Influence of Substrate Concentrations on the Performance of Fed-Batch and Perfusion Bioreactors: Insights from Mathematical Modelling

Abstract

Fed-batch and perfusion bioreactors are commonly used in biopharmaceutical production. This study applies mathematical models to investigate the influence of substrate concentration in the media added ($S_m$), operating substrate concentration in the bioreactor ($S$), and bioreaction time on the performance of both bioreactors. The performance parameters are titer, productivity, product yield, wasted substrate, and mean product residence time. The difference between the substrate concentration in the media and the operating substrate concentration has a major impact on performance parameters. For a fixed $S$, operating at higher values of $S_m$ is more beneficial to both fed-batch and perfusion performance. Higher productivities are obtained in perfusion, and mean product residence times are shorter. Furthermore, perfusion can obtain titers comparable to fed-batch when operated at similar substrate concentrations. All this suggests that perfusion is more advantageous. It is advantageous to operate the bioreactors over a longer bioreaction time. However, for fed-batch bioreactors, there exists an optimal time after which there is a major progressive reduction in productivity.

1. Introduction

Fed-batch and perfusion bioreactors are two of the most common types of reactors used in the industrial production of biopharmaceuticals [1]. Each mode of operation has its advantages and disadvantages. In most cases, the choice between fed-batch and perfusion is not a straightforward one, and many different criteria must be considered.

Fed-batch is not a new technology. It was first introduced in the 1980s as a method for increasing the productivity of other cell culture processes, which at the time were characterized by a number of inefficiencies and low titers [2]. Perfusion has also been used since the early 90s for the manufacture of different biomolecules such as factor-VIII and interferon beta-1a. For the past two decades, improvements in batch and fed-batch processes, including improved cell lines, expressions systems, media, equipment, and optimized operating conditions, have led to increased yield and process performance [2,3]. This eliminated the industry’s interest in perfusion and led to a fed-batch-dominated industry, with perfusion commonly only used for unstable proteins [2,4].

Fed-batch is typically performed in stainless-steel stirred tank reactors which can be as large as 40,000 L. Concentrated media is fed to the bioreactor incrementally throughout the bioreaction to prevent nutrient limitation. Therefore, the culture duration can be much longer than in batch mode, and the final productivity can be much greater [4]. The entire batch is harvested at the end of each run, where the dominant industrial primary recovery technologies are centrifugation and depth filtration [5,6]. Fed-batch processes can last anywhere from several days to three weeks [3]. The time profile of the media feed to the bioreactor is determined by substrate limitation; it should be designed so that the substrate concentration is always sufficient to support growth [5]. The duration of fed-batch bioreaction can be limited by the size of the bioreactor as the amount of media that can be added is restricted by the maximum working volume of the bioreactor. This can be overcome by using a high concentration of substrate in the media feed.

Perfusion is the most common method of continuous cell culture [7,8]. In perfusion, there is a constant feed of fresh media to the bioreactor and a simultaneous removal of cells and spent media. The volume within the bioreactor remains constant if the addition and removal rate are the same; thus, the maximum working volume of the bioreactor does not limit the amount of fresh media that can be added, unlike in fed-batch bioreactors. Perfusion processes require a cell retention device in order to separate the viable cells out, so they can be recycled back to the bioreactor to maintain the desired cell density [9]. Current continuous cell retention devices separate cells on the basis of either cell size or density; for example, continuous centrifugation and tangential filtration systems are commonly used [4,10,11,12]. Perfusion bioreactors can provide higher productivities, smaller physical footprints, and shorter residence times [13]. The cell retention enables the achievement of high cell concentrations in perfusion compared to fed-batch [14]. This results in the achievement of much higher productivities than in fed-batch. In steady-state operation, the cell culture can last for longer durations (up to months); thus, downtime is greatly reduced compared to batch or fed-batch [5]. The combination of high productivities and the potential for long operating durations allows for the implementation of continuous process intensification, with potential for greatly reduced physical footprint and cost [12,15]. A “cell bleed” is required in perfusion where cell biomass is removed from the bioreactor in order to achieve and maintain a constant cell density. The bleed rate should be minimized where possible in order to maximize yield [4].

Mammalian cells, specifically Chinese hamster ovary (CHO) cells, are the most common expression system for the large-scale production of biopharmaceuticals [16,17]. Mammalian cell culture is necessary for the production of many biopharmaceuticals because mammalian cells are particularly suited for the complex post-translational modifications that are required in many cases [17]. Most CHO cell lines can grow in either fed-batch or perfusion mode [18]. Fed-batch bioreactors are currently commonly used for the production of monoclonal antibodies (mAbs) despite the by-product accumulation, which can inhibit cell growth [19].

The performance of fed-batch and perfusion processes can be compared on the basis of a number of different performance indicators such as maximum cell density, product titer, and productivity [17,20]. The overall productivity of a biopharmaceutical plant will also depend on external factors, such as turnover times, scheduling, and other potential bottlenecks, which are not represented in mathematical models [21]. Perfusion titers are generally lower than those of fed-batch processes. However, this is balanced out by the higher cell densities achievable in perfusion reactions, which enables higher productivities [18,21]. Walther et al. [22] performed a head-to-head comparison of fed-batch and perfusion and found that while the fed-batch product concentration was 2.5 times greater than perfusion, the average productivity in perfusion was 7.5 times greater than fed-batch.

López-Mez et al. [17] identified the biopharmaceutical industry as a “niche wherein mathematical modelling has not been widely used”. Mathematical modelling of cell culture processes has shown promise for providing a quantitative description of the process, which would be useful for informing future process design [23]. A number of studies have been published on the application of mathematical modelling for multi-objective optimization of monoclonal antibody (mAb) production in fed-batch and perfusion bioreactors [6,24,25,26]. These incorporate the effect of variables, such as, temperature, rate of feed addition, biomass, glucose, protein and lactate concentrations, and how these can be optimized to maximize mAb productivity while minimizing nutrients’ requirement, wastage, and reactor volume. Some of these studies also include economic analysis [25,27], while others include environmental and sustainability aspects [9,28,29]. Kinetic modelling in particular is a useful tool for describing and assessing process performance and optimizing cell culture systems [19]. It provides an understanding of the relationship between process variables, which can be helpful when trying to improve process performance [17].

In the operation of fed-batch and perfusion bioreactors, the substrate concentration in the bioreactor is usually controlled to be at a certain value or within a range of values that is suitable or optimal for the cell culture. Furthermore, it may be required to control the concentration of a metabolite produced by the bioreaction so that it does not exceed a certain value that inhibits the cell culture. Also, it may be necessary to control the concentration of cells in the bioreactor so that it does not exceed a certain value.

In both bioreactors, control of these concentrations may be obtained by the addition of fresh media containing substrate. This addition may be intermittent or continuous over time. As the substrate concentration decreases due to the bioreaction, the addition of fresh media restores the substrate concentration back to its desired value or to within a range of desired values. This also has the effect of diluting an undesirable metabolite concentration and thus controlling it below a certain value. A critical factor in this control is the concentration of substrate in the media added because this influences the volume of media added.

The overall objective of the study is to use mathematical modelling to investigate and compare the performance of fed-batch and perfusion bioreactors. The following performance parameters are used in this study to assess and compare the performance of both the fed-batch and perfusion bioreactors:

• Product Yield: This is the mass of product produced from the substrate added. It is desirable to have a higher value.
• Productivity: This is the mass of product produced per bioreactor volume per unit time. This has a major influence on the size of the bioreactor required to produce a specified mass of product in a given time. A higher productivity is more desirable because this results in a smaller bioreactor size.
• Titer: This is the product concentration in the final working volume. It is desirable to have a higher value.
• Wasted Substrate: This is related to the mass of substrate added that is not used in the bioreaction and ends up being wasted, or requiring wastewater treatment. It is desirable to have a lower value of wasted substrate.
• Product Residence Time: This is the mean time that product spends in the bioreactor. It is desirable to have lower product residence times, especially for sensitive products that may be degraded over time.

In particular, the study investigates the influence of substrate concentration in the media added, operating substrate concentration in the bioreactor, and bioreaction time. The modelling results are used to provide a better understanding on how best to control the bioreactors in terms of performance and also highlighting performance trade-offs that may occur. The analysis is also used to compare the performances of both bioreactors. An outline of the mathematical modelling used is presented in the next section. This is followed by the Results and Discussion section, where the results from the mathematical modelling in terms of satisfying the objectives of the work are presented and discussed.

2. Mathematical Modelling

2.1. Bioreaction Kinetics

The intrinsic cell growth rate ($r_{xg}$) is modelled using the Logistic kinetic model in Equation (1) as follows:

$$r_{xg}=\mu X (1-{\displaystyle \frac{X_t}{X_m}})$$

(1)

where $X$ is viable cell concentration at time t, $X_t$ is the total cell concentration (viable + dead cells) at time t, $X_m$ is a physiological maximum cell concentration, and $\mu$ is the specific growth rate. This is modelled using a Monod type model (Equation (2)) as follows:

$$\mu ={\displaystyle \frac{{\mu }_{max}S}{K_s+S}}$$

(2)

where $S$ is the substrate concentration in the bioreactor liquid, and ${\mu }_{max}$ and $K_s$ are constants.

The rate of product production ($r_p$) is modelled using a non-growth associated model in Equation (3) as follows:

$$r_p=\beta X$$

(3)

where $\beta$ is a constant.

The rate of metabolite production ($r_g$) is also modelled using a non-growth associated model (Equation (4)) as follows:

$$r_g={\beta }_{g}X$$

(4)

where ${\beta }_g$ is a constant.

The rate of substrate utilization ($r_s$) is modelled using the linear substrate utilization model in Equation (5) as follows:

$$r_s=-\left(m_{s}X\right)$$

(5)

where $m_s$ is a constant.

Values for the bioreaction kinetic constants are provided in

Table 1. Values for constants in the bioreaction kinetic model.

$K_s$ (g L−1)	0.1	$\beta$ (h−1)	0.01
$m_s$ (h−1)	0.06	${\beta }_g$ (h−1	0.03
$X_m$ (g L−1)	50	${\mu }_{max}$ (h−1)	0.04

. The kinetic model equations used in this study are commonly used in the modelling of mammalian cell culture systems, and there are a number of studies presented in the literature that provide model kinetic constant values, which were mainly obtained from fitting the models to real experimental data [6,19,24,25,26,30,31,32]. There is variation in kinetic constant values presented in the literature, and this is for a number of reasons, including the fact that the products and cell cultures were different. The kinetic constant values presented in the literature were used as the basis for the selection of the values presented in Table 1. Consequently, these values are representative of mammalian cell culture systems. The maximum mammalian cell concentration ($X_m$) is reconned to be in the region of 2 × 10⁸ cells per mL [10,33]. A CHO cell has a dry cell mass of around 264 pg [34]. This results in a $X_m$ value of around 50 g L⁻¹, and this is used in this study. Sensitivity analysis is presented in Section 3.5 to provide insight into how varying the values of key kinetic constants influence the results and in particular the trends of how substrate concentrations impact on the performance of the bioreactors.

2.2. Bioreactor Mass Balances

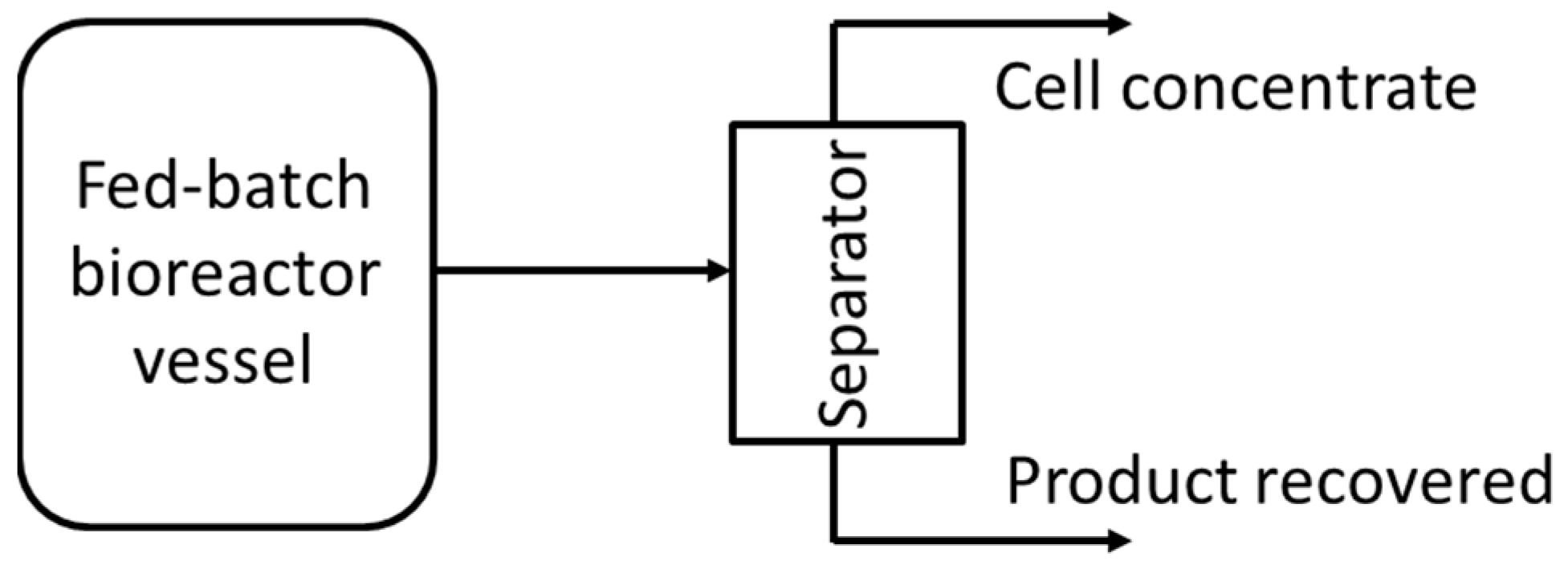
2.2.1. Fed-Batch

In fed-batch operation when no media is being added, the component mass balance equation is that of batch operation presented in Equation (6).

$${\displaystyle \frac{dZ}{dt}}=r_z$$

(6)

Here, $Z$ is the component concentration of interest, which is a substrate, cell, product, or metabolite.

The substrate concentration ($S$) is controlled within a range between an upper value ($S_U$) and a lower value ($S_L$). This is achieved by the intermittent addition of media when $S$ decreases to $S_L$. The volume of media added ($V_m$) to restore $S$ to $S_U$ depends on the concentration of substrate in the media ($S_m$). This is evaluated from a mass balance in Equation (7).

$$V_m={\displaystyle \frac{V_i\left(S_U-S_L\right)}{S_m-S_U}}$$

(7)

Here, $V_i$ is the working volume before media addition.

For product, cell, and metabolite concentrations, media addition will dilute their concentrations. For example, the product concentration ($P$) after adding a volume of media is modelled by a mass balance in Equation (8).

$$P={\displaystyle \frac{V_i P_i}{\left(V_m+V_i\right)}}$$

(8)

Here, $P_i$ is the product concentration before media addition. Similar expressions are applied to evaluate the cell and metabolite concentrations after media addition as these are also diluted by media addition. Media addition has the effect of controlling the increase in the concentrations of these components.

Continuous addition of media to maintain the substrate concentration very close to a constant steady-state value $S_S$ is also considered. This is modelled using the analysis above where $S_S=S_U$, and the difference between $S_U$ and $S_L$ is given a small value.

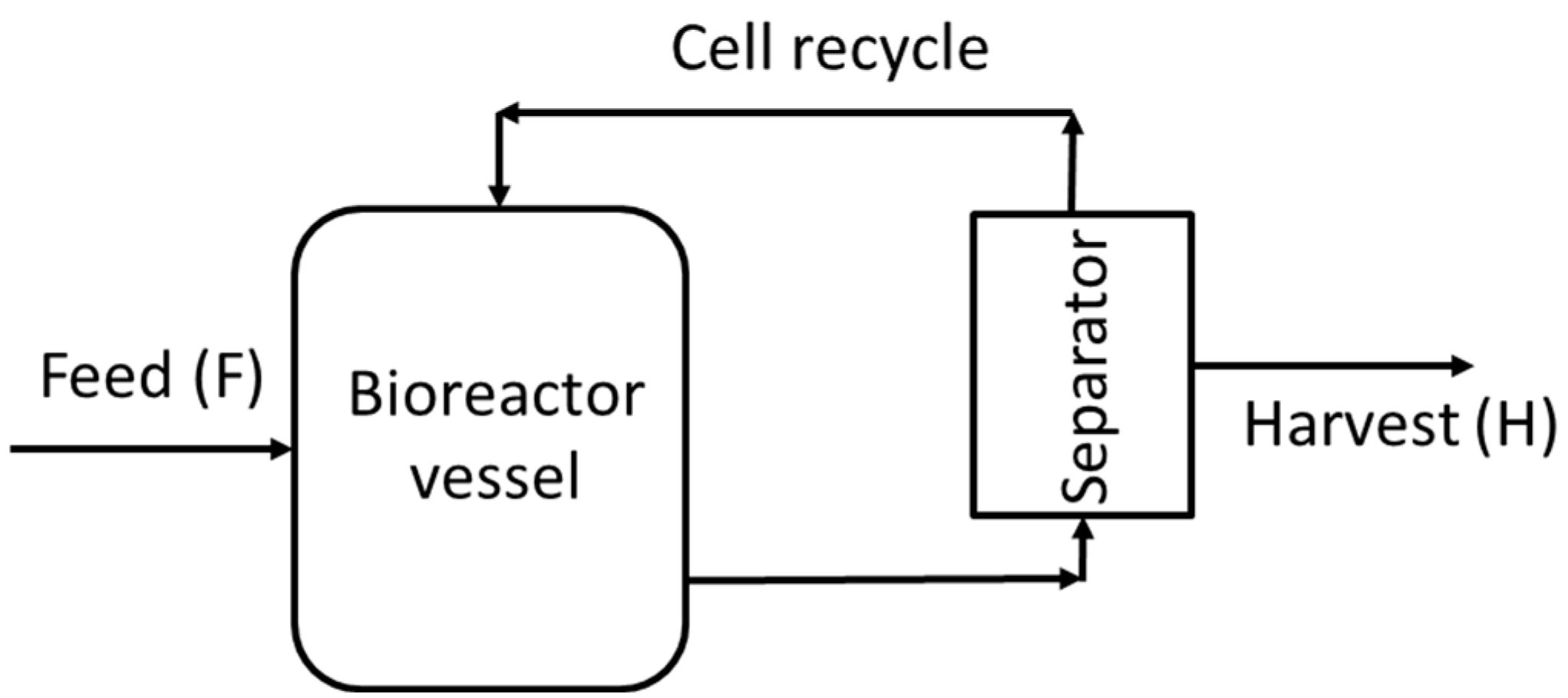
2.2.2. Perfusion

A schematic of the perfusion bioreactor is presented in Figure 1. The bioreactor is operated continuously, where $F$ is the media flowrate containing substrate concentrate ($S_m$) that is fed into the bioreactor vessel. The flow from the bioreactor vessel is fed to the separator, which retains the cells and recycles the cell suspension back into the bioreactor vessel. $H$ is the harvest or perfusion flowrate, and this is maintained at the same flowrate as the media flowrate. The media flowrate is controlled so as to maintain a constant substrate concentration ($S$) in the bioreactor vessel.

The component mass balance equations for the perfusion bioreactor are presented in Equations (9)–(12).

The viable cell mass balance equation is expressed as follows:

$$V{\displaystyle \frac{dX}{dt}}=r_{x}V$$

(9)

where $V$ is the bioreactor working volume.

The substrate mass balance equation is expressed as follows:

$$V{\displaystyle \frac{dS}{dt}}=F S_m+r_{s}V-H S$$

(10)

where $F$ is the media flowrate containing substrate concentrate ($S_m$), and $H$ is the harvest or perfusion flowrate.

The product mass balance equation is expressed as follows:

$$V{\displaystyle \frac{dP}{dt}}=r_{p}V-H P$$

(11)

where $P$ is the production concentration.

The metabolite mass balance equation is expressed as follows:

$$V{\displaystyle \frac{dG}{dt}}=r_{g}V-H G$$

(12)

where $G$ is the metabolite concentration.

In perfusion, the media feed flowrate ($F$) is controlled to maintain the substrate concentration at a constant steady-state concentration $\left(S_S\right)$. This will also influence the concentrations of product, cells, and metabolite.

2.3. Product Recovery

For the fed-batch operation, product recovery from the cell suspension after the fed-batch bioreaction process is required. This is carried out using a cell separator, as illustrated in Figure 2. This leads to some product being lost with the separated cells; thus, the mass of product recovered will be less than the total mass of product produced in the bioreactor.

The volume of recovered product solution ($V_P$) from the fed-batch bioreactor final working volume ($V_f$) can be estimated from the total and cell mass balances in Equations (13) and (14).

$$V_f {\rho }_f=V_C {\rho }_C+V_P{ \rho }_P$$

(13)

$$V_f{X}_{tf}=V_C{X}_{tC}$$

(14)

Here, $X_{tf}$ is the total cell concentrations at the end of the bioreaction, $V_C$ is the volume of the cell concentrate, $X_{tC}$ is the total cell concentration in the cell concentrate stream leaving the cell separator (this is given a value of 100 g L⁻¹), and $\rho$ is the density of the corresponding streams.

In the perfusion bioreactor, product is separated from the cells in the separator in the perfusion system, as illustrated in Figure 1. However, there will be some product in the perfusion bioreactor at the end of the process, and it may be desirable to recover additional product from the bioreactor at the end of the process and add it to the harvest. This additional volume of product solution is estimated using similar mass balances as in Equations (13) and (14).

2.4. Bioreactor Performance Parameters

The performance parameters used to assess and compare the performance of both the fed-batch and perfusion bioreactors are:

• Yield
• Wasted Substrate
• Productivity
• Titer (product concentration)
• Mean Product Residence Time

These are defined below for both bioreactors.

2.4.1. Yield

The yield is the product yield from substrate added. There are two yields defined as follows.

The first yield ($Yield1$) is defined as a percentage in Equation (15).

$$Yield1=100\ast {\displaystyle \frac{mass of product produced}{mass of substrate added}}$$

(15)

Here, the masses are the total mass of product produced and the total mass of substrate added during production.

Considering cell separation highlighted in Section 2.3, the second yield ($Yield2$) is defined as a percentage in Equation (16).

$$Yield2=100\ast {\displaystyle \frac{mass of product recovered}{mass of substrate added}}$$

(16)

For fed-batch, the mass of substrate added is the sum of the media substrate additions during the bioreaction time ($t_b$) plus the substrate in the vessel at the beginning, and this is evaluated in Equation (17).

$$mass of substrate added=\sum _{t=0}^{t=t_b}{V}_m{S}_m+V_O{S}_O$$

(17)

Here, $V_O$ and $S_O$ are the initial working volume and substrate concentration at time (t) = 0, respectively.

The mass of product produced is evaluated in Equation (18).

$$mass of product produced={V_f P}_f$$

(18)

Here, $V_f$ and $P_f$ are the working volume and product concentration at the end of the bioreaction or bioreaction time ($t_b$), respectively.

The mass of product recovered after cell separation is evaluated in Equation (19).

$$mass of product recovered={V_p P}_f$$

(19)

It is assumed that the product concentration is not affected by the cell separator and that its concentration is the same in both the recovered volume ($V_p$) and the bioreactor working volume.

For perfusion, the mass of substrate added is evaluated in Equation (20) as the mass of substrate added in the feed over the entire bioreaction time plus that in the bioreactor at the beginning of the bioreaction.

$$mass of substrate added={\int }_0^{t_b}F S_m dt+V S_O$$

(20)

Here, $V$ is the working volume of the bioreactor, and $S_O$ is the substrate concentration at time (t) = 0.

The mass of product produced is evaluated in Equation (21) as the mass of product harvested over the entire bioreaction time ($t_b$) plus that remaining in the bioreactor at the end of the bioreaction.

$$mass of product produced={\int }_0^{t_b}H P dt+V P_f$$

(21)

Here, $P_f$ is the product concentration at the end of the bioreaction.

The mass of product recovered consists of product in the harvest plus any additional product that is recovered from the bioreactor at the end of the bioreaction. This is evaluated in Equation (22).

$$mass of product recovered={\int }_0^{t_b}H P dt+V_p P_f$$

(22)

2.4.2. Wasted Substrate

The percentage of wasted substrate ($\%WS$) is defined as a percentage in Equation (23).

$$\%WS=100\ast {\displaystyle \frac{mass of unused substrate}{mass of substrate added}}$$

(23)

For fed-batch, the mass of unused substrate is the mass of substrate still in the fed-batch bioreactor at the end of the bioreaction, and this is evaluated in Equation (24).

$$mass of unused substrate=V_f S_f$$

(24)

where $V_f$ and $S_f$ are the working volume and substrate concentration at bioreaction time ($t_b$).

For perfusion, the mass of unused substrate is evaluated in Equation (25) as the mass of substrate that leaves the perfusion bioreactor in the harvest stream during the bioreaction time, plus that which is in the bioreactor at bioreaction time ($t_b$).

$$mass of unused substrate={\int }_0^{t_b}H S dt+V S$$

(25)

2.4.3. Titer

For fed-batch, the titer is the final product concentration at bioreaction time $t_b$.

For perfusion, the titer for perfusion is evaluated in Equation (26).

$$titre={\displaystyle \frac{{\int }_0^{t_b}H P dt+V_p P_f }{{\int }_0^{t_b}H dt +V_p}}$$

(26)

2.4.4. Productivity

The productivity is defined in Equation (27).

$$Producitivity={\displaystyle \frac{mass ofproduct recovered}{t_b V}}$$

(27)

Here, $t_b$ is the bioreaction time from the start to the end of the bioreaction.

For fed-batch, $V$ is the working volume of the bioreactor at bioreaction time ($t_b$).

For perfusion, $V$ is the working volume of the bioreactor.

2.4.5. Product Mean Residence Time

For fed-batch, the residence time of each product molecule varies as it depends on when the product molecule is formed. Product molecules formed at the beginning will have a residence time close to the bioreaction time, while product molecules formed near the end will have a short residence time close to zero. Consequently, the product residence time in the fed-batch reactor is estimated as a mean product residence time. Here, the bioreaction time ($t_b$) is divided up into n time increments, and the product mean residence time ($t_{res}$) is evaluated in Equation (28).

$$t_{res}=\sum _{i=1}^n\left(t_b-t_i\right)\left({\displaystyle \frac{\Delta M_{pi}}{M_p}}\right)$$

(28)

Here, $t_i$ is the bioreaction time at the ith increment, $\Delta M_{pi}$ is the mass of product produced during the ith increment, and $M_p$ is the mass of product produced during the bioreaction time ($t_b$).

For perfusion, the hydraulic residence time ($t_{hyd}$) is estimated in Equation (29).

$$t_{hyd}={\displaystyle \frac{\mathrm{V}}{F}}$$

(29)

However, $t_{hyd}$ will vary because the media flowrate ($F$) varies over the bioreaction time; thus, a mean flowrate ($F_{mean}$) is evaluated in Equation (30) for estimating the mean hydraulic residence time.

$$F_{mean}={\displaystyle \frac{{\int }_0^{t_b}F dt }{t_b}}$$

(30)

The mean hydraulic residence time in the perfusion bioreactor cannot be used as a measure of the mean product residence time as it will be an overestimate. Consider the hydraulic residence time associated with an element of liquid entering and leaving the bioreactor. During this time, product is being continually produced, some at the beginning and some at the end. This leads to a distribution of product residence times within the hydraulic residence time. To take this into account, the bioreaction time ($t_b$) is broken up into k increments, each having a one-hour duration. Within each one-hour time increment, the mean product residence for the kth increment ($t_{res\_k}$) is estimated in Equation (31).

$$t_{res\_k}=\sum _{j=k-1}^{j=k}{\displaystyle \frac{\left(t_k-t_j\right)}{\left(t_k-t_{k-1}\right)}}\left({\displaystyle \frac{\Delta M_{pj}}{\Delta M_{pk}}}\right)t_{hyd\_k}$$

(31)

Here,

$t_{hyd\_k}$ is the mean hydraulic residence time within the kth one-hour time increment;

$t_k$ is the bioreaction time at the end of the kth time increment;

$t_{k-1}$ is the bioreaction time at the beginning of the kth time increment;

$t_j$ is the bioreaction time during the kth time increment;

$\Delta M_{pk}$ is the mass of product produced during the kth time increment;

$\Delta M_{pj}$ is the mass of product produced during the jth time increment within the kth time increment.

The mean product residence time for the k increments was used to estimate the overall mean product residence time ($t_{res}$) in Equation (32).

$$t_{res}=\sum _{k=1}^{k=k_p}{t}_{res\_k}\left({\displaystyle \frac{\Delta M_{pk}}{M_p}}\right)$$

(32)

Here, $k_p$ is the total number of k increments within the bioreaction time $t_b$, and $M_p$ is the total mass of product produced during $t_b$.

2.5. Initial Conditions and Model Implementation

The initial cell concentration is given a value of 0.1 g L⁻¹, and product and metabolite concentrations are given initial values of 0 g L⁻¹. For the fed-batch simulations, the initial bioreactor working volume ($V_O$) is given a value of 0.05 m³, and the initial substrate concentration in the bioreactor is $S_O=S_U$. For the perfusion simulations, the bioreactor working volume is given a value of 1 m³, and this remains constant throughout the bioreaction. The initial substrate concentration in the bioreactor is given the same value as a constant steady-state concentration, i.e., $\left(S_O=S_S\right)$.

Algorithms using the equations above were formulated for both fed-batch and perfusion bioreactors. This included the implementation of a finite-difference approach for solving the differential equations. The time duration of the time steps used in the algorithms was 0.01 h. The coding and computations were implemented in MATLAB (https://www.mathworks.com/products/matlab.html, accessed on 1 July 2024, MathWorks, Natick, MA, USA).

3. Results and Discussion

Cell death and metabolite inhibition are important and will impact bioreactor performance; however, they are not included in this study. This is simply to reduce the complexity and gain a better understanding of the effects of the substrate concentrations on the performance of both bioreactors.

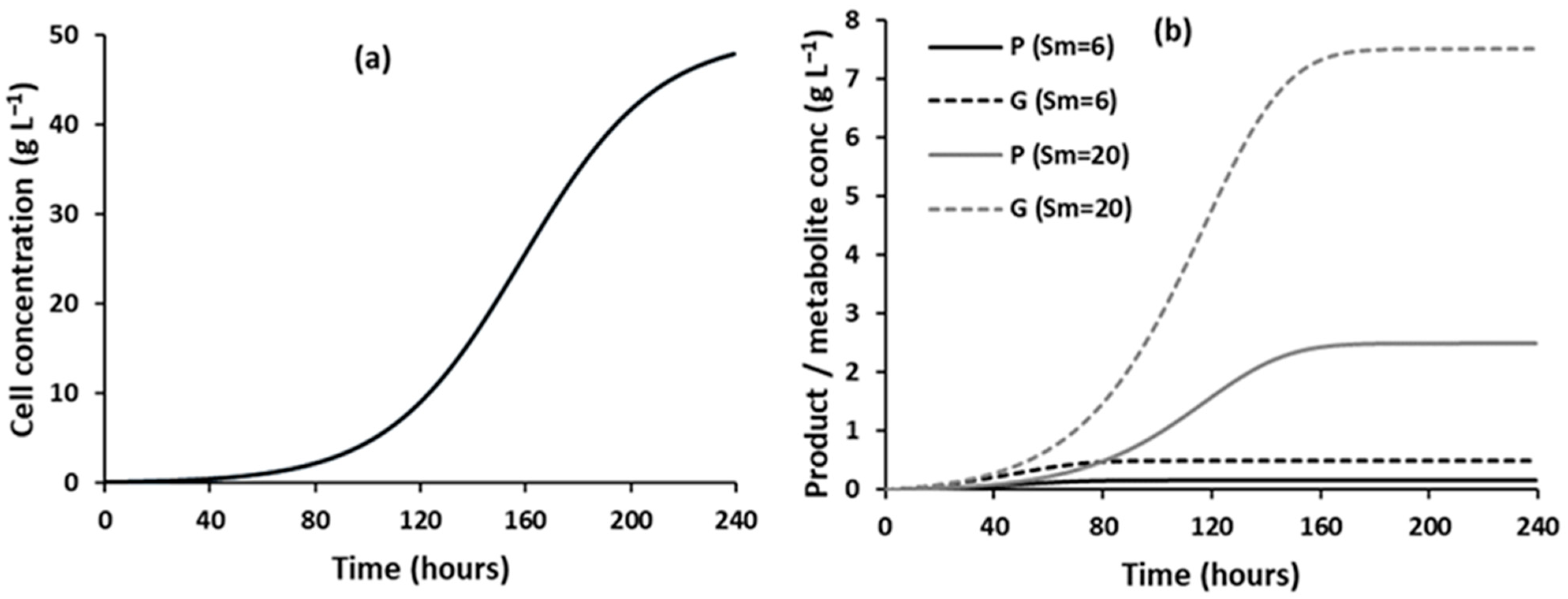
3.1. Effect of Substrate Concentrations on Fed-Batch Bioreactor Performance

3.1.1. Effect of Substrate Concentrations on the Evolution of Component Concentrations over Time

There are three substrate concentrations of interest. These are the substrate concentration in the media added ($S_m$) and the upper concentration value ($S_U$) and lower concentration value ($S_L$) within which the substrate concentration is controlled. In the simulation runs, $S_U$ was initially given a value of 5 g L⁻¹, $S_L$ was varied between 1 and 4 g L⁻¹, and $S_m$ was varied between 6 and 20 g L⁻¹. Within a substrate concentration range of 1 to 5 g L⁻¹, the substrate concentration is having little effect on the specific growth rate ($\mu$), as this is close to ${\mu }_{max}$ due to the value of $K_s$ (= 0.1 g L⁻¹).

The effect of $S_m$ on the evolution of the cell, product, and metabolite concentrations is illustrated in Figure 3 (for $S_m$ = 6 and 20 g L⁻¹). It can be seen that the higher $S_m$ results in higher cell concentrations, as illustrated in Figure 3a. This is due to a lower dilution effect when adding media that has a higher $S_m$ and is also coupled with higher cell growth rates at higher cell concentrations. Higher cell concentrations also result in faster product (and metabolite) production. Figure 3b illustrates that higher $S_m$ also results in higher concentrations of product and metabolite, which is also due to a lower dilution effect when adding media with a higher $S_m$.

Figure 4a shows the effect of $S_L$ on the evolution of cell concentration (for $S_L$ = 1 and 4 g L⁻¹). It shows that the cell concentration at $S_L$ = 4 g L⁻¹ overlaps toward the bottom of that at $S_L$ = 1 g L⁻¹. Consequently, the average cell concentration is higher at lower $S_L$ concentrations. Figure 4b shows the effect of $S_U$ on the evolution of cell concentration (for $S_U$ = 2 and 5 g L⁻¹). It shows that the cell concentration at $S_U$ = 2 g L⁻¹ overlaps toward the top of that at $S_U$ = 5 g L⁻¹. Consequently, the average cell concentration is higher at lower $S_U$ concentrations. All this is brought about by how the values of $S_U$ and $S_L$ influence the volume of media added (Equation (7)), which influences the dilution effect and the resultant cell concentrations (Equation (8)). Furthermore, similar trends occur for both product and metabolite concentrations.

3.1.2. Effect of Substrate Concentrations on Performance Parameters

In the section above, $S_m$ is shown to have a major impact on cell, product, and metabolite concentrations; thus, it is expected that it may significantly impact the performance parameters also. Simulations were performed to investigate the effect of $S_m$ on the performance parameters. The results are presented in

Table 2. Effect of $S_m$ on fed-batch performance for the case of $S_U$ = 5 g L⁻¹ and $S_L$ = 1 g L⁻¹ ($t_b$ = 240 h).

${\mathit{S}}_{\mathit{m}}$	$\mathit{T}\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ (g L−1)	Productivity (mg L−1 h−1)	${\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}$ (h)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}1$ (%)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}2$ (%)	$\%\mathit{W}\mathit{S}$ (%)	${\mathit{X}}_{\mathit{f}}$ (g L−1)
6	0.38	1.55	26.6	6.3	6.2	62.4	1.42
10	0.95	3.84	28.0	9.6	9.2	42.6	3.39
20	2.50	9.58	30.7	12.7	11.7	24.0	7.98

.

As already shown in Figure 3, the titer (or final product concentration) increases at higher $S_m$, which is due to lower dilution when media is added with a higher substrate concentration. The productivity also increases at higher $S_m$, which is due to increased reaction rates at higher cell concentrations. Table 2 shows that higher $S_m$ results in a small increase in the mean product residence time. $Yield2$ is similar to $Yield1,$ indicating that most of the product produced is being recovered and a relatively small amount is lost to the cell concentrate leaving the separator. This is because the cell concentrations are small at the end of the bioreaction in comparison to that in the cell concentrate of 100 g L⁻¹.

It is expected that $S_m$ should have a major impact on yields and $\%WS$, with higher yields and lower %WS expected at higher $S_m$. More of the added substrate should be utilized and converted into product at higher $S_m$. Consequently, less is wasted, and $\%WS$ should decrease at higher $S_m$. Table 2 broadly shows this trend with yields increasing and $\%WS$ decreasing as $S_m$ is increased from $S_m$ = 6 to 10 to 20 g L⁻¹.

More simulations were performed to investigate further how $S_m$ influences $Yield2$. This is presented in Figure 5, which shows a much more random behavior. What is happening is that $Yield2$ (and $\%WS$) is also influenced by the substrate concentration at the end of the fed-batch bioreaction, as this can randomly vary between $S_L$ and $S_U$. Figure 5 shows that there is a general trend that $Yield2$ increases with increasing $S_m$. However, it also shows that the final substrate concentration ($S_f$) is also having an influence, whereby lower $S_f$ values tend to increase $Yield2$, which is because there is less wasted substrate.

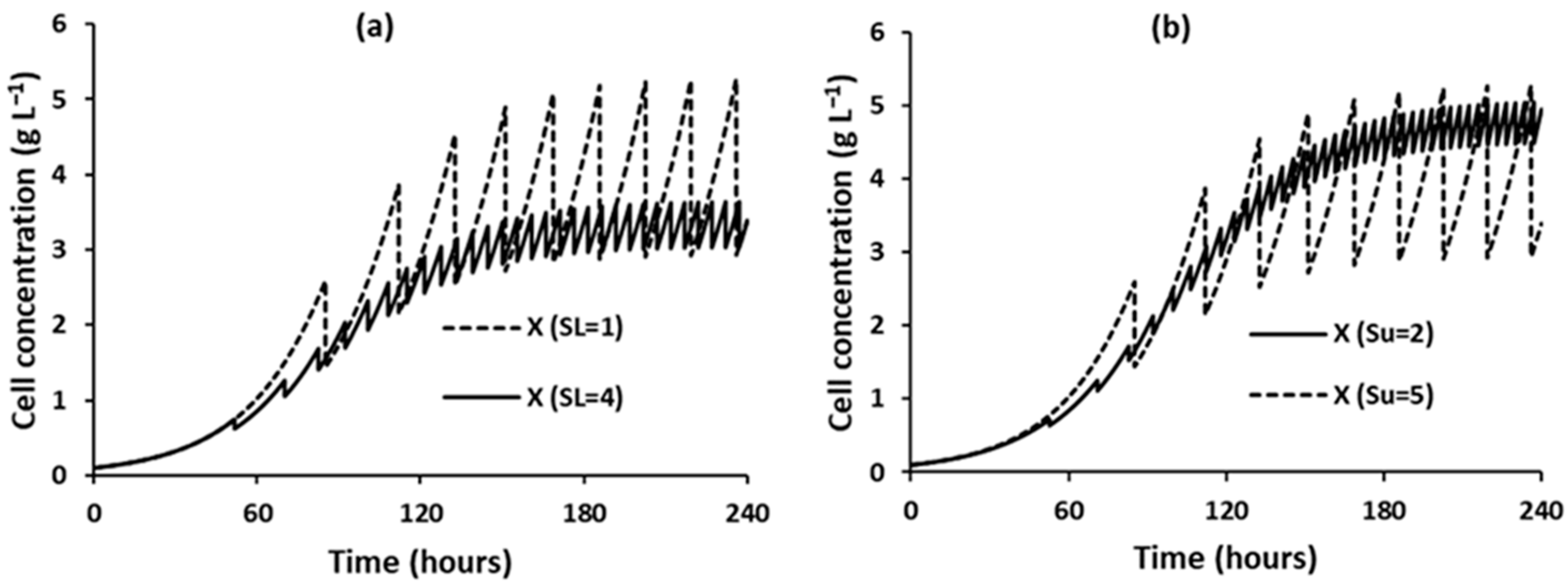
3.1.3. Effect of Substrate Concentrations on the Performance of a Fed-Batch Bioreactor Operated in Continuous Mode of Media Addition

To gain a clearer picture of how the substrate concentrations influence the performance parameters, it is necessary to remove the influence of fluctuating $S_f$ at the end of the fed-batch process. This can be achieved by decreasing the difference between $S_U$ and $S_L$ to a low value, whereby the fed-batch bioreactor is essentially operating in continuous mode of media addition. This is illustrated in Figure 6 for $S_U$ = 1 and 5 g L⁻¹, where the difference between $S_U$ and $S_L$ is 0.01 g L⁻¹. It shows that $Yield2$ continuously increases with higher $S_m$ for both cases, and there are no random fluctuations as seen in Figure 5. Furthermore, the relationship is not linear, as the rate of increase or slope of the curve decreases as $S_m$ increases. It also shows that the substrate concentration in the bioreactor ($S_U$ or $S_L$) also has a major influence on $Yield2$. The lower substrate concentration resulted in higher values of $Yield2$. This is due to the fact that there is less unused or wasted substrate at the end of the fed-batch bioreaction time at the lower substrate concentration.

The effects of $S_m$ and the substrate concentration inside the bioreactor on the performance parameters are presented in

Table 3. Effect of $S_m$ on fed-batch performance for $S_U$ = 1 g L⁻¹ and $S_U$ = 0.99 g L⁻¹ as well as for $S_U$ = 5 g L⁻¹ and $S_L$ = 4.99 g L⁻¹ ($t_b$ = 240 h).

${\mathit{S}}_{\mathit{m}}$	$\mathit{T}\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ (g L−1)	Productivity (mg L−1 h−1)	${\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}$ (h)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}1$ (%)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}2$ (%)	$\%\mathit{W}\mathit{S}$ (%)	${\mathit{V}}_{\mathit{f}}$ (m3)
$S_U$ = 1 g L−1 and $S_L$ = 0.99 g L−1
2	0.17	0.69	27.8	8.4	8.3	49.7	46.9
6	0.83	3.36	29.0	13.9	13.5	16.7	7.93
10	1.48	5.87	30.1	15.0	14.2	10.1	3.91
20	3.06	11.59	32.3	15.8	14.4	5.1	1.52
$S_U$ = 5 g L−1 and $S_L$ = 4.99 g L−1
2	-	-	-	-	-	-	-
6	0.17	0.69	25.8	2.8	2.8	83.3	85.4
10	0.83	3.35	27.1	8.3	8.1	50.1	13.8
20	2.46	9.43	29.8	12.5	11.4	25.3	3.30

. Here, increasing $S_m$ results in a major increase in the titer and productivity of the bioreactor. Increasing $S_m$ results in longer product residence time but it is not a major effect, and the effect of substrate concentration inside the bioreactor on product residence time is even less significant.

As highlighted in Figure 6, both substrate concentrations have a significant influence on the yields and the percentage of wasted substrate. Higher $S_m$ results in more of the substrate added being utilized, which results in higher yields and lower %WS. Lower substrate concentrations inside the bioreactor inherently result in less unused or wasted substrate and thus higher yields.

Table 3 also shows that $S_m$ has a significant impact on the final working volume of a fed-batch bioreactor ($V_f$). $V_f$ increases as $S_m$ is decreased, and there is a very large increase in $V_f$ as $S_m$ decreases and approaches $S_U$. This is due to the increased volume of media addition required (from Equation (7)) at lower values of $S_m$.

Overall, the results in Table 3 suggest that operating the fed-batch bioreactor at higher $S_m$ values is more beneficial as it increases titer, productivity, and yield and reduces wasted substrate and bioreactor volume, which are all desirable. On the other hand, the mean product residence time increases, but this is only a relatively small increase.

3.1.4. Effect of Rate-Limiting Bioreactor Substrate Concentration

Up to this point, the substrate concentration simulated inside the bioreactor resulted in specific growth rates that are close to the maximum and are thus not rate limiting (i.e., $\mu >0.9 {\mu }_{max}$). In this section, simulations were performed with a substrate concentration that reduces the specific growth rate to one-third of its maximum. Simulations were performed where the substrate concentration was controlled at around 1 g L⁻¹ (non-rate limiting) and 0.05 g L⁻¹ (rate limiting) for two values of $S_m$ (2 and 20 g L⁻¹). The effect on the performance parameters and final cell concentration ($X_f$) are presented in

Table 4. Effect of $S_m$ on fed-batch performance for $S_U$ = 1 g L⁻¹ and $S_f$ = 0.99 g L⁻¹ as well as for $S_U$ = 0.05 g L⁻¹ and $S_L$ = 0.04 g L⁻¹ ($t_b$ = 240 h).

${\mathit{S}}_{\mathit{m}}$	$\mathit{T}\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ (g L−1)	Productivity (mg L−1 h−1)	${\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}$ (h)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}1$ (%)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}2$ (%)	$\%\mathit{W}\mathit{S}$ (%)	${\mathit{X}}_{\mathit{f}}$ (L)	${\mathit{V}}_{\mathit{f}}$ (m3)
$S_U$ = 1 g L−1 and $S_L$ = 0.99 g L−1
2	0.17	0.69	27.8	8.4	8.3	49.7	0.60	46.9
20	3.06	11.6	32.3	15.8	14.4	5.1	9.22	1.52
$S_U$ = 0.05 g L−1 and $S_L$ = 0.04 g L−1 [rate-limiting]
2	0.27	1.11	67.9	16.2	16.2	2.6	0.35	0.28
20	1.02	4.21	68.2	16.5	16.3	0.8	1.32	0.07

.

Operating at the lower rate-limiting concentration slows down the cell growth kinetics; thus, it might be expected that productivity would be lower and that the titer may also be lower. However, Table 4 shows that for $S_m$ = 2 g L⁻¹, both productivity and titer are actually higher for the rate-limiting substrate concentration. Cell growth kinetics re slowed at the lower substrate concentration. However, on the other hand, ($S_m-S$) is greater at the low substrate concentration. As highlighted earlier, this results in a lesser dilution effect due to a lower volume of media being added (Equation (7)), which results in higher titer. The higher titer also results in higher productivity; however, this is misleading because the lower rate-limiting substrate concentration is leading to a much lower final working volume ($V_f$). This is indicative of the bioreaction progressing more slowly, resulting in a lower rate of product production.

For the higher $S_m$ value of 20 g L⁻¹, the ($S_m-S$) effect is not as great because their values are closer in value for both substrate concentrations. Thus, the slower growth kinetics at the low substrate concentration is having more of an effect, resulting in a much lower $X_f$, and the titer, productivity, and $V_f$ are also lower. In relation to the yields, these are significantly higher at the lower rate-limiting substrate concentration. This is because the wasted substrate is inherently lower due to the very low substrate concentration in the bioreactor.

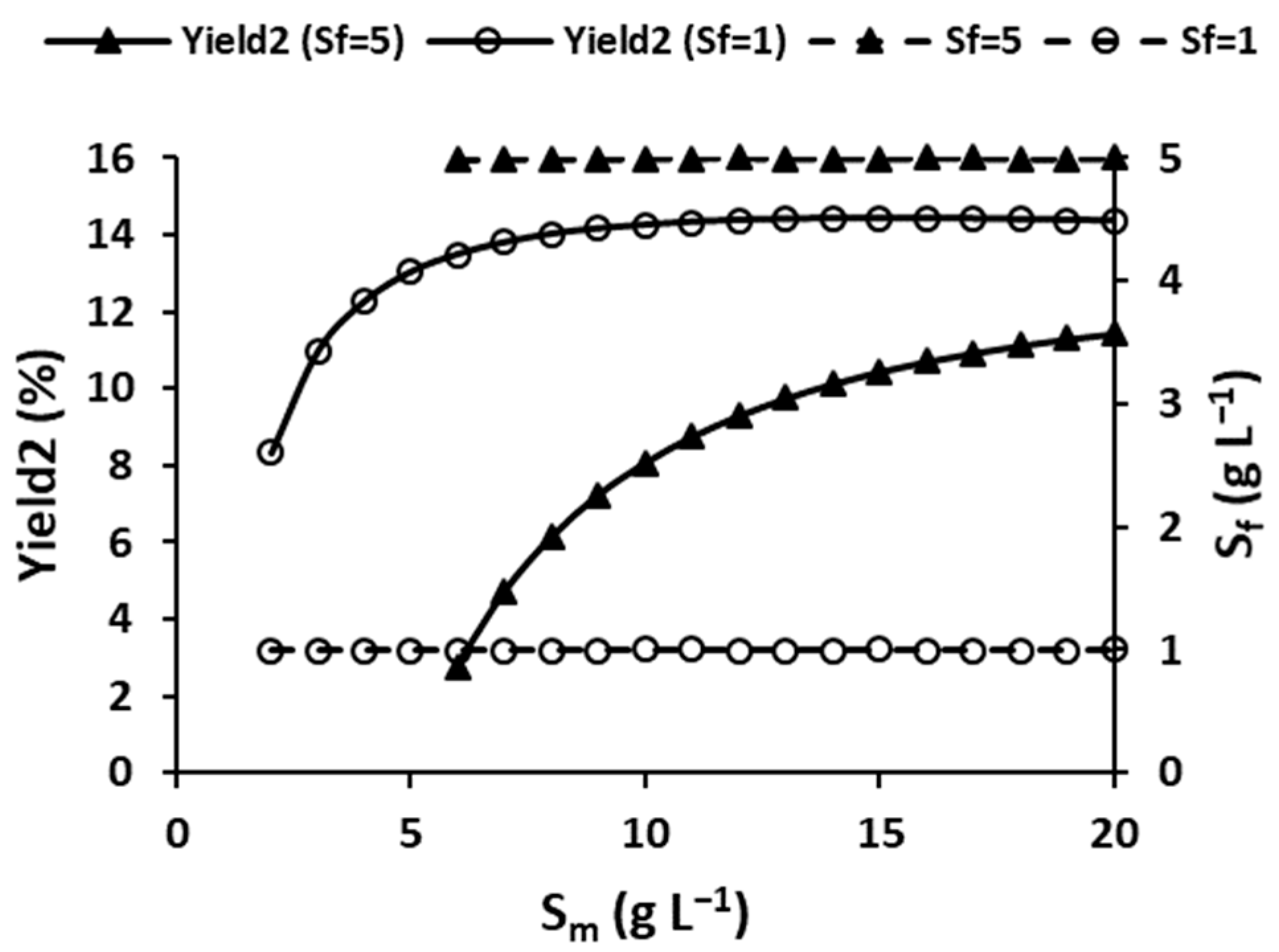
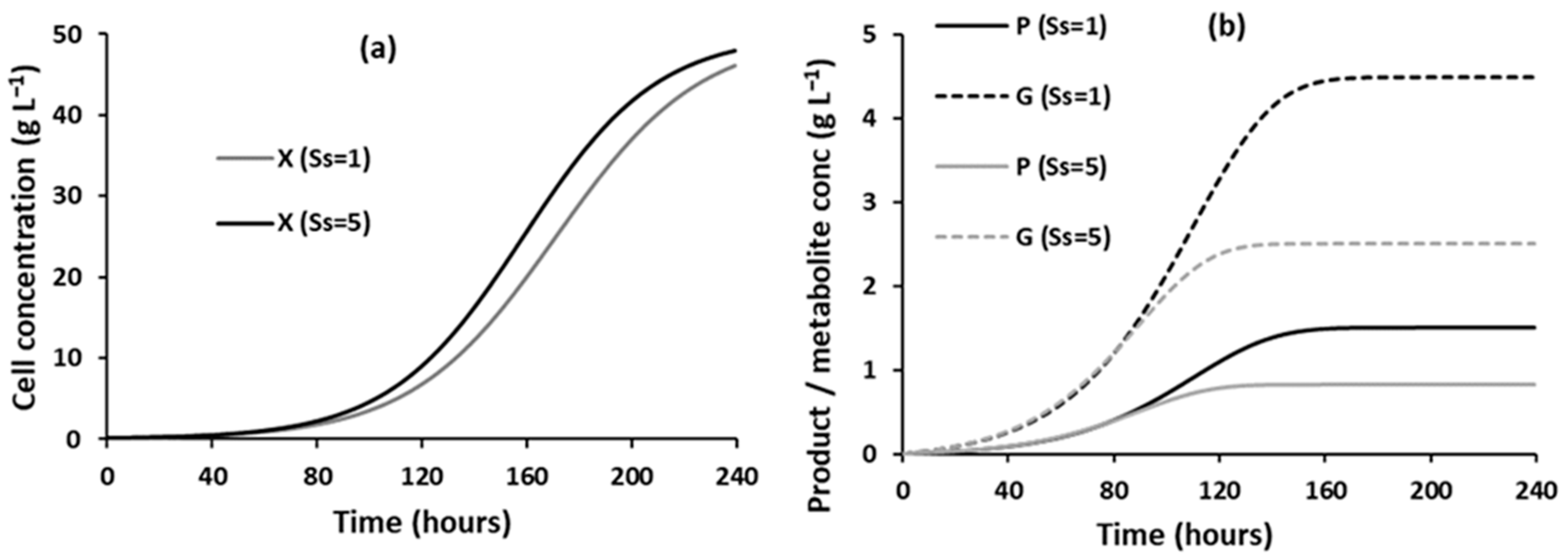
3.2. Effect of Substrate Concentrations on Perfusion Bioreactor Performance

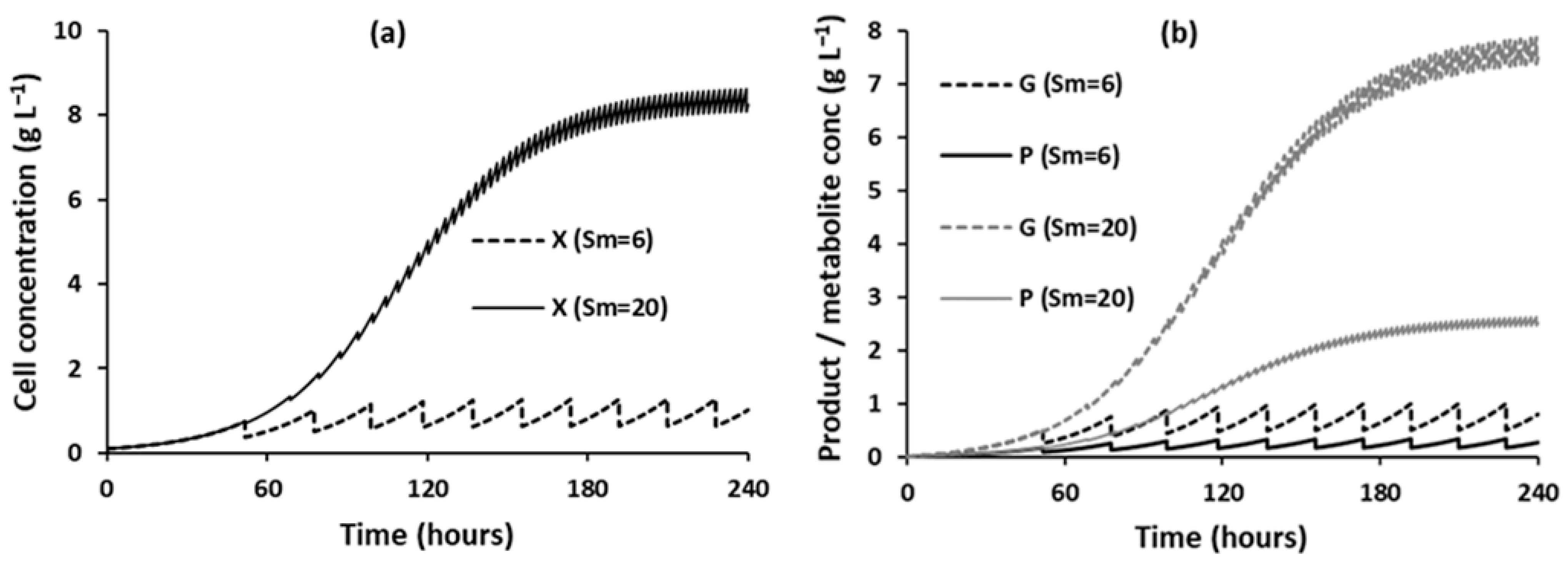
3.2.1. Effect of Substrate Concentrations on the Evolution of Component Concentrations over Time

In the simulation runs, the substrate concentration in the bioreactor $\left(S_S\right)$ was initially given a value of 5 g L⁻¹, and $S_m$ was varied between 6 and 20 g L⁻¹. The effect of $S_m$ on the evolution of the cell, product, and metabolite concentrations is illustrated in Figure 7 (for $S_m$ = 6 and 20 g L⁻¹).

$S_m$ has no effect on the cell concentration profile as the two profiles are plotting out on top of each other (Figure 7a). This is because the cells are not being diluted in the bioreactor system, as the cells are being retained in a constant volume bioreactor. On the other hand, $S_m$ does influence the concentration profiles of the product and metabolite, with higher $S_m$ values leading to higher product and metabolite concentrations. The substrate mass balance equation on the bioreactor vessel (Figure 1) for a constant steady-state $S_S$ is given in Equation (33).

$$0=F \left(S_m-S_S\right)+r_{s}V$$

(33)

From this, greater $\left(S_m-S_S\right)$ results in a smaller feed flowrate ($F$) to maintain $S_S$ at its fixed value. A lower feed flowrate results in longer hydraulic residence times in the bioreactor, which enables their concentrations to increase to higher values.

$S_S$ has only a small effect on the cell concentration profile (Figure 8a). This is due to the specific growth being a little lower at $S_S$ = 1 g L⁻¹. Figure 8b shows that $S_S$ does impact the product and metabolite concentration profiles. The effect is actually due to $\left(S_m-S_S\right)$ rather than just $S_S$ on its own. As highlighted earlier, greater $\left(S_m-S_S\right)$ results in a smaller feed flowrate ($F$) required, which results in a higher hydraulic residence time that enables the product and metabolite concentrations to achieve higher values.

3.2.2. Effect of Substrate Concentrations on Performance Parameters

Simulations were performed to investigate the effect of $S_m$ and $S_S$ on the performance parameters. The results are presented in

Table 5. Effect of $S_m$ and $S_S$ on perfusion performance ($t_b$ = 240 h).

${\mathit{S}}_{\mathit{m}}$	$\mathit{T}\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ (g L−1)	Productivity (mg L−1 h−1)	${\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}$ (h)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}1$ (%)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}2$ (%)	$\%\mathit{W}\mathit{S}$ (%)
$S_S$ = 1 g L−1
2	0.17	148	0.45	8.3	8.3	50.1
6	0.81	147	1.87	13.8	13.7	17.0
10	1.44	145	3.09	14.9	14.6	10.4
20	2.90	142	5.82	15.8	15.1	5.4
$S_S$ = 5 g L−1
2	-	-	-	-	-	-
6	0.17	172	0.40	2.8	2.8	83.4
10	0.82	170	1.65	8.3	8.2	50.5
20	2.35	167	4.27	12.3	12.0	26.1

. Increasing $S_m$ and reducing $S_S$ leads to higher titers. However, as discussed earlier, it is not $S_m$ or $S_S$ on their own that counts, it is the difference between them, whereby a higher $\left(S_m-S_S\right)$ results in higher titers.

The productivity changes very little with changes in $S_m$, and there are relatively small differences with changes in $S_S$. The productivity is given in Equation (27). This depends on the mass of product recovered from the bioreactor, which is given in Equation (22). In fact, if the mass of product produced was used in the productivity equation, then $S_m$ has no effect on productivity. The rationale for the substrate concentrations having little effect on productivity is attributed to the influence of $\left(S_m-S_S\right)$. Higher values of $\left(S_m-S_S\right)$ results in higher titers, which tends to increase productivity. However, this is counteracted by a decrease in the feed and harvest flowrates, which tends to reduce productivity. Consequently, the overall effect results in little or no change in the productivity.

The ratio of the mean product to mean hydraulic residence times is typically in the range of 0.3 to 0.5. The substrate concentrations influence the mean product residence time. However, once again it is not $S_m$ or $S_S$ on their own that counts; it is the difference between them. The reduction in feed flowrate, as $\left(S_m-S_S\right)$ increases, results in the mean product residence time increasing as $\left(S_m-S_S\right)$ increases. Consequently, $\left(S_m-S_S\right)$ may be used to control the mean product residence time.

As in the fed-batch bioreactor, $S_m$ has a major impact on the yields. Increasing $S_m$ and reducing $S_S$ results in higher yields. This is because more of the substrate in the feed is being utilized and less is wasted, as shown by the %WS values. Furthermore, lower $S_S$ results in less wasted substrate and thus higher yields.

In practice, $S_S$ is oftentimes constrained to suit the microorganisms, but $S_m$ can be varied. From Table 5, higher $S_m$ results in higher titers and yields and less wasted substrate, which are all desirable; however, it does result in higher product residence time, which may be undesirable although this depends on the product.

3.2.3. Effect of Rate-Limiting Bioreactor Substrate Concentration

Like in Section 3.1.4, the substrate concentration simulated inside the bioreactor resulted in a specific growth rate close to the maximum and is thus not rate limiting. Here, simulations were performed with a substrate concentration that reduces the specific growth rate to one-third of its maximum. Simulations were performed where substrate concentration ($S_S$) was controlled at 1 g L⁻¹ (non-rate limiting) and 0.05 g L⁻¹ (rate limiting) for two values of $S_m$ (2 and 20 g L⁻¹). The effects on the performance parameters and final cell concentration ($X_f$) are presented in

Table 6. Effect of $S_m$ and $S_S$ on perfusion performance ($t_b$ = 240 h).

${\mathit{S}}_{\mathit{m}}$	$\mathit{T}\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ (g L−1)	Productivity (mg L−1 h−1)	${\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}$ (h)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}1$ (%)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}2$ (%)	$\%\mathit{W}\mathit{S}$ (%)	${\mathit{X}}_{\mathit{f}}$ (g L−1)
$S_S$ = 1 g L−1
2	0.17	148	0.45	8.3	8.3	50.1	46.3
20	2.90	142	5.82	15.8	15.1	5.4	46.3
$S_S$ = 0.05 g L−1 [rate limiting]
2	0.27	7.2	15.5	16.2	16.1	3.0	2.34
20	1.13	7.1	128	16.5	16.2	0.73	2.34

.

As expected, $X_f$ is lower at $S_S$ = 0.05 g L⁻¹ because this substrate concentration is rate limiting. $S_m$ does not affect $X_f$ as discussed earlier. $S_m$ affects titer, product residence time, and productivity in a similar way at both substrate concentrations, as outlined earlier. At the low $S_S$, nearly all the substrate is utilized resulting in negligible wasted substrate; thus, the yields are consequentially higher, as shown in Table 6. A lower $S_S$ has a major impact on both productivity and product residence time, as shown in Table 6. This is all due to the slower reaction kinetics resulting in lower productivity. For a given $S_m$, lower productivity results in a lower feed flowrate requirement, which results in longer residence times.

The titer results are somewhat interesting. The lower rate-limiting $S_S$ results in higher titer at the low $S_m$, while the opposite occurs at higher $S_m$. What is happening here is that $\left(S_m-S_S\right)$ is significantly higher at the low $S_S$, and this is causing the higher titer. However, this effect is not significant at the high $S_m$, and it is the slower evolution of production concentration over time at the low $S_S$ that is resulting in the lower titer.

3.3. Effect of Bioreaction Time on Bioreactor Performance

The evolution of cell, product, and metabolite concentrations over time have been illustrated in a number of figures in the previous sections. This section focuses on the influence of bioreaction time on the performance of both fed-batch and perfusion bioreactors.

3.3.1. Fed-Batch

The effect of bioreaction time on the performance parameters is presented in

Table 7. Effect bioreaction time on fed-batch performance [$S_m$ = 20 g L⁻¹; $S_U$ = 1 g L⁻¹; $S_L$ = 0.99 g L⁻¹].

$\mathit{T}\mathit{i}\mathit{m}\mathit{e}$ (h)	$\mathit{T}\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ (g L−1)	Productivity (mg L−1 h−1)	${\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}$ (h)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}2$ (%)	$\%\mathit{W}\mathit{S}$ (%)	${\mathit{X}}_{\mathit{f}}$ (g L−1)	${\mathit{G}}_{\mathit{f}}$ (g L−1)	${\mathit{V}}_{\mathit{f}}$ (m3)
48	0.1	2.57	17.4	7.1	57.2	0.54	0.37	0.05
120	1.2	9.78	26.7	14.1	11.9	4.29	3.68	0.08
240	3.1	11.6	32.3	14.4	5.1	9.22	9.19	1.52
480	3.2	5.98	33.9	14.4	5.0	9.36	9.50	1799
960	3.2	2.99	33.9	14.4	5.0	9.36	9.50	2.6(109)

for fed-batch operation.

The main influences of bioreaction time are as follows:

• Titer, yield. and %WS: Final cell ($X_f$), final product, and final metabolite ($G_f$) concentrations all increase over time and eventually reach constant values. This is reflected in titer and yield behaving similarly and in %WS decreasing over time to a constant value.
• Bioreactor working volume: Bioreaction time has a major effect on the final bioreactor working volume ($V_f$), which is an exponential effect as illustrated in Figure 9. This is due to the mode of operation of fed-batch, whereby a greater volume of media addition is required to maintain the substrate concentration as the working volume increases over time. This increase in bioreactor working volume shows that the bioreaction time will be constrained in practice by the size of the bioreactor.
• Mean product residence time: Increasing the bioreaction time increases the residence time, but it does not affect it as one might intuitively expect, as illustrated in Figure 9. For example, one might expect that increasing the bioreaction time from 240 h to 960 h would significantly increase the product residence time. However, the product residence time for the 960 h bioreaction time is 33.9 h, which is only a little greater than the 32.3 h at the 240 h bioreaction time. The reason for this is due to the exponential increase in the bioreactor working volume; thus, most of the product is being produced in the latter part of the bioreaction time.
• Productivity: This initially increases as titer increases, achieves a maximum value, and then progressively decreases with increasing bioreaction time, in particular after 240 h, with productivity at 480 h being roughly half that at 240 h. The decrease in productivity is a consequence of the definition of productivity in Equation (27). As the bioreaction time doubles from 240 h to 480 h and then again to 960 h and the titer changes minimally, the net effect is that the productivity is reduced by half for each doubling of time. Figure 9 highlights that as the bioreaction time increases, more and more of the available working volume in a constant volume bioreactor is not being used, and this is contributing to the reduction in productivity over longer bioreaction times.

Considering the above, it is not advantageous to operate the fed-batch bioreactor over long periods of time beyond the productivity maximum because of the major reduction in productivity over time. Furthermore, the exponential increase in working volume will limit the bioreaction time. Overall, there is a trade-off between having a higher titer and sufficient final working volume on one hand and decreasing productivity and possibly longer product residence time on the other hand.

3.3.2. Perfusion

The effect of bioreaction time on the performance parameters is presented in

Table 8. Effect bioreaction time on perfusion performance [$S_m$ = 20 g L⁻¹; $S_S$ = 1 g L⁻¹].

$\mathit{T}\mathit{i}\mathit{m}\mathit{e}$ (h)	$\mathit{T}\mathit{i}\mathit{t}\mathit{e}\mathit{r}$ (g L−1)	Productivity (mg L−1 h−1)	${\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}$ (h)	$\mathit{Y}\mathit{i}\mathit{e}\mathit{l}\mathit{d}2$ (%)	$\%\mathit{W}\mathit{S}$ (%)	${\mathit{X}}_{\mathit{f}}$ (g L−1)	${\mathit{G}}_{\mathit{f}}$ (g L−1)
48	0.1	2.7	48	7.1	57.3	0.57	0.38
120	1.2	16	43	13.9	12.0	6.8	4.42
240	2.9	142	5.8	15.1	5.4	46.3	9.50
480	3.1	319	3.8	15.7	5.1	50.0	9.50
960	3.1	409	3.4	15.8	5.0	50.0	9.50

for perfusion operation.

The main influences of bioreaction time are as follows:

• Titer, yield, and %WS: Final cell ($X_f$), final product, and final metabolite ($G_f$) concentrations all increase over time and eventually reach constant steady-state values. This is reflected in titer and yield behaving similarly and in %WS decreasing over time to a constant value.
• Mean product residence time: This decreases over time, with residence times being much higher early on and then approaching a constant value. Bioreaction rates are very slow initially and increase over time. This leads to higher feed/harvest flowrates over time, which reduces residence times. These flowrates eventually attain steady-state values, leading to mean residence times approaching constant values.
• Productivity: The bioreaction time has significant impact on the productivity, with it increasing significantly over time. This is due to longer bioreaction times having higher titers and also higher harvest flowrates (which is evidence by the shorter residence times).

Considering the above, the analysis suggests that it advantageous to operate the perfusion bioreactor over a longer period of time.

3.4. Comparison of Fed-Batch and Perfusion Bioreactor Performance

When comparing the performance of fed-batch and perfusion bioreactors, it is important that values of $S_m$ and the substrate concentration inside the bioreactor ($S$) are the same. Considering this, Table 3 and Table 5 are used to compare the performance of the bioreactors for the case where there is no cell death and no metabolite inhibition.

An advantage of fed-batch operation is the ability to obtain high titers. However, if a perfusion bioreactor is operated at the same values of $S_m$ and $S$, then it can obtain a titer similar to that of fed-batch. Thus, bioreactors operated in perfusion mode can also achieve high titers if operated accordingly. Comparing these tables also shows that the yields and % wasted substrate are fairly similar.

A major advantage of perfusion over fed-batch is much higher productivity, which ranges from between 15 and 200 times when comparing the two tables, but this does depend on the substrate concentration values, the bioreaction time, and bioreaction kinetics. This is a very large difference in productivity, which greatly reduces the perfusion bioreactor volume required to provide a specified product production rate, and this subsequently greatly reduces its physical footprint and corresponding capital cost. This superior productivity is associated with the much higher cell concentration in perfusion mode and is also due to the available working volume not being in use all of the time in fed-batch mode. The perfusion bioreactor is able to obtain much higher cell concentrations than fed-batch because the cells are not being diluted due to their retention in a constant volume bioreactor. However, the cell concentration may sometimes become too high in perfusion, resulting in a need to bleed off or waste some of contents, thus lowering the productivity and yield.

Another potential major advantage of perfusion is a much lower mean product residence time ($t_{res}$), although this being an advantage does depend on the influence of $t_{res}$ on product stability. However, even for fed-batch, the $t_{res}$ values are less than 35 h, which is much shorter than the bioreaction time of 240 h in Table 3. Of course this does depend on the bioreaction kinetic models used. For perfusion, the $t_{res}$ values are much shorter at less than 5 h. In fed-batch, the value of $t_{res}$ does not vary much with variations in $S_m$ and $S$; thus, there is little scope for lowering $t_{res}$. On the other hand, in addition to having an inherently lower $t_{res}$, $S_m$ has a major influence on $t_{res}$. Consequently, reducing $S_m$ can be used to further reduce $t_{res}$, as can be seen in Table 5. This could be advantageous for an unstable product that requires a low $t_{res}$. However, reducing $S_m$ does negatively impact titer, yield, and % wasted substrate.

3.5. Sensitivity Analysis

Sensitivity analysis was conducted to investigate of how varying the values of key model parameters influences the results and the trends of how substrate concentrations impact on the performance of the bioreactors. The key model parameters tested were the kinetic constants in the kinetic model equations, i.e., ${\mu }_{max},$ $X_m,$ $K_s,$ $\beta$, and $m_s$. The kinetic constant values were varied by $\pm$20%. This was undertaken for combinations of $S_m$ and $S$, presented in Table 3 and Table 5, that provided ${(S}_m-S)$ values ranging from 1 to 19.

Table 9. Percentage change in performance parameters based on a $\pm$20% variation in the values of the kinetic constants (“All” refers to the case where all the kinetic constants are varied) [base-case: $S_m$ = 20 g L⁻¹; $S$ = 1 g L⁻¹, $t_b$ = 240 h].

	All −20%	Base- Case	All +20%	${\mathsf{\mu }}_{\mathit{m}\mathit{a}\mathit{x}}$ +20%	${\mathit{K}}_{\mathit{s}}$ +20%	${\mathit{X}}_{\mathit{m}}$ +20%	$\mathsf{\beta }$ +20%	${\mathit{m}}_{\mathit{s}}$ +20%
Fed-batch
$X_f$	−8	-	3	17	−2	3	0	−14
$Yield1$	−1	-	0	0	0	0	20	−17
Productivity	−9	-	2	1	0	0	20	−15
$Titre$	−9	-	3	2	0	0	20	−16
$\%WS$	11	-	−2	−2	0	0	0	0
$t_{res}$	20	-	−15	−12	1	−2	0	−2
Perfusion
$X_f$	−35	-	27	6	−1	18	0	0
$Yield1$	−1	-	0	0	0	0	20	−17
Productivity	−58	-	87	39	−4	12	20	1
$Titre$	−11	-	4	2	0	1	20	−16
$\%WS$	10	-	−4	−2	0	−1	0	−1
$t_{res}$	106	-	−40	−20	3	−11	0	−14

presents representative sensitivity analysis results for one substrate combination for both fed-batch and perfusion. As expected, changing the values of the model kinetic constants does impact the values of performance parameters. It is interesting to note that the effect is greater for perfusion than fed-batch. This is possibly due to the fact that the cell concentration is much higher in perfusion and is approaching the maximum value ($X_m$) at the bioreaction time of 240 h. Consequently, a 20% variation in $X_m$ has a much larger impact on the cell concentration in perfusion, which has a consequential impact on some of the performance parameters.

As already highlighted, variation in the values of the kinetic constants was expected to impact the values of the bioreactor performance parameters. However, the main interest of the sensitivity analysis was to see if variation in the values of the kinetic constants influences the trends of how the substrate concentrations impact the performance parameters for both bioreactors. This is important as it could influence the conclusions from the study as a whole. The results from the sensitivity analysis indicate that the variation in the values of the kinetic constants did not impact the trends between substrate concentrations and bioreactor performance; the trends remained the same. This is illustrated in Figure 10 for perfusion operation. Figure 10a shows that variation in the kinetic constants has a big impact on productivity, but the trend between substrate concentrations (represented by $S_m-S$) remains the same, i.e., increases in ($S_m-S$) result in only a very small change in productivity. Figure 10b shows that variation in the kinetic constants has only a small impact on titer and that the trend between ($S_m-S$) and titer remains unchanged, i.e., increases in ($S_m-S$) result in higher titers.

4. Conclusions

In both fed-batch and perfusion, the substrate concentration in the media added ($S_m$) has a major impact on the performance of the bioreactors. The operating substrate concentration in the bioreactor ($S$) also has an influence. In fact, it is the difference between $S_m$ and $S$, i.e., ${(S}_m-S),$ that is having the effect because this influences the dilution effect in fed-batch and the dilution rate ($F/V$) in perfusion. The operating substrate concentration in the bioreactor is often constrained or specified in practice; thus, $S_m$ may be the only substrate concentration that may be varied.

For both fed-batch and perfusion, increasing $S_m$ increases titer and yield and reduces % wasted substrate. For fed-batch, increasing $S_m$ also increases productivity and consequently reduces reactor working volume, although varying $S_m$ has only a small impact on mean product residence time ($t_{res}$). On the other hand for perfusion, varying $S_m$ has little or no effect on productivity but does impact $t_{res}$, with reduced $S_m$ resulting in lower $t_{res}$. Overall, operating at higher values of $S_m$ tends be more beneficial in terms of the performance of both fed-batch and perfusion. However, this will lead to higher values of $t_{res}$ for perfusion, which may be undesirable for unstable products; thus, there may be a trade-off here.

Reducing $S$ so that it slows the bioreaction will result in slower cell growth. This intuitively might be expected to lead to slower evolution of cell, product, and metabolite concentrations over time. However, it must also be kept in mind that as $S$ decreases, ${(S}_m-S)$ increases, and this has an opposite effect on the evolution of the concentrations over time. Consequently, there is an interplay between decreasing $S$ and increasing ${(S}_m-S)$ that will determine the actual evolution of the concentrations over time, which subsequently will influence the values of the performance parameters.

Fed-batch mode may be operated with the intermittent addition or continuous addition of media. For intermittent addition, there are upper and lower substrate concentration limits. It is important that at the end of the process, sufficient additional time is provided to allow the substrate concentration to reduce to the lower limit. Otherwise, this will result in unnecessary wasted substrate, lower yield, and lower titer. Another issue with fed-batch highlighted in the results is that productivity may sometimes be a misleading performance parameter for fed-batch bioreactors due to the varying working volume over time. Two different fed-batch bioreaction conditions may give rise to similar titers at a given bioreaction time, leading to similar productivities. However, the progression of the bioreactions could be very different, leading to different final working volumes and thus different rates of product production.

Bioreaction time is a key variable for fed-batch operation. Sufficient time is required to increase titer, yield, and productivity; however, too long a time leads to a major progressive reduction in productivity. Furthermore, the exponential growth in fed-batch bioreactor working volume may limit the bioreaction time. Overall, there is a trade-off between having a higher titer and sufficient final working volume on one hand and decreasing productivity on the other hand. For perfusion, it is advantageous to operate the perfusion bioreactor over a longer period of time due to increased titer and productivity and reduced product residence time.

Overall, the study shows that perfusion tends to outperform fed-batch, with much higher productivities and shorter mean product residence times. Furthermore, perfusion can obtain titers and yields comparable to fed-batch when operated at similar substrate concentrations. Finally, it is important to reiterate that the effects of cell death and metabolite inhibition are not presented in this work due to space limitations and to gain a better understanding of the effects of the substrate concentrations in isolation. The effects of cell death and metabolite inhibition will impact bioreactor performance, and it is envisaged that work undertaken to superimpose their effects on the current work will be published at a later stage.