Drilling Optimization Using Artificial Neural Networks and Empirical Models
Abstract
1. Introduction
2. Model Construction
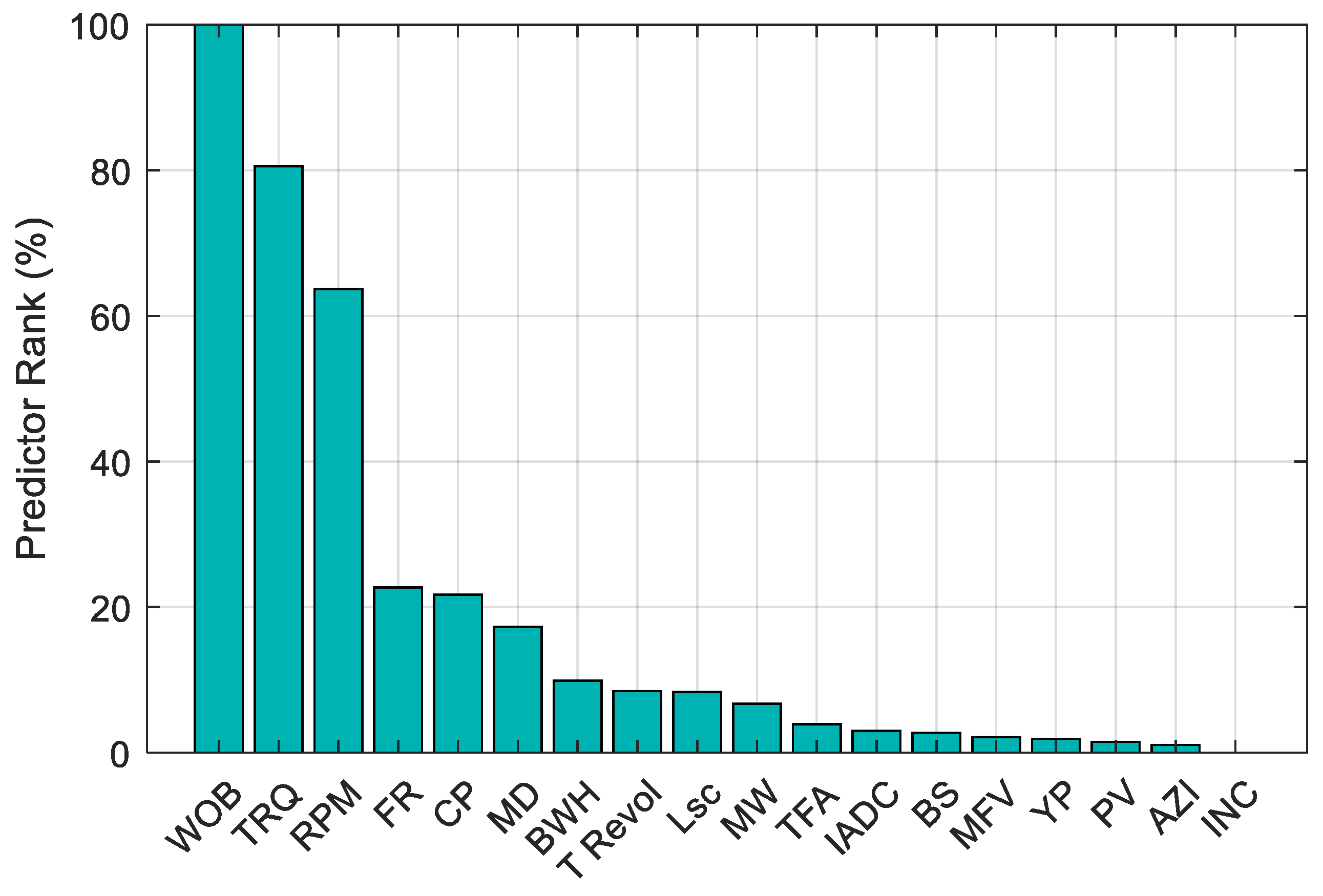
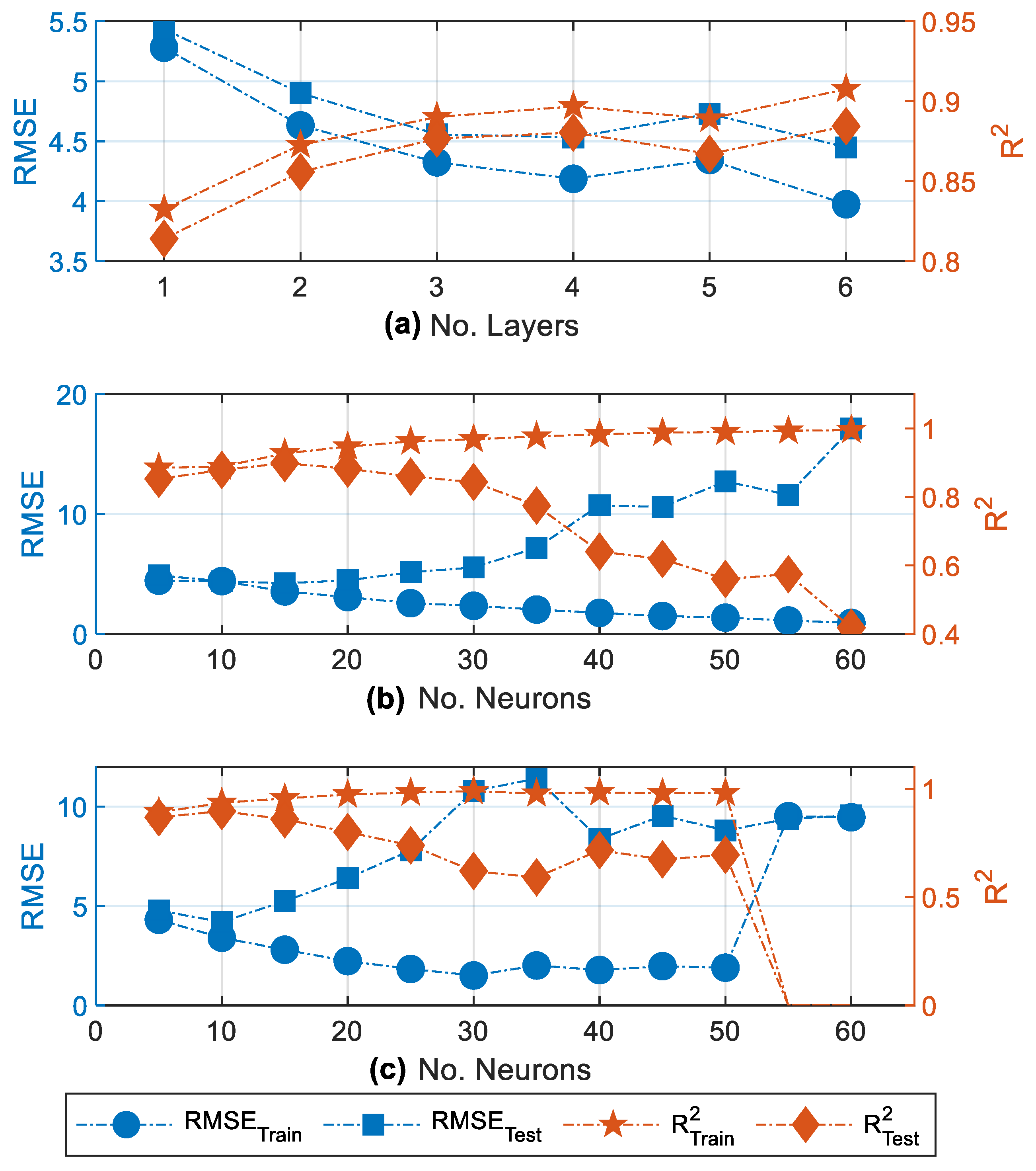
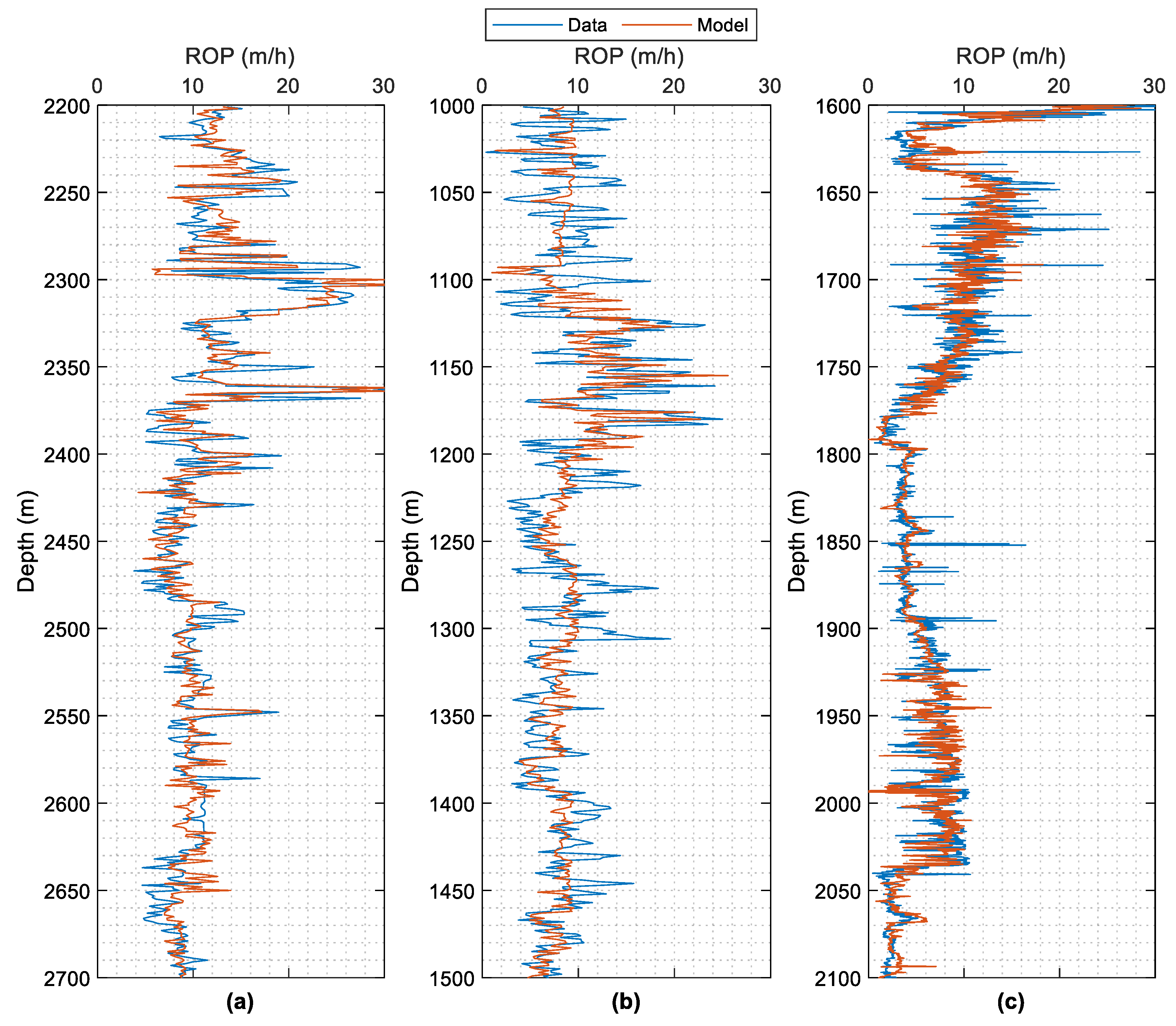
2.1. Data-Driven ANN Modeling
2.2. Empirical ROP Model
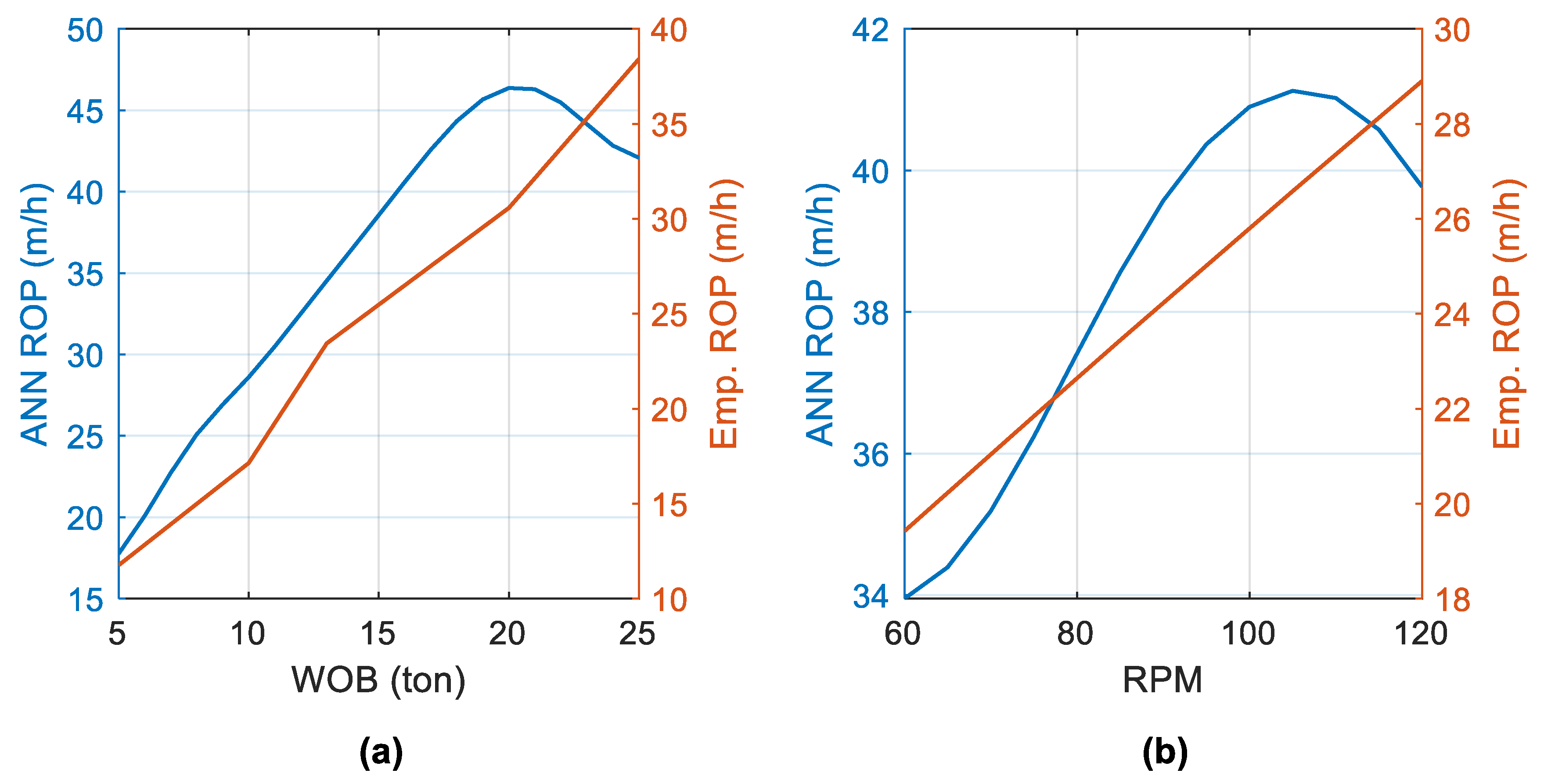
3. Sensitivity Analysis and Optimization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lummus, J.L. Factors to be Considered in Drilling Optimization. J. Can. Pet. Technol. 1969, 8, 138–146. [Google Scholar] [CrossRef]
- Staveley, C.; Thow, P. Increasing Drilling Efficiencies Through Improved Collaboration and Analysis of Real-Time and Historical Drilling Data. In Proceedings of the SPE Intelligent Energy Conference and Exhibition, Utrecht, The Netherlands, 23–25 March 2010. [Google Scholar] [CrossRef]
- Al Dushaishi, M.; Hellvik, S.; Aladasani, A.; Alsaba, M.; Okasha, Q. Application of Data Analytics to Improve Drilling Performance and Manage Drill Stem Vibrations. In Proceedings of the SPE International Heavy Oil Conference and Exhibition, Kuwait City, Kuwait, 10–12 December 2018. [Google Scholar] [CrossRef]
- Atashnezhad, A.; Al Dushaishi, M.F.; Hareland, G. A Graphical User Interface for Hard Rock Drilling Optimization System. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 12 February 2024. [Google Scholar] [CrossRef]
- Kolmer, H.P.; Cunningham, C.M.; Al-Dushaishi, M.F. ROP Optimization of Lateral Wells in SW Oklahoma: Artificial Neural Network Approach. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Houston, TX, USA, 20–21 September 2022. [Google Scholar] [CrossRef]
- Warren, T.M. Drilling Model for Soft-Formation Bits. J. Pet. Technol. 1981, 33, 963–970. [Google Scholar] [CrossRef]
- Motahhari, H.R.; Hareland, G.; James, J.A. Improved drilling efficiency technique using integrated PDM and PDC bit parameters. J. Can. Pet. Technol. 2010, 49, 45–52. [Google Scholar] [CrossRef]
- Kerkar, P.B.; Hareland, G.; Fonseca, E.R.; Hackbarth, C.J. Estimation of rock compressive strength using downhole weight-on-bit and drilling models. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 19–22 January 2014. [Google Scholar] [CrossRef]
- Akhtarmanesh, S.; Atashnezhad, A.; Hareland, G.; Al Dushaishi, M. ROP Model for PDC Bits in Geothermal Drilling. In Proceedings of the 55th U.S. Rock Mechanics/Geomechanics Symposium, Virtual, 20–23 June 2021; p. ARMA-2021-1214. [Google Scholar]
- Bataee, M.; Kamyab, M.; Ashena, R. Investigation of various ROP models and optimization of drilling parameters for PDC and roller-cone bits in Shadegan oil field. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar] [CrossRef]
- Soares, C.; Daigle, H.; Gray, K. Evaluation of PDC bit ROP models and the effect of rock strength on model coefficients. J. Nat. Gas Sci. Eng. 2016, 34, 1225–1236. [Google Scholar] [CrossRef]
- Macpherson, J.D.; Mason, J.S.; Kingman, J.E.E. Surface Measurement and Analysis of Drillstring Vibrations While Drilling. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 22–25 February 1993. [Google Scholar] [CrossRef]
- Dupriest, F.E.; Koederitz, W.L. Maximizing Drill Rates with Real-Time Surveillance of Mechanical Specific Energy. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 23–25 February 2005. [Google Scholar] [CrossRef]
- Al Dushaishi, M.; Nygaard, R.; Andersen, M.; Jeffery, C.; Hellvik, S.; Sassen, A.; Hareland, G. Selecting Optimum Drilling Parameters by Incorporating Vibration and Drilling Efficiency Models. In Proceedings of the IADC/SPE Drilling Conference and Exhibition held in Fort Worth, Fort Worth, TX, USA, 1–3 March 2016. [Google Scholar] [CrossRef]
- Wiktorski, E.; Kuznetcov, A.; Sui, D. ROP Optimization and Modeling in Directional Drilling Process. In Proceedings of the SPE Bergen One Day Seminar, Bergen, Norway, 5 April 2017. [Google Scholar] [CrossRef]
- Mehrad, M.; Bajolvand, M.; Ramezanzadeh, A.; Neycharan, J.G. Developing a new rigorous drilling rate prediction model using a machine learning technique. J. Pet. Sci. Eng. 2020, 192, 107338. [Google Scholar] [CrossRef]
- Elkatatny, S. New approach to optimize the rate of penetration using artificial neural network. Arab. J. Sci. Eng. 2018, 43, 6297–6304. [Google Scholar] [CrossRef]
- Ahmed, A.; Ali, A.; Elkatatny, S.; Abdulraheem, A. New artificial neural networks model for predicting rate of penetration in deep shale formation. Sustainability 2019, 11, 6527. [Google Scholar] [CrossRef]
- Gan, C.; Cao, W.H.; Liu, K.Z.; Wu, M.; Wang, F.W.; Zhang, S.B. A new hybrid bat algorithm and its application to the ROP optimization in drilling processes. IEEE Trans. Ind. Inform. 2019, 16, 7338–7348. [Google Scholar] [CrossRef]
- Aliyev, R.; Paul, D. A Novel Application of Artificial Neural Networks to Predict Rate of Penetration. In Proceedings of the SPE Western Regional Meeting, San Jose, CA, USA, 23–26 April 2019. [Google Scholar] [CrossRef]
- Brenjkar, E.; Biniaz Delijani, E.; Karroubi, K. Prediction of penetration rate in drilling operations: A comparative study of three neural network forecast methods. J. Pet. Explor. Prod. 2021, 11, 805–818. [Google Scholar] [CrossRef]
- Abbas, A.K.; Rushdi, S.; Alsaba, M.; Al Dushaishi, M.F. Drilling Rate of Penetration Prediction of High-Angled Wells Using Artificial Neural Networks. J. Energy Resour. Technol. 2019, 141, 112904. [Google Scholar] [CrossRef]
- Abbas, A.K.; Assi, A.H.; Abbas, H.; Almubarak, H.; Al Saba, M. Drill bit selection optimization based on rate of penetration: Application of artificial neural networks and genetic algorithms. In Proceedings of the International Petroleum Exhibition and Conference, Abu Dhabi, UAE, 11–14 November 2019. [Google Scholar] [CrossRef]
- Koulidis, A.; Ahmed, S. Advisory system for drilling optimization using artificial intelligence and in-cutter sensing data. In Proceedings of the SPE Middle East Intelligent Oil and Gas Symposium, Al Khobar, Saudi Arabia, 17–18 January 2023. [Google Scholar] [CrossRef]
- Hegde, C.; Daigle, H.; Millwater, H.; Gray, K. Analysis of rate of penetration (ROP) prediction in drilling using physics-based and data-driven models. J. Pet. Sci. Eng. 2017, 159, 295–306. [Google Scholar] [CrossRef]
- Barbosa, L.F.F.; Nascimento, A.; Mathias, M.H.; de Carvalho, J.A., Jr. Machine learning methods applied to drilling rate of penetration prediction and optimization-A review. J. Pet. Sci. Eng. 2019, 183, 106332. [Google Scholar] [CrossRef]
- Negara, A.; Saad, B. Combining Insight from Physics-Based Models into Data-Driven Model for Predicting Drilling Rate of Penetration. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 13–15 January 2020. [Google Scholar] [CrossRef]
- Chandrasekaran, S.; Kumar, G.S. Drilling efficiency improvement and rate of penetration optimization by machine learning and data analytics. Int. J. Math. Eng. Manag. Sci. 2020, 5, 381–394. [Google Scholar] [CrossRef]
- Soares, C.; Gray, K. Real-time predictive capabilities of analytical and machine learning rate of penetration (ROP) models. J. Pet. Sci. Eng. 2019, 172, 934–959. [Google Scholar] [CrossRef]
- Bourgoyn, A.T.; Millhem, K.K.; Chenevert, M.E.; Young, F.S. Applied Drilling Engineering, 9th ed.; SPE Textbook Series; SPE: Richardson, TX, USA, 2003; p. 232. [Google Scholar]
- Warren, T.M. Penetration Rate Performance of Roller Cone Bits. SPE Drill. Eng. 1987, 2, 9–18. [Google Scholar] [CrossRef]
- Rahimzadeh, H.; Mostofi, M.; Hashemi, A.; Salahshoor, K. Comparison of the penetration rate models using field data for one of the gas fields in Persian Gulf area. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar] [CrossRef]
- Hegde, C.; Pyrcz, M.; Millwater, H.; Daigle, H.; Gray, K. Fully coupled end-to-end drilling optimization model using machine learning. J. Pet. Sci. Eng. 2020, 186, 106681. [Google Scholar] [CrossRef]
- Al Dushaishi, M.F.; Abbas, A.K.; Alsaba, M.; Abbas, H.; Dawood, J. Data-driven stuck pipe prediction and remedies. Upstream Oil Gas Technol. 2021, 6, 100024. [Google Scholar] [CrossRef]
- Ozbayoglu, E.; Ozbayoglu, M.; Ozdilli, B.G.; Erge, O. Optimization of flow rate and pipe rotation speed considering effective cuttings transport using data-driven models. Energies 2021, 14, 1484. [Google Scholar] [CrossRef]
- Robnik-Šikonja, M.; Kononenko, I. An adaptation of Relief for attribute estimation in regression. In Machine Learning, Proceedings of the Fourteenth International Conference, San Francisco, CA, USA, 8–12 July 1997; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1997; Volume 5, pp. 296–304. [Google Scholar]
- Hareland, G.; Nygaard, R. Calculating Unconfined Rock Strength from Drilling Data. In Proceedings of the 1st Canada—U.S. Rock Mechanics Symposium, Vancouver, BC, Canada, 27–31 May 2007; p. ARMA-07-214. [Google Scholar]
- Hareland, G.; Rampersad, P.R. Drag-bit model including wear. In Proceedings of the SPE Latin America/Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, 27–29 April 1994. [Google Scholar] [CrossRef]
- Hareland, G.; Motahhari, H.R.; Hayes, J.P.; Qureshi, A. Increased Drilling Efficiency of Gas Storage Wells Proven Using Drilling Simulator. In Proceedings of the CIPC/SPE Gas Technology Symposium 2008 Joint Conference, Calgary, AB, Canada, 16–19 June 2008. [Google Scholar] [CrossRef]
- Rastegar, M.; Hareland, G.; Nygaard, R.; Bashari, A. Optimization of multiple bit runs based on ROP models and cost equation: A new methodology applied for one of the Persian Gulf carbonate fields. In Proceedings of the IADC/SPE Asia Pacific Drilling Technology Conference and Exhibition, Jakarta, Indonesia, 25–27 August 2008. [Google Scholar] [CrossRef]
- Hankins, D.; Salehi, S.; Karbalaei Saleh, F. An integrated approach for drilling optimization using advanced drilling optimizer. J. Pet. Eng. 2015, 2015, 281276. [Google Scholar] [CrossRef]
- Son, M.; Kim, J. Digital transformation of rotary hearth furnace for process automation and CO2 reduction: Hybrid model under limited operational data utilization. J. Manuf. Process. 2023, 101, 784–794. [Google Scholar] [CrossRef]
- Kim, J.; Son, M.; Han, S.S.; Yoon, Y.S.; Oh, H. Computational-cost-efficient surrogate model of vacuum pressure swing adsorption for CO separation process optimization. Sep. Purif. Technol. 2022, 300, 121827. [Google Scholar] [CrossRef]




| Parameter | Min. | Max. |
|---|---|---|
| Measure depth (MD) [m] | 610 | 3370 |
| Bit size (BS) [in] | 12.25 | 17.5 |
| Bit type (IADC) [-] | 223 | 527 |
| Total flow area (TFA) [in2] | 0.45 | 3.14 |
| Bit revolution (T Revol) [k Rev] | 0.06 | 1197 |
| Bit working hours (BWH) [h] | 0.01 | 124 |
| Rate of penetration (ROP) [m/h] | 0.13 | 75 |
| Weight on bit (WOB) [ton] | 0.01 | 40 |
| Rotational speed (RPM) [RPM] | 32 | 207 |
| Torque (TRQ) [kN.m] | 0.15 | 22.8 |
| Flow rate (FR) [L/min] | 425 | 3610 |
| Circulating pressure (CP) [psi] | 470 | 3851 |
| Mud weight (MW) [sg] | 1.07 | 1.28 |
| Marsh funnel viscosity (MFV) [s] | 45 | 74 |
| Plastic viscosity (PV) [cP] | 9 | 33 |
| Yield point (YP) [g/100 cm2] | 10 | 29 |
| Inclination (INC) [°] | 0.06 | 13.28 |
| Azimuth (AZI) [°] | 27.3 | 344 |
| Lithology factor (Lsc) [-] | 2 | 6.7 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| MD (m) | 1023 | FR (L/min) | 2900 |
| BS (in) | 17 ½ | CP (psi) | 1467 |
| IADC | 1415 | MW (sg) | 1.08 |
| TFA (in2) | 0.92 | MFV (s) | 55 |
| T Revol (krev) | 27 | PV (cp) | 10 |
| BWH (h) | 6 | YP (g/100 cm2) | 12 |
| WOB (ton) | 15 | AZI (°) | 86 |
| RPM | 85 | Lsc (-) | 6 |
| TRQ (kN·m) | 19.5 |
| No. | Bit | Bit Cost ($) | Length (m) | WOB (ton) | RPM | ROP (m/h) | Bit Wear | Cost ($/m) |
|---|---|---|---|---|---|---|---|---|
| 1 | Roller cone-A | 4000 | 240 | 11 | 92 | 4.74 | 4.5 | 2297 |
| 2 | PDC-A | 16,000 | 34 | 6 | 170 | 2.11 | 1 | 6157 |
| 3 | PDC-B | 19,000 | 857 | 5 | 173 | 7.17 | 2 | 1374 |
| 4 | Roller cone-B | 3200 | 30 | 14 | 94 | 1.06 | 6 | 12,368 |
| 5 | Roller cone-C | 3300 | 24 | 13 | 94 | 0.86 | 3 | 15,333 |
| 6 | Roller cone-D | 3200 | 52 | 14 | 96 | 2.25 | 3 | 6457 |
| Bits Used | Interval No. | WOB (ton) | RPM | FR (L/min) | Length (m) | ROP (m/h) | Time (h) | Bit Wear |
|---|---|---|---|---|---|---|---|---|
| PDC-A | 1 | 9 | 90 | 2500 | 153 | 17.32 | 8.83 | 0.8 |
| 2 | 14 | 130 | 2500 | 87 | 10.37 | 8.39 | 1.6 | |
| 3 | 18 | 150 | 2700 | 71 | 5.91 | 12.01 | 2 | |
| PDC-A | 1 | 12 | 100 | 2500 | 90 | 15.08 | 5.97 | 0.6 |
| 2 | 14 | 105 | 2500 | 50 | 17.35 | 2.88 | 0.8 | |
| 3 | 11 | 100 | 2500 | 70 | 10.92 | 6.41 | 1.1 | |
| 4 | 10 | 95 | 2500 | 80 | 12.54 | 6.38 | 1.3 | |
| 5 | 12 | 100 | 2600 | 60 | 13.00 | 4.62 | 1.4 | |
| 6 | 12.5 | 105 | 2500 | 210 | 11.15 | 18.83 | 2.4 | |
| 7 | 17 | 110 | 2600 | 130 | 10.96 | 11.86 | 3.0 | |
| 8 | 12 | 100 | 2600 | 130 | 11.68 | 11.13 | 3.2 | |
| PDC-B | 1 | 12 | 100 | 2500 | 19 | 10.65 | 1.78 | 0.3 |
| 2 | 25 | 200 | 2900 | 48 | 11.68 | 4.11 | 2.5 | |
| 3 | 15 | 180 | 2800 | 39 | 15.68 | 2.49 | 2.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Dushaishi, M.F.; Abbas, A.K.; Al Saba, M.T.; Wise, J. Drilling Optimization Using Artificial Neural Networks and Empirical Models. ChemEngineering 2025, 9, 37. https://doi.org/10.3390/chemengineering9020037
Al Dushaishi MF, Abbas AK, Al Saba MT, Wise J. Drilling Optimization Using Artificial Neural Networks and Empirical Models. ChemEngineering. 2025; 9(2):37. https://doi.org/10.3390/chemengineering9020037
Chicago/Turabian StyleAl Dushaishi, Mohammed F., Ahmed K. Abbas, Mortadha T. Al Saba, and Jarrett Wise. 2025. "Drilling Optimization Using Artificial Neural Networks and Empirical Models" ChemEngineering 9, no. 2: 37. https://doi.org/10.3390/chemengineering9020037
APA StyleAl Dushaishi, M. F., Abbas, A. K., Al Saba, M. T., & Wise, J. (2025). Drilling Optimization Using Artificial Neural Networks and Empirical Models. ChemEngineering, 9(2), 37. https://doi.org/10.3390/chemengineering9020037






