Performance Assessment of Novel Soda Ash Adsorbent Biogas Sweetening: Fixed Bed Studies, Adsorption Kinetics, and Adsorption Isotherms

Abstract

The reliance on greenhouse gas-emitting unrenewable energy sources such as coal, natural gas, and oil, increases climate change. Transitioning to renewable energy, such as biogas, is crucial to reducing environmental degradation and global warming. The existence of impurities such as hydrogen sulfide hampers the application of biogas. Utilizing natural resources for biogas purification is essential to improve access to clean energy for low-income communities. This study used soda ash derived from Lake Natron in Tanzania as a sorbent for H₂S removal. Effects of sorbent mass, flow rate, and particle size were investigated. Experimental data were analyzed using kinetic models, adsorption isotherms, and breakthrough curves. Soda ash of 280 μm particle size, a flow rate of 0.03 m³/h, and a mass of 75 g demonstrated the best performance, achieving an efficiency of 94% in removal and a sorption capacity of 0.02 g per 100 g in five repeated cycles. Freundlich and Jovanovich’s isotherms match the data with n = 0.4 and K_j = 0.003, respectively. Adsorption kinetics were best described by the intra-particle model (k_id = 0.14, c = 0.59 mg/g, and R² = 0.972). A breakthrough analysis indicated that the Yoon–Nelson model provided the best fit with an R² of 0.95. Soda ash from Lake Natron demonstrated great potential in biogas desulphurization, thus contributing to the production and access to clean energy.

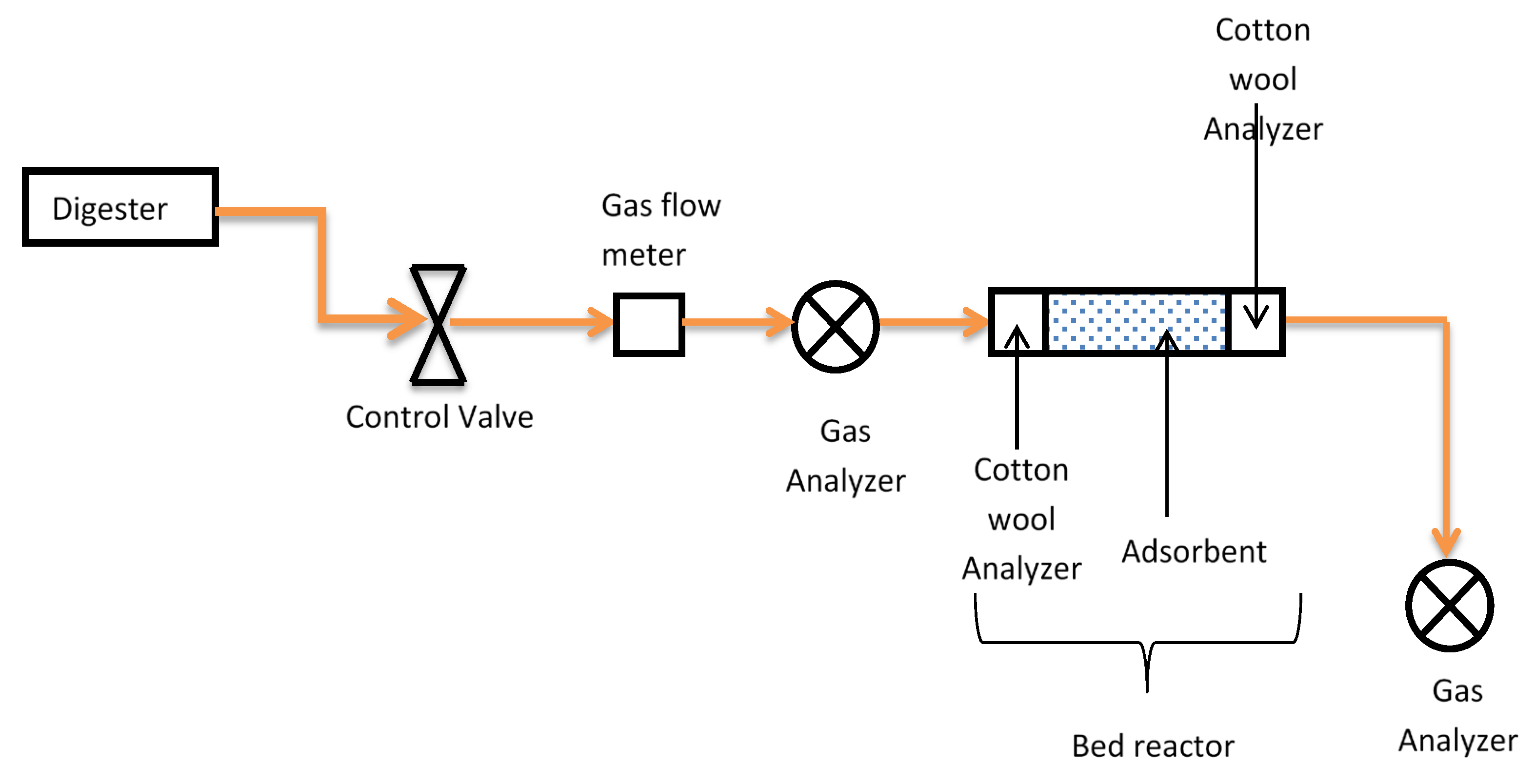
1. Introduction

Conventional energy resources, especially fossil fuels, have been a cornerstone of industrial advancement and economic growth. They include oil, coal, and natural gas, which have been instrumental in meeting the global energy demand for more than a century [1]. However, their continued use harms the environment and accelerates climate change. Fossil fuel combustion releases significant quantities of greenhouse gas emissions (GHGs) such as methane (CH₄), carbon dioxide (CO₂), and nitrous oxide (N₂O), which are the main contributors to the greenhouse effect and, subsequently, to global warming [2,3]. To address this challenge, the transition to renewable energy sources is appropriate to mitigate the effect of climate change, combat greenhouse gas emissions, and air pollution, and promote sustainability. The 2050 energy outlook envisions achieving net-zero emissions, which necessitates adopting clean and sustainable energy resources such as biofuels that align with SDG 7 [4].

Biogas is derived from the microbial decomposition of organic matter, like agricultural residues, food, human waste, biomass, and sewage. As such, biogas is an important renewable energy option with great potential to address the twin challenges of energy sustainability and waste management. The composition of biogas varies based on the type and amount of feedstock utilized. Generally, it contains methane (55–77%), carbon dioxide (30–45%), and minor constituents such as hydrogen sulfide, ammonia, nitrogen, and siloxane compounds [5]. The concentration of methane indicates the energy value of biogas, while the rest of the components are considered impurities. Biogas has a calorific value ranging from 25 to 30 MJ/m³, depending on the methane concentration, higher methane content in biogas corresponds to higher energy values [6].

Hydrogen sulfide in biogas is highly corrosive and can cause severe damage to metal components in biogas systems, such as pipes, valves, and engines. This corrosion can lead to increased maintenance costs, frequent repairs, and the reduced lifespan of equipment. The H₂S is a toxic gas with a characteristic rotten egg smell. High concentrations pose serious health risks, including respiratory problems, headaches, and, in extreme cases, life-threatening conditions [7]. Proper handling and monitoring are essential to ensure the safety of personnel working with biogas. When biogas containing H₂S is used in internal combustion engines or gas turbines, the H₂S can form sulfuric acid, affecting engine performance and efficiency. This can cause engine fouling, decreased power output, and increased maintenance needs. The presence of H₂S can negatively influence the efficiency of biogas utilization systems, reducing overall energy output and operational effectiveness [8]. When biogas is burned or processed, H₂S can react with oxygen to form sulfur dioxide (SO₂), which contributes to air pollution and acid rain. This environmental impact necessitates careful management of H₂S levels in biogas, thus upgrading technologies are required. In the process of upgrading biogas, H₂S must be removed to meet quality standards of biomethane for integration into natural gas networks or as fuel for vehicles.

Recently, several biogas desulphurization methods have been developed, including pressure swing adsorption, physical scrubbing, water scrubbing, and membrane separation. However, the application of these techniques in developing economies is limited by high maintenance and operational costs. This is because most current biogas desulphurization technologies are intended for large-scale operations. In contrast, using locally sourced organic materials for the elimination of hydrogen sulfide from biogas offers several advantages, including simplicity in design, ease of handling, and cost-effectiveness. In addition, this makes the technology easy to adapt and use in low-income areas and small-scale applications. Various sorbents, such as soda ash [7], activated sweet potato leaves [9], and red rock [10], have been utilized for biogas upgrading. The purified biogas, or bio-methane, can be transformed into bio-compressed natural gas (Bio-CNG), which facilitates its distribution through natural gas pipelines. The use of bio-compressed natural gas will increase from 2% in 2021 to 27% by 2050 [11,12].

Limited research exists on using low-cost materials for biogas purification. The few available studies have been conducted as batch studies, rather than column studies, which reflect practical applications. Our previous work investigated the characterization and use of soda ash collected from Lake Natron for the elimination of H₂S from biogas through batch studies [7]. The study determined that soda ash with 280 μm particle size, mass of 75 g, and gas flow rate of 0.03 m³/h gave the best performance. Within 15 min of application, the soda ash demonstrated a high removal efficiency of 94% and a sorption capacity of 0.02 g per 100 g of adsorbent. Given this strong performance, the objective of the present work was to apply existing kinetics of adsorption and breakthrough analysis models to the data from the experiment to determine key column design parameters. Such parameters include absorbent mass, column bed height, and biogas flow rate. They are useful for the design and optimization of biogas desulphurization systems. The adsorption kinetics were analyzed using the pseudo-first order, pseudo-second order, intra-particle diffusion models, and the Elovich model. Breakthrough curves were examined using the Yoon–Nelson, Thomas, and Adams–Bohart models. This study’s innovation lies in the application of a new adsorbent for H₂S removal from biogas and in deriving key design parameters from the models to support the scaling-up of the column. This approach aims to address the dual challenges of energy efficiency and safety using biogas.

2. Materials and Methods

2.1. Material Collection and Preparation

The materials employed included soda ash, cotton wool, sand, a fixed bed reactor, (for column packing), a 1/16-inch clear tube, and biogas. The equipment used comprised a grinder (model HK-820) from Food Machine, Zhengzhou, China, 12 mm × 50 m masking tape, sieves, a laboratory oven (model LDO-150) from Nabertherm GmbH, Lilienthal, Germany, an electronic balance (model HZT-A200) from EMIN Myanmar Co., Ltd., Yangon, Myanmar, aluminum foil, a flow meter (model JBD2-5-SA) from Pinnacle Biogas Technology, Nasarawa, Nigeria, and a biogas analyzer (Geotech 5000) from Cadmus Products Limited, Chelmsford, UK. The adsorbent was prepared by washing with tap water and packed in the column with some addition of pore-forming material to avoid the blockage of biogas, as shown Figure 1. Different variables, such as particle size, mass of the adsorbent, and biogas flow rate, were analyzed to evaluate the sorption capacity of soda ash. The experimental data obtained were then fitted to appropriate models for further analysis.

Experimental Description

Experiments were carried out in a household setting to evaluate the effectiveness of soda ash in removing hydrogen sulfide from biogas. A Geotech Biogas Analyzer 5000 (Cadmus Products Limited, Chelmsford, UK) was used to measure methane concentration and impurities before and after the adsorption process, while a flow meter monitored the biogas flow rate. The biogas composition and the feedstock used in the study were detailed in our previous publication [8]. All experiments were performed in triplicate and average values reported in the study.

2.2. Methods

2.2.1. Assessment of Fixed Bed Column Efficiency

Adsorption experiments were carried out at a household biogas plant that produced biogas from a 1:1:1 ratio blend of biomass, kitchen waste, and human waste. This mixture was combined with water in the same proportion, and the digester was fed twice daily. The co-digestion process improved biogas and methane production and ensured the stability of the system by maintaining balanced carbon-to-nitrogen (C/N). A fixed bed column, measuring 13 cm in height and 4 cm in width, was used. The column was packed with cotton wool and biogas was passed through without any sorbent material to confirm that the cotton did not react with the biogas. It was confirmed that no reaction occurred between the cotton wool and the biogas as the concentration of hydrogen sulfide remained the same. Soda ash, along with a non-reactive material to ensure smooth gas flow, was packed into the column, with both ends sealed with cotton wool. The setup was observed for about 15 min. The methane concentration measured before the introduction of the sorbent was identical to the amount recorded afterward. Additionally, the sorbent showed a preference for adsorbing hydrogen sulfide, meaning methane had minimal interaction with the soda ash. Figure 2 illustrates the experimental setup utilized. The results from the on-site experiments were validated through fixed bed adsorption studies, adsorption kinetics, and adsorption isotherms.

2.2.2. Impact of Different Process Parameters

The sorption capacity of soda ash was examined under varying conditions, including adsorbent particle size, sorbent mass, and flow rate with the findings presented in our previous study [7]. A particle size of 280 μm performs well because smaller particles offer a higher surface area-to-volume ratio, increasing the number of active sites present for the adsorption process. This enhanced surface area improves contact between the adsorbent and the biogas molecules, leading to more efficient adsorption. Additionally, the particle size is small enough to facilitate effective mass transfer. This balance makes 280 μm an optimal size for improved adsorption performance. The good performance in hydrogen sulfide removal at 0.03 m³/h biogas flow rate and a sorbent mass of 75 g is likely due to the increased time for interaction between the biogas and the adsorbent. At this lower flow rate, the gas moves more slowly through the system, allowing the hydrogen sulfide more time to interact with the sorbent, leading to more adsorption performance. Faster flow rates reduce this interaction time, which can lead to less effective hydrogen sulfide removal. The superior performance of 75 g of sorbent in removing hydrogen sulfide from biogas, compared to 50 g and 25 g, can be attributed to the increased amount of available surface area for the adsorption process. A larger sorbent mass provides more active sites for the hydrogen sulfide to bind to, which enhances the overall adsorption efficiency. In contrast, with 50 g or 25 g, the limited sorbent mass may not provide enough surface area to fully capture the hydrogen sulfide, particularly when dealing with larger volumes or higher concentrations of biogas, resulting in less efficient removal. A removal efficiency of 94% and a sorption capacity of 0.02 g/100 g were obtained with a particle size of 280 μm, a mass of 75 g, and a biogas flow rate of 0.03 m³/h.

2.2.3. Adsorption Isotherms

Adsorption equilibrium was evaluated using Freundlich, Langmuir, and Jovanovich isotherms, with equilibrium plots created in OriginPro version 9. The Langmuir model suggests that when adsorption reaches its maximum, a single layer of adsorbate molecules forms on the adsorbent, and no further sorption occurs on top of the already adsorbed molecules, but only on the unoccupied surface of the sorbent. The required parameters were calculated per the equation stipulated in our previously published paper on biogas sweetening. In contrast to the Langmuir adsorption isotherm, the Freundlich adsorption isotherm is an empirical model used to describe multilayer sorption on heterogeneous adsorption sites. It presumes changes in surface affinities and an uneven distribution of adsorption heat. The model accounts for the multilayer adsorption process on a non-uniform adsorbent surface. The Freundlich parameters can be calculated using the equations and procedures outlined in our previous study, through regression analysis of the log q_e vs. log C_e graph, to assess the applicability of the Freundlich isotherm. However, it is not effective for a wide range of data. The most common methods for validating the fit of the adsorption isotherm to the on-site data involve determining the R² value and comparing the experimental q_e with the estimated q_e.

The Jovanovich model follows similar assumptions to the classic Langmuir isotherm and successfully accounts for lateral interactions between adsorbed molecules. In contrast to the Langmuir isotherm, the Jovanovich isotherm considers the potential for mechanical interaction between the adsorbate and adsorbent [13]. It applies to both localized and mobile adsorption processes, the “n” parameter evaluates lateral interactions between adsorbed molecules. The Jovanovich isotherm saturates at high pressures, with the equation achieving maximum saturation when sorbate concentration is high. At low concentrations, the model simplifies to Henry’s law. In contrast to the Langmuir adsorption equation, the Jovanovich isotherm reaches saturation more gradually [14].

2.2.4. Kinetics of Adsorption

The batch kinetic studies were conducted in a closed chamber with a small opening. Biogas and soda ash adsorbent were contacted and readings taken at 15 min intervals for 150 min. The data were evaluated using pseudo-first order, pseudo-second order, and Elovich and intra-particles diffusion models as shown in

Table 1. Linear models of adsorption kinetics.

Adsorption Kinetics Model	Linear Form	Equation
Pseudo-first order	$q_t=q_e(1-e^{k_{1}t})$	(1)
Pseudo-second order	$\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$q_t=\frac{1}{k{q_e}^2}+\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$q_e$}\right.$}\right.$	(2)
Elovich model	$q_t={\displaystyle \frac{1}{\alpha }}ln\left(\alpha \beta \right)+{\displaystyle \frac{1}{\alpha }}Int$	(3)
Intra-particles diffusion model	$q_t=k_{id}{t}^{0.5}+C$	(4)

.

2.2.5. Adsorption Studies in a Fixed-Bed Column

The dynamic performance of the fixed bed in the column performance was studied using existing models summarized in

Table 2. Linear and non-linear fixed column models utilized in this study.

Models	Non-Linear	Linear	Plot Made	Reference
Adams–Bohart	$T=\left[{\displaystyle \frac{N_{oz}}{C_{ov}}}\right]-ln{\displaystyle \frac{(\frac{C_o}{C_t}-1)}{C_o{k}_{AB}}}$	$ln\left({\displaystyle \frac{C_t}{C_o}}\right)={\displaystyle \frac{k_{BA}{N}_{o}L}{U}}-k_{BA}{C}_{o}t$	$ln({\displaystyle \frac{C_t}{C_o}})Vs t$	[15]
Thomas	${\displaystyle \frac{C_t}{C_o}}={\displaystyle \frac{1}{[1+exp\left(k_{Th} q_{Th}m\right)]}}-k_{Th}{C}_{o}t$	$ln\left({\displaystyle \frac{C_t}{C_o}}-1\right)=\left({\displaystyle \frac{k_{Th}{q}_{Th}m}{Q}}\right)-k_{Th}{C}_{o}t$	$ln({\displaystyle \frac{C_t}{C_o}}-1)$ vs. t	[16]
Yoon–Nelson	${\displaystyle \frac{C_t}{C_o}}={\displaystyle \frac{1}{1+e^{K_{YN}(ɽ-T)}}}$	$ln({\displaystyle \frac{C_t}{C_O-C_t}})=K_{YN}t-ɽK_{YN}$	$ln({\displaystyle \frac{C_t}{C_o-C_t}})Vs t$	[16]

. Various variables were obtained from each model to describe the efficiency of the column. They were applied to fit the experimental data, and their performance was compared using correlation coefficient (R²).

Adam’s model relates the bed depth and the breakthrough time through a linear relationship (R²). This linearity simplifies the absorber design and analysis, and provides an easy method for conducting trial tests, as outlined in our previous work. Key parameters like N_o and k_AB were obtained from a plot of ln (C_t/C_o) versus time. N_o represents the maximal adsorption capacity (L/mg min), and k_AB is the Bohart–Adams constant.

On the other hand, the experimental data gathered from a fixed bed column during on-site testing were utilized to determine the maximal concentration of hydrogen adsorbed and the adsorption rate constant. This was achieved using the Thomas kinetic model. The parameters k_Th and q_o were obtained from the plot of ln [(C_o/C_t) − 1] against time, where k_Th represents Thomas’s constant parameter (mL/min mg), and q_o is the capacity of adsorption (mL/min mg). These variables were calculated using Equations (5) and (6). The Yoon–Nelson model is typically represented by the equations provided in Equations (7) and (8).

$$q_o={\displaystyle \frac{Intercept}{k_{Th}}},$$

(5)

$$k_{Th}=-\left({\displaystyle \frac{Slope}{C_o}}\right),$$

(6)

$${\tau }_{kY}=Intercept,$$

(7)

$$k_{YN}=Slope.$$

(8)

3. Results and Discussion

3.1. Biogas Composition and Summary of Material Characterization

The biogas compositions of the two digesters vary based on the quality and quantity of the feedstock used throughout the biogas production process, as shown in

Table 3. The constituent of biogas used in the current study.

Constituents	Bio-Digester 1	Bio-Digester 2
CH4 (v.%)	67–69.1	69–70.1
CO2 (v.%)	29.7–30.1	30.1–30.8
O2 (v.%)	0.1–0.2	0.1–0.2
H2S ppm	530–606	748–1480
NH3 ppm	331–421	331–530

. This variation occurs because the feedstock’s characteristics such as moisture level, organic content, and degradability directly influence microbial activity during digestion, thereby affecting the production and composition of biogas. Additionally, the amount of feedstock determines the availability of substrates for microorganisms, further affecting the gas yield and composition. The soda ash was characterized, and the results are reported in our previous study [8]. The multipoint BET analysis indicated that the material pores were mesoporous with pore sizes ranging from 2 to 50 nm. The SEM analysis showed that the material morphology is relatively rough with extremely hollow pores, and irregular crystal structures, which enhance H₂S removal.

3.2. Adsorption Isotherms

These were used to study the behavior of interaction between the active mesoporous sites of soda ash material and hydrogen sulfide from biogas. These isotherms describe the relationship between the equilibrium quantities of hydrogen sulfide adsorbed and those in the adsorbent phase.

3.2.1. The Langmuir Adsorption Model

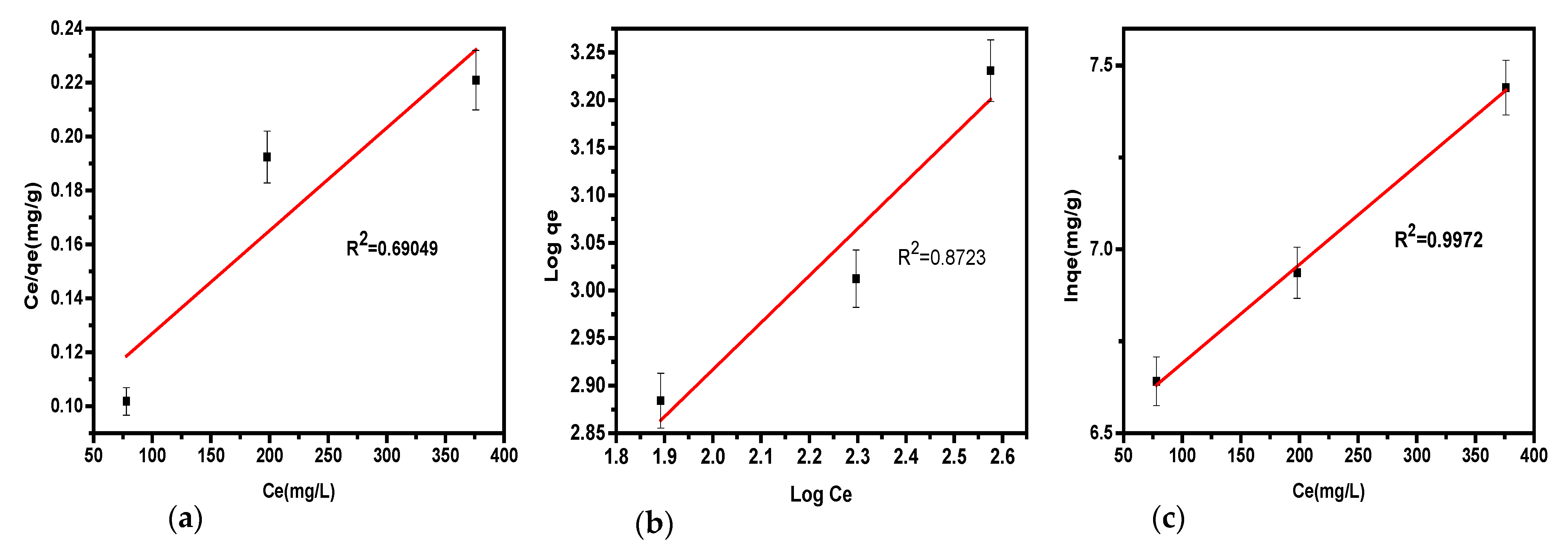
This model determined the maximal adsorption capacity, representing full monolayer coverage on the soda ash surface. The parameters of the model, presented in

Table 4. Condensed isotherm parameters for the adsorption of H₂S from biogas.

Model	Langmuir Isotherm				Freundlich Isotherm			Jovanovich Isotherm
Parameters	qmax (mg/g)	KL (L/mg)	RL	R2	kf	n	R2	qmax (mg/g)	Kj (L/g)	R2
H2S	11.25	233.8	3.45 × 10−6	0.69	84.9	0.4	0.87	6.42	0.003	0.997

, were obtained via equations detailed in our prior study, with plots illustrated in Figure 3a. From the intercept and slope of the linearized Langmuir plot of C_e/q_e versus C_e, key parameters like R_L, K_L, R², and q_m were derived. Adsorption efficiency was evaluated via the separation factor R_L: R_L = 1 suggests linear sorption, R_L > 1 indicates unfavorable adsorption, 0 < R_L < 1 shows favorable adsorption, and R_L = 0 implies irreversible adsorption. From the R² values in Table 4, the Langmuir isotherm does not appropriately describe hydrogen sulfide removal, as seen with an R_L of 3.45 × 10⁻⁶ and an R² of 0.69049, underscoring the model’s inadequacy for H₂S adsorption from biogas.

3.2.2. The Freundlich Isotherm

This model was used to estimate the sorption intensity, 1/n, of hydrogen sulfide on the surface of the soda ash sorbent. The model characterized the removal of H₂S as a multilayer adsorption process occurring on heterogeneous surfaces. The plots of log q_e versus log C_e illustrated in Figure 3b were utilized to obtain the parameters K_f, and n as shown in Table 4, offering insights into surface heterogeneity and adsorption intensity. By using this isotherm, the process is favorable only if 1< n < 10 or 0 < 1/n < 1. Alternatively, when n < 1 shows a slow sorption process, and n = 1 suggests a linear adsorption. In this study, the 1/n value for H₂S removal was found to be 0.4, with R² of 0.87. These results show that the adsorption of hydrogen sulfide aligns well with the model, as it achieved coefficients close to 1, and 1/n values fell within the expected range of 0 < 1/n < 1 consistent with the literature. This supports the conclusion that the Freundlich adsorption isotherm effectively modeled the adsorption of biogas impurities in this study.

3.2.3. The Jovanovich Isotherm Model for Adsorption

The Jovanovich model was evaluated, with the results presented in Table 4. A plot of ln q_e versus shown in Figure 3c, along with relevant equations, was used to determine the isotherm variables based on the data from the experiment. The results indicated adsorbent capacity is 6.42 mg/g for H₂S elimination (Table 4) with a correlation coefficient of 0.997. The data fitted well in the model as K_j was in the range of 0 < K_j < 1 agrees with the literature [17]. The low value of q_max indicates that the material has weak adsorption ability [18]. The Jovanovich isotherm adequately described the removal of hydrogen sulfide from biogas.

Here, K_L (L/mg) is the Langmuir constant, R_L (L/mg) is the Langmuir equilibrium constant, q_max (mg/g) is the maximum adsorption capacity, n is the adsorption intensity constant, k_f (L/g) is the Freundlich adsorption constant, and K_j (L/g) is the Jovanovich constant.

3.2.4. The Limitations of Langmuir Isotherms

The Langmuir isotherm assumes a homogenous adsorption surface with uniform energy levels, where adsorption occurs as a monolayer and each adsorption site can only hold one molecule without interactions between adsorbed molecules. These assumptions, while useful for ideal systems, limit the model’s applicability to more complex adsorption processes. In cases where the adsorbent surface is heterogeneous, such as soda ash, or where multilayer adsorption occurs due to varying binding energies and interactions, the Langmuir model fails to accurately describe the adsorption behavior. This limitation becomes evident when experimental data deviate significantly from the model’s predictions, as it cannot account for surface irregularities, variations in adsorption site energy, or the potential for molecules to adsorb onto previously adsorbed layers.

3.3. Adsorption Kinetics

The process of H₂S removal from biogas using soda ash material was investigated and the data from the experiment were analyzed using various kinetic models discussed here. Different equations for these models were converted into linear forms, enabling regression analysis based on the on-site results. The coefficient of correlation (R²) and the maximal adsorption (q_max) were then used to evaluate the alignment of the on-site data with the proposed adsorption kinetic models.

3.3.1. Pseudo-First Order Kinetics

The kinetics are considered valid for surface reactions-controlled adsorption kinetics, particularly under conditions of low adsorbate concentration or excess adsorbent, suggesting that each adsorbate molecule occupies a single active site on the surface. The model assumes that the adsorption process relies solely on the adsorbate concentration and is governed by diffusion. The linearized pseudo-first order (PFO) model requires an initial estimate of q_e to calculate other parameters through its equation. On the other hand, q_e can be estimated by deducing experimental data to t→+ꝏ. This involves the assumption of an initial q_e performing linear regression to obtain k₁, and iteratively refining q_e. The q_e, k₁, and R²-values are illustrated in

Table 5. Parameters of adsorption kinetics models for H₂S removal across four different models.

	Pseudo-First Order			Pseudo-Second Order			Elovich Model			Intra-Particle
Parameters	k1	R2	qe (mg/g)	k2	qe (mg/g)	R2	α	β	R2	kid	c	R2
value	2.3 × 10−4	0.561	11.5	3.2 × 10−6	10.5	0.903	1.9	0.03	0.892	0.14	0.59	0.972

, while the linear form of the model is depicted in Figure 4. The model highlights a direct correlation between the sorbent material’s surface area and the adsorption rate. However, the model’s accuracy is validated only when the calculated q_e (mg/g) closely matches the on-site q_e (mg/g). For hydrogen sulfide adsorption, the calculated q_e did not align with the value from the on-site experiment, indicating that the model failed to fit the experimental data.

3.3.2. Pseudo-Second Order Kinetics

The model can be expressed in a linear form, allowing the important variables to be determined, as shown in Table 5. Experimental data collected from on-site studies were utilized to create plot Figure 4b, from which the required parameters were derived. The adsorption kinetics for H₂S removal using the pseudo-second order model were studied in batch systems at ambient temperature. Figure 4b illustrates a rapid increase in H₂S adsorption during the first 50 min. The kinetic variables calculated from the pseudo-second order equation are summarized in Table 5. The correlation coefficient (R²) for hydrogen sulfide uptake using the pseudo-second order (PSO) model was found to be 0.903. However, the values of k, q_e, and R² indicate that the kinetics model did not adequately represent the experimental data [19]. Overall, the calculated q_e and R² for hydrogen sulfide adsorption demonstrate that the model failed to align with the on-site experimental results.

3.3.3. Elovich Model

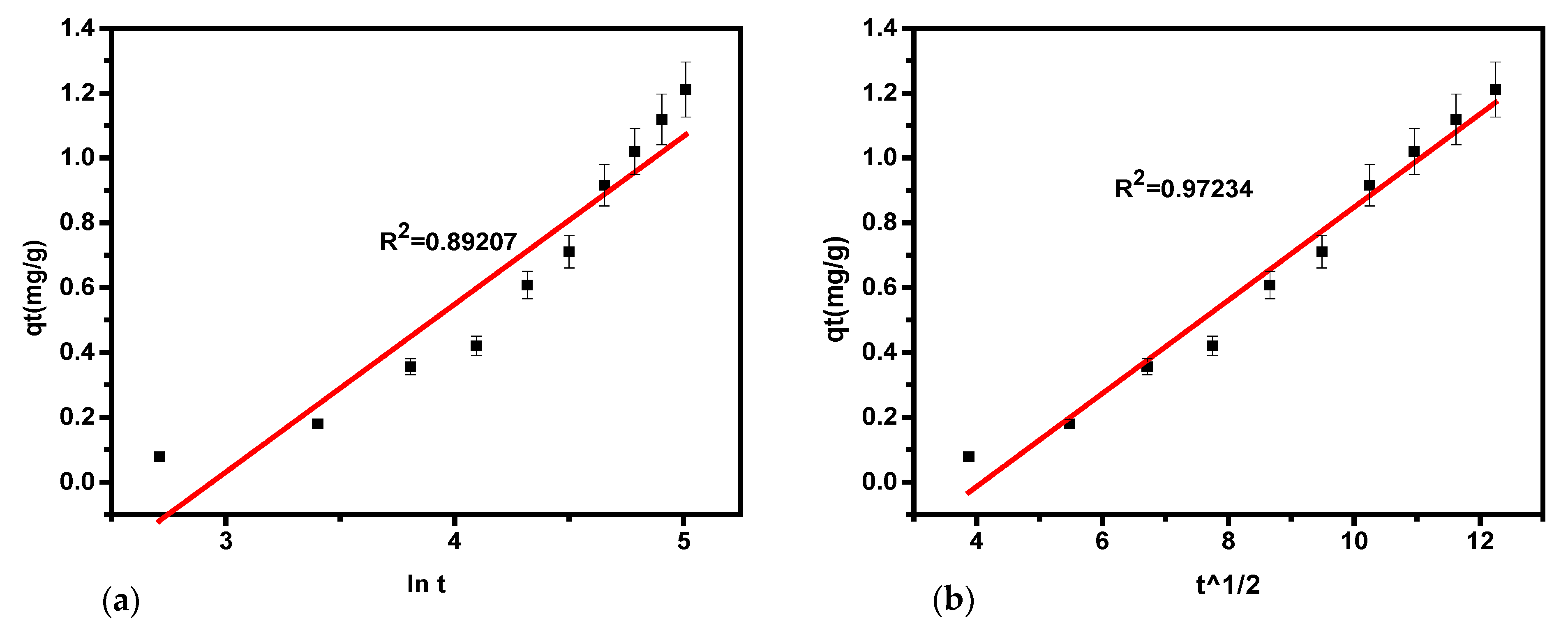
The parameters obtained for H₂S removal using this model are summarized in Table 5 and illustrated in Figure 5. The linear regression analysis for hydrogen sulfide removal based on the Elovich model yielded an R² value of 0.892. The availability of adsorption sites increases exponentially, following a multilayer adsorption process governed by chemisorption kinetics. This model suggests that the adsorption rate declines exponentially as the number of adsorbates increases, consistent with chemisorption mechanisms.

The kinetics of the model are defined by the parameters ᵦ, α, and R², which are derived from linear plots. The findings indicate strong chemisorption interactions between hydrogen sulfide and the sorbent material. Values for α, ᵦ, and R² were extracted from the plot of q_t versus lnt as demonstrated in Figure 5a, and the results are presented in Table 5. These results suggest that the Elovich kinetics model offers a moderate fit to the experimental data, as indicated by R² values below 0.89207.

It was further noted that the initial adsorption rate of hydrogen sulfide removal was minimal, at 1.9 mg/g·min. This observation aligns with findings from [19], suggesting that the desorption rate of hydrogen sulfide when using soda ash is relatively slow.

3.3.4. Intra-Particle Diffusion Model

A graph of q_t against t^1/2 illustrated a linear relationship between these parameters (Figure 5b). This indicates that the adsorption occurs through intra-particle mechanisms and surface adsorption. The c and k_id parameters are obtained from the plot of q_t versus t^1/2 as the slope and intercept, respectively, and are shown in Table 5. The high R² (closer to 1) concerning the previous models indicates the appropriateness of this mechanism. The values of k_id and c (mg/g) obtained suggest that soda ash sorbent can be used for chemisorption. Consequently, the intra-particle diffusion model best fits the on-site experimental data concerning the other models used in the current study.

The equation establishes a direct correlation between the square root of time and sorption capacity, as shown in Figure 5b. The graph of q_t against t^1/2 for H₂S adsorption using soda ash indicates that the adsorption occurs through both surface adsorption and intra-particle diffusion mechanisms. The parameters c and k_id (mg/g) can be derived from the slope and intercept of the q_t versus t^1/2 plot. These parameters are summarized in Table 5. The R² values for hydrogen sulfide removal are closer to 1 as compared to the remaining models, suggesting that the diffusion mechanism is a significant factor in the adsorption process. The values of k_id and c (mg/g) reflect the extent of the boundary layer and indicate that soda ash is a suitable sorbent for chemisorption.

3.4. Modeling

The Yoon–Nelson, Thomas, and Adams–Bohart models are widely utilized in adsorption studies to describe the dynamics of fixed-bed columns. The models help to understand and predict the breakthrough behavior during the removal of biogas contaminants, like hydrogen sulfide, from gaseous or liquid streams (Figure S1, Supplementary Materials). They enable the assessment of adsorbent performance and column design parameters, making them valuable tools in optimizing processes, such as hydrogen sulfide removal from biogas. In the adsorption experiments, the smallest particle size of 280 µm, with a flow rate of 0.03 m³/h and an initial hydrogen sulfide concentration of 1227 ppm, reached saturation at 160 min. The experiment demonstrated a high removal efficiency of 94% and a sorption capacity of 0.02 g per 100 g of adsorbent. The mass of the adsorbent used varied at 75 g, 50 g, and 25 g, while the bed volume changed correspondingly from 10 cm to 7 cm and 4 cm.

3.4.1. Adams–Bohart Model

This model is particularly effective in describing the initial phase of adsorption within a fixed column, as it focuses on the relationship between mass transfer and adsorption capacity. It was applied to describe the adsorption behavior of the material for hydrogen sulfide removal under varying conditions of initial sorbent concentrations and bed heights. The mass transfer coefficient (K_AB) and maximal adsorption ability (N_o) were obtained from the slope and intercept of the plots, respectively, Figure 6. The results presented in

Table 6. Parameters of models discussed based on linear regression analysis for biogas upgrading.

Adams–Bohart Model H2S Adsorption					Thomas Model			Yoon–Nelson Model
Co (%)	Z (cm)	kAB (L/mg min)	No (mg/L)	R2	kTh × 10−6 (mL/min mg)	qo (mL/min mg)	R2	kYN × 10−2 (min−1)	ɽ, (min)	R2
1227	4	7.09 × 10−6	1248	0.8722	3.62	1254	0.77680	4.4	74	0.7489
1227	7	1.04 × 10−5	693	0.9119	3.37	750	0.9485	3.9	62	0.8461
1227	10	1.49 × 10−5	480	0.9583	3.17	607	0.9559	3.1	50	0.9504

highlight the dependence of these parameters on the experimental conditions. An increase in bed height (e.g., 25 g to 75 g) was associated with higher values of (N_o) indicating that taller beds provided more active sites for adsorption. However, (K_AB) tended to increase with increased bed height, likely due to the extended contact time reducing the rate of mass transfer per unit area. Higher initial concentrations of hydrogen sulfide generally resulted in larger (K_AB) values, reflecting a stronger driving mechanism for mass transfer at the start of the sorption process. Similarly, (N_o) increased with concentration, demonstrating the ability of the adsorbent material to accommodate greater contaminant loads under higher input levels.

Overall, the results confirm the suitability of Adams’s model in assessing the kinetic behavior of the fixed-bed column, providing valuable insights into the adsorbent’s performance and its optimization for hydrogen sulfide removal. These findings emphasize the influence of operational variables, like bed height and influent concentration, on the adsorption efficiency. The Adams–Bohart model is often used for adsorption in fixed-bed systems and considers mass transfer limitations. Thus, the experimental data did not align well with this model, and it suggests that mass transfer resistance may not be the dominant factor in the adsorption process.

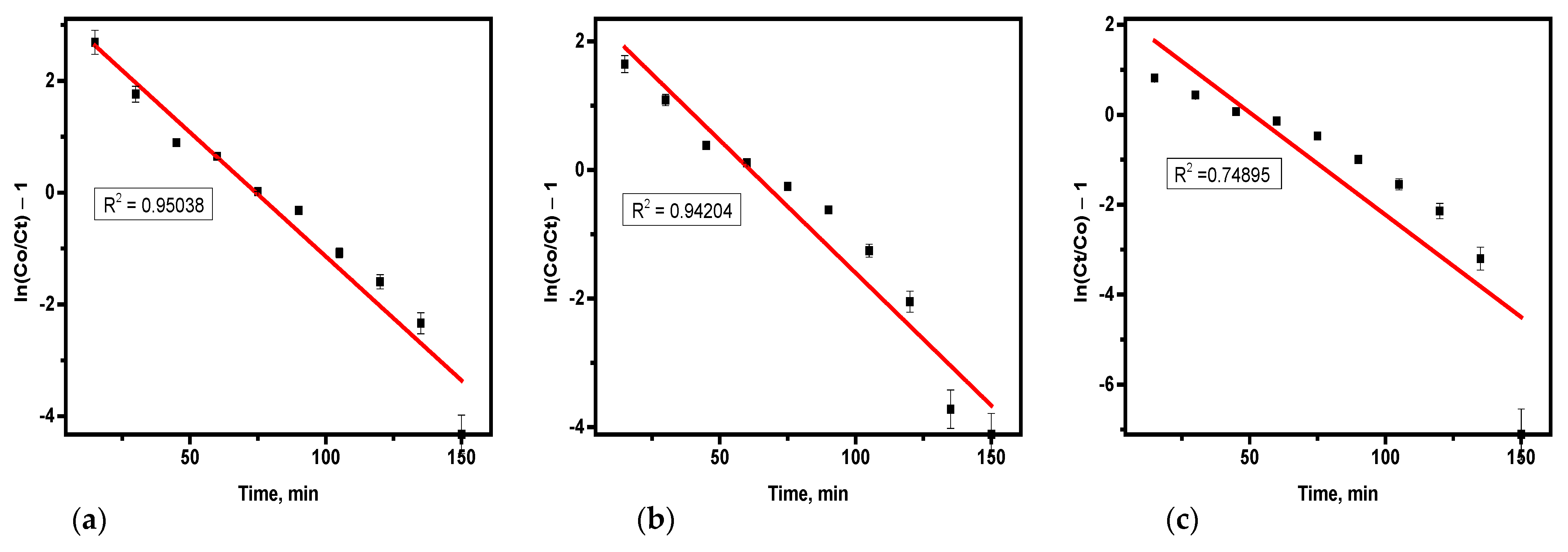
3.4.2. Thomas Model

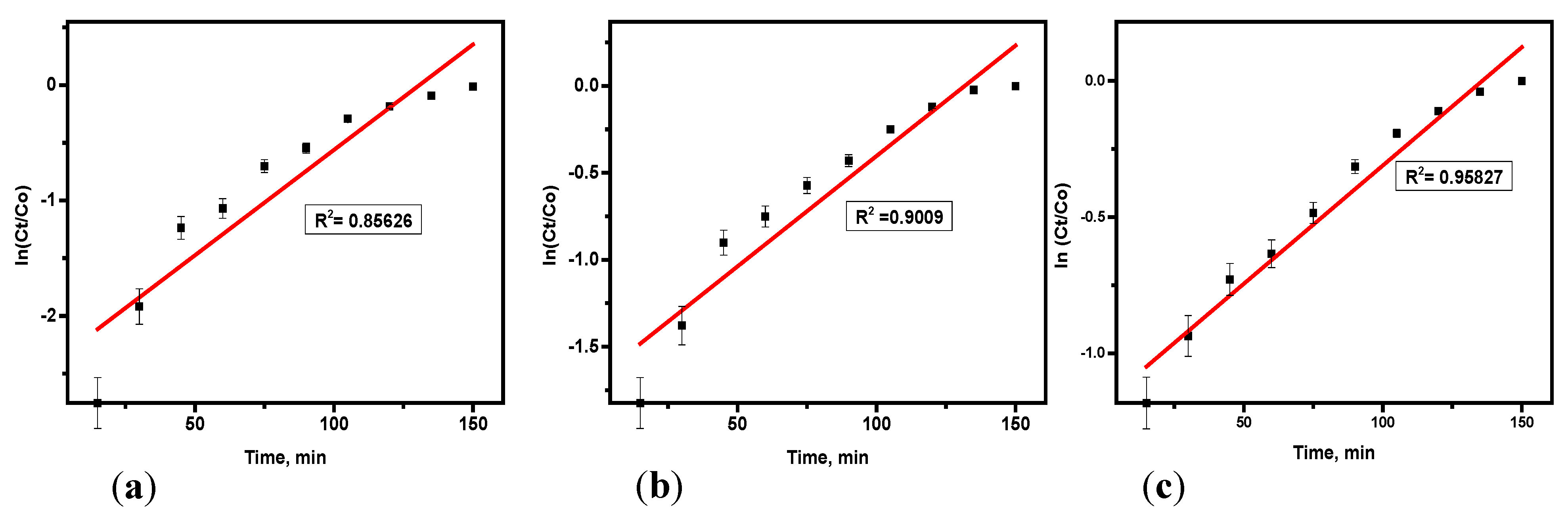
The model was used to fit the data from the experiments, with coefficients and related constants determined through linear regression analysis. Table 6 summarizes the results and was derived from Figure 7. The Thomas model exhibited R² values ranging from 0.95038 to 0.74895. Table 6 reveals that as bed depth increased, the k_Th values decreased, whereas higher flow rates and concentrations resulted in increased values for both k_TH and q_o [20]. The data from the experiment showed that as there is an increased bed height from 4 cm (Figure 7c)–10 cm (Figure 7a), q_o, k_TH decreased, consistent with findings in the literature [21]. This characteristic was contributed by the kinetics of adsorption influenced by concentration gradients. Thus, higher influent concentration, greater bed depth, and lower flow rate enhanced the sorption of hydrogen sulfide adsorption from biogas in the fixed column. The data from the experiment for the H₂S elimination aligned well with the Thomas model, with coefficients ranging from 0.74 to 0.95. The Thomas model assumes Langmuir kinetics and negligible axial dispersion, making it widely applicable in fixed-bed adsorption systems. The experimental data for hydrogen sulfide removal from biogas deviated from this model; it indicates that the adsorption mechanism does not strictly follow Langmuir isotherm assumptions and some external factors such as flow dynamics have influenced the adsorption performance of the soda ash sorbent. The terms C_o is the initial concentration, C_t is the concentration at time t, q_o is the equilibrium adsorption capacity and q_t is the adsorption capacity at time t.

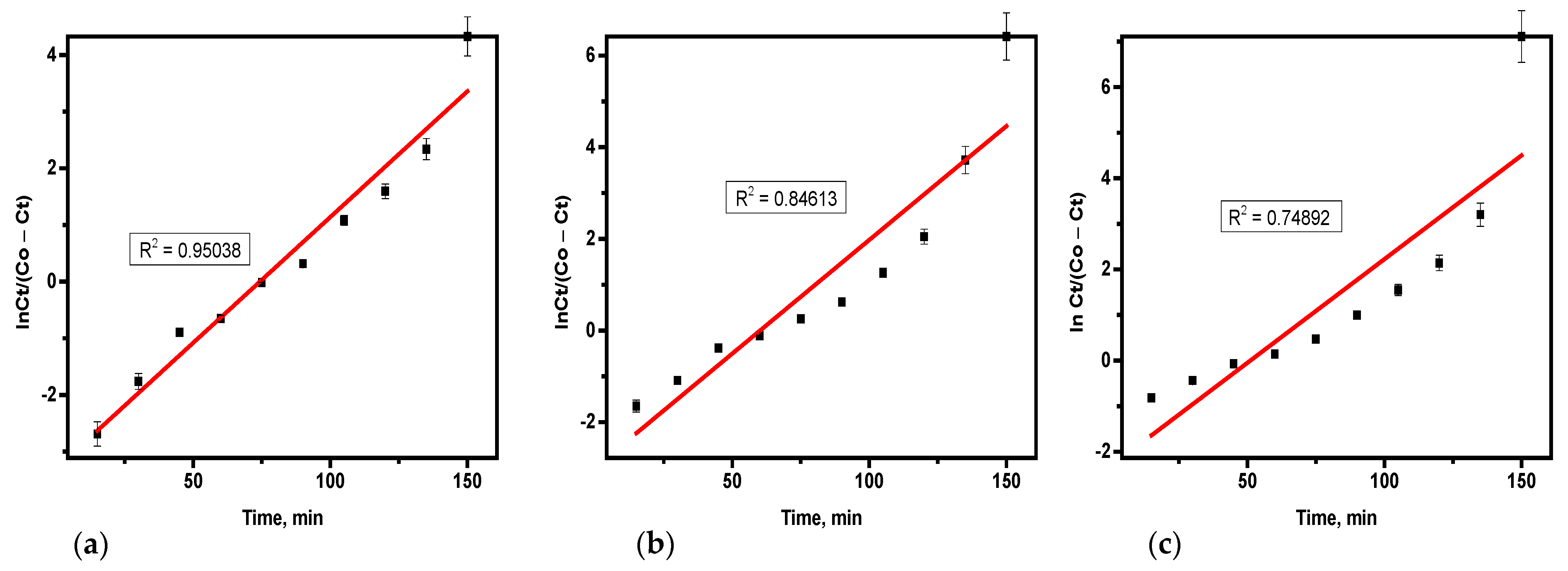
3.4.3. Yoon–Nelson Model

Variables such as ɽ (the time needed for 50% hydrogen sulfide breakthrough) and the rate constant (k_YN) were determined from the plot using the slope and intercept as illustrated in Table 6 and derived from Figure 8a–c. The values of k_YN increased as the flow rate and bed height decreased, while ɽ decreased as concentration increased and bed height. The rise in ɽ with higher flow rates suggests that a slower consumption rate of the adsorbent bed occurs, which is beneficial for the adsorption. The ɽ value indicates the time at which 50% of the adsorbent material in the column reaches the breakthrough point, with higher ɽ values reflecting improved column performance. Similar findings have been reported in the literature [21,22]. The Yoon–Nelson model is simpler than the Thomas model and only requires two parameters time required for 50% breakthrough (τ) and rate constant (k_YN). Its good fit suggests that the adsorption follows a predictable breakthrough behavior with a symmetrical adsorption and desorption process. This model’s consistency with the data indicates that breakthrough time prediction was accurate, and adsorption kinetics were stable under the given experimental conditions.

Therefore, the effect of the mass of the adsorbent on hydrogen sulfide elimination was evaluated via adsorbent quantities of 75 g, 50 g, and 25 g. Using the Adam-Bohart model, as the mass of soda ash increased, it resulted in a higher value of K_AB and a lower N_o value. Similarly, in the Thomas model, increasing the adsorbent mass led to a reduction in both K_TH and q_o. For the Yoon–Nelson model, a higher mass of adsorbent caused decreases in both K_YN and ɽ.

3.5. Study Limitations and Outlook

The study focused solely on soda ash as the adsorbent, which may limit the generalizability of the findings to other potential adsorbents with varying properties and efficiencies. Meanwhile, the range of particle sizes tested was narrow, and smaller or more varied particle sizes might provide additional insights into optimizing performance. The effect of external factors like temperature, pressure, and humidity on the adsorption efficiency was not extensively studied. The study recommended that investigating other adsorbents with higher adsorption capacities, better regeneration potential, or lower costs could enhance the efficiency and economic viability of the process. Similarly, comprehensive cost–benefit analyses and life cycle assessments should be conducted to ensure the long-term practicability of the process. These adsorption models can be applied in future reactor design and cost estimation for large-scale biogas purification systems through optimizing adsorbent usage. The best-fit model (Yoon–Nelson) can help predict breakthrough times, ensuring efficient adsorbent replacement schedules and model parameters can be extrapolated to design larger fixed-bed reactors with accurate residence times and adsorption capacities. Meanwhile, the Thomas and Adam–Bohart models can assist in understanding mass transfer limitations, guiding improvements in bed height, flow rate, and particle size for better performance. Additionally, models like Yoon–Nelson predict when a breakthrough occurs, helping estimate the frequency and cost of adsorbent replacement. Pressure drop refers to the decrease in pressure experienced by gas as it flows through a packed bed of solid adsorbent particles. This is caused by friction between the gas and the adsorbent particles as it moves through the bed. Generally, smaller particles result in higher pressure drop due to increased surface area for interaction with the gas. If we could be able to measure pressure drop, we could inform energy requirements for biogas flow through the reactor, contributing to operational cost estimates. The adsorption models, combined with cost data like adsorbent price, regeneration costs, and biogas flow rate, can help determine the cost-effectiveness of different adsorption setups before large-scale implementation. Thus, we recommend further studies to consider pressure drop in the bed reactor for a more accurate estimation of energy efficiency.

4. Conclusions

Soda ash sorbent was successfully used in the elimination of H₂S from biogas in a fixed column during the on-site experiment. The experimental data were analyzed using adsorption isotherms, kinetic models, and breakthrough curve models to derive valuable design parameters for scaling up. In this study, the 1/n value for H₂S removal was found to be 0.4, with R² of 0.87 while in the Jovanovich model, the sorption capacity is 6.42 mg/g for H₂S removal with a coefficient of 0.997. The results show that Freundlich and Jovanovich’s isotherm fits the onsite data. For the kinetics of adsorption, the values of R² from intra-particle diffusion were closer to unity than other models, indicating the mechanism for hydrogen sulfide diffusion from biogas with K_id and value of 0.14 and R² of 0.972. For the Yoon–Nelson model, a higher mass of adsorbent caused decreases in both K_YN and ɽ, thus it fits well with the on-site data with an R² of 0.9504. The extracted column parameters are useful for the design of effective biogas desulphurization systems especially for household and community use in resource-constrained areas.