Abstract
In this study, natural rubber (NR)/polybutadiene rubber (PB) blend-based composites were prepared using graphene as a partial replacement for carbon black (CB) in different parts per hundred rubber (phr) percentages. In a previous study, the vulcanization characteristics, viscoelastic behavior, and static mechanical properties were reported, and the compound labeled as compound 2 (with 2.5 phr of graphene and 52.5 phr of carbon black) showed optimum properties. Herein, we report the dynamic mechanical properties and the transport properties of the formulations to establish further characterization of the compounds. Three different organic solvents comprising benzene, toluene, and xylene were employed to analyze the sorption characteristics. The obtained data were also modeled with different theoretical predictions. The dynamic mechanical properties showed that certain compounds can be considered to be green tire formulations, as there were appreciable changes in the tanδ values at different temperatures (−25 °C to 60 °C). The thermogravimetric analysis showed that compound 2, with 2.5 phr of graphene, has a higher t50 value among the studied formulations, which indicates higher thermal stability than the base compound. The partial replacement of 2.5 phr of graphene in place of carbon black (total 55 phr) led to appreciable improvements in terms of thermal stability, transport properties, and dynamic mechanical properties.
1. Introduction
The tire industry is evolving due to advancements in formulations and the development of newer or hybrid fillers. Tire formulations are undergoing continuous developments to improve tire durability, safety, greater wet grip, lower fuel consumption, lower emission of greenhouse gases, negligible environmental risks, etc. [1]. Natural rubber (NR)/polybutadiene rubber (BR)-based blends and composites are used extensively for tire formulations [2]. Carbon black (CB) is an integral part of such formulations and there have been many studies related to the distribution of CB and tire property enhancement in recent years [3]. The effect of different types of carbon black on the properties of 60/40 NR/BR blends has been reported and the authors could obtain significant results for viscosity, bound rubber, resilience, heat build-up, tear strength, and dynamic properties [4].
Recently, attempts have been made to replace carbon black in tire formulations with nanofillers of different types, and improvements in various properties were reported [5,6,7,8]. The partial replacement of carbon black with graphene in rubber compounds, particularly for tire applications, has been the subject of research due to graphene’s superior properties, such as a fracture strength of 130 GPa, a Young’s modulus value of 1 TPa, and a low density of 1 g/cm3 [9,10]. Graphene can offer several advantages over carbon black when used in rubber and polymer formulations due to its inherent properties [11,12]. Graphene is highly conductive compared to carbon black, which means that it can reach percolation at lower concentrations, thereby being beneficial for applications requiring static charge dissipation and temperature management [13,14]. Due to its having much stronger mechanical properties, graphene can impart improved mechanical properties to the rubber formulation, especially regarding tensile strength and tear strength [15,16]. The flexibility of rubber formulations with graphene is higher than in those with carbon black [17,18,19]. Another important aspect of rubber formulations with graphene is that it can impart sensing properties and communication facilities, due to the high conductivity of the filler material [20,21]. For tires, temperature control is crucial and the thermal conductivity of graphene is advantageous for thermal management and the safer use of vehicles [22,23,24]. These advantages have encouraged many researchers to partially replace carbon black with graphene and study the technological and performance-related properties of these rubber formulations recently [9,16,25,26,27,28]. While graphene does present the advantages mentioned above, it is also important to note that it is currently more expensive than carbon black, especially in dissipative applications [29]. However, the potential improvements in material properties and performance can justify the cost in applications related to the safety, durability, and longevity of products.
Chitin nanofibers were used to replace carbon black in natural rubber formulations at up to 5 phr, keeping the carbon black loading constant (50 phr) [30]. The addition of 1 phr of nanofibers showed 47 and 160% improvement in tensile and tear strength, along with good rolling resistance (50% less) compared to formulation with carbon black alone. Shiva et al. studied a series of formulations with varying loadings in a hybrid filler system of highly dispersible silica, alumina, and organoclay in SBR (85)/BR(15), keeping the carbon black content at 53 phr [31]. The thermal conductivity coefficient improved appreciably, which can help faster curing with sulfur. The formulations also showed improved crack growth and weak abrasion behavior. Another interesting study replacing carbon black in tire formulations with nano cellulose obtained from rice husk has been reported recently [32]. Here, the total weight percentage of carbon black and nanocellulose was kept at 30, and various loadings of nanocellulose were used to make the compounds. The composites with 5 wt% of nanocellulose showed low rolling resistance, as evidenced by loss tangent measurements. The tan delta values at 60 °C became 0.06 from 0.2 for those composites having 5 wt% of nanocellulose and 25 wt% of carbon black. Silane coupling agent-treated aramid nanofiber was used recently along with carbon black to develop tire tread formulations [33]. The rolling resistance measured by tan delta at 60 °C showed a decrease from 0.116 to 0.099, and an increase of 11.3% in the abrasion resistance index was shown for a formulation with 1 phr of aramid nanofibers compared to the base formulation. In another study, CB was partially replaced by three different types of lignin, in the loading range of 5–20 phr, in NR/BR composites [34]. The incorporation of lignin up to 10 phr showed similar results to NR/BR/CB50 without lignin, as well as improvement in the aging and thermal properties. Dynamic mechanical analysis (DMA), transmission electron microscopy (TEM), and solid-state NMR were utilized to establish the distribution of CB in different phases. It was concluded that irrespective of the blend formulations, CB is more partitioned to the minor phase, that is, BR. In another study, octa vinyl-polyhedral oligomeric silsesquioxane (OV-POSS) was used as a compatibilizer for NR/BR blends [35]. DMA and contact angle studies indicated that the nanoparticles were located at the interface of the elastomers and contributed to improvements in the properties up to a certain loading. Precipitated silica/PCNSL modified kaolin hybrid filler has been used in NR/BR blends and improvements in properties such as tensile, tear strength and flex fatigue resistance were reported [36]. The lower heat build-up in composites is considered to be useful for tire applications. NR/BR composites were recently investigated by replacing a CB content of 50 phr to 25 phr, with the addition of 25 phr of nano silica, and improved mechanical, rheological, and hardness properties were reported [37]. Lan et al. used reclaimed rubber as a replacement for CB in NR/BR composites and the dynamic mechanical and flexing fatigue resistance were investigated [38]. The addition of reclaimed rubber showed improved dynamic mechanical properties and flexing fatigue resistance.
Solvent diffusion through rubber and rubber-based blends is critical to understanding the material’s permeation properties so that useful applications can be proposed. There is a large number of reports on this topic in the literature. Kaliyathan et al. recently investigated the effect of CB on the diffusion properties of NR/BR blends [39]. The experimental data were also validated with various theoretical models. The partial replacement of carbon black in NR/BR formulations with carbon nanotubes was researched by Poikelispaa et al. [7]. They studied the swelling and dynamic mechanical properties of the resulting composites and correlated the results with better filler matrix interactions, as well as the formation of regular crosslinks. The partial replacement of CB with graphene, based on a fixed phr of CB and replacing the filler, was performed previously by our research group [40]. The processability and mechanical properties were investigated and reported systematically. The compounds showed improved processability and static mechanical properties. It was one of the most novel studies in the literature of partially replacing carbon black with graphene and systematically studying the processing characteristics. In order to establish the performance of the tires, dynamic mechanical properties at different temperatures are recommended. Determination of the thermal stability of the compounds is important to understand the effect of graphene replacement in rubber formulations. Sorption through organic solvents is crucial to proposing applications of the products in different fields. The present work shows the effect of the partial replacement of CB with graphene on the dynamic mechanical and transport properties and thermal stability behavior of the NR/BR nanocomposites.
2. Experimental
2.1. Materials and Compound Formulations
The natural rubber (NR) used in the investigation was SMR CV60 with Mooney-viscosity ML (1 + 4, 100 °C) of 60 and polybutadiene rubber (BR) with a high cis-content grade (greater than 94%) (KBR 01). Elastomers, compounding ingredients and analytical grade solvents were purchased from local suppliers. Functionalized graphene (SDP 500) was donated by Perpetuus Advanced Materials, UK. Graphene (SDP 500) was characterized by scanning electron microscopy and the presence of oxygen on the surface was established through EDS analysis. Raman spectroscopy measurements revealed that the graphene used was multilayered and had defects on the surface [40]. An elastomer compound with 55 phr of carbon black loading was selected and only 5 phr of this carbon black was replaced with graphene in various ratios (1 phr, 2.5 phr, and 5 phr), keeping the overall filler loading at 55 phr. The details about the formulation and the compound preparation procedure are available in our previous publication [40]. Briefly, a two-stage process was followed for the preparation of compounds, as per their respective formulations. The first step was to prepare a master batch without curatives. An internal mixer (2.2 L, Comerio Ercole, Busto Arsizio (VA), Italy) was used for this operation. Mixing was carried out at a rotor speed of 80 rpm and the temperature was maintained at 75 °C. The second stage of compounding was carried out in a laboratory two-roll mill (Comerio Ercole, Busto Arsizio (VA), Italy) at room temperature, where curatives such as sulfur and accelerators were incorporated into the master batch obtained from the first stage. The compound was completely homogenized and sheets of approximately 5 mm in thickness were prepared. The compounds were compression-molded at a temperature of 150 °C for 60 min to prepare vulcanized sheets of 2 mm in thickness. The samples for various tests were punched out from these sheets.
2.2. Transport Characteristics
Swelling Studies
Swelling studies were performed according to ISO 1817: 2024. Approximately 1 g of the vulcanizates with dimensions of 30 × 5 × 2 mm3 were immersed in 75 mL of toluene at 25 °C for 72 h. The swollen samples were taken out and the excess toluene on the surfaces was removed, using a filter paper with light contact pressure, and immediately weighed. The samples were dried in a vacuum oven at 70 °C until a constant mass was obtained. The percentage increase in the mass of the samples was calculated using the equation:
where:
- m0 = initial mass of the vulcanizate samples
- m1 = mass of the swollen samples.
The crosslink density (Vc) calculations were performed using the Flory–Rehner equation [41,42], as given below:
where:
- Vr = volume fraction of swollen rubber
- m1 = mass of the swollen sample
- m2 = final dried mass of the sample
- mf = mass of filler
- ρp = density of the polymer
- ρs = density of solvent toluene (0.866 g/cm3)
- Mc = molecular weight between crosslinks
- Vs = molar volume of toluene (106.4 cm3/mol)
- χ = interaction parameter between the polymer and the solvent (0.382 for the NR/BR blend at a ratio of 80:20 [43,44]).
2.3. Equilibrium Sorption Experiments
Equilibrium sorption studies of the composites were carried out using benzene, toluene, and xylene as solvents. The three solvents selected differ only in the substituent and the number of methyl groups, and, thereby, the molecular weight. Due to the non-polar nature of the molecules, the three selected solvents are highly hydrophobic in nature. All these three solvents are immiscible in water and their solubility in water at 25 °C is 0.24, 0.2, and 0.18 g/L, respectively [45]. Although the molecular weights of the solvents are different, their viscosity at 25 °C is comparable (0.603, 0.59, and 0.58 mPa.s, respectively) [46]. The purity of the solvents was 99% or more, according to the data given by the manufacturers. The chemical compatibility of the solvents with elastomer compounds varies with the type of elastomers, concentration, and temperature [47]. The sorption measurements were conducted using a fixed concentration of solvents and temperature (25 °C). Rectangular samples were punched out of the vulcanizate sheets with dimensions of 20 × 20 × 2 mm3. The initial weight of the samples was noted. The samples were completely immersed in the solvents in separate glass diffusion bottles kept at a uniform temperature of 25 °C. The samples were carefully withdrawn from the diffusion bottles at specific time intervals and the excess solvent on the surface of the samples was removed using filter paper, after which they were quickly weighed. The samples were returned to the respective diffusion bottles and continued until equilibrium (in terms of swollen weight) was reached. At each time interval t during the experiment, the mole percentage uptake Qt for the solvents was calculated using the following equation [48]:
where Mt is the mass of the sample at any time t during the experiment, M0 is the initial mass of the sample taken, and MW is the molecular weight of the solvent used for the experiment. The sorption isotherms were then plotted with the mol percentage uptake of the solvent against time.
2.4. Dynamic Mechanical Properties
Dynamic mechanical analysis (DMA) of the compounds was carried out using Q800 DMA (TA Instruments, New Castle, DE, USA) with rectangular specimens (35 × 12 × 2 mm). The analysis was performed in dual cantilever mode with a temperature range from −60 to +60 °C, with a heating rate of 2 °C/min. A sinusoidal strain with a frequency of 1 Hz and an amplitude of 50 µm was applied to each specimen, and the loss modulus (E″), storage modulus (E′), and tanδ (ratio of E″ to E′) values were obtained.
2.5. Thermogravimetric Analysis (TGA)
Thermogravimetric analysis of the elastomer compounds was performed using a simultaneous thermogravimetric analyzer (STA 7200, Hitachi, Tokyo, Japan). The analysis was performed under a nitrogen atmosphere (50 mL/min) from ambient temperature to 750 °C, with a heating rate of 10 °C /min. The weight of the samples was continuously monitored throughout the entire temperature range and the thermograms were plotted from these data. The derivative thermograms (DTG) for the compounds were also plotted against the corresponding temperatures.
3. Results and Discussion
3.1. Swelling Studies
The calculated values for cross-link density and the molecular weight between crosslinks, according to the Flory–Rehner equations, are graphically shown in Figure 1. The swelling experiments generally yielded the cross-link density value, which had contributions from chemical crosslinks, physical entanglements, and polymer-filler interactions [49]. The cross-link density values exhibited a linear increasing trend with an increase in the replacement of carbon black with graphene, which indicates that the introduction of graphene into the compound resulted in the formation of more crosslinks and chain entanglements. Conversely, the molecular weight between cross-links (Mc) decreased with an increase in graphene content in the compounds on the expected line. Mc refers to the average molecular weight of polymer chains between two consecutive junctions. The junctions are also formed as a result of chemical cross-links, physical entanglements, and polymer-filler networks. Similar results were reported recently for an NR/BR system with expanded graphite incorporation [50]. Another report of NR/BR blends reinforced with a hybrid filler of kaolin silica also showed similar results related to chemical crosslink density [36]. The graphene used in the present study is functionalized so that different functional groups are present on the surface of the material. These functional groups can cause property enhancements; one indirect method to understand the effect of the functional groups is to monitor the crosslink density of the samples as a function of the increase in graphene content in the samples. The change in sorption behavior is correlated to the crosslink formation in elastomer compounds, which is greatly affected by the filler–filler and filler–polymer interactions through the various functional groups. The increase in cross-link density of the compounds containing graphene (compounds 1, 2, and 3) can be correlated with excess functional groups on the surface of the fillers.
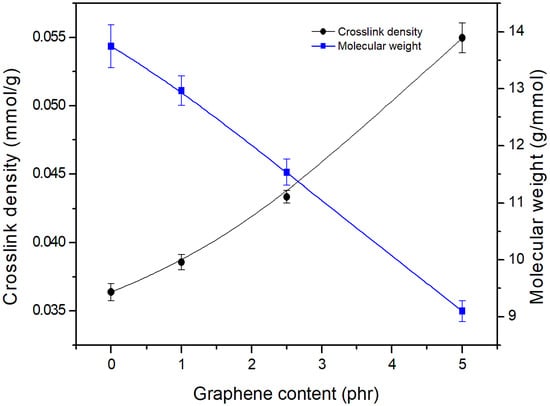
Figure 1.
Crosslink density and molecular weight between crosslinks (Mc) vs. graphene content.
3.2. Sorption Characteristics
The sorption curves are shown in Figure 2. Here, the moles of the solvent sorbed per 100 g of rubber, Qt, is plotted against the square root of time. The sorption curves generally exhibit two distinct regions, the initial steep curve and the equilibrium region. Initially, due to the large concentration gradient, the solvent uptake will be high, and an equilibrium will be reached with time. The equilibrium solvent uptake in mol% of the solvent against the graphene content in various elastomer compounds is plotted and shown in Figure 3. The uptake of benzene is the highest in all compounds, followed by toluene, with xylene being the least. This can be related to the increase in molecular weight from benzene to xylene. The effect of the partial replacement of carbon black with graphene (SDP 500) on the sorption behavior of the three different solvents is similar, as seen in Figure 3. Compound 0 has a higher solvent uptake than compound 1 and compound 2 for all three solvents. When 1 phr of graphene is added, the solvent uptake decreases, and, on further increase in graphene to 2.5 phr, the solvent uptake shows a further decrease. This decrease can be attributed to the better dispersion of the fillers, graphene, and carbon black in the vulcanized systems. The graphene added to the system develops a tortuous path for the organic solvents to pass through and, thereby, the solvent uptake decreases. However, when the graphene content is increased to 5 phr, the trend reverses. This can be ascribed to filler–filler agglomeration and efficient reinforcement is not generated thereby in the elastomer compound. If there is no efficient reinforcement in the compound, easy passage of the solvents will be achieved and the equilibrium solvent uptake will be more or less equal to the compound, without any partial replacement. Thus, the optimum partial replacement is at and around 2 to 3 phr of graphene in place of carbon back, while keeping the total amount of carbon materials at 55 phr. Similar results were obtained for static mechanical properties, rolling resistance, and hardness.
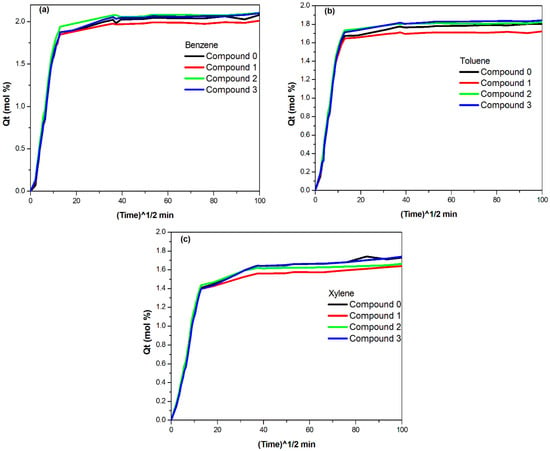
Figure 2.
Sorption curves for various compounds in (a) benzene, (b) toluene, and (c) xylene.
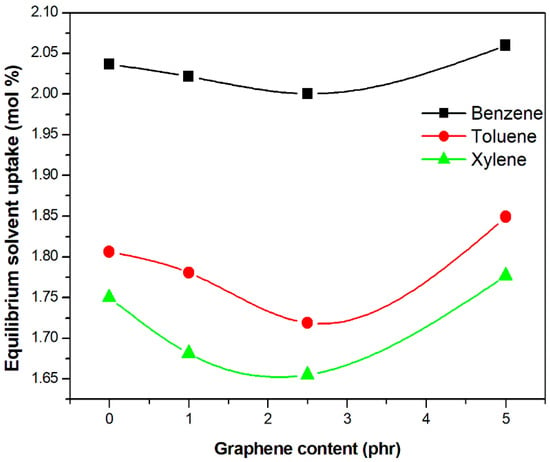
Figure 3.
Equilibrium solvent uptake vs. graphene content in the elastomer composites.
The diffusivity (D), sorption coefficient (S), and permeability (P) of the solvents through the samples were calculated using the following equations [51,52] and are summarized in Table 1:
where:

Table 1.
Transport coefficients of the various compounds.
- h = thickness of the specimen
- θ = slope of the initial linear portion of sorption curves
- Q∞ = equilibrium solvent uptake
- M∞ = mass of solvent uptake at equilibrium
- M0 = initial mass of the sample
- D = diffusivity
- S = solubility.
The following equation is used to understand the sorption mechanism, and data obtained from the equilibrium sorption experiments were fitted to this equation:
where Qt is the mol percentage uptake of solvent at time t, Q∞ is the mol percentage uptake at equilibrium, k is a constant indicating the interaction between the sample and the solvent, and the value of n indicates the type or mechanism of diffusion. The values of n and k are obtained from the linear portion of the plots of Qt against the square root of time (Figure 2) through regression analysis; the corresponding plots are shown in Figure 4 and the values are given in Table 2. All the n values are between 0.5 and 1, which indicates that the diffusion of benzene, toluene, and xylene through the compounds follows a non-Fickian mode of transport [39,53]. Compared to benzene, the values of n for toluene and xylene are lower, which may be due to the increase in molecular weight of the solvents. However, there is not much difference in the values of n for toluene and xylene [54].
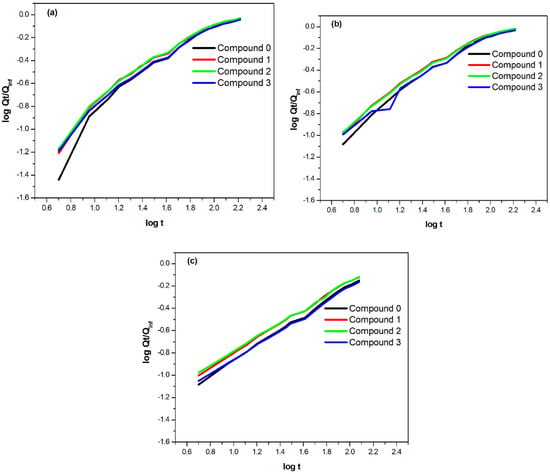
Figure 4.
Plots of log Qt/Q∞ against log t for (a) samples in benzene, (b) samples in toluene, and (c) samples in xylene.

Table 2.
Sorption parameters obtained from Equation (9).
To understand the mode of transport through these filled elastomer composites, four different mathematical models were utilized. These are the first-order kinetic equation, Higuchi model, Korsemayer–Peppas model, and Peppas–Sahlin model. The first-order kinetic equation is represented by the following equation:
where Qt is the mol percentage uptake of solvent at time t, Q∞ is the mol percentage uptake at equilibrium, and k is the first-order rate constant.
The Higuchi model equation given below (11) is based on a hypothesis that: (i) the diffusion is a one-dimensional process, (ii) the size of the diffusing species is extremely smaller compared with the size of the matrix through which diffusion takes place, (iii) diffusivity is considered as a constant, and (iv) the swelling of the matrix and the diffusion are also considered as constants [55].
Here, kh is the Higuchi dissolution constant. The Higuchi model equation was applied to the linear portion of the sorption curves given in Figure 2, while representative curves for compound 2 in benzene, toluene, and xylene are shown in Figure 5, and the corresponding values for the kinetic constants and the correlation factor are given in Table 3. The major factors affecting the sorption are the molecular weight of the solvents and swelling with the dissolution of the polymer matrix. Fickian diffusion is observed when the permeate mobility is overtaken by the relaxation rate. From Table 3, the Kh value, which is the Higuchi dissolution constant for compound 0, is 0.07265 for benzene, 0.07684 for toluene, and 0.06174 for xylene, respectively. The Kh values increased for compound 1 and compound 2 for all three solvents and they decreased for compound 3, which indicates the good synergetic dispersion of graphene and carbon black in the rubber matrix. Similar results are also reported for other systems [56,57]. Moreover, the mechanical properties of the composites also showed similar behavior.
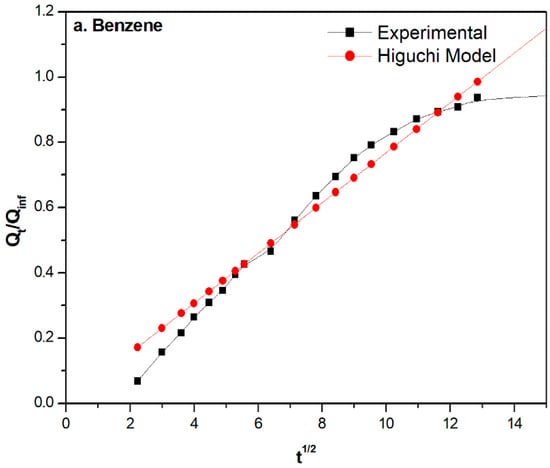
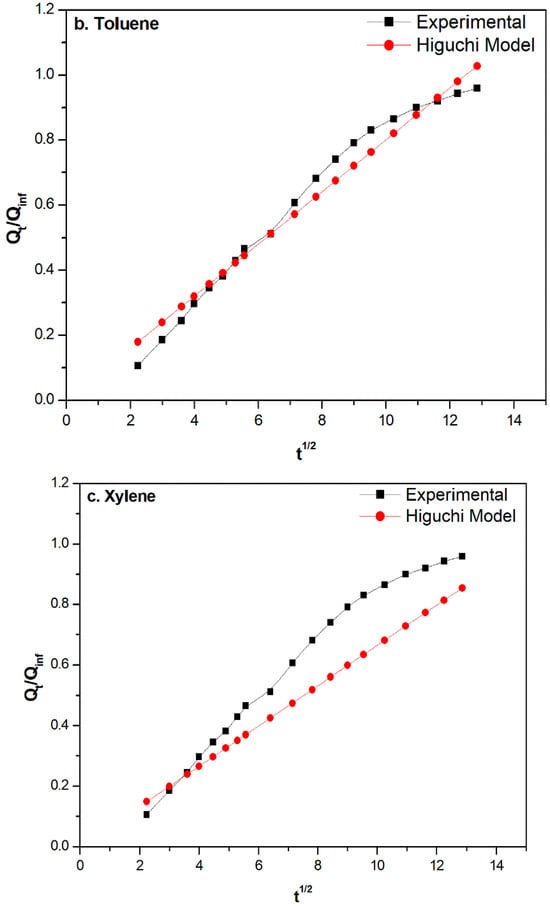
Figure 5.
Higuchi model applied to the linear portion of experimental data for compound 2 in (a) benzene, (b) toluene, and (c) xylene.

Table 3.
Constants and correlation coefficients from various mathematical models.
The first-order kinetic equation in its exponential form:
displays the relationship between t and the ratio Qt/Q∞ as asymptotic. As t increases, the ratio Qt/Q∞ approaches zero, whereas the experimental Qt/Q∞ increases with t initially and approaches saturation. The Higuchi model and the first-order kinetic equation have another common drawback, that of having just one constant k. As a result, there is a shortcoming in finding the best k that restores the ratio Qt/Q∞ in agreement with the experimental Qt/Q∞. Owing to this drawback, only the initial straight-line region in the time values is chosen for plotting.
This drawback is not found in the Korsemeyer–Peppas model and the Sahlin–Peppas model equations, as the former has two constants (k and m) and the latter has 3 constants (k1, k2, and m). As a result, the entire time values from beginning to saturation have been included in plotting for the Korsemeyer–Peppas and Sahlin–Peppas models.
The Korsemeyer–Peppas model [58] is given by the following exponential equation:
where k is the kinetic constant and the exponent n indicates the mechanism of transport.
The Peppas–Sahlin equation is based on the assumption that the transport properties of solvent through a matrix have both diffusional and relaxational components, which are generally additive in nature [59], and the model is given by Equation (14) [60], below:
where Mt and M∞ are the mass of solvent uptake at time t and equilibrium, respectively. The Fickian contribution (diffusion) for the solvent transport is given by the first term on the right-hand side of Equation (14), whereas the second term indicates the relaxation contribution of polymer chains and m is the Fickian diffusion exponent. The literature shows that if k1 > k2, then the transport mechanism is predominantly a diffusion-controlled one, and if k1 < k2, then it is a matrix-controlled one, and, if k1 = k2, then a combination of diffusion and matrix-controlled mechanisms is responsible for the transport of solvent through the matrix [55,61]. The Korsemeyer–Peppas model and the Peppas–Sahlin equation are applied to the entire sorption data, and the representative curves for compound 2 are shown in Figure 6a–c. In the Peppas–Sahlin model shown in Figure 6, the first term in the equation will always remain positive, as k1 tends to be positive for all t values. However, k2 and m tend to be negative. The first term in the equation remains positive since k1 is positive. However, the second term becomes more negative than the first term, making the whole result negative for low values of t. This is why the initial values of the Sahlin model are shown as negative values in Figure 6. Similar behavior has been reported in the literature [55]. The constants obtained from these two kinetic models and their respective correlation coefficients are given in Table 3. As can be seen from the figure, the Peppas–Sahlin model fits very well with the experimental data. The model considers both Fickian and case II relaxation processes. As per the prediction, the k1 values are higher than k2 for all compositions, as well as for the three solvents. There are slight changes in the k1 and k2 values for the different compositions. The values lead to the conclusion that the transport mechanism for the different organic solvents is diffusion-controlled, which is related to the chemical potential gradient [55]. Also, the large value of n for the Korsemeyer–Peppas model indicates that the swelling of the rubber matrix is important for the transport of the organic solvents [57,62].
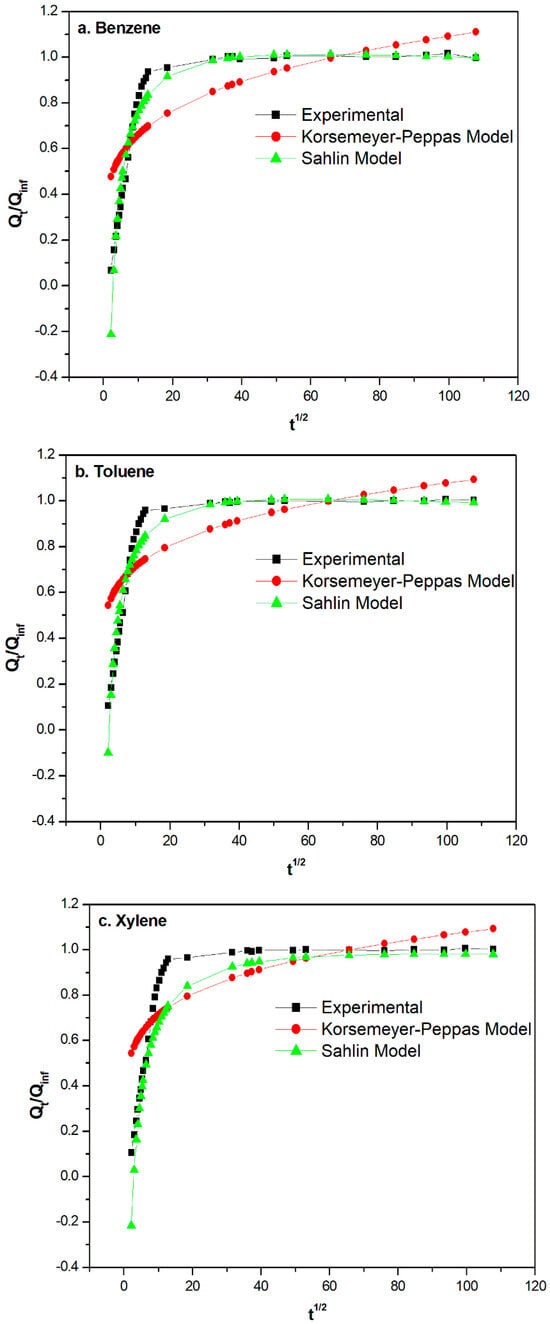
Figure 6.
The Korsemeyer–Peppas model and Peppas–Sahlin equation applied to the experimental data for compound 2 in (a) benzene, (b) toluene, and (c) xylene.
3.3. Dynamic Mechanical Analysis (DMA)
Viscoelastic properties are valuable tools to assess the suitability of a filled elastomer compound for load-bearing applications such as tire treads. The storage modulus and loss tangent values of the compounds obtained from DMA are plotted against temperature and are shown in Figure 7. The storage modulus shows a drastic decrease for the different elastomer compounds of around −50 °C, which can be correlated with the glass transition region for the compounds. The behaviors of the storage modulus for compounds 1 and 2 are different from those of compound 0 and compound 3. Compounds 1 and 2 show higher storage moduli than the other two compounds, indicating better filler–polymer interactions at low temperatures. The storage modulus is constant after the glass transition temperature for all compounds except for compound 2. Compound 2 exhibits different behavior compared to the other three formulations as it shows higher storage modulus values in the product utilization region. These values were reconfirmed by repeated analyses and can be attributed to better reinforcement happening due to the partial replacement of carbon black with graphene. This result also corroborates the static mechanical results.
Figure 7.
(a) The storage modulus against temperature curves and (b) tan delta against temperature curves.
It can be observed that the height of the tanδ peak for compound 2 is comparatively lower than for the other compounds. The restrictions on the mobilization of polymer chains due to the uniform distribution of nanophases of graphene can be ascribed to this reduction. This effective interaction between the filler and the polymer chains leads to the improved physical and chemical adsorption of polymer chain segments on the filler surfaces, leading to a reduction in the tanδ peak height during dynamic mechanical deformations [59]. The incorporation of a hybrid filler in a polymer matrix leads to the formation of a constrained region. It quantifies the elastomer chains immobilized by the hybrid fillers. The constrained region can be determined mathematically from the tanδ peak values using Equations (15)–(17) [3,63,64,65].
For the linear viscoelastic region, the energy loss factor W can be determined as:
where tanδ is the dissipation factor. The volume of the constrained region Cv can be determined from the dynamic viscoelastic region by using the following equation:
where W0 is the energy loss factor and C0 is the volume fraction of the constrained region of the base matrix. As the base matrix does not contain the hybrid filler system, C0 can be considered to be zero. The volume of the constrained region Cv then takes the form of Equation (17), as given below.
The calculated values for the volume of the constrained region Cv for the hybrid composites (compounds 1, 2, and 3) are given in Table 4. The volume of the constrained region increased from 0.0042 to 0.1829 for compound 2 when compared to compound 1. Then, it showed a decrease. Compound 3 has more graphene compared to compounds 1 and 2, which may lead to more and more filler–filler interaction, forming filler networks. This attribute may be influencing the mobility of the rubber chains more and decreasing the constrained region’s volume in compound 3. Similar results were reported recently in graphene/nano-silica hybrid-filled natural rubber composites [63].

Table 4.
Volume of the constrained region and degree of entanglement values for compounds.
The degree of entanglement (N) plays a major role in deciding the rubber-filler interaction and thereby influences the performance properties of the resulting hybrid composites. The values of N can be mathematically calculated from the storage modulus (E′) at the rubbery region (corresponding to 0 °C) using Equation (18) [63,66]:
where R is the universal gas constant and T is the absolute temperature (K). The calculated values of N are given in Table 4. The incorporation of graphene into the elastomer composites can lead to an increase in the degree of entanglements, as indicated by the higher values of N for compounds 1, 2, and 3. Compound 2 shows the highest value of N, and a further increase in the graphene content from 2.5 to 5 phr (in compound 3) results in a reduction in N, probably due to the agglomeration of the nanofillers within the elastomer matrix.
The loss tangent (tanδ) values corresponding to −20 °C, 0 °C, and +20 °C can be considered as an indication of grip and traction of tread compounds on icy, wet, and dry road surfaces, respectively [67], where tanδ values at +60 °C correlate to the rolling resistance of the tread compound [68,69]. A higher value of storage modulus (E′) at 30 °C is related to better dry handling characteristics [70]. The important parameters obtained from DMA are summarized in Table 5.

Table 5.
Parameters of the dynamic mechanical analysis.
The tanδ peak and the height of the elastomer compounds are highly useful in predicting the properties of tire formulations. From Table 5, it can be noted that the tanδ peak slightly shifted toward the lower side for the compound 2 formulation. The other two formulations showed a negligible shift compared to compound 0. Overall, the partial replacement of carbon black with graphene does not have much effect on the loss factor of the formulations. However, the storage modulus values at 30 °C show a prominent improvement for compound 2, compared to the other three formulations. Similar results were also obtained for the static mechanical properties [40]. Thus, it can be concluded that compound 2 exhibits the optimum loading of partial replacement of carbon black with graphene of these elastomer-blend compounds.
The tanδ peak height is important for assigning various properties to the tire formulations. It indicates the heat build-up in elastomer compounds. Normally, the peak height of the formulations will be lower than for the reference sample (neat) in elastomer compounds. The decrease in tanδ peak height is an indication of the hindrance that happens to the rubber chains through the filler particles. Tanδ values at 60 °C are a measure of the rolling resistance of the elastomer compounds. In the current study, compounds 1 and 3 show lower tanδ values at 60 °C than compound 0, which means that the rolling resistance is lower (lower hysteresis) than for the base material. A decrease in rolling resistance is shown by the decrease in the tanδ values at higher temperatures, which will enable fuel efficiency by reducing heat generation due to friction [71]. The compounds prepared by replacing carbon black with graphene show lower rolling resistance (~10%) than the base materials, which may lead to a 1–2% fuel consumption efficiency increase for the tires developed using these formulations [69,72,73]. The repeated destruction and reconstruction of the filler network owing to the replacement of carbon black with graphene is causing changes in tanδ values at higher temperatures [74].
The tanδ values at lower temperatures (−20 °C, 0 °C, 25 °C) are also tabulated in Table 5. It can be seen that the values for compound 2 are higher than that of the base material, compound 0. These higher values are an indication of the better grip properties of the tires on road surfaces, such as wet grip and grip on ice [69,75]. Sarkawi et al. reported that the higher tanδ at 0 °C is due to a higher degree of rubber–filler interaction in the elastomer compounds [76]. Similar results were obtained recently for natural rubber compounds with the rice-husk-derived nanocellulose replacement of carbon black [32]. In the present study, the optimum interaction is happening in compound 2, as evidenced by the tanδ values.
3.4. Thermogravimetric Analysis (TGA)
The TGA thermograms for the elastomer compounds are shown in Figure 8. From the figure, it can be seen that the incorporation of graphene as a partial replacement for carbon black in the elastomer compounds resulted in an improvement in the thermal degradation profiles of these compounds. An important parameter that can be obtained from the thermograms is t50, which is the temperature at which a 50% loss occurs for the weight of the samples. The t50 values are 436 °C, 466 °C, 468 °C, and 449 °C for compound 0, compound 1, compound 2, and compound 3, respectively. This indicates that the degradation temperature (t50) shifted to the higher side for those compounds that contain graphene as a partial replacement for carbon black, and, when its dosage reached 2.5 phr in the compound (compound 2), the t50 value showed a maximum. This agrees very well with the other results reported in this investigation. The weight loss at each thermal region is an important parameter obtained from the thermogravimetric analysis. The first derivative of the thermogravimetric curve, known as the DTG curve, shows distinct peaks corresponding to each stage of thermal degradation, which can be correlated with the degradation of individual components present in the compound. The DTG peak values are considered to be the maximum degradation temperature of these components [77]. The DTG curve for compound 0 that is included in Figure 8 shows two major peaks, one at 370 °C, which corresponds to the maximum degradation temperature of NR [78], and the other one at 447 °C, which corresponds to the maximum degradation temperature of the BR component [79] of the compound. The degradation peak temperatures, the sample weight loss at these peak temperatures, and the percentage residue remaining at 750 °C for all the compounds are summarized in Table 6. From the table, it can be seen that the incorporation of graphene in the compounds resulted in an overall decrease in weight loss corresponding to the degradation stages of NR and BR components in the blend, and the effect was more pronounced for compound 2. For compound 2, the first degradation peak shifted to a higher temperature (from 370 to 373.5 °C), with a reduction in weight loss from 29.38% to 12.80%, whereas, for the second degradation stage, the maximum degradation temperature remained almost the same for compounds 0, 1, and 2 (447 °C) and reduced to 443 °C for compound 3. The corresponding weight loss decreased from 53.51% (for compound 1) to 48.10% (for compound 3). The lowest weight loss was shown by compound 2. Hence, compound 2 can be considered to be more thermally stable compared with the thermal degradation characteristics of other compounds. The residue remaining at the end of the thermal degradation process gradually increased from compound 0 to compound 3, which indicates that the graphene present in the formulation succeeded in improving the filler–filler interactions in the compounds [80]. The increase in residue content is due to the increase in crosslink formations within the carbon black structure due to these improved filler–filler interactions [81].
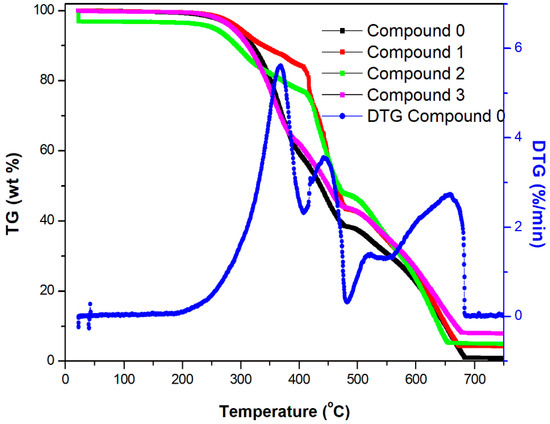
Figure 8.
Thermograms of the elastomer compounds from TGA.

Table 6.
Parameters obtained from a thermogravimetric analysis of the compounds.
4. Conclusions
The partial replacement of carbon black with graphene (SDP 500) in natural rubber/polybutadiene rubber-based formulations was studied on account of its transport properties, thermogravimetric analysis and dynamic mechanical properties. Sorption studies of the elastomer compounds were conducted with three different organic solvents, namely, benzene, toluene, and xylene. The equilibrium solvent uptake was minimal for compound 2, which had 2.5 phr of graphene incorporated in place of carbon black. Compared to the base material, compound 2 showed better properties in terms of sorption coefficient and diffusion coefficient. The sorption phenomena were theoretically modeled with different prediction models, and the Peppas–Sahlin model was fitted throughout the entire range of sorption curves. The dynamic mechanical analysis of the composites showed that compound 2 has optimal properties for the storage modulus and tan delta compared to the other formulations. The composites showed an appreciable reduction in rolling resistance from the dynamic mechanical analysis, which encourages us to propose the application of these formulations as tire treads for efficient fuel-saving products. The study also highlights the potential of achieving optimum properties through the partial replacement of carbon black with graphene, even though it is currently expensive.
Author Contributions
Conceptualization, K.P.R., A.G. and S.P.T.; methodology, K.P.R., A.G. and S.P.T.; software, K.P.R., M.R. and S.P.T.; validation, K.P.R., A.G. and S.P.T.; formal analysis, K.P.R., A.G., M.R., R.T. and S.P.T.; investigation, K.P.R., A.G. and S.P.T.; resources, K.P.R., A.G., M.R., R.T. and S.P.T.; data curation, K.P.R., A.G., M.R., R.T. and S.P.T.; writing—original draft preparation, K.P.R. and S.P.T.; writing—review and editing, K.P.R., A.G., M.R., R.T. and S.P.T.; visualization, K.P.R., A.G. and S.P.T.; supervision, K.P.R., A.G., M.R., R.T. and S.P.T.; project administration, K.P.R., A.G. and S.P.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thomas, J.; Patil, R. The Road to Sustainable Tire Materials: Current State-of-the-Art and Future Prospectives. Environ. Sci. Technol. 2023, 57, 2209–2216. [Google Scholar] [CrossRef] [PubMed]
- Railsback, H.E.; Cooper, W.T.; Stumpe, N.A. Cis-Polybutadiene-Natural Rubber Blends. Rubber Chem. Technol. 1959, 32, 308–320. [Google Scholar] [CrossRef]
- Kaliyathan, A.V.; Rane, A.V.; Huskic, M.; Kunaver, M.; Kalarikkal, N.; Rouxel, D.; Thomas, S. Carbon Black Distribution in Natural Rubber/Butadiene Rubber Blend Composites: Distribution Driven by Morphology. Compos. Sci. Technol. 2020, 200, 108484. [Google Scholar] [CrossRef]
- Hess, W.M.; Vegvari, P.C.; Swor, R.A. Carbon Black in NR/BR Blends for Truck Tires. Rubber Chem. Technol. 1985, 58, 350–382. [Google Scholar] [CrossRef]
- Polgar, L.M.; Van Essen, M.; Pucci, A.; Picchioni, F. Smart Rubbers: Synthesis and Applications; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2019; ISBN 3110639017. [Google Scholar]
- Parameswaran, S.K.; Bhattacharya, S.; Mukhopadhyay, R.; Naskar, K.; Bhowmick, A.K. Excavating the Unique Synergism of Nanofibers and Carbon Black in Natural Rubber Based Tire Tread Composition. J. Appl. Polym. Sci. 2021, 138, 49682. [Google Scholar] [CrossRef]
- Poikelispää, M.; Das, A.; Dierkes, W.; Vuorinen, J. The Effect of Partial Replacement of Carbon Black by Carbon Nanotubes on the Properties of Natural Rubber/Butadiene Rubber Compound. J. Appl. Polym. Sci. 2013, 130, 3153–3160. [Google Scholar] [CrossRef]
- Poikelispää, M.; Shakun, A.; Sarlin, E. Nanodiamond—Carbon Black Hybrid Filler System for Demanding Applications of Natural Rubber—Butadiene Rubber Composite. Appl. Sci. 2021, 11, 10085. [Google Scholar] [CrossRef]
- Ghosh, B.; Paul, S.; Kar, S.; Ghosal, R.; Roy, A.; Mondal, T.; Bhowmick, A.K. Graphene-Based Hybrid Fillers as New Reinforcing Agents in Rubber Compounds for the Tire Industry. In Graphene-Rubber Nanocomposites; CRC Press: Boca Raton, FL, USA, 2022; pp. 199–223. [Google Scholar]
- Tabandeh-Khorshid, M.; Kumar, A.; Omrani, E.; Kim, C.; Rohatgi, P. Synthesis, Characterization, and Properties of Graphene Reinforced Metal-Matrix Nanocomposites. Compos. Part B Eng. 2020, 183, 107664. [Google Scholar] [CrossRef]
- Innes, J.R.; Young, R.J.; Papageorgiou, D.G. Graphene Nanoplatelets as a Replacement for Carbon Black in Rubber Compounds. Polymers 2022, 14, 1204. [Google Scholar] [CrossRef] [PubMed]
- Sethulekshmi, A.S.; Jayan, J.S.; Saritha, A.; Joseph, K. Recent Developments in Natural Rubber Nanocomposites Containing Graphene Derivatives and Its Hybrids. Ind. Crops Prod. 2022, 177, 114529. [Google Scholar] [CrossRef]
- Marinho, B.; Ghislandi, M.; Tkalya, E.; Koning, C.E.; de With, G. Electrical Conductivity of Compacts of Graphene, Multi-Wall Carbon Nanotubes, Carbon Black, and Graphite Powder. Powder Technol. 2012, 221, 351–358. [Google Scholar] [CrossRef]
- Ke, K.; Sang, Z.; Chen, X.; Rohm, K.; Manas-Zloczower, I. Tuning Mechanical and Electrical Properties of Elastomer Composites with Hybrid Filler Network Containing Graphene for Stretchable Strain Sensors. Adv. Eng. Mater. 2022, 24, 2100703. [Google Scholar] [CrossRef]
- Leong, Y.L.; Lim, H.N.; Ibrahim, I. Graphene in Rubber Formulations: A Comprehensive Review and Performance Optimization Insights. Mol. Syst. Des. Eng. 2023, 8, 1229–1251. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Yang, L.; Liu, B.; Xie, S.; Qi, R.; Zhan, Y.; Xia, H. Graphene-Based Hybrid Fillers for Rubber Composites. Molecules 2024, 29, 1009. [Google Scholar] [CrossRef] [PubMed]
- Capezza, A.; Andersson, R.L.; Ström, V.; Wu, Q.; Sacchi, B.; Farris, S.; Hedenqvist, M.S.; Olsson, R.T. Preparation and Comparison of Reduced Graphene Oxide and Carbon Nanotubes as Fillers in Conductive Natural Rubber for Flexible Electronics. ACS Omega 2019, 4, 3458–3468. [Google Scholar] [CrossRef] [PubMed]
- Valentini, L.; Bon, S.B.; López-Manchado, M.A.; Verdejo, R.; Pappalardo, L.; Bolognini, A.; Alvino, A.; Borsini, S.; Berardo, A.; Pugno, N.M. Synergistic Effect of Graphene Nanoplatelets and Carbon Black in Multifunctional EPDM Nanocomposites. Compos. Sci. Technol. 2016, 128, 123–130. [Google Scholar] [CrossRef]
- Song, P.; Wang, G.; Zhang, Y. Preparation and Performance of Graphene/Carbon Black Silicone Rubber Composites Used for Highly Sensitive and Flexible Strain Sensors. Sens. Actuators A Phys. 2021, 323, 112659. [Google Scholar] [CrossRef]
- Khalifa, M.; Murugesan, S.; Anandhan, S. Graphene-Based Elastomer Nanocomposites: A Fascinating Material for Flexible Sensors in Health Monitoring. In Graphene-Rubber Nanocomposites; CRC Press: Boca Raton, FL, USA, 2022; pp. 347–375. [Google Scholar]
- Yin, F.; Niu, H.; Kim, E.; Shin, Y.K.; Li, Y.; Kim, N. Advanced Polymer Materials-based Electronic Skins for Tactile and Non-contact Sensing Applications. InfoMat 2023, 5, e12424. [Google Scholar] [CrossRef]
- Abbasi, S.; Peerzada, M.H.; Nizamuddin, S.; Mubarak, N.M. Functionalized Nanomaterials for the Aerospace, Vehicle, and Sports Industries. In Handbook of Functionalized Nanomaterials for Industrial Applications; Elsevier: Amsterdam, The Netherlands, 2020; pp. 795–825. [Google Scholar]
- Mirizzi, L.; Carnevale, M.; D’Arienzo, M.; Milanese, C.; Di Credico, B.; Mostoni, S.; Scotti, R. Tailoring the Thermal Conductivity of Rubber Nanocomposites by Inorganic Systems: Opportunities and Challenges for Their Application in Tires Formulation. Molecules 2021, 26, 3555. [Google Scholar] [CrossRef] [PubMed]
- Jayalakshmy, M.S.; Mishra, R.K. Applications of Carbon-Based Nanofiller-Incorporated Rubber Composites in the Fields of Tire Engineering, Flexible Electronics and EMI Shielding. In Carbon-Based Nanofillers and Their Rubber Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2019; pp. 441–472. [Google Scholar]
- Mondal, S.; Khastgir, D. Elastomer Reinforcement by Graphene Nanoplatelets and Synergistic Improvements of Electrical and Mechanical Properties of Composites by Hybrid Nano Fillers of Graphene-Carbon Black & Graphene-MWCNT. Compos. Part A Appl. Sci. Manuf. 2017, 102, 154–165. [Google Scholar]
- Debnath, M.; Adhikary, A. Use of Graphene in Rubber Nanocomposite, Its Processability, and Commercial Advantages. In Rubber Products: Technology and Cost Optimisation; Walter de Gruyter GmbH & Co. KG: Berlin, Germany, 2024; p. 151. [Google Scholar]
- Battig, A.; Fadul, N.A.-R.; Frasca, D.; Schulze, D.; Schartel, B. Multifunctional Graphene Nanofiller in Flame Retarded Polybutadiene/Chloroprene/Carbon Black Composites. e-Polymers 2021, 21, 244–262. [Google Scholar] [CrossRef]
- Roy, A.; Kar, S.; Ghosal, R.; Mukhopadhyay, R.; Naskar, K.; Bhowmick, A.K. Unique Graphene-carbon Black Hybrid Nanofiller by a Micromechanical Cleavage Technique as a Reinforcing Agent in Elastomers: Fundamental and Experimental Studies. J. Appl. Polym. Sci. 2023, 140, e53575. [Google Scholar] [CrossRef]
- Döscher, H.; Schmaltz, T.; Neef, C.; Thielmann, A.; Reiss, T. Graphene Roadmap Briefs (No. 2): Industrialization Status and Prospects 2020. 2D Mater. 2021, 8, 22005. [Google Scholar] [CrossRef]
- Mathew, M.; Midhun Dominic, C.D.; Neenu, K.V.; Begum, P.M.S.; Dileep, P.; Kumar, T.G.A.; Sabu, A.A.; Nagane, D.; Parameswaranpillai, J.; Badawi, M. Carbon Black and Chitin Nanofibers for Green Tyres: Preparation and Property Evaluation. Carbohydr. Polym. 2023, 310, 120700. [Google Scholar] [CrossRef]
- Shiva, M.; Akhtari, S.S.; Shayesteh, M. Effect of Mineral Fillers on Physico-Mechanical Properties and Heat Conductivity of Carbon Black-Filled SBR/Butadiene Rubber Composite. Iran. Polym. J. 2020, 29, 957–974. [Google Scholar] [CrossRef]
- Dominic, M.; Joseph, R.; Begum, P.M.S.; Kanoth, B.P.; Chandra, J.; Thomas, S. Green Tire Technology: Effect of Rice Husk Derived Nanocellulose (RHNC) in Replacing Carbon Black (CB) in Natural Rubber (NR) Compounding. Carbohydr. Polym. 2020, 230, 115620. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Sodano, H.A. Aramid Nanofiber Reinforced Rubber Compounds for the Application of Tire Tread with High Abrasion Resistance and Fuel Saving Efficiency. ACS Appl. Polym. Mater. 2020, 2, 4874–4884. [Google Scholar] [CrossRef]
- Mohamad Aini, N.A.; Othman, N.; Hussin, M.H.; Sahakaro, K.; Hayeemasae, N. Effect of Hybrid Carbon Black/Lignin on Rheological, Mechanical and Thermal Stability Properties of NR/BR Composites. Plast. Rubber Compos. 2022, 51, 293–305. [Google Scholar] [CrossRef]
- Ercan Kalkan, M.; Karakaya, N.; Özkoç, G. POSS Nanoparticles as a Potential Compatibilizer for Natural Rubber/Butadiene Rubber Blends. Polym. Adv. Technol. 2020, 31, 2290–2300. [Google Scholar] [CrossRef]
- Sreelekshmi, R.V.; Sudha, J.D.; Menon, A.R.R. Novel Organomodified Kaolin/Silica Hybrid Fillers in Natural Rubber and Its Blend with Polybutadiene Rubber. Polym. Bull. 2017, 74, 783–801. [Google Scholar] [CrossRef]
- Nayeeif, A.A.; Abed, M.S.; Abdulkhalik, H. Morphology, rheology and mechanical properties of NR, NR/BR and NR nanocomposite. J. Eng. Sci. Technol. 2022, 17, 3512–3525. [Google Scholar]
- Ma, L.; Zhang, Z.; Peng, Z.; Formela, K.; Wang, S. Dynamic Mechanical Properties and Flexing Fatigue Resistance of Tire Sidewall Rubber as Function of Waste Tire Rubber Reclaiming Degree. J. Appl. Polym. Sci. 2021, 138, 51290. [Google Scholar] [CrossRef]
- Kaliyathan, A.V.; Rane, A.V.; Jackson, S.; Thomas, S. Analysis of Diffusion Characteristics for Aromatic Solvents through Carbon Black Filled Natural Rubber/Butadiene Rubber Blends. Polym. Compos. 2021, 42, 375–396. [Google Scholar] [CrossRef]
- Rajan, K.P.; Gopanna, A.; Theravalappil, R.; Abdelghani, E.A.M.; Thomas, S.P. Partial Replacement of Carbon Black with Graphene in Natural Rubber/Butadiene Rubber Based Tire Compound: Investigation of Critical Properties. J. Polym. Res. 2022, 29, 1–17. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J., Jr. Statistical Mechanics of Cross-linked Polymer Networks I. Rubberlike Elasticity. J. Chem. Phys. 1943, 11, 512–520. [Google Scholar] [CrossRef]
- Hergenrother, W.L.; Hilton, A.S. Use of χ as a Function of Volume Fraction of Rubber to Determine Crosslink Density by Swelling. Rubber Chem. Technol. 2003, 76, 832–845. [Google Scholar] [CrossRef]
- Moon, B.; Lee, J.; Park, S.; Seok, C.-S. Study on the Aging Behavior of Natural Rubber/Butadiene Rubber (NR/BR) Blends Using a Parallel Spring Model. Polymers 2018, 10, 658. [Google Scholar] [CrossRef] [PubMed]
- Joseph, R.; George, K.E.; Francls, D.J.; Thomas, K.T. Polymer-Solvent Interaction Parameter for NR/SBR and NR/BR Blends. Int. J. Polym. Mater. 1987, 12, 29–34. [Google Scholar] [CrossRef]
- Farsouni Eydi, E.; Shariati, A.; Khosravi-Nikou, M.R. Separation of BTEX Compounds (Benzene, Toluene, Ethylbenzene and Xylenes) from Aqueous Solutions Using Adsorption Process. J. Dispers. Sci. Technol. 2019, 40, 453–463. [Google Scholar] [CrossRef]
- Al-Kandary, J.A.; Al-Jimaz, A.S.; Abdul-Latif, A.-H.M. Viscosities, Densities, and Speeds of Sound of Binary Mixtures of Benzene, Toluene, o-Xylene, m-Xylene, p-Xylene, and Mesitylene with Anisole at (288.15, 293.15, 298.15, and 303.15) K. J. Chem. Eng. Data 2006, 51, 2074–2082. [Google Scholar] [CrossRef]
- Niziolek, A.M.; Onel, O.; Floudas, C.A. Production of Benzene, Toluene, and Xylenes from Natural Gas via Methanol: Process Synthesis and Global Optimization. AIChE J. 2016, 62, 1531–1556. [Google Scholar] [CrossRef]
- Mathai, A.E.; Thomas, S. Transport of Aromatic Hydrocarbons through Crosslinked Nitrile Rubber Membranes. J. Macromol. Sci. Part B Phys. 1996, 35, 229–253. [Google Scholar] [CrossRef]
- Augustine, A.; Joseph, J.; Thomas, S.P.; Stephen, R. Effect of Halloysite Nanotubes and Organically Modified Bentonite Clay Hybrid Filler System on the Properties of Natural Rubber. J. Elastomers Plast. 2019, 0095244319865573. [Google Scholar]
- Bijina, V.; Jandas, P.J.; Jose, J.; Abhitha, K.; John, H. Tailoring of Performance Characteristics of Green Tyre Tread Formulation Using Thermally Exfoliated Graphite/Carbon Black Binary Filler System via Scalable and Competent Method. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Thomas, P.C.; Tomlal Jose, E.; Selvin Thomas, P.; Thomas, S.; Joseph, K. High-performance Nanocomposites Based on Arcylonitrile-butadiene Rubber with Fillers of Different Particle Size: Mechanical and Morphological Studies. Polym. Compos. 2010, 31, 1515–1524. [Google Scholar] [CrossRef]
- Balachandran, M.; Bhagawan, S.S. Mechanical, Thermal and Transport Properties of Nitrile Rubber (NBR)—Nanoclay Composites. J. Polym. Res. 2012, 19, 9809. [Google Scholar] [CrossRef]
- Igwe, I.O.; Ezeani, O.E. Studies on the Transport of Aromatic Solvents through Filled Natural Rubber. Int. J. Polym. Sci. 2012, 2012, 212507. [Google Scholar] [CrossRef]
- Nair, M.V.; Kumar, A.; Joseph, S.; Zachariah, A.K.; Maria, H.J.; Thomas, S. Synergistic Effect of Hybrid Fillers on Transport Behavior of NR/EPDM Blends. J. Integr. Sci. Technol. 2021, 9, 9–21. [Google Scholar]
- Abhisha, V.S.; Sisanth, K.S.; Thomas, S.; Stephen, R. Kinetic Studies on the Transport Behavior of Hybrid Filler Incorporated Natural Rubber (NR). Express Polym. Lett. 2023, 17, 1070. [Google Scholar] [CrossRef]
- Ravindran, A.; Kamaraj, M.; Vasanthmurali, N.; Meghavarshini, V.; Balachandran, M. Nanosilica Reinforced EPDM Silicone Rubber Blends: Experimental and Theoretical Evaluation of Mechanical and Solvent Sorption Properties. Mater. Today Proc. 2021, 46, 4381–4386. [Google Scholar] [CrossRef]
- Maria, H.J.; Lyczko, N.; Nzihou, A.; Mathew, C.; George, S.C.; Joseph, K.; Thomas, S. Transport of Organic Solvents through Natural Rubber/Nitrile Rubber/Organically Modified Montmorillonite Nanocomposites. J. Mater. Sci. 2013, 48, 5373–5386. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Gurny, R.; Doelker, E.; Buri, P.; Peppas, N.A. Mechanisms of Solute Release from Porous Hydrophilic Polymers. Int. J. Pharm. 1983, 15, 25–35. [Google Scholar] [CrossRef]
- Jose, J.P.; Thomas, S. XLPE Based Al2O3–Clay Binary and Ternary Hybrid Nanocomposites: Self-Assembly of Nanoscale Hybrid Fillers, Polymer Chain Confinement and Transport Characteristics. Phys. Chem. Chem. Phys. 2014, 16, 20190–20201. [Google Scholar] [CrossRef] [PubMed]
- Peppas, N.A.; Sahlin, J.J. A Simple Equation for the Description of Solute Release. III. Coupling of Diffusion and Relaxation. Int. J. Pharm. 1989, 57, 169–172. [Google Scholar] [CrossRef]
- Zachariah, A.K.; Kumar Chandra, A.; Mohamed, P.K.; Parameswaranpillai, J.; Thomas, S. Mixed Mode Morphology in Elastomeric Blend Nanocomposites: Effect on Vulcanization, Thermal Stability and Solvent Permeability. Polym. Compos. 2018, 39, E1659–E1668. [Google Scholar] [CrossRef]
- Kumar, N.; Singh, K.P.; Giri, A.; Singh, S.P. Transport Mechanism and Diffusion Kinetics of Kerosene through Polynorbornene Rubber/Natural Rubber Blends. Polym. Bull. 2021, 79, 5305–5325. [Google Scholar] [CrossRef]
- Prajitha, V.; Jibin, K.P.; Abitha, V.K.; Sisanth, K.S.; Huskic, M.; Meera, A.P.; George, J.S.; Thomas, S. Advancing Mechanical Performance in Sustainable Engineering: Synergistic Effects of Graphene Oxide/Nano-silica Hybrid Nanofiller via Latex Coagulation in Natural Rubber Composites. Polym. Compos. 2024, 45, 5980–5991. [Google Scholar] [CrossRef]
- Bindu, P.; Thomas, S. Viscoelastic Behavior and Reinforcement Mechanism in Rubber Nanocomposites in the Vicinity of Spherical Nanoparticles. J. Phys. Chem. B 2013, 117, 12632–12648. [Google Scholar] [CrossRef] [PubMed]
- Balakrishnan, P.; Sreekala, M.S.; Kunaver, M.; Huskić, M.; Thomas, S. Morphology, Transport Characteristics and Viscoelastic Polymer Chain Confinement in Nanocomposites Based on Thermoplastic Potato Starch and Cellulose Nanofibers from Pineapple Leaf. Carbohydr. Polym. 2017, 169, 176–188. [Google Scholar] [CrossRef] [PubMed]
- Oommen, Z.; Groeninckx, G.; Thomas, S. Dynamic Mechanical and Thermal Properties of Physically Compatibilized Natural Rubber/Poly (Methyl Methacrylate) Blends by the Addition of Natural Rubber-graft-poly (Methyl Methacrylate). J. Polym. Sci. Part B Polym. Phys. 2000, 38, 525–536. [Google Scholar] [CrossRef]
- Gopi, J.A.; Patel, S.K.; Chandra, A.K.; Tripathy, D.K. SBR-Clay-Carbon Black Hybrid Nanocomposites for Tire Tread Application. J. Polym. Res. 2011, 18, 1625–1634. [Google Scholar] [CrossRef]
- Hua, J.; Liu, K.; Wang, Z.; Geng, J.; Wang, X. Effect of Vinyl and Phenyl Group Content on the Physical and Dynamic Mechanical Properties of HVBR and SSBR. J. Appl. Polym. Sci. 2018, 135, 45975. [Google Scholar] [CrossRef]
- Sadat-Mansouri, S.N.; Hamrahjou, N.; Taghvaei-Ganjali, S.; Zadmard, R. Synthesis and Application of Silica Supported Calix [4] Arene Derivative as a New Processing Aid Agent for Reducing Hysteresis of Tread Rubber Compounds Used in Low Rolling Resistance Tires. Acta Chim. Slov. 2022, 69, 98–107. [Google Scholar] [PubMed]
- Mondal, T.; Bhowmick, A.K.; Ghosal, R.; Mukhopadhyay, R. Expanded Graphite as an Agent towards Controlling the Dispersion of Carbon Black in Poly (Styrene–Co-Butadiene) Matrix: An Effective Strategy towards the Development of High Performance Multifunctional Composite. Polymer 2018, 146, 31–41. [Google Scholar] [CrossRef]
- Thaptong, P.; Sae-Oui, P.; Sirisinha, C. Effects of Silanization Temperature and Silica Type on Properties of Silica-filled Solution Styrene Butadiene Rubber (SSBR) for Passenger Car Tire Tread Compounds. J. Appl. Polym. Sci. 2016, 133, 43342. [Google Scholar] [CrossRef]
- Gabriel, C.F.S.; Gabino, A.d.A.P.; de Sousa, A.M.F.; Furtado, C.R.G.; Nunes, R.C.R. Tire Tread Rubber Compounds with Ternary System Filler Based on Carbon Black, Silica, and Metakaolin: Contribution of Silica/Metakaolin Content on the Final Properties. J. Elastomers Plast. 2019, 51, 712–726. [Google Scholar] [CrossRef]
- Sae-oui, P.; Suchiva, K.; Thepsuwan, U.; Intiya, W.; Yodjun, P.; Sirisinha, C. Effects of Blend Ratio and SBR Type on Properties of Silica-Filled SBR/NR Tire Tread Compounds. Rubber Chem. Technol. 2016, 89, 240–250. [Google Scholar] [CrossRef]
- Schuring, D.J.; Futamura, S. Rolling Loss of Pneumatic Highway Tires in the Eighties. Rubber Chem. Technol. 1990, 63, 315–367. [Google Scholar] [CrossRef]
- Harper, M.; Tardiff, J.; Haakenson, D.; Joandrea, M.; Knych, M. Tire Tread Performance Modification Utilizing Polymeric Additives. SAE Int. J. Veh. Dyn. Stab. NVH 2017, 1, 179–189. [Google Scholar] [CrossRef]
- Sarkawi, S.S.; Aziz, A.A.; Kifli, A. Properties of Graphene Nano-Filler Reinforced Epoxidized Natural Rubber Composites. J. Polym. Sci. Technol. 2017, 2, 36–44. [Google Scholar]
- Prime, R.B.; Bair, H.E.; Vyazovkin, S.; Gallagher, P.K.; Riga, A. Thermogravimetric Analysis (TGA). Therm. Anal. Polym. Fundam. Appl. 2009, 241–317. [Google Scholar]
- Yahya, Y.S.R.; Azura, A.R.; Ahmad, Z. Effect of Curing Systems on Thermal Degradation Behaviour of Natural Rubber (SMR CV 60). J. Phys. Sci. 2011, 22, 1–14. [Google Scholar]
- De, D.; Panda, P.K.; Roy, M.; Bhunia, S. Reinforcing Effect of Reclaim Rubber on Natural Rubber/Polybutadiene Rubber Blends. Mater. Des. 2013, 46, 142–150. [Google Scholar] [CrossRef]
- Sircar, A.K. Analysis of Elastomer Vulcanizate Composition by TG-DTG Techniques. Rubber Chem. Technol. 1992, 65, 503–526. [Google Scholar] [CrossRef]
- Wunderlich, B. Thermal Analysis of Polymeric Materials; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; ISBN 3540236295. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).