Numerical Analysis of Gas Hold-Up of Two-Phase Ebullated Bed Reactor
Abstract
:1. Introduction
2. Materials and Methods
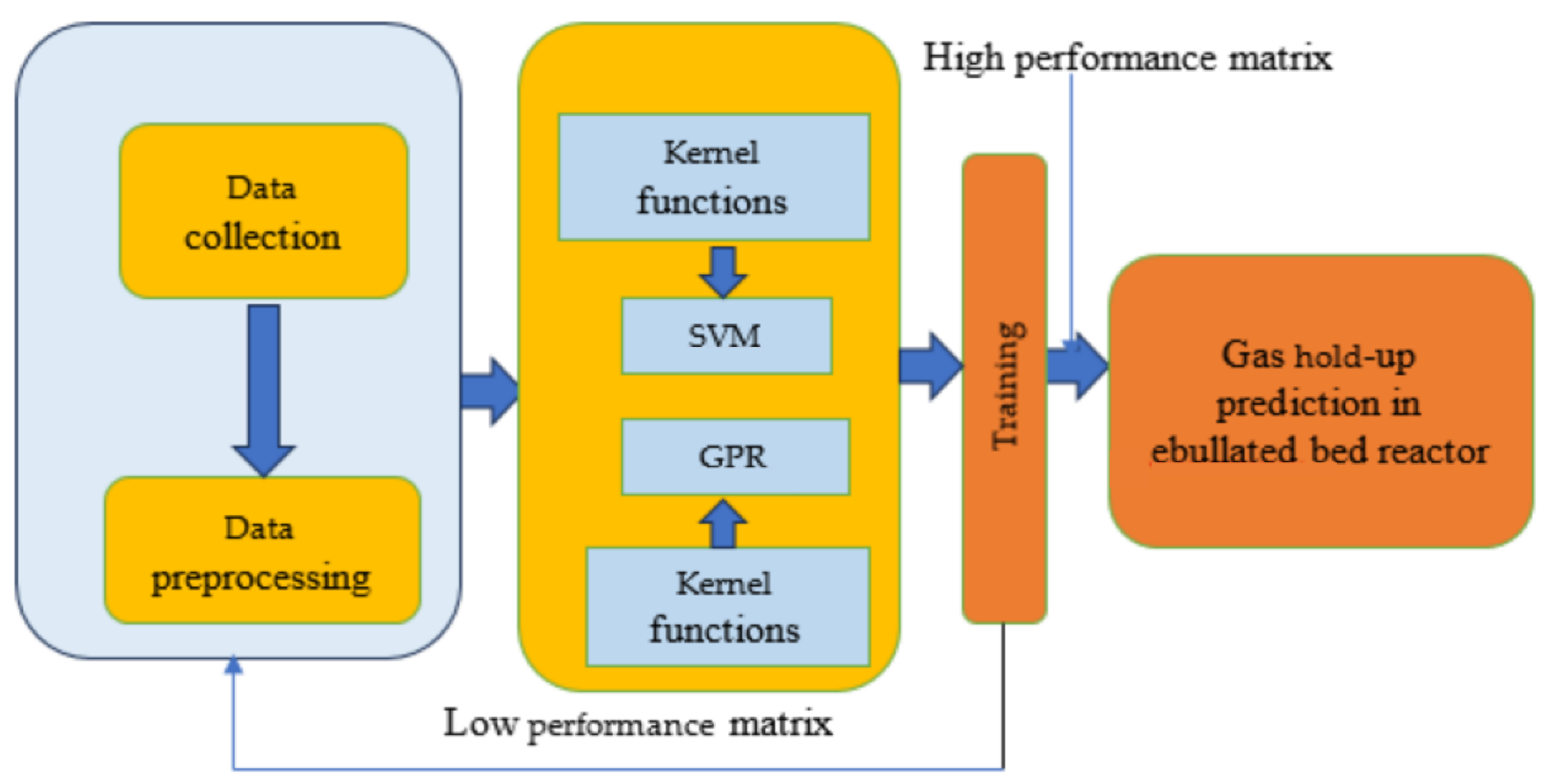
3. Model Description and Configurations
3.1. Support Vector Machine Regression
3.2. Gaussian Process Regression
3.3. Effect of Kernel Functions on Model Performance
3.4. Model Configuration and Training
3.5. Feature Selection
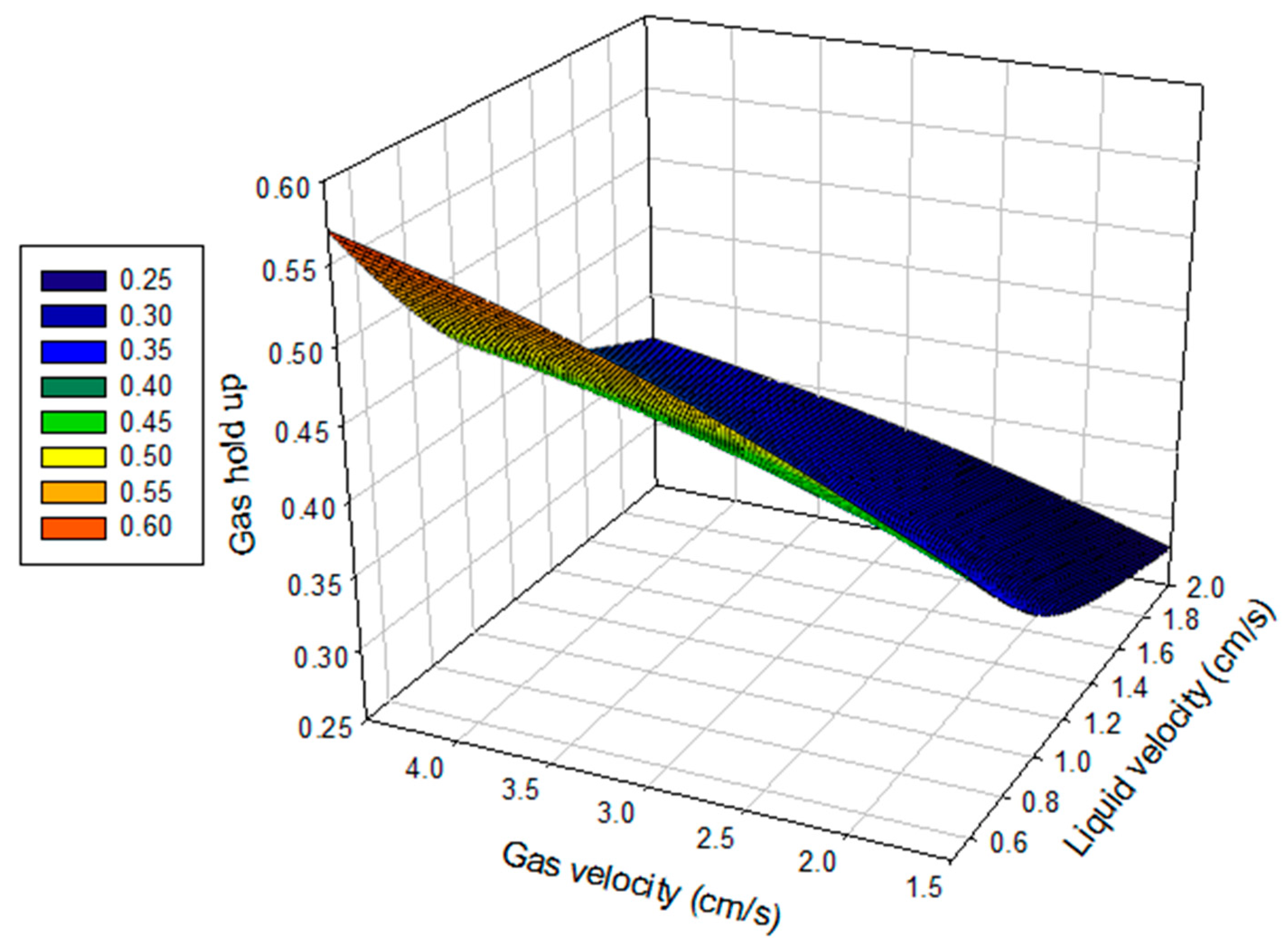
4. Results and Discussion
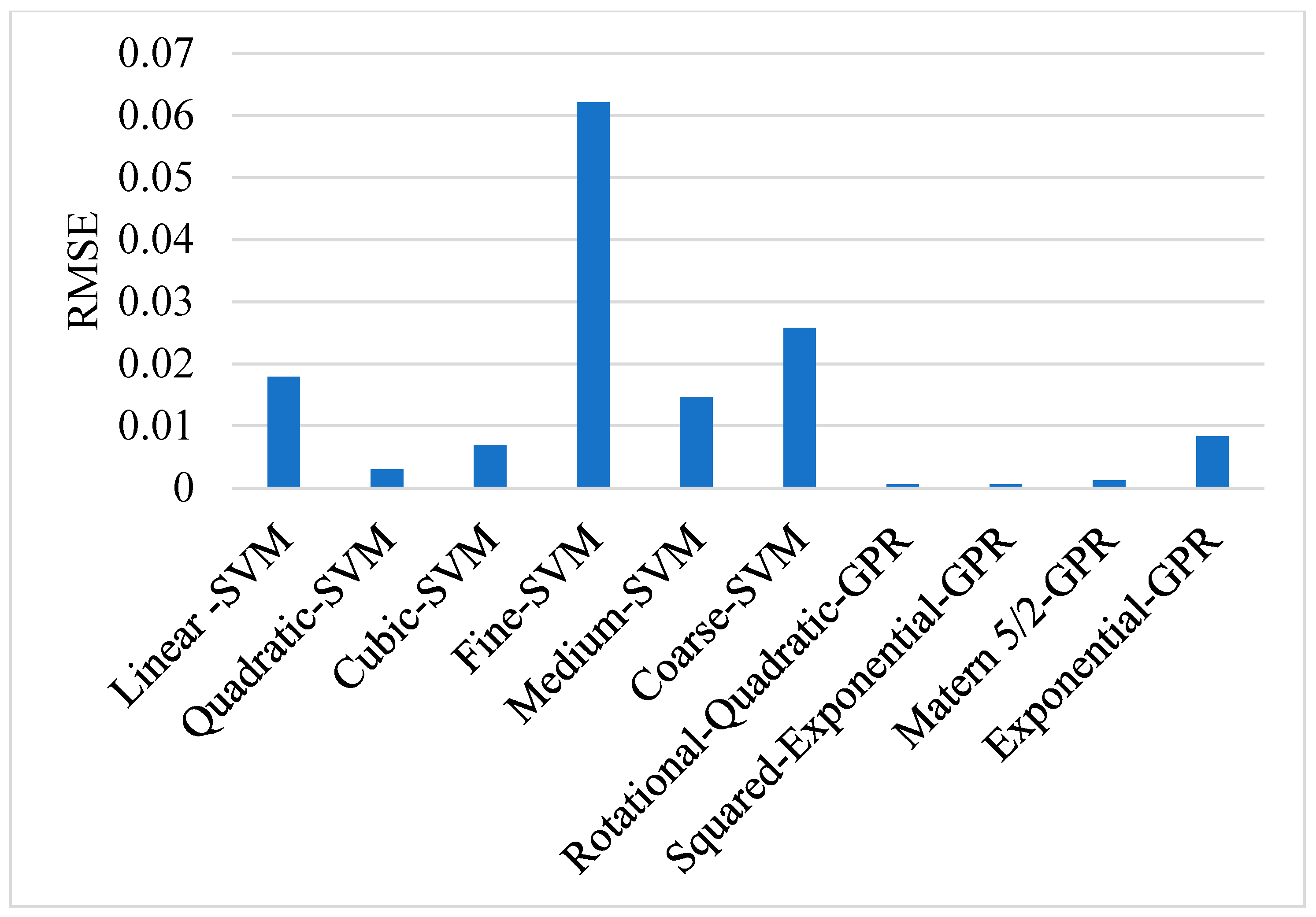
4.1. Hyperparameter Tuning
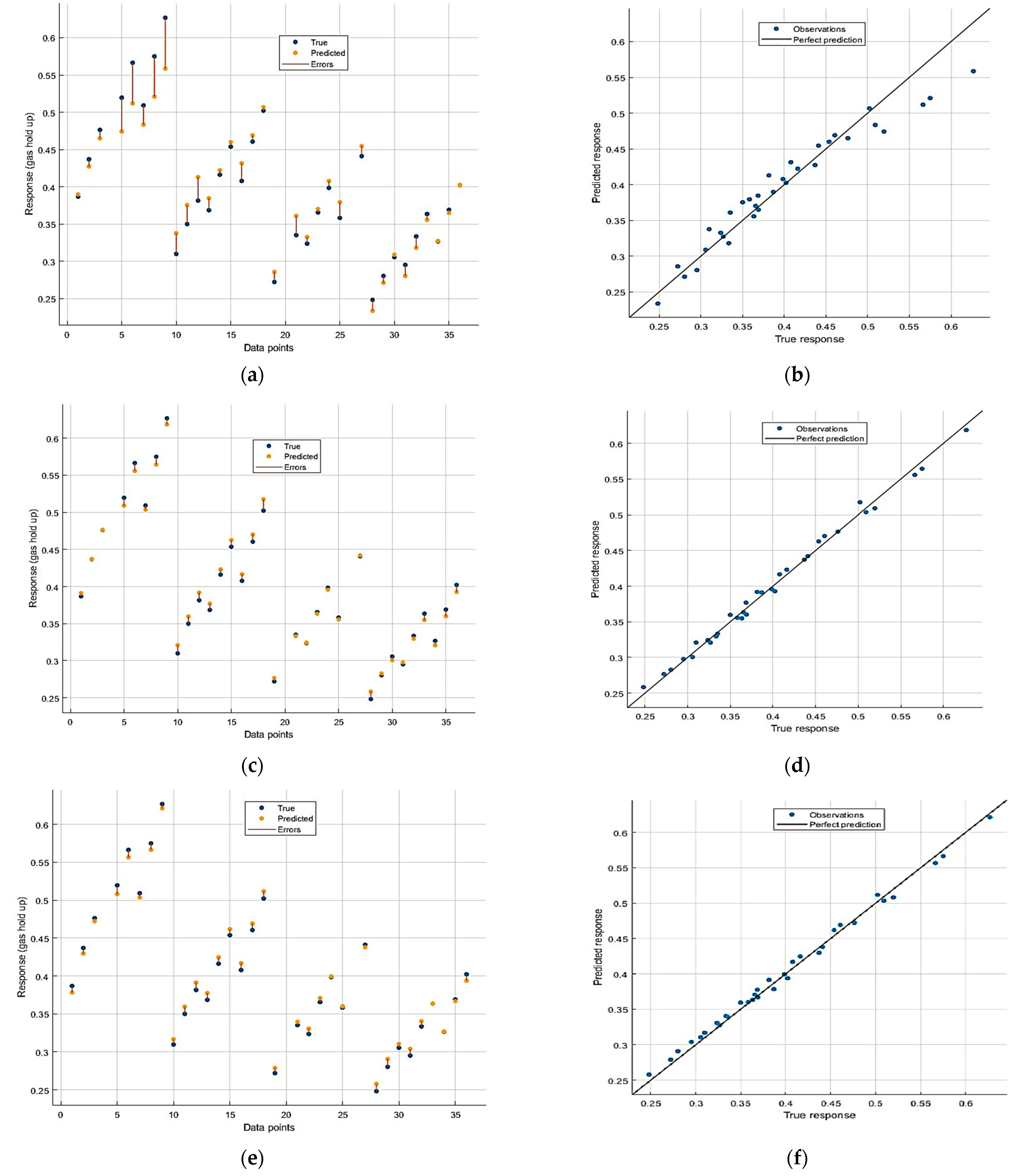
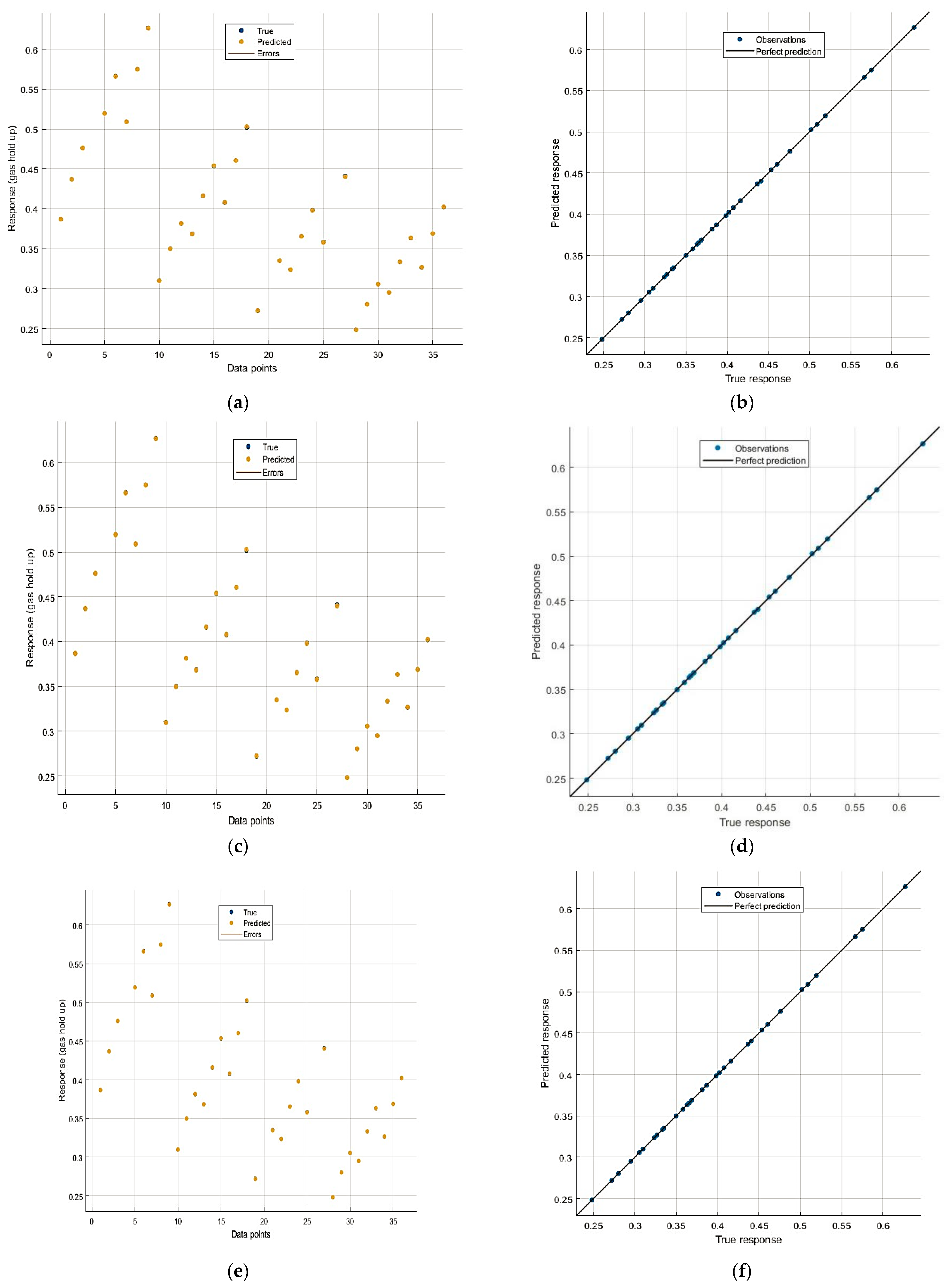
4.2. The Training and Testing Performance of the Models
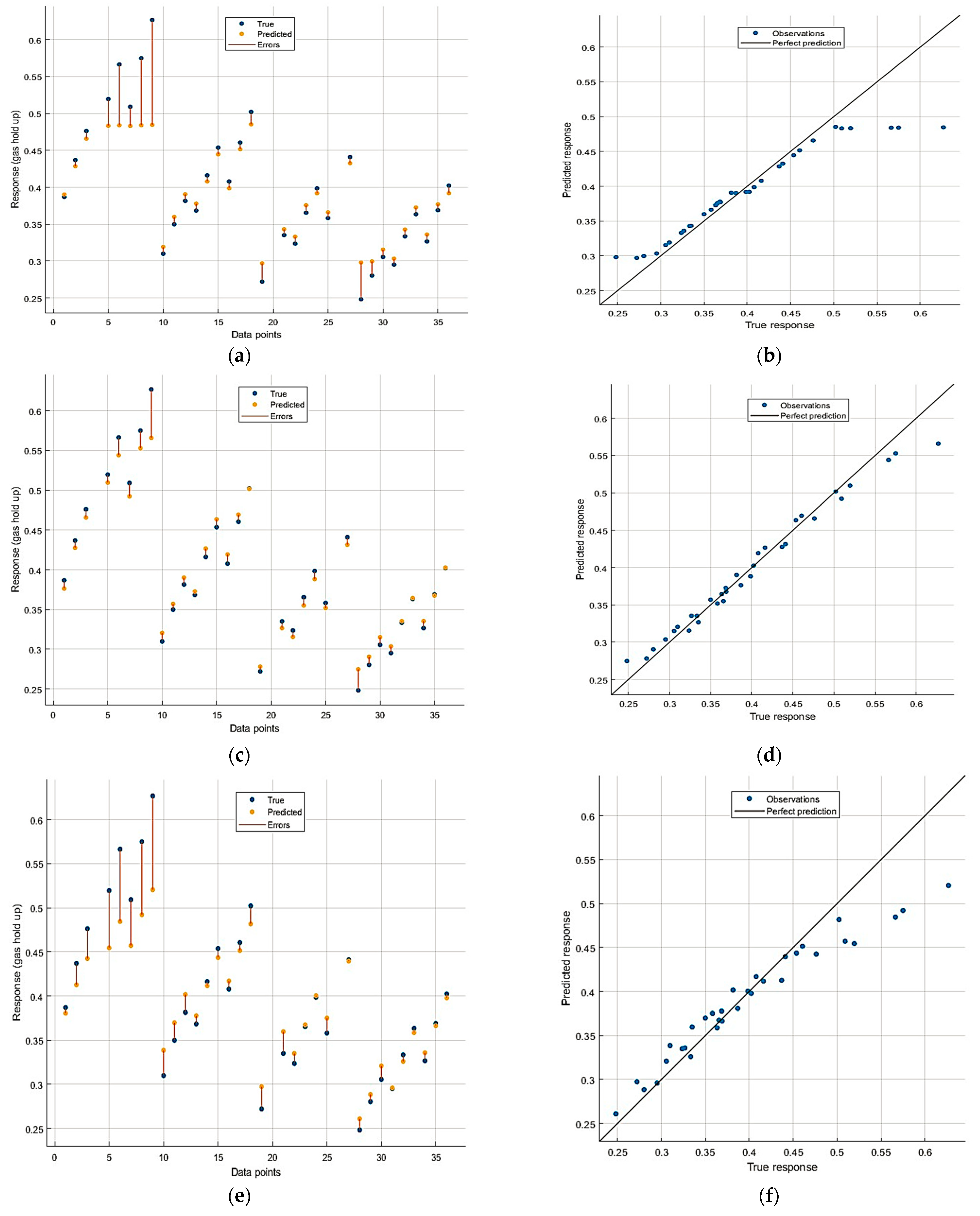
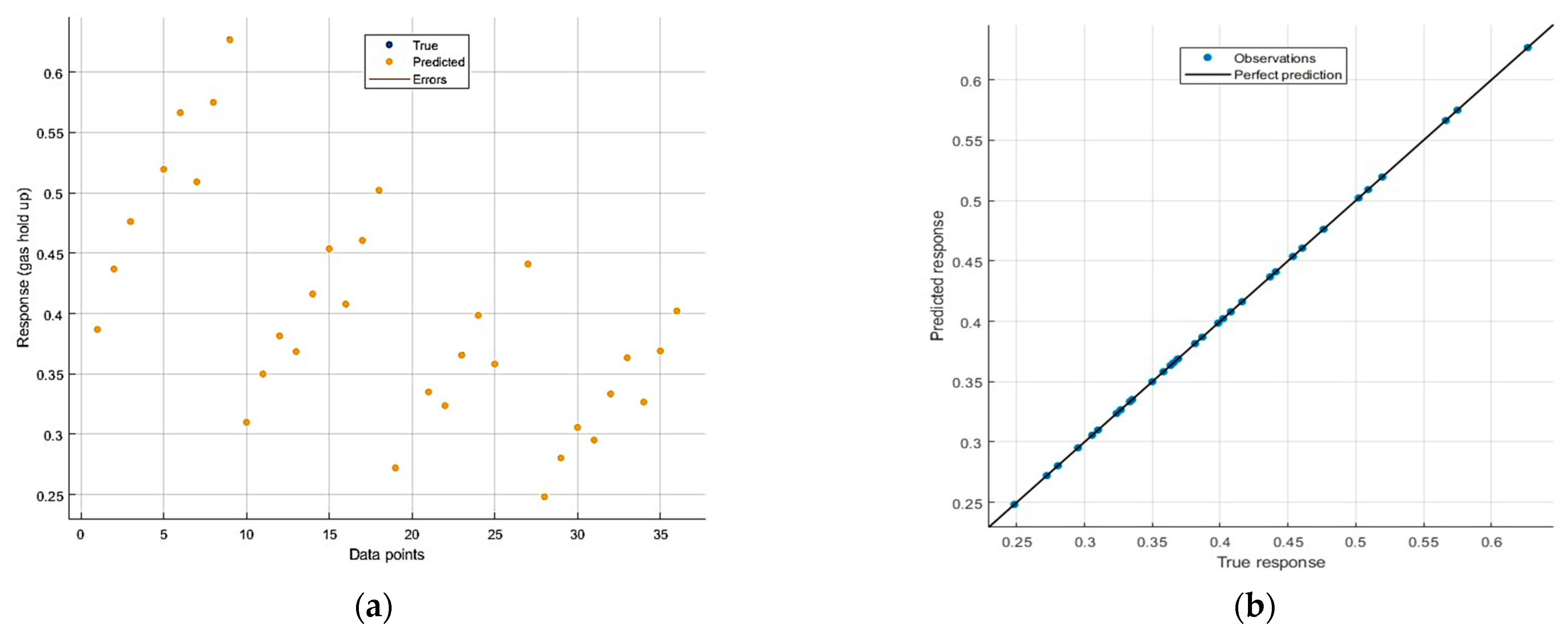
4.3. Predictive Performance of the Models
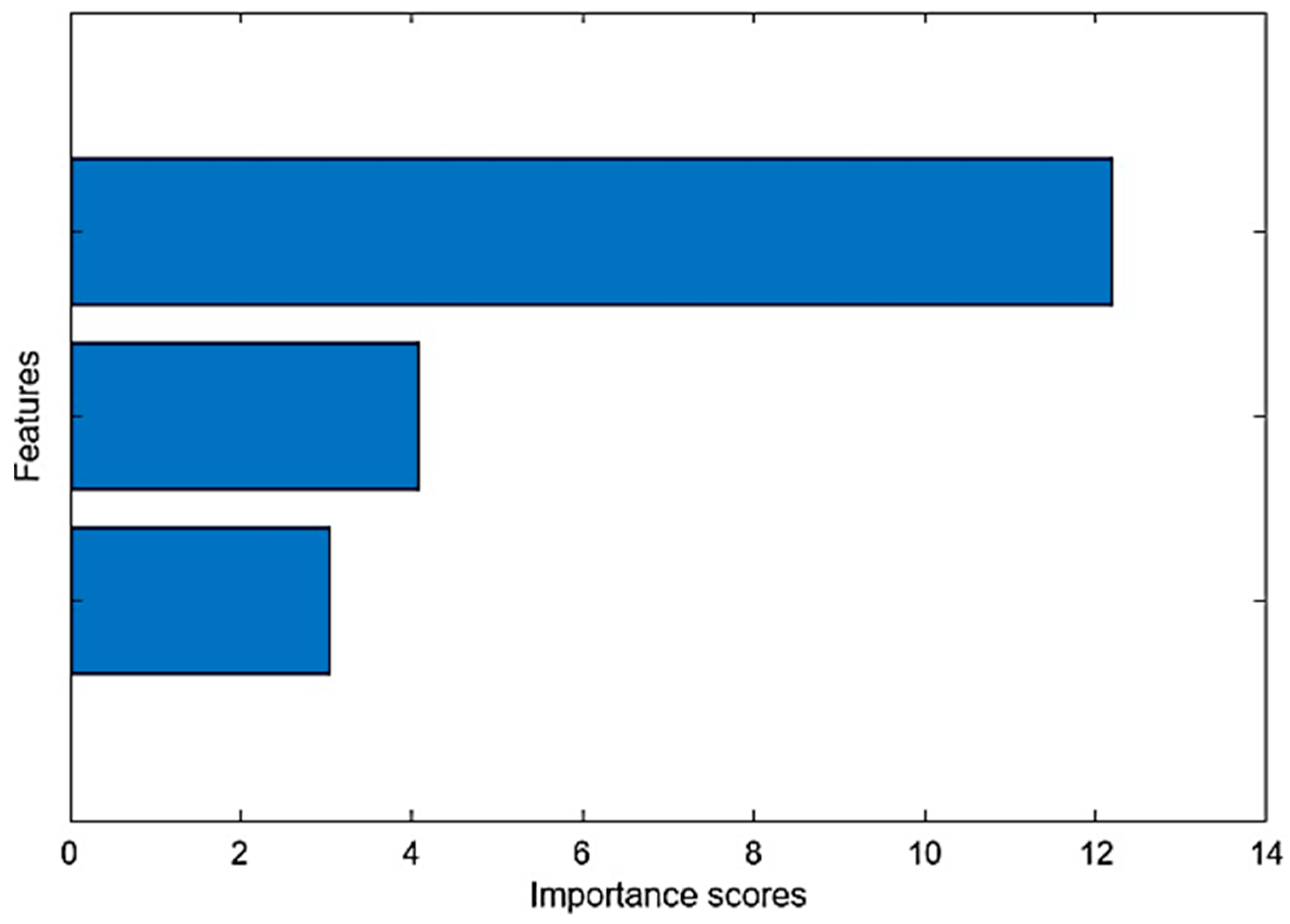
4.4. Feature Selection
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Chang, Y.; Li, J.; Wang, H.; Li, L.; Chen, C.; Zhao, Y.; Yuan, Y. Analysis of performance of novel hydrocyclones in ebullated bed reactor with different vortex finder structures. Chem. Eng. Res. Des. 2020, 158, 89–101. [Google Scholar] [CrossRef]
- Mowla, A.; Agnaou, M.; Treeratanaphitak, T.; Budman, H.M.; Abukhdeir, N.M.; Ioannidis, M.A. Gas segregation in a pilot-scale ebullated bed system: Experimental investigation and model validation. Chem. Eng. Res. Des. 2023, 194, 742–755. [Google Scholar] [CrossRef]
- Lane, C.D.; McKnight, C.A.; Wiens, J.; Reid, K.; Donaldson, A.A. Parametric analysis of internal gas separation within an ebullated bed reactor. Chem. Eng. Res. Des. 2016, 105, 44–54. [Google Scholar] [CrossRef]
- Parisien, V.; Pjontek, D.; McKnight, C.A.; Wiens, J.; Macchi, A. Impact of catalyst density distribution on the fluid dynamics of an ebullated bed operating at high gas holdup conditions. Chem. Eng. Sci. 2017, 170, 491–500. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Chang, Y.; Huang, Y.; Jiang, X.; Wang, H.; Li, L.; Chen, C.; Zhao, Y.; Yuan, Y. Cold model testing of in-situ catalyst activation by swirling self-rotation in ebullated bed reactor for biomass pyrolysis oils hydrogenation. Chem. Eng. J. 2021, 406, 126909. [Google Scholar] [CrossRef]
- Manek, E.; Haydary, J. Investigation of the liquid recycle in the reactor cascade of an industrial scale ebullated bed hydrocracking unit. Chin. J. Chem. Eng. 2019, 27, 298–304. [Google Scholar] [CrossRef]
- Tailleur, R.G. Effect of recycling the unconverted residue on a hydrocracking catalyst operating in an ebullated bed reactor. Fuel Process. Technol. 2007, 88, 779–785. [Google Scholar] [CrossRef]
- Mowla, A.; Ioannidis, M.A. Effect of particle wettability on the hydrodynamics of three-phase fluidized beds subject to foaming. Powder Technol. 2020, 374, 58–69. [Google Scholar] [CrossRef]
- Abid, M.F.; Ahmed, S.M.; AbuHamid, W.H.; Ali, S.M. Study on novel scheme for hydrodesulfurization of middle distillates using different types of catalyst. J. King Saud Univ. Eng. Sci. 2019, 31, 144–151. [Google Scholar] [CrossRef]
- Cheng, Z.-M.; Huang, Z.-B.; Yang, T.; Liu, J.-K.; Ge, H.-L.; Jiang, L.-J.; Fang, X.-C. Modeling on scale-up of an ebullated-bed reactor for the hydroprocessing of vacuum residuum. Catal. Today 2014, 220–222, 228–236. [Google Scholar] [CrossRef]
- Mach, J.; Donaldson, A.A.; Haelssig, J.; Wiens, J.; Adjaye, J.; MacChi, A. Fluid Dynamics Modeling of a Commercial Ebullated Bed Hydroprocessor. Ind. Eng. Chem. Res. 2020, 59, 19030–19044. [Google Scholar] [CrossRef]
- Kojić, P.; Omorjan, R. Predicting hydrodynamic parameters and volumetric gas–liquid mass transfer coefficient in an external-loop airlift reactor by support vector regression. Chem. Eng. Res. Des. 2017, 125, 398–407. [Google Scholar] [CrossRef]
- Gandhi, A.B.; Joshi, J.B. Unified correlation for overall gas hold-Up in bubble column reactors for various gas-liquid systems using hybrid genetic Algorithm-Support Vector Regression technique. Can. J. Chem. Eng. 2010, 88, 758–776. [Google Scholar] [CrossRef]
- Li, M.; Jia, G.; Mahmoud, H.; Yu, Y.H.; Tom, N. Physics-constrained Gaussian process model for prediction of hydrodynamic interactions between wave energy converters in an array. Appl. Math. Model. 2023, 119, 465–485. [Google Scholar] [CrossRef]
- Dai, X.; Andani, H.T.; Alizadeh, A.; Abed, A.M.; Smaisim, G.F.; Hadrawi, S.K.; Karimi, M.; Shamsborhan, M.; Toghraie, D. Using Gaussian Process Regression (GPR) models with the Matérn covariance function to predict the dynamic viscosity and torque of SiO2/Ethylene glycol nanofluid: A machine learning approach. Eng. Appl. Artif. Intell. 2023, 122, 106107. [Google Scholar] [CrossRef]
- Chatre, L.; Bataille, M.; Debacq, M.; Randriamanantena, T.; Nos, J.; Herbelet, F. Modelling of powder hydrodynamics in a screw reactor. Powder Technol. 2023, 420, 118367. [Google Scholar] [CrossRef]
- Vapnik, V. The Support Vector Method of Function Estimation. In Nonlinear Modeling: Advanced Black-Box Techniques; Suykens Johan, J.A.K., Vandewalle, Eds.; Springer: Boston, MA, USA, 1998; pp. 55–85. [Google Scholar] [CrossRef]
- Camastra, F.; Capone, V.; Ciaramella, A.; Riccio, A.; Staiano, A. Prediction of environmental missing data time series by Support Vector Machine Regression and Correlation Dimension estimation. Environ. Model. Softw. 2022, 150, 105343. [Google Scholar] [CrossRef]
- Goswami, K.; Samuel, G.L. Support vector machine regression for predicting dimensional features of die-sinking electrical discharge machined components. Procedia CIRP 2021, 99, 508–513. [Google Scholar] [CrossRef]
- Tong, H. Convergence rates of support vector machines regression for functional data. J. Complex. 2022, 69, 101604. [Google Scholar] [CrossRef]
- Chang, C.; Zeng, T. A hybrid data-driven-physics-constrained Gaussian process regression framework with deep kernel for uncertainty quantification. J. Comput. Phys. 2023, 486, 112129. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y. A Gaussian process regression machine learning model for forecasting retail property prices with Bayesian optimizations and cross-validation. Decis. Anal. J. 2023, 8, 100267. [Google Scholar] [CrossRef]
- Shi, C.; Xue, K.; Wang, C. Predicting global ionospheric TEC maps using Gaussian process regression. Adv. Space Res. 2023, 72, 3251–3268. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y. Price forecasts of ten steel products using Gaussian process regressions. Eng. Appl. Artif. Intell. 2023, 126, 106870. [Google Scholar] [CrossRef]
- Hossain, S.K.S.; Ayodele, B.V.; Almithn, A. Predictive Modeling of Bioenergy Production from Fountain Grass Using Gaussian Process Regression: Effect of Kernel Functions. Energies 2022, 15, 5570. [Google Scholar] [CrossRef]
- Zanaty, E.A.; Afifi, A. Generalized Hermite kernel function for support vector machine classifications. Int. J. Comput. Appl. 2020, 42, 765–773. [Google Scholar] [CrossRef]
- Rollbusch, P.; Becker, M.; Ludwig, M.; Bieberle, A.; Grünewald, M.; Hampel, U.; Franke, R. Experimental investigation of the influence of column scale, gas density and liquid properties on gas holdup in bubble columns. Int. J. Multiph. Flow 2015, 75, 88–106. [Google Scholar] [CrossRef]
- Besagni, G.; Di Pasquali, A.; Gallazzini, L.; Gottardi, E.; Colombo, L.P.M.; Inzoli, F. The effect of aspect ratio in counter-current gas-liquid bubble columns: Experimental results and gas holdup correlations. Int. J. Multiph. Flow 2017, 94, 53–78. [Google Scholar] [CrossRef]
- Rahimzadeh, A.; Ein-Mozaffari, F.; Lohi, A. Hydrodynamics and Gas Hold-Up of a Gas-Liquid Coaxial Mixing System at Different Scales Containing a Non-Newtonian Fluid. Eng. Proc. 2023, 37, 4. [Google Scholar] [CrossRef]
- Zhang, M.; Mahdi, W.A. Development of SVM-based machine learning model for estimating lornoxicam solubility in supercritical solvent. Case Stud. Therm. Eng. 2023, 49, 103268. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, P. A fault diagnosis methodology for nuclear power plants based on Kernel principle component analysis and quadratic support vector machine. Ann. Nucl. Energy 2023, 181, 109560. [Google Scholar] [CrossRef]
- Dagher, I. Quadratic kernel-free non-linear support vector machine. J. Glob. Optim. 2008, 41, 15–30. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, Y.; Park, J. Some companions of perturbed Ostrowski-type inequalities based on the quadratic kernel function with three sections and applications. J. Inequal. Appl. 2013, 2013, 226. [Google Scholar] [CrossRef]

| Parameters | Range | Minimum | Maximum | Mean | Std. Deviation | Variance |
|---|---|---|---|---|---|---|
| Liquid velocity (cm/s) | 1.50 | 0.50 | 2.00 | 1.25 | 0.57 | 0.32 |
| Gas velocity (cm/s) | 3.00 | 1.50 | 4.50 | 3.00 | 1.24 | 1.54 |
| Recycle ratio | 1.00 | 1.00 | 2.00 | 1.50 | 0.41 | 0.17 |
| Gas hold-up | 0.38 | 0.25 | 0.63 | 0.39 | 0.09 | 0.01 |
| Model | Kernel Function | Kernel Scale | Box Constraint | Standardize Data |
|---|---|---|---|---|
| Linear SVM | Linear | Automatic | Automatic | Yes |
| Quadratic SVM | Quadratic | Automatic | Automatic | Yes |
| Cubic SVM | Cubic | Automatic | Automatic | Yes |
| Fine Gaussian SVM | Gaussian | 0.43 | Automatic | Yes |
| Medium Gaussian SVM | Gaussian | 1.7 | Automatic | Yes |
| Coarse Gaussian SVM | Gaussian | 6.9 | Automatic | Yes |
| Rotational Quadratic GPR | Rotational quadratic | Automatic | Automatic | Yes |
| Squared-Exponential GPR | Squared-Exponential | Automatic | Automatic | Yes |
| Matern 5/2 GPR | Matern 5/2 | Automatic | Automatic | Yes |
| Exponential GPR | Exponential | Automatic | Automatic | Yes |
| Model Type | Kernel Function | Training | Testing | ||||
|---|---|---|---|---|---|---|---|
| RMSE | R2 | MAE | RMSE | R2 | MAE | ||
| SVM | Linear | 0.024 | 0.929 | 0.018 | 0.018 | 0.920 | 0.017 |
| SVM | Quadratic | 0.008 | 0.993 | 0.006 | 0.003 | 0.998 | 0.003 |
| SVM | Cubic | 0.007 | 0.993 | 0.007 | 0.007 | 0.988 | 0.006 |
| SVM | Fine | 0.036 | 0.843 | 0.021 | 0.062 | 0.030 | 0.054 |
| SVM | Medium | 0.015 | 0.972 | 0.011 | 0.015 | 0.946 | 0.014 |
| SVM | Coarse | 0.034 | 0.860 | 0.022 | 0.026 | 0.832 | 0.021 |
| GPR | Rotational-Quadratic | 0.000 | 0.999 | 0.000 | 0.001 | 0.999 | 0.001 |
| GPR | Squared-Exponential | 0.000 | 0.999 | 0.000 | 0.001 | 0.999 | 0.001 |
| GPR | Matern 5/2 | 0.000 | 0.999 | 0.000 | 0.001 | 0.999 | 0.001 |
| GPR | Exponential | 0.000 | 0.999 | 0.000 | 0.008 | 0.983 | 0.006 |
| Model | Kernel Functions | MAE | RMSE | R2 |
|---|---|---|---|---|
| SVM | Linear | 0.017 | 0.017 | 0.919 |
| SVM | Quadratic | 0.002 | 0.003 | 0.997 |
| SVM | Cubic | 0.005 | 0.006 | 0.988 |
| SVM | Fine | 0.054 | 0.062 | 0.029 |
| SVM | Medium | 0.013 | 0.014 | 0.946 |
| SVM | Coarse | 0.021 | 0.025 | 0.832 |
| GPR | Rotational-Quadratic | 0.001 | 0.001 | 0.999 |
| GPR | Squared-Exponential | 0.001 | 0.001 | 0.999 |
| GPR | Matern 5/2 | 0.001 | 0.001 | 0.999 |
| GPR | Exponential | 0.006 | 0.008 | 0.982 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almukhtar, R.S.; Yahya, A.A.; Mahdy, O.S.; Majdi, H.S.; Mahdi, G.S.; Alwasiti, A.A.; Shnain, Z.Y.; Mohammadi, M.; AbdulRazak, A.A.; Philib, P.; et al. Numerical Analysis of Gas Hold-Up of Two-Phase Ebullated Bed Reactor. ChemEngineering 2023, 7, 101. https://doi.org/10.3390/chemengineering7050101
Almukhtar RS, Yahya AA, Mahdy OS, Majdi HS, Mahdi GS, Alwasiti AA, Shnain ZY, Mohammadi M, AbdulRazak AA, Philib P, et al. Numerical Analysis of Gas Hold-Up of Two-Phase Ebullated Bed Reactor. ChemEngineering. 2023; 7(5):101. https://doi.org/10.3390/chemengineering7050101
Chicago/Turabian StyleAlmukhtar, Riyadh S., Ali Amer Yahya, Omar S. Mahdy, Hasan Shakir Majdi, Gaidaa S. Mahdi, Asawer A. Alwasiti, Zainab Y. Shnain, Majid Mohammadi, Adnan A. AbdulRazak, Peter Philib, and et al. 2023. "Numerical Analysis of Gas Hold-Up of Two-Phase Ebullated Bed Reactor" ChemEngineering 7, no. 5: 101. https://doi.org/10.3390/chemengineering7050101
APA StyleAlmukhtar, R. S., Yahya, A. A., Mahdy, O. S., Majdi, H. S., Mahdi, G. S., Alwasiti, A. A., Shnain, Z. Y., Mohammadi, M., AbdulRazak, A. A., Philib, P., Ali, J. M., Aljaafari, H. A. S., & Alsaedi, S. S. (2023). Numerical Analysis of Gas Hold-Up of Two-Phase Ebullated Bed Reactor. ChemEngineering, 7(5), 101. https://doi.org/10.3390/chemengineering7050101








