Synthetic Packed-Bed Generation for CFD Simulations: Blender vs. STAR-CCM+
Abstract
:1. Introduction
2. Methods
2.1. Packing Generation
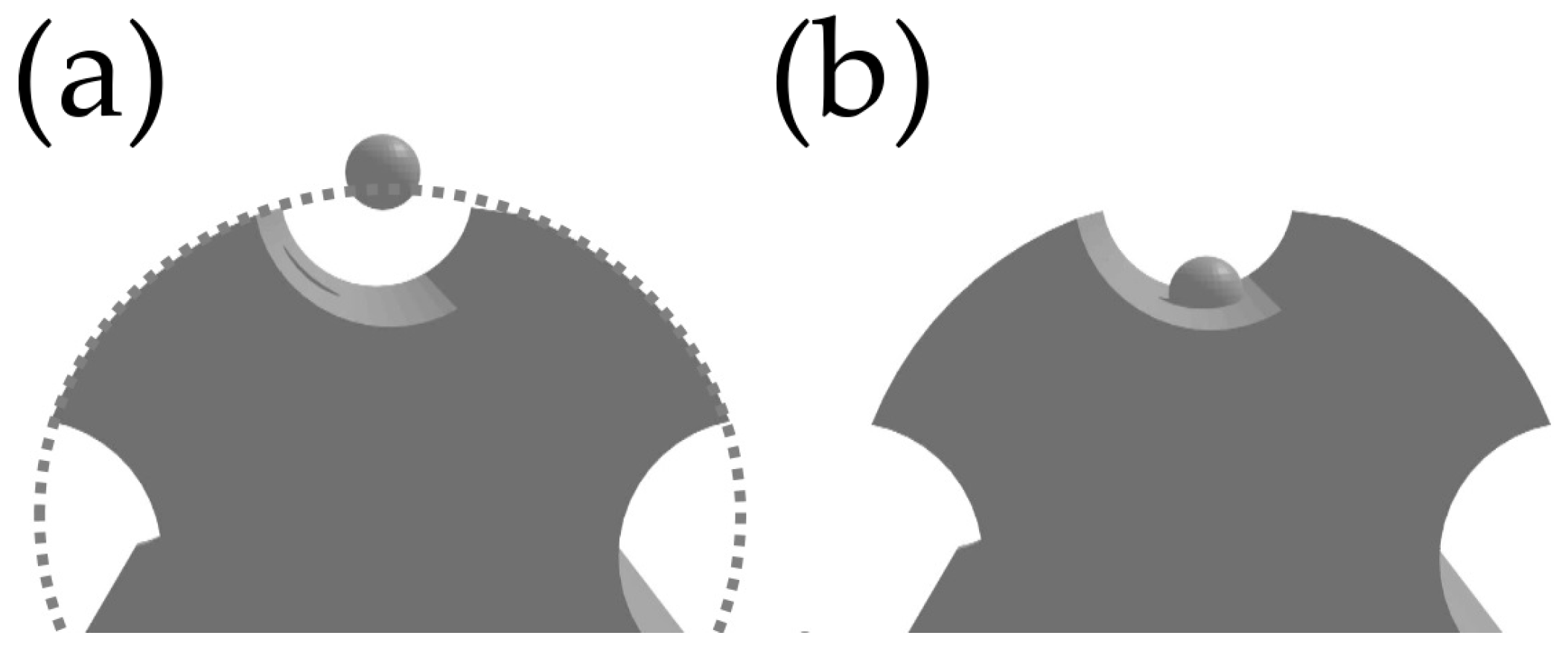
2.1.1. Discrete Element Method—Soft Body Approach in STAR-CCM+
- Density (used for calculation of the equivalent particle mass) (Equation (8))
- Young’s modulus (Equation (6))
- Poisson ratio (calculation of equivalent Young’s modulus) (Equation (6))
- Coefficient of restitution (Equation (7))
- Static friction factor (Equations (9) and (11))
2.1.2. Blender—Rigid Body Approach in Blender
2.2. CFD
2.2.1. Governing Equations
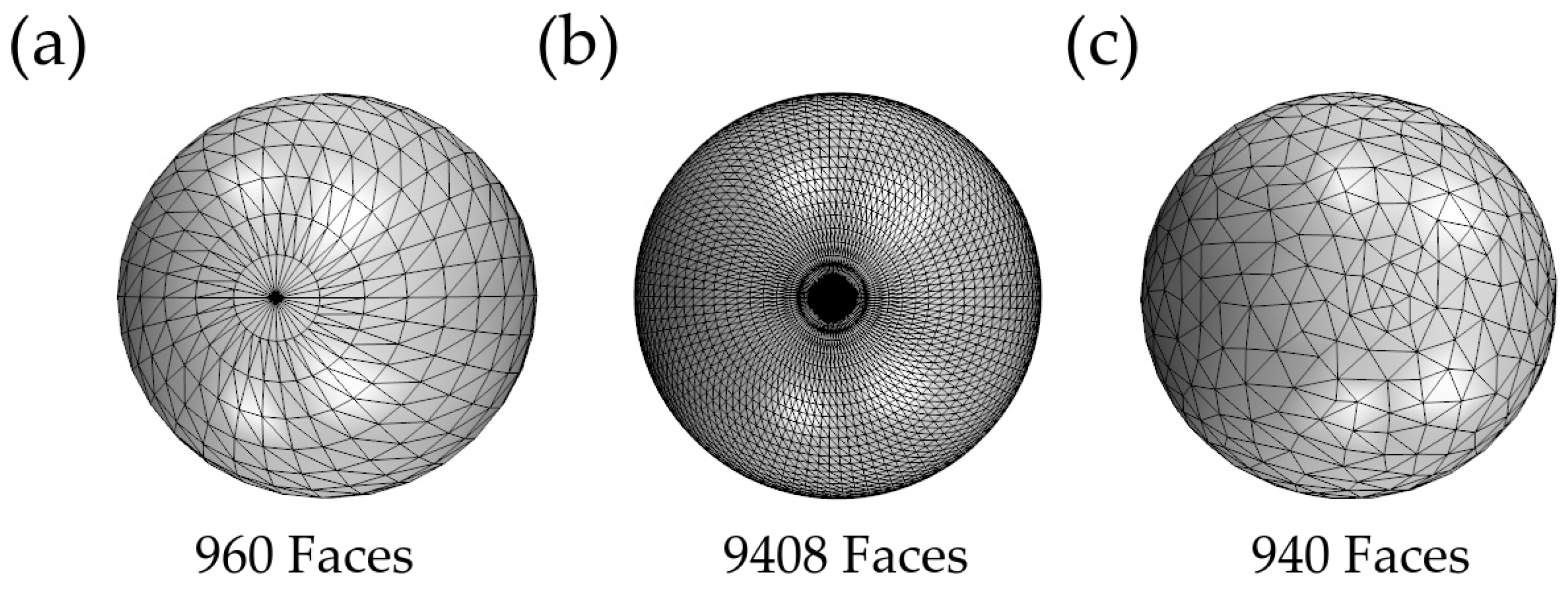
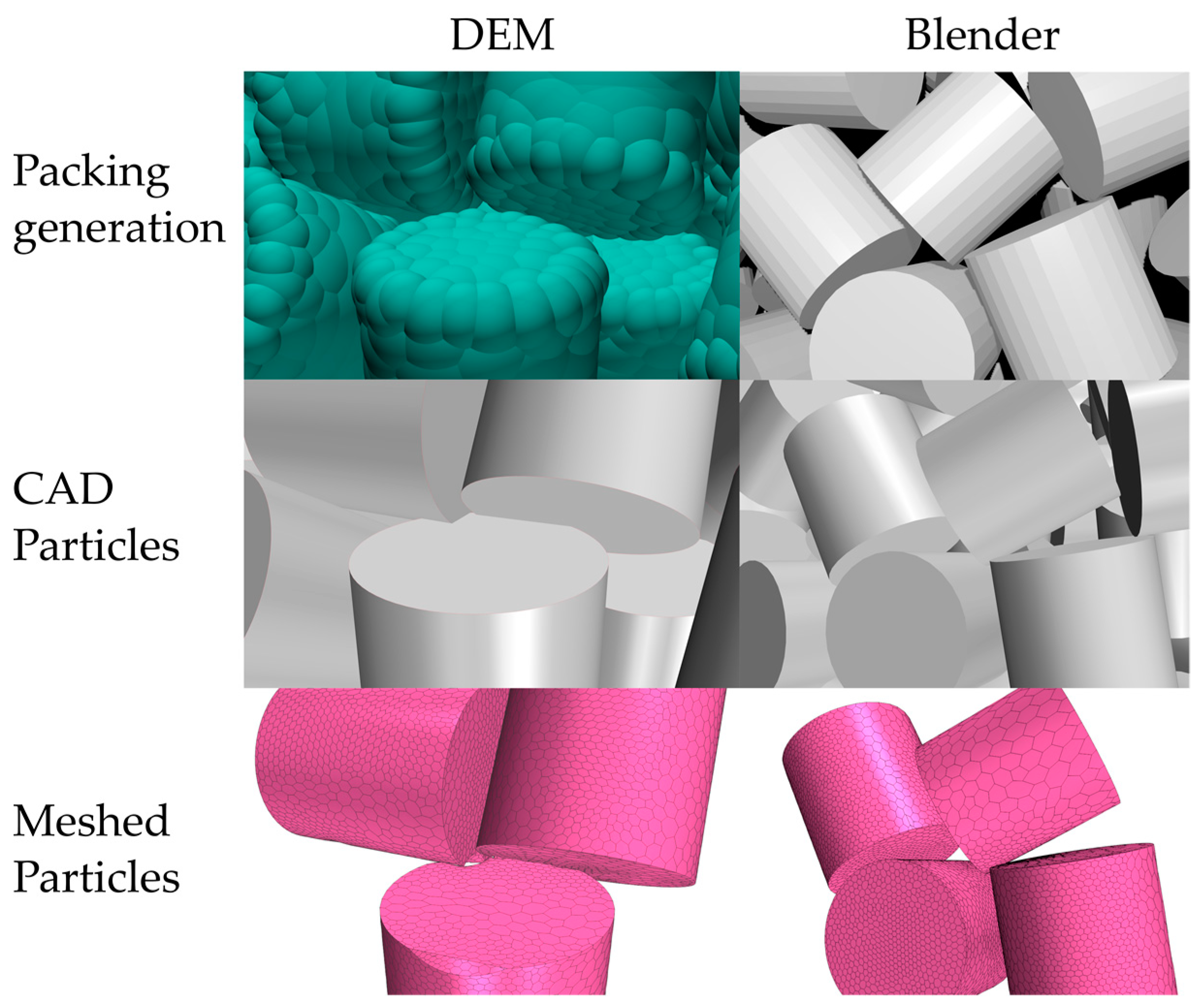
2.2.2. Meshing and Solving
2.2.3. Local Porosity Determination
2.2.4. Local Velocity Profiles
3. Numerical Setup
4. Results
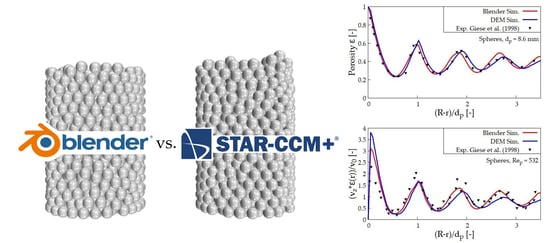
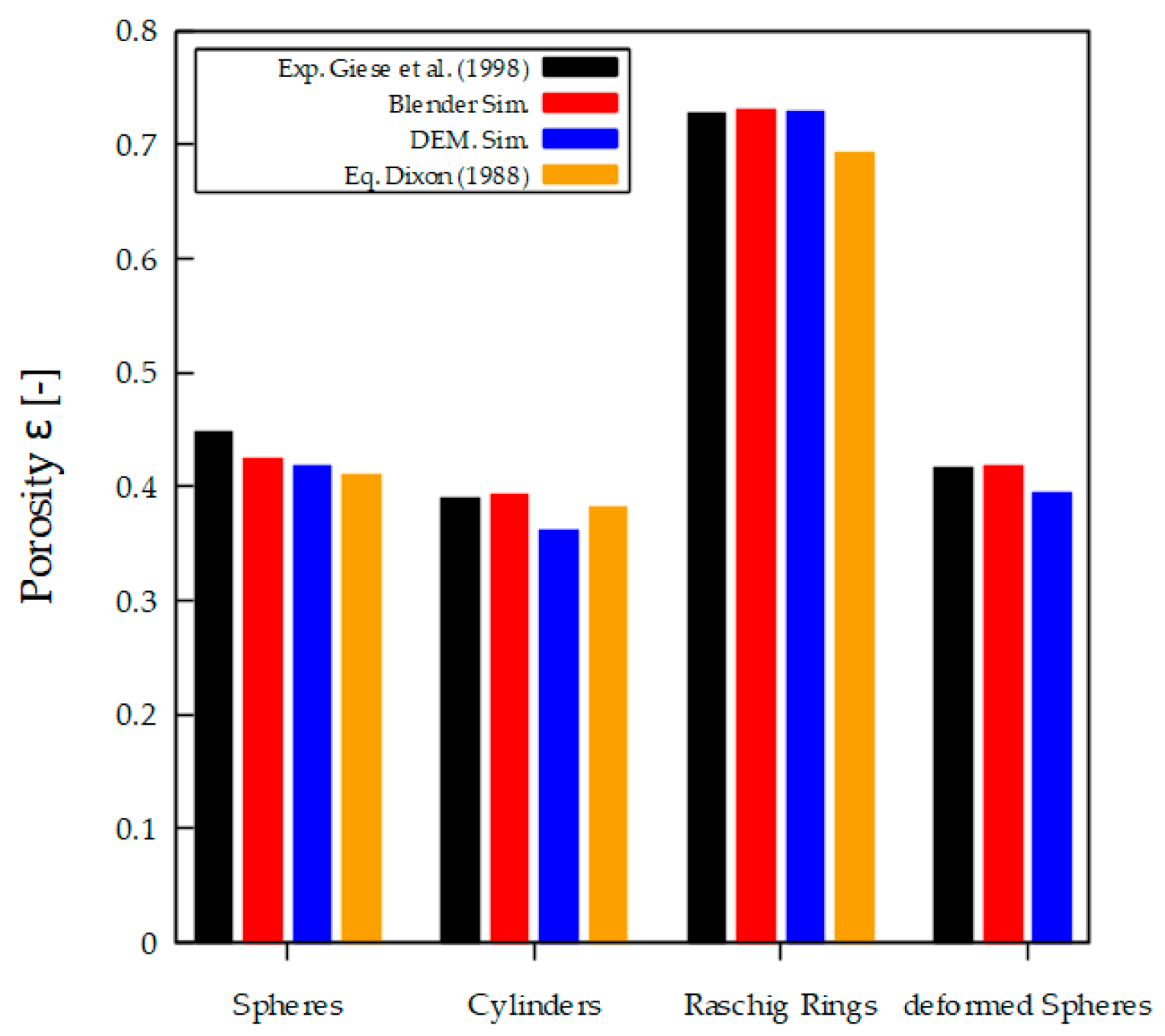
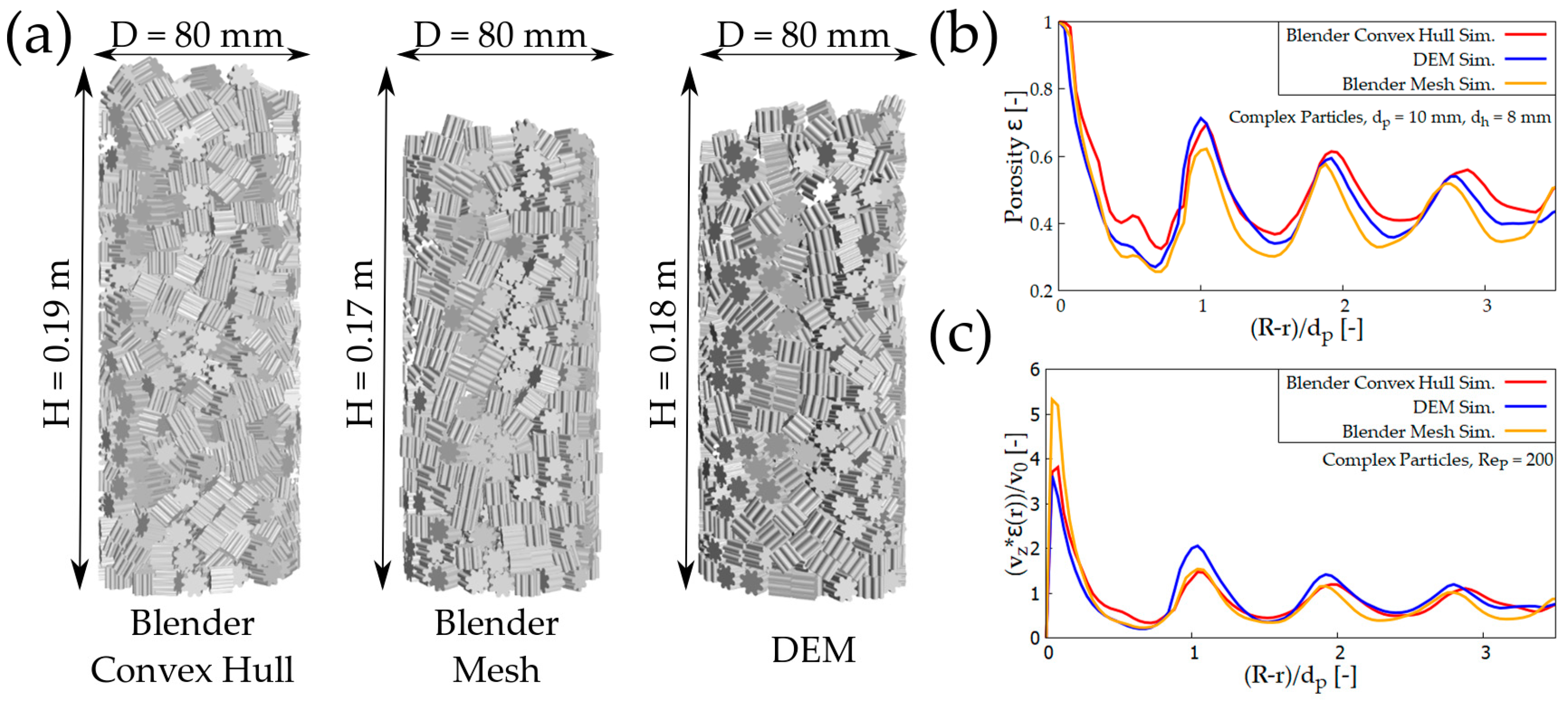
4.1. Overall Porosity
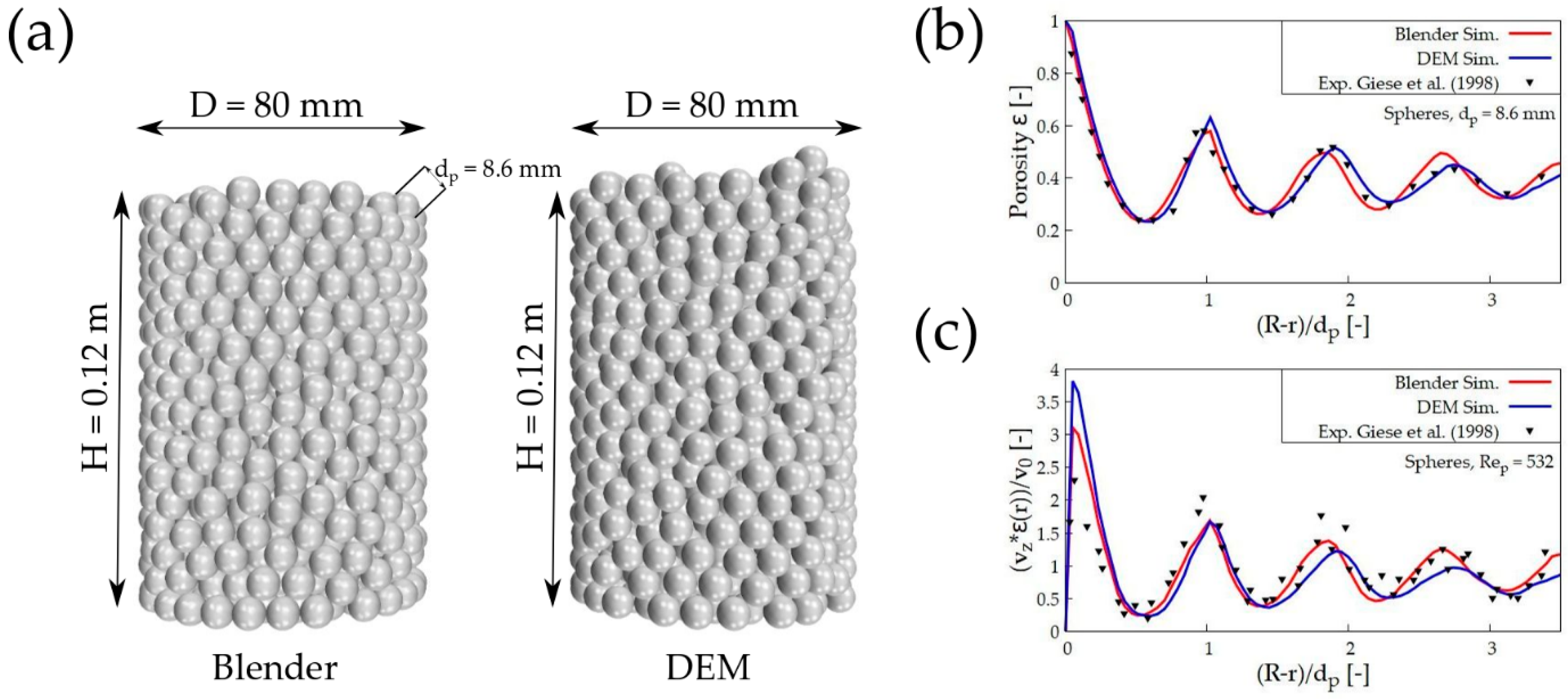
4.2. Spheres
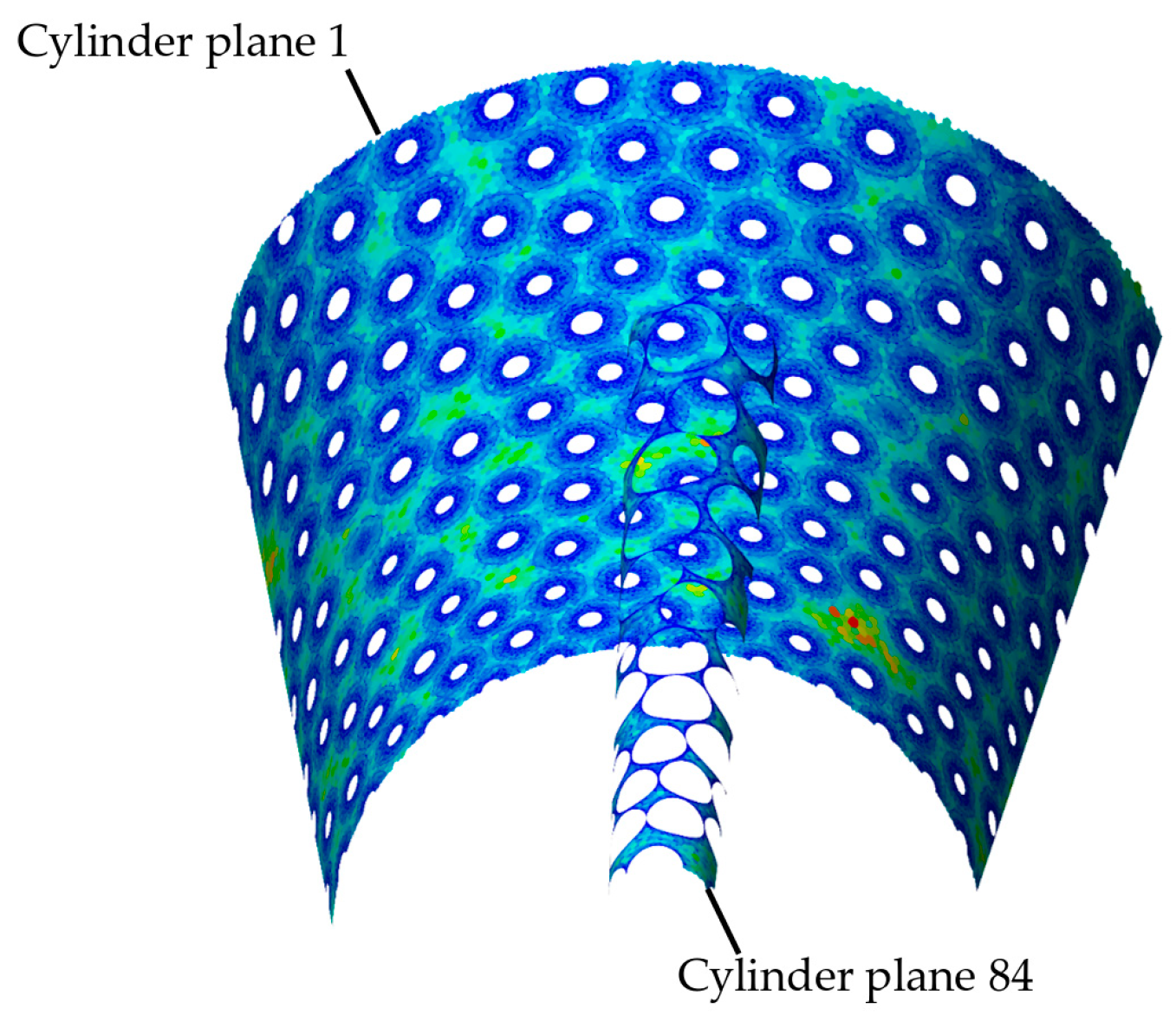
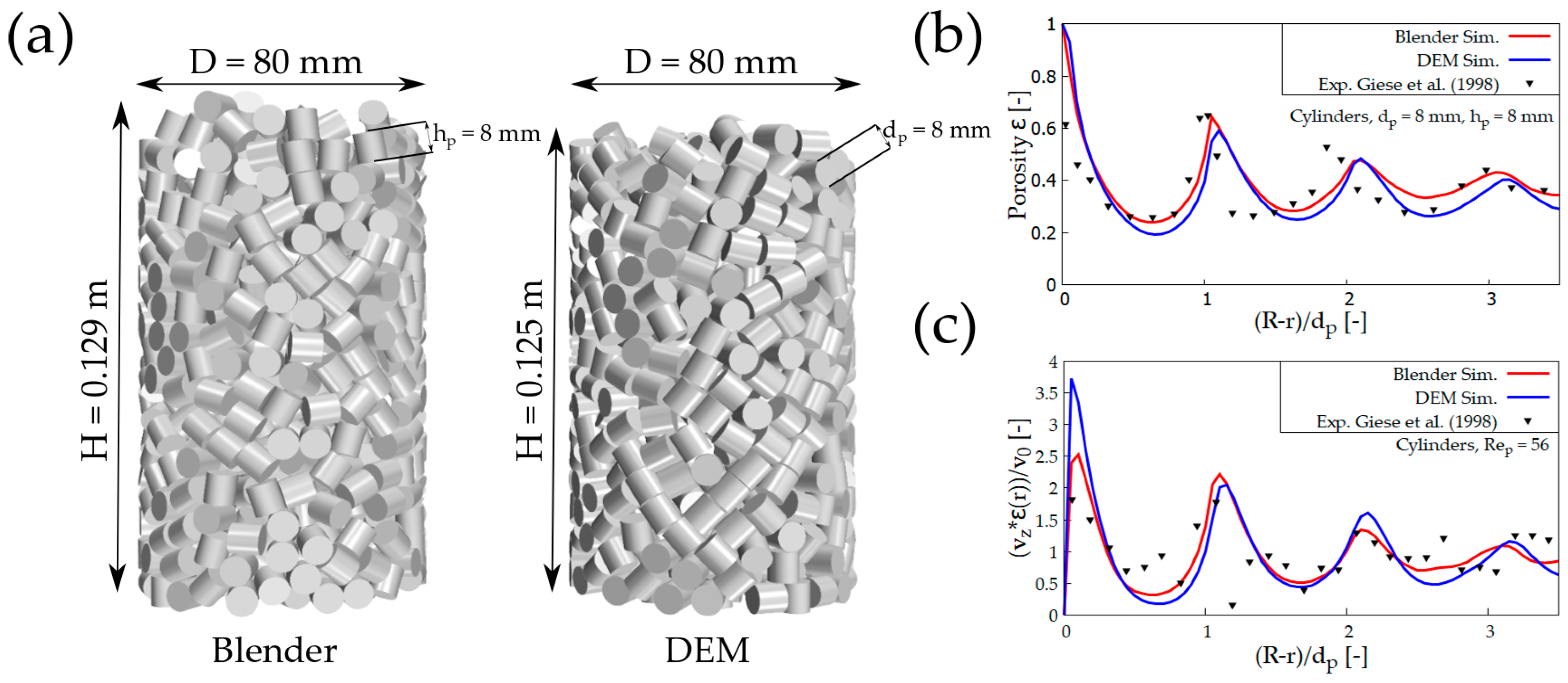
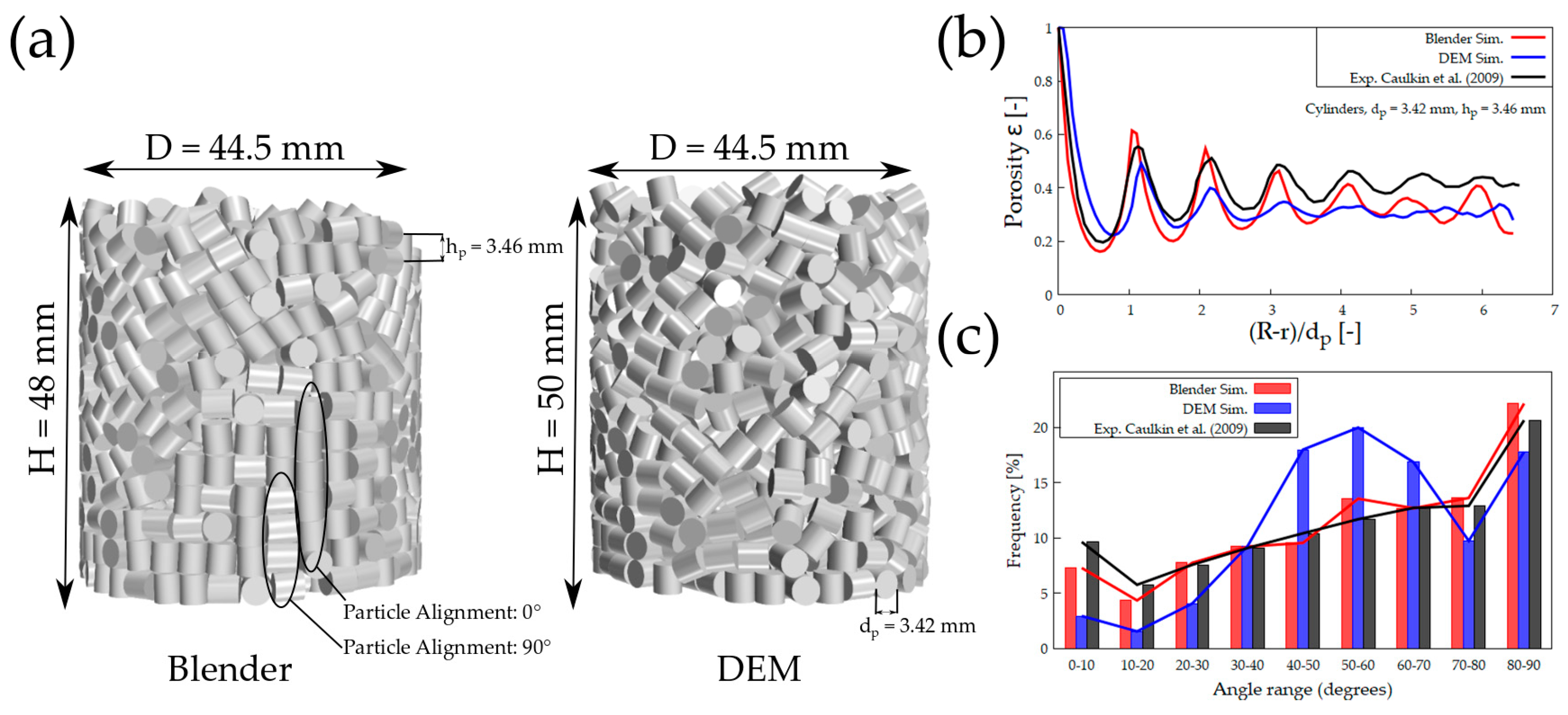
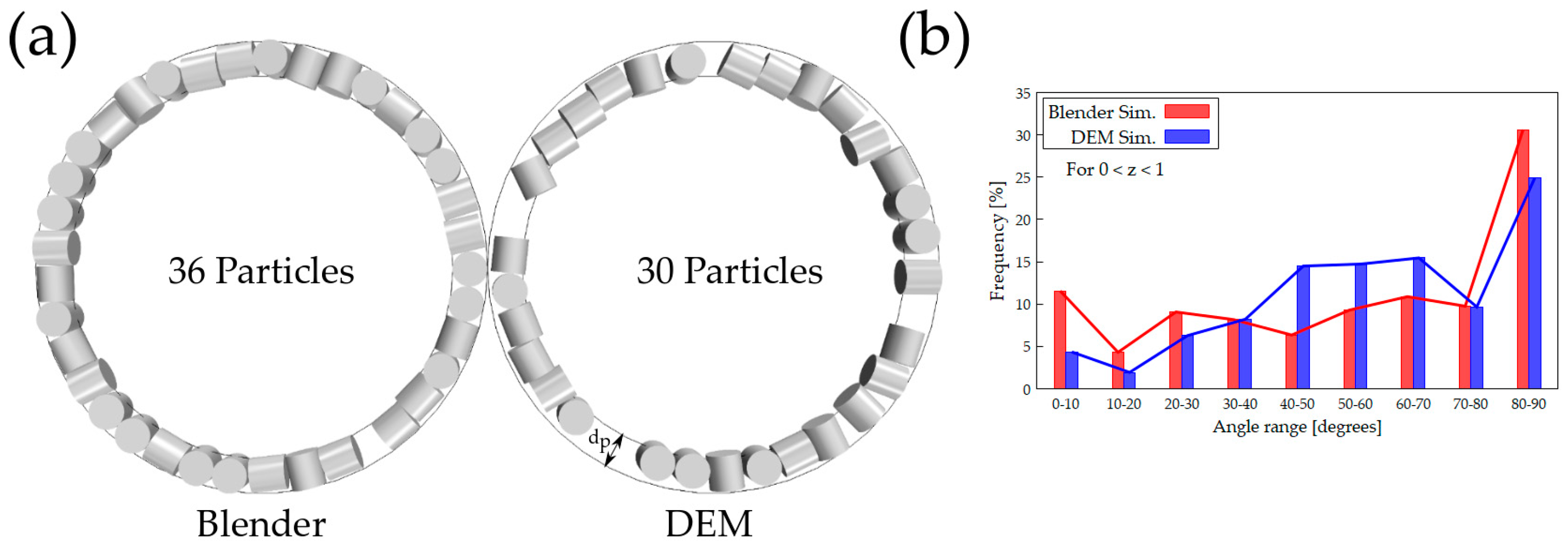
4.3. Cylinders
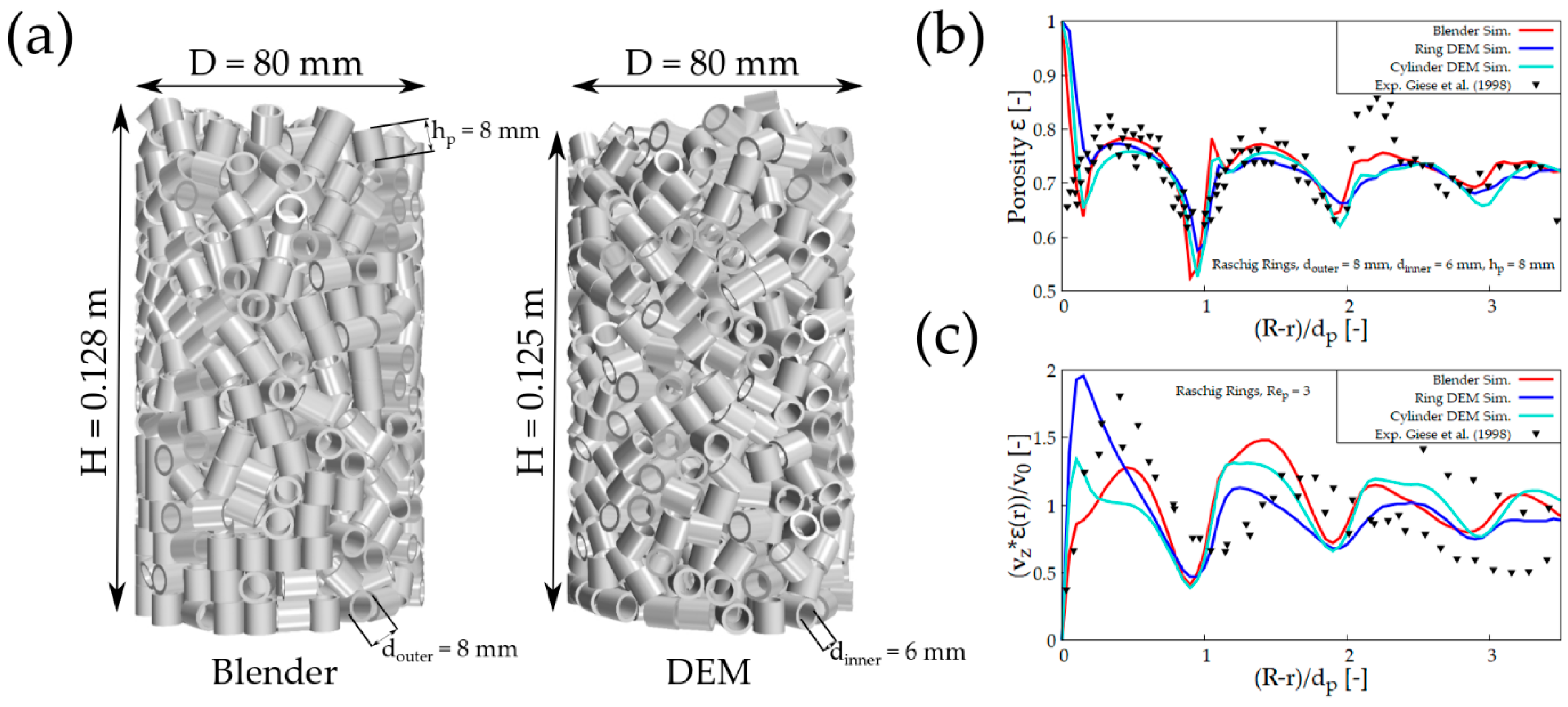
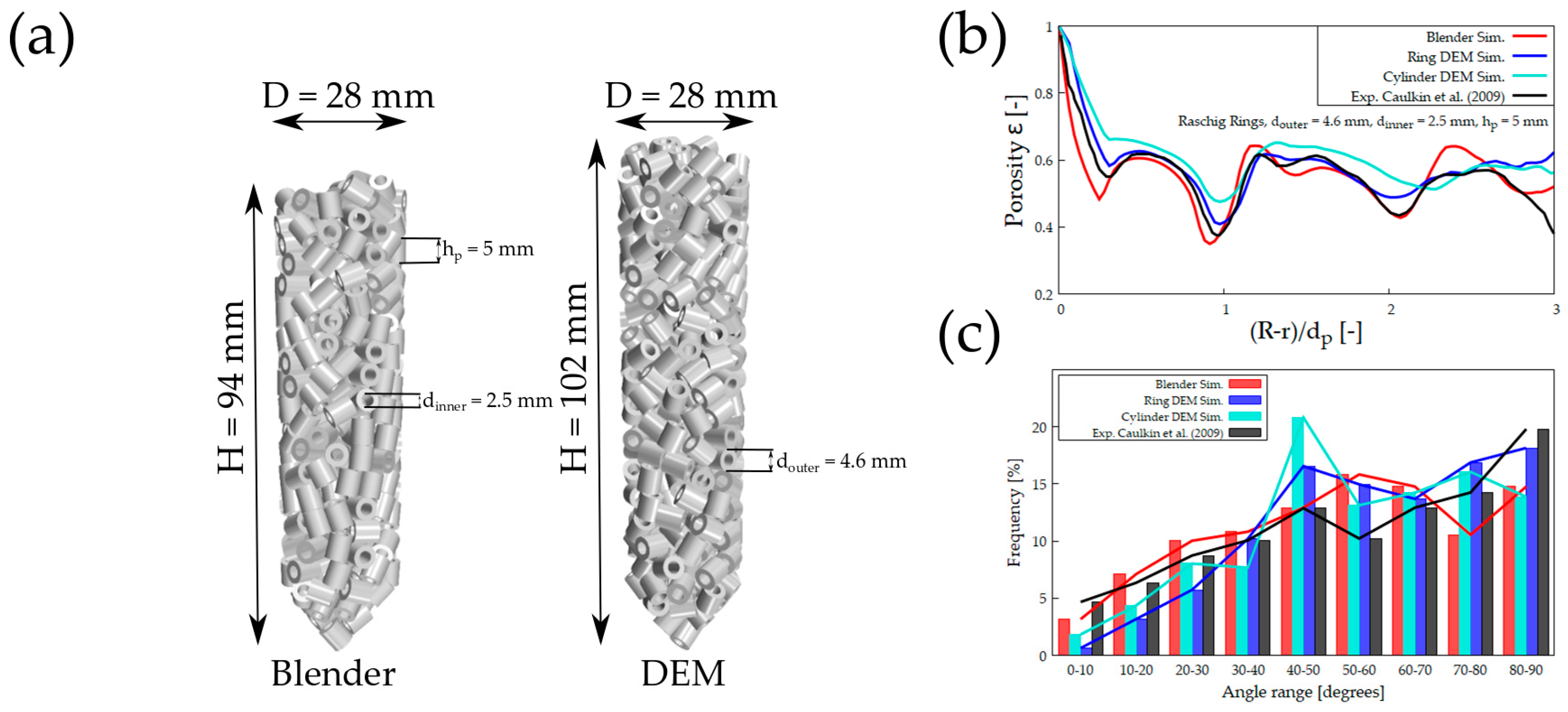
4.4. Raschig Rings
4.5. Complex Particles
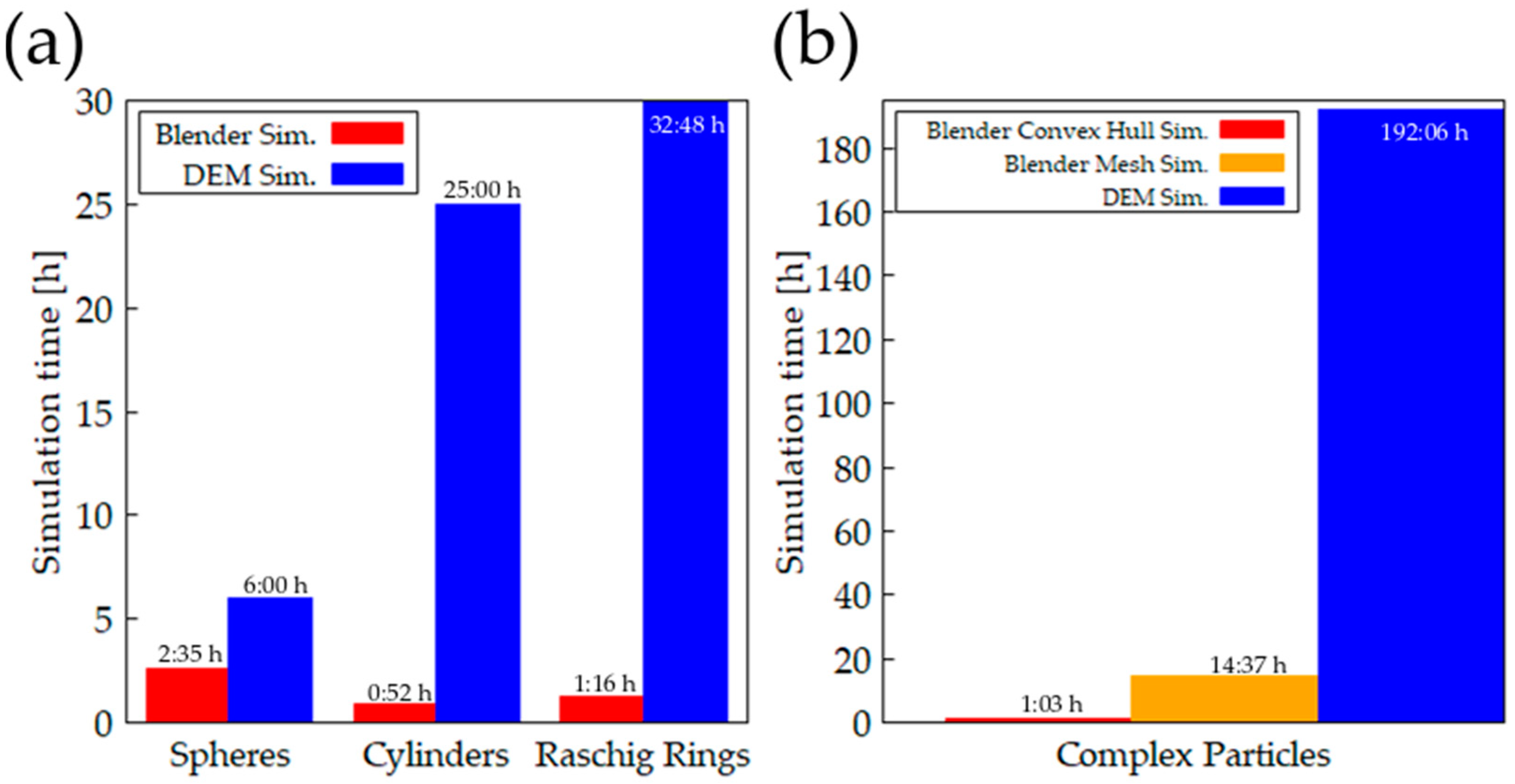
4.6. Simulation Time
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Latin Letters | ||
| area | ||
| overlaps | ||
| particle diameter | ||
| tube diameter | ||
| deformation tensor | ||
| coefficient of restitution | ||
| equivalent Young’s modulus | ||
| force (rigid body approach) | ||
| force (soft body approach) | ||
| body force | ||
| contact force | ||
| gravity force | ||
| surface force | ||
| height | ||
| moment of inertia | ||
| unit tensor | ||
| spring stiffness | ||
| mass | ||
| equivalent particle mass | ||
| unit normal vector | ||
| tube-to-particle-diameter ratio | ||
| damping | ||
| damping coefficient | ||
| pressure | ||
| radius | ||
| coefficient of determination | ||
| Reynolds number | ||
| equivalent radius | ||
| radius of radial position | ||
| unit normal vector | ||
| time | ||
| stress tensor | ||
| velocity | ||
| velocity | ||
| volume | ||
| Greek Letter | ||
| sliding speed | ||
| Boundary layer thickness | ||
| maximum overlap | ||
| porosity | ||
| dynamic viscosity | ||
| static friction coefficient | ||
| density | ||
| net moment | ||
| angular velocity | ||
| Subscripts | ||
| inlet | ||
| data obtained by the use of Blender | ||
| Blender object based pellet interaction | ||
| Blender object based container interaction | ||
| Phase based container-pellet interaction | ||
| part: Cylinder | ||
| part: Cylinder Plane | ||
| Data obtained by the use of DEM | ||
| amount of free space or volume | ||
| experimental data taken from Giese et al. (1998) | ||
| phase based pellet interaction | ||
| normal direction | ||
| tangential direction | ||
| amount of total space or volume | ||
| particle | ||
| additional tangential direction | ||
| specific radial velocity | ||
| Abbreviations | ||
| 3D | 3-dimensional | |
| DEM | Discrete Element Method | |
| CAD | Computer Aided Design | |
| CFD | Computational Fluid Dynamics | |
| CT | Computer Tomography | |
| MRI | Magnetic Resonance Imaging | |
| STL | Standard Triangulation Language | |
References
- Froment, G.F. Analysis and Design of Fixed Bed Catalytic Reactors Chemical Reaction Engineering; Bischoff, K.B., Ed.; American Chemical Society: Washington, DC, USA, 1972; Volume 109, pp. 1–55. [Google Scholar]
- Kulkarni, B.D.; Doraiswamy, L.K. Estimation of Effective Transport Properties in Packed Bed Reactors. Catal. Rev. 1980, 22, 431–483. [Google Scholar] [CrossRef]
- Eisfeld, B.; Schnitzlein, K. The influence of confining walls on the pressure drop in packed beds. Chem. Eng. Sci. 2001, 56, 4321–4329. [Google Scholar] [CrossRef]
- Andersson, K.E.B. Pressure drop in packed beds. Trans. Royal Inst. Technol. Stockholm 1963, 201. [Google Scholar]
- Dixon, A.G. Fixed bed catalytic reactor modelling-the radial heat transfer problem. Can. J. Chem. Eng. 2012, 90, 507–527. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. Packed Tubular Reactor Modeling and Catalyst Design using Computational Fluid Dynamics. In Advances in Chemical Engineering; Marin, G.B., Ed.; Elsevier textbooks, s.l.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 31, pp. 307–389. [Google Scholar] [CrossRef]
- Jurtz, N.; Kraume, M.; Wehinger, G.D. Advances in fixed-bed reactor modeling using particle-resolved computational fluid dynamics (CFD). Rev. Chem. Eng. 2018, 35. [Google Scholar] [CrossRef]
- Wang, Z.; Afacan, A.; Nandakumar, K.; Chuang, K.T. Porosity distribution in random packed columns by gamma ray tomography. Chem. Eng. Process. Process Intensif. 2001, 40, 209–219. [Google Scholar] [CrossRef]
- Baker, M.J.; Young, P.G.; Tabor, G.R. Image based meshing of packed beds of cylinders at low aspect ratios using 3d MRI coupled with computational fluid dynamics. Comput. Chem. Eng. 2011, 35, 1969–1977. [Google Scholar] [CrossRef]
- Hofmann, S.; Bufe, A.; Brenner, G.; Turek, T. Pressure drop study on packings of differently shaped particles in milli-structured channels. Chem. Eng. Sci. 2016, 155, 376–385. [Google Scholar] [CrossRef]
- Zeiser, T.; Steven, M.; Freund, H.; Lammers, P.; Brenner, G.; Durst, F.; Bernsdorf, J. Analysis of the flow field and pressure drop in fixed-bed reactors with the help of lattice Boltzmann simulations. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2002, 360, 507–520. [Google Scholar] [CrossRef] [PubMed]
- Caulkin, R.; Fairweather, M.; Jia, X.; Gopinathan, N.; Williams, R.A. An investigation of packed columns using a digital packing algorithm. Comput. Chem. Eng. 2006, 30, 1178–1188. [Google Scholar] [CrossRef]
- Caulkin, R.; Ahmad, A.; Fairweather, M.; Jia, X.; Williams, R.A. An investigation of sphere packed shell-side columns using a digital packing algorithm. Comput. Chem. Eng. 2007, 31, 1715–1724. [Google Scholar] [CrossRef]
- Caulkin, R.; Jia, X.; Fairweather, M.; Williams, R.A. Lattice approaches to packed column simulations. Particuology 2008, 6, 404–411. [Google Scholar] [CrossRef]
- Caulkin, R.; Jia, X.; Xu, C.; Fairweather, M.; Williams, R.A.; Stitt, H.; Nijemeisland, M.; Aferka, S.; Crine, M.; Léonard, A.; et al. Simulations of Structures in Packed Columns and Validation by X-ray Tomography. Ind. Eng. Chem. Res. 2009, 48, 202–213. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Kraume, M. CFD als Designtool für Festbettreaktoren mit kleinem Rohr-zu-Pelletdurchmesser-Verhältnis: Heute oder in Zukunft? Chem. Ingen. Tech. 2017, 89, 447–453. [Google Scholar] [CrossRef]
- Favier, J.F.; Abbaspour-Fard, M.H.; Kremmer, M.; Raji, A.O. Shape representation of axi-symmetrical, non-spherical particles in discrete element simulation using multi-element model particles. Eng. Comput. 1999, 16, 467–480. [Google Scholar] [CrossRef]
- Marigo, M.; Stitt, E.H. Discrete Element Method (DEM) for Industrial Applications: Comments on Calibration and Validation for the Modelling of Cylindrical Pellets. KONA 2015, 32, 236–252. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Cylindrical object contact detection for use in discrete element method simulations, Part II—Experimental validation. Chem. Eng. Sci. 2010, 65, 5863–5871. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Cylindrical object contact detection for use in discrete element method simulations. Part I—Contact detection algorithms. Chem. Eng. Sci. 2010, 65, 5852–5862. [Google Scholar] [CrossRef]
- Feng, Y.T.; Han, K.; Owen, D.R.J. A generic contact detection framework for cylindrical particles in discrete element modelling. Comput. Methods Appl. Mech. Eng. 2017, 315, 632–651. [Google Scholar] [CrossRef]
- Bender, J.; Erleben, K.; Trinkle, J. Interactive Simulation of Rigid Body Dynamics in Computer Graphics. Comput. Graph. Forum 2014, 33, 246–270. [Google Scholar] [CrossRef]
- Blender Org. Manual Homepage. Available online: https://docs.blender.org/manual/en/latest/game_engine/physics/introduction.html (accessed on 26 March 2019).
- Boccardo, G.; Del Plato, L.; Marchisio, D.; Augier, F.; Haroun, Y.; Ferre, D.; Icardi, M. Pore-scale simulation of fluid flow in packed-bed reactors via Rigid-Body simulations and CFD. In Proceedings of the 10th International Conference on CFD in Oil & Gas, Metallurgical and process Industries SINTEF, Trondheim, Norway, 17–19 June 2014. [Google Scholar]
- Boccardo, G.; Augier, F.; Haroun, Y.; Ferré, D.; Marchisio, D.L. Validation of a novel open-source work-flow for the simulation of packed-bed reactors. Chem. Eng. J. 2015, 279, 809–820. [Google Scholar] [CrossRef]
- Partopour, B.; Dixon, A.G. An integrated workflow for resolved-particle packed bed models with complex particle shapes. Powder Technol. 2017, 322, 258–272. [Google Scholar] [CrossRef]
- Fernengel, J.; Habla, F.; Hinrichsen, O. Scripting as an Approach to Automated CFD Simulation for Packed Bed Catalytic Reactor Modeling. Chem. Ingenieur Tech. 2018, 90, 685–689. [Google Scholar] [CrossRef]
- Pavlišič, A.; Ceglar, R.; Pohar, A.; Likozar, B. Comparison of computational fluid dynamics (CFD) and pressure drop correlations in laminar flow regime for packed bed reactors and columns. Powder Technol. 2018, 328, 130–139. [Google Scholar] [CrossRef]
- Giese, M.; Rottschäfer, K.; Vortmeyer, D. Measured and modeled superficial flow profiles in packed beds with liquid flow. AIChE J. 1998, 44, 484–490. [Google Scholar] [CrossRef]
- Siemens PLM STAR-CCM+ Homepage. Available online: https://mdx.plm.automation.siemens.com/star-ccm-plus (accessed on 14 March 2019).
- Blender Org. Manual Homepage. Available online: https://docs.blender.org/manual/de/dev/physics/rigid_body/introduction.html (accessed on 14 March 2019).
- MatWeb Material Property Data. Available online: http://www.matweb.com/search/DataSheet.aspx?MatGUID=c8c56ad547ae4cfabad15977bfb537f1 (accessed on 14 March 2019).
- MatWeb Material Property Data. Available online: http://www.matweb.com/search/DataSheet.aspx?MatGUID=cbe7a469897a47eda563816c86a73520 (accessed on 21 March 2019).
- Di Renzo, A.; Di Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Eppinger, T.; Jurtz, N.; Aglave, R. Automated workflof for spatially resolved packed bed reactors with spherical and non-spherical particles. In Proceedings of the 10th International Conference on CFD in Oil & Gas, Metallurgical and process Industries SINTEF, Trondheim, Norway, 17–19 June 2014. [Google Scholar]
- Wehinger, G.D.; Eppinger, T.; Kraume, M. Evaluating Catalytic Fixed-Bed Reactors for Dry Reforming of Methane with Detailed CFD. Chem. Ingenieur Tech. 2015, 87, 734–745. [Google Scholar] [CrossRef]
- Youtube. Available online: https://www.youtube.com/watch?v=Zz3I5Gbrguw (accessed on 7 April 2019).
- Blender Org. Manual Homepage. Available online: https://docs.blender.org/manual/de/dev/physics/rigid_body/properties.html (accessed on 11 July 2018).
- Dhole, S.D.; Chhabra, R.P.; Eswaran, V. A numerical study on the forced convection heat transfer from an isothermal and isoflux sphere in the steady symmetric flow regime. Int. J. Heat Mass Transf. 2006, 49, 984–994. [Google Scholar] [CrossRef]
- Eppinger, T.; Seidler, K.; Kraume, M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios. Chem. Eng. J. 2011, 166, 324–331. [Google Scholar] [CrossRef]
- Dixon, A.G. Correlations for wall and particle shape effects on fixed bed bulk voidage. Can. J. Chem. Eng. 1988, 66, 705–708. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Fütterer, C.; Kraume, M. Contact Modifications for CFD Simulations of Fixed-Bed Reactors: Cylindrical Particles. Ind. Eng. Chem. Res. 2017, 56, 87–99. [Google Scholar] [CrossRef]

| CAD-Geometry |  |  |  |  |
| Composite Particle of 100 Spheres |  |  |  |  |
| Composite Maximum |  560 spheres | 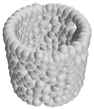 449 spheres |  543 spheres |  441 spheres |
| Size | Value |
|---|---|
| Base Size | |
| Target Surface Size | |
| Minimum Surface Size | |
| Prism Layer Total Thickness | (26) |
| Method | DEM | Rigid Body |
|---|---|---|
| Software |
|
|
| Solver settings |
|
|
|
| |
|
| |
| Friction |
|
|
| Restitution |
|
|
| Collision margin |
|
|
| Damping |
|
|
| Density |
|
|
| ||
| Young’s modulus |
|
|
| Poisson-Number |
|
|
| Particle shape |
|
|
| Source | Particle | Dimension | Boundary Conditions |
|---|---|---|---|
| Giese et al. [30] | Sphere | ||
| Cylinder | |||
| Raschig ring | |||
| Caulkin et al. [15] | Cylinder | ||
| Raschig ring | |||
| No reference | Complex Particles |
| Source | Particle | Packing Generation | ||
|---|---|---|---|---|
| Time Step | Solver Iterations | Number of Particles | ||
| Giese et al. [30] | Sphere | |||
| Cylinder | ||||
| Raschig Ring | ||||
| Caulkin et al. [15] | Cylinder | |||
| Raschig Ring | ||||
| No reference | Complex Particles | Blender Mesh: | Blender Mesh: | |
| Shape | ||
|---|---|---|
| Blender | DEM | |
| Spheres | ||
| Cylinders | ||
| Raschig rings | , | |
| Total | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flaischlen, S.; Wehinger, G.D. Synthetic Packed-Bed Generation for CFD Simulations: Blender vs. STAR-CCM+. ChemEngineering 2019, 3, 52. https://doi.org/10.3390/chemengineering3020052
Flaischlen S, Wehinger GD. Synthetic Packed-Bed Generation for CFD Simulations: Blender vs. STAR-CCM+. ChemEngineering. 2019; 3(2):52. https://doi.org/10.3390/chemengineering3020052
Chicago/Turabian StyleFlaischlen, Steffen, and Gregor D. Wehinger. 2019. "Synthetic Packed-Bed Generation for CFD Simulations: Blender vs. STAR-CCM+" ChemEngineering 3, no. 2: 52. https://doi.org/10.3390/chemengineering3020052
APA StyleFlaischlen, S., & Wehinger, G. D. (2019). Synthetic Packed-Bed Generation for CFD Simulations: Blender vs. STAR-CCM+. ChemEngineering, 3(2), 52. https://doi.org/10.3390/chemengineering3020052