Abstract
A common reactor type in the chemical and process industry is the fixed-bed reactor. Accurate modeling can be achieved with particle-resolved computational fluid dynamic (CFD) simulations. However, the underlying bed morphology plays a paramount role. Synthetic bed-generation methods are much more flexible and faster than image-based approaches. In this study, we look critically at the two different bed generation methods: Discrete element method (DEM) (in the commercial software STAR-CCM+) and the rigid-body model (in the open-source software Blender). The two approaches are compared in terms of synthetically generated beds with experimental data of overall and radial porosity, particle orientation, as well as radial velocities. Both models show accurate agreement for the porosity. However, only Blender shows similar particle orientation than the experimental results. The main drawback of the DEM is the long calculation time and the shape approximation with composite particles.
1. Introduction
Fixed-bed reactors are frequently used in the chemical and process industry, e.g., in heterogeneous catalysis, where the products are separated from the catalyst. Such catalytic fixed-bed reactors can be described with conventional engineering models on several levels of detail ranging from pseudo-homogeneous one-dimensional models to heterogeneous two-dimensional models [1,2]. For reactor arrangements with a low tube-to-particle diameter ratio , the effect of the confining walls have a large impact on the flow field and hence on the pressure drop [3,4], radial heat transfer [5] and consequently on the reaction rates. Over the last two decades, experiments of small N packed beds were accompanied with particle-resolved computational fluid dynamic (CFD) simulations in order to investigate the local interactions of transport phenomena, also in combination with local reaction kinetics [6,7].
In these particle-resolved CFD simulations, the fixed-bed morphology has to be as realistic as possible, which leads to additional challenges. Image-based methods provide more or less direct information of the bed morphology. For example, Wang et al. [8] conducted gamma-ray experiments to receive statistical information about a fixed bed consisting of Pall rings and evaluated them with a reconstruction algorithm. In another study, magnetic resonance imaging (MRI) was utilized to generate three-dimensional geometries for CFD simulations [9]. Similar to a two-dimensional image consisting of pixels, these images consist of three-dimensional voxels, which have to be converted into a surface description of the particle bed. The downside of a real image of a packed bed is the high expenditure of time and the special equipment required for scanning. In addition, the transition between the solid particles and the free space is mapped without a clear boundary, requiring an algorithm to precisely define the boundaries of the particle [10]. One possibility to create a random structure is the Monte Carlo method, where particles are randomly arranged in a container [11,12,13]. If a certain stability criterion is met, the particle is kept at this position, otherwise, it is deleted. This process is repeated until a certain fixed-bed height is reached. Whereas the bed porosity is satisfactorily reproduced by Monte Carlo algorithms, Caulkin et al. [14,15] showed that the local particle orientation was not in acceptable agreement with corresponding experiments.
The most widely used numerical method to generate synthetically packed-bed structures is the Discrete Element Method (DEM), based on the original work of Cundall and Strack [16]. In the DEM, the particles are filled into a container and Newton’s equation of motion are solved for the spherical particles. In the model, restitution and friction are taken into account. Furthermore, the contact forces between the particles (and between particles and the wall) are considered. The DEM has advantages over the Monte Carlo method, as it describes the physical process of filling more accurately. Wehinger and Kraume [17] showed satisfactory agreement of radial porosity profiles between packed beds of spheres and cylinders generated with DEM in comparison with experimental data. One disadvantage of the DEM is the very high computing effort since the contact forces for each generated particle must be determined. In addition, the contact forces are modeled on the basis of a sphere, so that the representation of non-spherical pellets results in composite pellet [18,19]. Kodam et al. [20,21] developed a sophisticated contact-detection algorithm for cylindrical particles. Based on different contact scenarios, the authors proposed equations to calculate the overlap, location, and normal vector of the contacts between two cylindrical particles and between the particle and the wall. More recently, this approach was generalized and included into a more comprehensive workflow [22].
Rigid body simulations, such as joints, motors, collisions and contacts with friction, are very common in computer games, animation software and film production. Consequently, over the last two decades, powerful software tools have been developed to capture such actions as realistic as possible [23]. One of them is Blender, an open source software, which has a physical library, Bullet Physics Library, included [24]. Recently, several research groups have been working on the possibility of using Blender for synthetic fixed-bed generation, see References [25,26,27,28,29].
Boccardo et al. [25] firstly mentioned the application of Blender to generate packed beds of different particle shapes. This possibility of the very fast and computationally efficient computer graphics code to simulate complex particles represents the main advantage of Blender, while the generated packings showed a realistic description. Later, Boccardo et al. [26] presented an open-source workflow for the CFD simulation of packed bed reactors, where spheres, cylindrical beads, and trilobes were tested. Partopour and Dixon [27] validated bed structures of different pellet shapes generated with Blender with correlations from literature and experimental data from Giese et al. [30]. In addition, the authors compared the particle alignment of cylinders with experimental data from Caulkin et al. [15]. They found a general agreement between simulations and experiments. However, modeling details of the bed generation process and simulations times were not presented. Due to the easy access and in Blender included Python scripting, the authors presented an own automation script for packed-bed generation. Fernengel et al. [28] also used a Python script for a workflow of CFD simulations for packed-bed reactors in OpenFOAM. Finally, Pavlišič et al. [29] applied Blender for beds of spherical and arbitrary particles (cylinders, trilobes and quadrilobes) and investigated with CFD simulations the pressure drop in packed beds. All these publications show that Blender is an easy-to-use open source tool for the synthetic generation of fixed beds with a high degree of automation.
Many authors claim that Blender is a computationally efficient tool to generate packed beds. To date, no comparison of different generation times has been shown. In addition, many studies compare the synthetically generated beds only with experimental data and not with alternative approaches. In this study, two approaches are applied to generate packings, of different particle shapes, i.e., the rigid body approach represented by Blender and the commonly used soft body DEM represented by STAR-CCM+ from Siemens PLM to generate packed beds made of different particle shapes [31]. The comparison between the two approaches involves accuracy with experimentally derived mean porosity values, radial porosity profiles, particle-orientation distribution, generation time, as well as CFD simulations based on the generated beds in terms of local velocity profiles. After a closer look at the methods, the results are presented and discussed, and finally, a conclusion with modeling recommendations are given.
2. Methods
2.1. Packing Generation
In this study, the discrete element method (DEM) is applied in the framework of the CAE software STAR-CCM+ from Siemens PLM [31]. DEM is a Soft Body Approach that takes into account the deformation of bodies under the influence of acting forces [16]. In Blender, on the contrary, the objects are assumed rigid and not deformable (Rigid Body Approach) [32]. This simplification is justified for most catalyst carriers since they consist of ceramic materials, which do not show any deformations under acting forces. They are characterized by a high shear modulus, i.e., the relationship between shear stress and shear strain. The typical shear modulus for ceramics is in the order of 150 GPa, whereas deformable materials such as rubber show values in the order of 0.2 GPa [33,34]. In the following, the applied methods for both approaches are presented and the possibility of adjustments will be discussed in more detail.
2.1.1. Discrete Element Method—Soft Body Approach in STAR-CCM+
The discrete element method is a soft body approach based on the original work Cundall and Strack [16]. It considers particles, in the original work spheres, as deformable bodies. Interactions between the objects are calculated with the momentum balance equation (Newton’s second law).
The contact forces between the objects are calculated using a spring-dashpot system. With its repulsive forces, the spring ensures that the particles are pushed apart representing the elastic part of a collision. The dashpot, on the other hand, represents the energy dissipation by reducing the collision forces simulating inelastic impacts. The forces are distributed in different directions. The normal force is represented by a parallel spring-dashpot system, while the force in the tangential direction to the contact surface is represented by a parallel spring-dashpot system connected in series with a slider. The contact force between two spheres is calculated according to (4) as the sum of the normal and tangential forces magnitudes and the unit normal vectors and .
In this soft body approach, the deformation of the particles under acting forces is characterized by allowing overlaps between each other. STAR-CCM+ offers various models for the calculation of these individual forces: Hertz-Mindlin no-slip contact model, linear spring contact model, and Walton Braun hysteretic contact model. The simplest model is the Linear Spring model, which assumes a linear relationship between the contact force and overlaps. A comparison of different models can be found elsewhere [35]. The description of the contact force in the normal direction is given by a term for the spring and the dashpot. It depends on the normal spring stiffness , the damping , the overlaps in normal direction and the velocity at the contact point .
Therefore the normal spring stiffness is calculated with the equivalent Radius of the contacting spheres, the maximum overlap and the equivalent Young’s modulus :
In order to determine damping, the damping coefficient is required, which is only dependent on the set coefficient of restitution :
With this damping coefficient, as well as the normal spring stiffness and the equivalent particle mass , the damping of the system in normal direction can be calculated:
The equations shown for the normal direction are also formulated equivalently for the tangential direction. As a special feature, therefore, only the contact force in tangential direction should be considered, since this depends on the condition shown in Equation (9).
The additional material property is the static friction coefficient , which is an important factor in fixed-bed filling processes. If the condition in Equation (9) is fulfilled, Equation (10) applies, otherwise Equation (11) applies.
For further information on the equations and other contact force models, please refer to the STAR-CCM+ manual and relevant DEM literature, e.g., Di Renzo and Di Maio [35], Zhu et al. [36]. In the equations above, the material property values are:
- Density (used for calculation of the equivalent particle mass) (Equation (8))
- Young’s modulus (Equation (6))
- Poisson ratio (calculation of equivalent Young’s modulus) (Equation (6))
- Coefficient of restitution (Equation (7))
- Static friction factor (Equations (9) and (11))
The contact forces are calculated on the basis of a sphere. However, this consideration becomes challenging, for non-spherical particles. The most frequently used method is the use of composite particles. Complex particles are approximated with a user-defined number of spheres. These are merged together in such a way that the shape of the composite particle approaches the original particle shape. The outer surface of the spheres is used for contact detection and force modelling [18]. With a higher number of spheres, the accuracy of the particle description is increasing. It has to be considered that a representation with few spheres allows faster simulations but due to the inaccurate representation of the particles with no sharp edges, the resulting solution might deviate largely. For further information please refer to Marigo and Stitt [19], where the effects of different shape approximations are investigated for two configurations for a rotating drum. As examples, in Table 1 the composite particle description for different particles and different accuracy are shown.

Table 1.
Different particle geometries and composite particle approximation.
Remember that a higher number of spheres leads to a more exact approximation (e.g., sharper edges), but also to higher simulation times. Therefore, the choice of the number of spheres represents a compromise between accuracy and calculation time. For complex particle shapes with convex and concave surfaces, even with a high number of spheres, the approximation is still far from the Computer Aided Design (CAD) model. In order to keep the particles to be simulated as simple as possible, cylindrical shapes with inner holes, such as Raschig rings or multi-hole cylinders, can be described by a full cylinder [37,38]. After the DEM simulation, the composite particle is transformed back into the original CAD particle shape. This approach was used in these publications for lowering of computational time since the full-cylinder approximation is made by a fewer number of composite DEM spheres. Since there is a difference in geometry and mass, there might be a difference in bed structure resulting from this approximation. In the presented references, there was no comparison made between the full-cylinder DEM approach and a DEM approximation of a hollow cylinder. For a closer look at the influence of the approximation methods on the bed structure, in this work, a Raschig ring shape was modeled based on a full-cylinder shape and an approximation of the hollow cylinder as shown in Table 1. The differences between porosity and velocity profiles, as well as simulation time, will be presented later in the results section.
2.1.2. Blender—Rigid Body Approach in Blender
Blender has various methods with which fixed beds can be generated. In addition to the rigid body simulation discussed here, it is also possible to consider a soft body approach. However, since this method is very computationally intensive, only the rigid body simulation will be referred to in the following. Rigid bodies are idealized bodies where the distance between each pair of points on the surface of the body never changes, even when forces are applied [23]. While catalyst pellets are from robust materials, it can be assumed that this approach of non-deformation is appropriate. For a comparison between a rigid body and soft body simulation in Blender see Reference [39]. The motion is modeled using the Newton-Euler equations, a system of differential equations based on Newton’s laws [23]. The net force acting on the body is equal to the change of the translation momentum ) with time (12):
For the description of the rotation movement, the net moment is represented by the change of the rotation moment with time Equation (13):
The force is the vector sum of all forces acting on the body, while is the vector sum of all moments of all forces and pure moments. To describe point contacts between objects, the Coulomb friction model is used, which requires contact at a single point. The contact force is divided into a normal component and two orthogonal components and . Similarly, the relative velocities between the contact points are divided into normal and tangential components. A negative speed in the normal direction is not allowed since this would be accompanied by an overlap of the objects. The Coulomb model uses a Friction Cone, which can be described by Equation (14). The contact force is larger than zero, because bodies only press against each other, but do not pull against.
The force depends on the static friction factor and the normal force used in Equations (15) and (16) to calculate the tangential force components and .
The other factors are the tangential velocity components and of velocity at the contact point, which are also used to calculate the sliding speed Equation (17).
For further information on the theory of rigid body simulation in video-animation programs, see e.g., Reference [23].
In contrast to the DEM, where contact forces are calculated based on a sphere, in Blender, the contact between objects is calculated based on the actual faces. This leads to the possibility to use the original three dimensional (3D) CAD model for the filling simulation. It has shown that simulation time of Blender is scaling with the number of faces so that a closer look at geometry approximation is necessary. If the particle geometry comes from a 3D-CAD program, the triangulation of surface mesh is very fine and leads to long simulation times. For this reason, the CAD surface has to be re-meshed in view of the trade-off between exact geometry representation (fine surface mesh) and computational cost (coarse surface mesh). A closer look at different surface triangulations of a sphere gives Figure 1. A sphere generated in Blender shows a total number of 960 triangles (Figure 1a). With STAR-CCM+, the sphere’s surface is approximated with 9408 faces (Figure 1b). Applying the option Decimate Geometry in Blender transforms the STAR-CCM+ surface into what is shown in Figure 1c. This procedure can be also applied in Blender for non-spherical pellets but might be also performed with other CAD software.
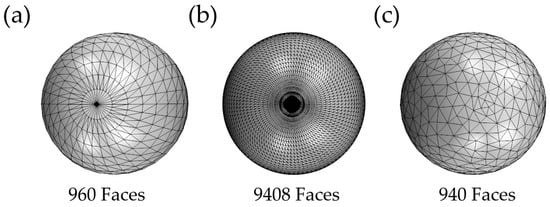
Figure 1.
Different surface triangulations of a sphere: (a) Blender, (b) STAR-CCM+, (c) using Blender option Decimate Geometry on (b).
While the triangulated sphere from Blender in Figure 1a and the 3D-CAD model sphere from STAR-CCM+ in Figure 1b have an inhomogeneous mesh, where faces get smaller in the direction of the pole, in the decimated geometry (Figure 1c) the triangle faces are equally sized. Such a distributed mesh is preferred because otherwise the restitution and friction are not independent on the location of the contact. The difference of the methods in terms of friction and restitution are the phase interaction approach in DEM and the object based approach in Blender. Friction and restitution can be directly defined for every object created in a Blender scene. For collisions between two objects, the static friction factor is calculated by multiplying friction factors of the single objects . The factor needs to be calculated from the static friction factor , belonging to the considered phase interaction. For the Blender object based friction factor of pellets and container (18) and (19) were used:
In analogy, the coefficient of restitution is defined in DEM for phase interactions and in Blender for single objects with the Equations (20) and (21):
The formulation in Blender makes it difficult to map more complex systems with more than two materials. The fixed-bed filling process, which only consists of two materials (container and pellets), can be simulated with the help of Equations (20) and (21). A further setting in Blender is the collision margin, which indicates the distance to the object at which the collision should occur. In order to correctly map the collisions between the particles and between particles and the wall, this value must be set to zero, as mentioned by Partopour et al. [27]. Otherwise, the collision does not occur at the surfaces of the bodies. The recommended value in Blender is 40 mm since the best results were achieved with values greater than zero [40]. In contrast to packed bed-filling processes, collision simulations in typical Blender applications take place at much larger dimensions.
2.2. CFD
2.2.1. Governing Equations
Computational fluid dynamics are based on the well-known conservation equations of mass, momentum, energy, and species mass. For details on CFD modeling for fixed-bed reactors, see e.g., Dixon et al. [6] and Jurtz et al. [7]. In this study, only steady-state cold flow CFD simulations were carried out. The conservation of mass is given by:
where is the fluid density and is the velocity vector. Furthermore, the conservation of momentum reads:
with as the stress tensor described by:
and as the mixture viscosity and as the unit tensor, is the pressure, and is the deformation tensor:
2.2.2. Meshing and Solving
For analysis of the porosity and local velocity fields all synthetic packed beds are meshed with STAR-CCM+. The Blender generated beds are imported as standard triangulation language (STL) files, a common file format for triangulated surfaces in CAD. The applied mesh properties of STAR-CCM+ are listed in Table 2, using the base size as reference for several relative size controls.

Table 2.
Meshing properties in STAR-CCM+.
The target surface size is the face size, which the mesher achieves when no controls for a smaller mesh are set. In order to capture complex features and allow more refinement, the minimum surface size should be decreased in comparison to the target size.
The boundary layer thickness is calculated according to Equation (26) [41] with the highest simulated particle Reynolds-Number Equation (27):
In order to prevent bad cells in contact regions, local flattening of point, line, and face contacts were applied, as described in earlier works for spheres [42] and for non-spherical particles [38]. A typical mesh of a bed of spheres is shown in Figure 2.

Figure 2.
Mesh for radial porosity profiles and CFD simulations.
2.2.3. Local Porosity Determination
The porosity calculation is based on the generated volume mesh. The overall porosity of the packed bed is the ratio of the free volume , which is interstitial region and likewise the sum of all computational cells, and the volume of the cylindrical container:
Experimental data from Giese et al. [30] were used for the validation. The overall porosity was extracted from the radial porosity profiles:
The theoretical overall porosity was calculated with the equations from Dixon [43]. For the determination of the radial porosity profiles of the simulations, a number of 100 cylindrical planes were placed in the container with equal distances, as seen in Figure 3. The porosity at the radial position results from the ratio of the free surface to the total surface of the cylinder , which is calculated with the height of the cylindrical plane :
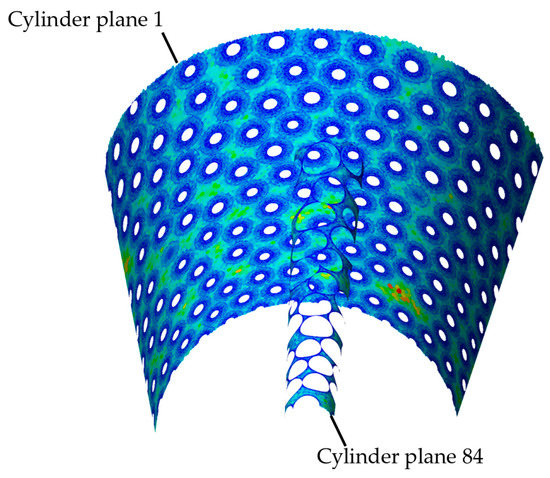
Figure 3.
Cylindrical planes for calculation of radial porosity and velocity profiles.
2.2.4. Local Velocity Profiles
The same cylindrical planes were used to determine the specific radial velocity profiles :
where is the velocity component in z-direction averaged over the cylindrical planes, is the radial porosity profile and is the inlet superficial velocity.
3. Numerical Setup
In Table 3 the settings of the DEM and rigid body simulations are summarized. As can be seen, not all of the sophisticated DEM models are implemented in Blender. Table 4 shows the geometric dimensions of all generated fixed beds as well as the boundary conditions. Finally, the solver settings are shown in Table 5. The Blender mesh method will be discussed in more detail later on.

Table 3.
Comparison of DEM and rigid body settings.

Table 4.
Boundary conditions of all simulations.

Table 5.
Solver Settings for packing generation.
4. Results
4.1. Overall Porosity
The porosity for different particle shapes is compared between simulations, experimental data from Giese et al. [30] and correlations from Dixon [43], see Figure 4. The overall agreement between experimental data and simulation is satisfactory. DEM shows, in general, a slightly smaller porosity than Blender, with a pronounced difference for beds made of cylinders.
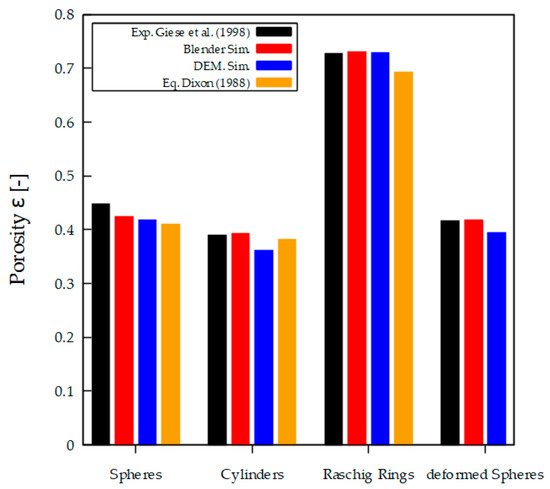
Figure 4.
Overall porosity of fixed beds made of different particle shapes. Experiments from Giese et al. [30]. Equations from Dixon [43].
4.2. Spheres
A packed bed of 1000 spheres was generated with STAR-CCM+ and Blender. Both beds were meshed in STAR-CCM+ with equal properties for calculation of radial porosity and CFD simulations. The injection method for both approaches, however, was slightly different. For DEM spheres were injected at a single point with a frequency of 100 s−1 and a velocity in the z-direction of 1 m s−1. This is more or less similar to the injection method in Blender. All particles were lined up at the beginning of the simulation above the cylindrical container. The Blender simulation also needed a physical time of for all particles to inject. Since glass beads were used in the original experiments, the corresponding physical properties were set in Blender and STAR-CCM+, see Table 4. The obtained packed beds are shown in Figure 5a as a 3D CAD model and in Figure 5b in terms of the radial porosity and Figure 5c radial velocity profiles.
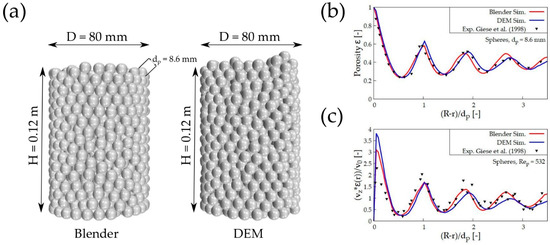
Figure 5.
(a) Comparison between synthetic generated packing of spheres, (b) radial porosity profiles, and (c) velocity profiles. Experiments from Giese et al. [30].
Both generated beds have an optical consistency with the same bed height. The overall porosity in Figure 4 shows a good agreement for the two synthetic packing methods, which result in a porosity lower than the experimental data but higher than in the theoretical equations. The radial porosity profile on Figure 5b of both methods is in excellent agreement with the experimental data from Giese et al. [30]. This can be shown with the coefficient of determination for the parity chart as a comparison between simulation data from both methods and experimental data. The coefficients of determination and are similar and show good agreement with the data. The velocity profiles (Figure 5c) follow the porosity profiles. Since the Blender bed is slightly looser, the near-wall maximum velocity (wall channeling) is slightly smaller than for the DEM bed.
4.3. Cylinders
Non-spherical pellets are widely used in industrial applications. Among those, the most simple shape is a cylinder. Based on two different experimental studies, beds made from cylinders were investigated with both generation methods. Firstly, experiments from Giese et al. [30] were reproduced synthetically with the same number of cylinders, see Figure 6a for a visual comparison between Blender and STAR-CCM+. The DEM bed shows a lower height than the Blender bed. This is also reflected in the lower overall porosity in Figure 4. It can be also seen that the radial porosity of the DEM bed is constantly below the Blender-generated bed (Figure 6b). Consequently, the velocity of the CFD simulation of DEM bed is higher in the near-wall region. One explanation of the overall lower porosity is the approximation of the cylinder shape in the DEM with the composite particle approach. This approximation leads to a deviation in comparison to the CAD particle especially at the edges of the cylinder. A closer look at this phenomenon gives Figure 7. Although in the DEM bed there are no overlaps of the composite particles, the transformation back to the CAD particles leads to overlaps in the STL file. This leads to a denser bed than in the Blender case, where there are no overlaps detected in the bed generation simulation, see Figure 7 right-hand side. These overlaps can be treated with the unite method or the caps method as was described in detail in Reference [44].
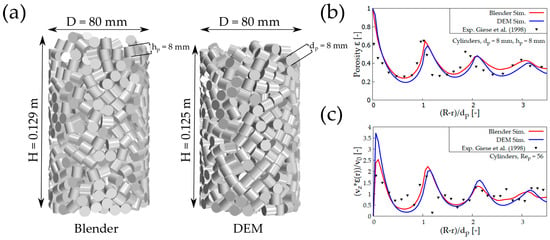
Figure 6.
(a) Comparison between synthetic generated packing of cylinders, (b) radial porosity profiles, and (c) velocity profiles. Experiments from Giese et al. [30].
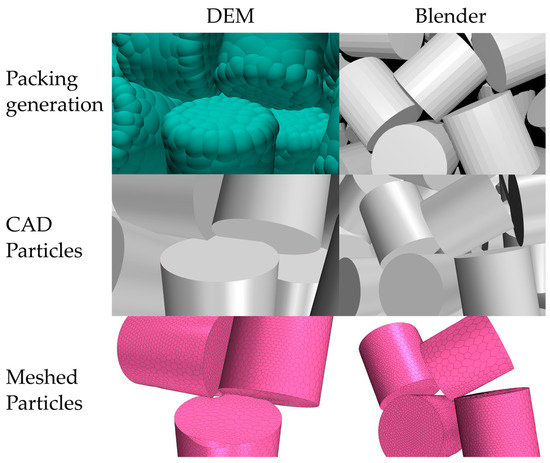
Figure 7.
Bed generation with DEM (left) and rigid body (right), CAD particle transformation, and resulting mesh.
At this point, the results show that the rigid body approach has advantages over DEM for the simulation of complex particle geometries. In addition, the agreement of the Blender simulation can be expressed by the coefficient of determination for the local porosity profile , which is larger than for the generated bed from DEM . There is a slight shift of the oscillating porosity profile of the simulations compared to the experimental data. This is one reason why the values are lower than for spheres, cf. Figure 6b. Nevertheless, the porosity profile maxima and minima are in a similar range. Another important aspect of packed bed morphology is the particle orientation. Particle-orientation distribution was evaluated experimentally with computer tomography (CT) data by Caulkin et al. [15]. This data set is compared with synthetically generated beds of Blender and STAR-CCM+ in Figure 8.
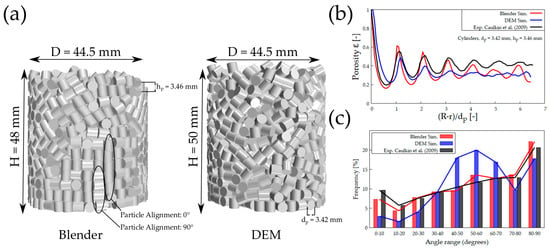
Figure 8.
(a) Comparison between synthetic generated packing of cylinders, (b) radial density distribution, and (c) particle alignment. Experiments from Caulkin et al. [15].
The optical height of the generated beds in Figure 8a is not exactly similar, however, the near-wall particles show different orientations. In the Blender bed, the cylinders stack over each other, while in the DEM bed most of the cylinders are inclined. The porosity profile of the Blender bed is more pronounced than the DEM bed and furthermore lower than the DEM bed (Figure 8b). This is different from the observation of the particle bed in Figure 6b where Blender has a higher porosity than the DEM bed. The particle arrangement in Figure 8c shows differences between the two synthetic methods. The angle range is calculated for an angle in comparison to the normal z-direction. An angle of 0° is a standing cylinder, while 90° is a horizontally oriented cylinder. The Blender bed is characterized by a higher frequency of stacked particles, as already noticed in Figure 8a. In addition, the alignment of DEM particles shows a higher frequency for particles from 40° to 70°. The comparison with experimental data from Caulkin et al. [15] shows an acceptable agreement with the Blender bed (Figure 8c). For many applications, the near-wall region is of great interest, e.g., due to critical radial heat transfer from the wall to the gas etc. Therefore, a closer look at the bed morphology in this region is crucial. Figure 9a shows one layer of particles close to the container wall for a Blender bed and a STAR-CCM+ bed. The Blender particles arrange either standing or lying resulting in more particles fitting into the outer ring. On the contrary, the DEM bed is characterized by a looser morphology and therefore more particles with angles in the mid-range, cf. Figure 9b. The alignment of the Blender cylinders shows a significantly higher frequency in the range up to 30 degrees than with the DEM. This observation shows why the fixed bed from Blender has a lower bed height and a lower porosity than the DEM bed (Figure 8a), despite the fact of overlapping particles.
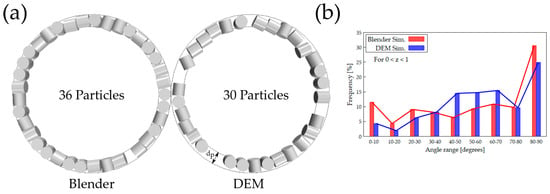
Figure 9.
(a) One layer of cylinders touching the container wall. (b) Orientation distribution of near-wall cylinders.
4.4. Raschig Rings
Another frequently used particle shape is the Raschig ring. In this study, the approximation of a Raschig ring with the composite approach is compared against a full cylinder, as well as the rigid approach. The advantage of the full cylinder approximation is that a smaller amount of composite spheres is needed, cf. Table 1. The number of spheres can be reduced from 449 to only 100 per particle. By using a full cylinder, it is possible to generate with only one DEM simulation a certain amount of different particle shapes by transforming the cylinders into rings or more hole cylinders [37,38]. It can be doubted that the different ballistics of a full cylinder and a one-hole cylinder give similar bed morphologies. In addition, the packing density between these methods might be different, because the additional free space inside the hollow cylinders can be filled with edges of other particles. In Figure 10 the comparison between Blender, full cylinder DEM, and “ring” DEM, as shown in Table 1, against experimental data is shown. In Figure 10a only the Blender bed and ring DEM is shown for brevity reasons. Again, the two differently generated beds show similar heights, but different particle orientation.
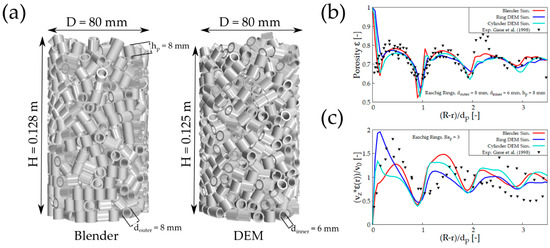
Figure 10.
(a) Comparison between synthetic generated packing of Raschig Rings, (b) radial porosity profiles, and (c) velocity profiles. Experiments from Giese et al. [30].
It can be seen, that the Blender Bed porosity in the near wall region shows a low deviation from experimental data (Figure 10b). Reasons for this will be presented later, where different Blender simulation methods will be presented. In addition, the ring DEM has lower maxima and minima and represents the experimental data in near-wall regions rather well. A difference in experimental data and all three simulations can be seen at a wall distance of , where the results of experiments are larger than simulation predictions. The values of determination for this case are for Blender Simulation, and . One of the reasons for the large deviation is also the wide scattering of the experimental data as shown in Figure 10b. For the fluid simulation (Figure 10c), a large difference between the three methods can be noticed especially in the near-wall region. This leads to the assumption that the particle orientation has to be different.
An additional bed setup from Caulkin et al. [15] was used to evaluate the orientation of the particles. Notice that the dimensions are different. Again, synthetic beds with Blender and the two DEM methods were generated and compared. In Figure 11a the Blender and DEM bed are shown for illustrative comparison.
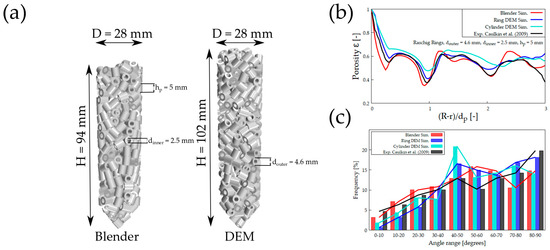
Figure 11.
(a) Comparison between synthetic generated packing of Rachig Rings, (b) radial density distribution, and (c) particle alignment. Experiments from Caulkin et al. [15].
The radial porosity profile (Figure 11b) shows that the data from Blender and the DEM ring simulation have a small deviation from the experimental data. The DEM generated with the full cylinder composite particles shows a strong deviation in the value at the minimum at . In addition, the porosity of this bed is steadily higher than the data of the others. A glance at the alignment of the particles in Figure 11c shows that the general trend is well captured by the simulations. This time the Blender and ring DEM bed shows similar particle orientation to the experiments. The data of the cylinder DEM, on the other hand, show a strong deviation in which the majority of the particles have an angle between 40° and 50°. The coefficients of determination are listed in Table 6 for the different particle shapes and as summarized as a total value over all Blender and DEM simulations.

Table 6.
Coefficients of determination.
4.5. Complex Particles
The filling process of complex particles is challenging due to the difficult particle approximation for the DEM composite approach and due to collision detection. A further comparison between Blender and the DEM is conducted with a complex particle shape. For this purpose, a previously unmentioned setting within Blender will be discussed at first. In Blender’s rigid body approach, different collision shapes can be selected, which affects the detection of the collision. Commonly in Blender, the convex hull method is applied. With this option, a convex approximation is drawn around the particle for collision detection. Advantage of this method is the high performance and simulation stability. However, the convex hull method cannot be used to represent a cylinder with a curved outer surface. As shown in Figure 12a, a small object will collide with the pellet at the dashed position for the convex hull method. Another collision shape in Blender is the mesh method, which is based on the real shape of the object [40]. For the mesh method in Figure 12b, the collision detection takes place at the correct surface of the particle.
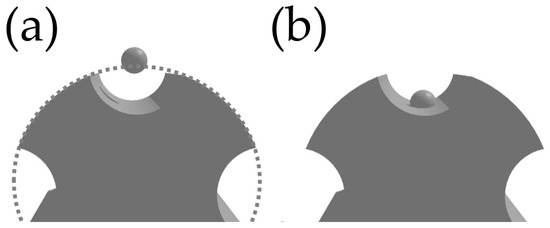
Figure 12.
Different collision shapes in Blender. (a) Convex hull method and (b) Mesh method.
Since the complex particle shown in Table 1 has a more complex shape, a simulation based on the mesh collision method should be considered. However, the disadvantage of this method is the much longer simulation time and the instability of the solution [40]. In order to consider the differences, synthetic beds with both Blender methods and with the DEM are presented. The composite particle method used in the DEM corresponds to the composite maximum shown in Table 1.
The resulting beds in Figure 13 show different heights. The convex hull method yields a significantly higher bed than the mesh method. The reason for this is that the gearwheel-shaped pellets can interlock. The bed generated with DEM, on the other hand, has only a minimally larger height. This optical observation is proven with the radial porosity profile shown in Figure 13b. The convex hull method profile shows a difference in velocity for the near-wall region. The results highlight that the convex hull method applied for such complex particles leads to unrealistic loose packings. However, solution stability is more robust than for the mesh collision method.
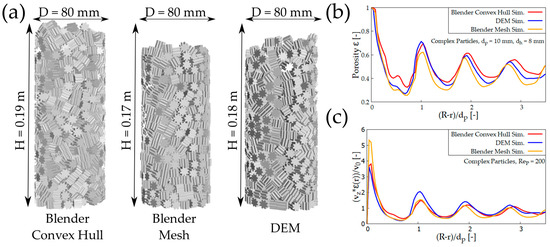
Figure 13.
(a) Comparison between synthetic generated packing of complex particles, (b) radial porosity profiles, and (c) velocity profiles.
4.6. Simulation Time
A further criterion for the selection of synthetic packed bed generation is the total simulation time. Since the DEM scales with the number of spheres for the composite particle, the simulation time is in general longer for particles that are more complex. Figure 14 summarizes the calculation time on one CPU (Intel Xeon x5660) of all simulations. In general, Blender shows shorter simulation times in comparison to DEM. While the time increases with the DEM when changing from spheres to cylinders, it decreases with Blender. This can be explained by the fact that Blender scales with the number of surfaces of the particles. Since more surfaces are required for a sphere than for a cylinder, the simulation time is shorter. The time of Raschig rings is shown for ring DEM. Time savings are possible by using a simple cylinder, leading to the same simulation time as the shown cylinders. In Figure 14a it can be seen that the time advantage of Blender is getting higher with the complexity of the particle shape. While for spheres the DEM time is nearly doubled, for Raschig rings it is 26 times larger than Blender. Due to the stable and fast simulation, the Blender method convex hull method was used for the particles shown on the left. Since this method is no longer suitable for complex particles, the slower mesh method was shown here. Nevertheless, for these complex particles, which are difficult to represent, the Blender Mesh simulation is clearly 13 times faster than STAR-CCM+.
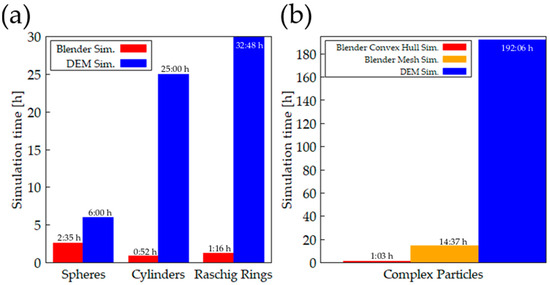
Figure 14.
Simulation Time of Blender and DEM for different particle shapes. (a) Spheres, Cylinders and Raschig Rings; (b) Complex Particles.
5. Conclusions
In particle-resolved CFD simulations of fixed-bed reactors, the underlying bed morphology plays a paramount role. Synthetic bed-generation methods are much more flexible and faster than image-based approaches. Typical decision aspects for synthetic bed generators are realistic bed structure generation (accuracy against experimental data), easy-to-handle use, exportability of bed structure, flexibility for different shapes, physically relevant models, and finally low computational costs. In this study, we looked critically at the commonly used DEM approach and compared the resulting bed morphology with the more recently presented rigid-body method incorporated into the Blender software.
Both methods show large flexibility for different particle shapes originating from an external CAD modeler and the option to export the particle bed via the STL format. In addition, both methods come with a graphical user interface, which is easy-to-use and furthermore automation processes can be included, i.e., python for Blender and Java scripting for STAR-CCM+. Whereas the commercially available STAR-CCM+ software is well documented in the own user guide and own internet forum, the documentation of the open-source bullet physics is rather vague. However, both methods show physically meaningful models to simulate the filling process of fixed-bed reactors, whereas the soft-body approach in STAR-CCM+ is more sophisticated than the rigid-body model. In terms of accuracy, the picture is less clear. Both models can predict experimental porosity profiles with satisfactory accuracy, cf. Table 6 for values between synthetically generated beds and experimental data. Particle orientation is captured more accurately with Blender. However, the experimental data basis is rather scarce. The main disadvantage of the DEM is the approximation of non-spherical particles with the composite particle approach. This approximation can lead in general to denser beds and to overlaps of particles, which in turn results in meshing challenges. Additionally, it was shown that the use of a full-cylinder DEM approximating a Raschig ring leads to differences in the bed structure and the velocity profile, especially due to different pellet orientation. For more complex particle shapes, the fast but simple convex hull collision method in Blender clearly shows its limits. The mesh collision method in Blender resolves the actual particle shape, which requires additional computational costs. Still, Blender is in general clearly faster for the bed generation process, especially, when the complexity of the particle is high, cf. Figure 14.
Future studies should incorporate experimental data from complex particle shapes in order to judge the accuracy of the different collision methods in Blender. In addition, special attention should be drawn to the damping forces applied to the moving particles, since this can violate the law of conservation of linear and angular momentum and energy over each time.
Author Contributions
S.F. and G.D.W. conceived and designed the computer experiments; S.F. performed the simulations; S.F. and G.D.W. analyzed the data; S.F. wrote the paper, whereas G.D.W. supervised the project.
Funding
This research received no external funding.
Acknowledgments
This publication is based upon work supported and financed by the Clausthal University of Technology, project Catalytic and microbial methanation as basis for sustainable energy storage (CliMb).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Latin Letters | ||
| area | ||
| overlaps | ||
| particle diameter | ||
| tube diameter | ||
| deformation tensor | ||
| coefficient of restitution | ||
| equivalent Young’s modulus | ||
| force (rigid body approach) | ||
| force (soft body approach) | ||
| body force | ||
| contact force | ||
| gravity force | ||
| surface force | ||
| height | ||
| moment of inertia | ||
| unit tensor | ||
| spring stiffness | ||
| mass | ||
| equivalent particle mass | ||
| unit normal vector | ||
| tube-to-particle-diameter ratio | ||
| damping | ||
| damping coefficient | ||
| pressure | ||
| radius | ||
| coefficient of determination | ||
| Reynolds number | ||
| equivalent radius | ||
| radius of radial position | ||
| unit normal vector | ||
| time | ||
| stress tensor | ||
| velocity | ||
| velocity | ||
| volume | ||
| Greek Letter | ||
| sliding speed | ||
| Boundary layer thickness | ||
| maximum overlap | ||
| porosity | ||
| dynamic viscosity | ||
| static friction coefficient | ||
| density | ||
| net moment | ||
| angular velocity | ||
| Subscripts | ||
| inlet | ||
| data obtained by the use of Blender | ||
| Blender object based pellet interaction | ||
| Blender object based container interaction | ||
| Phase based container-pellet interaction | ||
| part: Cylinder | ||
| part: Cylinder Plane | ||
| Data obtained by the use of DEM | ||
| amount of free space or volume | ||
| experimental data taken from Giese et al. (1998) | ||
| phase based pellet interaction | ||
| normal direction | ||
| tangential direction | ||
| amount of total space or volume | ||
| particle | ||
| additional tangential direction | ||
| specific radial velocity | ||
| Abbreviations | ||
| 3D | 3-dimensional | |
| DEM | Discrete Element Method | |
| CAD | Computer Aided Design | |
| CFD | Computational Fluid Dynamics | |
| CT | Computer Tomography | |
| MRI | Magnetic Resonance Imaging | |
| STL | Standard Triangulation Language | |
References
- Froment, G.F. Analysis and Design of Fixed Bed Catalytic Reactors Chemical Reaction Engineering; Bischoff, K.B., Ed.; American Chemical Society: Washington, DC, USA, 1972; Volume 109, pp. 1–55. [Google Scholar]
- Kulkarni, B.D.; Doraiswamy, L.K. Estimation of Effective Transport Properties in Packed Bed Reactors. Catal. Rev. 1980, 22, 431–483. [Google Scholar] [CrossRef]
- Eisfeld, B.; Schnitzlein, K. The influence of confining walls on the pressure drop in packed beds. Chem. Eng. Sci. 2001, 56, 4321–4329. [Google Scholar] [CrossRef]
- Andersson, K.E.B. Pressure drop in packed beds. Trans. Royal Inst. Technol. Stockholm 1963, 201. [Google Scholar]
- Dixon, A.G. Fixed bed catalytic reactor modelling-the radial heat transfer problem. Can. J. Chem. Eng. 2012, 90, 507–527. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. Packed Tubular Reactor Modeling and Catalyst Design using Computational Fluid Dynamics. In Advances in Chemical Engineering; Marin, G.B., Ed.; Elsevier textbooks, s.l.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 31, pp. 307–389. [Google Scholar] [CrossRef]
- Jurtz, N.; Kraume, M.; Wehinger, G.D. Advances in fixed-bed reactor modeling using particle-resolved computational fluid dynamics (CFD). Rev. Chem. Eng. 2018, 35. [Google Scholar] [CrossRef]
- Wang, Z.; Afacan, A.; Nandakumar, K.; Chuang, K.T. Porosity distribution in random packed columns by gamma ray tomography. Chem. Eng. Process. Process Intensif. 2001, 40, 209–219. [Google Scholar] [CrossRef]
- Baker, M.J.; Young, P.G.; Tabor, G.R. Image based meshing of packed beds of cylinders at low aspect ratios using 3d MRI coupled with computational fluid dynamics. Comput. Chem. Eng. 2011, 35, 1969–1977. [Google Scholar] [CrossRef]
- Hofmann, S.; Bufe, A.; Brenner, G.; Turek, T. Pressure drop study on packings of differently shaped particles in milli-structured channels. Chem. Eng. Sci. 2016, 155, 376–385. [Google Scholar] [CrossRef]
- Zeiser, T.; Steven, M.; Freund, H.; Lammers, P.; Brenner, G.; Durst, F.; Bernsdorf, J. Analysis of the flow field and pressure drop in fixed-bed reactors with the help of lattice Boltzmann simulations. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2002, 360, 507–520. [Google Scholar] [CrossRef] [PubMed]
- Caulkin, R.; Fairweather, M.; Jia, X.; Gopinathan, N.; Williams, R.A. An investigation of packed columns using a digital packing algorithm. Comput. Chem. Eng. 2006, 30, 1178–1188. [Google Scholar] [CrossRef]
- Caulkin, R.; Ahmad, A.; Fairweather, M.; Jia, X.; Williams, R.A. An investigation of sphere packed shell-side columns using a digital packing algorithm. Comput. Chem. Eng. 2007, 31, 1715–1724. [Google Scholar] [CrossRef]
- Caulkin, R.; Jia, X.; Fairweather, M.; Williams, R.A. Lattice approaches to packed column simulations. Particuology 2008, 6, 404–411. [Google Scholar] [CrossRef]
- Caulkin, R.; Jia, X.; Xu, C.; Fairweather, M.; Williams, R.A.; Stitt, H.; Nijemeisland, M.; Aferka, S.; Crine, M.; Léonard, A.; et al. Simulations of Structures in Packed Columns and Validation by X-ray Tomography. Ind. Eng. Chem. Res. 2009, 48, 202–213. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Kraume, M. CFD als Designtool für Festbettreaktoren mit kleinem Rohr-zu-Pelletdurchmesser-Verhältnis: Heute oder in Zukunft? Chem. Ingen. Tech. 2017, 89, 447–453. [Google Scholar] [CrossRef]
- Favier, J.F.; Abbaspour-Fard, M.H.; Kremmer, M.; Raji, A.O. Shape representation of axi-symmetrical, non-spherical particles in discrete element simulation using multi-element model particles. Eng. Comput. 1999, 16, 467–480. [Google Scholar] [CrossRef]
- Marigo, M.; Stitt, E.H. Discrete Element Method (DEM) for Industrial Applications: Comments on Calibration and Validation for the Modelling of Cylindrical Pellets. KONA 2015, 32, 236–252. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Cylindrical object contact detection for use in discrete element method simulations, Part II—Experimental validation. Chem. Eng. Sci. 2010, 65, 5863–5871. [Google Scholar] [CrossRef]
- Kodam, M.; Bharadwaj, R.; Curtis, J.; Hancock, B.; Wassgren, C. Cylindrical object contact detection for use in discrete element method simulations. Part I—Contact detection algorithms. Chem. Eng. Sci. 2010, 65, 5852–5862. [Google Scholar] [CrossRef]
- Feng, Y.T.; Han, K.; Owen, D.R.J. A generic contact detection framework for cylindrical particles in discrete element modelling. Comput. Methods Appl. Mech. Eng. 2017, 315, 632–651. [Google Scholar] [CrossRef]
- Bender, J.; Erleben, K.; Trinkle, J. Interactive Simulation of Rigid Body Dynamics in Computer Graphics. Comput. Graph. Forum 2014, 33, 246–270. [Google Scholar] [CrossRef]
- Blender Org. Manual Homepage. Available online: https://docs.blender.org/manual/en/latest/game_engine/physics/introduction.html (accessed on 26 March 2019).
- Boccardo, G.; Del Plato, L.; Marchisio, D.; Augier, F.; Haroun, Y.; Ferre, D.; Icardi, M. Pore-scale simulation of fluid flow in packed-bed reactors via Rigid-Body simulations and CFD. In Proceedings of the 10th International Conference on CFD in Oil & Gas, Metallurgical and process Industries SINTEF, Trondheim, Norway, 17–19 June 2014. [Google Scholar]
- Boccardo, G.; Augier, F.; Haroun, Y.; Ferré, D.; Marchisio, D.L. Validation of a novel open-source work-flow for the simulation of packed-bed reactors. Chem. Eng. J. 2015, 279, 809–820. [Google Scholar] [CrossRef]
- Partopour, B.; Dixon, A.G. An integrated workflow for resolved-particle packed bed models with complex particle shapes. Powder Technol. 2017, 322, 258–272. [Google Scholar] [CrossRef]
- Fernengel, J.; Habla, F.; Hinrichsen, O. Scripting as an Approach to Automated CFD Simulation for Packed Bed Catalytic Reactor Modeling. Chem. Ingenieur Tech. 2018, 90, 685–689. [Google Scholar] [CrossRef]
- Pavlišič, A.; Ceglar, R.; Pohar, A.; Likozar, B. Comparison of computational fluid dynamics (CFD) and pressure drop correlations in laminar flow regime for packed bed reactors and columns. Powder Technol. 2018, 328, 130–139. [Google Scholar] [CrossRef]
- Giese, M.; Rottschäfer, K.; Vortmeyer, D. Measured and modeled superficial flow profiles in packed beds with liquid flow. AIChE J. 1998, 44, 484–490. [Google Scholar] [CrossRef]
- Siemens PLM STAR-CCM+ Homepage. Available online: https://mdx.plm.automation.siemens.com/star-ccm-plus (accessed on 14 March 2019).
- Blender Org. Manual Homepage. Available online: https://docs.blender.org/manual/de/dev/physics/rigid_body/introduction.html (accessed on 14 March 2019).
- MatWeb Material Property Data. Available online: http://www.matweb.com/search/DataSheet.aspx?MatGUID=c8c56ad547ae4cfabad15977bfb537f1 (accessed on 14 March 2019).
- MatWeb Material Property Data. Available online: http://www.matweb.com/search/DataSheet.aspx?MatGUID=cbe7a469897a47eda563816c86a73520 (accessed on 21 March 2019).
- Di Renzo, A.; Di Maio, F.P. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chem. Eng. Sci. 2004, 59, 525–541. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Eppinger, T.; Jurtz, N.; Aglave, R. Automated workflof for spatially resolved packed bed reactors with spherical and non-spherical particles. In Proceedings of the 10th International Conference on CFD in Oil & Gas, Metallurgical and process Industries SINTEF, Trondheim, Norway, 17–19 June 2014. [Google Scholar]
- Wehinger, G.D.; Eppinger, T.; Kraume, M. Evaluating Catalytic Fixed-Bed Reactors for Dry Reforming of Methane with Detailed CFD. Chem. Ingenieur Tech. 2015, 87, 734–745. [Google Scholar] [CrossRef]
- Youtube. Available online: https://www.youtube.com/watch?v=Zz3I5Gbrguw (accessed on 7 April 2019).
- Blender Org. Manual Homepage. Available online: https://docs.blender.org/manual/de/dev/physics/rigid_body/properties.html (accessed on 11 July 2018).
- Dhole, S.D.; Chhabra, R.P.; Eswaran, V. A numerical study on the forced convection heat transfer from an isothermal and isoflux sphere in the steady symmetric flow regime. Int. J. Heat Mass Transf. 2006, 49, 984–994. [Google Scholar] [CrossRef]
- Eppinger, T.; Seidler, K.; Kraume, M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios. Chem. Eng. J. 2011, 166, 324–331. [Google Scholar] [CrossRef]
- Dixon, A.G. Correlations for wall and particle shape effects on fixed bed bulk voidage. Can. J. Chem. Eng. 1988, 66, 705–708. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Fütterer, C.; Kraume, M. Contact Modifications for CFD Simulations of Fixed-Bed Reactors: Cylindrical Particles. Ind. Eng. Chem. Res. 2017, 56, 87–99. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).