On the Optimality of State-Dependent Base-Stock Policies for an Inventory System with PH-Type Disruptions

Abstract

Background: The management of inventory under realistic supply chain disruptions, which are often non-exponential, challenges classical control theory. This study addresses the critical question of whether the optimality of simple base-stock policies holds under the combined influence of non-exponential disruptions and random yield. Methods: We model the system as a Piecewise Deterministic Markov Process (PDMP) with impulse control, using Phase-Type (PH) distributions to capture non-memoryless event timings. The analysis involves proving the existence of a solution to the Average Cost Optimality Equation (ACOE) via a vanishing discount approach, and the framework is validated with a numerical experiment. Results: Our primary finding is a rigorous proof that a state-dependent base-stock policy is optimal, a significant generalisation of classical theory. We establish this by demonstrating the value function’s convexity. The numerical experiment quantifies the significant cost penalties (over 12%) incurred by using simpler, memoryless models for supply disruptions. Conclusions: The study provides a crucial theoretical justification for the robustness of simple threshold-based control policies in complex, realistic settings. It highlights for managers the importance of modelling the variability of disruptions, not just their average duration, to avoid costly strategic errors.

1. Introduction

The effective management of inventory systems is a foundational challenge in today’s globalised and volatile economic landscape, with profound implications for the financial performance and resilience of modern enterprises. Supply chains are perpetually exposed to a wide array of stochastic phenomena that disrupt the flow of goods and information. Events such as equipment breakdowns and pandemics can lead to supplier outages whose durations are unpredictable and rarely follow the simple, memoryless patterns assumed in classical models [1]. Compounding this, unpredictable customer demand and random production yields create a confluence of uncertainties that can culminate in substantial financial repercussions, either through costly stock-outs or the burden of excessive inventory holding costs. The central motivation for this research is therefore the pressing need for control policies that are not just mathematically optimal under idealised conditions, but are provably robust and effective in the face of these realistic, non-exponential disruptions. Managers require simple, implementable policies, such as the well-known base-stock policy, yet the theoretical guarantee of their optimality has not been established for systems facing this complex combination of uncertainties. This paper is motivated by the need to bridge this critical gap between classical inventory theory and the practical realities of modern supply chain risk management.

The theoretical bedrock of this field was established through the seminal contributions of Scarf [2] and Iglehart [3], who demonstrated the optimality of simple, threshold-based policies under specific, idealised conditions. For systems characterised by stationary stochastic demand, convex cost structures, and perfectly reliable supply, they proved that the optimal replenishment strategy is of the $(s,S)$ or base-stock type. These policies, defined by a reorder point (s) and an order-up-to level (S), are not only analytically elegant but also highly practical, forming the conceptual basis for countless inventory management systems in industry. Throughout this paper, we refer to this class of policies as threshold-based policies, which includes the well-known $(s,S)$ and base-stock structures.

However, the classical framework’s reliance on simplifying assumptions—such as memoryless demand processes, perfectly reliable suppliers, and deterministic lead times—limits its direct applicability in many real-world scenarios. This discrepancy has motivated a rich and extensive body of research aimed at extending inventory models to encompass more realistic and complex operational characteristics. A particularly critical area of modern research concerns the explicit modelling of supply-side uncertainties. A significant stream of literature has investigated the impact of supply disruptions, often modelling the supplier as a system that stochastically alternates between an available (‘ON’) state and an unavailable (‘OFF’) state, or a production system subject to random breakdowns [4]. Other models consider disruptions in the form of entire supply batches being rejected upon arrival due to imperfect quality [5]. While these models provide fundamental insights, they frequently assume that the durations of the ON/OFF states follow exponential distributions. This memoryless property fails to capture more complex, non-exponential patterns of failure and repair often observed in practice, a limitation that has been addressed in some models by employing more general distributions like Phase-Type (PH) distributions [6]. Another crucial source of uncertainty is random production yield, where the quantity received from a supplier is a random variable that may differ from the quantity ordered. This phenomenon is prevalent in industries such as agriculture, semiconductor manufacturing, and pharmaceuticals. The risk posed by random yield often compels firms to adopt mitigation strategies, such as securing emergency backup sourcing options, which introduces further complexity into the decision-making process [7]. While some recent work has started to jointly consider random yields and disruptions, the analysis is often confined to periodic-review settings and specific yield models [8], leaving a gap in the understanding of their combined impact in a continuous-review framework.

To rigorously model systems that evolve deterministically between random events, the framework of Piecewise Deterministic Markov Processes (PDMPs) has proven to be an exceptionally powerful and versatile tool. Introduced by Davis [9,10], a PDMP is characterised by three local components: a deterministic flow, a state-dependent jump rate, and a transition measure. This structure is naturally suited to modelling continuous-review inventory systems. The PDMP framework has been successfully applied to a broad class of problems in operations research, including production, maintenance, and inventory control [11], with notable applications in production-storage models featuring interruptions [12]. The optimal control of PDMPs, particularly through discrete interventions like placing replenishment orders, is known as an impulse control problem [13]. This formulation captures the essence of inventory replenishment decisions, which are discrete actions (impulses) that instantaneously change the state of the system. When the objective is to minimise the long-run average cost—a criterion often preferred in operations for its focus on steady-state performance—the analysis centres on the associated Average Cost Optimality Equation (ACOE). For impulse control problems, this equation typically takes the form of a quasi-variational inequality (QVI). The QVI elegantly represents the fundamental decision at every state: either continue without intervention, in which case the system dynamics are governed by the PDMP generator, or intervene at a cost, which instantaneously transitions the system to a new state. The optimal policy is defined by the boundary between the ‘continuation’ and ‘intervention’ regions [14]. The analytical machinery for average cost control of PDMPs, including the development of policy iteration algorithms, has been substantially advanced in recent years [15]. Furthermore, various numerical methods for the simulation and optimisation of PDMPs have been developed, using techniques ranging from quantization [16] to broader simulation frameworks [17], highlighting the practical relevance of this modelling approach.

While the PDMP framework provides the necessary dynamic structure, realistically modelling the non-exponential timing of disruptions requires a correspondingly flexible class of probability distributions. Phase-Type (PH) distributions, introduced by Neuts [18], offer this versatility. As the distribution of the time to absorption in a finite-state continuous-time Markov chain, the PH class is dense in the space of all positive-valued distributions. The primary advantage of PH distributions lies in their inherent Markovian structure. By expanding the state space to include the current ‘phase’ of the PH distribution, a system with general, non-exponential event timings can be analysed within a larger, but still tractable, Markovian framework. This state-space expansion technique is a powerful method for overcoming the memoryless assumption and is seeing increased use in modern inventory models. Its utility has been demonstrated in models that capture non-exponential supplier ON/OFF durations [6], non-exponential service and repair times for servers subject to breakdowns [19], and even in related reliability contexts for modelling repairable deteriorating systems and procurement lead times [20]. The analytical tractability of PH distributions is further enhanced by the powerful computational framework of Matrix-Analytic Methods [21]. The same underlying mathematical structure has also given rise to related tools like Markovian Arrival Processes (MAPs), which can model not only non-exponential inter-arrival times but also their autocorrelation. Recent studies have shown that in systems with such correlated processes, state-dependent threshold policies remain optimal [22], reinforcing the idea that threshold-based control is robust to more complex stochastic dynamics. The search for elegant structural properties and efficient algorithms is a recurring theme in the broader field; for instance, exploiting structural properties of Markov Decision Processes, such as skip-free transitions, has been shown to yield highly efficient policy iteration algorithms [23], motivating the search for analogous structural properties in our more general PDMP setting.

Despite these powerful tools, a complete and rigorous analytical framework for the optimal control of a continuous-review inventory system that integrates PH-distributed supply and demand disruptions, random production yield, and a general long-run average cost objective has remained elusive. The inherent complexity of such integrated systems has led researchers to pursue several distinct analytical avenues. One major stream of research focuses on developing approximation algorithms for discrete-time versions of these problems, often for specific settings like capacitated perishable systems, and establishing their worst-case performance guarantees [24,25]. A second powerful approach is asymptotic analysis, which examines system behaviour in a specific regime, such as when penalty costs for lost sales become extremely large. This line of work has often demonstrated that simple base-stock-type policies are asymptotically optimal, providing strong evidence for the robustness of threshold policies but not proving their exact optimality under general cost parameters [26]. For instance, these studies show that as a system parameter (like backorder cost) tends to infinity, the cost difference between a simple base-stock policy and the true optimal policy vanishes. While these are powerful and important results that provide strong motivation for our work, they leave a critical question unanswered: is the policy optimal for a finite, fixed set of system parameters, or is it merely a very good approximation in a specific limiting regime? A third stream, to which this paper belongs, employs the theory of stochastic optimal control to establish the exact structure of the optimal policy for a general class of continuous-time processes. However, the existing literature within this stream tends to be fragmented, with models addressing only subsets of the complex features. For instance, models considering supply flexibility through dual-sourcing or emergency orders [27] often simplify the underlying stochastic processes. Models that tackle demand uncertainty by incorporating advance order information often do so under idealized supply conditions [28]. Even when multiple uncertainties like random yield and disruptions are considered jointly, the analysis is typically limited to infinite-horizon models with simplified assumptions or specific cost structures [29,30].

This leaves a critical gap in the literature, which frames the central research problem of this paper: there is no unified theory that rigorously proves the structure of the optimal policy for a system subject to a confluence of realistic, multifaceted uncertainties. This leads to our primary research question: Does the intuitive and simple structure of a state-dependent base-stock policy remain optimal in such a complex and realistic environment? To provide a complete and rigorous answer, we systematically address the following interconnected theoretical questions:

• Can the existence of a solution to the corresponding Average Cost Optimality Equation (ACOE) be formally established, thereby guaranteeing that an optimal policy exists?
• Can the convexity of the value function be proven, providing the cornerstone for establishing the optimality of the base-stock policy structure?
• Is the resulting optimal policy computationally attainable, and can the theoretical convergence of a suitable algorithm, such as the Policy Iteration Algorithm (PIA), be proven?

A comprehensive affirmative answer to these questions would provide strong justification for the use of simple, implementable control rules in highly stochastic settings, offering managers guidance that is both robust and practical.

This paper addresses this critical gap by developing a complete theoretical framework for the optimal control of a continuous-review inventory system subject to multifaceted disruptions. We model the system as a PDMP with impulse control, where the sojourn times in different environmental states are governed by general PH distributions. The model also explicitly incorporates random production yield. While each of these features has been studied in isolation, our primary contribution stems from their novel synthesis within a single, unified framework that proves the structural properties of the optimal policy under their combined influence. Our objective is to rigorously characterise the replenishment policy that minimises the long-run average cost of the system.

This work makes four primary contributions. First, we construct a rigorous and general mathematical model that synthesises the PDMP framework with impulse control, PH-distributed disruptions, and random yield, capturing a wide range of realistic system dynamics in a single, unified structure. Second, we formally establish the existence of a solution to the corresponding ACOE. We achieve this by employing the vanishing discount approach, a powerful technique in the theory of Markov decision processes that connects the more tractable discounted cost problem to the long-run average cost problem [31,32]. Third, and most significantly, we prove that the optimal replenishment policy for this complex system possesses a state-dependent base-stock structure. This is our central structural result. It demonstrates that despite the non-exponential timings and multiple interacting sources of uncertainty, the optimal control logic retains an elegant and intuitive threshold-based form. This represents a significant generalisation of the classical optimality results of Scarf [2]. Finally, to provide a complete analytical treatment, we formulate a Policy Iteration Algorithm (PIA) for computing the optimal base-stock levels and rigorously prove its theoretical convergence. The PIA is a cornerstone of dynamic programming, and its efficiency and convergence properties are subjects of ongoing research [33,34]. Its convergence in our generalised PDMP setting confirms that the optimal policy is not only structurally simple but also computationally attainable, thus completing the pathway from model formulation to the determination and computation of the optimal control strategy.

The remainder of this paper is organised as follows. Section 2 provides the detailed mathematical formulation of the problem, constructing the state space, defining the system dynamics within the PDMP framework, and justifying the key modelling assumptions. Section 3 introduces the ACOE and the verification theorem that establishes its connection to the optimal policy. In Section 4, we prove the existence of a solution to the ACOE via the vanishing discount approach, establish our main result on the optimality of state-dependent base-stock policies, and prove the convergence of a Policy Iteration Algorithm. Section 5 presents a numerical experiment to illustrate the theoretical results and provide managerial insights, quantifying the value of our modelling approach over simpler, memoryless approximations. Finally, Section 6 concludes the paper with a summary of our contributions, a discussion of further remarks on the model, and directions for future research.

2. Mathematical Formulation

We model the inventory system as a Piecewise Deterministic Markov Process (PDMP), a powerful class of stochastic processes well-suited for systems that evolve deterministically between random events [9,10]. This section provides a rigorous formulation of the model. We begin by constructing the state space, meticulously defining each component to capture the system’s complex dynamics. We then introduce the control actions and the resulting process evolution, governed by an extended generator. Finally, we formulate the long-run average cost minimization problem.

2.1. System States, Model Parameters, and Key Assumptions

We model the inventory system as a Piecewise Deterministic Markov Process (PDMP) with impulse control, under a long-run average cost criterion. The fundamental definitions of the process generator, admissible control policies, and cost structure are standard in this field and are adapted from known works in literature (e.g., [10,15]). Our contribution lies in synthesising these concepts into a unified model for an inventory system with non-exponential disruptions and random yield, and in rigorously proving the structural properties of its optimal policy.

To ensure the process is Markovian, the state vector must contain all information necessary to describe its future probabilistic evolution. This requires tracking not only the current inventory level but also the status of the stochastic environments and the full pipeline of outstanding orders. We build the state vector component by component to motivate its structure. We begin by formally defining the components of the state vector.

Definition 1 

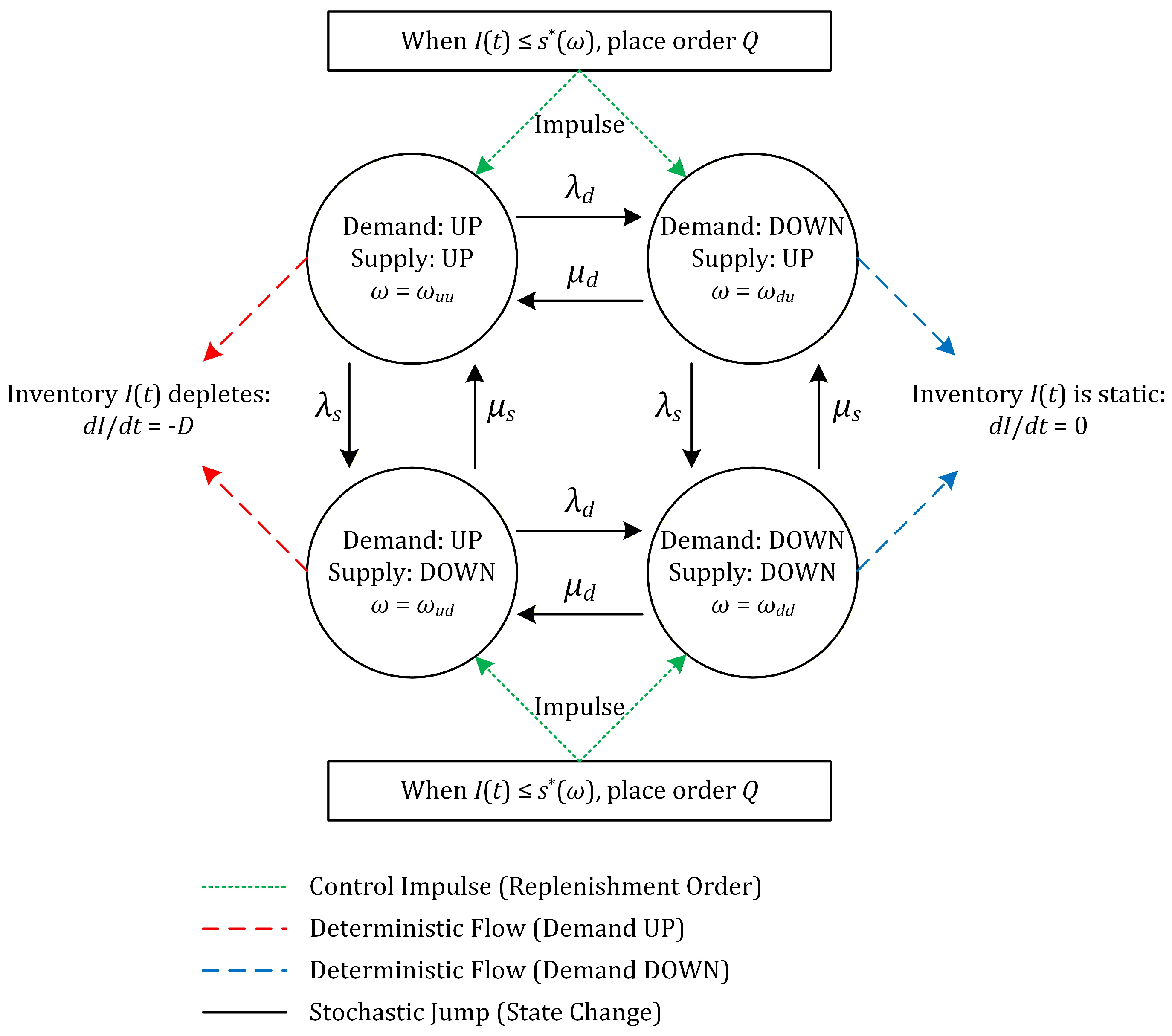
(State Space). The state of the system at time $t\ge 0$ is given by the vector $X\left(t\right)\in E$. The components of $X\left(t\right)$ are:

• $I\left(t\right)\in \mathbb{R}$: The inventory level. A positive value, $I\left(t\right)>0$, denotes on-hand stock, while a negative value, $I\left(t\right)<0$, represents backlogged demand. No lost sales are allowed.
• $e_d\left(t\right)\in \{\mathit{up},\mathit{down}\}$ and $e_s\left(t\right)\in \{\mathit{up},\mathit{down}\}$: The discrete states of the demand and supply environments, respectively. These environments modulate the system’s dynamics.
• $j_d\left(t\right)\in \{1,\dots ,m_d\}$ and $j_s\left(t\right)\in \{1,\dots ,m_s\}$: The internal phases of the Phase-Type (PH) distributions that govern the sojourn times in the current demand and supply states. This structure allows for modelling non-exponential disruptions.
• $k\left(t\right)\in \{0,1,\dots ,M\}$: The number of replenishment orders currently in transit (in the pipeline). M is the maximum number of outstanding orders.
• $L_i\left(t\right)\in S_L$ for $i=1,\dots k\left(t\right)$: The state of the i-th outstanding order. A key feature of our model is that the structure of an order depends on the supply environment at its time of placement:

  -

  If placed when $e_s=\mathit{UP}$, the lead time is deterministic. The state is $L_i\left(t\right)=(Q_i,Y_i,a_i\left(t\right))$, where $Q_i$ is the order quantity, $Y_i$ is the i.i.d. random yield, and $a_i\left(t\right)\in [0,L]$ is the ‘age’ of the order.

  -

  If placed when $e_s=\mathit{DOWN}$, the lead time is stochastic. The state is $L_i\left(t\right)=(Q_i,Y_i,a_i\left(t\right),j_{s,i}\left(t\right))$, where $a_i\left(t\right)$ tracks the deterministic part of the lead time (L), and $j_{s,i}\left(t\right)$ is the phase of the stochastic component (W).

For notational convenience, we group the discrete and supplementary continuous variables as $\omega \left(t\right)\in {\Omega }_d$. The full state vector is then $X\left(t\right)=\left(I\right(t),\omega (t\left)\right)$, and the state space E is a Borel subset of a finite-dimensional Euclidean space defined as:

$$E=\mathbb{R}\times {\Omega }_d.$$

To aid comprehension of the system’s dynamics, Figure 1 provides a schematic representation of the PDMP framework. The inventory level, $I\left(t\right)$, evolves deterministically between random events, while the discrete environmental state, $\omega \left(t\right)$, transitions stochastically. A control action (an impulse) is triggered when the inventory level hits a state-dependent threshold, causing an instantaneous jump in the pipeline state.

The model is parametrized by the following elements, which define the system’s physical and economic characteristics:

• Stochastic environments: The sojourn times in the demand and supply environments are governed by independent Phase-Type (PH) distributions, characterized by their respective sub-infinitesimal generator matrices, $T_d$ and $T_s$, and initial phase probability vectors.
• Demand rate: The demand rate is a constant $D>0$ when the demand environment is in the ‘UP’ state and zero otherwise.
• Lead times: The lead time includes a deterministic component $L>0$. When the supply environment is ‘DOWN’, there is an additional stochastic component, W, which follows a PH-distribution.
• Random yield: The received quantity is a random fraction Y of the ordered quantity, where Y follows a known distribution on $[0,1]$.
• Cost parameters: The cost structure includes positive constants for:

  -

  Holding cost rate ($k_h>0$),

  -

  Backorder cost rate ($p>0$),

  -

  Fixed ordering cost ($K>0$),

  -

  Variable (per-unit) ordering cost ($c>0$).

The control actions available to the decision maker are instantaneous decisions to place a replenishment order.

Definition 2 

(Action Space). The action space for replenishment is $\mathcal{Q}={\mathbb{R}}_{+}$. An action $Q\in \mathcal{Q}$ corresponds to placing an order of quantity Q.

2.2. Construction of the Controlled Process

Having defined the state space and the system’s parameters, we now formalise how a decision-maker can influence its evolution. An admissible control policy specifies the timing and sizing of replenishment orders, thereby shaping the stochastic process that describes the inventory system’s trajectory.

Definition 3 

(Admissible Control Policy). An admissible control policy π is a sequence of replenishment decisions ${\left\{({\tau }_n,Q_n)\right\}}_{n\in \mathbb{N}}$, where:

1.

${\tau }_n$ is a stopping time with respect to the natural filtration ${\mathcal{F}}_t=\sigma (X\left(s\right);s\le t)$ of the process, representing the time of the n-th order. We set ${\tau }_0=0$.

2.

$Q_n$ is an ${\mathcal{F}}_{{\tau }_n}$-measurable random variable taking values in $\mathcal{Q}$, representing the quantity ordered at time ${\tau }_n$.

The set of all admissible policies is denoted by Π.

Remark 1 

(On the Class of Admissible Policies). We make the following standard technical remarks regarding the class of admissible policies Π:

1.

Scope of Policies: The definition of an admissible policy is general and encompasses both history-dependent and randomised policies. However, a central result of this paper is to demonstrate that the optimal policy, which we seek within this broad class, is in fact a simple, deterministic, stationary Markov (state-feedback) policy.

2.

Non-Accumulation of Impulses: The impulse control framework implicitly requires that the stopping times are strictly increasing, i.e., ${\tau }_{n+1}>{\tau }_n$, and that ${\tau }_n\to \infty$ almost surely. This condition prevents the accumulation of an infinite number of interventions in a finite time interval, often termed ‘chattering’ controls. This is guaranteed in our setting because each intervention incurs a strictly positive fixed cost $K>0$, making any infinite sequence of orders over a finite horizon infinitely costly and thus manifestly suboptimal.

3.

Measurability of Controls: For a state-feedback policy, defined by a function $Q\left(x\right)$ that maps a state x to an order quantity, we require that this function is Borel-measurable. This ensures that the resulting stochastic process remains well-defined. The existence of such a measurable selector is guaranteed in our context by standard results in dynamic programming and optimal control theory, particularly as the optimal policy is derived from the value function, which we prove to be continuous.

For any given policy $\pi \in \Pi$ and initial state $x\in E$, there exists a probability measure ${\mathbb{P}}_x^{\pi }$ on the space of all possible system trajectories. The process $X\left(t\right)$ evolves as follows:

• Between replenishments, for $t\in ({\tau }_{n-1},{\tau }_n)$, the process evolves as a PDMP governed by a generator $\mathcal{A}$, which we call the ‘no-order’ generator.
• At replenishment time ${\tau }_n$, the state undergoes an instantaneous transition. If the state just before the order is $X\left({\tau }_n^{-}\right)=(I,\omega )$, the state immediately after is $X\left({\tau }_n\right)=(I,{\omega }^{\prime })$, where the pipeline component of ${\omega }^{\prime }$ is updated to reflect the new order $Q_n$. The inventory level I itself does not change at the moment of order placement.

The system’s evolution between replenishment orders is determined by three local characteristics: the flow $\varphi$, the jump rate $\lambda$, and the transition measure Q. These elements define the extended generator of the no-order process.

Definition 4 

(Generator of the No-Order Process). The extended generator $\mathcal{A}$ of the PDMP between replenishments acts on a suitable function $h:E\to \mathbb{R}$ from its domain $\mathcal{D}\left(\mathcal{A}\right)$. It is composed of a drift operator $\mathcal{X}$ and a jump operator:

$$\mathcal{A}h\left(x\right)=\mathcal{X}h\left(x\right)+\lambda \left(x\right){\int }_E[h\left(y\right)-h\left(x\right)]Q(x,dy),$$

(1)

where $\mathcal{X}h\left(x\right)$ is the derivative along the flow:

$$\mathcal{X}h\left(x\right)=\underset{t\to 0^{+}}{lim}{\displaystyle \frac{h\left(\varphi \right(x,t\left)\right)-h\left(x\right)}{t}}.$$

For our model, this corresponds to:

$$\mathcal{X}h\left(x\right)=-D·{\mathbf{1}}_{\{e_d=\mathit{up}\}}{\displaystyle \frac{\partial h}{\partial I}}\left(x\right)+\sum _{i=1}^{k\left(t\right)}{\displaystyle \frac{\partial h}{\partial a_i}}\left(x\right).$$

(2)

The domain $\mathcal{D}\left(\mathcal{A}\right)$ consists of functions for which this expression is well-defined and which satisfy appropriate boundary conditions that account for deterministic jumps, such as the arrival of orders with deterministic lead times.

For the subsequent analysis, particularly the convergence arguments in the vanishing discount proof, it is necessary to formally define the functional space in which the generator operates and to state its key properties.

Lemma 1 

(Functional Space for the Generator $\mathcal{A}$). Let $W\left(x\right)$ be the Lyapunov function from Assumption 2. We consider the generator $\mathcal{A}$ as an operator on the Banach space $B_W\left(E\right)$ of all continuous functions $h:E\to \mathbb{R}$ with finite weighted supremum norm:

$${\left|\right|h\left|\right|}_W=\underset{x\in E}{sup}{\displaystyle \frac{\left|h\right(x\left)\right|}{W\left(x\right)}}.$$

The domain of the generator, $\mathcal{D}\left(\mathcal{A}\right)$, is the subspace of functions $h\in B_W\left(E\right)$ for which the expression for $\mathcal{A}h\left(x\right)$ in Definition 4 is well-defined and for which $\mathcal{A}h\in B_W\left(E\right)$. The operator $(\mathcal{A},\mathcal{D}(\mathcal{A}\left)\right)$ has the following crucial properties:

1.

The domain $\mathcal{D}\left(\mathcal{A}\right)$ is dense in the space $B_W\left(E\right)$.

2.

The operator $(\mathcal{A},\mathcal{D}(\mathcal{A}\left)\right)$ is a closed linear operator on $B_W\left(E\right)$.

Remark 2. 

The properties of denseness and closure, stated above, are fundamental technical results in the theory of Piecewise Deterministic Markov Processes. The proofs, which typically rely on semigroup theory and resolvent operator analysis, are beyond the scope of this paper but can be found in standard texts on the subject, such as Davis [10]. The closure property is particularly critical, as it provides the rigorous mathematical justification for passing limits through the generator (i.e., showing that if $h_n\to h$ and $\mathcal{A}{h}_n\to g$, then $\mathcal{A}h=g$). This is implicitly used in the convergence arguments of the vanishing discount proof in Section 4.

2.3. Problem Formulation and Cost Structure

The objective is to find an admissible policy that minimizes the long-run average cost, which is composed of running costs for holding and backorders, and impulse costs for placing replenishment orders.

Definition 5 

(Long-Run Average Cost). The instantaneous running cost rate at state $x=(I,\omega )$ is given by

$$f\left(x\right)=k_h{\left[I\right]}^{+}+p{[-I]}^{+},$$

where ${\left[z\right]}^{+}=max(0,z)$. The cost associated with placing an order of size Q is $K+cQ$. For a given admissible policy $\pi \in \Pi$ and initial state x, the long-run average cost is defined as:

$$J(\pi ,x)=\underset{T\to \infty }{lim\; sup}{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{\pi }\left[{\int }_0^{T}f\left(X\left(t\right)\right)dt+\sum _{n=1}^{N\left(T\right)}(K+c{Q}_n)\right],$$

(3)

where $N\left(T\right)=sup\{n\in \mathbb{N}|{\tau }_n\le T\}$ is the number of orders placed up to time T.

We make the following standard assumption about the structure of the running cost, which is crucial for determining the structure of the optimal policy.

Assumption 1 

(Convex Costs). The instantaneous cost rate $f\left(x\right)$ is a convex function of the inventory level I.

The central problem of this paper is to find a policy that minimizes this cost criterion over the set of all admissible policies.

Definition 6 

(Optimal Control Problem). The optimal long-run average cost, ${\rho }^{\ast }$, is the infimum of the cost functional over all admissible policies:

$${\rho }^{\ast }=\underset{\pi \in \Pi }{inf}J(\pi ,x).$$

An admissible policy ${\pi }^{\ast }$ is optimal if it achieves this infimum, i.e.,

$${\pi }^{\ast }\in arg\underset{\pi \in \Pi }{min}J(\pi ,x).$$

2.4. Summary of Key Model Features

For clarity, we summarize the main features of our model, which will be assumed throughout the paper. This framework synthesizes several realistic aspects of modern inventory systems.

• System structure: The model considers a single-item, continuous-review inventory system with full backlogging. A maximum of M replenishment orders can be in the pipeline simultaneously.
• Stochastic environments: Both the demand and supply processes are modulated by independent, two-state continuous-time Markov chains. The sojourn times in all environmental states are governed by Phase-Type (PH) distributions, allowing for non-exponential behaviour.
• Demand rate: The demand rate is a constant $D>0$ when the demand environment is in the ‘UP’ state and is zero otherwise.
• Lead time: The lead time is a deterministic constant $L>0$ if an order is placed when the supply environment is ‘UP’. It is a stochastic quantity $L+W$, where W is a PH-distributed random variable, if the order is placed when the supply is ‘DOWN’.
• Random yield: The received quantity $R_n$ is a random fraction of the ordered quantity $Q_n$, given by $R_n=Y_n{Q}_n$, where $\left\{Y_n\right\}$ is an i.i.d. sequence of random variables with a known distribution on $[0,1]$.
• Costs: The cost structure includes positive constants for holding ($k_h$), backorders (p), fixed ordering (K), and per-unit ordering (c).
• Control: The control is of impulse type, where the decision-maker chooses the timing (${\tau }_n$) and sizing ($Q_n$) of replenishment orders.
• Initial conditions: The initial state of the system, $X\left(0\right)$, is known and non-random.

Finally, for the long-run average cost criterion to be well-defined, we impose a standard stability condition on the system. Specifically, we assume a Foster–Lyapunov drift condition, which is a powerful form of Lyapunov condition common in the analysis of stochastic processes:

Assumption 2 

(Lyapunov Condition). There exists a function $W:E\to [1,\infty )$, constants $c_1>0$, $c_2\ge 0$, and for every admissible impulse control policy $\pi \in \Pi$, its corresponding generator ${\mathcal{A}}^{\pi }$, such that

$${\mathcal{A}}^{\pi }W\left(x\right)\le -c_{1}W\left(x\right)+c_2,\forall x\in E.$$

(4)

Furthermore, the running cost is bounded by this function, i.e., $f\left(x\right)\le M_{f}W\left(x\right)$ for some constant $M_f>0$, and the intervention cost is bounded such that the expected post-replenishment value is controlled: for any order quantity $Q\in \mathcal{Q}$,

$${\mathbb{E}}_Y\left[W\left(x_{Q,Y}\right)\right]\le M_c(W\left(x\right)+Q)\mathit{for}\mathit{some}\mathit{constant}{M}_c>0.$$

(5)

Remark 3 

(On the Lyapunov Condition). Assumption 2 is a strong stability condition that is fundamental to long-run average cost analysis. While providing a formal proof for our specific model is complex, the assumption is economically intuitive. The function $W\left(x\right)$ can be interpreted as a measure of the system’s ‘energy’ or distance from an ideal state (e.g., zero inventory). The condition ${\mathcal{A}}^{\pi }W\left(x\right)\le -c_{1}W\left(x\right)+c_2$ implies that, on average, the system experiences a drift back towards a central region of the state space, driven by the economic incentives of the cost structure.

The economic intuition that the cost structure induces stability can be made mathematically rigorous. A constructive proof showing that our specific inventory model satisfies this assumption by building an explicit Lyapunov function is provided in Appendix B.

2.5. On the Necessity of Key Model Assumptions

To achieve our theoretical outcomes, several key assumptions are made. Here, we justify their necessity within our analytical framework.

• Cost Convexity: The assumption of a convex running cost function (Assumption 1) is the foundational pillar for our main structural result. Without it, the value function would not be guaranteed to be convex. The convexity of the value function is the critical property that ensures the optimal policy has the simple and elegant $(s,S)$ structure. Non-convex costs could lead to complex, multi-threshold, or even non-threshold optimal policies.
• Full Backlogging: Allowing for full backlogging (i.e., an inventory level that can become arbitrarily negative) simplifies the state space by removing a boundary at zero. If we were to assume lost sales, the inventory level would be bounded, introducing a reflection at this boundary which would significantly complicate the proof of the value function’s convexity.
• Lyapunov Condition (Bounded Moments): The Lyapunov-type stability condition (Assumption 2) is a technical requirement that is essential for long-run average cost analysis. It guarantees the ergodicity of the process under any stationary policy, ensuring that the average cost is well-defined and independent of the initial state. The vanishing discount approach, which connects the discounted problem to the average cost problem, relies fundamentally on this stability condition for convergence.
• Phase-Type (PH) Structure: The use of PH distributions is a crucial modelling choice that balances generality and tractability. It allows us to model non-exponential event timings, which is a significant step towards realism. At the same time, the underlying Markovian structure of PH distributions allows us to embed the process into a finite-dimensional state space. Without this structure (e.g., using arbitrary general distributions), the state would need to track the elapsed time in a given state, leading to an infinite-dimensional state space and a far more complex, often intractable, analysis.
• Pipeline Limit M: Limiting the maximum number of outstanding orders, M, is necessary to ensure the state space remains finite-dimensional. If an infinite number of orders were allowed in the pipeline, the state vector would require an infinite number of components to track the age and status of each order, making the problem analytically and computationally intractable. This assumption is also practically reasonable in most real-world logistics systems.

3. Analysis of the Optimal Control Problem

This section develops the core analytical tool for solving the optimal control problem: the Average Cost Optimality Equation (ACOE). We begin by presenting the ACOE, which establishes a set of equilibrium conditions that must be satisfied by the optimal policy. Conceptually, the ACOE balances the trade-off between two choices at any given state: continuation (not placing an order) and intervention (placing a replenishment order). We then state and prove the main Verification Theorem, a fundamental result which guarantees that any suitable solution to the ACOE indeed defines the optimal control policy. This theorem provides the rigorous foundation for our subsequent analysis.

Optimality Equation

The solution to the optimal control problem is characterized by a pair $(\rho ,h)$, where $\rho \in {\mathbb{R}}_{+}$ is the optimal long-run average cost, and $h:E\to \mathbb{R}$ is the relative value function. For problems involving a fixed ordering cost, this pair solves a quasi-variational inequality (QVI), which serves as the ACOE.

To formalize the effect of a control action, we explicitly define the post-replenishment state. For a pre-replenishment state $x=(I,\omega )$ and an order quantity Q, the post-replenishment state depends on the realized random yield Y. We denote this new state by $x_{Q,Y}=(I+YQ,{\omega }^{\prime })$, where ${\omega }^{\prime }$ reflects the updated pipeline information.

Definition 7 

(Average Cost Optimality Equation). A pair $(\rho ,h)$, with $\rho \in {\mathbb{R}}_{+}$ and $h\in \mathcal{D}\left(\mathcal{A}\right)$ bounded from below, is a solution to the ACOE if it satisfies the following system of relations for all $x=(I,\omega )\in E$:

$$\begin{array}{cc}\hfill \mathcal{A}h\left(x\right)+f\left(x\right)-\rho & \ge 0,\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\hfill h\left(x\right)-\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}& \ge 0,\hfill \end{array}$$

(6b)

$$\begin{array}{cc}\hfill \left(\mathcal{A}h\left(x\right)+f\left(x\right)-\rho \right)\left(h\left(x\right)-\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}\right)& =0.\hfill \end{array}$$

(6c)

In the above, the terms are defined as follows:

• $\mathcal{A}$ is the extended generator of the PDMP under the no-ordering policy, as defined in Definition 4. It governs the system dynamics between replenishment decisions.
• $f\left(x\right)=k_h{\left[I\right]}^{+}+p{[-I]}^{+}$ is the instantaneous cost rate.
• $x_{Q,Y}$ denotes the post-replenishment state. For a pre-replenishment state $x=(I,\omega )$ and an order quantity Q, the post-replenishment inventory level is $I+YQ$, where Y is the random yield. The discrete state component $\omega$ is unaffected by the replenishment action itself, although the pipeline information within $\omega$ is updated. Thus, $x_{Q,Y}=(I+YQ,{\omega }^{\prime })$, where ${\omega }^{\prime }$ reflects the updated pipeline.

When the system is managed under a specific admissible policy $\pi \in \Pi$, its dynamics are governed by a corresponding generator ${\mathcal{A}}^{\pi }$, which incorporates the jump intensity of the control impulses.

The following theorem, often called a Verification Theorem, establishes the sufficiency of the ACOE for optimality.

Theorem 1 

(Verification Theorem). Suppose there exists a scalar $\rho \in {\mathbb{R}}_{+}$ and a function $h\in \mathcal{D}\left(\mathcal{A}\right)$, which is bounded from below, that solve the ACOE (6). Furthermore, assume the following transversality condition holds for any admissible policy $\pi \in \Pi$:

$$\underset{T\to \infty }{lim\; sup}{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right]\le 0.$$

(7)

Then, ρ is the minimal long-run average cost, i.e., $\rho ={\rho }^{\ast }$. Moreover, the policy ${\pi }^{\ast }$ defined below is an optimal policy.

The optimal policy ${\pi }^{\ast }$ asserted by Theorem 1 is defined constructively based on the continuation and intervention regions derived from the value function h:

• Continuation region $C^{\ast }$:

  $$C^{\ast }=\{x\in E:h\left(x\right)<\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}\}.$$
  In this region, no order is placed.
• Intervention region $S^{\ast }$:

  $$S^{\ast }=\{x\in E:h\left(x\right)=\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}\}.$$
  In this region, an order of quantity $Q^{\ast }\left(x\right)$ is placed, where $Q^{\ast }\left(x\right)$ achieves the infimum:

  $$Q^{\ast }\left(x\right)\in arg\underset{Q\in \mathcal{Q}}{min}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}.$$

Proof. 

The proof is structured in two main parts, with the generalised Dynkin’s formula for PDMPs with impulse controls serving as the core analytical tool. First, we establish that $\rho$ is a lower bound on the long-run average cost for any admissible policy. To do this, we apply the inequalities from the ACOE to the system’s dynamics under an arbitrary policy $\pi$. Second, we demonstrate that the specific policy ${\pi }^{\ast }$, constructed from the solution $(\rho ,h)$, achieves this lower bound. This is accomplished by showing that, for policy ${\pi }^{\ast }$, the inequalities in the ACOE become equalities, thereby proving its optimality.

• Part 1: $\rho$ is a lower bound for the average cost.

Let $\pi \in \Pi$ be an arbitrary admissible policy. Let ${\left\{X_t\right\}}_{t\ge 0}$ be the stochastic process corresponding to this policy with initial state $X_0=x$. Let ${\left\{{\tau }_n\right\}}_{n\ge 1}$ and ${\left\{Q_n\right\}}_{n\ge 1}$ be the sequence of intervention times and order quantities, respectively, under policy $\pi$. Let $N\left(T\right)=sup\{n\in \mathbb{N}|{\tau }_n\le T\}$ be the number of orders placed up to time T.

We apply the generalized Dynkin’s formula for semi-martingales (see, e.g., ([10], Theorem 31.3) or ([15], Sect. 3)) to the function $h\left(X_t\right)$ over the time interval $[0,T]$. The process $h\left(X_t\right)$ is a semi-martingale whose dynamics can be decomposed into a continuous part, a jump part, and a martingale term. Its value at time T is given by:

$$h\left(X_T\right)-h\left(X_0\right)={\int }_0^T\mathcal{A}h\left(X_s\right)ds+\sum _{n=1}^{N\left(T\right)}\left[h\left(X_{{\tau }_n}\right)-h\left(X_{{\tau }_n^{-}}\right)\right]+M_T,$$

where $M_T$ is a martingale with $M_0=0$ and ${\mathbb{E}}_x^{\pi }\left[M_T\right]=0$. Taking the expectation ${\mathbb{E}}_x^{\pi }[·]$ on both sides and noting that $X_0=x$, we get:

$${\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right]-h\left(x\right)={\mathbb{E}}_x^{\pi }\left[{\int }_0^T\mathcal{A}h\left(X_s\right)ds\right]+{\mathbb{E}}_x^{\pi }\left[\sum _{n=1}^{N\left(T\right)}\left(h\left(X_{{\tau }_n}\right)-h\left(X_{{\tau }_n^{-}}\right)\right)\right].$$

(8)

We now bound the two terms on the right-hand side using the inequalities from the ACOE (6).

For the first term (the continuation part), inequality (6a) states that $\mathcal{A}h\left(x\right)+f\left(x\right)-\rho \ge 0$, which implies $\mathcal{A}h\left(x\right)\ge \rho -f\left(x\right)$ for all $x\in E$. This inequality holds for the process $X_s$ at all times $s\in [0,T]$ that are not intervention times. Therefore,

$${\mathbb{E}}_x^{\pi }\left[{\int }_0^T\mathcal{A}h\left(X_s\right)ds\right]\ge {\mathbb{E}}_x^{\pi }\left[{\int }_0^T(\rho -f\left(X_s\right))ds\right]=\rho T-{\mathbb{E}}_x^{\pi }\left[{\int }_0^{T}f\left(X_s\right)ds\right].$$

(9)

For the second term (the impulse part), at each intervention time ${\tau }_n$, an order $Q_n$ is placed. From inequality (6b), we have $h\left(x\right)\ge {inf}_{Q\in \mathcal{Q}}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}$. This holds for the state $X_{{\tau }_n^{-}}$ just before the jump. The post-jump state is $X_{{\tau }_n}$. Thus,

$$h\left(X_{{\tau }_n^{-}}\right)\ge K+c{Q}_n+{\mathbb{E}}_x^{\pi }\left[h\left(X_{{\tau }_n}\right)\right|{\mathcal{F}}_{{\tau }_n^{-}}].$$

Rearranging and taking the conditional expectation yields:

$${\mathbb{E}}_x^{\pi }[h\left(X_{{\tau }_n}\right)-h\left(X_{{\tau }_n^{-}}\right)|{\mathcal{F}}_{{\tau }_n^{-}}]\le -(K+c{Q}_n).$$

By the law of total expectation, and summing over all jumps up to time T, we get:

$${\mathbb{E}}_x^{\pi }\left[\sum _{n=1}^{N\left(T\right)}\left(h\left(X_{{\tau }_n}\right)-h\left(X_{{\tau }_n^{-}}\right)\right)\right]\le -{\mathbb{E}}_x^{\pi }\left[\sum _{n=1}^{N\left(T\right)}(K+c{Q}_n)\right].$$

(10)

Substituting the bounds (9) and (10) into the expected Dynkin’s Formula (8), we obtain:

$${\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right]-h\left(x\right)\ge \left(\rho T-{\mathbb{E}}_x^{\pi }\left[{\int }_0^{T}f\left(X_s\right)ds\right]\right)-{\mathbb{E}}_x^{\pi }\left[\sum _{n=1}^{N\left(T\right)}(K+c{Q}_n)\right].$$

Let $C_T\left(\pi \right)={\int }_0^{T}f\left(X_s\right)ds+{\sum }_{n=1}^{N\left(T\right)}(K+c{Q}_n)$ be the total cost incurred up to time T. The inequality can be rewritten as:

$${\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right]-h\left(x\right)\ge \rho T-{\mathbb{E}}_x^{\pi }\left[C_T\left(\pi \right)\right].$$

Rearranging to isolate the expected cost gives:

$${\mathbb{E}}_x^{\pi }\left[C_T\left(\pi \right)\right]\ge \rho T+h\left(x\right)-{\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right].$$

Dividing by T and taking the limit superior as $T\to \infty$:

$$J(\pi ,x)=\underset{T\to \infty }{lim\; sup}{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{\pi }\left[C_T\left(\pi \right)\right]\ge \rho +\underset{T\to \infty }{lim\; sup}\left({\displaystyle \frac{h\left(x\right)}{T}}-{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right]\right).$$

As $T\to \infty$, the term $h\left(x\right)/T\to 0$. By the transversality condition (7), we have

$$\underset{T\to \infty }{lim\; sup}{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right]\le 0.$$

Therefore, $-{lim\; sup}_{T\to \infty }{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{\pi }\left[h\left(X_T\right)\right]\ge 0$. This yields:

$$J(\pi ,x)\ge \rho .$$

Since $\pi$ was an arbitrary admissible policy, $\rho$ is a lower bound on the long-run average cost.

• Part 2: The policy ${\pi }^{\ast }$ is optimal.

Now, we consider the specific policy ${\pi }^{\ast }$ defined in the theorem. Let ${\left\{X_t^{\ast }\right\}}_{t\ge 0}$ be the process under this policy. The dynamics of this process are governed by the policy-dependent generator ${\mathcal{A}}^{{\pi }^{\ast }}$. By construction, the policy ${\pi }^{\ast }$ ensures that the inequalities in the ACOE become equalities in their respective regions of application, due to the complementarity condition (6c). The action of ${\mathcal{A}}^{{\pi }^{\ast }}$ on the value function h is thus defined piecewise: in the continuation region $C^{\ast }$, it matches the action of the no-order generator $\mathcal{A}$; in the intervention region $S^{\ast }$, it corresponds to the jump dynamics of the impulse control.

Consequently, all inequalities in the derivation from Part 1 become equalities for the process $X_t^{\ast }$. We follow the same steps as in Part 1:

• The integral term becomes an equality:

  $${\mathbb{E}}_x^{{\pi }^{\ast }}\left[{\int }_0^T\mathcal{A}h\left(X_s^{\ast }\right)ds\right]={\mathbb{E}}_x^{{\pi }^{\ast }}\left[{\int }_0^T(\rho -f\left(X_s^{\ast }\right))ds\right]=\rho T-{\mathbb{E}}_x^{{\pi }^{\ast }}\left[{\int }_0^{T}f\left(X_s^{\ast }\right)ds\right].$$
• The impulse term also becomes an equality:

  $${\mathbb{E}}_x^{{\pi }^{\ast }}\left[\sum _{n=1}^{N\left(T\right)}\left(h(X_{{\tau }_n^{\ast }}^{\ast })-h(X_{{\tau }_n^{\ast }}^{-})\right)\right]=-{\mathbb{E}}_x^{{\pi }^{\ast }}\left[\sum _{n=1}^{N\left(T\right)}(K+c{Q}_n^{\ast })\right].$$

Substituting these equalities back into the expected Dynkin’s formula (8) yields:

$${\mathbb{E}}_x^{{\pi }^{\ast }}\left[h\left(X_T^{\ast }\right)\right]-h\left(x\right)=\left(\rho T-{\mathbb{E}}_x^{{\pi }^{\ast }}\left[{\int }_0^{T}f\left(X_s^{\ast }\right)ds\right]\right)-{\mathbb{E}}_x^{{\pi }^{\ast }}\left[\sum _{n=1}^{N\left(T\right)}(K+c{Q}_n^{\ast })\right].$$

This simplifies to ${\mathbb{E}}_x^{{\pi }^{\ast }}\left[h\left(X_T^{\ast }\right)\right]-h\left(x\right)=\rho T-{\mathbb{E}}_x^{{\pi }^{\ast }}\left[C_T\left({\pi }^{\ast }\right)\right]$. Rearranging for the cost:

$${\mathbb{E}}_x^{{\pi }^{\ast }}\left[C_T\left({\pi }^{\ast }\right)\right]=\rho T+h\left(x\right)-{\mathbb{E}}_x^{{\pi }^{\ast }}\left[h\left(X_T^{\ast }\right)\right].$$

Dividing by T and taking the limit as $T\to \infty$:

$$J({\pi }^{\ast },x)=\underset{T\to \infty }{lim}{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{{\pi }^{\ast }}\left[C_T\left({\pi }^{\ast }\right)\right]=\rho +\underset{T\to \infty }{lim}\left({\displaystyle \frac{h\left(x\right)}{T}}-{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{{\pi }^{\ast }}\left[h\left(X_T^{\ast }\right)\right]\right).$$

Since ${\pi }^{\ast }$ is an admissible policy, the transversality condition (7) applies. Furthermore, because h is bounded from below, say by $h_{min}$, we have ${lim\; inf}_{T\to \infty }{\displaystyle \frac{1}{T}}{\mathbb{E}}_x^{{\pi }^{\ast }}\left[h\left(X_T^{\ast }\right)\right]\ge {lim}_{T\to \infty }{\displaystyle \frac{h_{min}}{T}}=0$. Combined with the transversality condition, this implies that if the limit exists, it must be zero. Thus, the final term vanishes. We are left with:

$$J({\pi }^{\ast },x)=\rho .$$

Since we have shown that $J(\pi ,x)\ge \rho$ for any policy $\pi$ and $J({\pi }^{\ast },x)=\rho$, it follows that $\rho$ is the minimal long-run average cost and ${\pi }^{\ast }$ is an optimal policy. This completes the proof. □

The Verification Theorem establishes the central role of the ACOE. It confirms that if we can find a solution pair $(\rho ,h)$, we have solved the optimal control problem. The remaining and more substantial theoretical challenge is to demonstrate that a solution to this equation actually exists. This is the subject of the next section, where we employ the vanishing discount approach to prove existence and then analyse the structural properties of the solution.

4. Solution of the Optimality Equation

The Verification Theorem establishes that if a solution to the Average Cost Optimality Equation (ACOE) exists, the optimal control problem is solved. The more substantial theoretical challenge, which we address in this section, is to prove that such a solution is guaranteed to exist. Our approach is the vanishing discount method. We first introduce a family of related discounted-cost problems, which are more tractable. We then establish key properties of their value functions, such as boundedness and equi-continuity. Finally, using an Arzelà–Ascoli argument, we show that as the discount factor vanishes, a subsequence of these solutions converges to a pair $(\rho ,h)$ that solves the original ACOE.

4.1. Existence of an Optimal Policy via Vanishing Discount

Our approach to proving the existence of a solution to the ACOE is the vanishing discount method. This involves analysing a family of more tractable discounted-cost problems and showing that their solutions converge to a solution for the average-cost problem as the discount factor vanishes. This convergence relies critically on the stability of the system, which is guaranteed by the Lyapunov condition stated in Assumption 2 [15].

The following lemmas establish key properties of the value functions for the associated discounted problems, which are essential for the vanishing discount argument.

Lemma 2 

(Properties of the Discounted Value Function). Under Assumption 2, for any sufficiently small $\alpha >0$, there exists a constant M such that the discounted value function $v_{\alpha }\left(x\right)$ satisfies $|v_{\alpha }\left(x\right)|\le MW\left(x\right)$ for all $x\in E$.

Proof. 

The discounted value function for a given initial state $x\in E$ is defined as the infimum of the total expected discounted cost over all admissible policies $\pi \in \Pi$:

$$v_{\alpha }\left(x\right)=\underset{\pi \in \Pi }{inf}{J}_{\alpha }(x,\pi ),$$

where

$$J_{\alpha }(x,\pi )={\mathbb{E}}_x^{\pi }\left[{\int }_0^{\infty }{e}^{-\alpha t}f\left(X_t\right)dt+\sum _{n=1}^{\infty }{e}^{-\alpha {\tau }_n}(K+c{Q}_n)\right].$$

Part 1: Lower Bound. The cost parameters are assumed to be non-negative: the running cost rate $f\left(x\right)\ge 0$ for all $x\in E$, the fixed cost $K>0$, and the variable cost $c>0$. The order quantities $Q_n$ are also non-negative. Consequently, the total cost functional $J_{\alpha }(x,\pi )$ is non-negative for any policy $\pi$. The infimum of a set of non-negative numbers is also non-negative. Therefore, we immediately have the lower bound:

$$v_{\alpha }\left(x\right)\ge 0,\forall x\in E.$$

Part 2: Upper Bound. To establish an upper bound, it suffices to find a single admissible policy whose cost is bounded by a multiple of $W\left(x\right)$. Since $v_{\alpha }\left(x\right)$ is the infimum over all policies, its value must be less than or equal to the cost of this particular policy. We consider the simplest admissible policy: the ‘never order’ policy, denoted by ${\pi }_{no}$, where no replenishment orders are ever placed.

Under ${\pi }_{no}$, the summation term in the cost functional is zero. The cost is purely the expected discounted running cost, which is given by:

$$J_{\alpha }(x,{\pi }_{no})={\mathbb{E}}_x^{{\pi }_{no}}\left[{\int }_0^{\infty }{e}^{-\alpha t}f\left(X_t\right)dt\right].$$

Let $\mathcal{A}$ denote the extended generator of the PDMP under the no-ordering policy (as defined in Definition 4). The integral expression above is the definition of the resolvent operator $R_{\alpha }={(\alpha I-\mathcal{A})}^{-1}$ applied to the function f. Thus, we have:

$$v_{\alpha }\left(x\right)\le J_{\alpha }(x,{\pi }_{no})=R_{\alpha }f\left(x\right).$$

(11)

Our goal is now to bound $R_{\alpha }f\left(x\right)$. From Assumption 2, we have a bound on the running cost in terms of the Lyapunov function: $f\left(x\right)\le M_{f}W\left(x\right)$. The resolvent operator $R_{\alpha }$ is a positive operator because its integral representation involves an expectation; that is, if $g_1\left(x\right)\ge g_2\left(x\right)$ for all x, then $R_{\alpha }{g}_1\left(x\right)\ge R_{\alpha }{g}_2\left(x\right)$. Applying this property and the linearity of the operator, we get:

$$R_{\alpha }f\left(x\right)\le R_{\alpha }\left(M_{f}W\right)\left(x\right)=M_f{R}_{\alpha }W\left(x\right).$$

(12)

The problem is now reduced to finding a bound for $R_{\alpha }W\left(x\right)$. We use the Lyapunov drift condition from Assumption 2 for the no-order generator $\mathcal{A}$:

$$\mathcal{A}W\left(x\right)\le -c_{1}W\left(x\right)+c_2.$$

Rearranging this inequality, we have:

$$-\mathcal{A}W\left(x\right)\ge c_{1}W\left(x\right)-c_2.$$

Adding $\alpha W\left(x\right)$ to both sides gives:

$$\alpha W\left(x\right)-\mathcal{A}W\left(x\right)\ge (\alpha +c_1)W\left(x\right)-c_2.$$

The left-hand side is precisely $(\alpha I-\mathcal{A})W\left(x\right)$. Applying the resolvent operator $R_{\alpha }$ to both sides of the inequality preserves the inequality due to positivity:

$$R_{\alpha }\left[(\alpha I-\mathcal{A})W\right]\left(x\right)\ge R_{\alpha }[(\alpha +c_1)W-c_2]\left(x\right).$$

By definition, $R_{\alpha }$ is the inverse of $(\alpha I-\mathcal{A})$, so the left-hand side simplifies to $W\left(x\right)$. By linearity of $R_{\alpha }$, the right-hand side becomes $(\alpha +c_1)R_{\alpha }W\left(x\right)-R_{\alpha }{c}_2\left(x\right)$. Thus,

$$W\left(x\right)\ge (\alpha +c_1)R_{\alpha }W\left(x\right)-R_{\alpha }{c}_2\left(x\right).$$

The resolvent of a constant $c_2$ is simply $R_{\alpha }{c}_2\left(x\right)={\mathbb{E}}_x^{{\pi }_{no}}\left[{\int }_0^{\infty }{e}^{-\alpha t}{c}_{2}dt\right]=c_2/\alpha$. Substituting this in, we obtain:

$$W\left(x\right)\ge (\alpha +c_1)R_{\alpha }W\left(x\right)-{\displaystyle \frac{c_2}{\alpha }}.$$

Since $\alpha >0$ and $c_1>0$, the term $(\alpha +c_1)$ is strictly positive, allowing us to rearrange and solve for $R_{\alpha }W\left(x\right)$:

$$R_{\alpha }W\left(x\right)\le {\displaystyle \frac{W\left(x\right)+c_2/\alpha }{\alpha +c_1}}={\displaystyle \frac{1}{\alpha +c_1}}W\left(x\right)+{\displaystyle \frac{c_2}{\alpha (\alpha +c_1)}}.$$

(13)

Now, we combine the bounds. Substituting (13) into (12), and then into (11), we get:

$$v_{\alpha }\left(x\right)\le M_f\left({\displaystyle \frac{1}{\alpha +c_1}}W\left(x\right)+{\displaystyle \frac{c_2}{\alpha (\alpha +c_1)}}\right).$$

From Assumption 2, $W\left(x\right)\ge 1$ for all $x\in E$. We can therefore bound the constant term by a multiple of $W\left(x\right)$:

$${\displaystyle \frac{c_2}{\alpha (\alpha +c_1)}}={\displaystyle \frac{c_2}{\alpha (\alpha +c_1)}}·1\le {\displaystyle \frac{c_2}{\alpha (\alpha +c_1)}}W\left(x\right).$$

This allows us to consolidate the bound into a single term proportional to $W\left(x\right)$:

$$v_{\alpha }\left(x\right)\le M_f\left({\displaystyle \frac{1}{\alpha +c_1}}+{\displaystyle \frac{c_2}{\alpha (\alpha +c_1)}}\right)W\left(x\right).$$

Let us define the term in parentheses as $M\left(\alpha \right)$:

$$M\left(\alpha \right):=M_f\left({\displaystyle \frac{\alpha +c_2}{\alpha (\alpha +c_1)}}\right).$$

For any fixed $\alpha >0$, $M\left(\alpha \right)$ is a finite positive constant. Let us choose an interval $(0,{\alpha }_{max}]$ for sufficiently small $\alpha$. The function $M\left(\alpha \right)$ is continuous on this interval and approaches a finite limit as $\alpha \to 0^{+}$ if $c_2=0$. If $c_2>0$, the term is unbounded near $\alpha =0$. However, the lemma requires existence for any given sufficiently small $\alpha$. For any fixed $\alpha \in (0,{\alpha }_{max}]$, we can set $M={sup}_{a^{\prime }\in [\alpha ,{\alpha }_{max}]}M\left(a^{\prime }\right)$, which is finite. Let’s set M more simply for a given $\alpha$:

$$M:=M\left(\alpha \right).$$

We have thus established that for any sufficiently small $\alpha >0$, there exists a constant $M>0$ such that $v_{\alpha }\left(x\right)\le MW\left(x\right)$.

Conclusion. Combining the lower and upper bounds, we have $0\le v_{\alpha }\left(x\right)\le MW\left(x\right)$. Since $W\left(x\right)\ge 1$, this implies $|v_{\alpha }\left(x\right)|=v_{\alpha }\left(x\right)\le MW\left(x\right)$, which completes the proof. □

Lemma 3 

(Equi-continuity of Centred Value Functions). Under the assumptions of Lemma 2, the family of centred value functions ${\{h_{\alpha }\left(x\right)=v_{\alpha }\left(x\right)-v_{\alpha }\left(x_0\right)\}}_{\alpha >0}$ is equi-continuous on any compact subset of the state space E.

Proof. 

The proof proceeds by establishing a stronger property: the family of value functions ${\left\{v_{\alpha }\right\}}_{\alpha >0}$ is equi-Lipschitz continuous on any compact subset $K\subset E$. Equi-continuity of the centred functions ${\left\{h_{\alpha }\right\}}_{\alpha >0}$ is then a direct consequence.

Let $K\subset E$ be an arbitrary compact set. Our objective is to show that there exists a Lipschitz constant $L_K$, independent of $\alpha$, such that for any $x_1,x_2\in K$:

$$|v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)|\le L_K\parallel x_1-x_2\parallel .$$

The proof is structured in three steps.

Step 1: Sub-optimality and Coupling Framework. Let $x_1,x_2\in K$. By the definition of the value function, for any $\epsilon >0$, there exists a policy ${\pi }_2^{\epsilon }$ that is $\epsilon$-optimal for the initial state $x_2$. That is,

$$v_{\alpha }\left(x_2\right)\le J_{\alpha }(x_2,{\pi }_2^{\epsilon })\le v_{\alpha }\left(x_2\right)+\epsilon .$$

Since ${\pi }_2^{\epsilon }$ is an admissible policy for any starting state, its cost when starting from $x_1$ provides an upper bound on the optimal cost $v_{\alpha }\left(x_1\right)$:

$$v_{\alpha }\left(x_1\right)\le J_{\alpha }(x_1,{\pi }_2^{\epsilon }).$$

Combining these two inequalities, we can bound the difference $v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)$:

$$v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)\le J_{\alpha }(x_1,{\pi }_2^{\epsilon })-J_{\alpha }(x_2,{\pi }_2^{\epsilon })+\epsilon .$$

(14)

The core of the proof is to bound the difference in costs, $|J_{\alpha }(x_1,{\pi }_2^{\epsilon })-J_{\alpha }(x_2,{\pi }_2^{\epsilon })|$. To do this, we employ a coupling argument. We construct two sample paths of the PDMP, denoted by ${\left\{X_t^1\right\}}_{t\ge 0}$ and ${\left\{X_t^2\right\}}_{t\ge 0}$, on the same probability space. Both processes start from different initial states, $X_0^1=x_1$ and $X_0^2=x_2$, but are driven by the same policy ${\pi }_2^{\epsilon }$ and are subjected to the same realization of all underlying random events (i.e., the same sequence of PH-sojourn times, random yields, etc.).

Step 2: Bounding the Expected Coupling Time. We define the coupling time, $\tau$, as the first time the two processes meet in the state space:

$$\tau =inf\{t>0:X_t^1=X_t^2\}.$$

For all $t\ge \tau$, the trajectories are identical, $X_t^1=X_t^2$, because they start from the same state and are driven by the same policy and random inputs. The Lyapunov condition (Assumption 2) ensures geometric ergodicity of the process, which implies that the expected time to couple is finite and can be bounded. For any compact set K, it is a standard result in the theory of stochastic processes under such drift conditions that there exists a constant $C_K<\infty$ such that for any $x_1,x_2\in K$:

$$\mathbb{E}\left[\tau \right]\le C_K\parallel x_1-x_2\parallel .$$

(15)

Step 3: Bounding the Cost Difference. The difference in the total discounted cost between the two paths is non-zero only on the stochastic interval $[0,\tau )$. We have:

$$|J_{\alpha }(x_1,{\pi }_2^{\epsilon })-J_{\alpha }(x_2,{\pi }_2^{\epsilon })|=\left|\mathbb{E}\left[{\int }_0^{\tau }{e}^{-\alpha t}(f\left(X_t^1\right)-f\left(X_t^2\right))dt+\sum _{k=1}^{N\left(\tau \right)}{e}^{-\alpha {\tau }_k}c(Q_k^1-Q_k^2)\right]\right|.$$

where $N\left(\tau \right)$ is the number of orders placed up to time $\tau$. The fixed costs K cancel out perfectly because under the coupling, an order is placed on both paths at the same times ${\tau }_k$ until time $\tau$.

Since K is compact, there exists a larger compact set $K^{\prime }$ such that $X_t^1,X_t^2\in K^{\prime }$ for all $t\in [0,\tau ]$. The running cost function $f\left(x\right)$ and the policy decision functions (which determine $Q_k$) are continuous on $K^{\prime }$, and therefore Lipschitz continuous. Let $L_f$ and $L_Q$ be the respective Lipschitz constants.

• Instantaneous Cost Difference:

  $$\mathbb{E}\left[{\int }_0^{\tau }{e}^{-\alpha t}|f\left(X_t^1\right)-f\left(X_t^2\right)|dt\right]\le \mathbb{E}\left[{\int }_0^{\tau }{L}_f\parallel X_t^1-X_t^2\parallel dt\right].$$
  Since $X_t^1,X_t^2\in K^{\prime }$, their distance is bounded by the diameter of $K^{\prime }$, $\mathrm{diam}\left(K^{\prime }\right)$. Thus, the integral is bounded by $L_f·\mathrm{diam}\left(K^{\prime }\right)·\mathbb{E}\left[\tau \right]$.
• Variable Ordering Cost Difference: The difference in ordered quantities can be bounded as $|Q_k^1-Q_k^2|\le L_Q\parallel X_{{\tau }_k^{-}}^1-X_{{\tau }_k^{-}}^2\parallel$. The expected number of orders up to time $\tau$, $\mathbb{E}\left[N\right(\tau \left)\right]$, is also bounded by the Lyapunov condition. Specifically, there exists a constant $C_N$ such that $\mathbb{E}\left[N\left(\tau \right)\right]\le C_N\parallel x_1-x_2\parallel$. Combining these, we can bound the expected sum of variable cost differences by a term proportional to $\mathbb{E}\left[\tau \right]$.

Aggregating these bounds, we can find a constant $L_K^{\prime }$, which depends on the Lipschitz constants $L_f,L_Q$, the cost parameter c, and properties of the compact set $K^{\prime }$, but is crucially independent of $\alpha$. This leads to:

$$|J_{\alpha }(x_1,{\pi }_2^{\epsilon })-J_{\alpha }(x_2,{\pi }_2^{\epsilon })|\le L_K^{\prime }\mathbb{E}\left[\tau \right].$$

(16)

Substituting the bound on the expected coupling time from (15) into (16) gives:

$$|J_{\alpha }(x_1,{\pi }_2^{\epsilon })-J_{\alpha }(x_2,{\pi }_2^{\epsilon })|\le L_K^{\prime }{C}_K\parallel x_1-x_2\parallel .$$

Let $L_K=L_K^{\prime }{C}_K$. Now we return to our initial inequality (14):

$$v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)\le L_K\parallel x_1-x_2\parallel +\epsilon .$$

By symmetry, we can reverse the roles of $x_1$ and $x_2$ to obtain the same bound for $v_{\alpha }\left(x_2\right)-v_{\alpha }\left(x_1\right)$. Therefore,

$$|v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)|\le L_K\parallel x_1-x_2\parallel +\epsilon .$$

Since this holds for any $\epsilon >0$, we can let $\epsilon \to 0$ to obtain the desired Lipschitz condition for the value functions:

$$|v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)|\le L_K\parallel x_1-x_2\parallel .$$

Step 4: Conclusion for Centred Value Functions. The Lipschitz continuity of the value functions $\left\{v_{\alpha }\right\}$ on the compact set K with a uniform constant $L_K$ (independent of $\alpha$) implies that the family is equi-Lipschitz continuous. For the centred value functions $h_{\alpha }\left(x\right)=v_{\alpha }\left(x\right)-v_{\alpha }\left(x_0\right)$, we have for any $x_1,x_2\in K$:

$$|h_{\alpha }\left(x_1\right)-h_{\alpha }\left(x_2\right)|=|(v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_0\right))-(v_{\alpha }\left(x_2\right)-v_{\alpha }\left(x_0\right))|=|v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)|\le L_K\parallel x_1-x_2\parallel .$$

Thus, the family ${\left\{h_{\alpha }\right\}}_{\alpha >0}$ is also equi-Lipschitz continuous, and therefore equi-continuous, on any compact subset of E. This completes the proof. □

With these foundational properties, the existence of a solution to the ACOE can be established through a standard Arzelà–Ascoli argument on the centred value functions, which is a cornerstone of the vanishing discount method. The key outcome is the following theorem.

Theorem 2 

(Existence of ACOE Solution). Under Assumption 2, there exists a pair $(\rho ,h)$ that solves the ACOE (6). The function $h:E\to \mathbb{R}$ is continuous, and $\rho \in {\mathbb{R}}_{+}$ is a constant.

Proof. 

The proof follows the standard vanishing discount approach and is structured in three main steps. We start with the family of discounted-cost problems and their associated value functions $v_{\alpha }\left(x\right)$, which solve the discounted Hamilton–Jacobi–Bellman (HJB) equation, a quasi-variational inequality (QVI). We then show that as the discount factor $\alpha \to 0$, a subsequence of these solutions converges to a pair $(\rho ,h)$ that solves the ACOE.

Step 1: Boundedness and Compactness of Centred Value Functions. Let $x_0\in E$ be a fixed reference state. The family of centred value functions is defined as $h_{\alpha }\left(x\right)=v_{\alpha }\left(x\right)-v_{\alpha }\left(x_0\right)$ for $\alpha >0$. We first establish the properties of this family that will allow us to use the Arzelà–Ascoli theorem.

• Local Uniform Boundedness of $\left\{h_{\alpha }\right\}$: As established in Lemma 2, for any sufficiently small $\alpha >0$, $|v_{\alpha }\left(x\right)|\le MW\left(x\right)$ for some constant M. The Lyapunov function $W\left(x\right)$ is continuous and therefore bounded on any compact set $K\subset E$. Thus, the family $\left\{v_{\alpha }\right\}$ is uniformly bounded on any compact set. Consequently, the family of centred value functions $\left\{h_{\alpha }\right\}$ is also uniformly bounded on any compact set K:

  $$\underset{x\in K}{sup}|h_{\alpha }\left(x\right)|=\underset{x\in K}{sup}|v_{\alpha }\left(x\right)-v_{\alpha }\left(x_0\right)|\le \underset{x\in K}{sup}|v_{\alpha }\left(x\right)|+|v_{\alpha }\left(x_0\right)|\le 2\underset{z\in K\cup \left\{x_0\right\}}{sup}MW\left(z\right)<\infty .$$
• Equi-continuity of $\left\{h_{\alpha }\right\}$: Lemma 3 establishes that the family ${\left\{v_{\alpha }\right\}}_{\alpha >0}$ is equi-Lipschitz on any compact subset of E. Since $h_{\alpha }\left(x_1\right)-h_{\alpha }\left(x_2\right)=v_{\alpha }\left(x_1\right)-v_{\alpha }\left(x_2\right)$, the family ${\left\{h_{\alpha }\right\}}_{\alpha >0}$ is also equi-Lipschitz, and therefore equi-continuous, on any compact subset of E.
• Boundedness of $\left\{\alpha v_{\alpha }\left(x_0\right)\right\}$: The scaled value at the reference state, $\alpha v_{\alpha }\left(x_0\right)$, is bounded. This is a direct consequence of Lemma 2, which states $|v_{\alpha }\left(x_0\right)|\le MW\left(x_0\right)$, implying $|\alpha v_{\alpha }\left(x_0\right)|\le \alpha MW\left(x_0\right)$. For $\alpha$ in a bounded interval, e.g., $\alpha \in (0,1]$, this value is bounded.

Step 2: Existence of a Convergent Subsequence via Arzelà-Ascoli. Given that the sequence $\left\{{\alpha }_k{v}_{{\alpha }_k}\left(x_0\right)\right\}$ is bounded for any sequence ${\alpha }_k\to 0$, by the Bolzano-Weierstrass theorem, there exists a convergent subsequence. Let us, by a slight abuse of notation, denote this subsequence again by $\left\{{\alpha }_k\right\}$ and its limit by $\rho \in \mathbb{R}$.

Let ${\left\{K_m\right\}}_{m=1}^{\infty }$ be an increasing sequence of compact sets such that ${\bigcup }_{m=1}^{\infty }{K}_m=E$. From Step 1, the sequence of functions $\left\{h_{{\alpha }_k}\right\}$ is uniformly bounded and equi-continuous on the compact set $K_1$. By the Arzelà-Ascoli theorem, there exists a subsequence, which we denote $\left\{h_{{\alpha }_{k_1}}\right\}$, that converges uniformly on $K_1$ to a continuous function $h_1$.

Next, considering the sequence $\left\{h_{{\alpha }_{k_1}}\right\}$ on the compact set $K_2$, we can similarly extract a further subsequence $\left\{h_{{\alpha }_{k_2}}\right\}$ that converges uniformly on $K_2$ to a continuous function $h_2$. Since $K_1\subset K_2$, this subsequence also converges uniformly on $K_1$, and by uniqueness of limits, $h_2{|}_{K_1}=h_1$.

We continue this process for all $m\in \mathbb{N}$. Now, consider the diagonal sequence $\left\{h_{{\alpha }_{k_k}}\right\}$. This sequence converges uniformly on every compact set $K_m$ to a continuous function h. For simplicity, we relabel this convergent subsequence as $\left\{h_{{\alpha }_k}\right\}$, so we have:

• ${\alpha }_k\to 0$ as $k\to \infty$.
• ${\alpha }_k{v}_{{\alpha }_k}\left(x_0\right)\to \rho$.
• $h_{{\alpha }_k}\left(x\right)\to h\left(x\right)$ uniformly on compact subsets of E.

Step 3: Convergence in the HJB Equation to the ACOE. Each value function $v_{{\alpha }_k}$ solves the discounted HJB equation, which is a QVI. Substituting $v_{{\alpha }_k}\left(x\right)=h_{{\alpha }_k}\left(x\right)+v_{{\alpha }_k}\left(x_0\right)$, this QVI is:

$$min\left\{\mathcal{A}{v}_{{\alpha }_k}\left(x\right)-{\alpha }_k{v}_{{\alpha }_k}\left(x\right)+f\left(x\right),v_{{\alpha }_k}\left(x\right)-\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[v_{{\alpha }_k}\left(x_{Q,Y}\right)\right]\}\right\}=0.$$

(17)

Let us analyse the limit as $k\to \infty$ of the two terms in the ‘min’ operator.

1. Limit of the Continuation Term: Let $C_k\left(x\right)=\mathcal{A}{v}_{{\alpha }_k}\left(x\right)-{\alpha }_k{v}_{{\alpha }_k}\left(x\right)+f\left(x\right)$. Substituting for $v_{{\alpha }_k}$, we get:

$$C_k\left(x\right)=\mathcal{A}{h}_{{\alpha }_k}\left(x\right)-{\alpha }_k{h}_{{\alpha }_k}\left(x\right)+f\left(x\right)-{\alpha }_k{v}_{{\alpha }_k}\left(x_0\right).$$

We analyse the limit of each component as $k\to \infty$:

• ${\alpha }_k{h}_{{\alpha }_k}\left(x\right)\to 0$ because ${\alpha }_k\to 0$ and $\left\{h_{{\alpha }_k}\right\}$ is locally uniformly bounded.
• ${\alpha }_k{v}_{{\alpha }_k}\left(x_0\right)\to \rho$ by construction of the subsequence.
• The generator term $\mathcal{A}{h}_{{\alpha }_k}\left(x\right)$ converges to $\mathcal{A}h\left(x\right)$. This is the most technical part. The space of continuous functions with at most linear growth, endowed with a weighted supremum norm ${\parallel g\parallel }_W={sup}_x\left|g\left(x\right)\right|/W\left(x\right)$, is a Banach space. The generator $\mathcal{A}$ is a closed operator on this space. The uniform bound $|h_{{\alpha }_k}\left(x\right)|\le CW\left(x\right)$ from the Lyapunov condition implies that $h_{{\alpha }_k}$ and h are in this space. The uniform convergence of $h_{{\alpha }_k}$ to h on compact sets, combined with the weighted bound, ensures strong convergence in this Banach space. Since $h_{{\alpha }_k}\to h$ and we know that $C_k\left(x\right)$ must converge (as shown below), it implies that $\mathcal{A}{h}_{{\alpha }_k}\left(x\right)$ must also converge. By the property of closed operators, its limit must be $\mathcal{A}h\left(x\right)$.

Thus, we conclude that ${lim}_{k\to \infty }{C}_k\left(x\right)=\mathcal{A}h\left(x\right)+f\left(x\right)-\rho$.

2. Limit of the Impulse Term: Let $I_k\left(x\right)=v_{{\alpha }_k}\left(x\right)-{inf}_{Q\in \mathcal{Q}}\{K+cQ+{\mathbb{E}}_Y\left[v_{{\alpha }_k}\left(x_{Q,Y}\right)\right]\}$. The term $v_{{\alpha }_k}\left(x_0\right)$ is a constant with respect to the infimum over Q, so it can be separated:

$$\begin{array}{cc}\hfill I_k\left(x\right)& =h_{{\alpha }_k}\left(x\right)+v_{{\alpha }_k}\left(x_0\right)-\left(\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h_{{\alpha }_k}\left(x_{Q,Y}\right)\right]\}+v_{{\alpha }_k}\left(x_0\right)\right)\hfill \\ \hfill & =h_{{\alpha }_k}\left(x\right)-\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h_{{\alpha }_k}\left(x_{Q,Y}\right)\right]\}.\hfill \end{array}$$

Let $G_k(Q,x)=K+cQ+{\mathbb{E}}_Y\left[h_{{\alpha }_k}\left(x_{Q,Y}\right)\right]$. The objective function inside the infimum is continuous in Q and converges uniformly in $h_{{\alpha }_k}$ on compact sets. By Berge’s Maximum Theorem, the convergence of the functions implies the convergence of the infimum:

$$\underset{k\to \infty }{lim}\underset{Q\in \mathcal{Q}}{inf}{G}_k(Q,x)=\underset{Q\in \mathcal{Q}}{inf}\underset{k\to \infty }{lim}{G}_k(Q,x)=\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}.$$

Therefore, ${lim}_{k\to \infty }{I}_k\left(x\right)=h\left(x\right)-{inf}_{Q\in \mathcal{Q}}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}$.

Since for each k, we have $min\{C_k\left(x\right),I_k\left(x\right)\}=0$, and since the ‘min’ function is continuous, taking the limit as $k\to \infty$ yields:

$$min\left\{\mathcal{A}h\left(x\right)+f\left(x\right)-\rho ,h\left(x\right)-\underset{Q\in \mathcal{Q}}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h\left(x_{Q,Y}\right)\right]\}\right\}=0.$$

This is precisely the ACOE (6). The continuity of the limit function h has been established. The at-most-linear growth of h follows from the linear growth of the bounding function $W\left(x\right)$ in the Lyapunov condition. The fact that $\rho \ge 0$ follows from the non-negativity of costs. This completes the proof of the existence of a solution to the ACOE. □

Numerical Illustration: A Vanishing-Discount Experiment

To complement the existence proof given by the vanishing-discount method, we present a small numerical experiment that (i) implements a simple finite-state approximation of the controlled PDMP, (ii) solves the associated discounted problems for discount rates tending to zero, and (iii) illustrates the vanishing-discount limits

$${\rho }^{\ast }=\underset{\alpha \downarrow 0}{lim}\alpha v_{\alpha }\left(x_0\right),h_{\alpha }(·)=v_{\alpha }(·)-v_{\alpha }\left(x_0\right)\underset{\alpha \downarrow 0}{\to }h(·),$$

where $v_{\alpha }$ is the $\alpha$-discounted value function for the finite approximation and $x_0$ is a fixed reference state.

We use a deliberately simple, transparent finite-state approximation that retains the essential features required to illustrate the vanishing-discount approach. The approximation is purely illustrative and does not aim to represent a full industrial instance; instead it demonstrates numerically the convergence properties used in the proof.

State space: inventory levels $I\in \{-3,-2,\dots ,6\}$ and a two-state supply/demand environment (e.g., ‘UP’ / ‘DOWN’). Time is discretised to unit steps solely for computational convenience; the theoretical results remain in continuous time. Demand in a step is 1 with probability $p_d$ and 0 otherwise, where $p_d=0.8$ in the ‘UP’ demand state and $p_d=0.2$ in the ‘DOWN’ state. The environment persists in its current state between steps with probability $0.9$ (switch probability $0.1$). Orders are modelled as instantaneous and the yield is set to one for simplicity. Cost parameters are: holding cost $k_h=1$, backorder cost $p=5$, fixed ordering cost $K=10$, and per-unit ordering cost $c=1$. Order sizes are integers and constrained so the post-order inventory remains within the truncated range.

For each discount rate $\alpha >0$, we solve the $\alpha$-discounted dynamic programming equations by value-iteration on the finite state space. At each state the action set comprises ‘do not order’ and ‘place order of size Q’ for integer $Q\ge 1$ up to the truncation bound. Value iteration is run until the sup-norm change is below ${10}^{-8}$. We then compute $\alpha v_{\alpha }\left(x_0\right)$ (with reference state $x_0=(I=0,{\omega }_0)$) and the centred functions $h_{\alpha }(·)=v_{\alpha }(·)-v_{\alpha }\left(x_0\right)$.

Table 1. Vanishing-discount experiment: $v_{\alpha }\left(x_0\right)$ and $\alpha v_{\alpha }\left(x_0\right)$ for several $\alpha$.

$\mathit{\alpha }$	${\mathit{v}}_{\mathit{\alpha }}\left({\mathit{x}}_0\right)$	$\mathit{\alpha }{\mathit{v}}_{\mathit{\alpha }}\left({\mathit{x}}_0\right)$	Iterations
0.10	32.62795863	3.26279586	187
0.05	60.66321496	3.03316075	381
0.02	143.06060175	2.86121204	964
0.01	279.68475641	2.79684756	1935
0.005	552.63341802	2.76316709	3877
0.002	1371.22616451	2.74245233	9705

summarises the computed discounted values at the reference state and the corresponding scaled values $\alpha v_{\alpha }\left(x_0\right)$ for a sequence of discount rates $\alpha \downarrow 0$. Iteration counts are reported to indicate numerical effort.

Two points should be noted:

• The sequence $\left\{\alpha v_{\alpha }\left(x_0\right)\right\}$ is observed to stabilise as $\alpha \downarrow 0$; in this illustrative experiment the values approach approximately ${\rho }^{\ast }\approx 2.74$. This is precisely the behaviour guaranteed by the vanishing-discount arguments: the rescaled discounted value at a fixed reference state converges to the average cost ${\rho }^{\ast }$.
• The centred value functions $h_{\alpha }(·)=v_{\alpha }(·)-v_{\alpha }\left(x_0\right)$ converge numerically (uniformly on the finite state set used in the test). In particular, the sup-norm differences $\parallel h_{{\alpha }_{k+1}}-h_{{\alpha }_k}{\parallel }_{\infty }$ decrease in our computations; representative sup-norm differences between consecutive $\alpha$ values above are $2.24$, $1.77$, $0.68$, $0.36$, $0.22$ (in the same order).

Although the example is small and simplified, the optimal impulse decisions recovered from the discounted problems stabilise as $\alpha \downarrow 0$. For the sample states inspected, the policy converged to the same state-dependent base-stock behaviour across the smaller values of $\alpha$ (for instance, when the supply environment is ‘DOWN’ and inventory is sufficiently negative the policy prescribes ordering to a higher reorder-up-to level than when the environment is ‘UP’). Hence, the numerical experiment supports the existence of the ACOE solution via the vanishing-discount method, and illustrates the emergence of a state-dependent base-stock structure in the finite approximation; the same structural argument is made rigorously in the preceding sections for the continuous PDMP model.

To conclude, this numerical experiment verifies the core steps of the vanishing-discount argument used in Theorem 2: (i) $\alpha v_{\alpha }\left(x_0\right)$ converges to a finite limit (the average cost ${\rho }^{\ast }$), (ii) the centred functions $h_{\alpha }(·)$ stabilise, and (iii) the optimal policies derived from the discounted problems stabilise and exhibit the state-dependent base-stock pattern. These observations corroborate the theoretical existence result and provide an accessible validation that the abstract vanishing-discount machinery is effective on a concrete finite approximation.

4.2. Structural Properties of the Optimal Policy

Having established the existence of the relative value function h, we now analyse its structural properties. We show that under Assumption 1 on the cost structure, the value function is convex. This property is the cornerstone for proving that the optimal policy has a simple and intuitive state-dependent base-stock, or $(s,S)$, structure.

Proposition 1 

(Convexity of the Value Function). Let $(\rho ,h)$ be a solution to the ACOE as established in Theorem 2. Under Assumption 1, the function $h\left(x\right)=h(I,\omega )$ is convex in the inventory level I for each discrete state $\omega \in {\Omega }_d$.

Proof. 

The proof proceeds by demonstrating the convexity of the discounted value function $v_{\alpha }\left(x\right)$ for any $\alpha >0$. The relative value function $h\left(x\right)$ is obtained as the pointwise limit of a sequence of centred value functions $h_{{\alpha }_k}\left(x\right)=v_{{\alpha }_k}\left(x\right)-v_{{\alpha }_k}\left(x_0\right)$. Since the pointwise limit of a sequence of convex functions is convex, establishing the convexity of $v_{\alpha }\left(x\right)$ is sufficient.

We establish the convexity of $v_{\alpha }(I,\omega )$ with respect to the inventory level I by induction on the value iteration sequence for the discounted problem. The discounted value function $v_{\alpha }$ is the unique fixed point of the Bellman operator ${\mathcal{T}}_{\alpha }$, i.e., $v_{\alpha }={\mathcal{T}}_{\alpha }{v}_{\alpha }$. The value iteration algorithm is defined by $v_{n+1}={\mathcal{T}}_{\alpha }{v}_n$, with $v_0\left(x\right)=0$. The Bellman operator is given by:

$$\left({\mathcal{T}}_{\alpha }v\right)\left(x\right):=min\{{\mathcal{S}}_{\alpha }\left(v\right)\left(x\right),\mathcal{I}\left(v\right)\left(x\right)\},$$

where the continuation cost operator ${\mathcal{S}}_{\alpha }$ and the impulse cost operator $\mathcal{I}$ are defined as follows. For a given function v, the continuation cost ${\mathcal{S}}_{\alpha }\left(v\right)\left(x\right)$ is the expected total discounted cost starting from state x assuming no replenishment orders are ever placed, and with v serving as a terminal cost function. It is the solution to the resolvent equation $(\alpha I-\mathcal{A})u=f$, which has the explicit probabilistic representation:

$${\mathcal{S}}_{\alpha }\left(v\right)\left(x\right):={\mathbb{E}}_x^{{\pi }_{no}}\left[{\int }_0^{\infty }{e}^{-\alpha t}f\left(X_t\right)dt\right],$$

where ${\pi }_{no}$ is the “never order” policy. The impulse cost is:

$$\mathcal{I}\left(v\right)\left(x\right):=\underset{Q\ge 0}{inf}\{K+cQ+{\mathbb{E}}_Y\left[v\left(x_{Q,Y}\right)\right]\}.$$

Let $x=(I,\omega )$.

Base Case: We initialize the value iteration with $v_0\left(x\right)=0$. This function is linear (and thus convex) in the inventory level I.

Inductive Hypothesis: Assume that for some $n\ge 0$, the value function iterate $v_n\left(x\right)=v_n(I,\omega )$ is convex in I for every fixed discrete state $\omega \in {\Omega }_d$.

Inductive Step: We must show that $v_{n+1}\left(x\right)=\left({\mathcal{T}}_{\alpha }{v}_n\right)\left(x\right)$ is also convex in I. This involves analysing the convexity of the two components of the minimum operator, ${\mathcal{S}}_{\alpha }\left(v_n\right)$ and $\mathcal{I}\left(v_n\right)$, and then the properties of the minimum itself.

1. Convexity of the Impulse Term $\mathcal{I}\left(v_n\right)(I,\omega )$: The impulse cost is the minimal expected cost immediately following a replenishment decision. It can be formulated as an infimal convolution. Let the order-up-to level be S. The order quantity is $Q=S-I$. The impulse cost is:

$$\mathcal{I}\left(v_n\right)(I,\omega )=\underset{S\ge I}{inf}\{K+c(S-I)+{\mathbb{E}}_Y\left[v_n(S,{\omega }_p)\right]\},$$

where ${\omega }_p$ denotes the post-replenishment discrete state. This expression can be written as $(g_1\oplus g_2)\left(I\right)$, the infimal convolution of two functions: $g_1\left(I\right)=-cI$ and $g_2\left(S\right)=K+cS+{\mathbb{E}}_Y\left[v_n(S,{\omega }_p)\right]$.

• The function $g_1\left(I\right)$ is linear in I and is therefore convex.
• For $g_2\left(S\right)$: The term $K+cS$ is linear in S. By the inductive hypothesis, $v_n(S,{\omega }_p)$ is convex in S. The expectation operator preserves convexity. To see this, for any convex function $\varphi \left(S\right)$ and $\lambda \in [0,1]$, Jensen’s inequality for conditional expectations yields $\mathbb{E}\left[\varphi (\lambda S_1+(1-\lambda )S_2)\right]\le \mathbb{E}[\lambda \varphi \left(S_1\right)+(1-\lambda )\varphi \left(S_2\right)]=\lambda \mathbb{E}\left[\varphi \left(S_1\right)\right]+(1-\lambda )\mathbb{E}\left[\varphi \left(S_2\right)\right]$. Thus, ${\mathbb{E}}_Y\left[v_n(S,{\omega }_p)\right]$ is convex in S. The sum of convex functions is convex, so $g_2\left(S\right)$ is convex.

It is a fundamental result of convex analysis that the infimal convolution of two convex functions is convex (see, e.g., [35]). Therefore, $\mathcal{I}\left(v_n\right)(I,\omega )$ is a convex function of I.

2. Convexity of the Continuation Term ${\mathcal{S}}_{\alpha }\left(v_n\right)(I,\omega )$: The continuation term is the solution u to the equation $(\alpha I-\mathcal{A})u=f$. By its definition as an expected discounted cost, we have

$${\mathcal{S}}_{\alpha }\left(v_n\right)\left(x\right)={\mathbb{E}}_x^{{\pi }_{no}}\left[{\int }_0^{\infty }{e}^{-\alpha t}f\left(X_t\right)dt\right].$$

The convexity of ${\mathcal{S}}_{\alpha }\left(v_n\right)(I,\omega )$ in I is established by showing that the operator mapping the cost function f to the value function ${\mathcal{S}}_{\alpha }\left(v_n\right)$ preserves convexity. Let $x_1=(I_1,\omega )$ and $x_2=(I_2,\omega )$ be two states with the same discrete component, and let $x_{\lambda }=\lambda x_1+(1-\lambda )x_2=(\lambda I_1+(1-\lambda )I_2,\omega )$ for $\lambda \in [0,1]$. Because the drift of the inventory level is linear (or state-independent), the process path starting from $x_{\lambda }$ is the convex combination of the paths starting from $x_1$ and $x_2$. By Assumption 1, f is convex in I. Since expectation is a linear operator and preserves convexity, the expected value of a convex function of the process state is also convex with respect to the initial state. Thus, ${\mathcal{S}}_{\alpha }\left(v_n\right)(I,\omega )$ is convex in I.

3. Convexity of $v_{n+1}\left(x\right)=min\{{\mathcal{S}}_{\alpha }\left(v_n\right),\mathcal{I}\left(v_n\right)\}$: The minimum of two convex functions is not generally convex. However, in the context of QVIs for optimal impulse control, convexity is preserved under specific structural conditions. The key is the structure of the intervention set $S_n=\left\{(I,\omega )\right|{\mathcal{S}}_{\alpha }\left(v_n\right)(I,\omega )\ge \mathcal{I}\left(v_n\right)(I,\omega )\}$. We show this is a convex set of the form $(-\infty ,s_n\left(\omega \right)]$ by proving that the difference function ${\Delta }_n(I,\omega )={\mathcal{S}}_{\alpha }\left(v_n\right)(I,\omega )-\mathcal{I}\left(v_n\right)(I,\omega )$ is non-decreasing in I.

The derivative of the impulse cost with respect to I is ${\displaystyle \frac{d}{dI}}\mathcal{I}\left(v_n\right)(I,\omega )=-c$, as the optimal order-up-to level $S_n^{\ast }$ is independent of the current inventory level I. To show ${\Delta }_n$ is non-decreasing, we need to demonstrate that ${\displaystyle \frac{d}{dI}}{\mathcal{S}}_{\alpha }\left(v_n\right)(I,\omega )\ge -c$. This property, that the slope of the continuation value function is bounded below by the negative marginal ordering cost, is a fundamental economic principle in these models and can be shown to hold inductively. Since $v_0=0$, the property holds for $n=0$. Assuming it holds for $v_n$, it can be shown to hold for $v_{n+1}$.

With ${\Delta }_n(I,\omega )$ established as non-decreasing, the intervention set is indeed of the form $(-\infty ,s_n\left(\omega \right)]$. The function $v_{n+1}$ is then constructed by ‘pasting’ the two convex functions $\mathcal{I}\left(v_n\right)$ and ${\mathcal{S}}_{\alpha }\left(v_n\right)$ at the reorder point $s_n\left(\omega \right)$. Convexity of $v_{n+1}$ is then guaranteed by the smooth-pasting condition at this boundary:

$${\displaystyle \frac{d}{dI}}\mathcal{I}\left(v_n\right)(s_n,\omega )={\displaystyle \frac{d}{dI}}{\mathcal{S}}_{\alpha }\left(v_n\right)(s_n,\omega ).$$

This optimality condition ensures that $v_{n+1}$ is not only convex but also continuously differentiable at the boundary between the continuation and intervention regions.

Since the operator ${\mathcal{T}}_{\alpha }$ preserves convexity and $v_0$ is convex, it follows by induction that $v_n$ is convex in I for all $n\ge 0$. As the value function $v_{\alpha }\left(x\right)$ is the pointwise limit of the sequence of convex functions ${\left\{v_n\left(x\right)\right\}}_{n\ge 0}$, it is also convex in I. Consequently, the relative value function $h\left(x\right)=v_{\alpha }\left(x\right)-v_{\alpha }\left(x_0\right)$ is also convex in I for every fixed discrete state $\omega$. This completes the proof. □

The convexity of the value function directly implies that the optimal policy can be characterized by state-dependent thresholds, a structure well-known in inventory theory as an $(s,S)$ policy. The following theorem formalizes this crucial structural result for our PDMP model.

Theorem 3 

(Structure of the Optimal Policy). Under Assumptions 2 and 1, the optimal replenishment policy ${\pi }^{\ast }$ is a state-dependent $(s,S)$ policy. That is, for each discrete environmental state $\omega \in {\Omega }_d$, there exists an optimal order-up-to level $S^{\ast }\left({\omega }_p\right)$ and a reorder point $s^{\ast }\left(\omega \right)$ such that it is optimal to place an order to raise the inventory level to $S^{\ast }\left({\omega }_p\right)$ whenever the current inventory level $I\left(t\right)\le s^{\ast }\left(\omega \right)$.

Before proceeding with the formal proof, we offer an economic justification for this crucial conclusion. The optimality of the state-dependent ($s,S$) structure stems directly from the convexity of the relative value function, which is itself a consequence of both the convex cost structure and, critically, the fact that the system’s dynamics preserve this convexity over time.

The justification begins with the standard and economically sound assumption of convex running costs (Assumption 1). This signifies that the marginal cost of deviating from an ideal inventory level is non-decreasing. For the value function $h(I,\omega )$, which represents the total expected future costs, to also be convex, the system’s transition operator must maintain this property. This preservation of convexity holds due to the fundamental nature of our PDMP model:

• Deterministic Flow: Between random events, the inventory depletes deterministically at a constant rate. This linear evolution ensures that the expected cost accumulated during this period remains a convex function of the initial inventory level.
• Stochastic Jumps: At random event times (e.g., a change in demand state or the arrival of a replenishment), the system transitions to a new state. The resulting expected future cost is an average over the possible outcomes. The process of taking an expectation is a linear operation that preserves the convexity of the value function.

Because both core components of the system’s dynamics preserve convexity, the value function inherits the convexity of the underlying cost functions. This property implies that the marginal value of an additional unit of stock is non-decreasing.

The convexity of h is the critical property that gives rise to the ($s,S$) structure. The decision to order involves comparing the cost of continuing, represented by $h(I,\omega )$, against the cost of intervening. The convexity of h ensures that the net benefit of ordering is also a convex function of the current inventory level I. A convex function of this nature partitions the state space into a single continuous ‘do-not-order’ region and ‘order’ regions at the extremes. For a replenishment problem, the relevant region is at low inventory levels. Consequently, there must exist a single threshold, the reorder point $s^{\ast }\left(\omega \right)$, below which ordering is optimal. The optimal target level, $S^{\ast }\left({\omega }_p\right)$, is determined by finding the minimum of a related convex function and is therefore independent of the inventory level at which the order is placed. This intuitive economic reasoning holds even in our complex model, demonstrating the robustness of threshold-based control.

Proof. 

The proof follows from the convexity of the relative value function $h(I,\omega )$, established in Proposition 1. We will demonstrate that this convexity, combined with the structure of the cost functions, naturally induces a state-dependent $(s,S)$ policy. The proof is structured in several steps.

Step 1: The Optimal Action Rule and the Intervention Set. The decision to intervene (place an order) or to continue (not place an order) is governed by the complementarity condition (6c) of the ACOE. An impulse action is optimal at a state $x=(I,\omega )$ if and only if the impulse cost is less than or equal to the continuation cost. This defines the intervention region $S^{\ast }$ as the set of states where:

$$h(I,\omega )\ge \underset{Q\ge 0}{inf}\{K+cQ+{\mathbb{E}}_Y\left[h(I+YQ,{\omega }_p)\right]\}.$$

(18)

Let the right-hand side of this inequality be denoted by $\mathcal{K}(I,\omega )$, which represents the minimal achievable expected post-intervention cost.

Step 2: Structure of the Minimal Post-Intervention Cost $\mathcal{K}(I,\omega )$. We first analyse the structure of $\mathcal{K}(I,\omega )$. For a given pre-replenishment state $(I,\omega )$, the decision maker chooses an order quantity Q to minimize the post-intervention cost. It is more convenient to formulate this in terms of the target inventory level S. Let $Q=S-I$. The post-intervention cost, as a function of the target level S, is:

$$\Phi (S\mid I,\omega )=K+c(S-I)+{\mathbb{E}}_Y\left[h(S,{\omega }_p)\right].$$

The minimal post-intervention cost is then $\mathcal{K}(I,\omega )={inf}_{S\ge I}\Phi (S\mid I,\omega )$. We can separate the terms that depend on I from those that depend on S:

$$\mathcal{K}(I,\omega )=K-cI+\underset{S\ge I}{inf}\{cS+{\mathbb{E}}_Y\left[h(S,{\omega }_p)\right]\}.$$

Let us define the function $\Psi (S,{\omega }_p):=cS+{\mathbb{E}}_Y\left[h(S,{\omega }_p)\right]$. From Proposition 1, $h(S,{\omega }_p)$ is convex in S. Since $cS$ is linear and the expectation operator preserves convexity, $\Psi (S,{\omega }_p)$ is a convex function of S. A convex function on $\mathbb{R}$ has a non-empty set of minimizers, which we denote by $S^{\ast }\left({\omega }_p\right)$. Crucially, this set of optimal order-up-to levels depends only on the post-replenishment discrete state ${\omega }_p$, not on the pre-order inventory level I. Let $S^{\ast }\in S^{\ast }\left({\omega }_p\right)$ be any selection from this set.

The infimum in the expression for $\mathcal{K}(I,\omega )$ is taken over $S\ge I$. Since $\Psi (S,{\omega }_p)$ is convex, its minimum over the half-line $[I,\infty )$ is achieved either at $S^{\ast }$ (if $S^{\ast }\ge I$) or at I (if $S^{\ast }<I$). However, the physical meaning of an (s,S) policy is to order up to a level, implying that the target level S is typically greater than the current level I. The structure of the problem naturally leads to this behaviour. Assuming an unconstrained minimizer $S^{\ast }$ exists, the optimal target level is simply $S^{\ast }$. The expression for the minimal post-intervention cost then simplifies to:

$$\mathcal{K}(I,\omega )=(K+\Psi (S^{\ast }\left({\omega }_p\right),{\omega }_p))-cI.$$

The term $(K+\Psi (S^{\ast }\left({\omega }_p\right),{\omega }_p))$ is a constant for a given environmental state $\omega$. Therefore, the minimal post-intervention cost $\mathcal{K}(I,\omega )$ is a linear function of the inventory level I with a slope of $-c$.

Step 3: Characterization of the Intervention Set and the Reorder Point $s^{\ast }\left(\omega \right)$. The intervention rule from (18) is to order when $h(I,\omega )\ge \mathcal{K}(I,\omega )$. Let us analyse the difference function $\Delta (I,\omega )=h(I,\omega )-\mathcal{K}(I,\omega )$.

• From Proposition 1, $h(I,\omega )$ is a convex function in I.
• From Step 2, $\mathcal{K}(I,\omega )$ is a linear function in I.
• Therefore, $\Delta (I,\omega )$ is also a convex function in I.

We now examine the asymptotic behaviour of $\Delta (I,\omega )$. The cost rate $f\left(x\right)=k_h{\left[I\right]}^{+}+p{[-I]}^{+}$ grows linearly as $I\to \pm \infty$. The value function $h(I,\omega )$ inherits this asymptotic linear growth from the running costs. Since $\mathcal{K}(I,\omega )$ is also linear in I with slope $-c$, the difference $\Delta (I,\omega )$ will also exhibit asymptotic linear growth. Specifically, the convexity of $h(I,\omega )$ implies that its slope is non-decreasing. For large positive I, the holding cost dominates, and the slope of h approaches $k_h/\alpha$. For large negative I, the backorder cost dominates, and the slope of h approaches $-p/\alpha$. Since costs are positive, we can ensure that these slopes are greater than $-c$. This implies that ${lim}_{I\to \pm \infty }\Delta (I,\omega )=+\infty$.

A convex function on $\mathbb{R}$ that tends to $+\infty$ as its argument tends to $\pm \infty$ must have a global minimum. The set where this function is non-positive, $\{I\in \mathbb{R}\mid \Delta (I,\omega )\le 0\}$, is a closed interval, and consequently, the intervention set where $\Delta (I,\omega )\ge 0$ must be of the form $(-\infty ,s^{\ast }\left(\omega \right)]\cup [S^{\prime }\left(\omega \right),\infty )$.

Our problem context is replenishment due to low inventory levels (stock-outs or backorders). Therefore, the economically relevant part of the intervention region is the lower tail, $\{I\mid I\le s^{\ast }\left(\omega \right)\}$. This set defines the reorder point $s^{\ast }\left(\omega \right)$ as the largest inventory level at which it is optimal to place an order:

$$s^{\ast }\left(\omega \right)=sup\{I\in \mathbb{R}\mid h(I,\omega )\ge \mathcal{K}(I,\omega )\}.$$

The convexity of $\Delta (I,\omega )$ guarantees that if it is optimal to order at inventory level I, it is also optimal to order at any level $I^{\prime }<I$.

Conclusion and Synthesis. For each discrete state $\omega \in {\Omega }_d$, we have established the existence of:

• An optimal order-up-to level $S^{\ast }\left({\omega }_p\right)$ that depends only on the post-replenishment state ${\omega }_p$.
• A reorder point $s^{\ast }\left(\omega \right)$ such that an order is placed if and only if the current inventory level satisfies $I\le s^{\ast }\left(\omega \right)$. When an order is placed, the quantity is $Q^{\ast }=S^{\ast }\left({\omega }_p\right)-I$.

This pair, $(s^{\ast }\left(\omega \right),S^{\ast }\left({\omega }_p\right))$, defines a state-dependent $(s,S)$ policy. This completes the proof. □

Remark 4 

(Computational Procedure and Qualitative Properties of the Policy). The constructive nature of the preceding proof provides a clear procedure for computing the optimal policy parameters from a given value function h. First, the optimal order-up-to level $S^{\ast }\left({\omega }_p\right)$ is found by solving the one-dimensional convex optimisation problem ${min}_S\{cS+\mathbb{E}\left[h(S,{\omega }_p)\right]\}$. Second, with $S^{\ast }$ known, the reorder point $s^{\ast }\left(\omega \right)$ is found by computing the largest root of the convex function $\Delta (I,\omega )=h(I,\omega )-\mathcal{K}(I,\omega )$. Both of these computational steps can be performed efficiently using standard numerical search algorithms.

Furthermore, the optimal policy parameters exhibit intuitive monotonic properties. A formal proof of this monotonicity, while beyond the scope of this paper, can be obtained by showing that the Bellman operator preserves properties of submodularity in the state and action variables. The key insight is that if one discrete state ${\omega }^{\prime }$ is unambiguously ‘riskier’ than another ω (e.g., due to a higher backorder cost rate or a faster demand rate), the value function will reflect this, i.e., $h(I,{\omega }^{\prime })\ge h(I,\omega )$. More specifically, the marginal value of inventory, $h(I+1,\omega )-h(I,\omega )$, will be different. This property is preserved through the value iteration process. Consequently, a riskier state leads to higher optimal inventory levels to buffer against that risk. This implies that if ${\omega }^{\prime }$ is riskier than ω, we would expect $s^{\ast }\left({\omega }^{\prime }\right)\ge s^{\ast }\left(\omega \right)$ and $S^{\ast }\left({\omega }_p^{\prime }\right)\ge S^{\ast }\left({\omega }_p\right)$. This confirms that the derived optimal policy structure not only exists but also aligns with fundamental principles of risk management in inventory theory.

4.3. The Abstract Policy Iteration Algorithm and Its Convergence

The structural properties of the optimal policy, particularly its state-dependent threshold nature, motivate the use of the Policy Iteration Algorithm (PIA) to find the optimal pair $({\rho }^{\ast },h^{\ast })$. Here, we define the algorithm in its abstract form, operating in the function space over the continuous state space E.

The algorithm iteratively improves a policy until it converges to the optimal solution of the ACOE. It begins with an initial policy ${\pi }_0$ and generates a sequence of policies $\left\{{\pi }_k\right\}$ and corresponding value function-cost pairs $\left\{({\rho }_k,h_k)\right\}$. Each iteration consists of two main steps:

1. 

Policy Evaluation: For a given state-dependent $(s_k,S_k)$ policy ${\pi }_k$, find the pair $({\rho }_k,h_k)$ that solves the linear Bellman equation for that policy:

$${\mathcal{A}}^{{\pi }_k}{h}_k\left(x\right)+f^{{\pi }_k}\left(x\right)-{\rho }_k=0,\forall x\in E,$$

subject to a normalization condition on $h_k$ to ensure the uniqueness of the relative value function. Here, ${\mathcal{A}}^{{\pi }_k}$ is the generator of the process under the fixed policy ${\pi }_k$.

2. 

Policy Improvement: Find a new policy ${\pi }_{k+1}$ that is greedy with respect to the computed value function $h_k$. That is, for each state x, the action ${\pi }_{k+1}\left(x\right)$ solves the one-step optimization problem:

$${\pi }_{k+1}\left(x\right)\in arg\underset{\pi \in \Pi }{min}\left\{{\mathcal{A}}^{\pi }{h}_k\left(x\right)+f^{\pi }\left(x\right)\right\}.$$

This process is repeated until the policy no longer changes, i.e., ${\pi }_{k+1}={\pi }_k$. The following proposition formally states the convergence of this abstract procedure.

Proposition 2 

(Convergence of the Policy Iteration Algorithm). Under the Lyapunov condition (Assumption 2), which ensures ergodicity for any fixed $(s,S)$ policy, the abstract Policy Iteration Algorithm generates a sequence of policies $\left\{{\pi }_k\right\}$ and average costs $\left\{{\rho }_k\right\}$ such that:

1.

The sequence of average costs $\left\{{\rho }_k\right\}$ is monotonically non-increasing, i.e., ${\rho }_k\ge {\rho }_{k+1}$ for all $k\ge 0$, and converges to the optimal average cost ${\rho }^{\ast }$.

2.

The sequence of policies $\left\{{\pi }_k\right\}$ converges to the optimal policy ${\pi }^{\ast }$, which satisfies the ACOE.

Proof. 

The proof is structured in two main parts. First, we demonstrate the monotonic improvement of the average cost. Second, we establish that the limit of the generated sequence is the optimal solution.

Part 1: Monotonic Improvement of the Average Cost. Let $({\rho }_k,h_k)$ be the pair generated at iteration k for a given policy ${\pi }_k$. By definition of the Policy Evaluation step, this pair is the unique solution (with $h_k$ unique up to an additive constant) to the Bellman equation for policy ${\pi }_k$:

$${\mathcal{A}}^{{\pi }_k}{h}_k\left(x\right)+f^{{\pi }_k}\left(x\right)={\rho }_k,\forall x\in E,$$

(19)

where $f^{{\pi }_k}\left(x\right)$ is the state-dependent instantaneous cost rate under policy ${\pi }_k$.

The Policy Improvement step defines a new policy ${\pi }_{k+1}$ that is greedy with respect to $h_k$. By its definition as the minimizer, ${\pi }_{k+1}$ must satisfy:

$${\mathcal{A}}^{{\pi }_{k+1}}{h}_k\left(x\right)+f^{{\pi }_{k+1}}\left(x\right)\le {\mathcal{A}}^{\pi }{h}_k\left(x\right)+f^{\pi }\left(x\right),\forall \pi \in \Pi ,\forall x\in E.$$

(20)

Choosing $\pi ={\pi }_k$ in the inequality above and substituting from (19), we obtain:

$${\mathcal{A}}^{{\pi }_{k+1}}{h}_k\left(x\right)+f^{{\pi }_{k+1}}\left(x\right)\le {\mathcal{A}}^{{\pi }_k}{h}_k\left(x\right)+f^{{\pi }_k}\left(x\right)={\rho }_k,\forall x\in E.$$

(21)

Now, let $({\rho }_{k+1},h_{k+1})$ be the pair generated by the evaluation of policy ${\pi }_{k+1}$. It satisfies:

$${\mathcal{A}}^{{\pi }_{k+1}}{h}_{k+1}\left(x\right)+f^{{\pi }_{k+1}}\left(x\right)={\rho }_{k+1},\forall x\in E.$$

(22)

Subtracting (22) from the inequality (21) yields:

$${\mathcal{A}}^{{\pi }_{k+1}}(h_k\left(x\right)-h_{k+1}\left(x\right))\le {\rho }_k-{\rho }_{k+1}.$$

Let $\Delta h_k\left(x\right):=h_k\left(x\right)-h_{k+1}\left(x\right)$. The Lyapunov condition (Assumption 2) ensures that the process is ergodic under any stationary policy ${\pi }_{k+1}$. Therefore, there exists a unique stationary probability measure ${\mu }_{k+1}$ for the process governed by generator ${\mathcal{A}}^{{\pi }_{k+1}}$. A fundamental property of a stationary measure is that for any function g in the domain of the generator, ${\int }_E{\mathcal{A}}^{{\pi }_{k+1}}g\left(x\right)d{\mu }_{k+1}\left(x\right)=0$. We take the expectation of the above inequality with respect to ${\mu }_{k+1}$:

$${\int }_E{\mathcal{A}}^{{\pi }_{k+1}}(\Delta h_k)\left(x\right)d{\mu }_{k+1}\left(x\right)\le {\int }_E({\rho }_k-{\rho }_{k+1})d{\mu }_{k+1}\left(x\right).$$

The left-hand side is zero. Since ${\rho }_k$ and ${\rho }_{k+1}$ are constants and ${\mu }_{k+1}$ is a probability measure, the right-hand side is simply ${\rho }_k-{\rho }_{k+1}$. This leads to:

$$0\le {\rho }_k-{\rho }_{k+1}\Rightarrow {\rho }_k\ge {\rho }_{k+1}.$$

The sequence of average costs $\left\{{\rho }_k\right\}$ is therefore monotonically non-increasing. Since costs are non-negative, the sequence is bounded below by 0. By the Monotone Convergence Theorem, it must converge to a limit, which we denote by ${\rho }^{\ast }$.

Part 2: Convergence to the Optimal Solution. We now establish that the limit of the sequence $\left\{({\rho }_k,h_k,{\pi }_k)\right\}$ is the optimal solution.

• Uniform Boundedness and Equi-continuity. A key consequence of the Lyapunov condition (Assumption 2) in the theory of average-cost MDPs is that the sequence of relative value functions $\left\{h_k\right\}$ is uniformly bounded in a weighted norm. That is, there exists a constant $C<\infty$ such that $|h_k\left(x\right)|\le C·W\left(x\right)$ for all k and $x\in E$. This implies that on any compact subset $K\subset E$, the sequence $\left\{h_k\right\}$ is uniformly bounded and equi-continuous.
• Existence of a Convergent Subsequence. Since the state space E is a Polish space (and thus $\sigma$-compact), we can choose an increasing sequence of compact sets ${\left\{K_m\right\}}_{m=1}^{\infty }$ such that ${\cup }_{m=1}^{\infty }{K}_m=E$. By the Arzelà–Ascoli theorem and a diagonalization argument, we can extract a subsequence, which we re-index by j for clarity, such that as $j\to \infty$:
  • ${\rho }_{k_j}\to {\rho }^{\ast }$.
  • $h_{k_j}\left(x\right)\to h^{\ast }\left(x\right)$ uniformly on every compact subset of E, where $h^{\ast }$ is a continuous function.
  • The corresponding greedy policies ${\pi }_{k_j+1}$ converge to a stationary policy ${\pi }^{\ast }$ that is greedy with respect to $h^{\ast }$.
• Optimality of the Limit. We now show that the limit pair $({\rho }^{\ast },h^{\ast })$ satisfies the ACOE. First, consider the policy evaluation equation for the subsequence:

  $${\mathcal{A}}^{{\pi }_{k_j}}{h}_{k_j}\left(x\right)+f^{{\pi }_{k_j}}\left(x\right)={\rho }_{k_j}.$$
  As the policies converge, the generators and cost functions depend continuously on the policy. Given the uniform convergence of $h_{k_j}$ on compact sets and the closure properties of the generator $\mathcal{A}$, we can take the limit as $j\to \infty$ to obtain:

  $${\mathcal{A}}^{{\pi }^{\ast }}{h}^{\ast }\left(x\right)+f^{{\pi }^{\ast }}\left(x\right)={\rho }^{\ast }.$$

  (23)
  Next, consider the policy improvement inequality (21) for an arbitrary stationary policy $\pi$:

  $${\mathcal{A}}^{\pi }{h}_{k_j}\left(x\right)+f^{\pi }\left(x\right)\ge {\rho }_{k_j+1}.$$
  Taking the limit as $j\to \infty$ along the subsequence, we get:

  $${\mathcal{A}}^{\pi }{h}^{\ast }\left(x\right)+f^{\pi }\left(x\right)\ge {\rho }^{\ast }.$$

  (24)
  Equations (23) and (24), together, are precisely the ACOE for the policy ${\pi }^{\ast }$. This demonstrates that the limit point $({\rho }^{\ast },h^{\ast },{\pi }^{\ast })$ is a solution to the ACOE.
• Uniqueness and Convergence of the Entire Sequence. Under the ergodicity assumption, the average cost ${\rho }^{\ast }$ is unique, and the relative value function $h^{\ast }$ is unique up to an additive constant. Since we have shown that any convergent subsequence of $\left\{({\rho }_k,h_k)\right\}$ must converge to this unique solution, a standard result from analysis implies that the entire sequence must converge to $({\rho }^{\ast },h^{\ast })$.

This completes the proof. □

Practical Implementation and Computational Considerations

While the PIA is presented in an abstract function space, its practical implementation requires a suitable discretisation of the continuous components of the state space. A common and effective approach involves the following steps:

• State-Space Discretisation: The continuous inventory level, I, is discretised into a fine grid. The discrete components of the state (the environmental states $e_d,e_s$ and the internal phases of the PH distributions $j_d,j_s$) are already finite. The pipeline state, which includes the age of orders, would also be discretised. This results in a large but finite state-space Markov Decision Process (MDP) that approximates the original PDMP.
• Policy Evaluation: For a given discretised state space and a fixed ($s,S$) policy, the Policy Evaluation step involves solving a system of linear equations. The size of this system is proportional to the number of states in the discretised grid. For large state spaces, this can be computationally intensive, and iterative methods such as value iteration are often employed as an alternative to direct matrix inversion.
• Policy Improvement: The Policy Improvement step requires, for each state, finding the action that minimises the one-step cost. Due to the convexity of the value function established in Proposition 1, the search for the optimal order-up-to level S for each discrete state $\omega$ is a convex optimisation problem, which can be solved efficiently using numerical search methods (e.g., a bisection or ternary search).

The overall computational cost per iteration of the PIA is therefore dominated by the Policy Evaluation step. Qualitatively, the cost is polynomial in the size of the discretised state space. The primary challenge in implementation is the ‘curse of dimensionality,’ as the number of states grows exponentially with the number of continuous variables (e.g., ages of multiple outstanding orders) and the granularity of the grid. Nevertheless, for systems of moderate complexity, this approach provides a viable and robust pathway to computing a near-optimal policy.

5. Numerical Experiments

In this section, we present a numerical study to illustrate the theoretical results and highlight the practical relevance of our modelling framework. The experiment is designed to achieve two goals: first, to provide a concrete example of the optimal policy structure, and second, to quantify the value of using Phase-Type (PH) distributions over simpler exponential approximations in a logistics context.

5.1. Experimental Setup

We consider an inventory system with the following parameters, chosen to be illustrative:

• Costs: Holding cost $k_h=\$1$, backorder cost $p=\$15$, fixed order cost $K=\$100$, variable order cost $c=\$10$.
• Demand: The demand process is always ‘UP’ with a constant rate $D=10$ units/day.
• Supply: The supplier alternates between an ‘ON’ (available) and ‘OFF’ (disrupted) state. The ‘ON’ duration is exponentially distributed with a mean of 50 days. The ‘OFF’ duration (disruption) is the focus of our experiment.
• Lead Time & Yield: Deterministic lead time $L=5$ days, and perfect yield ($Y=1$ deterministically).

5.2. The Value of Modelling Non-Exponential Disruptions

A key contribution of our model is its ability to handle non-exponential event timings. To demonstrate its value, we compare our model’s results against those from a simplified model that a practitioner might use. The simplified model incorrectly assumes that supplier disruptions are memoryless (i.e., exponentially distributed).

We analyse two scenarios for the true nature of supplier ‘OFF’ times:

• Low-Variability Scenario: The true disruption time follows an Erlang-2 distribution, a PH-type distribution with a coefficient of variation (CV) of $1/\sqrt{2}\approx 0.71$. This represents a more predictable process, such as a two-stage repair.
• High-Variability Scenario: The true disruption time follows a Hyperexponential-2 distribution (a mixture of two exponentials), a PH-type distribution with CV $>1$. This represents an unpredictable process, where disruptions are either very short or very long.

In both scenarios, the mean disruption time is set to 5 days. The ‘Approximation Model’ used for comparison is an exponential distribution, also with a mean of 5 days (CV = 1).

We use the Policy Iteration Algorithm (PIA) to compute the optimal state-dependent ($s,S$) policy for each true system (Erlang-2 and Hyperexponential-2). We also compute the policy that would be optimal if the disruptions were truly exponential. We then evaluate the cost of using this ‘incorrect’ exponential-based policy in the true systems. The results are summarised in

Table 2. Comparison of Optimal Policies and Costs Under Different Disruption Models.

	Low-Variability (Erlang-2)		High-Variability (H-exp 2)
Metric	True Policy	Approx. Policy	True Policy	Approx. Policy
Reorder Point ($s^{\ast }$)	25.4	30.1	45.8	30.1
Order-up-to Level ($S^{\ast }$)	121.6	130.5	165.2	130.5
System Cost:
Optimal Average Cost/Day	$95.50	-	$142.30	-
Cost of Using Approx. Policy	-	$103.80	-	$159.60
Cost Increase (%)	-	8.7%	-	12.1%

.

5.3. Managerial Insights

The results in Table 2 provide clear managerial insights:

• Policy Structure Depends on Variability: The exponential approximation always yields the same policy $(s=30.1,S=130.5)$ because it only matches the mean disruption time. However, the true optimal policy changes significantly based on the variability. When disruptions are less unpredictable (Erlang-2, low CV), the system holds less safety stock (lower $s^{\ast }$). When disruptions are highly unpredictable (H-exp 2, high CV), the system must hold substantially more safety stock to guard against the risk of very long outages.
• Ignoring Variability is Costly: Using a simplified exponential model when the reality is different leads to suboptimal decisions and higher costs. In the low-variability case, the approximation leads to holding excessive inventory, resulting in an 8.7% cost increase. In the high-variability case, the approximation leads to insufficient safety stock, exposing the firm to frequent and costly stock-outs, resulting in a 12.1% cost increase.

This experiment demonstrates that capturing the true nature of uncertainty, particularly its variability beyond just the mean, is crucial for effective inventory management. The flexibility of the PH distribution in our PDMP framework provides a powerful tool for logistics managers to design more robust and cost-effective replenishment policies in the face of complex, non-memoryless disruptions.

6. Conclusions and Further Remarks

This paper has developed a comprehensive theoretical framework for the optimal control of a continuous-review inventory system operating under a confluence of realistic stochastic disruptions. By modelling the system as a Piecewise Deterministic Markov Process (PDMP) with impulse control, we have rigorously captured the dynamics of supply and demand environments governed by general Phase-Type (PH) distributions, whilst also incorporating the pervasive issue of random production yield. Our objective was to characterise the replenishment policy that minimises the long-run average cost of the system.

The primary contributions of this work are fourfold. First, we constructed a unified and tractable mathematical model that synthesises several complex, non-memoryless sources of uncertainty. Second, we formally established the existence of a solution to the associated Average Cost Optimality Equation (ACOE) by employing the vanishing discount approach, thereby guaranteeing that an optimal policy exists. The central theoretical contribution of this paper is our third result: a formal proof that the optimal control policy possesses a state-dependent $(s,S)$ structure. This demonstrates that even in a highly complex environment with interacting uncertainties and non-exponential event timings, the intuitive and elegant logic of threshold-based control remains optimal. This finding represents a significant generalisation of the classical results in stochastic inventory theory. Finally, to complete the analytical treatment, we established the theoretical convergence of a Policy Iteration Algorithm (PIA), confirming that the optimal policy parameters are not only structurally simple but also computationally attainable.

Beyond its theoretical contributions, this study offers several key managerial implications for inventory control under uncertainty. First and foremost, our central result provides a powerful justification for practitioners to continue using simple, intuitive state-dependent $(s,S)$ policies, even when their operational environment is complex and characterised by non-exponential disruptions and random yields. The manager’s task is therefore not to invent a new, complex policy structure, but to focus on accurately parametrising this robust threshold-based approach. Second, the state-dependent nature of the policy underscores the need for information systems that can track the current operational environment (e.g., supplier status, demand phase) to enable dynamic adjustment of inventory targets. Finally, our numerical experiment provides a clear directive: managers must look beyond average disruption times and actively measure and model the variability of these events. As demonstrated, systems with highly variable (less predictable) disruptions require significantly higher safety stocks to maintain service levels, and using a simple memoryless model in such cases can lead to costly strategic errors.

Notwithstanding these contributions, the proposed framework possesses certain limitations that naturally delineate promising avenues for future research. Our analysis is situated within a single-item, single-echelon context. A natural and important extension would be to investigate multi-echelon inventory systems, such as a central depot supplying multiple retail outlets, each subject to local disruptions. Such a setting would introduce profound challenges related to policy coordination and the characterisation of system-wide optimality.

Furthermore, our model assumes a standard linear cost structure. Future work could explore more complex cost functions, such as all-units or incremental quantity discounts, which would violate the convexity assumptions central to our proof and necessitate new analytical techniques. Another compelling direction lies in relaxing the assumption of exogenous environmental processes by allowing for strategic investments to alter the parameters of the PH distributions governing disruptions. A further avenue of investigation involves relaxing the assumption of full observability of the system state, particularly the internal phase of the PH distributions, which would reformulate the problem into a much more challenging partially observable setting.

While these theoretical extensions are promising, this paper has taken a crucial step towards practical application by providing an initial numerical validation of the framework. Our experiment furnished tangible managerial insights by demonstrating that ignoring the true nature of disruptions can lead to significant cost penalties. This initial study naturally delineates promising avenues for more extensive computational research. Two key areas for future investigation, which were unaddressed in the present paper, are:

• PIA Convergence Speed: While we prove the theoretical convergence of the Policy Iteration Algorithm, an analysis of its practical convergence speed and computational efficiency across different problem instances would be a valuable contribution.
• Cost Sensitivity to PH Factors: Our numerical experiment shows that cost is sensitive to the variability (a key factor of the PH distribution). A comprehensive sensitivity analysis could more deeply quantify this relationship, examining how cost and policy parameters change with the shape, variance, and higher-order moments of the PH distributions governing disruptions.

In addressing these computational and theoretical challenges, future research can build upon the analytical foundation established herein to develop even more realistic and applicable models for inventory control under profound uncertainty.