From Chaos to Coherent Structure (Pattern): The Mathematical Architecture of Invisible Time—The Critical Minute Theorem in Ground Handling Operations in an Aircraft Turnaround on the Ground of an Airport

Abstract

Background: In the dynamic world of commercial aviation, the efficient management of ground handling (GH) operations in aircraft turnarounds is an increasingly complex challenge, often perceived as operational chaos. Methods: This paper introduces the “Critical Minute Theorem” (CMT), a novel framework that integrates mathematical architecture principles into the optimization of GH processes. CMT identifies singular temporal thresholds, $t_k^{\mathrm{*}}$ at which small local disturbances generate nonlinear, system-wide disruptions. Results: By formulating the turnaround as a set of algebraic dependencies and nonlinear differential relations, the case studies demonstrate that delays are not random but structurally determined. The practical contribution of this study lies in showing that early recognition and intervention at these critical minutes significantly reduces propagated delays. Three case analyses are presented: (i) a fueling delay initially causing 9 min of disruption, reduced to 3.7 min after applying CMT-based reordering; (ii) baggage mismatch scenarios where CMT-guided list restructuring eliminates systemic deadlock; and (iii) PRM assistance delays mitigated by up to 12–15 min through anticipatory task reorganization. Conclusions: These results highlight that CMT enables predictive, non-technological control in turnaround operations, repositioning the human analyst as an architect of time capable of restoring structure where the system tends to collapse.

1. Introduction

Commercial aviation has become one of the most complex operational ecosystems in the modern world. Airlines and airports must orchestrate a wide array of interdependent activities under conditions of uncertainty, variability, and growing demand. Among these activities, aircraft turnaround—the set of ground handling (GH) operations performed between arrival and departure—plays a decisive role in safety, punctuality, and efficiency [1]. Although often treated as a routine procedure, turnaround is in fact a dynamic system of tightly coupled tasks, each vulnerable to perturbations that can propagate across the entire operation.

The relevance of turnaround operations has increased in the context of the “smart airport” paradigm, which integrates digital technologies, big data, and automation to optimize efficiency [2,3,4,5]. Emerging concepts, such as Airport 4.0 [3], based on open data and advanced prediction tools, envision airports as intelligent ecosystems capable of detecting delays in advance, allocating resources dynamically, and maintaining operational resilience. Reports from the Civil Aviation Administration of China (CAAC) [4] and studies from international hubs [2,5] highlight that future airports are expected to minimize delays, anticipate risks, and maximize utilization. Yet, despite these advances, operational disturbances remain inevitable, often leading to unpredictable disruptions.

Related studies have approached the problem of flight delays and ground handling efficiency through different methodological perspectives:

1. 

Data-driven and machine learning approaches.

Considerable work has been dedicated to predicting flight delays based on statistical and artificial intelligence techniques. Khaksar et al. [6] used machine learning to show the impact of weather and scheduling on delay propagation in the US network. Truong et al. [7] employed decision trees and Bayesian inference to construct delay prediction models. Wu et al. [8] developed a deep SE-DenseNet model that improved accuracy by 1.8% when integrating weather and operational data. Esmaeilzadeh et al. [9] applied support vector machines to identify main delay factors. Choi et al. [10] compared supervised learning algorithms, with random forests achieving highest predictive accuracy under severe weather. Ye et al. [11] tested multiple regression and ensemble learning, finding LightGBM to be superior. Thiagarajan et al. and also Shai et al. [12,13] further confirmed that gradient boosting approaches outperform other algorithms.

2. 

Probabilistic and scheduling models.

Earlier foundational work by Liu and Layland [14] introduced the critical instant theorem, later refined by Sha et al. [15] and expanded to probabilistic settings by Maxim and Cucu-Grosjean [16]. These studies advanced the concept of critical time zones [17], emphasizing the moments when system response time is maximized, and explored probabilistic convolution methods [17,18,19,20,21,22,23,24,25,26,27]. Such models offer analytical rigor but often assume simplified task arrival patterns, making their direct application to complex turnaround environments challenging.

3. 

Deterministic and algebraic approaches.

A smaller body of literature has explored deterministic frameworks to model task dependencies and system fragility [18,19,20,21,22,23,24,25,26,27,28,29]. These studies suggest that certain structural thresholds—points where convexity is lost or singularities appear in delay propagation functions—can be identified algebraically. Such approaches resonate with systems theory [14], which classifies operational processes as stable, unstable, or marginally stable. However, the application of deterministic models to real-time airport operations remains underdeveloped.

Knowledge gap. Despite the substantial advances in predictive analytics and probabilistic modeling, existing studies primarily focus on forecasting delays rather than structurally identifying the exact moment when small perturbations escalate into systemic instability. Most machine learning models require large volumes of historical data, while probabilistic methods often rely on assumptions that are difficult to satisfy in live operations. There remains a lack of frameworks capable of revealing invisible time—the latent moments where minor disruptions transition into exponential delay propagation—without the need for extensive datasets or simulations.

Purpose and hypothesis. This paper addresses that gap by proposing the Critical Minute Theorem (CMT). It is hypothesized that turnaround operations exhibit an underlying mathematical architecture that governs how perturbations evolve. Specifically, this study posits the existence of singular operational moments, denoted $\left(t_k^{\mathrm{*}}\right)$, at which minimal local disturbances trigger nonlinear system-wide disruptions. Identifying these moments algebraically provides a structural tool for anticipatory intervention.

Aims and objectives. The objectives of this study are as follows:

• To formally define the Critical Minute Theorem as a deterministic framework for turnaround analysis;
• To demonstrate, through algebraic modeling, how fragility points can be detected in real time;
• To apply the theorem to case studies (fueling delays, baggage mismatch, PRM assistance) and quantify its effectiveness in reducing propagated delays.

Significance and contribution. By integrating theoretical mathematics with operational case studies, this research contributes to both academic understanding and industry practice. Unlike data-driven models, CMT does not require historical datasets but instead leverages algebraic dependencies to reveal hidden fragility points. Our findings show that targeted interventions at the critical minute reduce delays significantly (e.g., 9 → 3.7 min in fueling, 12–15 min in PRM assistance). Beyond predictive analytics, this work positions the turnaround manager as an architect of time, capable of detecting the invisible threshold between order and chaos and acting before systemic failure occurs.

To reflect recent progress, the study also considers contributions published in the last three years that apply modern machine learning and optimization techniques to delay management and turnaround processes [30,31,32,33,34,35,36]. These studies confirm the strong trend towards data-driven prediction and real-time optimization, yet they remain heavily dependent on large training datasets or simulation environments. This reinforces the research gap addressed in this paper: the need for a deterministic, algebraic framework capable of identifying fragility thresholds without reliance on historical data.

The overall value of this study lies in bridging a critical gap between theoretical modeling and operational practice in airport logistics. While most existing research relies on probabilistic or machine learning approaches that require large historical datasets, this work introduces a deterministic, algebraic framework—the Critical Minute Theorem—that identifies hidden fragility points in real time. By formalizing the concept of “invisible time” as singular temporal thresholds $\left(t_k^{\mathrm{*}}\right)$, the model reveals how minor disturbances can escalate into systemic disruptions and how minimal compensatory action can restore stability. This dual contribution, both theoretical and practical, provides a novel tool for anticipating and mitigating delays in ground handling operations, thereby offering predictive insight that complements existing data-driven methods.

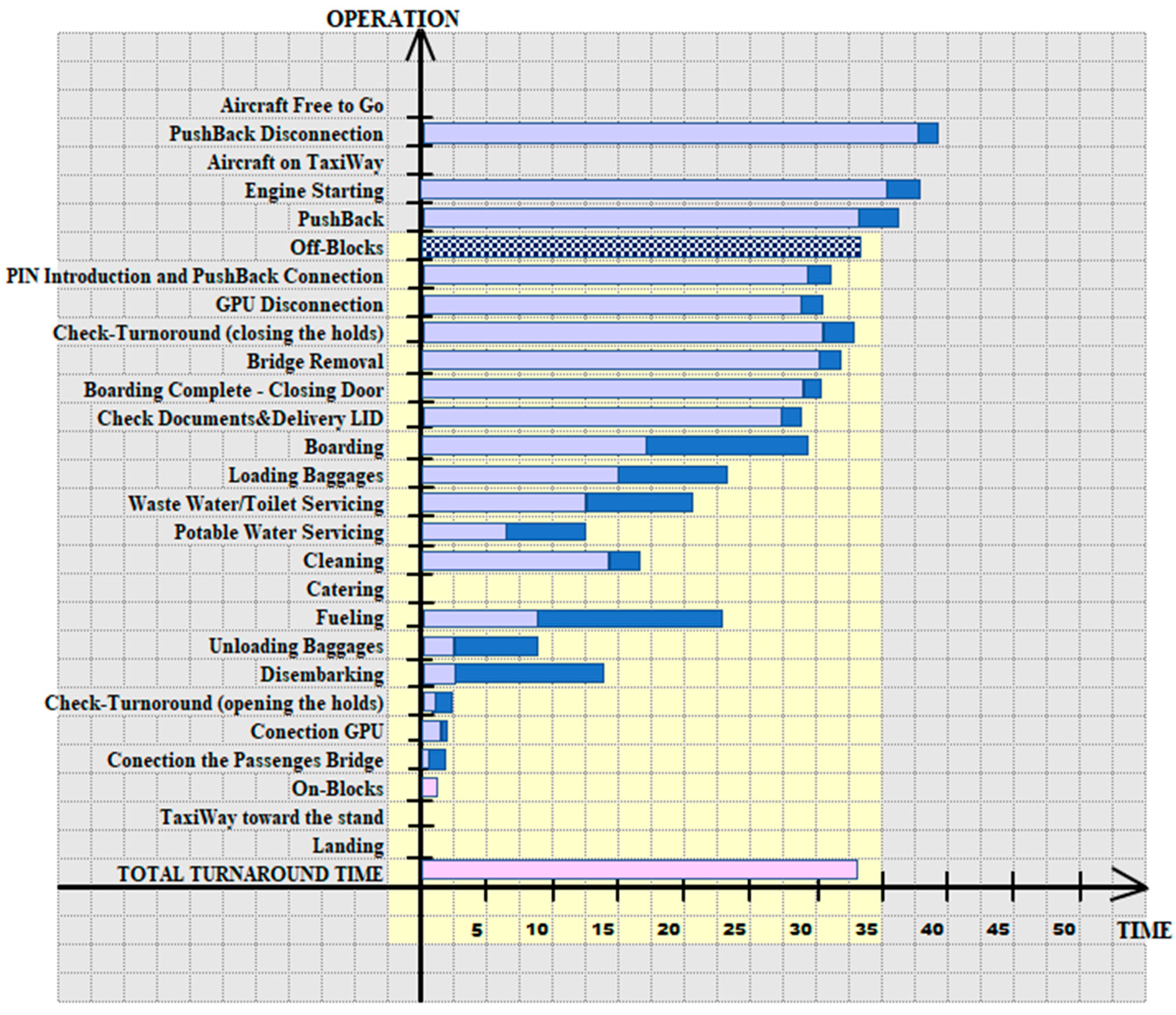
2. Turnaround and Its Tasks

Turnaround is the period between the arrival of an aircraft at an airport and its departure on the next flight from the same airport. It is a critical operational process involving various tasks, such as disembarking passengers from the arriving flight and then boarding the next departing flight without a break, refueling, cleaning, servicing, and loading baggage and cargo for the next flight. In fact, behind the scenes, it is a real logistical game. Teams spring into action to unload passengers and cargo, refuel the aircraft, clean the cabin, carry out quick maintenance checks, and get everything ready for the next departure. It is a fast, precise, and carefully organized process, as shown in Figure 1, which captures the outside view of a typical turnaround flight.

Turnarounds are arguably the most unappreciated task for flight crews. These are flights in which the crew makes a round trip with the aircraft without a break at the destination. Basically, they fly immediately round trip. The crew will remain on board and, once the cleaning and catering procedures and re-fueling are completed, begin boarding and return to base.

Obviously, this is the most economical option for airlines, and they will always try to take advantage of it before granting a turnaround. However, in some cases (which are not uncommon), the airline has no other option. If duty time exceeds what is allowed by law, for safety reasons, the airline will be obliged to provide a turnaround for the crew.

This paper presents a recovery method with only 27 different tasks commonly used on Boeing 737-800, 737-8200, and even Airbus 320 aircraft, although on flights with longer turnarounds there may be more than 27 tasks.

Figure 1 represents a photographic image of the 27 tasks, while Figure 2 reflects the tasks plotted on a Cartesian chart and their respective time measured in minutes.

The exact sequence of the 27 turnaround actions in the order of their execution is as follows:

• Landing;
• TaxiWay towards the stand;
• On-Blocks;
• Connection of the passenger bridge;
• GPU connection;
• Check turnaround (opening the holds);
• Disembarking;
• Unloading baggage;
• Fueling;
• Catering;
• Cleaning;
• Potable water servicing;
• Waste water/toilet servicing;
• Loading luggage;
• Boarding;
• Check documents and delivery LID;
• Boarding complete—closing door;
• Bridge removal;
• Check turnaround (closing the holds);
• GPU disconnection;
• PIN introduction and pushback connection;
• Off-Blocks;
• Pushback;
• Engine starting;
• Aircraft on TaxiWay;
• Pushback disconnection;
• Aircraft free to go.

3. The Critical Minute: What It Is, How to Identify and Localize It, Why It Is Invisible, and How to Act Once Localized

3.1. What Is It and How Does It Manifest Itself?

The critical minute is not simply a moment in the turnaround sequence of ground handling operations; it is the invisible inflection point at which the structured order of the GH. process begins to drift towards chaos. It is not announced by alarms or sensors, but its presence is manifested by its consequences: congestion, lack of coordination, and systemic delay [30,31].

3.2. How to Identify and Localize the Critical Minute?

The ways to clearly identify the critical minute are as follows:

• Knowing to perfection the operational structure and order of realization of all of the GH operations of a turnaround;
• Knowing where bottlenecks tend to accumulate;
• Mentally projecting the consequences of a delay that has not yet occurred;
• Using structural intuition by clearly understanding that operational time is not a sum of minutes but a network of synchronicities.

But, detecting and localizing the critical minute is achieved as follows.

Observing the fragility of the system:

• The critical minute occurs when a seemingly minor action, such as a delay in refueling or waiting for a PRM elevator, causes a chain reaction of other activities. This is not about time itself but rather its position in the web of dependencies.
• What was once flexible now becomes rigid, and what was once coordinated becomes stuck. The system loses its ability to absorb disturbances.

Synchronicity break detection:

• Recovery is a complex choreography in which many tasks occur in parallel or sequentially. The critical minute occurs when one task no longer aligns harmoniously with the others; it cannot be delayed further without disrupting the overall structure.
• The balance is broken. Tasks no longer “wait” their turn but start competing for time, space, and priority.

Recognizing the transition from flexibility to urgency:

• A normal structured system has margins: controlled downtime, independent tasks, and sufficient buffers. But, in the critical minute, this margin of maneuver disappears. Every minute starts costing another minute. Time stops being linear and becomes exponential, “expensive.”
• The careful operator perceives this before the data reflect it and sees how decisions become tense, how teams overlap, and how room for maneuver disappears.

3.3. Why Is It Invisible?

Because the critical minute is not a “screaming” moment but a “whisper” in the system’s structure, it is not an observable event like the arrival of a vehicle or the closing of doors; it has no alarm or red flag in the program. The critical minute is not perceived on clocks but in the latent relationships between dependent tasks, in the way one action feeds into another, and in the way their sequence can subtly change from “fragile” to “indeterminate”.

The critical minute is essentially a transition in the operating regime. As happens in nonlinear dynamical systems, there is a point—often not directly visible—at which the system loses its ability to self-regulate. Loads no longer align naturally, and decisions begin to propagate with an amplification effect.

The critical minute is structural, not punctual. It emerges from the fabric of additions, not from a specific hour. Nothing seems to change on the outside, but the system is not the same on the inside. A topological threshold emerges where previous states are no longer sufficient to absorb the error.

From a mathematical point of view, this is a change in the stable topology of the system. Technically, it is the moment when the derivative of the overall efficiency ${\displaystyle \frac{d{T}_{op}}{dt}}$ starts to become positive or when an eigenvalue of the Jacobian matrix of interdependencies shifts from the left to the right zone of the complex plane. At the operational level, it is something even deeper; it is the moment when the logic of recovery disintegrates. That is why it is invisible—because it does not appear as a consequence of an action but as the result of an invisible accumulation of interactions. It is a phase shift, a subtle shift between tolerable and irreversible.

And yet, if you analyze carefully at the edges of sequences, in the sequencing of tasks, in the gaps in buffer zones, the critical minute can be sensed and subsequently made visible not by what happens but by what stops the flow, the course of evolution.

3.4. How to Act Once Localized

The critical minute cannot be eliminated, but it can be neutralized. When it is detected, the following is possible:

• Reorder actions to regain synchronization.
• Introduce new strategic edges (slack).
• Coordinate key decisions before cascading effects accumulate.

In short, the critical minute is the threshold at which time stops flowing like a line and starts branching like a network. Detecting it is an act of structural insight, not computation.

4. Critical Minute Theorem and the Mathematical Structure of Airport Turnaround

4.1. Critical Minute Theorem

In every finite sequence of mutually dependent actions whose objective is the operational return to ground maintenance of an aircraft, there is a singular moment—not directly observable but algebraically deductible—at which the change in local time generates a global break in the sequential equilibrium. That moment is referred to as the critical minute, denoted by $t_k^{\mathrm{*}}.$

If the accumulated delay at that point exceeds a threshold ${\delta }_c$, then the total response time $T$ becomes an increasing nonlinear function of the initial delay, and its derivative with respect to the partial time perturbs the entire system of dependencies.

Formally stated, if there exists an operational $\mathrm{Փ}\left(t_1,t_2,t_3,...,t_n\right)$ flow function such that

$$T=\mathrm{Փ}\left(t_1,t_2,t_3,...,t_n\right)$$

(1)

with functional dependencies $t_i=f_i\left(t_j\right)$, then there exists at least one $t_k\in \left\{t_1,t_2,...,t_n\right\}$, such that ${\displaystyle \frac{\mathsf{\partial }T}{{\mathsf{\partial }}_{t_k}}}\to \mathrm{\infty }$ when $t_k\to t_k+{\delta }_c$.

The existence of such a point $t_k$ defines a structural point of instability, and its early identification allows for minimal intervention with maximum overall impact.

Definition:

Let $\mathcal{T}$= {$T_1,T_2,T_3,...T_n$ } be a set of interdependent actions performed during an aircraft turnaround process, where each activity has the following:

• An initial launch (start) time $S_i$.
• A duration $t_i$.
• A completion time $E_i=S_i+t_i$.
• And either $\mathcal{C}\subseteq \mathcal{T}$ subset of activities that make up the critical path, such that the total turnaround time is as follows:
• As a formal definition, $t_k\in {\mathbb{R}}^{+}$ is the point in time at which the task starts, $T_k.$
• $k=1,2,3...,27$, following the complete task sequence from aircraft landing to takeoff.
• $t_1$ is the time of landing.
• $t_{27}$ is the moment when the airplane is free to take off.
• The crowd {${\mathrm{t}}_{\mathrm{k}}$} is nondescending because the activities follow a sequential or partially ordered order with functional dependencies.
• In the context of the Critical Minute Theorem (CMT), ${\mathrm{t}}_{\mathrm{k}}$ represents the actual operating time in which activity number k in the turnaround process is executed or should be executed.

The critical minute ${\mathrm{t}}_{\mathrm{k}}^{\mathrm{*}}$ occurs when a small variation in a previous activity produces a nonlinearly amplified effect on a future dependent task.

If ${\displaystyle \frac{{\mathcal{d}}^2\mathrm{T}\left({\mathrm{t}}_{\mathrm{k}}\right)}{{\mathcal{d}\mathrm{t}}^2}}<0,\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}$ ${\displaystyle \frac{\mathcal{d}\mathrm{T}\left({\mathrm{t}}_{\mathrm{k}}\right)}{\mathcal{d}\mathrm{t}}}$ changes abruptly, so ${\mathrm{t}}_{\mathrm{k}}^{\mathrm{*}}$ is considered a critical moment.

This indicates the following:

• Return stability curve.
• Start of dynamic bifurcation: small causes → large effects.
• In sum, ${\mathrm{t}}_{\mathrm{k}}$ is the operational moment at which activity k occurs.
• ${\mathrm{t}}_{\mathrm{k}}^{\mathrm{*}}$ is the critical operational moment at which a minimal disturbance generates a structural break in the activity chain.

An important observation in the formulation of the CMT is that the critical moment ${\mathrm{t}}_{\mathrm{k}}^{\mathrm{*}}$, although mentioned as a key dynamic inflection point, does not directly appear as an explicit variable in the equations of the theorem. This omission is neither accidental nor incomplete; it responds to a deep structural logic within the model.

CMT is not a direct localization formula but rather a set of existence and recognition criteria. It defines analytical conditions that guarantee the occurrence of a moment $t_k$ at which the stability of the turnaround system is disrupted, either by

• Loss of convexity in the dispersion function of critical loads,$T\left(t_k\right)$;
• The occurrence of a local singularity in the differential equations modeling the dependencies;
• Divergence of the second-order derivative on the propagation curve;
• Bifurcation in the operational equilibrium of the system.

From this perspective, the critical minute is not a number to be computed but an observable consequence that occurs when the system responds abnormally to a disturbance and enters a zone of instability. At that moment, the turnaround evolution curve changes its geometry, and its analysis allows us to infer the existence of the point $t_k^{\mathrm{*}}$, even if it was not explicitly predicted from the beginning.

Philosophically, just as a doctor cannot predict the exact moment of a heart attack but knows how to recognize the signs that precede it, CMT does not directly “predict”${ t}_k^{\mathrm{*}}$ but provides the analytical tools to recognize it before it becomes irreversible.

This approach makes CMT a more flexible and operational tool adaptable to different real-world recovery settings and useful even in the absence of artificial intelligence or predictive simulations.

4.2. Algebraic Modeling of Turnaround Using Differential Equations

Turnaround is considered a system of time-interdependent processes. Each process $P_i$ has a duration $t_i\left(t\right)$ and may depend on one or more preceding processes, reflecting a network of causal dependencies. These dependencies are modeled using a system of nonlinear coupled differential equations.

Operational variables:

• $t_i\left(t\right)\in {\mathbb{R}}^{+}$: The accumulated time of the process $P_i$ at continuous time $t$ represents the elapsed time from the beginning of the process to continuous time $t. {\mathbb{R}}^{+}$ represents the crowd of positive real numbers, i.e., ${\mathbb{R}}^{+}=\left\{\mathcal{x}\in \mathbb{R}\mid \mathcal{x}>0\right\}$.
• $T\left(t\right)\in {\mathbb{R}}^{+}$ is the total cumulative execution time up to the moment $t$, given by
• $T\left(t\right)=\sum _{\mathcal{i}=1}^{\mathcal{n}}{t}_i\left(t\right)$
• $R_i\left(t\right)\in {\mathbb{R}}^{+}$ is the cumulative delay of the process $P_i$ with respect to its nominal schedule, up to time t. This delay can also propagate to dependent processes.
• ${\alpha }_{\mathcal{i}\mathcal{j}}$ is the sensitivity of process i to the delay of process j.
• ${\lambda }_i$ is the operational efficiency of process i.

General model:

$${\displaystyle \frac{{dt}_i}{d_t}}={\lambda }_i-\sum _{j<i}{\alpha }_{ij}{R}_j\left(t\right)$$

(2)

$${\displaystyle \frac{{dR}_i}{dt}}=\left\{\begin{array}{c}0 \mathrm{for} R_{i-1}\left(t\right)<{\delta }_c\\ {\gamma }_{\mathcal{i}}·R_{\mathcal{i}-1}{\left(t\right)}^2 \mathrm{for} R_{i-1}\left(t\right)\ge {\delta }_c\end{array}\right.$$

(3)

Here, the quadratic term models the nonlinear propagation of delays once the critical threshold has been crossed, ${\delta }_c$. The nonlinearity reflects the amplification of the impact due to congestion, rescheduling, or resource conflicts.

Example: for a chain of three processes

Assume a backlink with three successive processes: download $P_1$, cleanup $P_2$, and upload $P_3$. The differential equations are defined as

$${\displaystyle \frac{{dt}_i}{d_t}}={\lambda }_i, t_1(0)=0$$

(4)

$${\displaystyle \frac{{dR}_2}{dt}}=\left\{\begin{array}{c}0 \mathrm{for} R_1\left(t\right)<{\delta }_c\\ {\gamma }_2·R_1{\left(t\right)}^2 \mathrm{for} R_1\left(t\right)\ge {\delta }_c\end{array}\right.$$

(5)

$${\displaystyle \frac{{dt}_2}{d_t}}={\lambda }_2-{\alpha }_{21}{R}_1\left(t\right)$$

(6)

$${\displaystyle \frac{{dt}_3}{d_t}}={\lambda }_3-{\alpha }_{32}{R}_2\left(t\right)$$

(7)

• ${\alpha }_{21};{\alpha }_{32}$ are the coupling or transfer coefficients between activities; the index indicates that the effect passes from one activity to another (${\alpha }_{21}$ destination activity: 2 ← source activity: 1).
• ${\alpha }_{21}$ measures the effect that the resource of activity 1 has on reducing the delay of activity 2.

Specifically, it is a parameter of sensitivity or efficiency of mitigation.

• ${\alpha }_{21}>0$ indicates that the resource used in activity 1 helps reduce the delay in activity 2.
• The larger ${\alpha }_{21}$ is, the stronger the influence of activity 1 on activity 2 will be.

Analytic simulation or numerical integration shows that over $R_1\left(t\right)>{\delta }_c$, the total duration, $T=t_1+t_2+t_3$ is triggered in a nonlinear fashion, confirming the behavior predicted by the Critical Minute Theorem.

The crucial aspect of the model is that it is not concerned with simulating events but rather with inferring their structural dynamics via differential relations. The identification of a critical minute involves finding values for $t_k$ for which the sensitivity ${\mathsf{\partial }\mathrm{T}/\mathsf{\partial }t}_k$ is divergent, i.e., where small local perturbations generate disproportionate global consequences.

This approach removes the reliance on large volumes of data or training of AI algorithms and re-establishes the central role of structural mathematical thinking as a tool for precise and minimalistic interventions in airport logistics. In this context, “training an algorithm” means exposing a mathematical or computational model to large amounts of historical or simulated data so that it learns underlying patterns, relationships, and rules. The algorithm can then make predictions or decisions when presented with new information.

4.3. Critical Minute Detection and Avoidance

It is important to emphasize that once a disturbance occurs, operations are necessarily affected, as the system has already departed from its original equilibrium. The purpose of the Critical Minute Theorem (CMT) is therefore not to preserve operations untouched but to minimize disruption by applying a compensatory action. Unlike a correction, which seeks to restore the system to its previous equilibrium (no longer available once instability emerges), a compensatory action introduces a corrective–adaptive influence, such as task reordering, temporary buffer insertion, or targeted resource reallocation, that absorbs the disturbance and redirects the process towards a new stable equilibrium. In this sense, operations are intentionally and minimally altered in order to avoid the far greater impact of uncontrolled delay propagation.

Critical Minute Detection is based on analyzing the local behavior of the partial derivatives of the total time T with respect to each subprocess $t_k$. The analytical procedure consists of three steps.

A. 

Modeling the system of functional dependencies:

Construct the system of differential equations and explicitly define ${\alpha }_{\mathcal{i}\mathcal{j}}{\gamma }_i$ and ${\lambda }_i$ from empirical data or direct observations.

B. 

Evaluation of partial derivatives:

Compute ${\displaystyle \frac{\mathsf{\partial }T}{{\mathsf{\partial }}_{t_k}}}$ for each execution thread. A sensitivity spike is identified when this derivative tends to increase sharply or becomes divergent near a certain value of $t_k$, i.e.,

$$\underset{t_k\to t_k^{\mathrm{*}}}{\mathit{lim}}{\displaystyle \frac{\mathsf{\partial }T}{{\mathsf{\partial }}_{t_k}}}\to \mathrm{\infty }$$

(8)

This signals the presence of a critical minute $t_k^{\mathrm{*}}$.

C. 

System Stabilization Analysis:

By analyzing the sign and curvature of the functions $R_i\left(t\right)$, temporal bifurcations are identified where small local perturbations qualitatively change the global dynamics (e.g., transitions from stability to operational chaos).

Once a critical minute has been identified $t_k^{\mathrm{*}}$, the system can be stabilized through minimal but specific strategies:

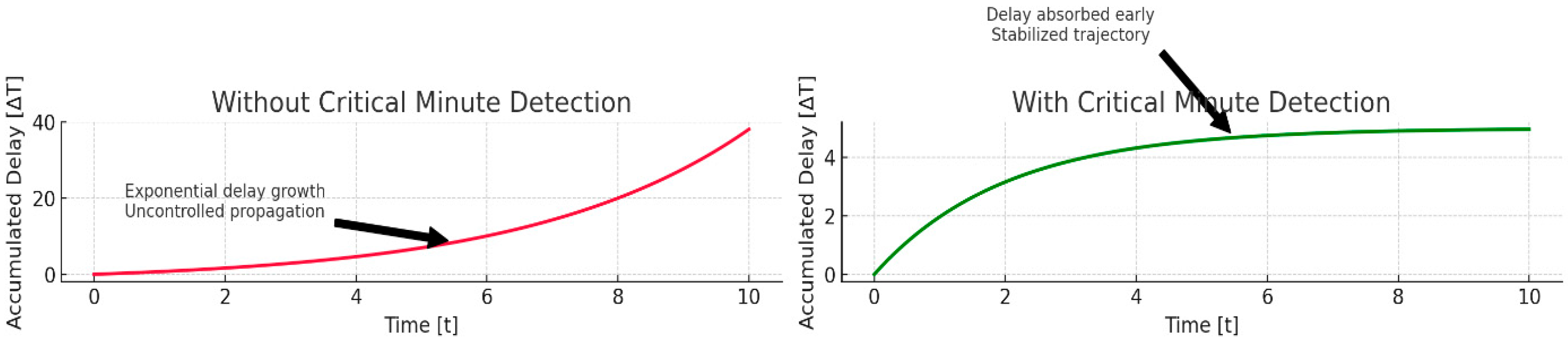
• Early local intervention—allocate additional staff or resources exclusively to the critical subprocess before it reaches $t_k^{\mathrm{*}}$, maintaining $R_k\left(t\right)<{\delta }_c$
• Dependency decoupling—the operational sequence is temporarily redesigned to reduce or eliminate the direct dependencies of downstream processes on the critical process, i.e., minimize ${\alpha }_{\mathcal{i}k}$ through operational scheduling.
• Reduce timing rigidity—introduce structured tolerance in downstream processes using dynamic buffers so that small delays do not result in cascading effects.
• Real-time adaptive prioritization—operational priorities are dynamically reassigned when a process enters a critical area, with resources shifted from non-critical areas into a controlled framework.

$t_k^{\mathrm{*}}$ is the critical minute of an activity k, i.e., the last possible moment at which a corrective intervention applied to activity k can prevent the critical propagation of a delay along the critical path of the system.

• $t$ indicates a time or temporal moment;
• The subscript k indicates the specific activity (debark, refuel, etc.) or node in the graph;
• * indicates that it is a critical time (threshold or optimum);
• $t_k^{\mathrm{*}}$ is not a given moment but one that meets a critical threshold condition:

$${\delta }_k\left(t_k^{\mathrm{*}}\right)={\delta }_c$$

(9)

where

• ${\delta }_k\left(t\right)$ is the propagated delay from activity k as a function of time t.
• ${\delta }_c$ is the critical threshold of tolerable spread.

In short, the introduction of the CMT allows us to move from an empirical and adaptive perspective of recovery to a structural, algebraic, and anticipatory perspective. The greatest advantage lies in the fact that mathematical modeling of the system enables the detection of weaknesses that remain invisible to inductive or statistical models. Thus, optimization is not based on probabilistic prediction but structural understanding.

5. Analytical Criterion of the Existence of the Critical Minute

5.1. Critical Minute Detection Within the Critical Path

The critical route is the set of GH activities during turnaround, the delay of which has a direct impact on the total turnaround time of the aircraft $T_{turnaround}$. It is the longest path in terms of time dependency between interconnected tasks.

The critical minute is a specific point in the critical path where

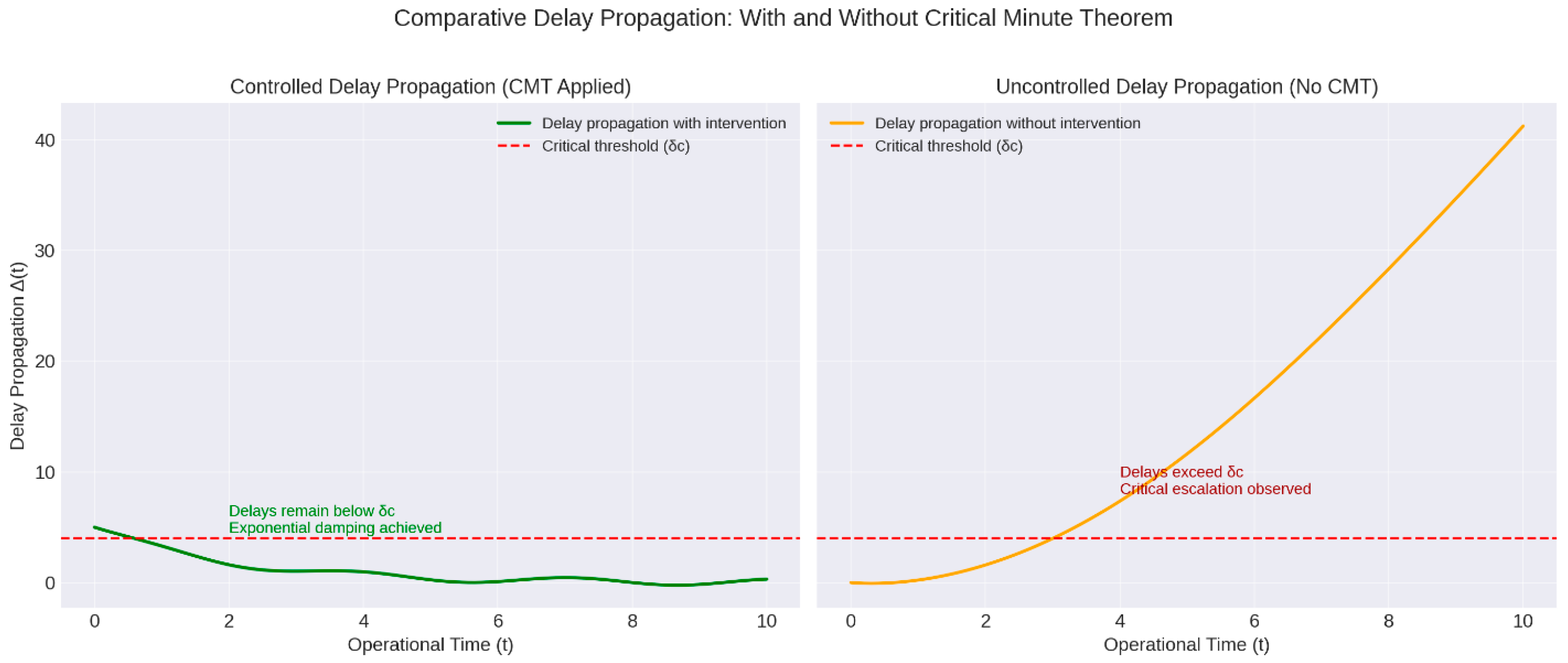
• A small perturbation produces a nonlinear propagation effect.
• The time convexity of the system is lost.
• A singularity or functional discontinuity occurs in the derivative of the total time with respect to the partial times.

5.2. Theoretical and Mathematical Basis

Consider the turnaround time as a system of dependent events $\left\{A_1\right\}\begin{array}{c}n\\ i=1\end{array}$ and let $T\left(t_k\right)$ be the function representing the total return time as a function of time $t_k$ of a critical task $A_k$.

$\left\{A_1\right\}\begin{array}{c}n\\ i=1\end{array}$ represents the crowd of elements $A_i$, indexed by i, from i = 1 to i = n.

The critical minute exists when a small perturbation in the duration of a process $t_k$ produces a disproportionate perturbation in the total execution time T due to the structure of dependencies between processes. This condition is translated into a partial derivative analysis

$${\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }{t}_k}}={\displaystyle \frac{\mathsf{\partial }\Phi }{\mathsf{\partial }{t}_k}}$$

(10)

from which only two conditions (formal and alternative) can be derived.

The variable Φ represents a dynamic propagation function, i.e., a function that models how the system responds to the delay at the critical time $t_k$ and can incorporate cumulative effects, logistic responses, consumed buffers, resource saturations, etc. In the context of CMT, Φ captures the dynamics of the logistic system under time pressure.

Criterion 1—Formal condition (differential functional singularity)

The critical minute occurs at a time $t_k^{\mathrm{*}}$, such that

$$\underset{ϵ\to 0}{\lim }\left|{\displaystyle \frac{dT\left(t_k^{\mathrm{*}}+ϵ\right)}{d{t}_k}}-{\displaystyle \frac{dT\left(t_k^{\mathrm{*}}-ϵ\right)}{d{t}_k}}\right|\to \mathrm{\infty }$$

(11)

That is, there is a point of non-differentiability (singularity) in the total time function.

Or, there exists a critical minute in the process $t_k$ if

$$\underset{t_k\to t_k^{\mathrm{*}}}{\mathit{lim}}\left|{\displaystyle \frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{t}_k^2}}\right|\to \mathrm{\infty }$$

(12)

or, equivalently, if ${\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }{t}_k}}$ loses continuity or increases exponentially.

This usually happens when $t_k$ influences several downstream processes with high sensitivity coefficients ${\alpha }_{ik}$, causing explosive delay propagation.

Criterion 2—Alternative condition (loss of convexity)

Because the ideal system has a convex evolution (i.e., the marginal impact of each delay decreases with time), the critical minute also manifests as a loss of convexity in the total function, $T\left(t_k\right)$.

Geometric Criterion:

$${\displaystyle \frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{t}_k^2}}<0$$

(13)

This implies that the system enters a region of structural instability; small perturbations $t_k$ are no longer absorbed but amplified. This is the point at which the system practically goes from a stable state to a fragile state, indicating a critical minute.

6. Critical Minute Detection and Prevention

6.1. Detection

The critical minute is detected by analyzing the sensitivity of the process network. There are three complementary methods:

• Partial derivative calculation:
  Identifies ${\displaystyle \frac{\mathsf{\partial }T}{\mathsf{\partial }{t}_k}}\gg 1$
  or loss of continuity in the second-order derivatives.

2.

Propagated delay analysis:

${\displaystyle \frac{d{R}_i}{dt}}={\gamma }_i\cdot R_j{\left(t\right)}^2$ when $R_j\ge {\delta }_c$

Detects when a delay $R_j$ exceeds the threshold ${\delta }_c$.

3.

Stability bifurcation monitoring—this is detected when the system changes its qualitative behavior (e.g., from damped to unstable). In dynamic systems, such as operational recovery, a bifurcation is a point at which the behavior of the system changes qualitatively in response to a small change in a key variable (e.g., a delay, a saturation, a failed resource). This is detected by monitoring the derivative or Jacobian of the system with respect to a critical parameter. A sign change in the key derivative occurs when

${\displaystyle \frac{d^2{T}_{op}}{d{t}^2}}>0$ (accelerated increase in delay)

or when the first derivative changes sign,

${\displaystyle \frac{d{T}_{op}}{dt}}\to 0^{+}=\succ$ critical inflection or saturation.

This indicates a loss of damping and a possible bifurcation.

6.2. Prevention

Once a critical minute is detected (or anticipated), it can be prevented through the following:

• Local specific intervention—temporary increase of resources (equipment, personnel) in the critical process.
• Sequential adjustment—changing the logical order to decouple sensitive processes.
• Dynamic anticipated buffer (DB)—the introduction of micro-temporal buffers before the critical process. DB is a proactively built-in, real-time-adjusted time buffer based on operational variables designed to prevent the propagation of a localized disturbance (delay, failure, or absence) along the critical task chain.

In order to avoid the critical minute, the theorem sets a condition for operational intervention:

$R_t\left(t\right)<{\delta }_c$$\forall j\in \mathcal{D}\left(i\right)$

This implies that each antecedent process must keep its delay below a ${\delta }_c$ predetermined, empirically adjusted critical threshold.

The intervention consists of the following:

• Value reduction $R_t\left(t\right)$ through operational reorganization.
• Reduce dependency ${\gamma }_{ ij}$ through restructuring.
• Sequential order reorganization (change of functional topology).

7. Discussion and Examples of Application of the Critical Minute Theorem

Recent research has also addressed ground handling delays and operational stability through complementary methodological lenses. For example, Aircraft Turnaround Bottlenecks: Addressing Ground Handling Delays for Operational Excellence [37] examines root causes of ground handling inefficiencies using empirical case studies, identifying resource constraints, adverse weather, and procedural lag as major contributors to turnaround disruption. Additionally, The Application of Multi-Criteria Decision Analysis in Gaining a Premier Sort of Stability in Airplane Safety [38] uses multi-criteria decision analysis to evaluate safety and stability in aircraft operations, offering insight into how decision frameworks can help prioritize stability alternatives under multiple conflicting criteria. These studies confirm that recent trends are not only about prediction but also about combining decision frameworks and empirical validation to enhance operational resilience—reinforcing the gap that the Critical Minute Theorem seeks to fill by providing a structural, algebraic, threshold-based tool for anticipating instability.

Algebraic generalization: A boarding process $P_5$ that depends on the refueling process $P_4$, and the latter on the technical process $P_3$. The propagation model would be

$${\displaystyle \frac{d{R}_4}{dt}}={\gamma }_{43}\cdot R_3^2\left(t\right)$$

(14)

$${\displaystyle \frac{d{R}_5}{dt}}={\gamma }_{54}\cdot R_4^2\left(t\right)$$

(15)

Cascade replacement:

$${\displaystyle \frac{d{R}_5}{dt}}={\gamma }_{54}\cdot {{\left({\gamma }_{43}\cdot R_3^2\left(t\right)\right)}^2={\gamma }_{54}\cdot {\gamma }_{43}^{2}R}_3^4\left(t\right)$$

(16)

This shows how a moderate delay in $P_3$ can be amplified $P_5$ up to order $R_3^4$, resulting in explosive behavior if uncontrolled.

7.1. Case 1: Fuel Supply Delay

Scenario:

The tanker arrives 9 min late from the scheduled time $t_{fuel}$.

The shift had already started the bag unloading sequence, but the refueling team was not available.

Immediate impact:

The delay impacts some operations with a high dependency on downstream resources; without loaded fuel, no start-up, pushback, or “Ready for Engine Start” mode can be initiated. The operation enters a blocking node in the dependency network.

Applied pattern:

Either

• $R_{fuel}\left(t\right)$ fuel accumulation delay function;
• $T_{toal}\left(t\right)$ total response time as compound function.

The “Fueling” node is defined as

$${\displaystyle \frac{\mathcal{d}{R}_{fuel}}{\mathcal{d}t}}={\lambda }_{fuel}-{\alpha }_f·S\left(t\right)$$

(17)

where

• ${\lambda }_{fuel}$ is the delay onset rate;
• ${\alpha }_f$ is the effectiveness of the mitigation team (action of the team leader);
• $S\left(t\right)$ is the corrective intervention function (task reorganization).

CMT Application:

Point $t_k^{\mathrm{*}}$ is identified when

${\displaystyle \frac{{\mathcal{d}}^2{T}_{total}}{{\mathcal{d}t}^2}}>0$ and ${\displaystyle \frac{\mathcal{d}{R}_{fuel}}{\mathcal{d}t}}>\gamma$

• where γ is a divergence threshold. The CMT is activated, simultaneously rerouting the cleaning and water supply sequence, advancing non-fuel-dependent tasks.

Result:

Partially absorbed delay: reduced from 9 to 3.7 min propagated. The critical node was disabled through nonlinear reordering, as plotted in Figure 3.

7.2. Case 2: Baggage Mismatch—Physical Baggage More than Official Check-In (Bingo)

Scenario:

When loading baggage, the ramp equipment detects 125 physical bags, while the system reports only 121 valid tags (bingo). This discrepancy indicates four bags with no official traceability, which immediately activates the security protocol to isolate the cargo, as its origin and contents cannot be guaranteed.

Main risk:

This scenario completely blocks the departure operation of the aircraft with a larger number of bags and additionally without tag verification. The existence of more physical baggage than checked baggage poses a potential threat of unauthorized introduction of hazardous materials (explosives, weapons, narcotics, etc.).

Operational impact:

The operation is frozen on two levels:

• Security: Until the additional baggage is identified and removed or validated, no shipment can be made.
• Functional dependencies: Cargo lane closure, flight dispatch, and TaxiWay authorization are directly affected.

Mathematical modeling:

Note the following:

• $M_f\left(t\right)$ is the amount of physical baggage counted during time t;
• $M_r\left(t\right)$ is the number of checked bags at bingo;
• ${∆}_m\left(t\right)=M_f\left(t\right)-\left(t\right)$ is a dynamic discrepancy;
• $R_{seg}\left(t\right)$ is a system-perceived risk.

The system triggers blocking when

$${∆}_m\left(t_k\right)>0=\succ R_{seg}\left(t\right)=\mathrm{\infty }$$

(18)

At that time, $t_k=t_k^{\mathrm{*}},$ the safety critical minute is defined, considering that $t_k$ is the operational time at which task k occurs.

This can be formalized as

$\underset{t\to t_k^{-}}{\lim }{\displaystyle \frac{{dT}_{op}}{dt}}<0$  and $\underset{t\to t_k^{+}}{\mathit{lim}}{\displaystyle \frac{{dT}_{op}}{dt}}=0$

GH activities during turnaround suddenly flatten out, revealing a zone of operational collapse.

• $T_{op}$ means the remaining operational time left; it is the useful time left to perform GH tasks before the scheduled departure time (STD). In other words, it measures how much free space there is to operate without suffering delays.
• $t_k^{-}$ is the time immediately before the critical minute and represents the time just before the system goes out of balance. The superscript “-” indicates an approach to the critical minute $t_k^{\mathrm{*}}$ on the left, i.e., before operational collapse occurs.
• $t_k^{+}$ is the moment immediately after the critical minute and refers to the moment immediately after the critical minute threshold has been crossed, when the system has already started to show serious disruptions (backlogs of unperformed activities, loss of synchronization, risk of imminent delay).

Summarizing the equation,

$$\underset{t\to t_k^{-}}{\lim }{\displaystyle \frac{{dT}_{op}}{dt}}<0,$$

(19)

describes a critical warning signal. The limit shows that when approaching the critical minute before, the derivative of the remaining running time is negative. That is, the useful operating margin decreases rapidly. In practical terms, the system loses running time and, unless immediate action is taken, the critical minute $t_k^{\mathrm{*}}$ will be reached, where the bifurcation or disturbance effect is triggered.

In this type of situation, one of the factors aggravating delays is the disorganization of the passenger list and the associated bingo cards:

• The lists are not delivered in numerical order of passenger sequence but by first or last name.
• The physical bingo tags are not logically correlated or matched.
• This turns an already critical check into a chaotic and error-prone search.

Applying CMT in this scenario:

At this point, the team leader not only intervenes operationally but also generates a “virtual simulation block:”

• The discrepancy is isolated.
• A temporary load route is generated for the already checked baggage.
• Immediate validation of the correctly labeled bags is requested from the passage.

This reduces the exponential increase in delay at a temporary plateau.

Proposed solution (not yet approved by the company): structural reorganization of the list.

Delivering the passenger list in ascending sequential order, coupled with correlative bingo tags, is a direct entropy reduction in the system.

Dynamically,

$${\tau }_{verif}=\mathrm{ʄ}\left(E\right)$$

(20)

where E is the entropy of the mating system.

By reducing $E\to {\tau }_{verif}\downarrow$, it has a direct impact on the following:

• The operational validation time, which becomes shorter.
• Reduced risk of deadlock due to possible false positives.
• Almost eliminating the occurrence of CMT in this node.

${\tau }_{verif}$↓ the time required to perform an operational check. In this case, there is a downward trend or a decrease. By sorting the passenger list in ascending order of sequence number, this results in ${\tau }_{verif}$↓, thereby enabling considerable time savings in baggage checking.

This example of Case 2 baggage number mismatch demonstrates a clear distinction between critical minutes due to inefficiency and critical minutes due to security. While the former can be addressed by reordering, the latter can only be avoided by preventing structural and logical data. An improvement in information format and baggage traceability is as powerful as a physical intervention on the runway. Figure 4 clearly represents the comparative delay propagation in this case.

7.3. Case 3: Delay Due to PRM Service

Operational scenario:

During turnaround GH activities (

Table 1. Calculation of time sequence and delay. Total accumulated time.

Stage	Estimated Time	Comments
Remote Park allocation	+3 min	Scheduling change by ATC
Waiting for ambu-lift	+10 min	Unscheduled rerouting
WCHC passenger assistance	+7 min	Careful and slow handling
Rear access locking	+3 min	Interference with boarding logistics
Resuming boarding	+5 min	Security coordination and verification

$∆T_{prm}=3+10+7+5=28 \mathrm{m}\mathrm{i}\mathrm{n}.$

), the flight arriving is carrying four PRMs (Persons with Reduced Mobility) requiring specific assistance to disembark. Initially, the aircraft was assigned a position in a standard terminal parking lot provided with a gangway for disembarkation, but due to the domino effect of a previous severely delayed flight, the control tower was forced to reassign the aircraft to a remote position without a gangway.

This involved the following:

• PRM passenger transfer by specialized vehicle.
• Urgent need for an ambulatory elevator machine (ambu-lift), taking an additional 10 min to reach the new location.
• One of the passengers is in a wheelchair with complete immobility (WCHC), involving the following:

  ○

  Intervention of two PRM agents on board.

  ○

  Removal of the passenger from their seat through a narrow aisle, controlled lift, and transfer to the ambu-lift.

This process disrupts access from the rear of the aircraft and delays the start of boarding for new passengers, as, according to the regulation, boarding cannot start while people with reduced mobility are assisted on board.

Delay Propagation:

This type of incident has a nonlinear delay profile, which propagates according to almost exponential dynamics if no action is taken in the critical minute $t_k^{\mathrm{*}}.$

Approximate Modeling:

Computing the derivative of the running time with respect to the real time ${\displaystyle \frac{{dT}_{op}}{dt}}$ shows the following.

• Before the PRM event:

$${\displaystyle \frac{{dT}_{op}}{dt}}\approx 0$$

(21)

• During the delay caused by ambu-lift and WCHC:

$$\underset{t\to t_k^{-}}{\lim }{\displaystyle \frac{{dT}_{op}}{dt}}<0 (\mathrm{rapid} \mathrm{decline})$$

(22)

With ambu-lift delay at critical time $t_k^{\mathrm{*}}$, the team leader activates early containment logistic measures, such as the following:

• Sequential reorganization of the boarding order (boarding first through the front door).
• Anticipation of other parallel services (catering, cleaning, fuel).
• Immediate request for a second ambu-lift on standby (if available).
• Direct communication with terminal agents to mobilize the remaining passengers afterwards.

Result:

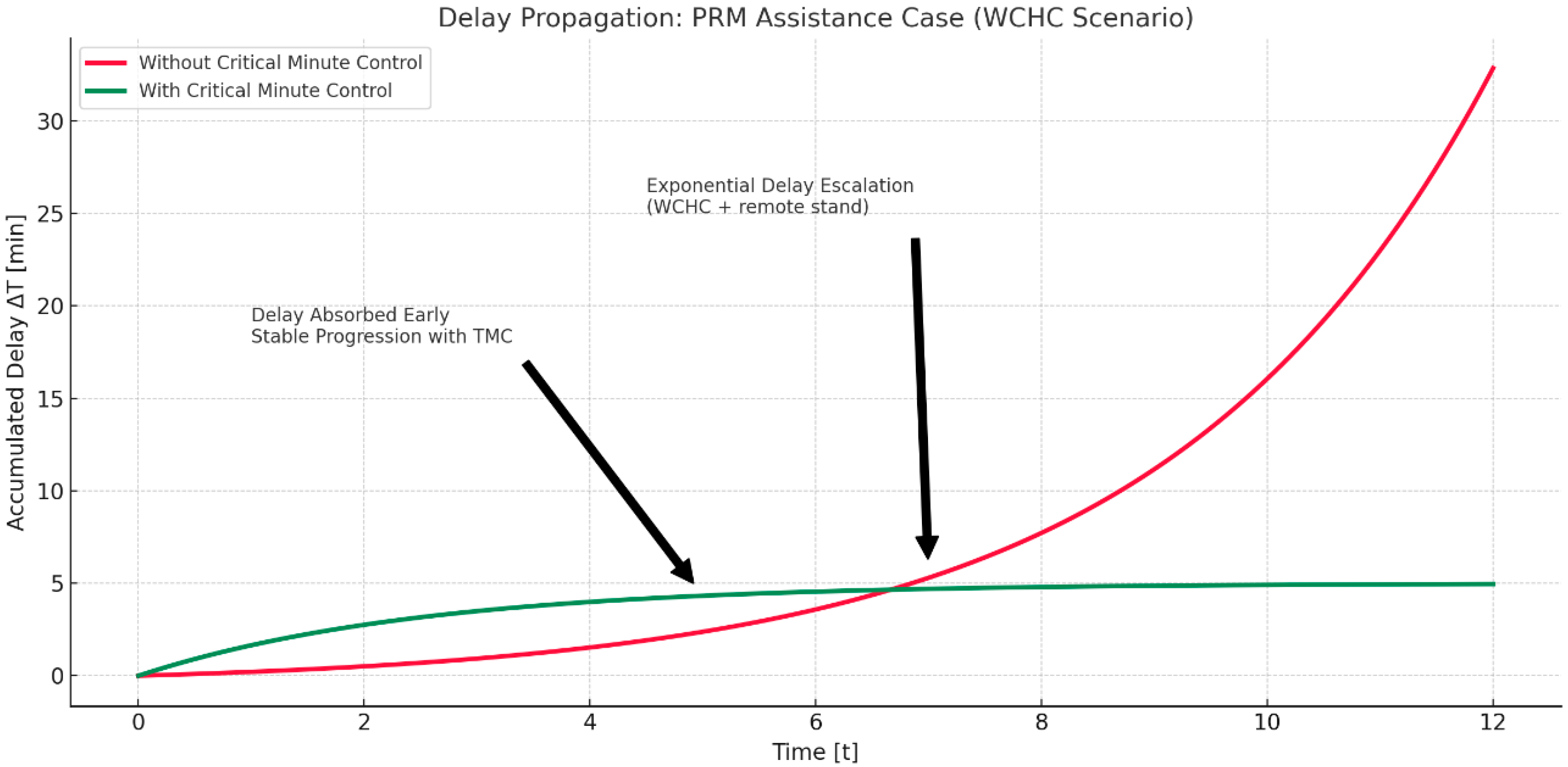
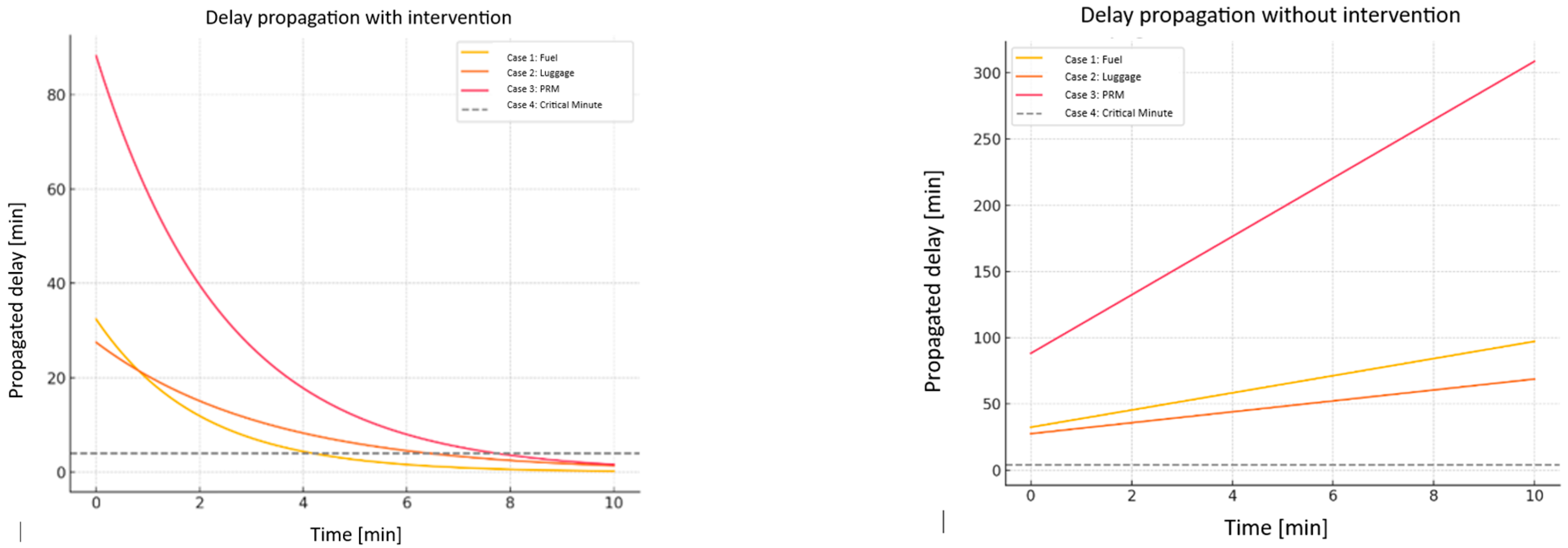
• Total effective blockage time is reduced.
• The propagated time loss is estimated to be shortened by up to 12–15 min, depending on the degree of anticipation.
• If CMT is applied immediately after ambu-lift delay identification.

Possibility of early logistical isolation → effective reduction of up to 12–15 min:

• ${\tau }_P$ is late ambu-lift arrival time = 10 min;
• $∆T_{emb}$ is additional time that is extended until boarding due to waiting for PRM;
• D unit is propagated delay.

No intervention:

$$D_{total}^{noTMC}={\tau }_P+∆T_{emb}, D_{total}^{noTMC}=10+5=15 \mathrm{m}\mathrm{i}\mathrm{n}.$$

With CMT application:

Early queue reduction at logistics.

Ground tasks overlap with recovery management:

$$D_{total}^{TMC}={\tau }_P-ϵ+∆{T\mathrm{’}}_{emb} (\mathrm{where} ϵ>0, ∆{T\mathrm{’}}_{emb}<∆T_{emb})$$

$$D_{total}^{TMC}\approx 10-4+1=7\mathrm{m}\mathrm{i}\mathrm{n}$$

Therefore, an improvement is evident:

${∆D=D_{total}^{noTMC}-D}_{total}^{TMC}=15-7=8$ (up to 12–15 min in extended scenarios);

• $∆T_{emb}$ is the total delivery delay without the application of CMT (full distribution);
• $∆{T\mathrm{’}}_{emb}$ is boarding delays after applying CMT (mitigated spread);
• $∆D_{emb}$ is recovered time = the difference between the two.

Conclusion

CMT allows for action in $t_k^{\ast }$ just before the logistic inflection point, avoiding a nonlinear escalation of delays. Due to this early response, the following occurs:

• The initial chaos is reabsorbed.
• The domino effect is substantially reduced.
• And, most importantly, the overall stability of the rotation period is maintained, complying with regulations without compromising operational punctuality.

Delay propagation is shown in Figure 5 and Figure 6.

Figure 7 shows the comparative delay propagation curves of all three cases previously exposed in the same graph.

Previous studies on delay management have largely relied on data-driven methods, such as machine learning, probabilistic modeling, and simulation-based approaches (e.g., Khaksar et al. [6]; Wu et al. [8]; Thiagarajan et al. [12]). These methods are effective at predicting the probability of delay events but depend heavily on large training datasets and remain limited in novel or unprecedented scenarios. In contrast, the Critical Minute Theorem provides a deterministic, algebraic framework that does not require historical data but instead identifies fragility points in real time through structural analysis. For example, in the fueling delay case, the reduction of propagation from 9 to 3.7 min illustrates a predictive control mechanism comparable in effectiveness to reported machine-learning-based mitigations but achieved without algorithmic training. Similarly, the PRM service case shows mitigation of up to 12–15 min, an effect consistent with operational improvements described in delay propagation studies but here derived from analytical recognition of bifurcation points rather than statistical forecasting. This positions the present work as complementary to the existing literature; while predictive models estimate if delays will occur, CMT provides a structural mechanism to determine when and where a small disturbance becomes critical, enabling earlier and more targeted interventions.

Much more than that, the results of the case studies illustrate the dual significance of the Critical Minute Theorem (CMT). On a theoretical level, CMT reframes turnaround operations as an algebraic system in which critical thresholds $t_k^{\mathrm{*}}$ govern stability and instability. This structural perspective contrasts with conventional machine learning or probabilistic methods, which primarily estimate the likelihood of delay without revealing the precise mechanism of amplification. On the operational level, the case results demonstrate that early recognition of critical minutes allows for minimal, targeted interventions that reduce propagated delays by more than 50% in some scenarios. This finding underscores that the cost of small, proactive adjustments is far lower than the cumulative cost of uncontrolled cascades.

Nevertheless, CMT has its limitations. The current model focuses on temporal and algebraic dependencies between tasks but does not yet incorporate resource heterogeneity (e.g., crew skill variability, equipment availability) or external constraints (e.g., weather shocks, regulatory procedures). These factors will need to be integrated in future refinements. Furthermore, while the theorem establishes a deterministic mechanism, its operational implementation still relies on human decision makers to interpret signals and apply compensatory action effectively.

In this sense, the contribution of CMT lies not only in proposing a mathematical architecture but also in redefining the human role as an architect of time. By shifting the focus from corrective to counter-perturbative action, CMT highlights a paradigm where operational disruptions are not merely managed but structurally anticipated. This dual lens—mathematical and operational—provides depth to the discussion and situates our results as a complementary approach to the existing body of predictive and probabilistic research.

It is important to note that the case studies reported in this paper are based on real turnaround operations where the Critical Minute Theorem was experimentally applied. The fueling delay, baggage mismatch, and PRM assistance cases were not simulated but derived from actual operational contexts. However, due to strict data protection regulations and confidentiality policies of the collaborating company, the raw datasets cannot be disclosed at this stage. This represents a limitation of the present paper not in terms of validation but in terms of data availability for external verification. Future research will focus on developing formal agreements with industry partners to allow for official release of anonymized operational data, thereby enabling full empirical transparency and independent replication of our results.

8. Conclusions

This study introduced the Critical Minute Theorem (CMT) as a deterministic, algebraic framework for understanding fragility in aircraft turnaround operations. The central result is the identification of singular temporal thresholds $t_k^{\mathrm{*}}$, where small local disturbances generate nonlinear, system-wide disruptions.

But, far from the contemporary fascination with artificial intelligence, this study also shows that turnarounds are more than a technical problem; they are a dynamic architecture of human decisions, a system of fragile equilibria in which the smallest perturbation, if not detected in time, can propagate with exponential consequences. The Critical Minute Theorem does not arise from the lack of sensors or predictive algorithms but is generated by observing the internal structure of operational time from the mathematics of the moment before collapse.

According to systems theory, any dynamic structure can be categorized as stable, unstable, or marginally stable [14]. Far from being a strictly mechanical or predictable process, the turnaround behaves in practice like a marginally stable system; it operates in equilibrium if it is not disturbed, but a small deviation—a minimal delay, an omitted activity, a late reaction—is enough to break that equilibrium, and the system enters a critical transition phase.

What is really fascinating is that a turnaround does not crash completely; it naturally seeks a new equilibrium state, even if it is different from the initial one. This behavior, so characteristic of living and adaptive systems, is exactly what CMT harnesses. When applied correctly, CMT allows us to identify the exact moment when an intervention can reconfigure the system to restore stability, preventing the disorder from amplifying and spreading.

In this context, the team leader becomes more than a mere coordinator of activities, as he or she becomes the dynamic regulator of the system and the architect of the momentary equilibrium. It is his or her ability to read the operational flow in real time, anticipate breaking points, and act before the critical moment that makes the difference between a controlled recovery and irreversible disruption.

But, there is a hidden obstacle that is much harder to neutralize than any external contingency: the human tendency towards repetitive habits and towards the common comfort familiar to all. As Aristotle (384-322 BC) said more than two thousand years ago: “Thought conditions action, action determines behavior, repeated behavior creates habit, habit structures character, and character defines destiny.” In critical operations like the turnaround, many significant delays are not due to technical failures or force majeure but rather the weight of routine, including automatic decisions, assumed operational sequences, and signals ignored out of habit. In these moments, CMT is not just a tool to manage time but a wake-up call for operational success. Its application requires focus, clarity, and the courage to intervene even when everything seems “normal.”

The case studies provide empirical confirmation of the theorem’s operational relevance. In fueling operations, a 9 min disturbance was reduced to 3.7 min through CMT-guided task reordering. In baggage handling, the theorem prevented systemic deadlock by restructuring the loading sequence. In PRM assistance, anticipated interventions reduced propagated delays by 12–15 min.

These findings demonstrate that CMT enables predictive, non-technological control of turnaround operations, offering a complementary alternative to machine learning and probabilistic models. By revealing invisible fragility points and enabling minimal compensatory action, the theorem provides a practical contribution towards increasing efficiency and stability in ground handling processes.

While mathematics can give us the key to balance, only human judgment can prevent us from losing that balance. For, after all, precision is not a property of machines but a virtue of character.

Reflection between Precision and Silent Chaos

The Critical Minute Theorem is not simply an operational management tool. It is a living mathematical architecture capable of detecting deviations from equilibrium in complex dynamic systems before instability becomes irreversible. It acts as a silent compass that guides the team leader through multiple variables under stress, interpreting the airport symphony when it seems about to turn to noise.

In this context, balance is neither imposed nor decreed. It is deciphered. It is sensed in the subtlest vibrations of the system, even before the disorder becomes visible.

And yet, like a whisper in a whisper, the inevitable is already looming: a future in which robots will be part of the ecosystem of GH. But even then, human judgment—not in execution, but in direction—will be what keeps the logic of CMT alive. Wherever there is a system that works, there will still be a need for someone to listen.

“Turnaround,” that temporal theater of human decisions, is already beginning to prepare space for a new generation of actors, including automated robots, mechanical arms, artificial intelligence, and precision. The future—even if not immediately—will not be able to resist the temptation to automate even the hands that close airplane holds, fill tanks, count suitcases, or push wheelchairs. It will be a silent, gradual, almost invisible movement, just like the transition from paper to digital. Yet this future cannot be completely free of human judgment. Because, including in the machine world, someone will have to decide when to intervene, what constitutes an error, and when a pattern of behavior is a critical anomaly. Someone will have to understand what machines cannot imagine. And that is why, even if math helps us model chaos and machines will one day execute it accurately, post-humanist architecture on Earth will still require human thinking, at least until the human being can program intuition.

This is all because according to Adrian Bejan’s Constructal Law, “flow is nothing but knowledge, and knowledge is that capacity to lead to making changes in the design (blueprint, sketch, draft, drawing, form, etc.)… of the concept itself” [32]. Knowledge is not merely information contained in an article or a book, and a book is not a means to light a fire.