Efficient Simulation Algorithm and Heuristic Local Optimization Approach for Multiproduct Pipeline Networks
Abstract
1. Introduction
2. Literature Review
2.1. Network Layout
- Straight pipelines,
- Tree-like pipeline networks,
- Mesh-like or arbitrary pipeline networks.
2.2. Model Constraints
2.3. Objective
2.4. Modeling Techniques
2.5. Simulation Approaches
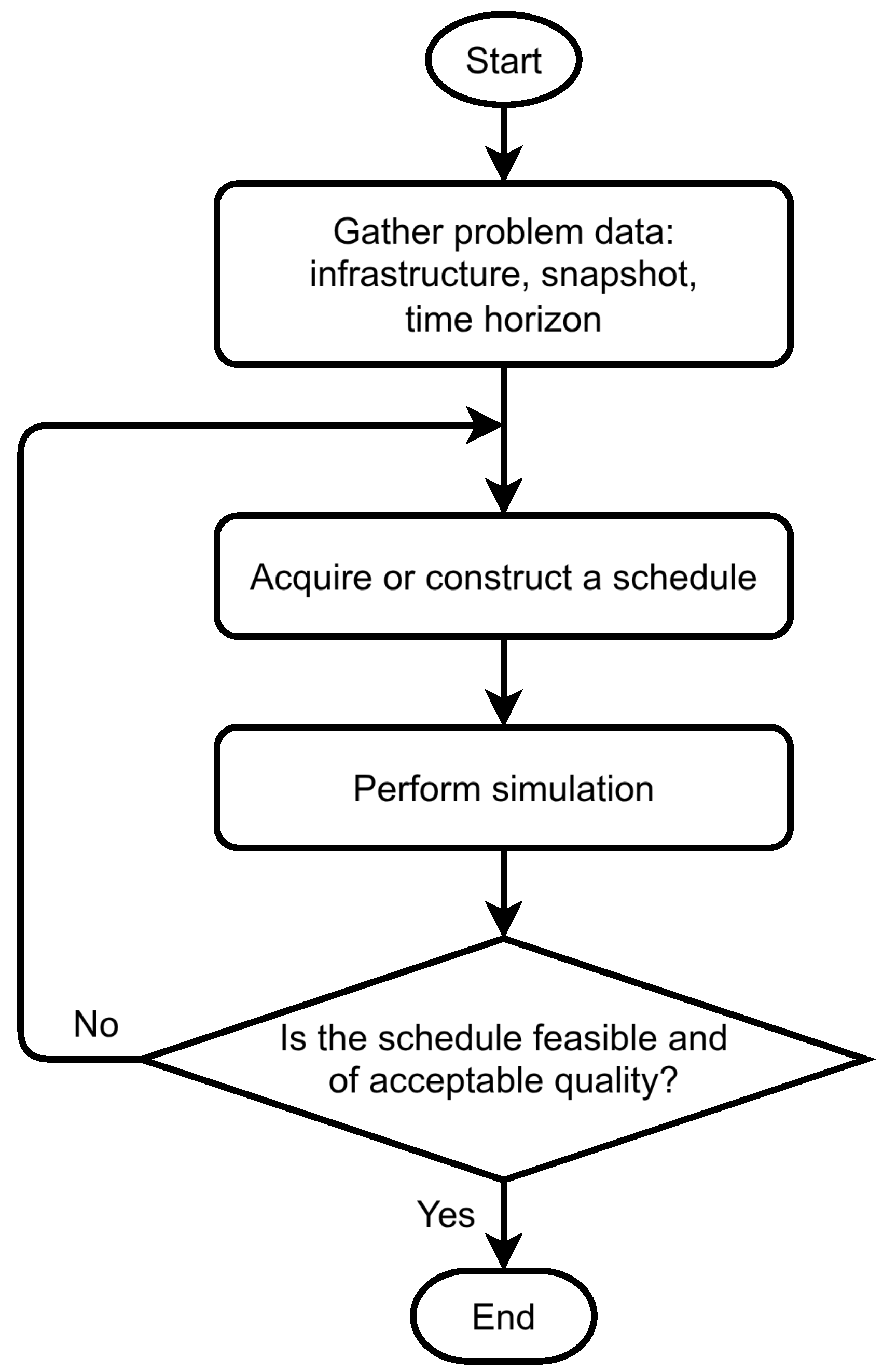
3. Proposed Method
3.1. Problem Formulation
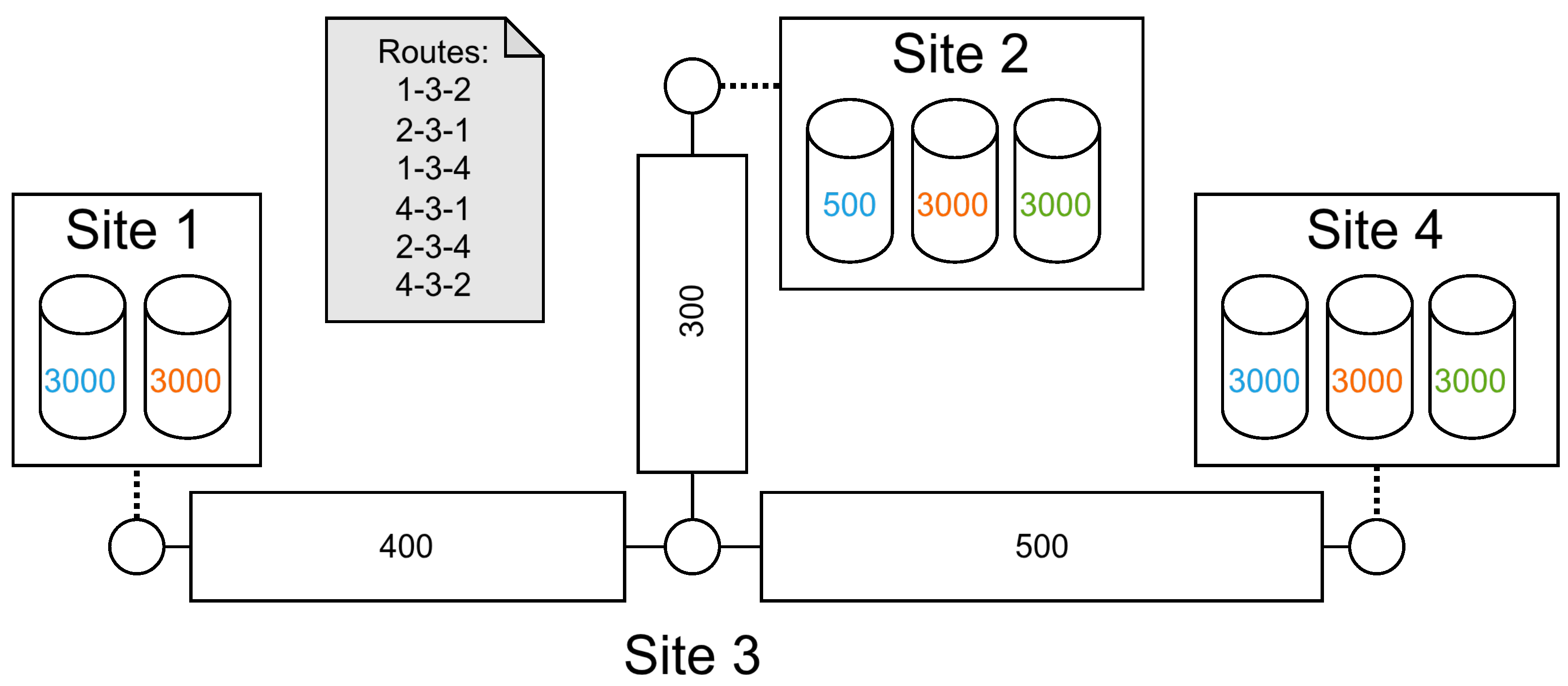
3.1.1. Infrastructure Data
- Petroleum products managed in the network.
- Sites that contain an aggregate maximum tank capacity for each product. The minimum tank capacity is assumed to be zero. Sites are the nodes of the pipeline network.
- Pipe segments, or simply called pipes, which have a fixed volume and connect two distinct sites.
- Routes, which are paths connecting a source and a target site, consisting of adjacent pipes. A pumping operation can be performed over a route.
- Flow rates of considered pumping operations, inflows and outflows.
- The roles of sites are not determined. A site can be a production site, an intermediate node, a delivery station, or any combination of these. These are rather decided in the snapshot part, in the form of the planned inflows and outflows.
- A pumping operation is allowed not only via a single pipe, but a path of interconnected pipes from a source and a remote target site. A route may contain intermediate sites which do not participate in the pumping operation. However, not all such paths in the network are valid for pumping; therefore, allowed routes are explicitly listed in the problem description.
- A site may participate in multiple simultaneous pumping operations, via different routes. However, a pipe may participate in a single pumping operation at any given time.
- Site 1 cannot store product 3 (green).
- Site 2 can store a limited 500 of product 1 (blue).
- Site 3 has no tanks, and it cannot store any products. It is an intermediate node.
3.1.2. Snapshot Data
- Current tank inventory for all products in all sites.
- Current pipe contents, which are a list of plugs of different products.
- Given future inflows and outflows that are expected to happen. Each inflow or outflow is described by a start time, a site, a product, and an amount.
- Aggregate tanks are assumed. Therefore, each site is supposed to contain a single tank for each product. Operations relying on dedicated tanks (e.g., blending operations) are not directly modeled.
- Tank inventories should be between the minimum and maximum capacities, which are zero and the capacity given by the infrastructure, respectively.
- Plugs in a pipe must always sum up to the constant volume of the pipe.
- Other than product type, no additional information is stored per plug. In particular, plugs are not assigned to specific batches or specific target sites, but simply end up being pushed out somewhere, influenced by subsequent pumping operations.
- Inflows and outflows represent material flows coming inside and going outside the pipeline network. Such flows only happen at site tanks, never from the pipes directly. These can model receiving of products from outside, production, blending operations, delivery, and other operations.
- Inflows and outflows are not instantaneous but continuous. For the sake of simplicity, the flow rates for inflows and outflows each are assumed to be constants given as infrastructure data.
- For product 1 (blue), there is a stock of 2000 at site 1, and 400 is already present in two pipes, as three distinct plugs of sizes 100 , 100 , and 200 .
- For product 2 (orange), there is a stock of 1000 at site 4, and 800 in three different pipes, in plugs of size 200 , 300 , and 300 .
- For product 3 (green), there is a stock of 1200 at site 4.
3.1.3. Schedule Description
- The infrastructure of the pipeline network,
- A snapshot of the given infrastructure,
- A time horizon of length H, which starts at the time point the snapshot corresponds to.
- Starting time (within the time horizon).
- Ending time (after the starting time, within the time horizon).
- The route on which the pumping operation is performed.
- The product which is being pumped.
- A schedule determines what happens in the pipeline network in full detail.
- Pumping volumes are indirectly determined by the pumping start and end times and the flow rates. Expressing pumping operations by time rather than volume makes it easier to design a contradiction-free schedule.
- Source and target sites, as well as the involved pipes are determined by the route chosen.
- The product which is pushed out at the target site and uploaded to a tank is indirectly determined by the actual pipe contents at the last pipe of the route. Therefore, the product pushed out at the target site may change during the same pumping operation, but the product pumped at the source site always remains the same.
- Condition 1: Two pumping operations overlap for which the routes have a common pipe.
- Condition 2: The stored amount of a product at a site goes below zero or above tank capacity.
3.1.4. Expected Simulator Output
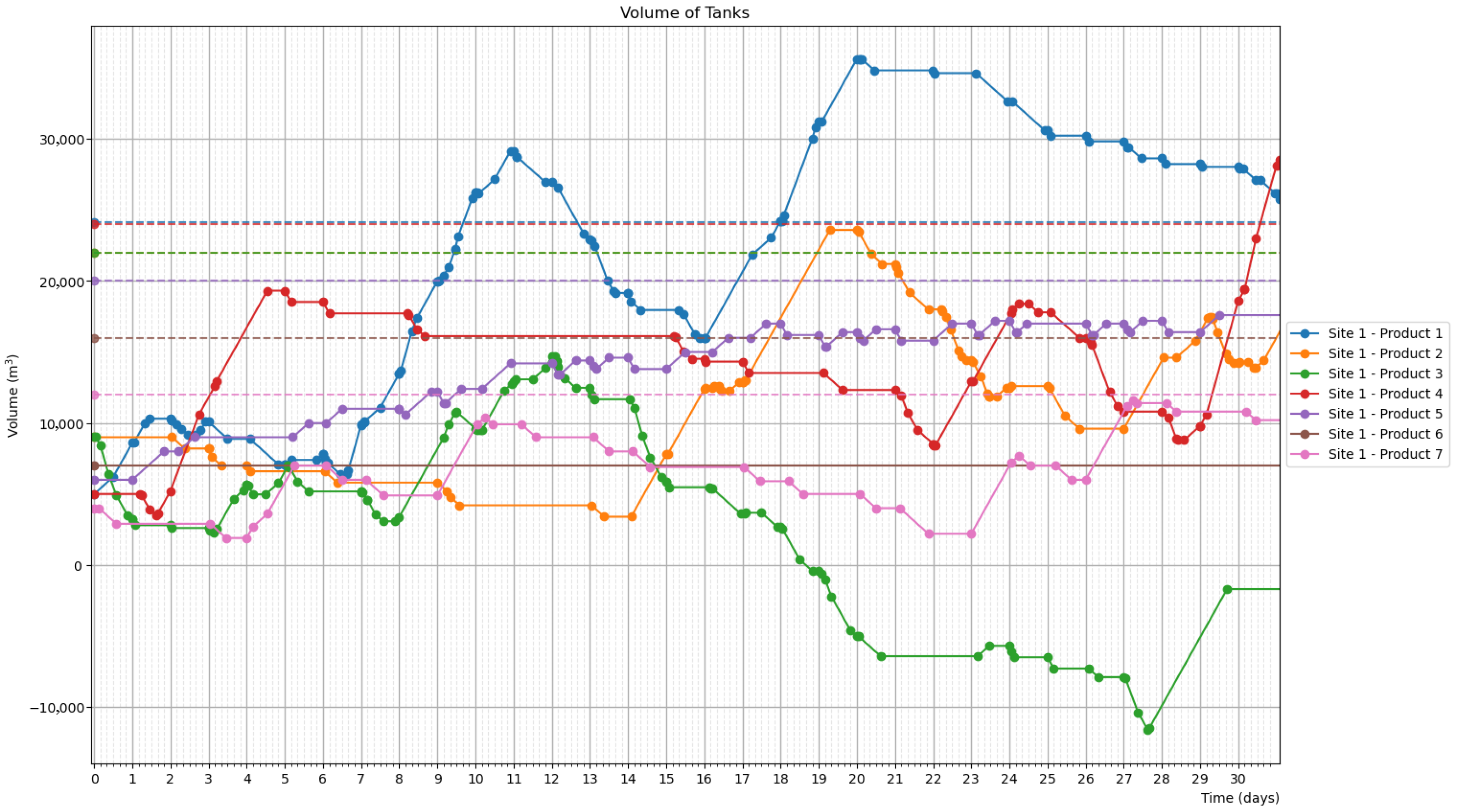
- Detailed tank level profiles for each product at each site.
- Detailed pipe contents for each pipe segment.
- Tracking of interfaces.
- Quality measures.
- Number of interfaces (already present or created).
- Total persistence duration of interfaces.
- Number of flow reversals.
- Number of pumping operations.
3.2. Simulation Algorithm
3.2.1. Event System
| Algorithm 1 Main event loop of the simulation algorithm. |
(time horizon start) set of initially generated events while
do Choose so that StartTime(e) is minimal StartTime(e) Process(e) NextEvents(e) end while |
- Inflow (and outflow) start events are known a priori, so only the next one is considered.
- An inflow (and outflow) end is only considered after its corresponding start.
- Plug events describe structural changes during a pumping operation, and at each such event, only the next one can be and needs to be calculated.
3.2.2. Pumping Events
- The tank of the source product at the source site that is currently being pumped.
- The tank of the product currently being pushed out at the target site.
- The plugs in the pipes on the route of the pumping operation.
- Interfaces between plugs.
- The source tank and all shrinking plugs are decreased by .
- The target tank and all growing plugs are increased by .
- Plugs with a remaining volume of zero are removed.
- If p was the last pipe of the route, the product that is pushed out might change, so the target tank flow rates are updated. Otherwise, a new growing plug is inserted to the pipe after p, with a volume of zero.
3.2.3. Interface Management
- Interfaces exist initially between plugs of different products.
- New interfaces are created only at pumping start events at the beginning of a pipe in the route (see Figure 9).
- Interfaces are only removed when arriving at a target site.
- Interfaces may move from one pipe to another during a plug event when a corresponding plug shrinks to zero.
3.3. Optimization by Local Search-Based Algorithms
- Exhaustive variant.
- Look-ahead variant.
- Simulated annealing variant.
3.3.1. Two-Stage Fitness Function
- Global earliest tank violation time:
- Time-adjusted sum of first tank violation times:
- Time-adjusted sum of violation volumes:
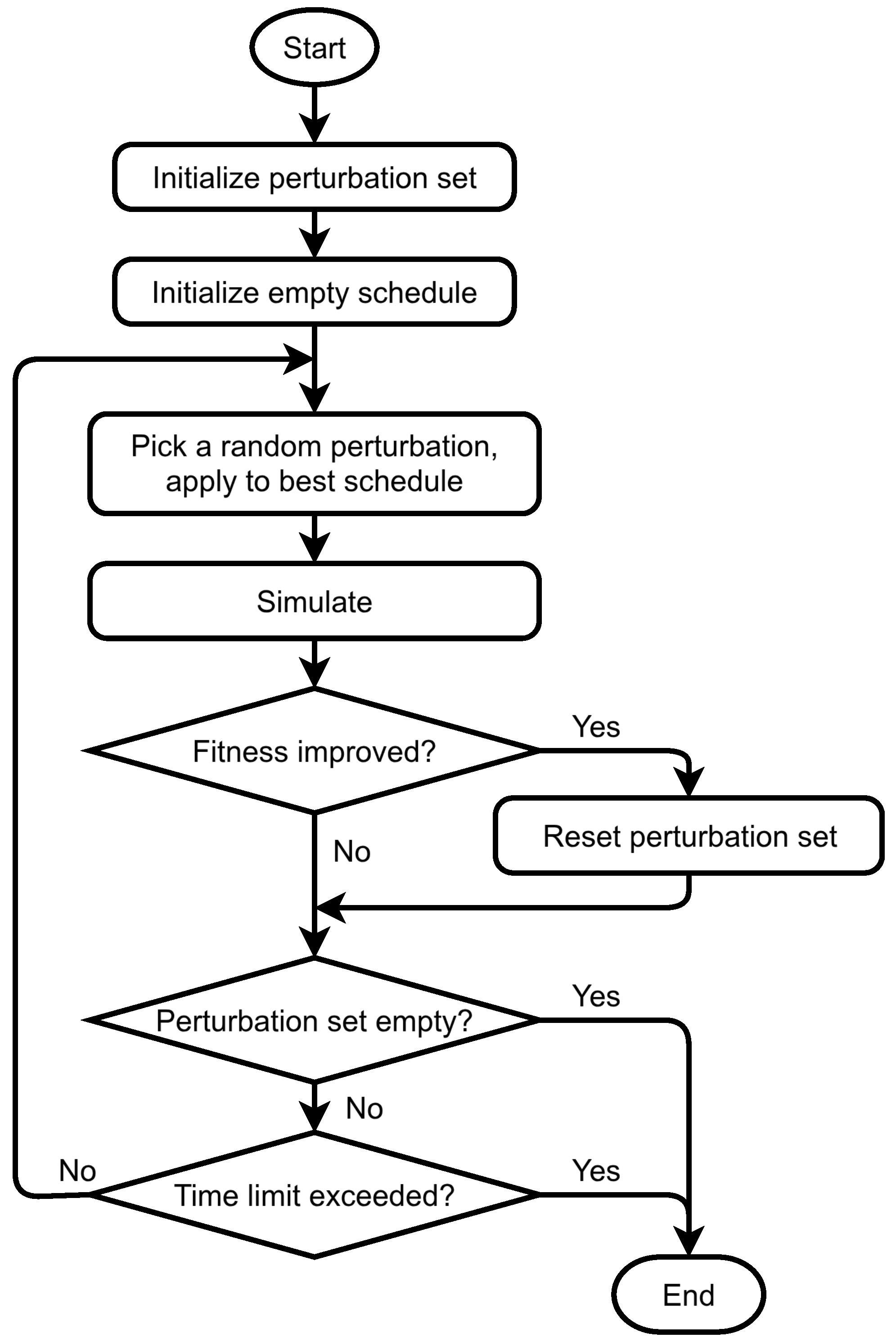
3.3.2. Exhaustive Optimizer
- For , define perturbations for and for all routes and products, as adding a pumping operation at , by insertion or replacement (for two perturbations in total). Insertion differs from replacement in that the overwritten pumping operations are shifted forward.
- For , define perturbations for as clearing the schedule between , shifting down to x, grouping the same type of pumping operations together within , reversing the schedule within , and moving a pumping operation at x from y, or vice versa (for six perturbations in total).
- For , for time points , define perturbations as clearing, filling, or shifting one pumping operation below and above x (for six perturbations in total).
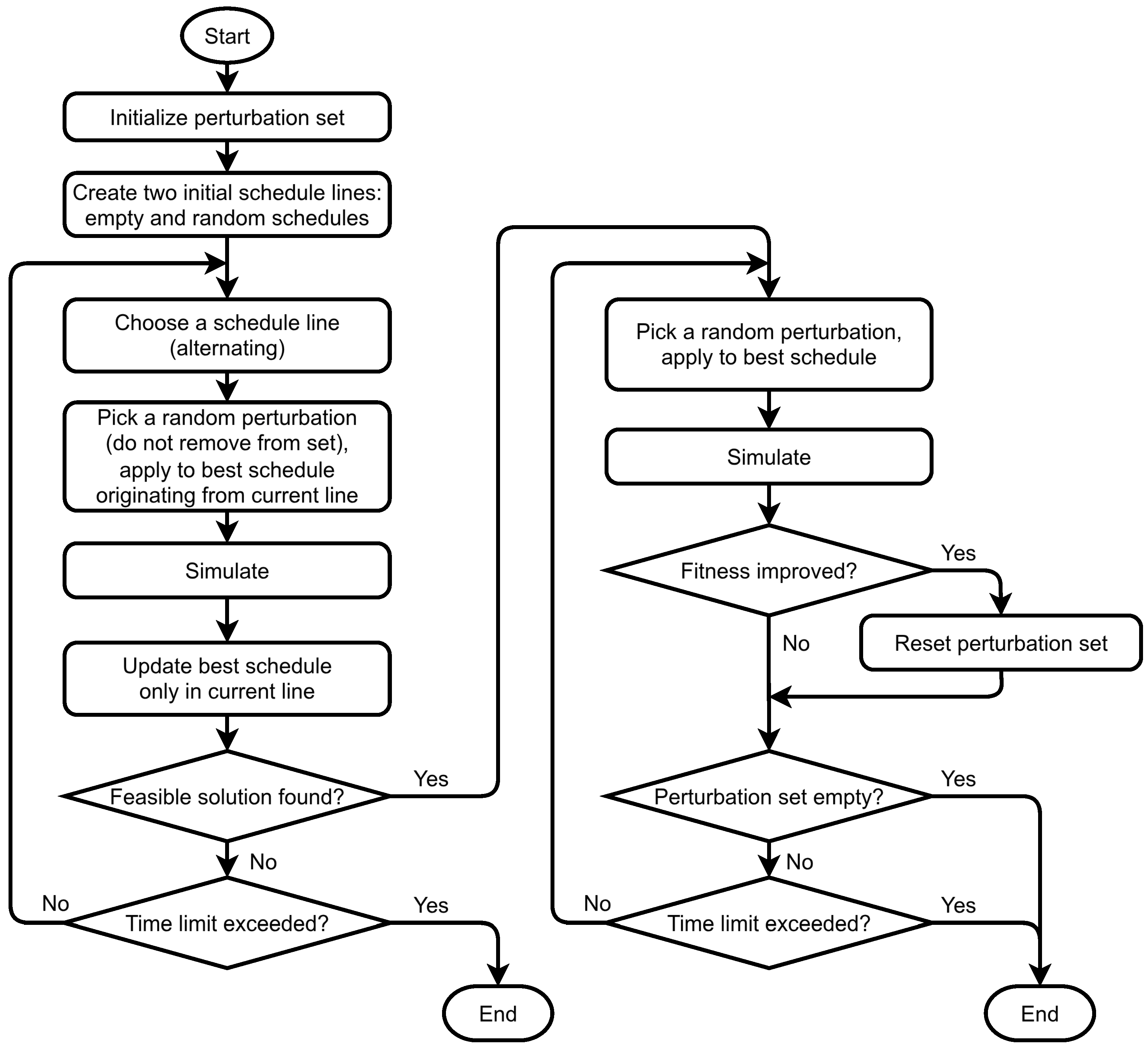
3.3.3. Look-Ahead Optimizer
- Instead of the empty schedule, the look-ahead proceeds on two separate, alternately improved lines using two starting schedules: one line starting with an empty schedule and one line starting with a schedule randomly filled with pumping operations of length . These are alternatively perturbed until the first feasible solution is found.
- Pumping operations are not from a set of perturbations to be exhausted. There is an chance of adding a pumping operation. After the first feasible schedule is found, this chance is set to .
- When adding a pumping operation, a random starting time is always chosen before the first tank violation. Then, there is a chance to set the pumping duration to a fixed , or a chance to set it by looking ahead. The look-ahead setting performs a new simulation, assuming the added pumping ends at the end of the time horizon. Then, the first tank violation denotes the chosen end time of the added pumping operation. This algorithm uses two simulations in total for performing one perturbation. The rationale behind this look-ahead mechanism is not to cause infeasible situations while performing as much pumping at once as possible with a single perturbation.
3.3.4. Simulated Annealing Optimizer
- The starting value of temperature T is the number of possible route–product pairs for pumping.
- An exponential cooling and acceptance regime is applied [35]. The acceptance probability p is given by Equation (7).The objectives before and after perturbation are and . Depending on whether a feasible schedule was already found, either the first stage or second-stage objective is used.
- Each time acceptance is considered, and T is multiplied by .
- When the first feasible schedule is found, T is reset. Afterwards, an infeasible schedule is never accepted.
3.4. Possible Extensions
- Aggregate tanks are currently assumed. Dedicated tanks could be handled by the simulator, provided that a logic is available for choosing an appropriate tank at the source and target sites. This is not expected to significantly affect the computational cost of a simulation. A policy for automatic choice of the tank by the simulator is a possibility and already used in practice. Alternatively, dedicated tanks can be coded as a scheduling decision, but that could introduce a new kind of infeasibility: when the product arriving at a target site does not match the target tank.
- Tank availability changes are rare but can be possibly planned. When a tank is down (for example, due to maintenance or opening hours), any pumping-related inventory change can be included in the first-stage fitness function as a penalty and handled in the same manner as for tank level violations.
- Forbidden product pairs for interface formation are currently not handled. However, since the simulation already tracks interfaces, large penalties can be introduced if specific products become in contact.
- The simulation algorithm can handle parallel pumping operations, but the optimization algorithms currently do not consider this possibility. Parallel pumping operations would require a more sophisticated perturbation mechanism, which permits multiple, non-conflicting routes to be chosen for pumping in overlapping time intervals. Note that the simulation model can already handle tank flow rate changes from different sources, as pumping operations, inflows, and outflows may already overlap.
- Arbitrary flow rates could also be used. The simulator currently assumes as the pumping flow rate, where is a constant for the problem instance. Other flow rates could be implemented as follows.
- −
- If the flow rate is a time-independent constant, the algorithm can be used without change to the event loop. An example scenario is when the pumping flow rate depends on the route and pumped product only, as if .
- −
- If the flow rate depends on current pipe contents, then can be calculated as normal. Since there are no further effects until the next plug event occurs besides the volume changes of and , Equation (1) can be solved for t. An example scenario is when the pumping flow rate depends on some weighted average of pipe contents.
4. Computational Results
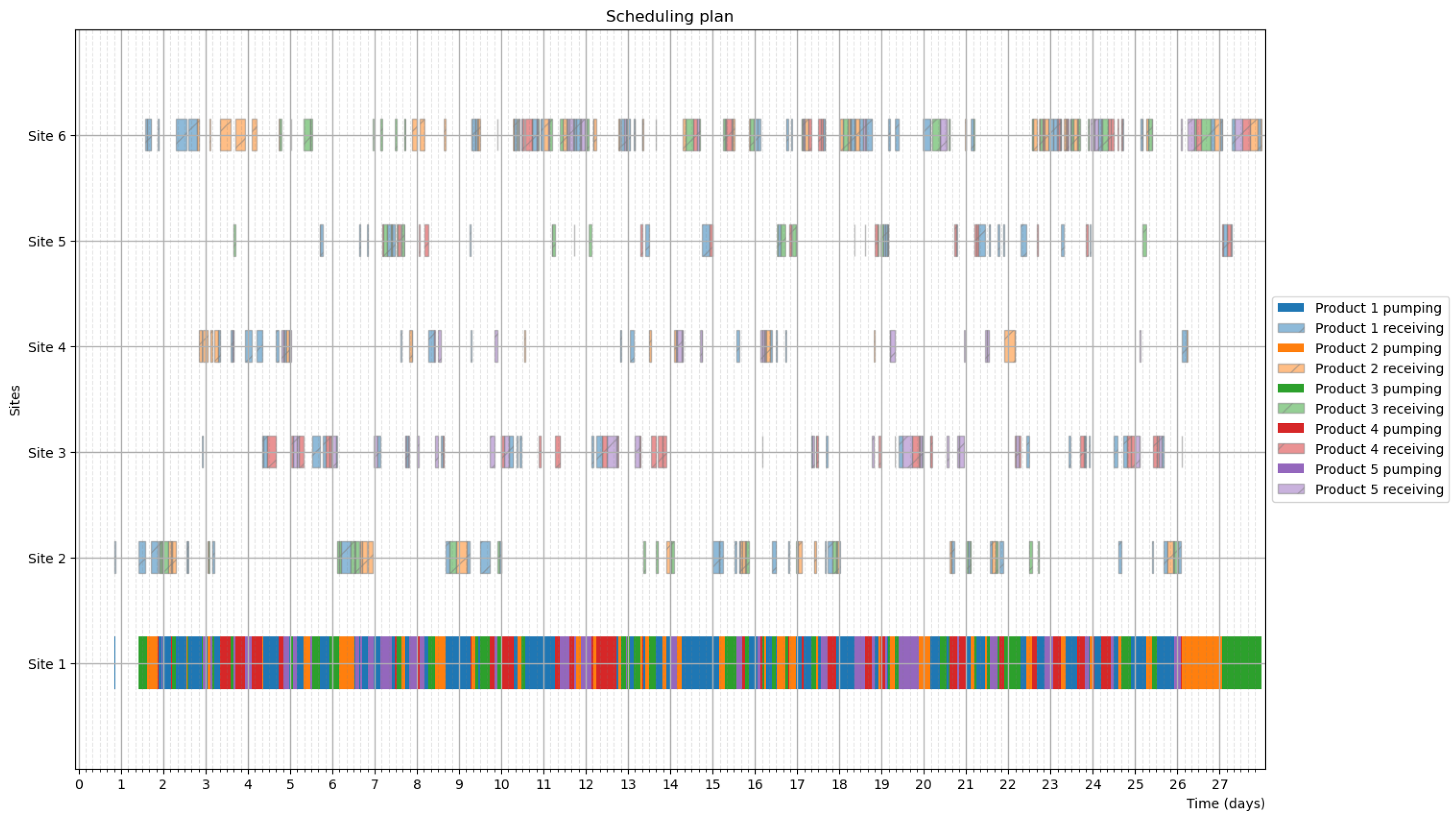
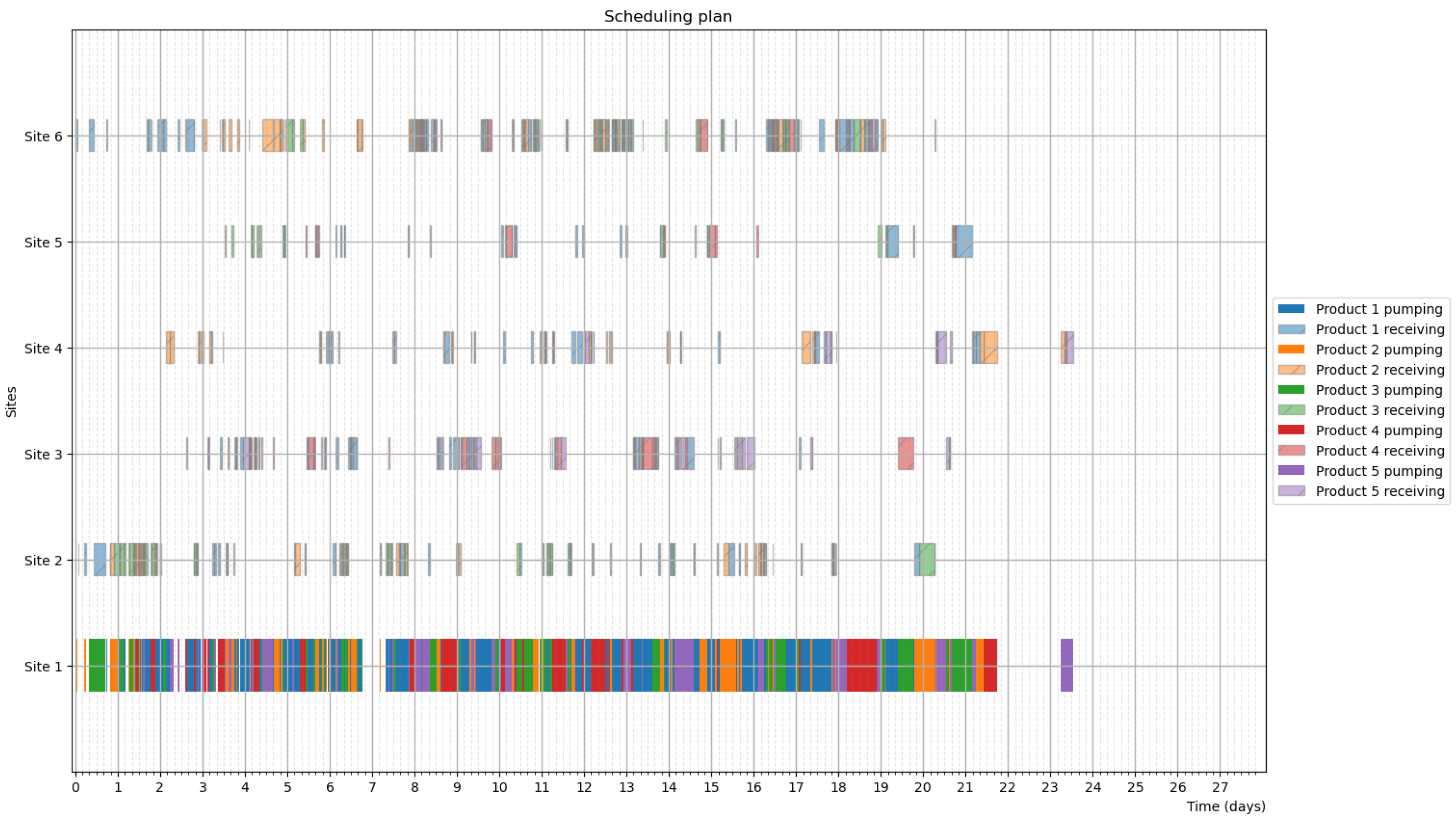
4.1. Scheduling Problems
- Problem 1: y-junction network, with large tank capacities.
- Problem 2: y-junction network, with tight tank capacities.
- Problem 3: Straight network.
- Problem 4: Large-scale mesh-like network.
4.2. Testing Circumstances
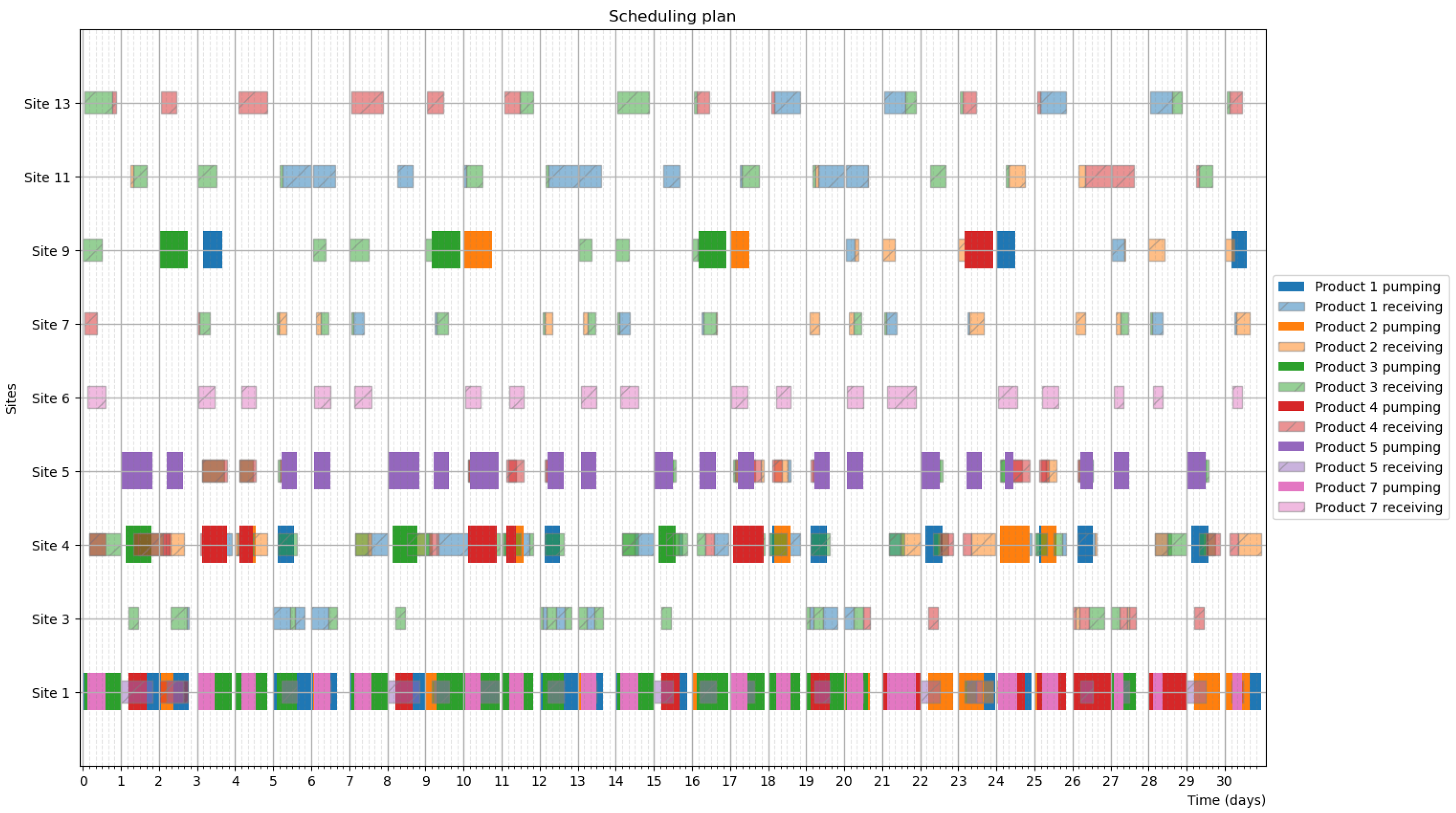
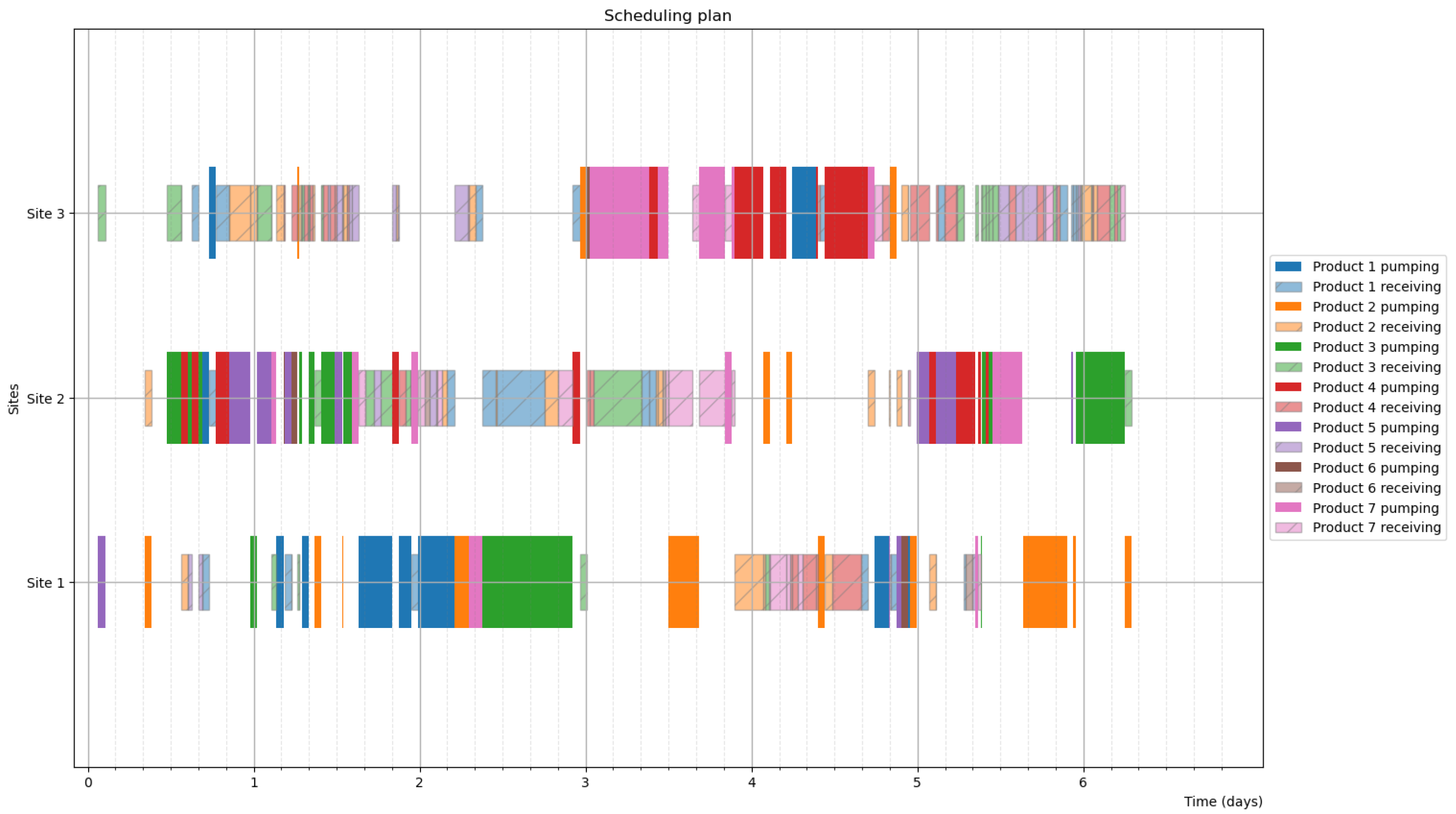
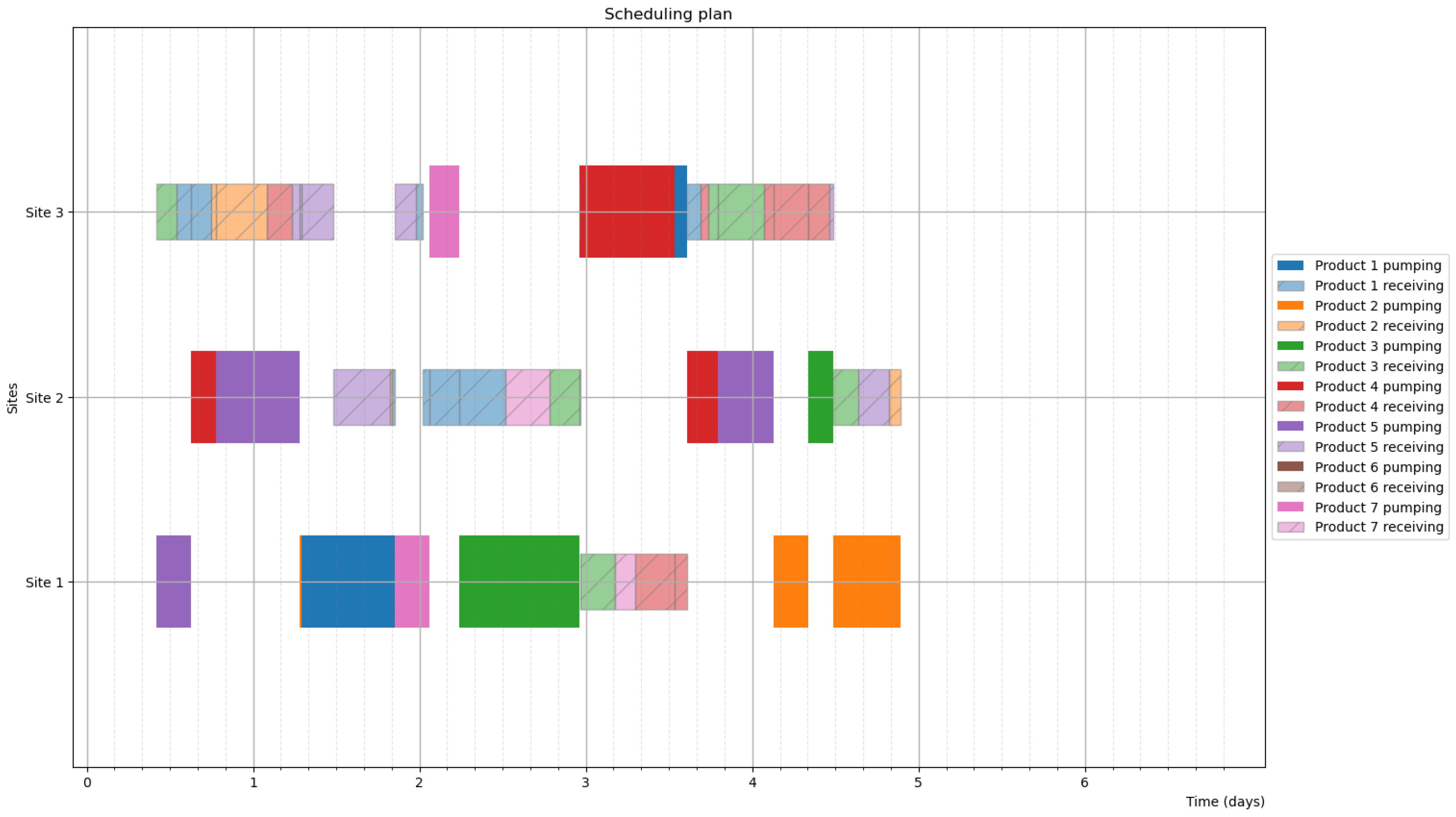
4.3. Simulation Results
4.4. Optimization Results
- The Ex variant terminated before finding a feasible schedule for the illustrative problem, but the Lo and SA variants succeeded.
- The Lo variant could not reach a feasible schedule for Problem 2, 28-day horizon; the best schedule is infeasible from Day 12. However, the Ex and SA variants succeeded.
- The Lo and SA variants could not reach a feasible schedule for Problem 3, 28-day horizon; the best schedules are infeasible from Day 13 and Day 17, but the Ex variant succeeded.
- For Problem 1, the Lo variant produced the best result for 7 and 14 days, and the SA was the best for 28 days.
- For Problem 2, the Ex variant was the best for 4 days and 28 days, and the SA was the best for 7 days and 14 days.
- For Problem 3, the SA variant was the best for 4 days and 14 days, the Lo was the best for 7 days, and the Ex was the best for 28 days.
- First tank violation time or feasible horizon: for a feasible schedule, this is 100%.
- First-stage objective, for feasibility, in a logarithmic scale.
- Second-stage objective, for quality.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACO | Ant Colony Optimization |
| CLP | Constraint Logic Programming |
| DES | Discrete-Event Simulation |
| Ex | Exhaustive, the name of a proposed optimization algorithm variant |
| GA | Genetic Algorithm |
| Lo | Look-ahead, the name of a proposed optimization algorithm variant |
| MILP | Mixed-Integer Linear Programming |
| SA | Simulated Annealing, and also the name of a proposed optimization algorithm variant |
Appendix A. Optimization Algorithms
| Algorithm A1 The exhaustive variant of the local search-based optimization algorithm. |
function
OptimizeExhaustive set of all considered perturbations empty schedule Simulate(s) while ¬TimeLimitExceeded() do Random(P) Apply() Simulate() if then end if end while return s end function |
Appendix B. Computational Results
- H: is the time horizon in days
- Alg: algorithm variant: Ex(haustive), Lo(ok-ahead), or SA (simulated annealing).
- Run (s): runtime of the algorithm in seconds (I/O, image generation excluded).
- Stage 1 and Stage 2: before and after finding the first feasible schedule.
- Sim #: number of simulations performed.
- Imp #: number of times the best fitness improved.
- Sim time, %: percent of runtime spent to performing simulations.
- Sim time, #/s: average simulations per second.
- Best schedule fitness: statistics of the schedule with the best fitness found.
| Run | Stage 1 | Stage 2 | Sim Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H | Alg | (s) | Sim # | Imp # | Sim # | Imp # | % | #/s | Best Schedule Fitness |
| 2 | Ex | 0.14 | 11,152 | 50 | 0 | 0 | 89% | 77,063.63 | IF/Day 01, 21:10/1005.29 |
| 2 | Lo | 0.15 | 3692 | 57 | 10,990 | 41 | 88% | 96,333.67 | F/678/7/2580/1/5 |
| 2 | SA | 0.43 | 8630 | 32 | 33,501 | 84 | 89% | 97,492.63 | F/674/7/2340/2/5 |
| Run | Stage 1 | Stage 2 | Sim Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H | Alg | (s) | Sim # | Imp # | Sim # | Imp # | % | #/s | Best Schedule Fitness |
| 2 | Ex | 0.09 | 1 | 1 | 9451 | 0 | 86% | 105,436.40 | F/0/0/0/0/0 |
| 2 | Lo | 0.03 | 1 | 1 | 3305 | 0 | 84% | 100,679.67 | F/0/0/0/0/0 |
| 2 | SA | 0.64 | 1 | 1 | 66,197 | 0 | 86% | 103,480.27 | F/0/0/0/0/0 |
| 4 | Ex | 0.30 | 1 | 1 | 22,891 | 0 | 88% | 76,806.03 | F/0/0/0/0/0 |
| 4 | Lo | 0.10 | 1 | 1 | 7448 | 0 | 88% | 73,825.45 | F/0/0/0/0/0 |
| 4 | SA | 1.06 | 1 | 1 | 79,880 | 0 | 88% | 75,628.25 | F/0/0/0/0/0 |
| 7 | Ex | 2.32 | 391 | 35 | 101,796 | 65 | 91% | 44,054.84 | F/748/6/3480/2/6 |
| 7 | Lo | 1.26 | 5080 | 44 | 46,787 | 52 | 91% | 41,297.31 | F/718/6/3180/2/6 |
| 7 | SA | 2.69 | 4219 | 55 | 100,154 | 299 | 91% | 38,742.80 | F/756/6/3360/3/6 |
| 14 | Ex | 17.16 | 1562 | 155 | 349,949 | 176 | 93% | 20,484.30 | F/3440/29/15,000/12/25 |
| 14 | Lo | 10.76 | 20,139 | 146 | 197,329 | 421 | 92% | 20,207.82 | F/2174.1/18/8941/10/18 |
| 14 | SA | 22.74 | 12,463 | 169 | 385,926 | 1204 | 92% | 17,525.92 | F/3162/26/13,120/14/27 |
| 28 | Ex | 100.25 | 9471 | 626 | 1,031,066 | 736 | 93% | 10,379.20 | F/6294.5/52/27,445/21/53 |
| 28 | Lo | 100.06 | 98,609 | 671 | 607,124 | 1487 | 92% | 7053.57 | F/12,181.9/94/55,219/43/110 |
| 28 | SA | 100.07 | 148,632 | 853 | 636,766 | 2014 | 92% | 7849.35 | F/5751/46/25,210/21/51 |
| Run | Stage 1 | Stage 2 | Sim Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H | Alg | (s) | Sim # | Imp # | Sim # | Imp # | % | #/s | Best Schedule Fitness |
| 2 | Ex | 0.09 | 1 | 1 | 9451 | 0 | 85% | 105,871.33 | F/0/0/0/0/0 |
| 2 | Lo | 0.03 | 1 | 1 | 3305 | 0 | 85% | 102,328.34 | F/0/0/0/0/0 |
| 2 | SA | 0.50 | 1 | 1 | 51,883 | 0 | 86% | 103,518.76 | F/0/0/0/0/0 |
| 4 | Ex | 0.64 | 60 | 7 | 41,941 | 24 | 90% | 65,496.59 | F/314/3/1440/0/2 |
| 4 | Lo | 0.24 | 543 | 13 | 14,419 | 18 | 88% | 61,280.86 | F/631/6/2410/2/5 |
| 4 | SA | 1.17 | 621 | 13 | 75,070 | 86 | 90% | 64,469.44 | F/362/3/1620/1/3 |
| 7 | Ex | 6.33 | 817 | 77 | 205,170 | 213 | 92% | 32,565.74 | F/1871.5/16/8115/5/16 |
| 7 | Lo | 5.84 | 15,657 | 106 | 130,506 | 426 | 92% | 25,028.43 | F/2335/20/9850/8/19 |
| 7 | SA | 10.92 | 5405 | 74 | 347,967 | 623 | 91% | 32,378.11 | F/1673/13/7730/6/13 |
| 14 | Ex | 61.23 | 10,189 | 399 | 1,023,148 | 565 | 93% | 16,875.22 | F/4568.5/39/20,085/12/37 |
| 14 | Lo | 65.15 | 126,954 | 413 | 719,669 | 933 | 92% | 12,996.77 | F/7518.7/59/35,287/22/60 |
| 14 | SA | 59.86 | 103,887 | 421 | 823,030 | 1350 | 92% | 15,489.18 | F/3775/30/17,350/11/32 |
| 28 | Ex | 100.16 | 51,659 | 1296 | 636,333 | 1061 | 92% | 6869.25 | F/12,678/100/60,180/31/104 |
| 28 | Lo | 100.00 | 586,571 | 1035 | 0 | 0 | 92% | 5865.48 | IF/Day 12, 10:39/4.28503 |
| 28 | SA | 100.02 | 355,041 | 1102 | 155,585 | 2021 | 92% | 5105.50 | F/24,339.7/192/104,997/92/240 |
| Algorithm A2 The look-ahead variant of the local search-based optimization algorithm. |
function AddPumping(s) random start time up to first tank violation if Random01() < 0.25 then else Apply(s, PumpingBetween()) FirstTankViolation(Simulate()) end if return Apply(s, PumpingBetween() end function function
OptimizeLookAhead set of all considered non-pumping-adding perturbations empty schedule random schedule, full with pumping operations Simulate() Simulate() while ¬TimeLimitExceeded() ¬FeasibleScheduleFound() do alternately 1 and 2 if Random01() < 0.85 then AddPumping() else Random(P) Apply(, p) end if Simulate() if then end if end while s, best schedule so far and its fitness while ¬TimeLimitExceeded() do if Random01() < 0.15 then AddPumping(s) else Random(P) Apply(s, p) end if Simulate() if then end if end while return s end function |
| Algorithm A3 The simulated annealing variant of the local search-based optimization algorithm. Note that the only difference from Algorithm A2 is the conditional acceptance by AcceptNext(), based on the current temperature T. |
function AddPumping(s) random start time up to first tank violation if Random01() < 0.25 then else Apply(s, PumpingBetween()) FirstTankViolation(Simulate()) end if return Apply(s, PumpingBetween() end function function
OptimizeWithSimulatedAnnealing set of all considered non-pumping-adding perturbations empty schedule random schedule, full with pumping operations Simulate() Simulate() starting temperature while ¬TimeLimitExceeded() ¬FeasibleScheduleFound() do alternately 1 and 2 if Random01() < 0.85 then AddPumping() else Random(P) Apply(, p) end if Simulate() if AcceptNext() then end if end while s, best schedule so far and its fitness starting temperature while ¬TimeLimitExceeded() do if Random01() < 0.15 then AddPumping(s) else Random(P) Apply(s, p) end if Simulate() if AcceptNext() then end if end while return s end function |
| Run | Stage 1 | Stage 2 | Sim time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H | Alg | (s) | Sim # | Imp # | Sim # | Imp # | % | #/s | Best Schedule Fitness |
| 2 | Ex | 0.10 | 4 | 2 | 7776 | 0 | 88% | 78,997.55 | F/10/0/0/0/1 |
| 2 | Lo | 0.06 | 91 | 2 | 4486 | 0 | 87% | 81,384.81 | F/10/0/0/0/1 |
| 2 | SA | 0.42 | 571 | 5 | 33,018 | 23 | 88% | 80,303.64 | F/10/0/0/0/1 |
| 4 | Ex | 1.29 | 220 | 23 | 55,264 | 125 | 91% | 43,016.70 | F/1845/9/13,250/0/7 |
| 4 | Lo | 0.75 | 468 | 16 | 32,730 | 72 | 90% | 44,195.97 | F/2233/10/16,430/0/9 |
| 4 | SA | 1.95 | 818 | 16 | 89,532 | 113 | 91% | 46,263.30 | F/1571.8/9/10,418/0/8 |
| 7 | Ex | 4.97 | 2093 | 99 | 10,5783 | 98 | 93% | 21,697.89 | F/8798/24/72,880/0/31 |
| 7 | Lo | 3.06 | 4366 | 62 | 68,061 | 201 | 92% | 23,635.80 | F/8591.8/22/72,218/0/27 |
| 7 | SA | 17.34 | 25,230 | 117 | 320,050 | 1099 | 92% | 19,919.13 | F/9328.5/27/76,385/0/34 |
| 14 | Ex | 100.15 | 11,935 | 421 | 764,621 | 443 | 93% | 7753.96 | F/38,825/98/327,650/0/116 |
| 14 | Lo | 100.03 | 188,693 | 353 | 409,349 | 888 | 93% | 5978.89 | F/63,663.5/132/553,035/0/176 |
| 14 | SA | 100.06 | 140,346 | 446 | 600,594 | 1019 | 93% | 7405.72 | F/38,184.1/98/319,241/0/136 |
| 28 | Ex | 100.06 | 40,501 | 1270 | 288,377 | 678 | 95% | 3286.73 | F/107,162/220/934,420/0/272 |
| 28 | Lo | 100.00 | 394,815 | 909 | 0 | 0 | 93% | 3947.99 | IF/Day 13, 19:58/9.96707 |
| 28 | SA | 100.00 | 428,493 | 808 | 0 | 0 | 93% | 4284.74 | IF/Day 17, 14:58/2.14598 |
Appendix C. Nomenclature
| H | Time horizon for scheduling. |
| Flow rate function, cumulated volume change after t time elapsed. | |
| Volume of the last, shrinking plug of a pipe, during a pumping operation. | |
| Network-wide constant flow rate. | |
| Constant flow rate, depending on source site and product pumped. | |
| Threshold volume used by the simulation algorithm for ignoring very small flows between last plug event and pumping end. | |
| Globally earliest tank violation time. Candidate for first-stage objective. | |
| Time-adjusted sum of first tank violation times. Candidate for first-stage objective. | |
| Time-adjusted sum of violation volumes. Candidate for first-stage objective. | |
| First time point where tank h was filled above its maximum capacity. | |
| First time point where tank h was depleted below its minimum capacity (zero). | |
| Tank level, volume of product in tank h at time point t. | |
| Maximum capacity of tank h. | |
| Minimum capacity of tank h (zero). | |
| Constant rate used for time-adjusting violations. | |
| Number of interfaces during the time horizon. | |
| Total duration of interfaces existing in the time horizon, in minutes. | |
| Number of flow reversals or backtransports per pipe during the time horizon. | |
| Number of pumping operations during the time horizon. | |
| Quality measure for the schedule. Used as second-stage objective. | |
| L | Time slot length for generating perturbations. |
| Intervals for generating perturbations, based on time slot length L. | |
| T | Temperature used by the SA variant. |
| Objective before perturbation (in the context of the SA variant). | |
| Objective after perturbation (in the context of the SA variant). |
References
- Mostafaei, H.; Alipouri, Y.; Zadahmad, M. A mathematical model for scheduling of real-world tree-structured multi-product pipeline system. Math. Methods Oper. Res. 2015, 81, 53–81. [Google Scholar] [CrossRef]
- Jittamai, P. Analysis of Oil-Pipeline Distribution of Multiple Products Subject to Delivery Time-Windows. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2004. [Google Scholar]
- Sidki, M.; Tchernev, N.; Féniès, P.; Ren, L.; Elfirdoussi, S. Multiproduct pipeline scheduling: A comprehensive bibliometric analysis and a systematic literature review. Comput. Chem. Eng. 2025, 192, 108911. [Google Scholar] [CrossRef]
- Csontos, B.; Halász, L.; Heckl, I. Improved event-driven simulation method for fuel transport in a mesh-like pipeline network. Comput. Chem. Eng. 2022, 168, 108066. [Google Scholar] [CrossRef]
- Polli, H.L.; Magatão, L.; Magatão, S.N.B.; Neves, F.J.; Arruda, L.V.R. Collaborative Approach Based on Heuristic Algorithm and MILP Model To Assignment and Sequencing of Oil Derivative Batches in Pipeline Networks. Ind. Eng. Chem. Res. 2017, 56, 2492–2514. [Google Scholar] [CrossRef]
- Maruyama Mori, F.; Lüders, R.; Valéria Ramos de Arruda, L.; Yamamoto, L.; Vicente Bonacin, M.; Luis Polli, H.; Correia Aires, M.; Fernando de Jesus Bernardo, L. Simulating the operational scheduling of a realworld pipeline network. Comput. Aided Chem. Eng. 2007, 24, 691–696. [Google Scholar] [CrossRef]
- Magatão, L.; Arruda, L.; Neves, F. A mixed integer programming approach for scheduling commodities in a pipeline. Comput. Chem. Eng. 2004, 28, 171–185. [Google Scholar] [CrossRef]
- Cafaro, D.C.; Cerdá, J. Optimal scheduling of multiproduct pipeline systems using a non-discrete MILP formulation. Comput. Chem. Eng. 2004, 28, 2053–2068. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, Y.; Liao, Q.; Wu, M.; Yan, X. A hybrid computational approach for detailed scheduling of products in a pipeline with multiple pump stations. Energy 2017, 119, 612–628. [Google Scholar] [CrossRef]
- Cafaro, D.C.; Cerdá, J. Operational scheduling of refined products pipeline networks with simultaneous batch injections. Comput. Chem. Eng. 2010, 34, 1687–1704. [Google Scholar] [CrossRef]
- Cafaro, D.C.; Cerdá, J. A Rigorous Mathematical Formulation for the Scheduling of Tree-Structure Pipeline Networks. Ind. Eng. Chem. Res. 2011, 50, 5064–5085. [Google Scholar] [CrossRef]
- Boschetto, S.N.; Magatão, L.; Brondani, W.M.; Neves, F., Jr.; Arruda, L.V.R.; Barbosa-Póvoa, A.P.F.D.; Relvas, S. An Operational Scheduling Model to Product Distribution through a Pipeline Network. Ind. Eng. Chem. Res. 2010, 49, 5661–5682. [Google Scholar] [CrossRef]
- Liao, Q.; Castro, P.M.; Liang, Y.; Zhang, H. New batch-centric model for detailed scheduling and inventory management of mesh pipeline networks. Comput. Chem. Eng. 2019, 130, 106568. [Google Scholar] [CrossRef]
- Chen, H.; Wu, C.; Zuo, L.; Diao, F.; Wang, L.; Wang, D.; Song, B. Optimization of Detailed Schedule for a Multiproduct Pipeline Using a Simulated Annealing Algorithm and Heuristic Rules. Ind. Eng. Chem. Res. 2017, 56, 5092–5106. [Google Scholar] [CrossRef]
- Mostafaei, H.; Castro, P.M.; Relvas, S.; Harjunkoski, I. A holistic MILP model for scheduling and inventory management of a multiproduct oil distribution system. Omega 2021, 98, 102110. [Google Scholar] [CrossRef]
- Dimas, D.; Murata, V.V.; Neiro, S.M.; Relvas, S.; Barbosa-Póvoa, A.P. Multiproduct pipeline scheduling integrating for inbound and outbound inventory management. Comput. Chem. Eng. 2018, 115, 377–396. [Google Scholar] [CrossRef]
- Chen, H.; Zuo, L.; Wu, C.; Li, Q. An MILP formulation for optimizing detailed schedules of a multiproduct pipeline network. Transp. Res. Part E: Logist. Transp. Rev. 2019, 123, 142–164. [Google Scholar] [CrossRef]
- Cafaro, V.G.; Cafaro, D.C.; Méndez, C.A.; Cerdá, J. Oil-derivatives pipeline logistics using discrete-event simulation. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010; pp. 2101–2113. [Google Scholar] [CrossRef]
- Liao, Q.; Zhang, H.; Xu, N.; Liang, Y.; Wang, J. A MILP model based on flowrate database for detailed scheduling of a multi-product pipeline with multiple pump stations. Comput. Chem. Eng. 2018, 117, 63–81. [Google Scholar] [CrossRef]
- Liao, Q.; Liang, Y.; Xu, N.; Zhang, H.; Wang, J.; Zhou, X. An MILP approach for detailed scheduling of multi-product pipeline in pressure control mode. Chem. Eng. Res. Des. 2018, 136, 620–637. [Google Scholar] [CrossRef]
- García-Sánchez, Á.; Arreche, L.M.; Ortega-Mier, M. Combining Simulation and Tabu Search for Oil-derivatives Pipeline Scheduling. In Metaheuristics for Scheduling in Industrial and Manufacturing Applications; Xhafa, F., Abraham, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 301–325. [Google Scholar] [CrossRef]
- Castro, P.M.; Mostafaei, H. Batch-centric scheduling formulation for treelike pipeline systems with forbidden product sequences. Comput. Chem. Eng. 2019, 122, 2–18. [Google Scholar] [CrossRef]
- Haoran, Z.; Yongtu, L.; Qi, L.; Yun, S.; Xiaohan, Y. A self-learning approach for optimal detailed scheduling of multi-product pipeline. J. Comput. Appl. Math. 2018, 327, 41–63. [Google Scholar] [CrossRef]
- Rejowski, R.; Pinto, J. Scheduling of a multiproduct pipeline system. Comput. Chem. Eng. 2003, 27, 1229–1246. [Google Scholar] [CrossRef]
- Rejowski, R.; Pinto, J. Efficient MILP formulations and valid cuts for multiproduct pipeline scheduling. Comput. Chem. Eng. 2004, 28, 1511–1528. [Google Scholar] [CrossRef]
- Chen, H.; Zuo, L.; Wu, C.; Wang, L.; Diao, F.; Chen, J.; Huang, Y. Optimizing detailed schedules of a multiproduct pipeline by a monolithic MILP formulation. J. Pet. Sci. Eng. 2017, 159, 148–163. [Google Scholar] [CrossRef]
- Magatão, S.N.B.; Magatão, L.; Luis Polli, H.; Neves, F.J.; de Arruda, L.V.R.; Relvas, S.; Barbosa-Póvoa, A.P.F.D. Planning and Sequencing Product Distribution in a Real-World Pipeline Network: An MILP Decomposition Approach. Ind. Eng. Chem. Res. 2012, 51, 4591–4609. [Google Scholar] [CrossRef]
- Magatão, L.; Arruda, L.V.R.; Neves, F., Jr. A combined CLP-MILP approach for scheduling commodities in a pipeline. J. Sched. 2011, 14, 57–87. [Google Scholar] [CrossRef]
- Crane, D.S.; Wainwright, R.L.; Schoenefeld, D.A. Scheduling of multi-product fungible liquid pipelines using genetic algorithms. In Proceedings of the 1999 ACM Symposium on Applied Computing, San Antonio, TX, USA, 28 February–2 March 1999. [Google Scholar]
- de la Cruz García, J.; Risco Martín, J.; Herrán González, A.; Fernández Blanco, P. Hybrid heuristic and mathematical programming in oil pipelines networks. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Portland, OR, USA, 19–23 June 2004; Volume 2, pp. 1479–1486. [Google Scholar] [CrossRef]
- Ribas, P.C.; Yamamoto, L.; Polli, H.L.; Arruda, L.; Neves, F., Jr. A micro-genetic algorithm for multi-objective scheduling of a real world pipeline network. Eng. Appl. Artif. Intell. 2013, 26, 302–313. [Google Scholar] [CrossRef]
- Sasikumar, M.; Ravi Prakash, P.; Patil, S.M.; Ramani, S. PIPES: A heuristic search model for pipeline schedule generation1Revised version of the article originally published in Knowledge-based Computer Systems: Research and Applications. (Eds K.S.R. Anjaneyulu, M. Sasikumar and S. Ramani) Narosa Publishing House, New Delhi, 1997.1. Knowl.-Based Syst. 1997, 10, 169–175. [Google Scholar] [CrossRef]
- Csontos, B.; Halász, L.; Heckl, I. Event-driven simulation method for fuel transport in a mesh-like pipeline network. Comput. Chem. Eng. 2022, 157, 107611. [Google Scholar] [CrossRef]
- Strachotová, D.; Dyntar, J. Support of Scheduling of Multiproduct Pipeline Systems Using Simulation in Witness. Int. J. Simul. Model. 2021, 20, 536–546. [Google Scholar] [CrossRef]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
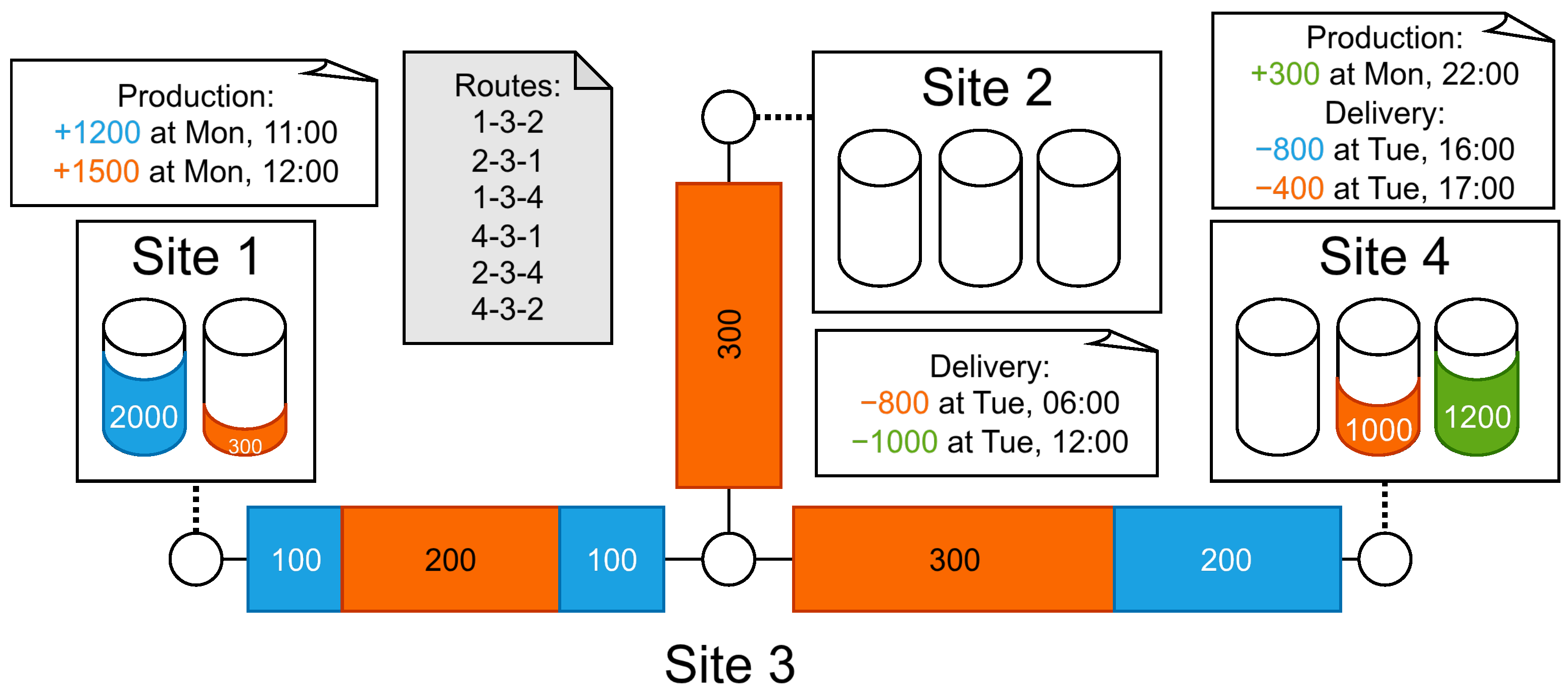
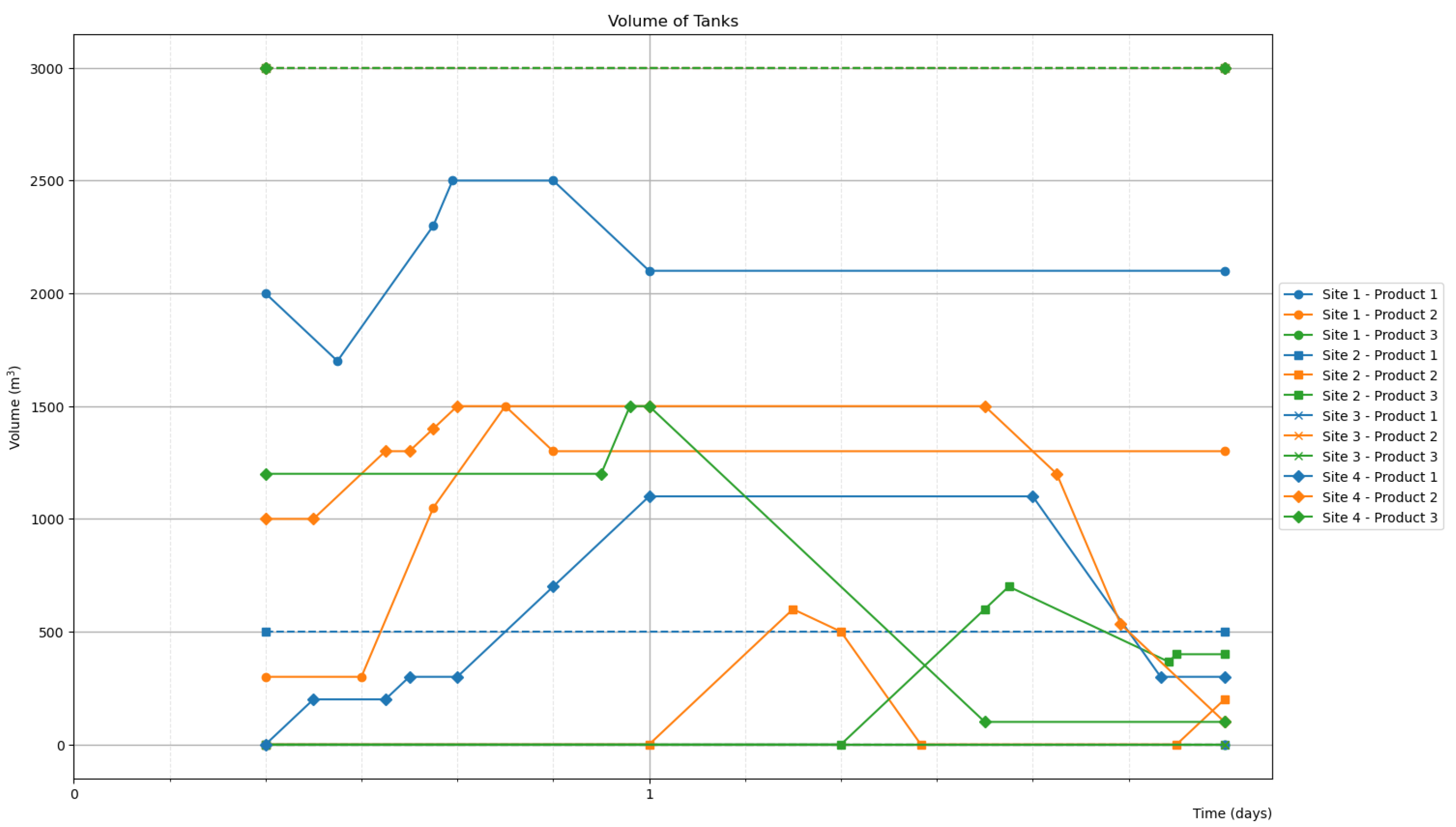
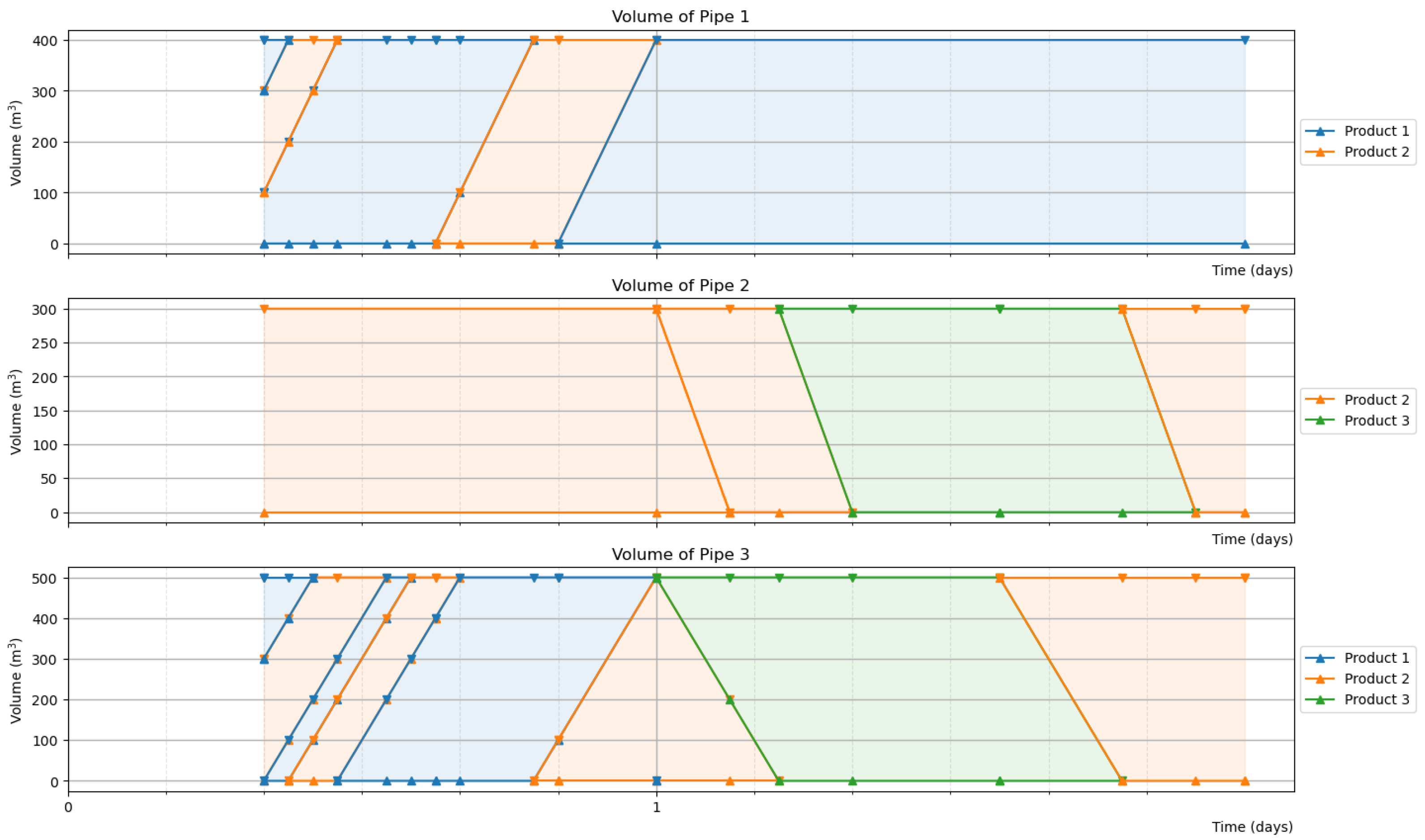
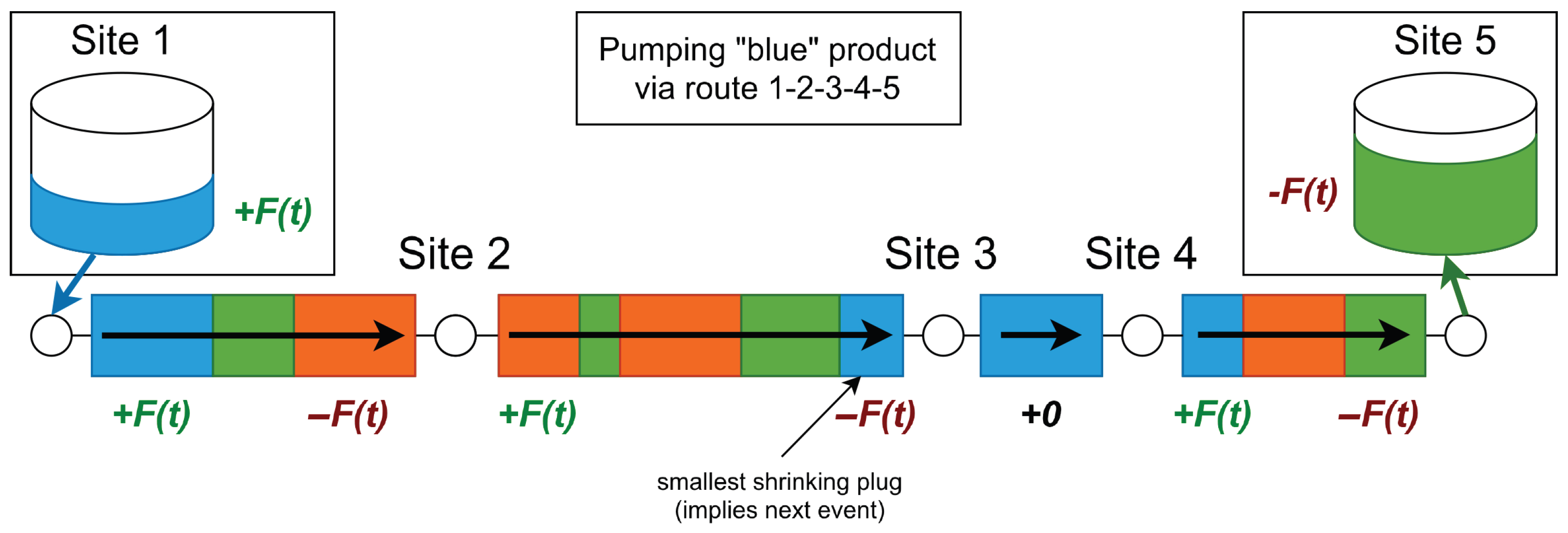


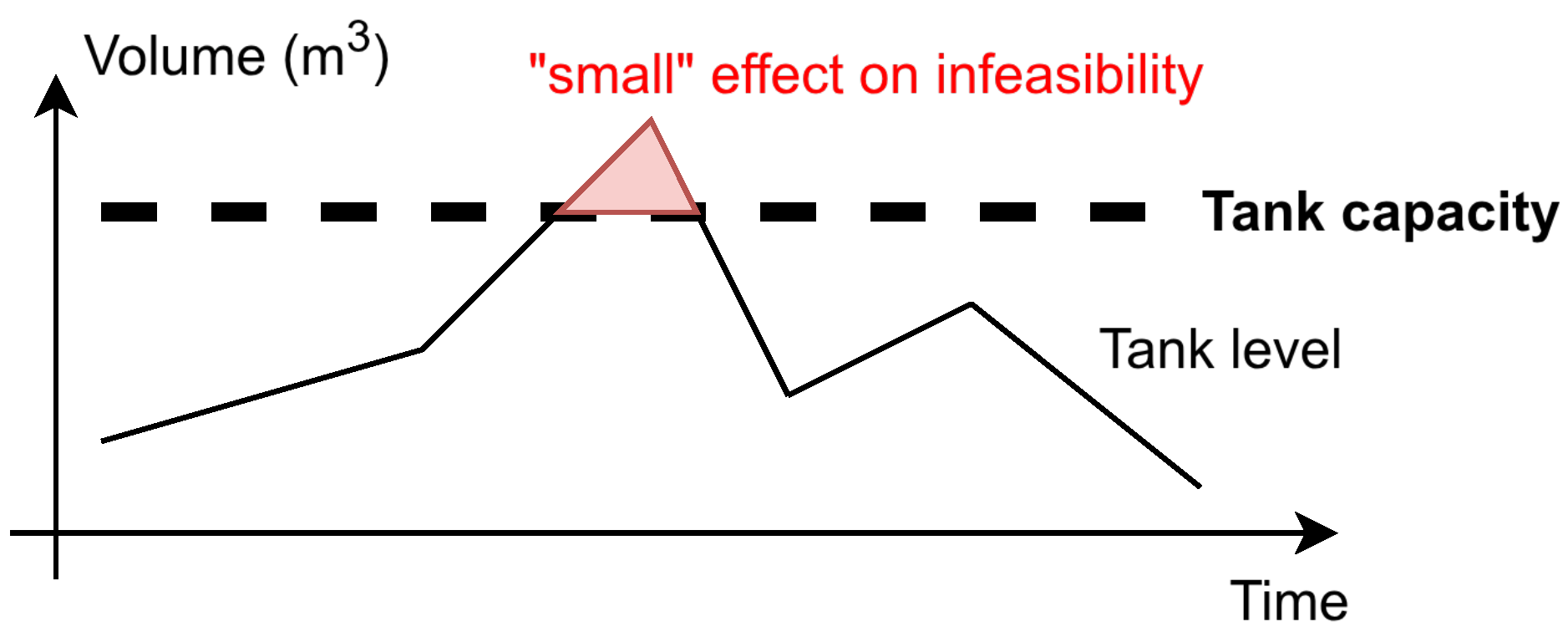




| Start Time | Site | Product | Amount | In/Out |
|---|---|---|---|---|
| Day 1, 11:00 | Site 1 | Product 1 (blue) | 1200 | Inflow |
| Day 1, 12:00 | Site 1 | Product 2 (orange) | 1500 | Inflow |
| Day 2, 06:00 | Site 2 | Product 2 (orange) | 800 | Outflow |
| Day 2, 12:00 | Site 2 | Product 3 (green) | 1000 | Outflow |
| Day 1, 22:00 | Site 4 | Product 3 (green) | 300 | Inflow |
| Day 2, 16:00 | Site 4 | Product 1 (blue) | 800 | Outflow |
| Day 2, 17:00 | Site 4 | Product 2 (orange) | 400 | Outflow |
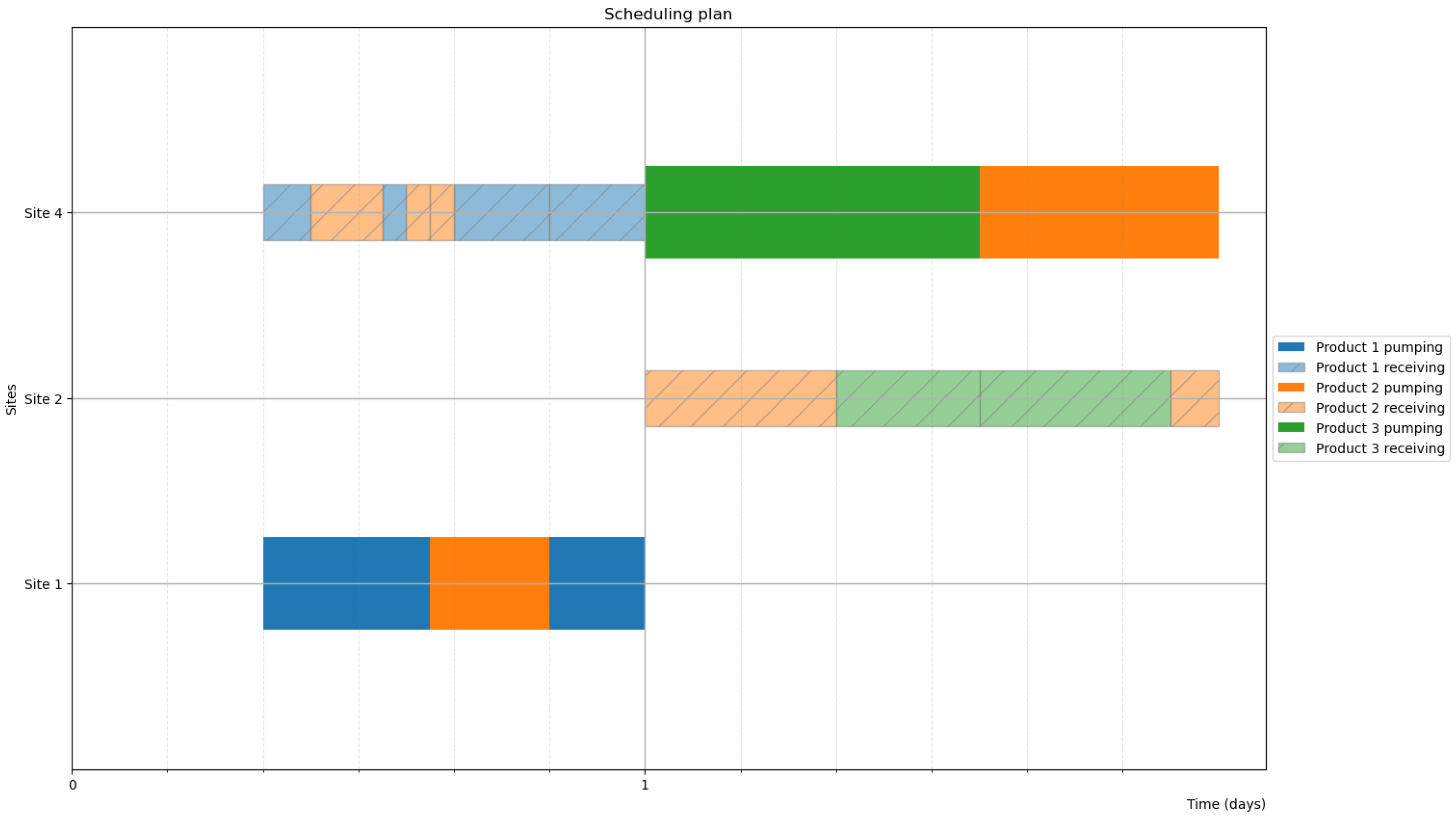
| Start Time | End Time | Route | Product |
|---|---|---|---|
| Day 1, 08:00 | Day 1, 15:00 | 1-3-4 | 1 (blue) |
| Day 1, 15:00 | Day 1, 20:00 | 1-3-4 | 2 (orange) |
| Day 1, 20:00 | Day 2, 00:00 | 1-3-4 | 1 (blue) |
| Day 2, 00:00 | Day 2, 14:00 | 4-3-2 | 3 (green) |
| Day 2, 14:00 | Day 2, 00:00 | 4-3-2 | 2 (orange) |
| Event Type | Tank FR Increase | Tank FR Decrease | Plug FR Change | Interface Change | Next Event(s) Possibly Generated |
|---|---|---|---|---|---|
| Inflow start | Yes | No | No | No | Inflow end, start |
| Inflow end | No | Yes | No | No | Inflow start |
| Outflow start | No | Yes | No | No | Outflow end, start |
| Outflow end | Yes | No | No | No | Outflow start |
| Pumping start | Yes | Yes | Usually | Possible | Plug event, pumping end |
| Plug event | Possible | Possible | Yes | Yes | Plug event, pumping end |
| Pumping end | Yes | Yes | Usually | Possible | Pumping start |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Éles, A.; Heckl, I. Efficient Simulation Algorithm and Heuristic Local Optimization Approach for Multiproduct Pipeline Networks. Logistics 2025, 9, 114. https://doi.org/10.3390/logistics9030114
Éles A, Heckl I. Efficient Simulation Algorithm and Heuristic Local Optimization Approach for Multiproduct Pipeline Networks. Logistics. 2025; 9(3):114. https://doi.org/10.3390/logistics9030114
Chicago/Turabian StyleÉles, András, and István Heckl. 2025. "Efficient Simulation Algorithm and Heuristic Local Optimization Approach for Multiproduct Pipeline Networks" Logistics 9, no. 3: 114. https://doi.org/10.3390/logistics9030114
APA StyleÉles, A., & Heckl, I. (2025). Efficient Simulation Algorithm and Heuristic Local Optimization Approach for Multiproduct Pipeline Networks. Logistics, 9(3), 114. https://doi.org/10.3390/logistics9030114






