1. Introduction
Globalization and the societal shift toward individualization pose significant challenges for logistics, particularly intralogistics. The growing demand for customized products, delivered at specific times and locations, has led to increased transport volumes and an atomization of shipments [
1]. In response to rising customer expectations and competitive pressures, intralogistics has evolved into a value-adding process [
2]. Purchasing decisions are increasingly influenced by immediate availability, and intralogistics enables the efficient fulfillment of diverse, individualized customer demands with minimal inventory. Shorter product life cycles further demand rapid and flexible responses to change [
2]. Traditional centrally organized processes struggle to meet these requirements, necessitating modular structures and decentralized decision-making [
1,
2]. Agent-based systems offer a promising approach, consisting of autonomous software entities capable of flexibly achieving specific goals [
3]. The paradigm of the agent (or software agent) has been proposed as a means of modeling and controlling complex systems [
4]. An agent is “[…] a computer system, situated in some environment, that is capable of flexible autonomous action in order to meet its design objectives” [
5]. Agents are usually attributed to properties like autonomy, reactivity, proactivity, deliberativeness, and communicative abilities and thus enable self-organization of systems and Industry 4.0 applications [
6]. These systems allow for the decomposition of complex problems into manageable modules that can be flexibly replaced as needed, enhancing resilience through decentralized control and eliminating single points of failure [
7,
8].
Automated Guided Vehicles (AGVs), a key component of intralogistics, are still predominantly centrally controlled [
9]. This limits flexibility, complicates system adjustments and slows system recovery after disruptions [
10]. Furthermore, solving the problem of collision avoidance optimally by a centralized solver brings with it the problem of limited scalability, while heterarchical systems also exhibit problems with exceeding numbers of required messages [
11]. Adapting AGVs to modern intralogistics demands a shift to decentralized control structures [
10] while providing scalable solutions for large systems. For some applications, AGVs are increasingly being replaced by Autonomous Mobile Robots (AMRs) [
12]. The primary difference between AMR and AGV lies in their navigation capabilities. AMRs can move autonomously within their environment without relying on predefined paths, such as guidelines or centralized path planning. Additionally, AMRs require less installation effort since they navigate using their own sensors and do not need guidelines or centralized control systems. However, Uttendorf [
12] highlights that the distinction between AMRs and AGVs is becoming increasingly blurred, as modern AGVs may also feature automatic path planning, free navigation, and numerous additional sensors. Due to the decreasing differentiation between AMRs and AGVs noted by Uttendorf [
12], this work does not enforce a strict separation between the terms. Instead, the term AGV is used broadly to include AMRs. This trend, however, of blurring lines between the paradigms also enables new concepts and ideas that utilize the gray area between centrally controlled AGVs and fully autonomous AMRs.
A major challenge in controlling AGVs is collision avoidance between vehicles [
13]. Areas prone to vehicle conflicts are referred to in this work as interaction zones. The problem of collision avoidance and, in a broader sense, conflict resolution between the vehicles is also relevant for systems that already exhibit decentralized control architectures. As Purwin et al. [
14] point out, many common approaches are based on reactive heuristics, often without cooperation between the vehicles. Such architectures can lead to sub-optimal behavior due to congestion and the lack of prioritization between the vehicles. In these applications it remains to be seen which degree of decentralization results in the optimal performance depending on the system context.
This work aims to determine the optimal degree of decentralization by developing an agent-based control system for interaction zones, addressing the need for flexibility and prioritization. The degree of decentralization, i.e., the entities and locations where decisions should take place can range from fully centrally deciding architectures, with known disadvantages in terms of reactivity, flexibility, scalability, and robustness, to fully decentralized systems where everything is decided on the vehicles.
This work investigates the benefits of different degrees of decentralization and cooperation by providing the two concepts of hierarchical interaction zone management and full distribution of coordination decisions. These alternative agent-based concepts are compared to (a) a simple heuristic rule (First Come, First Served (FCFS)) with no cooperation and (b) a centrally optimizing Mixed-Integer Linear Program (MILP) model.
Thus, the contributions of this paper are as follows:
Provision of two agent-based architectures, differing in level of decentralization.
Comparison of the different architectures in terms of solution quality and scalability.
Comparison of the agent-based approaches with a simple heuristic and a central optimization approach.
The results can be used by practitioners to further determine the optimal degree of decentralization for their specific systems.
Section 2 introduces the fundamentals of intralogistics and control tasks in AGVs, focusing on collision avoidance. It concludes with an overview of agent systems and the problem of collision-free control in interaction zones.
Section 4 reviews the state of the art in collision avoidance for automated vehicles, identifies gaps in research, and evaluates approaches based on the requirements of modern intralogistics. In
Section 5, the 2DECS methodology is used to design hierarchical and heterarchical agent systems, including control processes and algorithms for conflict detection and resolution. The developed systems are tested in a simulation study, detailed in
Section 6, which also explains the design, execution, and evaluation of the simulation. The results are also discussed in this section. The work concludes with a summary and an outlook on future research directions in
Section 7.
2. Fundamentals
After briefly providing some background on AGV control approaches, this section describes the problem context in more detail and postulates the requirements for a suitable control method.
The control of AMRs and AGVs involves several key tasks, which can be categorized as follows:
Task assignment: assigning tasks to individual AGVs, often described as the Multi-Robot Task Allocation problem [
10,
13].
Navigation: ensuring vehicles can navigate their environment effectively [
15].
Positioning of idle vehicles: optimally placing idle vehicles to minimize response times for future tasks [
10].
Path/route planning: calculating the shortest path to a given destination while minimizing costs such as time or energy [
13].
Motion control/route execution: ensuring safe route execution by avoiding collisions and deadlocks [
13,
16]. According to [
17], two types of collisions can be distinguished. First, following collisions must be prevented. These occur when an AGV collides with another AGV ahead of it on the same route. Second, lateral collisions occur when two AGVs approach the same point from different directions at the same time.
Vehicle management: monitoring vehicle status, including battery levels and maintenance needs [
13].
This work focuses on collision avoidance, i.e., motion control and route execution as these are critical for responding to operational changes and ensuring system flexibility. Efficient motion control allows dynamic responses to unexpected obstacles and altered requirements, ensuring smooth operations and adaptability. Collision avoidance for AGVs occurs on multiple levels. Within the classification of control previously presented, it can be associated with motion planning or route execution. However, collision avoidance is not limited to the control level. It can also be addressed during the design of a new system. According to [
18,
19], collision avoidance can be broadly divided into three areas: design, zone control, and control. As design is not the focus of this paper, the interested reader is refferred to literature reviews by Vis [
19] and Le-Anh and De Koster [
20].
Zone control is widely used in traditional strategies [
21]. In its static form, the network is divided into fixed, non-overlapping zones, with only one vehicle allowed per zone, ensuring collision prevention without influencing route planning or execution [
21]. Dynamic zone control improves on this by adapting zone boundaries to system load. Ho [
21] introduced a dynamic approach for loop-based systems, aiming to balance system utilization. Ho and Liao [
18] extended this method to all systems and demonstrated its advantages over static zone control in throughput and inventory efficiency. In their model, each vehicle has its own adjustable zone, requiring transfer stations for handovers between zones. A recent method by Lee and Park [
22] incorporates vehicle geometry into zone division, crucial for tight layouts. Their algorithm also prevents deadlocks, as shown in simulation experiments.
Ho and Liao [
18] and Schmidt et al. [
23] classify collision avoidance approaches on the control level into two main categories. The first category includes planning-based approaches, where vehicle routes are planned collision-free from the outset, combining path and motion planning. The second category, reactive approaches, separates route planning from motion execution, addressing collisions only during execution [
23].
Planning-based approaches are further divided: one assumes all tasks are known in advance, allowing optimization-based solutions [
21,
24,
25], while the other addresses systems with dynamic task arrivals, often linked to the multi-agent path finding problem [
26,
27]. Hybrid methods combining planning and reactive approaches also exist, such as [
28], where conflicts are resolved reactively if planning fails.
Reactive approaches are categorized into cooperative and non-cooperative types [
14]. Non-cooperative methods rely solely on local sensor data, requiring worst-case scenario planning due to the lack of communication [
14]. Cooperative methods involve communication or negotiation between vehicles, either hierarchically, where specific vehicles or managers have decision authority, or heterarchically, where vehicles are equal and coordinate autonomously. For such approaches, the paradigm of software agents is frequently used. Multi-Agent Systems (MASs), originating from distributed artificial intelligence, have become increasingly relevant in software engineering [
7]. MASs consist of autonomous, interactive agents pursuing specific goals [
29]. Agents are characterized by autonomy, social interaction, reactivity, and proactivity [
30]. Agent systems excel in dynamic environments, enabling modular, low-risk adaptations and distributed information handling [
3]. They simplify complex problems by dividing them into manageable, reusable parts [
3].
3. Problem Description
To prevent collisions effectively, it may suffice to focus on intersections and manage them to avoid conflicts, provided the system’s paths are designed such that conflicts only occur at these points [
31]. This requires that AGVs cannot overtake one another, as this would introduce additional collision risks. Since conflict-prone areas are not limited to intersections, they are referred to here as interaction zones. This term includes intersections but also encompasses any areas where conflicts may arise and require management.
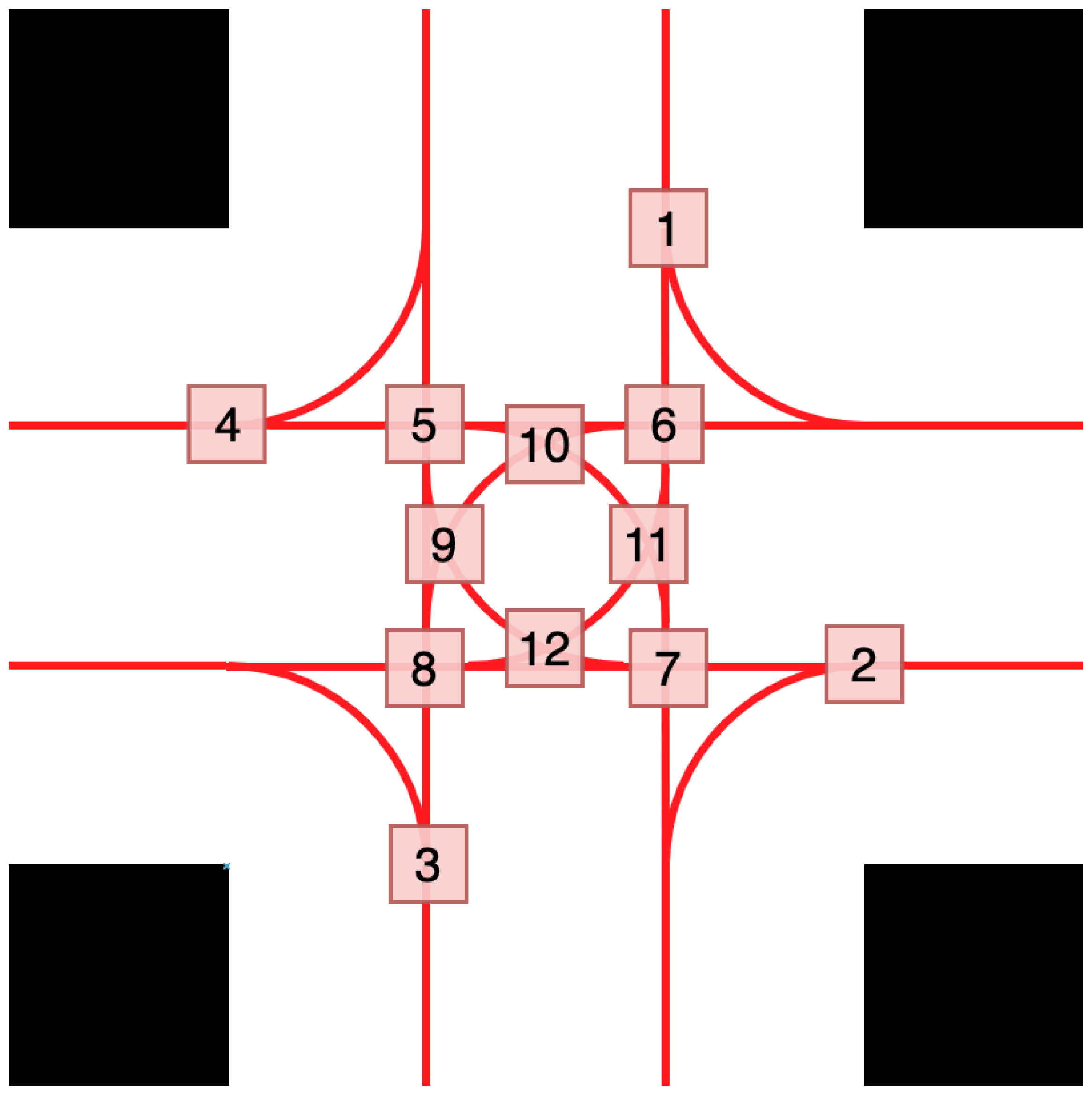
The collision avoidance problem is exemplified by a four-way omnidirectional intersection (
Figure 1), with one lane per direction, enabling vehicles to pass in opposite directions without collisions. Vehicles are assumed to move freely but follow predefined routes in the intersection to simplify the control task [
32]. This assumption aligns with real-world logistics centers or production environments, where structural layouts naturally restrict vehicle paths.
Each vehicle entering the intersection can move straight, turn left, or turn right, resulting in 12 distinct routes. These routes create 12 conflict points, where collisions may occur, as shown in
Figure 1.
The aim of this work is to develop a method that ensures efficient collision avoidance at the intersection while minimizing tardiness and waiting times. The priority of a task, ranging from one (low) to ten (high), is considered in the control system: tasks with higher priority should experience minimal delays. Collision avoidance is the primary focus and must be guaranteed.
The following assumptions are made for the considered system:
The number of vehicles n is known.
Each vehicle has the ability to communicate with other vehicles and, if applicable, with the infrastructure.
Task assignment to the vehicles is completed prior to collision avoidance and is not part of this work.
Each vehicle conducts its path planning decentrally, has knowledge of its surroundings, and detects obstacles and preceding vehicles using sensors.
Vehicles adhere to the specified maximum speed and maintain a safe distance from the vehicle ahead.
The resulting method should enable safe and priority-oriented route execution to prevent collisions, minimize delays, and thereby maximize the efficiency of the transport system.
3.1. Mathematical Model of the Collision Avoidance Problem
The sets and variables displayed in
Table 1 as well as the following equations describe the collision avoidance problem for AGVs in interaction areas. The model includes vehicle dynamics, collision prevention, priority handling, and safe distance constraints.
Minimize the weighted total travel time based on priority:
Vehicle dynamics ensure realistic movement behavior:
Collision avoidance constraints ensure no two vehicles occupy the same conflict point:
Safe following distances prevent collisions:
Entry and exit conditions ensure vehicles reach their destinations:
3.2. Requirements
To successfully solve the problem previously described, the control system must meet various requirements. These requirements are divided into three mandatory (M) and seven optional (O) criteria. While mandatory criteria ensure the functionality of collision-free control within interaction areas, optional criteria aim to enable optimal solutions and enhance the efficiency of complex systems.
A scoring system is derived to evaluate the suitability of different control approaches. Each requirement is scored on fulfillment: full compliance receives one point, partial compliance may receive fractional points, and non-compliance is scored as zero. An approach failing to meet any mandatory criterion is considered unsuitable. The total score is obtained by summing points across all requirements.
3.2.1. Mandatory Requirements
- M1
Collision-Free Operation
The primary requirement is that the control system reliably prevents collisions. Full collision avoidance earns 1 point, partial prevention earns 0.5 points, and failure to reliably prevent collisions scores 0.
- M2
Support for Interaction Areas
The control must be capable of managing an intersection, as previously described. Systems treating the intersection superficially as a network node score 0.5 points. Managing a similar intersection with fewer than four directions scores 0.75 points, while full compliance earns 1 point.
- M3
Online Capability
Control systems must respond to real-time changes within a reasonable timeframe, such as new task assignments. Approaches requiring complete prior knowledge of tasks and routes are scored zero. Fully online-capable systems earn one point.
3.2.2. Optional Requirements
- O1
Decentralization
Decentralized control is preferred due to its robustness and scalability. Hierarchically decentralized approaches score 0.5 points, while fully heterarchical systems with no single point of failure earn 1 point.
- O2
Cooperation
Communication between vehicles is essential. Systems enabling information exchange in general score 0.5 points, while those supporting cooperative behavior earn 1 point.
- O3
Adherence to Target Times
Systems aiming to minimize delays alongside collision prevention score 1 point, and systems ignoring delays score 0.
- O4
Number of Vehicles in Conflict Areas
Systems allowing multiple vehicles in the intersection based on actual conflicts earn 1 point. Static limits above one vehicle score 0.5 points, while single-vehicle restrictions score 0.
- O5
Task Prioritization
Systems distinguishing between normal and high-priority tasks score 0.5 points. Finer prioritization earns 1 point.
- O6
Autonomy
Fully autonomous systems reacting adaptively to different scenarios score 1 point. Static responses earn 0.5 points, while systems lacking autonomy score 0.
- O7
System Complexity
Systems are evaluated on:
Handling the standard scenario of four vehicles earns 0.25 points, with no fixed vehicle limits earning an additional 0.25 points.
Accounting for heterogeneous fleets scores 0.25 points.
Managing offline vehicles, such as manually operated forklifts, earns 0.25 points.
4. Literature Review
This section first briefly describes the applied research methodology and afterward describes the findings separated into non-cooperative and cooperative approaches. Finally, the research gap is explained.
4.1. Methodology
The control of autonomous vehicles at interaction areas, particularly intersections, has gained increasing attention in recent years, partly due to the advancements in autonomous driving. This section presents the works deemed most relevant by the authors. A systematic literature review was not conducted. Instead, various literature reviews, such as those by [
10,
13,
19,
33], served as a starting point. Many sources cited in this section are directly drawn from these reviews.
The selected approaches focus on intersection control, particularly collision avoidance, as described in the problem statement. Additionally, various approaches were included to provide a broad overview. Beyond the literature identified in reviews, targeted searches were conducted in Google Scholar, Scopus, and IEEE databases to address gaps. For instance, market-based approaches, mentioned by De Ryck et al. [
13], were not detailed in the reviews, necessitating further exploration.
To highlight the diverse application areas of intersection control approaches, two different search strings were created for Scopus. The first search string focused on logistics and intralogistics:
((‘Automated Guided Vehicle*’ OR ‘Autonomous Mobile Robot*’) AND ‘Intersection’ AND (‘Collision’ W/3 ‘Avoid*’) AND (‘Decentral*’ OR ‘Distributed’))
Keywords such as ‘Automated Guided Vehicle*’ and ‘Autonomous Mobile Robot*’, appearing in the title, abstract, or keywords, ensured a logistical context. The wildcard (*) allowed for variations in word endings. This search yielded five results [
34,
35,
36,
37,
38], all addressing collision-free vehicle control at intersections, making them relevant to this work.
A significant application area for intersection control lies in road traffic, where terms like AMR or AGV are not used. Instead, vehicles are referred to as Connected Automated Vehicles (CAVs) or ‘Autonomous Vehicles’, and terms like ‘Autonomous Driving’ are common. Thus, a second search string was tailored for road traffic applications:
(((‘connect*’ W/3 ‘automated’ W/3 ‘vehicle*’) OR (‘Autonomous’ W/3 ‘vehicle*’) OR (‘autonomous’ W/3 ‘driving’)) AND ‘Intersection’ AND (‘Collision’ W/3 ‘Avoid*’) AND (‘Decentral*’ OR ‘Distributed’))
This search yielded 52 results, approximately ten times more than the logistics-focused search string. While neither search captured all relevant literature in their respective domains, the results emphasize that most intersection control approaches originate from road traffic applications. As [
36] noted, many road-traffic approaches can be adapted for intralogistics.
A comprehensive analysis of road-traffic literature is beyond the scope of this work. The following selection provides an overview of various approaches.
4.2. Non-Cooperative Approaches
This section introduces methods where vehicles do not communicate with each other and adapt their routes reactively. In these approaches, vehicles have no knowledge of the future paths of others, relying solely on their sensors to detect the current state of surrounding vehicles. Non-cooperative approaches include reactive evasive methods, predictive methods that estimate others’ routes, and rule-based approaches inspired by traffic regulations.
4.2.1. Reactive Evasive Methods
One well-known approach is the virtual force field method, introduced by [
39], which uses virtual force fields for local obstacle avoidance. Vehicles detect obstacles via sensors and assign a “certainty” value to grid cells representing the environment. These cells exert virtual repulsive forces on the vehicle, while an attractive force from the target directs its movement. The method, initially designed for static obstacles, was later extended by [
40] to account for moving obstacles, including vehicles. A related method utilizes virtual force histograms, developed by [
41], which improves virtual force fields by constructing a polar histogram around the vehicle to identify viable directions. Zhu et al. [
42] adapted virtual force histograms for mobile obstacles, reducing computational complexity and incorporating collision risk in direction selection. Another approach is Optimal Reciprocal Collision Avoidance (ORCA) by [
43], which guarantees collision avoidance for a large number of vehicles without requiring communication. Vehicles calculate permissible velocity spaces based on nearby robots and select optimal speeds using linear optimization. Alonso-Mora et al. [
44] extended ORCAs to handle non-holonomic vehicles with movement constraints. These approaches are effective for obstacle avoidance but fail in structured coordination, making it unsuitable for complex intersections as they do not allow cooperation, prioritization and are purely based on immediate sensor data.
4.2.2. Predictive Methods
Predictive methods forecast others’ movements to avoid collisions. Missura and Bennewitz [
45] extended the dynamic window approach [
46] by integrating dynamic obstacles into its velocity-based framework. Unlike ORCAs, this approach does not assume uniform control algorithms for all vehicles. Obstacles are modeled as polygons, and collision risks are calculated over a defined time horizon. The optimized velocity minimizes collision risk and aligns with the target direction. Chen et al. [
47] proposed a DRL-based approach for scenarios without reliable communication. Vehicles predict the trajectories of others based on observed states and solve a collision avoidance optimization problem offline. Simulation results showed faster arrival times compared to ORCAs. Predictive methods are more advanced than reactive approaches but still lack direct vehicle cooperation and task prioritization.
4.2.3. Rule-Based Methods
Traffic-rule-based approaches, such as those by Kato et al. [
31], prevent collisions by applying rules similar to road traffic. Rules are categorized into positional (e.g., stop signs), situational (e.g., right-of-way at intersections), and safety rules. Kato’s method emphasizes optimizing system-wide behavior rather than individual vehicles. By reducing collision-prone areas and introducing traffic rules, such as a “right-before-left” rule, the likelihood of collisions can be significantly reduced. Vehicles identify intersection rules via a map and use sensors to determine priority at crossings. Such methods require centralized rules and lack cooperation possibilities. Furthermore, no prioritization is possible.
4.3. Cooperative Approaches
This section presents cooperative algorithms for managing intersections, focusing on both hierarchical and heterarchical methods.
4.3.1. Hierarchical Methods
Hierarchical approaches use a higher-level instance, typically an Intersection Manager (IM) or an auctioneer, to control intersections and avoid collisions. The following sections summarize key approaches, grouped into optimization-based control and market-based control.
Intersection manager control methods use a central IM to coordinate vehicle movements. Bichiou and Rakha [
48] propose an optimization model to minimize vehicle travel times while incorporating constraints for acceleration and collision prevention. The model relies on full communication between vehicles and the IM, sharing speed and position data. Simulation results show reduced delays and emissions compared to traffic signals or roundabouts, but the high computational demand limits real-time applicability. Abdelhameed et al. [
49] describe a simpler intersection management system where an IM monitors potential collisions and sends acceleration or braking commands to vehicles. This control is based on a fuzzy controller optimized offline using a genetic algorithm. The method improves throughput compared to traffic signals but restricts vehicle autonomy. Li et al. [
50] use a sequencing problem solved by a genetic algorithm to manage a more complex intersection with two lanes per direction. Vehicles receive entry time slots from the IM and adjust their speeds accordingly. However, this method does not support vehicle priority, limiting its applicability.
Hierarchical methods can support intersection management but display only limited online capability. They are not fully decentralized and autonomous, but allow for cooperation between vehicles.
Market-based control methods apply auction mechanisms to allocate intersection access. Carlino et al. [
51] propose an auction system where vehicles bid based on their utility, and the IM determines winners using the Clarke–Groves mechanism. While flexible, this approach struggles with fairness and system efficiency without additional interventions such as subsidies for specific vehicles.
While Carlino et al. [
51] focus on auction-based intersection management, De Ryck et al. [
52] extend this concept to a broader decentralized task allocation framework for AGV systems. Their approach incorporates routing constraints within an auction-based mechanism, using a delegate Multi-Agent System (MAS) to dynamically optimize task assignments. This integration enhances system performance by balancing workload distribution and reducing execution times in industrial settings.
Market-based approaches often rely on central auctioneers but generally allow for prioritization, cooperation and online adaption.
4.3.2. Heterarchical Methods
Heterarchical approaches rely on decentralized decision-making for collision avoidance. The following methods can be classified into network-level and intersection-level strategies.
Network-level collision avoidance methods focus on coordination at a broader network scale. Wang and Premvuti [
37] introduce a decentralized control system for AMR operating in networks with limited intersection capacities. Vehicles communicate only with neighbors via a Sign-Board system. While effective for simple layouts, the method does not fully meet complexity requirements. Jager and Nebel [
53] propose a temporary hierarchy for collision management, where vehicles negotiate right-of-way using coordination links. However, this method is prone to deadlocks, limiting its practicality.
Intersection-level collision avoidance methods focus on vehicle coordination at individual intersections. Difilippo et al. [
54] use a consensus algorithm to coordinate vehicles at a four-way intersection, iteratively adjusting entry times and speeds to avoid collisions. While effective for small numbers of vehicles, it does not account for vehicle priorities. Majer et al. [
35] apply game theory to coordinate AMR at intersections without predefined paths. Vehicles iteratively optimize their strategies based on the movements of others, but the approach has only been tested with small numbers of vehicles and lacks support for heterogeneous systems. Miyamoto et al. [
34] develop traffic rules for intersections in logistics centers, allowing AMR to negotiate priority based on their status and goals. Although formally verified, this rule-based system does not consider task priorities and simplifies intersection complexity.
Unlike the previous methods, which rely on consensus, game theory, or predefined rules for intersection management, Grosset et al. [
55] take a broader approach to cooperative vehicle coordination. By leveraging standardized communication protocols such as cooperative awareness messages and decentralized environmental notification messages, their work enables autonomous vehicles to exchange situational data dynamically. Through simulations and real-world experiments in ROS2 and Gazebo, they show how message-based cooperation enhances collision avoidance and overall system efficiency in industrial environments.
Network-level and intersection-level collision avoidance usually do not allow for prioritization even though they enable cooperation and decentralized architectures.
4.4. Research Gap
All cooperative control approaches presented were evaluated based on the established evaluation framework. The results of these evaluations are summarized in
Table 2, highlighting that none of the reviewed approaches fully satisfies all defined requirements. Among the methods that meet all mandatory requirements, the heterarchical approach by Difilippo et al. [
54] achieves the highest score of 72.5%. Among the hierarchical methods, Carlino et al. [
51] and Li et al. [
50] are the best performers, each scoring approximately 67%. These results underline that while some approaches address a significant number of the requirements, no existing method fully meets all criteria. Additionally, only 4 out of the 15 reviewed approaches fulfill all mandatory requirements.
It is noteworthy that only a few control methods originate from intralogistics, with most of the examined approaches being developed for road traffic applications. The top-performing methods also stem from traffic management, rendering them suboptimal for the specific needs of intralogistics. For instance, many approaches neglect to account for priority orders or varying priorities among orders, and adherence to target times is rarely implemented. Furthermore, traffic-based methods often exhibit limited cooperation and autonomy. In contrast, intralogistics systems typically feature a clear common goal for all AGVs, making cooperation more significant and easier to achieve. Additionally, intralogistics operates within a known, finite space with a defined number of vehicles, simplifying reliable communication and coordination.
This analysis reveals a deficit in control approaches tailored to the specific requirements of intralogistics. The objective of this study is thus to develop two control methods designed to meet these requirements. The first method will employ a hierarchical architecture with a (de-)centralized intersection manager, decentralized in the sense that each intersection in a system can be managed by a dedicated manager. The second method will use a heterarchical structure, enabling fully decentralized vehicle control.
Finally, the two approaches will be compared to each other as well as with an FCFS heuristic and a MILP approach using simulation studies to determine under which conditions which method is more suitable and to evaluate the advantages they offer.
5. Agent-Based Control Architectures
This section introduces two new control approaches to address the problem described in
Section 2. First, the development method used to create the agent systems is briefly explained. Then, the development process, control workflow, and conflict resolution algorithms are described for both the hierarchical and heterarchical system designs.
5.1. Development Methodology
The MAS was developed following a structured and systematic approach based on the 2DECS method [
61]. The development process included requirements elicitation, goal modeling, capability definition, role assignment, and interaction modeling, leading to the design of agent-based control architectures. Specific adaptations were made to fit the scope of this work. For a detailed description of the methodology, refer to [
61].
5.2. Hierarchical Architecture
This section introduces the control flow for managing the interaction area using a hierarchically structured agent architecture, followed by the conflict resolution algorithm executed by the IM.
5.2.1. Control Flow of the Hierarchical System
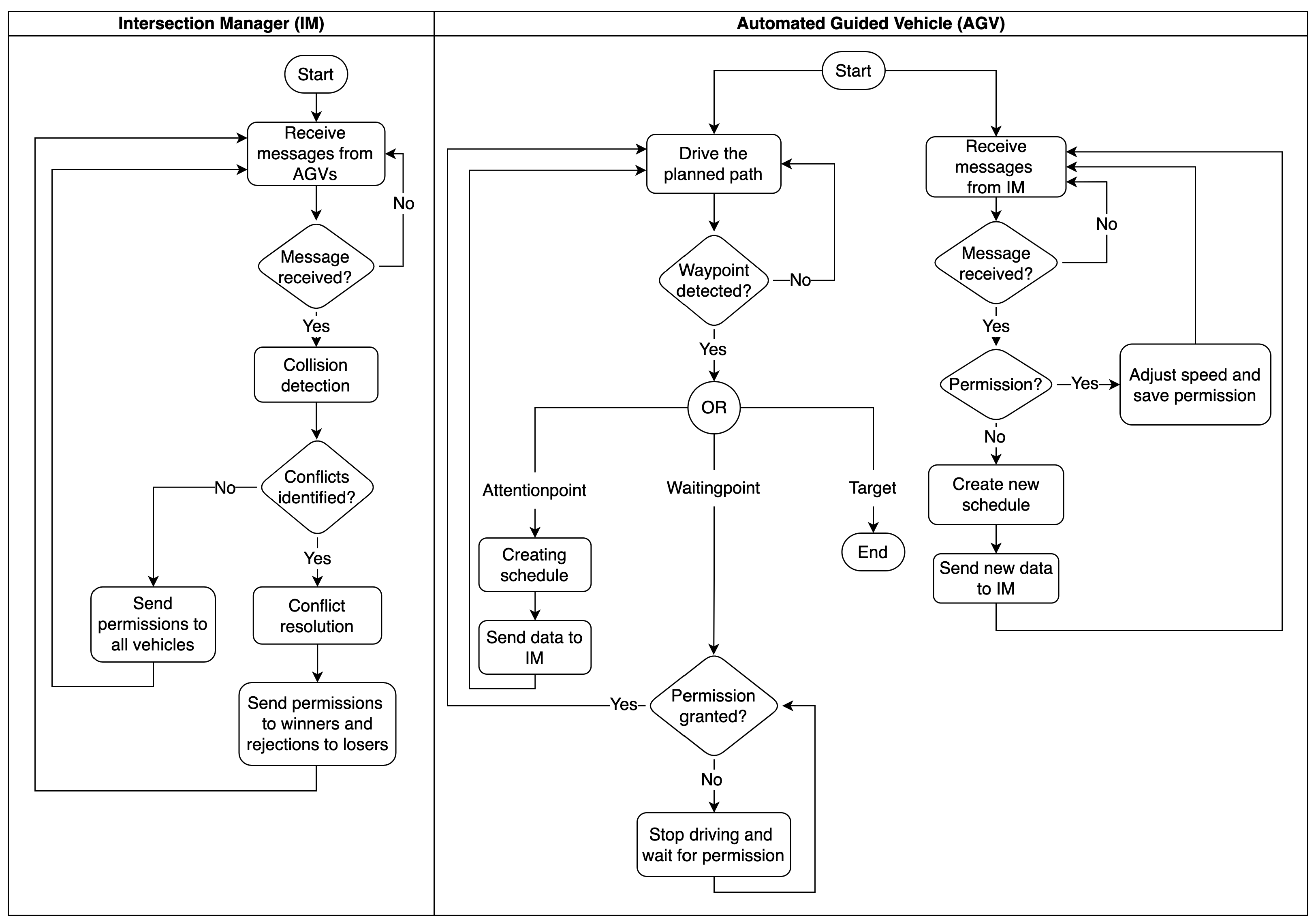
The hierarchical collision avoidance system utilizes two agent types: the IM-Agent at each intersection manages conflict detection and resolution, while AGV-Agents independently handle vehicle control and crossing time planning.
An intersection is divided into two zones, the communication zone (outer zone) where AGV-Agents communicate with the IM upon entry and begin crossing planning. Further, there is the conflict zone (inner area) where potential collisions between vehicles on different routes may occur. This zone can only be accessed with explicit permission from the IM. This clustering is common in the literature [
50,
56,
57].
The control flow (
Figure 2) focuses on preventing lateral collisions. The following collisions are assumed to be managed by vehicle sensors.
Upon entering the communication zone, detected via a so-called Attention Point (AP), the AGV-Agents calculate an ideal crossing schedule and record the timestamp
. In the conflict zone, 12 predefined Conflict Points (CPs) (
Figure 1) mark critical points where collisions may occur. Each AGV-Agent computes the crossing times
for the CP it needs to traverse, along with buffer times
, determined by vehicle size and speed.
AGV-ID for identification
Priority of the task
Timestamps and (entry into conflict zone)
Crossing times and buffer for all CPs
Status of waypoint crossing
The IM evaluates the received schedule for conflicts. If none are detected, the AGV-Agents receive approvals. Otherwise, the IM resolves the conflict by prioritizing one vehicle and rejecting the other’s schedule. Permissions can be revoked before a vehicle enters the conflict zone to ensure optimal scheduling.
Vehicles with approved schedules adjust their speed to reach the conflict zone at the scheduled time, avoiding stops. Rejected AGV-Agents adjust their schedules by incrementing and resubmit them until approval is received.
5.2.2. Hierarchical Conflict Resolution
The IM-Agent initiates conflict detection upon receiving a request from an AGV-Agent. By identifying the first CP (), the direction and position of the requesting AGV in the queue are determined. Based on this position, the algorithm ensures compliance with the no-overtaking rule and calculates occupancy intervals for each CP.
If it is determined that the proposed schedule of the requesting AGV does not violate the overtaking prohibition, the conflict check is continued. Otherwise, the conflict check can be terminated, as the schedule is already deemed invalid and can be rejected. For the conflict check to be conducted, the time intervals during which the requesting AGV intends to occupy the CP must first be calculated. This is done based on the known times
and the buffer
, as shown in Equation (
10):
If the time intervals for all CPs to be traversed by two AGVs are known, the two inequalities (
11) can be used to check if their intervals overlap at a CP.
An overlap exists only if both inequalities are satisfied. Otherwise, no conflict exists, as the start and end times for each AGV are either entirely before or after those of the other. This check must be performed for all CPs and all other vehicles, as described in Algorithm 1. If a conflict is detected between AGV
i and AGV
j at CP
c, the variable
, indicating the presence of a conflict, is set to 1 by the IM-Agent.
| Algorithm 1 Conflict Assessment for AGVs i |
| 1: for do |
| 2: for and do |
| 3: if and then |
| 4: |
| 5: end if |
| 6: end for |
| 7: end for |
If no conflict is detected during the conflict check, the IM-Agent sends approval to the requesting AGV-Agent. If a conflict is identified, the priority between the conflicting AGVs must be determined. The conflict resolution Algorithm A1 evaluates various criteria in descending priority until a clear decision is made. Once a criterion resolves the conflict, subsequent checks are skipped. The algorithm checks whether a Waypoint (WP) has already been passed, i.e., if the inner area of the conflict zone has been entered and thus no more changes to the schedule are possible. If AGV i has priority over AGV j at CP c, the IM-Agent sets to 1 and to 0. If no conflict exists between AGV i and j at CP c, both and are set to 1. The AGV with priority is referred to as the winner, while the other, which must adjust its schedule, is called the loser.
If an AGV has already entered the intersection zone, it cannot adjust its schedule, and the other AGV must adapt its plan. If both are outside the zone, priority is given based on task priority—higher-priority tasks win. For equal priorities, the first to reach to AP wins. In rare cases of identical priority and entry time, the lower AGV-ID is used to decide. The IM-Agent calculates
for each AGV, which equals 1 if the schedule is approved or 0 if rejected. Equation (
12) ensures that
can only equal 1 if
equals 1 for all
j and
c, meaning that AGV
i either has no conflict with another AGV or is determined to be the winner in all conflict resolutions. If, however, AGV
i is the loser in at least one conflict resolution,
takes the value 0, and a rejection must be sent to AGV
i by the IM-Agent.
Rejections trigger plan adjustments, and all affected agents are notified. This ensures consistent updates for all AGVs near the interaction zone.
A problem arising from the overtaking prohibition is that high-priority vehicles may have to wait if a low-priority vehicle is ahead at the intersection. For instance, if an AGV with much higher priority arrives with another AGV of low priority in front of it, which has to yield to other higher-prioritized vehicles before crossing, it causes a delay for the high priority AGV. To prevent this, the IM-Agent adjusts priorities before executing Algorithm A1, ensuring each AGV has at least the same priority as vehicles further back in the queue. This adjustment is detailed in Algorithm 2.
| Algorithm 2 Algorithm for AGV priority adjustment |
| for do |
| for and do |
| if then |
| if then |
| |
| end if |
| end if |
| end for |
| end for |
5.3. Heterarchical Architecture
The following first describes the control process of the heterarchical system. Subsequently, the algorithms used for conflict resolution in the heterarchical system are presented, with a primary focus on the differences from the algorithms in the hierarchical system.
5.3.1. Control Flow of the Heterarchical System
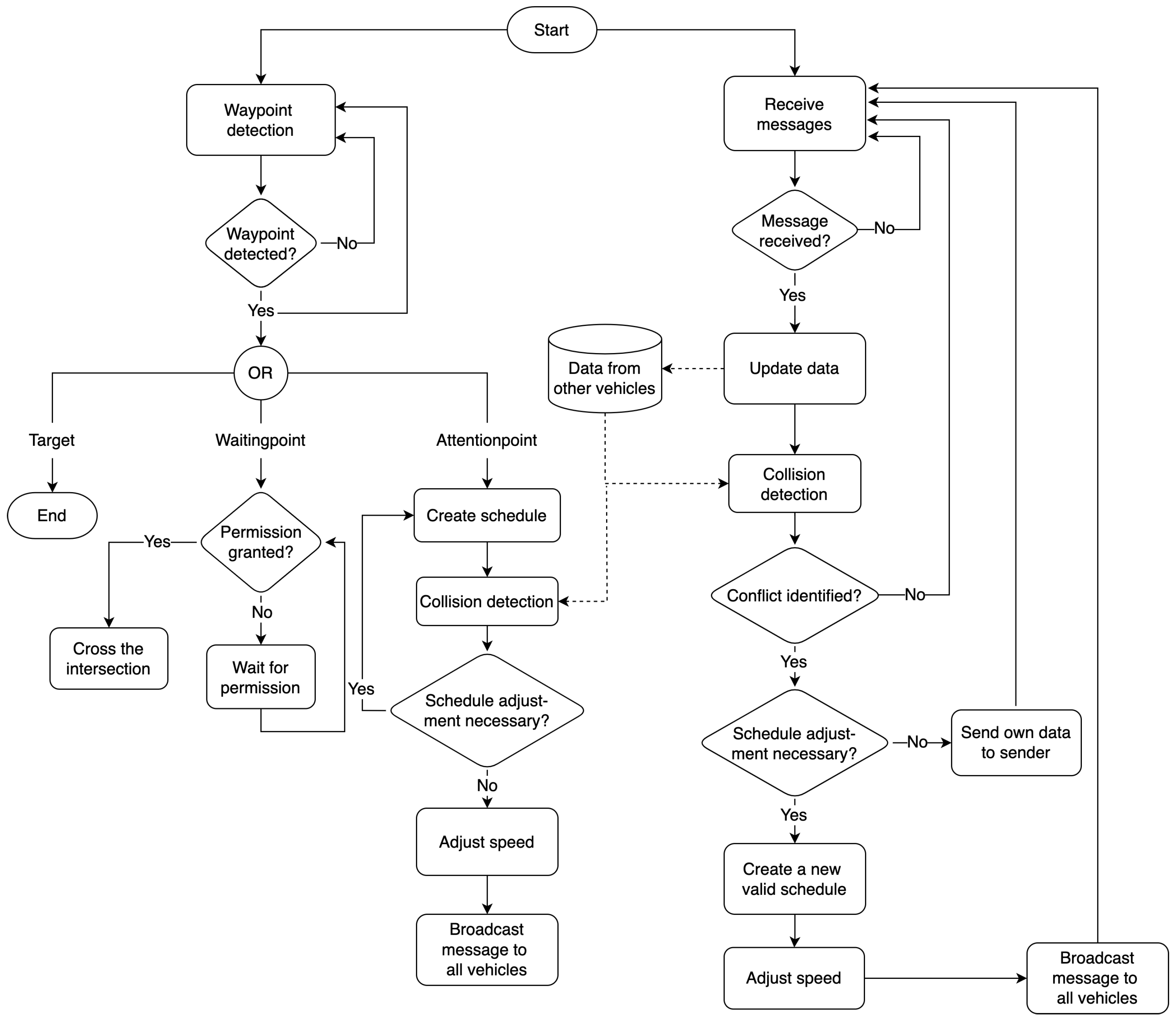
The fundamental structure of the interaction area, divided into a communication zone and a conflict zone, as described in
Section 5.2.1, remains unchanged in the heterarchical system. However, unlike the hierarchical system, the heterarchical system consists of only one agent type—the AGV-Agent. Each vehicle in the system is assigned an AGV-agent. This agent is responsible for performing both the tasks managed by the IM-Agent in the hierarchical setup and the tasks carried out by the AGV-Agents in the hierarchical system.
Waypoint Detection and Time Planning: The fundamental process of waypoint detection, as carried out by the AGV-Agents in the hierarchical system, is retained in the heterarchical system. The AGV-Agent in the heterarchical system continuously checks for waypoints during its journey. When a waypoint is identified, the waypoint detection continues even if the waypoint’s action has already been triggered (see
Figure 3). If an AP is detected by the AGV, the agent begins calculating its own schedule for crossing the interaction area. Unlike the hierarchical system, the developed schedule is not directly communicated to other AGV-Agents or an IM-Agent.
Conflict Detection and Resolution: In the heterarchical system, each AGV can independently detect conflicts using available information from other AGVs. If a conflict is identified and the AGV is required to adjust its schedule, e.g., because of lower priority, a fixed value to the times and is added. This process mirrors the adjustment logic of the hierarchical system. The adjusted schedule undergoes repeated conflict checks until no conflicts remain. The step size for adjustments has minimal impact on message frequency, as the schedule is only shared once it is valid. However, it affects computation time: larger steps lead to faster but less optimal adjustments, while smaller steps provide finer results but require more iterations.
Speed Adjustment and Information Sharing: Once a valid schedule is created, the AGV adjusts its speed to avoid stopping. The new schedule and additional details (e.g., AGV ID, priority) are broadcast to all AGVs. Unlike the hierarchical system, the schedule must specify the correct interaction zone, as no central agent manages the assignments.
Approval Granting: Unlike the hierarchical system, where approval is granted by the IM-Agent, an AGV in the heterarchical system can approve its own schedule after resolving conflicts. When an AGV detects a waypoint, it checks if it is authorized to proceed. If approval exists, the waypoint is crossed. Otherwise, the AGV waits. Upon reaching its destination, the task is completed, and a new task can begin.
Response to Incoming Messages: When an AGV receives information about another AGV heading toward the same interaction zone, it updates its internal data storage. It then checks for conflicts between its schedule and the incoming one. If no conflict exists, no further action is taken, and no response is sent to minimize communication load.
If a conflict is identified that requires adjustment of the recipient AGV’s schedule, it updates its plan accordingly and shares the revised schedule via a broadcast. If the conflict demands adjustment of the sender’s schedule, the recipient sends relevant information back, prompting the sender to resolve the conflict. This ensures that only valid schedules are broadcast, reducing message traffic.
5.3.2. Heterarchical Conflict Resolution
The heterarchical system employs two variants of the conflict resolution algorithm. The first is executed when an AGV adjusts its own schedule, checking if the new schedule conflicts with others and, if necessary, modifying it. The second variant is triggered when an AGV receives new information from another AGV, requiring it to verify and resolve conflicts involving both its own and the sender’s schedule. These two variants are detailed below.
Before executing either algorithm, the direction and relative position of each AGV must be determined, as described in
Section 5.2.2. The occupancy intervals for key points (CPs) are also calculated similarly. The compliance with overtaking restrictions is checked, but only for the relevant AGVs in the triggered variant.
Both variants rely on the same conflict detection logic (Algorithm 1) as in the hierarchical system. They prioritize vehicles entering the conflict zone or determine precedence based on task priority or FCFS rules, as detailed in
Section 5.2.2. To handle long waits for high-priority AGVs stuck behind lower-priority ones, the priority adjustment algorithm (Algorithm 2) is also applied here, but executed autonomously by each AGV.
Algorithm A2 describes the first variant, used when an AGV updates its own schedule. It checks all CPs and other AGVs to determine whether the schedule is feasible. If conflicts exist, they are resolved using the same priority logic as in the hierarchical system. The variable
tracks whether AGV
i has precedence at CP
c, with
derived using Equation (
13):
If , the AGV shares its schedule via broadcast; otherwise, it modifies its schedule and rechecks conflicts.
Algorithm A3 handles conflicts when an AGV receives updates from another AGV. Here, only conflicts between the two AGVs are checked. The variables and indicate precedence for AGVs i and j at CP c. If either AGV lacks precedence ( or ), adjustments are made. If no conflict exists ( and ), no further action is needed.
6. Simulation Study
To compare the performance and scalability of the proposed control architecture and further algorithms, this section describes the implementation, the conducted simulation experiments, as well as the results. Finally, the results are discussed.
6.1. Implementation
The simulation utilizes an existing Python-based framework (
https://github.com/hsu-aut/RIVA_Decentralized_Communication, accessed on 2 April 2025) adapted for interaction area control. The software, built on Pygame, allows environment creation, vehicle movement, and obstacle placement. Key modifications include restricting vehicle movements to fixed lanes, integrating waypoint detection, collision avoidance, and implementing scheduling and speed adjustments.
Communication between agents, based on
FIPA-ACL, is managed via Python Agent Development Environment (PADE) [
62] scripts (
https://github.com/NiklasJobs/Agent-based_Control_of_Interaction_Area, accessed on 2 April 2025) and CSV files. The hierarchical system follows Algorithm A1, while the heterarchical system uses Algorithms A2 and A3 for conflict resolution. Vehicles generate schedules upon entering the communication area and adjust them as needed based on agent interactions.
Simulations consist of random vehicle arrivals with predefined destinations and priorities. The 800 × 800-pixel simulated environment represents 80 × 80 m, with vehicles modeled as circles. Reproducible results are ensured by fixing random seeds.
Figure 4 shows an example setup, where vehicles start outside the communication zone and adjust their speed based on generated schedules.
In the hierarchical system, AGVs send schedule updates via JSON messages to the central IM-Agent, which resolves conflicts and communicates approvals or rejections through FIPA-ACL messages. Vehicles adjust their schedules or speeds based on these responses.
In the heterarchical system, AGVs independently check for conflicts using Algorithm A2. Approved schedules are shared via FIPA-ACL, while rejections trigger schedule adjustments. If conflicts involve external vehicles, Algorithm A3 determines which vehicle must adjust its schedule.
Communication between Pygame and PADE scripts relies on CSV files for data exchange. Vehicles calculate schedules based on Manhattan distances and predefined parameters, ensuring smooth and collision-free operation.
6.2. Design and Execution of Simulation Experiments
The general simulation setup involves generating a fixed number of vehicles with random start positions and destinations. These vehicles simultaneously approach and cross the interaction area, creating varying scenarios rather than a constant traffic flow. This approach allows isolated analysis of scenarios, highlighting strengths and weaknesses of the control methods.
Each experiment consists of
runs, which is sufficient to identify behavior patterns while keeping computation time manageable. The evaluation is based on the following metrics: the message count tracks the number of messages exchanged between agents, providing insights into the communication load, which is critical for real-world network design. Note that the messages between the agents for the FCFS do not imply cooperation, as they are simply exchanging arrival times whereas in the other approaches the agents work on a synchronized common plan. Furthermore, the delay of vehicles is tracked, i.e., the additional time needed compared to an unobstructed crossing of the interaction area. Finally, the priority-weighted delay is measured as described in Equation (
A1), as well as the average delay of high-priority vehicles.
First, the two agent-based architectures are compared in detail with the scenarios displayed in
Table 3. Experiments with 8, 16, 24, 32 and 40 vehicles simulate varying congestion levels, while vehicle priorities are uniformly distributed between 1 and 5.
Following this detailed comparison, further experiments are conducted for 8, 16 and 32 vehicles comparing the agent-based approaches with the FCFS heuristic and the MILP approach. The MILP approach is based on the model described in
Section 3.1. The detailed model is shown in
Appendix A. The aim of this comparison is, on the one hand, to evaluate the approaches presented against the optimal solution of the MILP and, on the other hand, compare the scalability of a centralized optimal solution compared to decentralized approaches, particularly in terms of computing time.
In addition to the MILP, a simple FCFS logic is implemented as a reference algorithm. In this approach, vehicles are assigned crossing permissions strictly based on their arrival order in the interaction area, without considering priority values or optimization techniques. This provides a straightforward benchmark to assess the benefits and limitations of the agent-based control methods in terms of priority-depending delays. The FCFS approach represents a naive but commonly used method in decentralized traffic coordination, making it a useful comparison algorithm.
6.3. Results
Freedom of collisions, which occur when the distance between two vehicles falls below the sum of their radii, as defined in Equation (
14), was determined for all approaches.
This demonstrates the functionality of both control approaches for conflict detection and resolution and ensures comparability of all the described approaches.
Comparison of Agent-Based Approaches
Table 4 shows the results for the different vehicle counts.
Delays per vehicle increase with more vehicles due to higher conflict frequency. For 8 vehicles, delays are minimal (1.04 s for hierarchical and 1.12 s for heterarchical). At 16 vehicles, delays rise significantly (6.50 s for hierarchical and 6.61 s for heterarchical). With 32 vehicles, average delays exceed 20 s, which is caused by the resulting congestion at the intersection. This clearly linear trend reflects the increased likelihood of conflicts as vehicle density grows. Such delays, although high for a single interaction area, must be assessed relative to the overall system and could indicate systemic overloading rather than control inefficiency. Persisting congestion in a real system would necessitate layout or material flow adjustments. Similarly, the priority-weighted delay increases but the results show that both approaches exhibit very similar behavior in the case of general average delays and priority-weighted delays.
Another key metric from the simulation experiments is the number of messages sent per simulation run. To ensure comparability, the total number of messages is divided by the number of vehicles, yielding the average number of messages per vehicle. In the hierarchical case, this also includes messages sent by the IM agent, reflecting the communication overhead per vehicle crossing.
Table 4 shows that the heterarchical control consistently generates about three times more messages per vehicle than the hierarchical approach. Additionally, the message count per vehicle increases with the number of vehicles. The highest value, approximately 130 messages per vehicle, occurs with 32 vehicles using heterarchical control, while the lowest, about 8 messages per vehicle, is observed with 8 vehicles under hierarchical control.
Summarizing this comparison, both approaches exhibit similar properties in terms of delays but the hierarchical approach requires significantly less messages.
6.4. Comparison of Agent-Based, FCFS and MILP Approaches
In the following, the agent-based approaches are compared to the MILP and FCFS logic to assess if the agent-based approach does outperform the FCFS in terms of priority-oriented delays, to assess solution quality compared to the optimal solution, and to determine the degree of scalability in terms of algorithmic complexity and computation time of the agent-based vs. the central optimization approach.
Table 5 displays the results of the experiments for 8, 16 and 32 vehicles (24 and 40 are neglected here for the sake of brevity as they do not yield additional insights in this case).
The results show that the simple exchange of arrival times in the FCFS requires even less messages to be exchanged than the hierarchical approach. The MILP does not require any exchange of messages in the current implementation as it possesses all required information from the start. The solution quality, i.e., the average delays and the sum of priority-weighted delays show that for 8 vehicles, the realized delay of the heuristic approaches is about half a second larger than the calculated optimum (1 s. vs. 0.4 s). For 16 vehicles, the number of runs was reduced to 10 due to the long computation times of the optimal solving MILP. The experiments were conducted on a macOS 13 notebook with Intel
® Core™ i7-7700HQ CPU @2.90 GHz and 16.0 GB RAM. The results are displayed in
Table 6.
With growing problem size, the optimality gap significantly increases for all heuristic approaches. The FCFS heuristic exhibits smaller average delays than the agent-based approaches; however, as it does not incorporate priorities, the delay for high-priority vehicles is larger. This is displayed in more detail in
Figure 5.
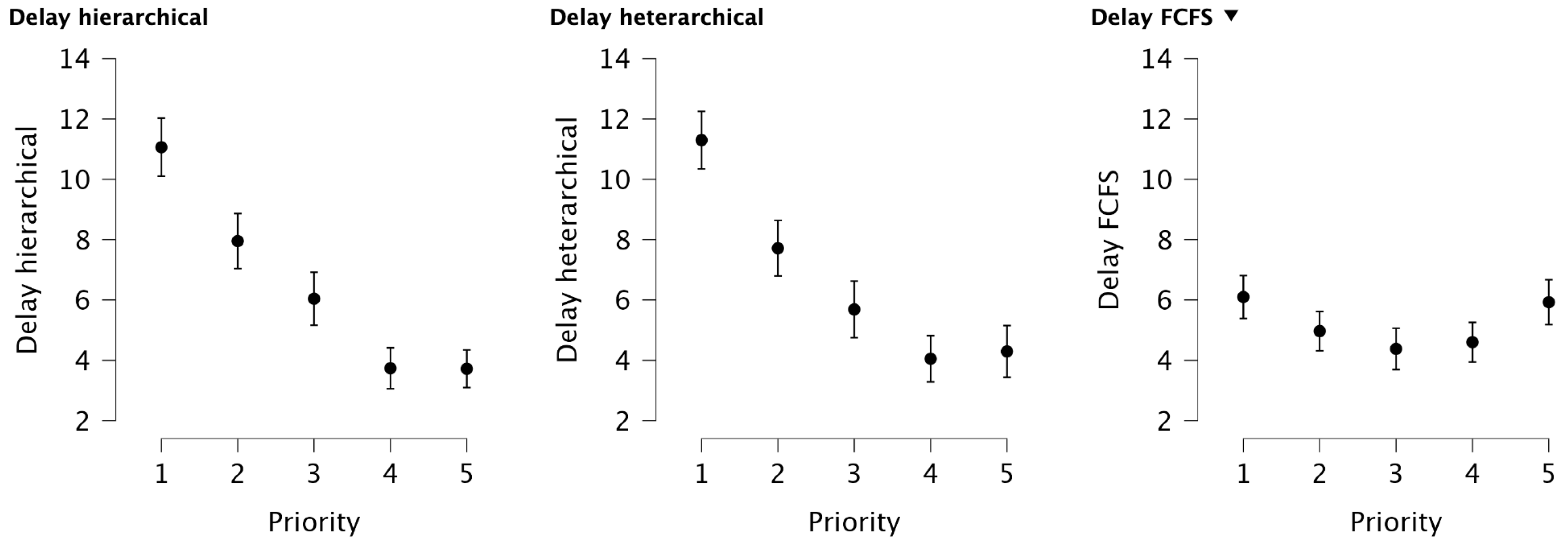
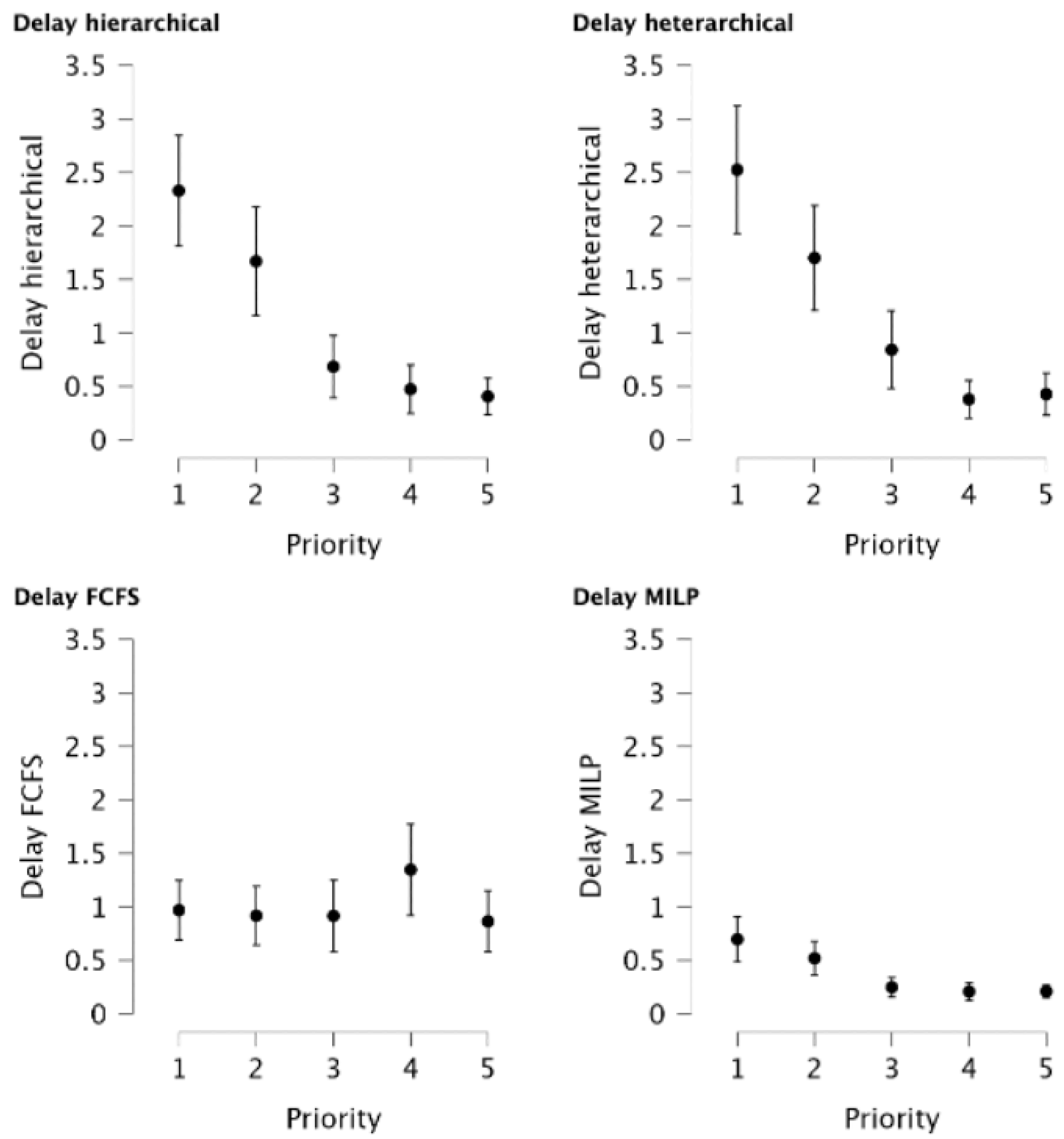
Figure 5 shows the average delays per priority for both approaches and for the FCFS logic and the MILP as a baseline, which resulted from the simulation with 8 vehicles. In addition to the average delay, the 95% confidence intervals are also shown. It becomes clear that the average delays decrease significantly with higher priority for both the hierarchical and the heterarchical approach, while the average delays remain approximately constant across the priorities according to FCFS logic. In addition, the confidence intervals for the two developed approaches become noticeably smaller with higher priority. Therefore,
Figure 5 clearly shows that the two developed approaches accept higher delays for the low-priority vehicles so that the delays of the high-priority vehicles can be significantly reduced. On average, the delay of the high-priority vehicles is below the average delay achieved with the FCFS logic. As with the two agent-based approaches, the optimal solution of the MILP shows that the delay decreases with increasing vehicle priority. However, the overall level of delays is significantly lower. The experiments with 16 and 32 vehicles have also shown that the average delay decreases with both approaches as the priority of the vehicles increases (see
Figure A1 and
Figure A2).
In order to determine whether the described differences in the delays of vehicles with different priorities in the new approaches are statistically significant, an analysis of variance with a significance level of 5% was conducted for all simulation experiments. Since for the experiments with 8 and 16 vehicles the null hypothesis of homogeneity of variances can be rejected, which is required for analysis of variance [
63], this assumption is considered not fulfilled. Therefore, the Welch analysis of variance, which does not rely on the assumption of homogeneity of variances, was conducted for all simulation experiments [
64]. For all simulation experiments, the p-value is significantly below the significance level of 0.05. Thus, for all conducted simulation experiments, the null hypothesis that there are no significant differences in delays between vehicles with different priorities can be rejected.
Another important aspect to consider is the computation time and complexity.
Table 7 displays the average computation times for the 8 vehicle experiments. Here, the total amount of time is the sum of the serial portion (i.e., the part that can not be paralyzed, in this case the intersection manager) plus the number of vehicles times the calculation time per vehicle. Assuming that the calculation of a solution is required as soon as a vehicle leaves a prior interaction area and needs to be solved before any part of the solution implies a change in real-world behavior of the vehicles, the computation time if the MILP already exceeds practical applicability for this small problem size. The average computation time for 16 vehicles obtained in 10 runs, with 916.16 s, further supports that claim.
6.5. Discussion
This section highlights the results of the conducted experiments and points out limitations and further research directions.
The simulation studies confirmed that all presented approaches enable collision-free navigation within the interaction area. In the cases with 8 and 16 vehicles, the average vehicle delay with the hierarchical approach was approximately 0.1 s less than with the heterarchical approach. However, there is no significant difference between the two approaches.
In the 32-vehicle experiment, the heterarchical approach shows a 1.18-s advantage in average delay. In the experiment with 40 vehicles, the average delay is approximately 0.4 s less with the heterarchical approach. Overall, there are no clear differences between the two approaches in terms of average delays. The reason for this can be found in the shared decision logic of both approaches.
Both approaches were benchmarked against a pure FCFS logic. This showed that high-priority vehicles experienced fewer delays with the two approaches presented than with control based on FCFS logic. In order to achieve this, higher delays for low-prioritized vehicles had to be accepted. In addition, both approaches were compared against an optimal solution obtained by an MILP approach. Although the optimal solution is significantly better in terms of the average delay, the computing time for the optimal solution is significantly higher, which prevents it from being used in real systems.
Mapping the developed approaches to the postulated requirements, there are some inherent limitations: the hierarchical structure only partially supports decentralization, as the IM-Agent limits vehicle autonomy, and offline vehicles are not fully integrated. The latter is also valid for the heterarchical approach, but in general, an integration in the hierarchical architecture might be easier to realize but at the cost of lower robustness due to a single point of failure. Both approaches meet most requirements, especially the heterarchical one, which offers significant improvements for the studied scenario. However, the evaluation framework is not exhaustive and could be expanded with additional criteria tailored to specific application domains.
As expected, significant differences in communication overhead were observed. On average, the heterarchical approach required 2.74 times more messages per vehicle than the hierarchical approach.
6.5.1. Broader Implications and Limitations
The developed control approaches were tested on a standard intersection with four entry and exit directions but can be generalized to other interaction areas where vehicles follow fixed routes, predefined waypoints, and attention points. The results highlight the potential of decentralized, agent-based approaches for managing complex systems, offering flexible and efficient solutions for coordination and conflict resolution, especially when vehicle priorities or similar vehicle-specific properties such as weights or battery status, which can be translated to priorities, are important.
Certain limitations warrant further research. The unidirectional schedule adjustments could be refined. Allowing schedules to shift forward in specific scenarios, such as when a high-priority vehicle approaches a low-priority one, could reduce overall delays.
Communication reliability is another factor not addressed in the simulations, which assumed error-free communication. In practice, communication failures could pose challenges, particularly for the heterarchical approach, where missing messages might lead to critical information gaps. Redundancy in message exchange or requiring mutual approval for schedules could mitigate such risks but would increase communication overhead.
Finally, the isolated intersection simulations limit the applicability of the results to broader logistics or production environments. Future studies should explore these approaches within realistic networked scenarios to evaluate their impact on delivery reliability and overall system throughput. Expanding the analysis to include a wider variety of hierarchical and heterarchical approaches would also strengthen the generalizability of the findings.
6.5.2. Influence of Vehicle Arrival Order on Delays
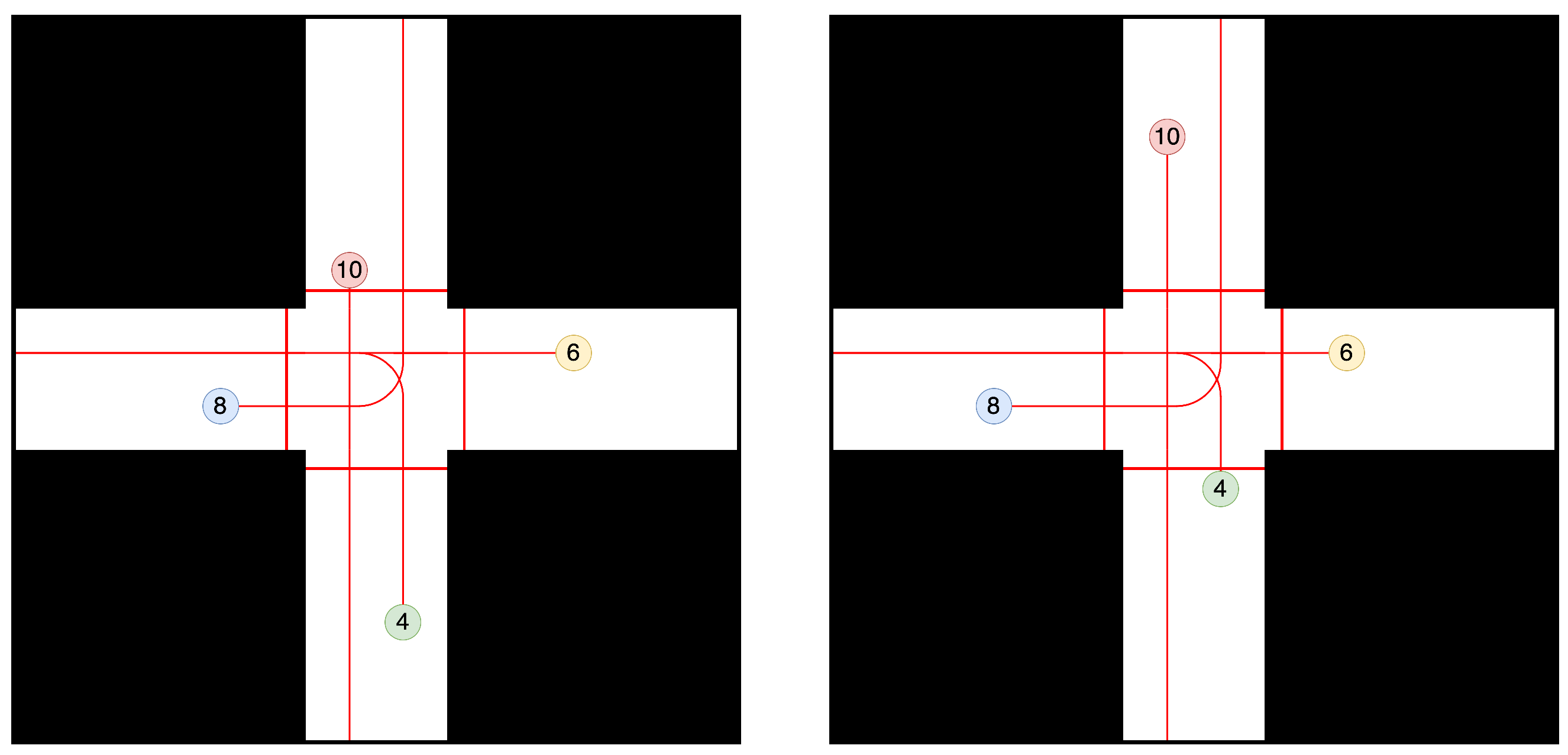
This section demonstrates, using a simple example, how the order in which vehicles approach the interaction area affects their delays.
Figure 6 illustrates two scenarios where the same four AGVs with identical priorities approach an interaction area. It is assumed that all vehicles have the same maximum speed. In the left scenario, the AGVs arrive at the intersection in descending order of priority. The highest-priority vehicle (the red AGV with priority 10) arrives first, followed by the second-highest priority vehicle (the blue AGV with priority 8), and so on. This arrival order is ideal for the control approaches presented, as vehicles arrive at the interaction area according to their priority, minimizing wait times.
In contrast, the right scenario shows the same vehicles approaching the intersection in reverse order. If the time gaps between vehicles reaching the intersection are sufficiently small, all vehicles may have to wait for the red AGV with priority 10. Subsequently, all vehicles would have to allow the blue AGV with priority 8 to pass, followed by the green AGV waiting for the yellow AGV with priority 6. In this case, the order in which vehicles cross the interaction area would be the reverse of their arrival order, resulting in maximum delays for the vehicles.
This example illustrates that minimizing vehicle delays depends not only on the distribution of task priorities but also on the order in which vehicles arrive at the interaction area.
7. Summary and Outlook
Intralogistics systems, such as AGV-based systems, face growing challenges that centralized control approaches can no longer adequately address. Modern systems demand high levels of flexibility, reconfigurability, scalability, and availability—requirements that centralized systems struggle to meet in complex environments. Despite this, most AGVs currently used in industry rely on centralized control, including for critical tasks like collision avoidance, limiting their adaptability to modern intralogistics demands.
Agent-based systems present a promising alternative. Their decentralized structure and autonomous agents reduce control complexity by dividing the overall problem into smaller, locally solvable tasks based on available information. This decentralized approach offers significant advantages over centralized systems.
This study aimed to develop a decentralized, agent-based control approach for collision avoidance in AGV-based systems, focusing on managing interaction areas where potential vehicle collisions may occur. Additionally, the study explored how the architecture of the MAS influences solution quality by developing both hierarchical and heterarchical agent systems. The two architectures developed differ in terms of the degree of decentralization and required communication. Both systems were designed to meet intralogistics requirements, particularly prioritizing tasks.
Two agent-based system architectures were developed using a structured methodology: the hierarchical system includes two agent types, IM-Agents and AGV-Agents, while the heterarchical system consists solely of AGV-Agents. Algorithms for conflict detection and resolution were designed for both systems, following a clear hierarchy: vehicles with higher task priorities are given precedence. Furthermore, a simple FCFS and an optimally solving MILP approach were developed. These approaches, demarking the extremess of full decentralization with no cooperation (FCFS) and centrally optimizing solution techniques MILP, were compared to the agent-based architectures in a simulation study.
The simulations demonstrated that decentralized, agent-based approaches are well-suited for managing interaction areas in intralogistics. All approaches ensured collision-free navigation in all runs. However, the agent-based approaches emphasized the priority aspect. The MILP mechanism exhibited unpractical computation times for such dynamic applications. In terms of performance, all heuristic approaches exhibit a rising optimality gap with growing problem size. However, the delay, especially for high-priority vehicles for the agent-based systems, is within acceptable boundaries.
This work demonstrates the suitability of agent-based approaches for controlling complex intralogistics systems, suggesting that agent-based systems could replace the currently predominant centralized AGV control architectures.
While the functionality of the proposed approaches was established, the simulations focused on isolated interaction areas. Future studies could incorporate these areas into transport networks, reflecting real-world applications. Another open question in this regard is, how this integration in a wider network is possible in the different architectures, i.e., if, for example, the hierarchical architecture enables an easier exchange of information between different interaction zones.
Communication disruptions, such as interruptions or delays, were largely excluded from this study. Future research should investigate the resilience of agent-based systems to such disturbances compared to centralized approaches.
Additionally, future research should examine the impact of autonomy levels on system performance. The degree of autonomy, i.e., in how far vehicles follow predefined routes and plans, could further improve system performance.












































































































































































 not fulfilled
not fulfilled  partially fulfilled
partially fulfilled  half fulfilled
half fulfilled  nearly fulfilled
nearly fulfilled  fully fulfilled.
fully fulfilled.





