Dynamical System Modeling for Disruption in Supply Chain and Its Detection Using a Data-Driven Deep Learning-Based Architecture
Abstract
1. Introduction
- system dynamics model for analyzing and modeling supply chain disruptions, focusing on receiving delays in the automotive sector;
- artificial intelligence was used to detect disruptions using the data generated by a system dynamics model by designing a neural network based on deep learning.
2. Materials and Methods
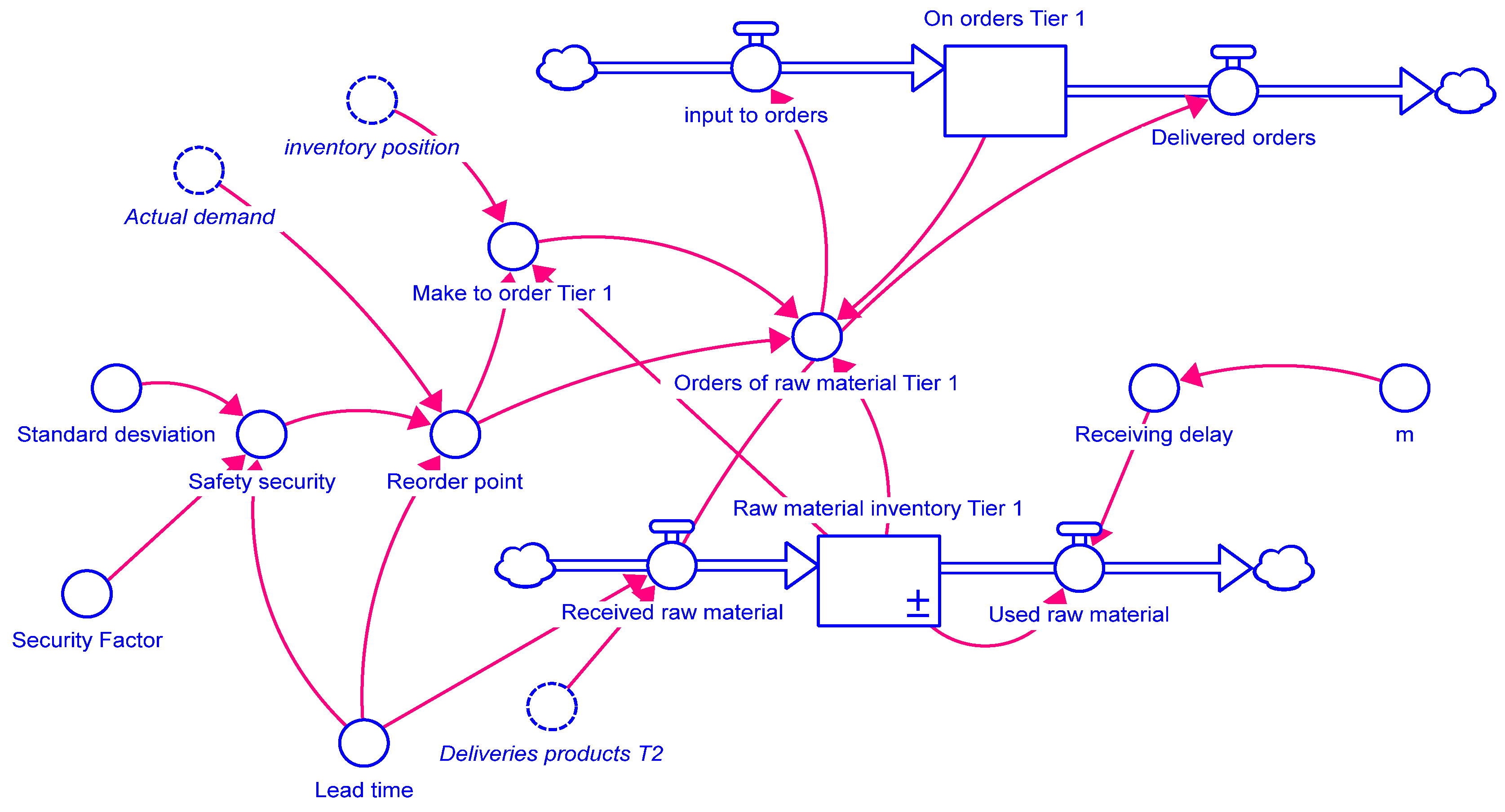
2.1. Dynamics System Modeling
2.1.1. Definition of Equations and Parameters
2.1.2. Integrating Information into Stella
2.1.3. Evaluating Causal Model of Disruption
2.1.4. Interpretation of the Performance of Results
2.2. Artificial Neural Networks Based on the Detection of Disruptions
2.2.1. Data Monitoring
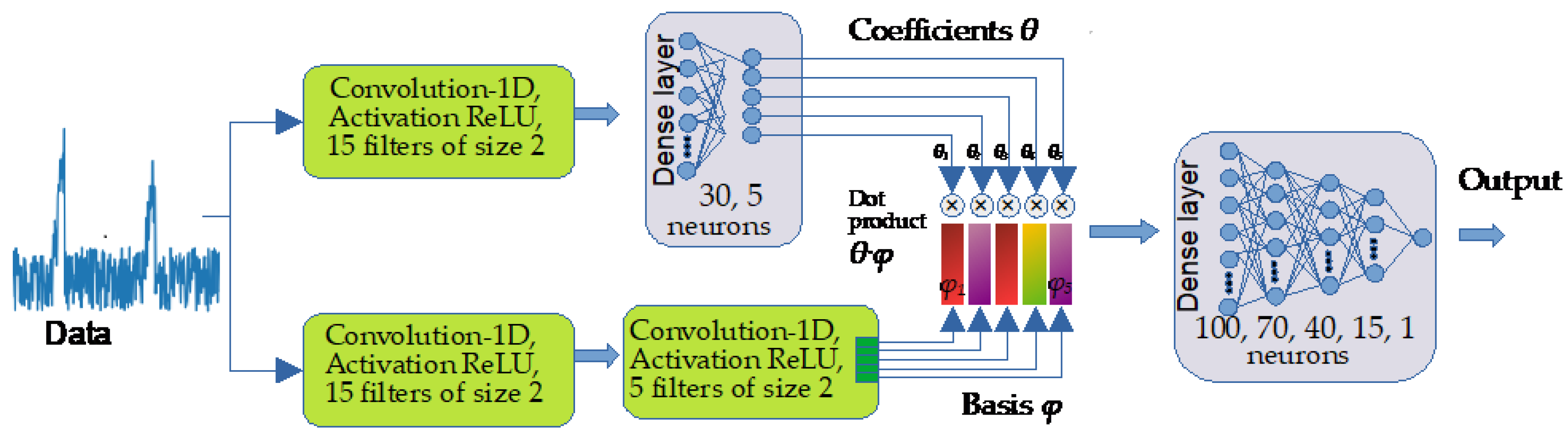
2.2.2. Deep Learning Architecture for Disruption Detection
2.2.3. Model Implementation
3. Results
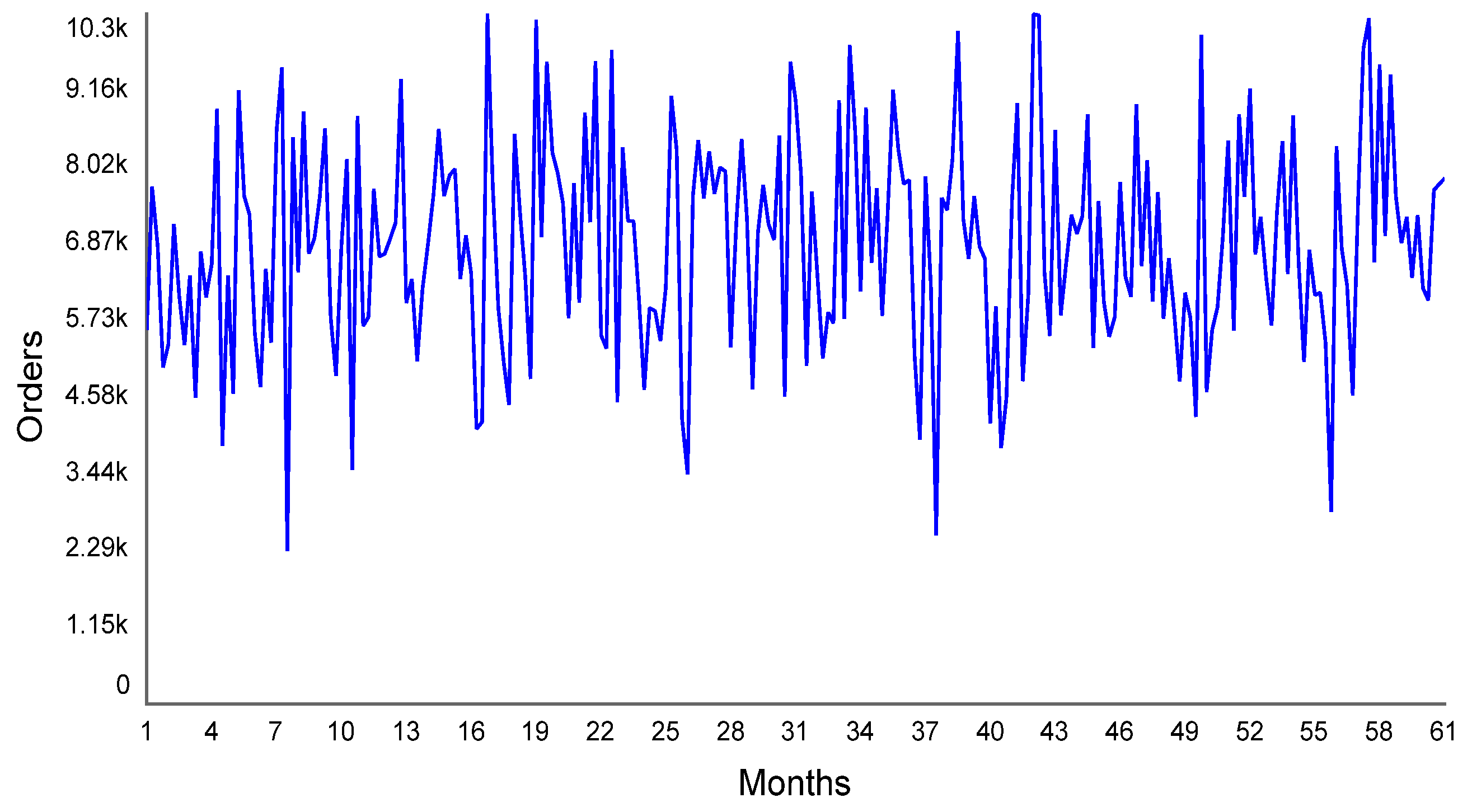
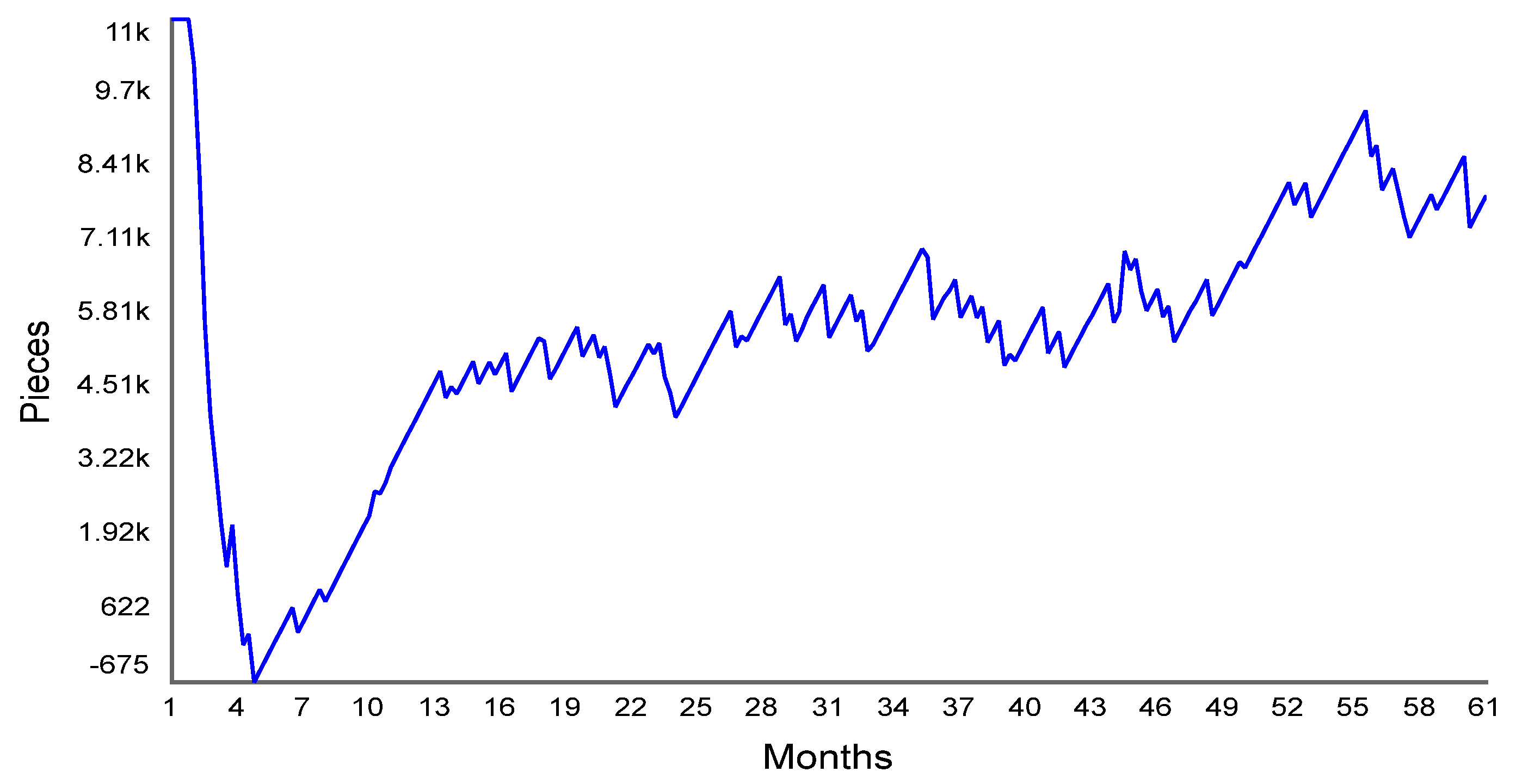
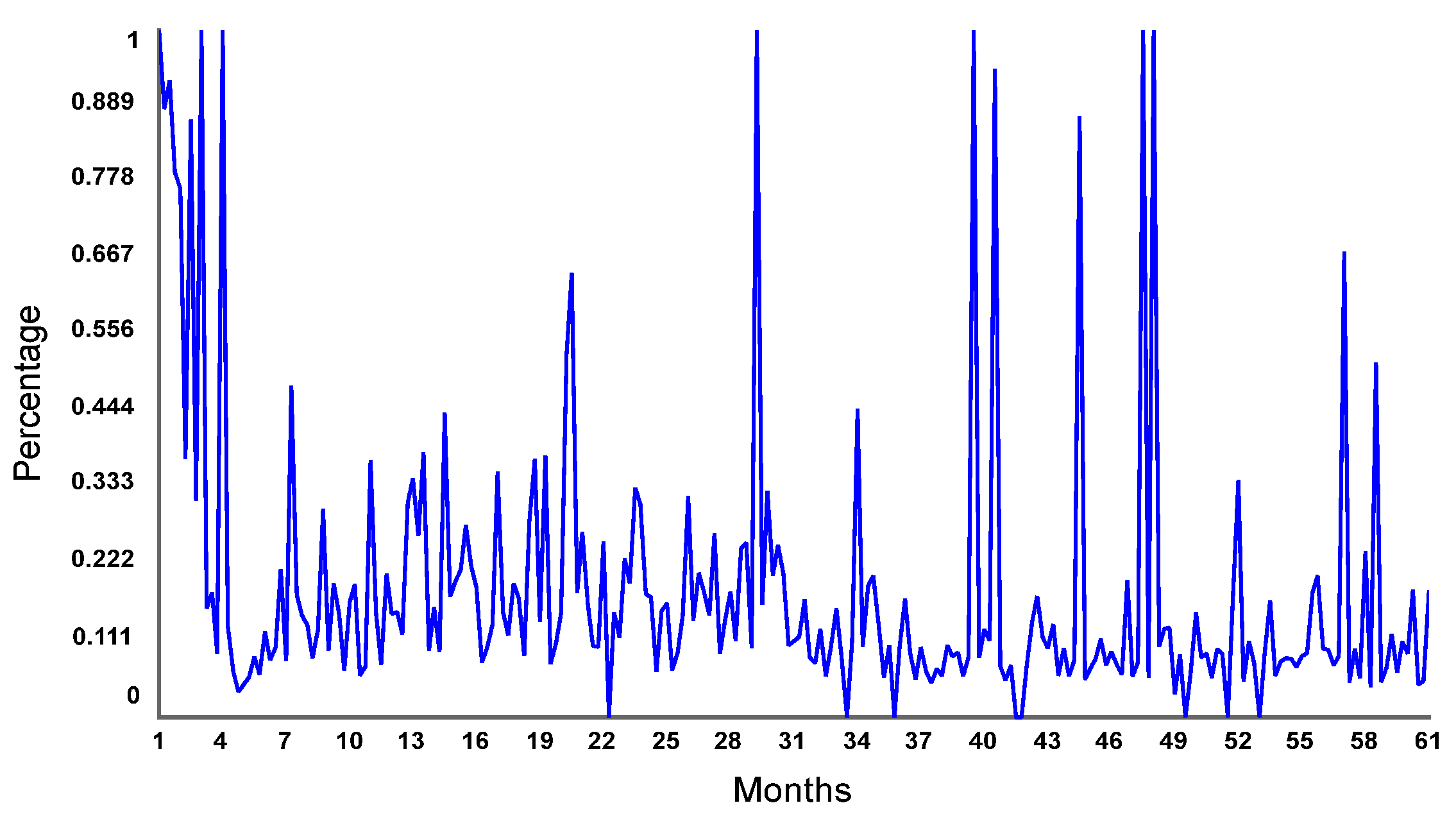
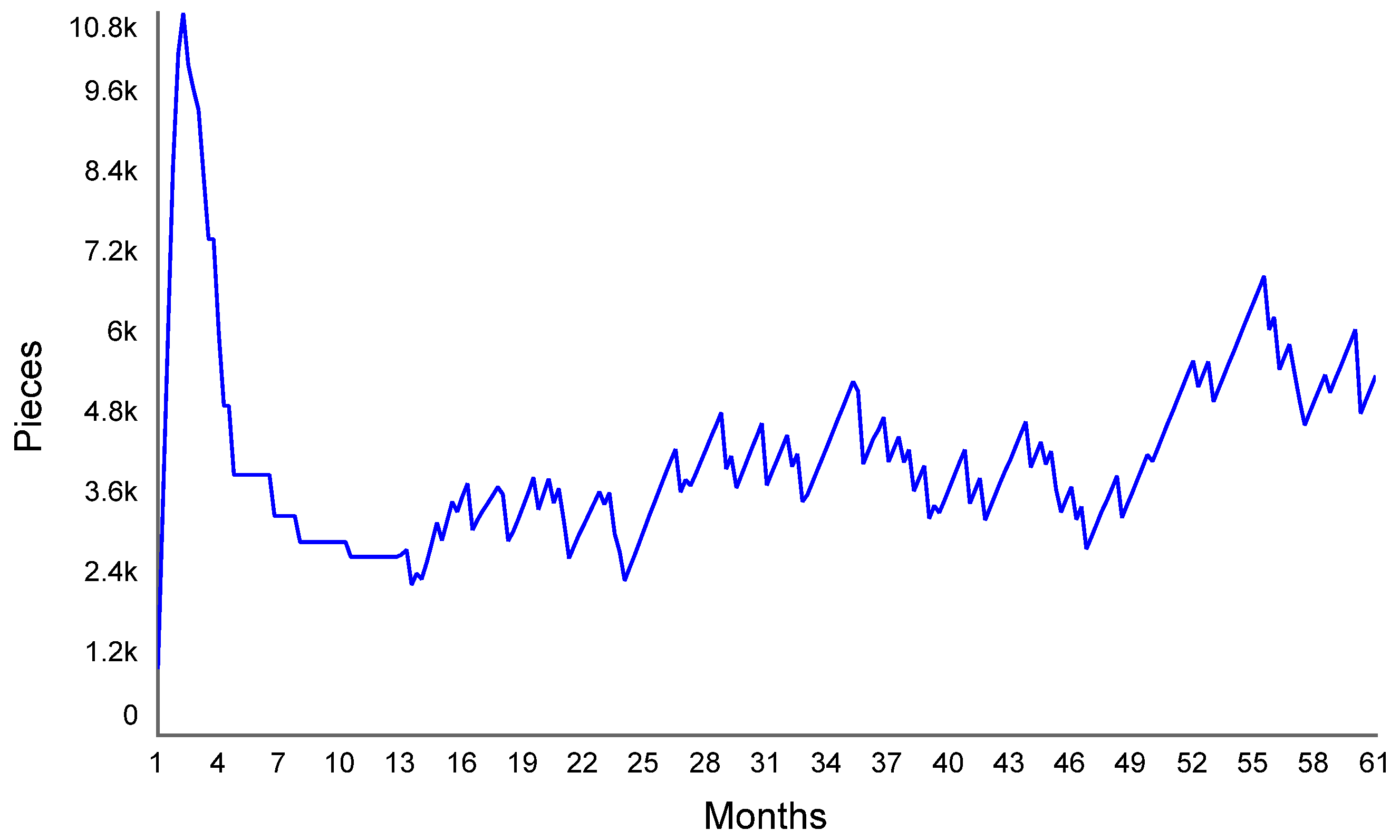
3.1. System Dynamics Model Results
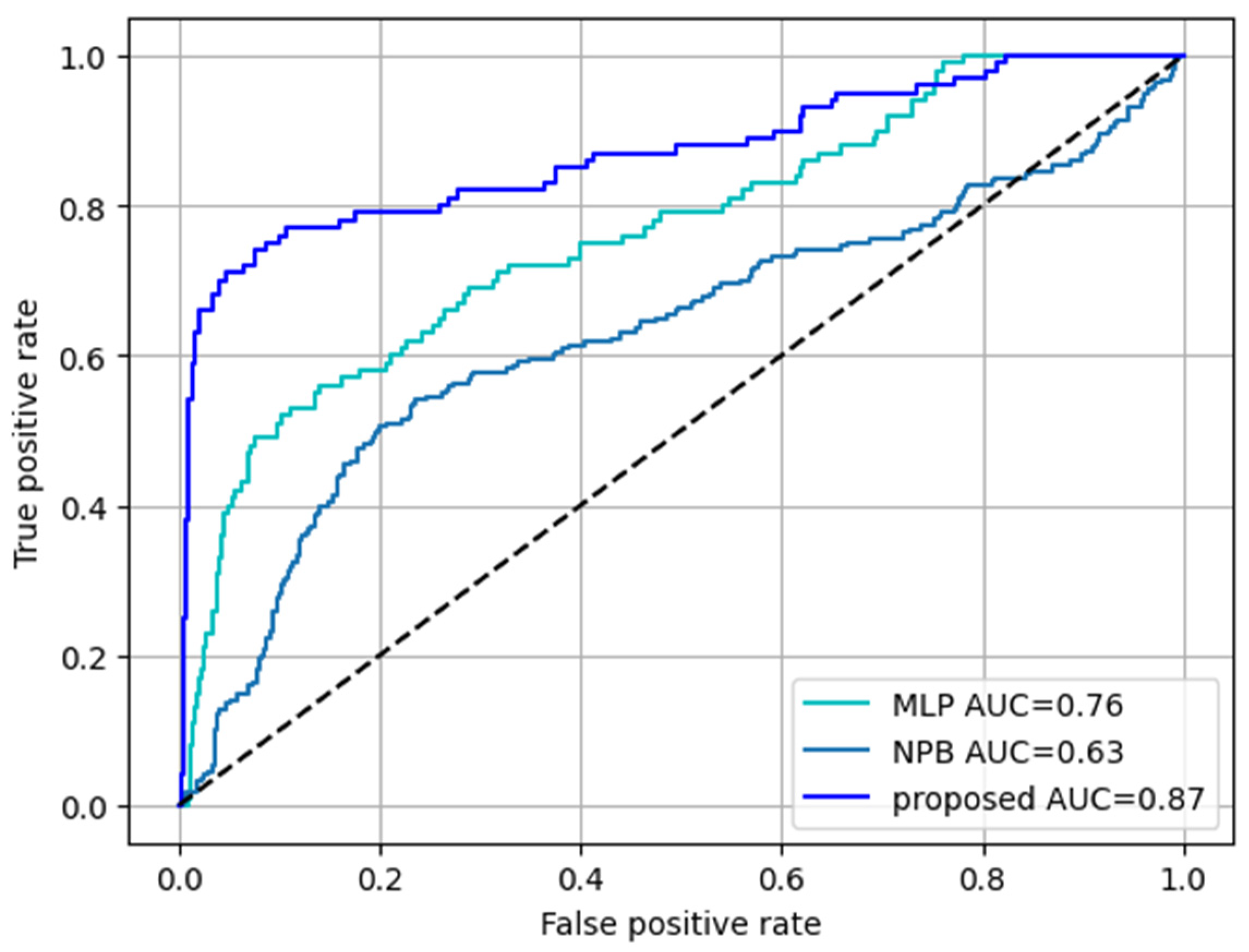
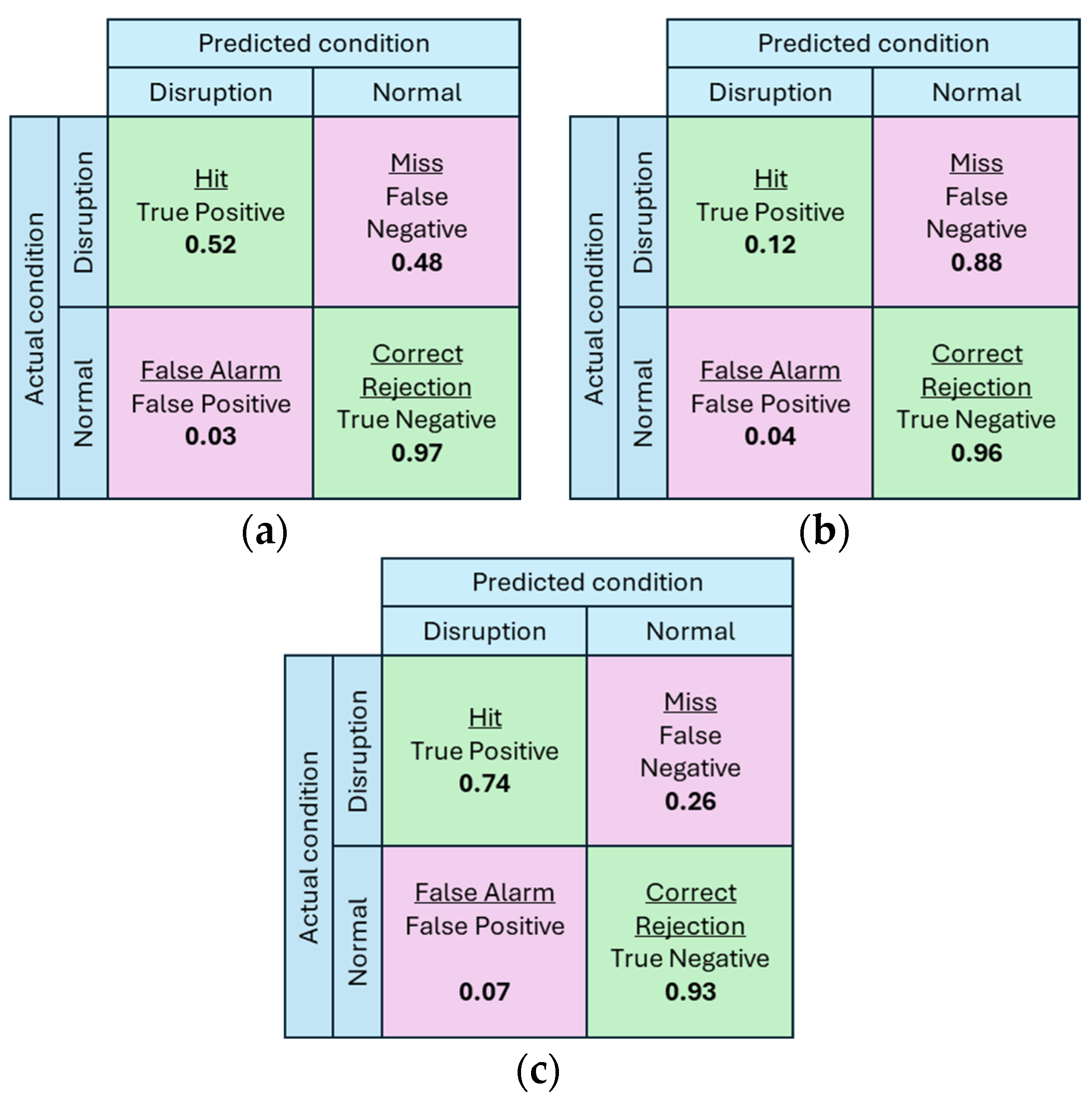
3.2. Network Evaluation in the Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| Tier 1 | Supplier 1 |
| Tier 2 | Supplier 2 |
| SC | Supply chain |
| OEE | Assembly plant |
| SD | Systems dynamic |
References
- Remko, V.H. Research opportunities for a more resilient post-COVID-19 supply chain-closing the gap between research findings and industry practice. Int. J. Oper. Prod. Manag. 2020, 40, 341–355. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A. OR-methodsfor coping with the ripple effect in supply chains during COVID-19 pandemic:Managerial insights and research implications. Int. J. Prod. Econ. 2021, 232, 107921. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101922. [Google Scholar] [CrossRef] [PubMed]
- Cannella, S.; Ponte, B.; Dominguez, R.; Framinan, J.M. Proportional order-up to policies for closed-loop supply chain: The dynamic effects of inventory controllers. Int. J. Prod. Resc. 2021, 59, 3323–3337. [Google Scholar] [CrossRef]
- Matsuo, H. Implications of the Tohoku earthquake for Toyo ota׳s coordination mechanism: Supply chain disruption of automotive semiconductors. Int. J. Prod. Econ. 2015, 161, 217–227. [Google Scholar] [CrossRef]
- Ivanov, D.; Tsipoulanidis, A.; Schönberger, J. Supply Chain Risk Management and Resilienc. In Global Supply Chain and Operations Management: A Decision-Oriented Introduction to the Creation of Value; Ivanov, D., Tsipoulanidis, A., Schönberger, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 485–520. [Google Scholar]
- Mashud, A.H.M.; Hasan, M.R.; Daryanto, Y.; Wee, H.-M. A resilient hybrid payment supply chain inventory model for post COVID-19 recovery. Comput. Ind. Eng. 2021, 157, 107249. [Google Scholar] [CrossRef]
- Saleheen, F.; Habib, M.M. Global Supply Chain Disruption Management Post COVID-19. Am. J. Ind. Bus. Manag. 2022, 12, 376–389. [Google Scholar] [CrossRef]
- Kinra, A.; Ivanov, D.; Das, A.; Dolgui, A. Ripple effect quantification by supplier risk exposure assessment. Int. J. Prod. Res. 2019, 58, 5559–5578. [Google Scholar] [CrossRef]
- Zhong, J.; Jia, F. Supply chain risk transmition monitoring based on graphic evaluation and review technique. Heliyon 2025, 11, e41462. [Google Scholar] [CrossRef]
- Xu, X.; Tatge, L.; Xu, X.; Lio, Y. Block chain application in the supply chain management in German automotive industry. Prod. Plan. Con. 2022, 56, 917–931. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B.; Solovyeva, I.; Dolgui, A.; Jie, F. Dynamic recovery policies for time-critical supply chains under conditions of ripple effect. Int. J. Prod. Res. 2016, 54, 7245–7258. [Google Scholar] [CrossRef]
- Ivanov, D. Simulation-based ripple effect modeling in the supply chain. Int. J. Prod. Res. 2017, 55, 2083–2101. [Google Scholar] [CrossRef]
- Rozhkov, M.; Rozhkov, M. ScienceDirect for capacity production-inventory for capacity production-inventory. IFAC-PapersOnLine 2018, 51, 1448–1452. [Google Scholar] [CrossRef]
- Dolgui, A.; Ivanov, D.; Sokolov, B. Ripple effect in the supply chain: An analysis and recent literature. Int. J. Prod. Res. 2018, 56, 414–430. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A.; Sokolov, B. Scheduling of recovery actions in the supply chain with resilience analysis considerations. Int. J. Prod. Res. 2018, 56, 6473–6490. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A. Low-Certainty-Need (LCN) supply chains: A new perspective in managing disruption risks and resilience. Int. J. Prod. Res. 2019, 57, 5119–5136. [Google Scholar] [CrossRef]
- Ivanov, D. Disruption tails and revival policies: A simulation analysis of supply chain design and production-ordering systems in the recovery and post-disruption periods. Comput. Ind. Eng. 2019, 127, 558–570. [Google Scholar] [CrossRef]
- Hosseini, S.; Ivanov, D.; Dolgui, A. Ripple effect modeling of supplier disruption: Integrated Markov chain and dynamic Bayesian network approach. Int. J. Prod. Res. 2020, 58, 3284–3303. [Google Scholar] [CrossRef]
- Llaguno, A.; Mula, J.; Campuzano-Bolarin, F. State of the art, conceptual framework and simulation analysis of the ripple effect on supply chains. Int. J. Prod. Res. 2021, 60, 2044–2066. [Google Scholar]
- Dolgui, A.; Ivanov, D.; Dolgui, A. Ripple effect and supply chain disruption management: New trends and research directions. Int. J. Prod. Res. 2021, 59, 102–109. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, X.; Feng, L.; Yang, W. Disruption risks in supply chain management: A literature review based on bibliometric analysis. Int. J. Prod. Res. 2020, 58, 3508–3526. [Google Scholar] [CrossRef]
- Ali, S.M.; Bari, A.B.M.M.M.; Rifat, A.A.M.M.; Alharbi, M.; Choudhary, S.; Luthra, S. Modelinging supply chain disruption analytics under insufficient data: A decision support system based on Bayesian hierarchical approach. Int. J. Inf. Manag. Data Insights 2022, 2, 100121. [Google Scholar] [CrossRef]
- Sawik, T. Stochastic optimization of supply chain resilience under ripple effect: A COVID-19 pandemic related study. Omega 2022, 109, 102596. [Google Scholar] [CrossRef]
- Lai, X.; Chen, Z.; Wang, X.; Chiu, C.H. Risk propagation and mitigation mechanisms of disruption and trade risks for a global production network. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 103013. [Google Scholar] [CrossRef]
- Badakhshan, E.; Ball, P. Deploying hybrid modeling to support the development of a digital twin for supply chain master planning under disruptions. Int. J. Prod. Res. 2023, 62, 3606–3637. [Google Scholar] [CrossRef]
- Wilson, M.C. The impact of transportation disruptions on supply chain performance. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 295–320. [Google Scholar] [CrossRef]
- Bueno-solano, A.; Cedillo-campos, M.G. Dynamic impact on global supply chains performance of disruptions propagation produced by terrorist acts. Transp. Res. Part E 2014, 61, 1–12. [Google Scholar] [CrossRef]
- Sánchez-Ramírez, C.; Ramos-Hernández, R.; Fong, J.R.M.; Alor-Hernández, G.; García-Alcaraz, J.L. A system dynamics model to evaluate the impact of production process disruption on order shipping. Appl. Sci. 2020, 10, 208. [Google Scholar] [CrossRef]
- Thomas, V.A.; Mahanty, B. Assessment of emergency sourcing strategy of a supply chain through dynamic simulation approach. J. Ind. Prod. Eng. 2020, 37, 56–69. [Google Scholar] [CrossRef]
- Badakhshan, E.; Humphreys, P.; Maguire, L.; Mcivor, R. Using simulation-based system dynamics and genetic algorithms to reduce the cash flow bullwhip in the supply chain. Int. J. Prod. Res. 2020, 58, 5253–5279. [Google Scholar] [CrossRef]
- Olivares-Aguila, J.; ElMaraghy, W. System dynamics modeling for supply chain disruptions. Int. J. Prod. Res. 2021, 59, 1757–1775. [Google Scholar] [CrossRef]
- Duan, W.; Ma, H.; Xu, D.S. Analysis of the impact of COVID-19 on the coupling of the material flow and capital flow in a closed-loop supply chain. Adv. Prod. Eng. Manag. 2021, 16, 5–22. [Google Scholar] [CrossRef]
- Chen, X. Optimizing Agility in the Pharmaceutical Supply Chain using Digital Twins to Cope with the Ripple Effect. Front. Bus. Econ. Manag. 2024, 17, 338–352. [Google Scholar] [CrossRef]
- Birkie, S.E.; Trucco, P. Do not expect others do what you should! Supply chain complexity and mitigation of the ripple effect of disruption. Int. J. Logist. Manag. 2020, 31, 123–144. [Google Scholar] [CrossRef]
- Konder, B.; Maheut, J.; Konle, M. Simulation methods and digital strategies for supply chains facing disruptions: Insights from a systematic literature review. Sustainability 2024, 16, 5957. [Google Scholar] [CrossRef]
- Garvey, M.D.; Carnovale, S. The rippled newsvendor: A new inventory framework for modeling supply chain risk severity in the presence of risk propagation. Int. J. Prod. Econ. 2020, 228, 105772. [Google Scholar] [CrossRef]
- Lochan, S.A.; Rozanova, T.; Bezpalov, V.V.; Fedyunin, D. Supply chain management and risk management in an environment of stochastic uncertainty (retail). Risk 2021, 9, 197. [Google Scholar] [CrossRef]
- Bhuvaraghavan, S.T.; Hameed, U.M. Visualizing the ripple effect: COVID-19’s impact and predictive insights. Int. J. Eng. Res. Sustain. Technol. 2024, 2, 1–8. Available online: https://www.ijerst.drmgrjournals.org/index.php/ijerst/article/view/70 (accessed on 25 March 2024).
- Ghadge, A.; Er, M.; Ivanov, D.; Chaudhuri, A. Visualization of ripple effect in supply chains under long-term, simultaneous disruptions: A system dynamics approach. Int. J. Prod. Res. 2021, 60, 6173–6186. [Google Scholar] [CrossRef]
- Ivanov, D.; Tsipoulanidis, A.; Schonberger, J. Inventory Management. In Global Supply Chain and Operations Management: A Decision-Oriented Introduction to the Creation of Value; Ivanov, D., Tsipoulanidis, A., Schönberger, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 385–433. [Google Scholar] [CrossRef]
- Bala, B.K.; Arshad, F.M.; Noh, K.M. System Dynamics: Modeling and Simulation; Springer Text in Business and Economics; Springer Nature: Dordrecht, The Netherlands, 2017; Volume 274. [Google Scholar] [CrossRef]
- Liu, C.; Shu, T.; Chen, S.; Wang, S.; Lai, K.K.; Gan, L. An improved grey neural network model for predicting transportation disruptions. Expert Syst. Appl. 2016, 45, 331–340. [Google Scholar]
- Bodendorf, F.; Sauter, M.; Franke, J. A mixed methods approach to analyze and predict supply disruptions by combining causal inference and deep learning. Int. J. Prod. Econ. 2023, 256, 108708. [Google Scholar] [CrossRef]
- Tang, H.; Yuan, Y.; Gong, T. Industrial Chain Disruption Events Monitoring with Deep Learning Methods: A Practical Application in China. Int. J. Intell. Syst. 2023, 2023, 3338184. [Google Scholar] [CrossRef]
- Bradley, J.R. An improved method for managing catastrophic supply chain disruptions. Bus. Horiz. 2014, 57, 483–495. [Google Scholar] [CrossRef]
- Sheffi, Y. Preparing for Disruptions Through Early Detection. J. MIT Sloan Manag. Rev. 2015, 57, 31. [Google Scholar]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. arXiv 2019, arXiv:1905.10437. [Google Scholar] [CrossRef]
- Teuteberg, F. Supply Chain Risk Management: A Neural Network Approach. In Strategies and Tactics in Supply Chain Event Management; Ijioui, R., Emmerich, H., Ceyp, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 99–118. [Google Scholar]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Int. J. Forecast. 1988, 44, 837–845. [Google Scholar] [CrossRef]


| Authors | Research Problem | Methodology | Variables | Limitations |
|---|---|---|---|---|
| [20] | Analyze the impact of the ripple effect in the supply chain | System dynamic approach | Inventory level and service level | Disruption short |
| [21] | The ripple effect analyze | State of the art | Inventory, Capacity | Empirical research |
| [22] | Disruption risk in the supply chain | Bibliometric analysis | Mitigation of disruption risk | Ignoring automotive industry |
| [25] | Disruption risk in the supply chain | System dynamic simulation model risk | Safety stock, inventory level service level, supply disruption | Constant lead time, empirical validation |
| [27] | The effect of transportation disruption on the supply chain | Systems dynamic approach | Customer demand, inventory policy and transportation capacity | Risk mitigation is not covered |
| [28] | Dynamic disruption in the supply chain caused by terrorist acts | System dynamic model | Inventory level, service level, constant lead time, customer demand | Disruption time is short, Availability of data ignored |
| [29] | Impact production process disruption on order shipping | System dynamic model | Order shipping rate, Finish good inventory | Exclude the service level |
| [30] | Analysis of sourcing strategies for supply chain disruption | System dynamic model and control theory | Service level. Lead time, backlog | Generic model and exclude inventory control |
| [31] | Mitigate the costs of inventory and backorder | Combinate system dynamic and genetic algorithms | Inventory cost, backlog cost | Exclude replenishment policies and reorder point |
| [32] | Understanding supply chain disruption | System dynamics | Level service, inventory level, lead time, Backlog | Exclude the variability demand and disruptive risk |
| [33] | Analysis of the disruptions of the material flow | System dynamic modeling | Inventory level, sakes rate | Disruption in short term |
| [34] | Analysis of uncertainty in supply chain disruption | Digital Twin technology | Inventory level, Order fulfillment rate, Delivery time | No including artificial neuronal network |
| [35] | Analize the complexity in supply chain disruption | Multiple regression model approach | Demand, lead time fluctuations | Exclude the severity disruption |
| [36] | Analysis and mitigate the ripple effect in supply chain | Hybrid simulation with artificial neuronal network | Inventory level. Demand | Empirical research |
| [37] | Minimizing supply risk severity | Bayesian network model | Inventory level, Cost, Service level | Assumed that the inventory level and demand were uniform |
| [38] | Analysis of complexity in supply chain risk | Simulation modeling | Demand uncertain, lead time, inventory level, service level | Disruption in short term |
| [39] | Visualizing the ripple effect in supply chain | Machine learning | Demand, accuracy level | Dates of one year |
| [40] | Visualization of the ripple effect in supply chain | System dynamics approach | Inventory level, service level, lead time | Use secondary data |
| Scenarios | Demand Variation | Disrupted Capacity Rate | Lead Time | Delay |
|---|---|---|---|---|
| 1 | 0 | 0 | 0.25 | 0.25 |
| 2 | 0.2 | 0.5 | 0.5 | 0.5 |
| 3 | 0.50 | 0.50 | 0.50 | 0.50 |
| 4 | −0.20 | 0.50 | 0.50 | 0.50 |
| 5 | −0.50 | 0.50 | 0.50 | 0.50 |
| 6 | 0.2 | 0.7 | 1 | 1 |
| 7 | 0.50 | 0.7 | 1 | 1 |
| 8 | 0.7 | 0.7 | 1 | 1 |
| 9 | −0.2 | 0.7 | 1 | 1 |
| 10 | −0.5 | 0.7 | 1 | 1 |
| Class | Method | Precision | Recall | F1-Score |
|---|---|---|---|---|
| MLP | 0.92 | 0.97 | 0.94 | |
| Normal | NP | 0.72 | 0.96 | 0.82 |
| Proposed | 0.95 | 0.93 | 0.94 | |
| MLP | 0.76 | 0.52 | 0.62 | |
| Disruption | NP | 0.57 | 0.12 | 0.20 |
| Proposed | 0.65 | 0.74 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de la Cruz Madrigal, V.H.; Avelar Sosa, L.; Mejía-Muñoz, J.-M.; García Alcaraz, J.L.; Jiménez Macías, E. Dynamical System Modeling for Disruption in Supply Chain and Its Detection Using a Data-Driven Deep Learning-Based Architecture. Logistics 2025, 9, 51. https://doi.org/10.3390/logistics9020051
de la Cruz Madrigal VH, Avelar Sosa L, Mejía-Muñoz J-M, García Alcaraz JL, Jiménez Macías E. Dynamical System Modeling for Disruption in Supply Chain and Its Detection Using a Data-Driven Deep Learning-Based Architecture. Logistics. 2025; 9(2):51. https://doi.org/10.3390/logistics9020051
Chicago/Turabian Stylede la Cruz Madrigal, Víctor Hugo, Liliana Avelar Sosa, Jose-Manuel Mejía-Muñoz, Jorge Luis García Alcaraz, and Emilio Jiménez Macías. 2025. "Dynamical System Modeling for Disruption in Supply Chain and Its Detection Using a Data-Driven Deep Learning-Based Architecture" Logistics 9, no. 2: 51. https://doi.org/10.3390/logistics9020051
APA Stylede la Cruz Madrigal, V. H., Avelar Sosa, L., Mejía-Muñoz, J.-M., García Alcaraz, J. L., & Jiménez Macías, E. (2025). Dynamical System Modeling for Disruption in Supply Chain and Its Detection Using a Data-Driven Deep Learning-Based Architecture. Logistics, 9(2), 51. https://doi.org/10.3390/logistics9020051








