A Bi-Objective Mixed-Integer Linear Programming Model for a Sustainable Agro-Food Supply Chain with Product Perishability and Environmental Considerations
Abstract
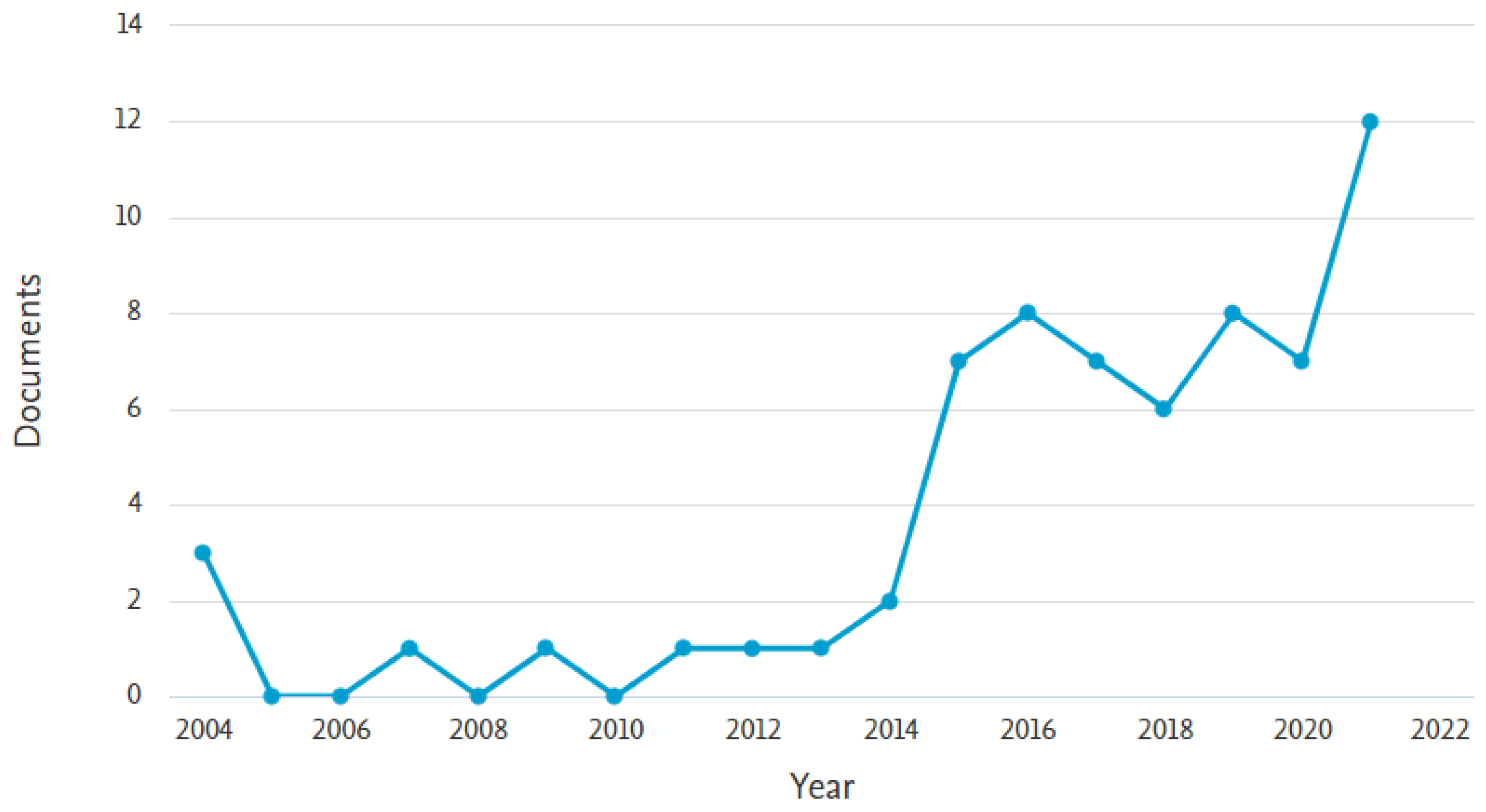
1. Introduction
- The development of a mixed-integer linear programming (MILP) model for AFSC design;
- The integration of crop rotation planning into SC design, considering factors such as crop allocation and the timing of harvesting;
- The incorporation of tactical decisions in the SCN, including transportation, storage, processing, demand fulfillment, and waste management;
- The consideration of seasonality of yield and demand, as well as the perishability of crops and products;
- An analysis of multiple cropping seasons through a rotation cycle.
2. Literature Review
2.1. Special Features of AFSCs
2.2. The Design of AFSCs
2.2.1. Economic Objective
2.2.2. Economic and Environmental Objectives
2.2.3. Economic, Environmental, and Social Objectives
2.3. Research Gaps and Article Contributions
- Inadequate consideration of agricultural decisions in the context of AFSC, such as the seasonality and perishability of crops and the timing of harvesting;
- Insufficient attention to the design of an AFSC for multiple products with different planning levels over a multi-period planning horizon;
- Limited focus on optimizing the environmental dimension of sustainability in an AFSC.
- It proposes a novel strategic tactical decision support planning model that integrates agricultural decisions represented in strategic crop rotation schedules, with the tactical design of an AFSC that includes transportation, inventory, processing decisions, and waste disposal;
- It accounts for the seasonal variability of agro-materials and the perishable nature of non-processed and processed products by directly incorporating shelf life constraints while simultaneously maximizing profits across the entire SC and minimizing the negative environmental impact represented in CO2 emissions.
3. Problem Description
- The agricultural stage;
- The coupling and transportation stage;
- The industrial stage.

4. Proposed Mathematical Model
- The selection of plots to be planted as well as the crops to be planted on them in addition to the planting period;
- The selection of the harvesting period as well as estimating the harvested quantity from each crop in each plot at each period;
- The calculation of the transported quantity from each farm to each processing facility per period as well as the number of trips needed to transport such quantity;
- The determination of the processed quantity of products at each processing facility per period;
- The estimation of the total stored quantity from both non-processed and processed products at each processing facility per period;
- The determination of the satisfied demand and lost sales, if any.
4.1. Model Assumptions
- The estimated yield for each crop in each period is known, which mainly depends on the harvested period and its maturation level;
- The farm consists of homogenous plots of standard sizes; therefore, the obtained yield is the same in any plot;
- The expected crop yield and irrigation water depend only on the present crop, regardless of the preceding crop;
- The total annual available water is constant for all the years in the rotation cycle;
- Each crop has a known deterministic demand in each period;
- There is no water stored in the soil;
- The harvested quantity is transported to the processing facility immediately after harvesting in the same harvesting period;
- Inventory is held at the processing facilities only; hence, there is no inventory on the fields;
- Processing facilities have a fixed processing capacity;
- Crops and products which exceed their shelf life are disposed of immediately in the same period;
- The age of crops used to process a specific product has no effect on its shelf life after processing.
4.2. Model Nomenclature
| Set of crops | ||
| Set of periods | ||
| Set of years in the rotation cycle | ||
| Allowable harvesting periods for crop in year | ||
| Set of crop families where represents the legume family and represents the fallow periods (unplanted periods) | ||
| Set of plots | ||
| Set of processing facilities | ||
| Set of vehicles | ||
| Set of products produced from a specific crop (e.g., is the set of products produced from crop 1) | ||
| Index indicating the age of a crop since its harvesting in periods | ||
| Index indicating the age of a product since its production in periods |
| Starting period of planting crop in year , with ∈ | |
| Production time required for planting crop (maturation period) | |
| Ending period of harvesting crop in year , with ∈ | |
| Number of crop families | |
| Expected harvested percentage of crop harvested in period on plot (%) | |
| Optimum yield quantity of crop planted on plot (ton/ha) | |
| Minimum threshold on the required plots from crop in year | |
| Maximum threshold on the required plots from crop in year | |
| Number of plots available per year | |
| The required amount of water for irrigating crop () | |
| The total annual available amount of water () | |
| Planting frequency of crop during the rotation cycle | |
| Frequency modification factor for crop | |
| The reciprocal of frequency of crop | |
| The rotation cycle length in years | |
| TS | Annual time slots |
| PS | Number of different planting seasons per year |
| Minimum maturation period for crop , | |
| Maximum maturation period for crop , | |
| Truck capacity for transporting crops using vehicle (ton) | |
| Maximum number of trips from plot | |
| Total number of trips for vehicle during period | |
| Maximum required supply from crop in period to facility (ton/period) | |
| Processing capacity of product in period in facility (ton/period) | |
| The conversion factor for producing product in facility (ton/ton) | |
| The demand of product in period at facility (ton) | |
| Distance between plot and facility (km) | |
| Cost per km of transporting crop using vehicle (EUR/km⋅ton) | |
| Holding cost of crop in period in facility (EUR/ton⋅period) | |
| Holding cost of product in period in facility (EUR/ton⋅period) | |
| Agriculturally related CO2-eq emissions of the production of crop (ton CO2-eq/hectare) | |
| Transportation-related CO2-eq emissions for transporting crop using vehicle (ton CO2-eq/ton⋅km) | |
| Processing related CO2-eq emissions of product in facility | |
| Disposal-related CO2-eq emissions of crop (ton CO2-eq/ton) | |
| Disposal-related CO2-eq emissions of product (ton CO2-eq/ton) | |
| Maximum shelf life of crop (periods) | |
| Maximum shelf life of product (periods) | |
| Minimum threshold of the fulfilled demand from product during the rotation cycle (ton) | |
| Maximum threshold of the fulfilled demand from product during the rotation cycle (ton) | |
| Processing cost of product in facility (EUR/ton) | |
| Price of selling product (EUR/ton) | |
| Disposal cost of crop (EUR/ton) | |
| Disposal cost of product (EUR/ton) | |
| Penalty cost of lost sales from product (EUR/ton) |
4.3. Model Formulation
4.3.1. Decision Variables
| Harvested quantity from crop harvested in period from plot | |
| Shipped quantity of crop harvested in period from plot to facility using vehicle | |
| Required number of trips to transport crop harvested in period from plot to facility using vehicle | |
| Available quantity from crop in period at facility with age | |
| Inventory of crop in period at facility with age | |
| Processed quantity of product in period in facility made from crop of age | |
| Inventory of product in period at facility with age | |
| Disposed waste from crop in period facility with age | |
| Disposed waste from product in period facility with age | |
| Fulfilled demand from product in period from facility of age | |
| Lost sales from product in period from facility |
4.3.2. Objective Functions
- Cost of shipping the crops from plots to the processing facilities;
- Holding cost of storing crops and products in the processing facilities;
- Cost of disposing waste from crops and products which exceed their shelf lives;
- The processing cost of products;
- Penalty cost of unfulfilled product demand.
4.3.3. Constraints
- Each crop has its criteria, including the planting and harvesting dates and the associated demand;
- Each crop requires different amounts of water for irrigation that must be satisfied at a given time period;
- Crops belong to different botanic families. The same crops or crops from the same family cannot be planted in succession;
- At least one legume crop should be planted on each plot during the rotation cycle; this would positively affect the soil and the yield obtained;
- Every cycle should involve at least one fallow period to allow the soil to restore its moisture and fertility content.
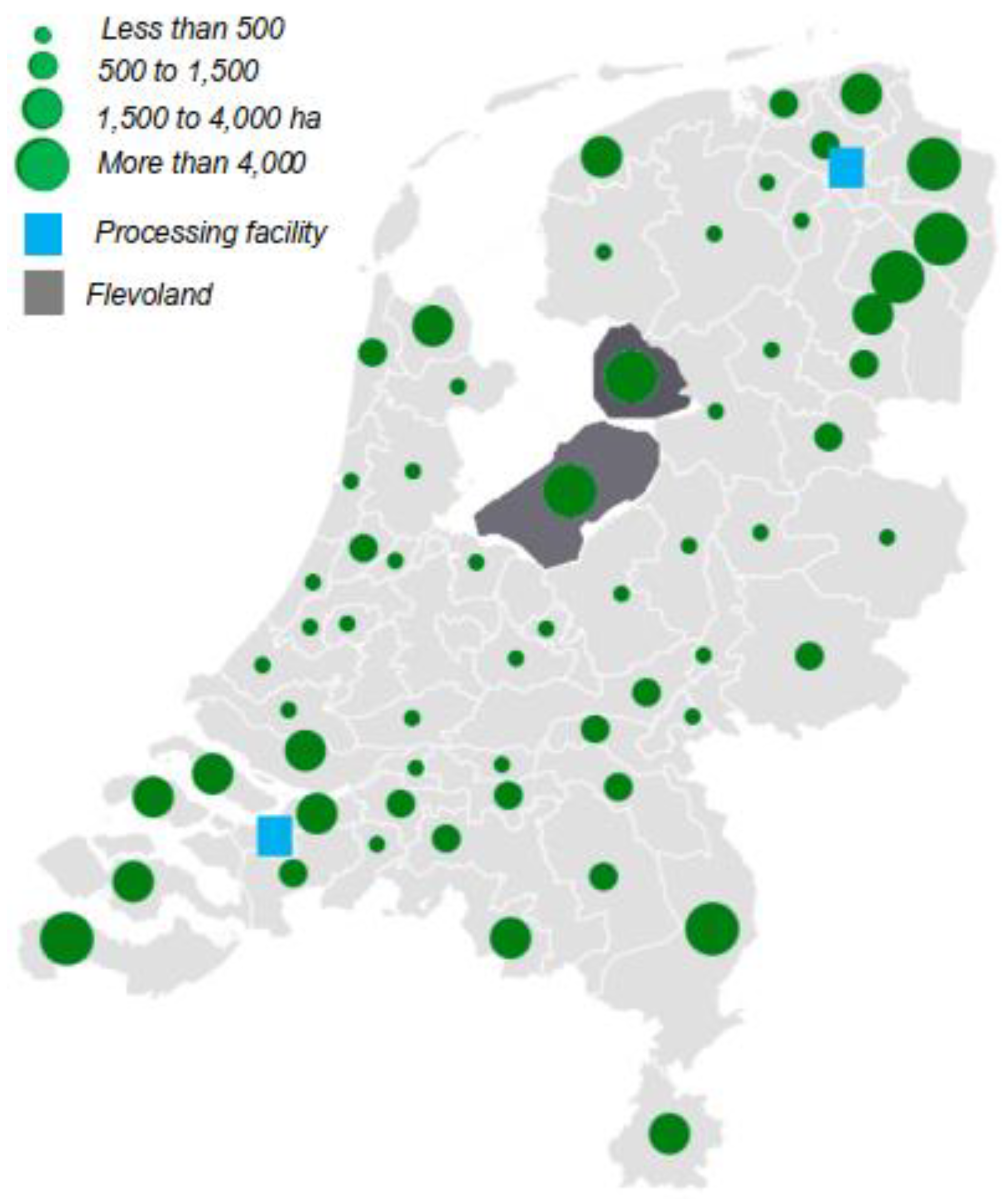
5. Case Study Description
| Crop | Family | [36] ( ) | Yield [37] (tons/ha) | Sowing Date [39] | Harvesting Date [39] | Maturity Period [39] (Days) |
|---|---|---|---|---|---|---|
| Sugar beet | Chenopodiaceae | 1/4 | 90–100 | April | October–November | 285–305 |
| Winter wheat | grass (Cereal) | 1/4 | 8.7 | September–October | August | 210–230 |
| Green peas | Legumes | 1/6 | 5.7 | March | November | 300–315 |
| Seed potato | Nightshade | 1/4 | 38.7 | March–April | July–September | 220–230 |
| Seed onion | Amaryllidaceae | 1/6 | 37 | March | June-July | 215–235 |
| Winter rapeseed | Brassica | 1/4 | 3.5 | January | December | 300–315 |
| Barley (spring) | grass (Cereal) | 1 | 6.3 | April | September | 215–235 |
| Maize (silage) | grass (Cereal) | 1 | 40.8 | April | November | 275–295 |
| Onions | Amaryllidaceae | 1/6 | 58.4 | March | July–August | 235–250 |
| Potatoes (ware) | Nightshade | 1/3 | 56.8 | March–April | August–September | 255–275 |
| Wheat (spring) | grass (Cereal) | 1/2 | 7.8 | April | September | 215–235 |
| Winter carrot | Apiaceae | 1/6 | 70 | September–October | September–October | 70–80 |
| Parameter | Value |
|---|---|
| Truck capacity | 50 ton |
| White sugar conversion rate [40] | 0.14625 ton/ton |
| Daily processing capacity [41] | 10 ton |
| Parameter | Value |
|---|---|
| White sugar selling price [41] | 500 EUR/ton |
| Transportation cost [40] | 0.1 EUR/ton⋅km |
| White sugar processing cost in a traditional facility design [41] | 65.49 EUR/ton |
| Holding cost of white sugar [2] | 0.1 EUR/day⋅ton |
| Holding cost of sugar beet [7] | 0.15 EUR/day⋅ton |
| Disposal cost of white sugar [2] | 10 EUR/ton |
| Disposal cost of sugar beet | 10 EUR/ton |
| Penalty for lost sales | 250 EUR/ton |
6. Results and Discussion
6.1. Model Verification and Validation
6.2. Case Results and Discussion
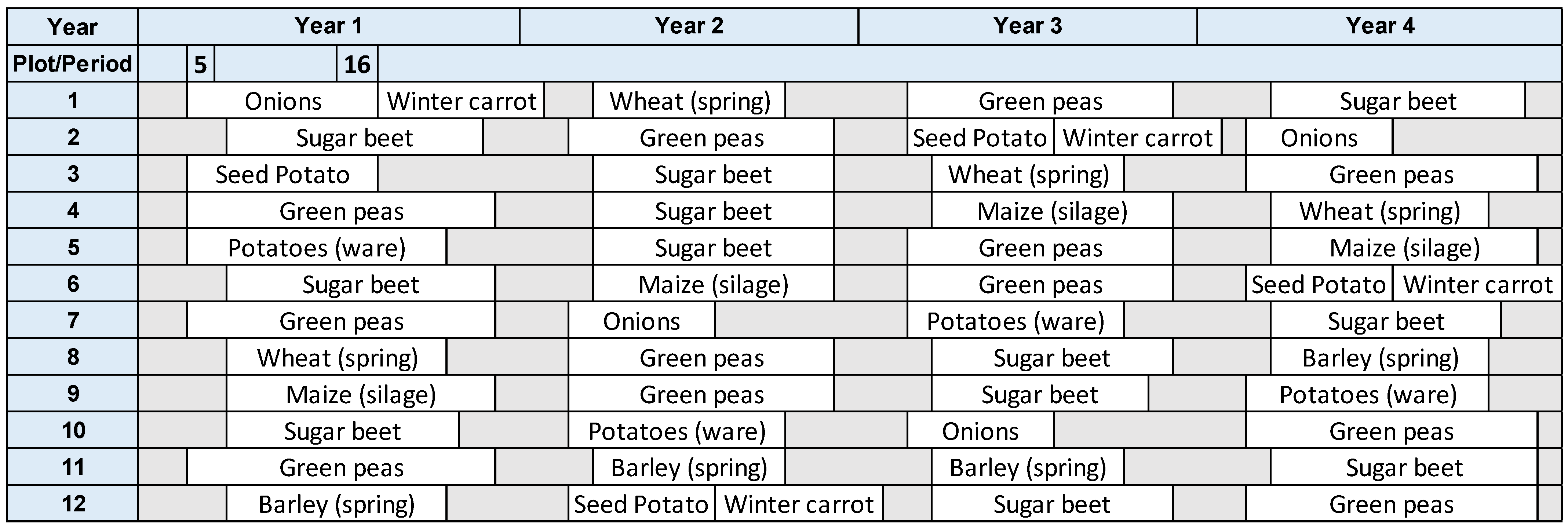
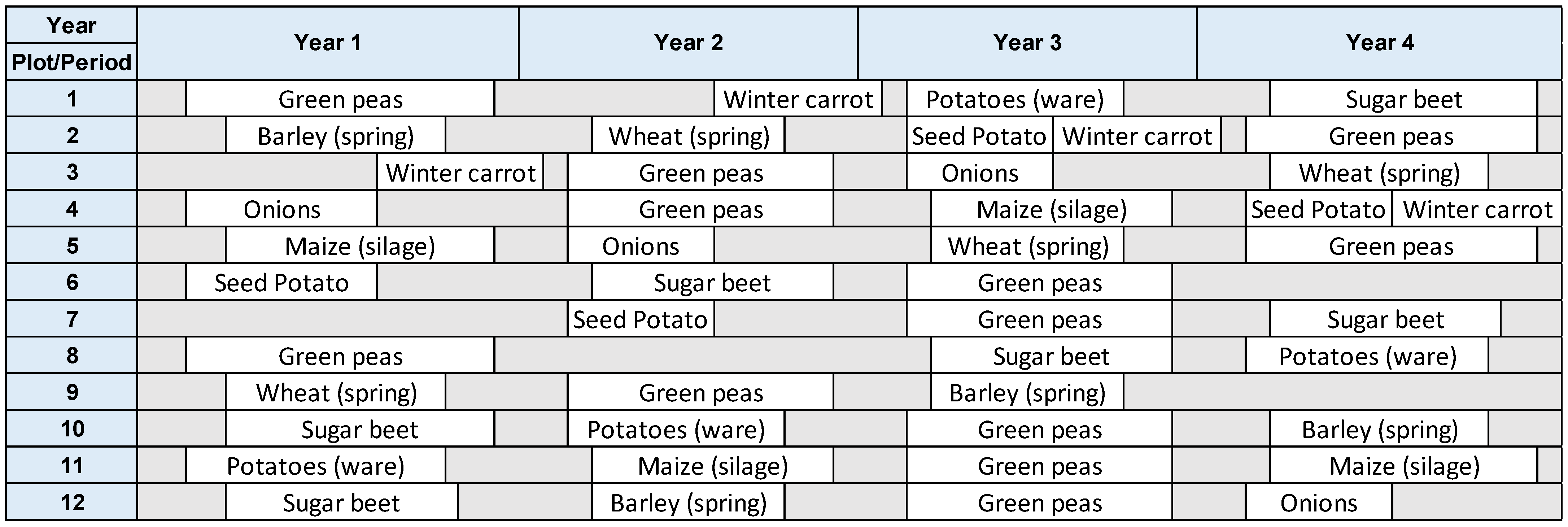
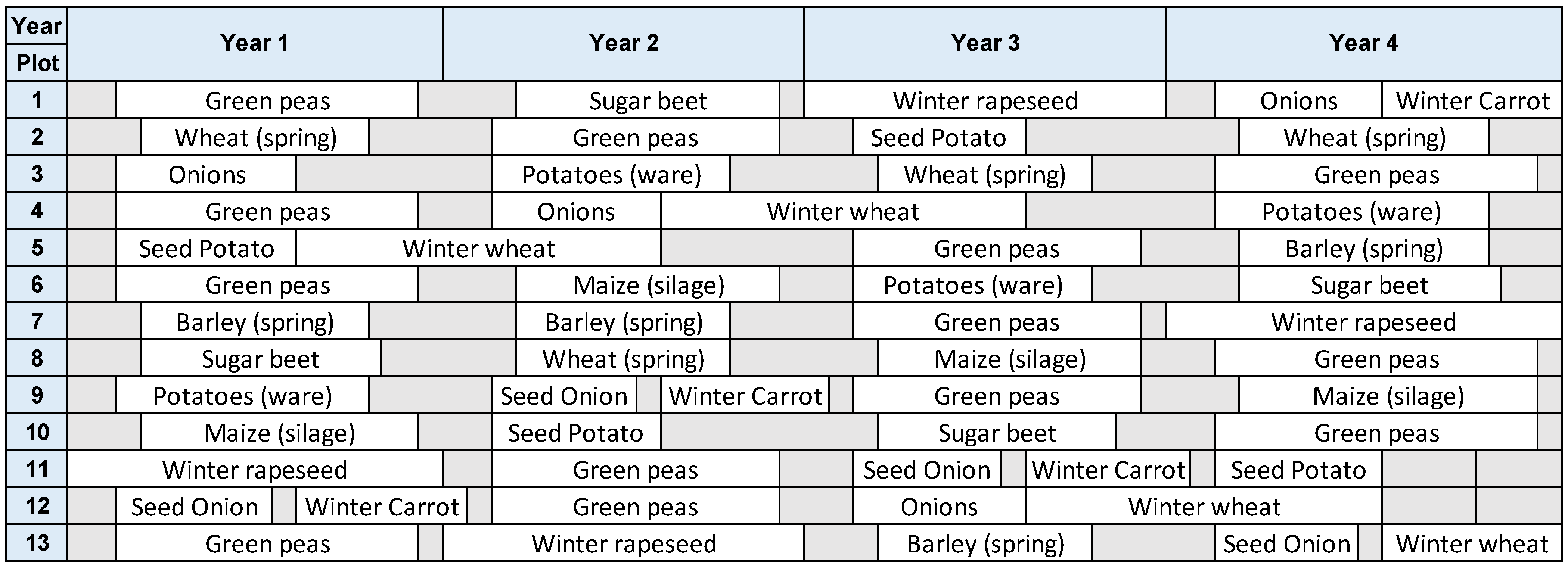
6.2.1. Farm Schedule
- Which crops will be planted in which plots and in which period?
- When should planted crops be harvested?
- Scenario 1 entails satisfying a certain demand from each crop (e.g., contract farming) where a maximum and minimum threshold on the number of annual plots that should be planted with specific crops are used;
- Scenario 2 entails that each crop should be planted annually during the rotation cycle (crop mix).
6.2.2. Optimum SCN
- The model tends to keep inventory from processed products (white sugar) rather than from crops (sugar beet) because of two main reasons. The first reason is that storing crops costs more than storing processed products due to the need for special setups that would prevent crops from spoiling. The second reason is that processing positively affects the perishability of products resulting in products with a longer shelf life that can be stored and kept longer across the SC;
- There was no waste generated across the SC which is due to the relatively long shelf life of sugar beet and white sugar in addition to the model’s tendency to minimize waste whatever the objective is because disposing of waste is of a high cost and emits CO2 emissions with no added value to the SCN.
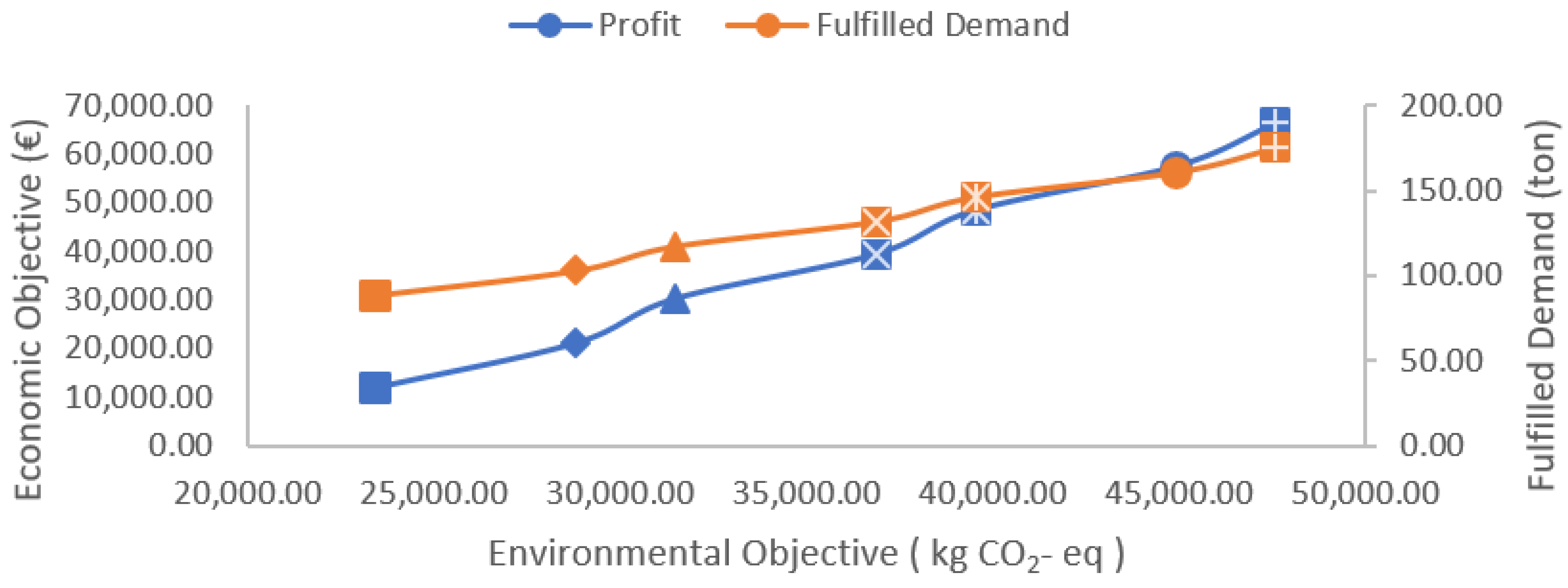
6.2.3. Multi-Objective Optimization and Trade-Off Analysis
| Algorithm 1. Multi-Objective Optimization Algorithm Using ε-constraint Method. |
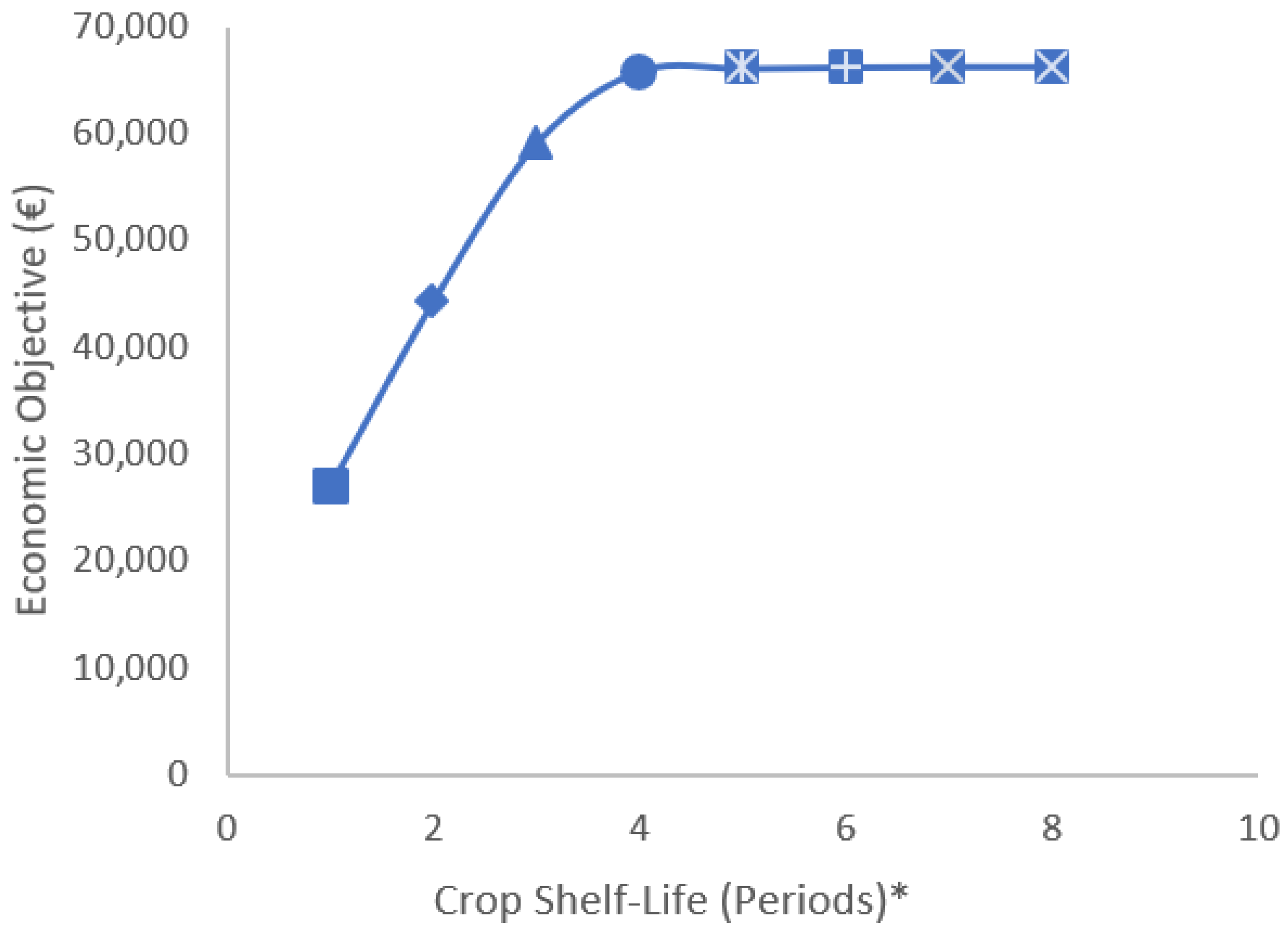
6.2.4. Quantifying the Impact of Perishability on the Economic Objective
6.2.5. Managerial Insights
6.3. Model Performance Test
7. Conclusions and Directions of Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- van der Goot, A.J.; Pelgrom, P.J.M.; Berghout, J.A.M.; Geerts, M.E.J.; Jankowiak, L.; Hardt, N.A.; Keijer, J.; Schutyser, M.A.I.; Nikiforidis, C.V.; Boom, R.M. Concepts for Further Sustainable Production of Foods. J. Food Eng. 2016, 168, 42–51. [Google Scholar] [CrossRef]
- Jonkman, J.; Barbosa-Póvoa, A.P.; Bloemhof, J.M. Integrating Harvesting Decisions in the Design of Agro-Food Supply Chains. Eur. J. Oper. Res. 2019, 276, 247–258. [Google Scholar] [CrossRef]
- Gustavsson, J. (Ed.) Global Food Losses and Food Waste: Extent, Causes and Prevention; Study Conducted for the International Congress Save Food! At Interpack 2011, [16–17 May], Düsseldorf, Germany; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011; ISBN 978-92-5-107205-9. [Google Scholar]
- Naylor, R. Expanding the Boundaries of Agricultural Development. Food Secur. 2011, 3, 233–251. [Google Scholar] [CrossRef]
- Ahumada, O.; Villalobos, J.R. Application of Planning Models in the Agri-Food Supply Chain: A Review. Eur. J. Oper. Res. 2009, 196, 1–20. [Google Scholar] [CrossRef]
- Soto-Silva, W.E.; Nadal-Roig, E.; González-Araya, M.C.; Pla-Aragones, L.M. Operational Research Models Applied to the Fresh Fruit Supply Chain. Eur. J. Oper. Res. 2016, 251, 345–355. [Google Scholar] [CrossRef]
- Fikry, I.; Gheith, M.; Eltawil, A. An Integrated Production-Logistics-Crop Rotation Planning Model for Sugar Beet Supply Chains. Comput. Ind. Eng. 2021, 157, 107300. [Google Scholar] [CrossRef]
- Fikry, I.; Gheith, M.; Eltawil, A. A New Mathematical Model for the Deterministic Crop Rotation Planning Problem. In Proceedings of the 2019 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Macao, China, 15–19 December 2019; IEEE: Piscataway, NI, USA, 2019; pp. 314–318. [Google Scholar]
- Zegada-Lizarazu, W.; Monti, A. Energy Crops in Rotation. A Review. Biomass Bioenergy 2011, 35, 12–25. [Google Scholar] [CrossRef]
- Kusumastuti, R.D.; van Donk, D.P.; Teunter, R. Crop-Related Harvesting and Processing Planning: A Review. Int. J. Prod. Econ. 2016, 174, 76–92. [Google Scholar] [CrossRef]
- Accorsi, R.; Cholette, S.; Manzini, R.; Pini, C.; Penazzi, S. The Land-Network Problem: Ecosystem Carbon Balance in Planning Sustainable Agro-Food Supply Chains. J. Clean. Prod. 2016, 112, 158–171. [Google Scholar] [CrossRef]
- New FAO Analysis Reveals Carbon Footprint of Agri-Food Supply Chain. Available online: https://news.un.org/en/story/2021/11/1105172 (accessed on 30 January 2022).
- Banasik, A.; Kanellopoulos, A.; Bloemhof-Ruwaard, J.M.; Claassen, G.D.H. Accounting for Uncertainty in Eco-Efficient Agri-Food Supply Chains: A Case Study for Mushroom Production Planning. J. Clean. Prod. 2019, 216, 249–256. [Google Scholar] [CrossRef]
- Chaabane, A.; Ramudhin, A.; Paquet, M. Designing Supply Chains with Sustainability Considerations. Prod. Plan. Control 2011, 22, 727–741. [Google Scholar] [CrossRef]
- Quariguasi Frota Neto, J.; Walther, G.; Bloemhof, J.; van Nunen, J.A.E.E.; Spengler, T. A Methodology for Assessing Eco-Efficiency in Logistics Networks. Eur. J. Oper. Res. 2009, 193, 670–682. [Google Scholar] [CrossRef]
- Esteso, A.; Alemany, M.M.E.; Ortiz, Á. Impact of Product Perishability on Agri-Food Supply Chains Design. Appl. Math. Model. 2021, 96, 20–38. [Google Scholar] [CrossRef]
- Lucas, M.T.; Chhajed, D. Applications of Location Analysis in Agriculture: A Survey. J. Oper. Res. Soc. 2004, 55, 561–578. [Google Scholar] [CrossRef]
- Rong, A.; Akkerman, R.; Grunow, M. An Optimization Approach for Managing Fresh Food Quality throughout the Supply Chain. Int. J. Prod. Econ. 2011, 131, 421–429. [Google Scholar] [CrossRef]
- de Keizer, M.; Akkerman, R.; Grunow, M.; Bloemhof, J.M.; Haijema, R.; van der Vorst, J.G.A.J. Logistics Network Design for Perishable Products with Heterogeneous Quality Decay. Eur. J. Oper. Res. 2017, 262, 535–549. [Google Scholar] [CrossRef]
- Institute of Food Science and Technology of the United Kingdom. Shelf Life of Foods Guidelines for Its Determination and Prediction; Institute of Food Science and Technology: London, UK, 1993. [Google Scholar]
- Akkerman, R.; Farahani, P.; Grunow, M. Quality, Safety and Sustainability in Food Distribution: A Review of Quantitative Operations Management Approaches and Challenges. OR Spectr. 2010, 32, 863–904. [Google Scholar] [CrossRef]
- van Elzakker, M.A.H.; Zondervan, E.; Raikar, N.B.; Hoogland, H.; Grossmann, I.E. Optimizing the Tactical Planning in the Fast Moving Consumer Goods Industry Considering Shelf-Life Restrictions. Comput. Chem. Eng. 2014, 66, 98–109. [Google Scholar] [CrossRef]
- Hajimirzajan, A.; Vahdat, M.; Sadegheih, A.; Shadkam, E.; Bilali, H.E. An Integrated Strategic Framework for Large-Scale Crop Planning: Sustainable Climate-Smart Crop Planning and Agri-Food Supply Chain Management. Sustain. Prod. Consum. 2021, 26, 709–732. [Google Scholar] [CrossRef]
- Sinha, A.K.; Anand, A. Optimizing Supply Chain Network for Perishable Products Using Improved Bacteria Foraging Algorithm. Appl. Soft Comput. 2020, 86, 105921. [Google Scholar] [CrossRef]
- Fikry, I.; Eltawil, A.; Gheith, M. A Robust Crop Rotation Optimization Model With Water Scarcity and Net Return Uncertainty Considerations. IEEE Access 2021, 9, 128938–128950. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Sohrabi, M.; Rabbani, M.; Molana, S.M.H.; Werner, F. Sustainable Phosphorus Fertilizer Supply Chain Management to Improve Crop Yield and P Use Efficiency Using an Ensemble Heuristic–Metaheuristic Optimization Algorithm. Agronomy 2023, 13, 565. [Google Scholar] [CrossRef]
- Jaehn, F. Sustainable Operations. Eur. J. Oper. Res. 2016, 253, 243–264. [Google Scholar] [CrossRef]
- Liu, A.; Zhu, Q.; Xu, L.; Lu, Q.; Fan, Y. Sustainable Supply Chain Management for Perishable Products in Emerging Markets: An Integrated Location-Inventory-Routing Model. Transp. Res. Part E Logist. Transp. Rev. 2021, 150, 102319. [Google Scholar] [CrossRef]
- Allaoui, H.; Guo, Y.; Choudhary, A.; Bloemhof, J. Sustainable Agro-Food Supply Chain Design Using Two-Stage Hybrid Multi-Objective Decision-Making Approach. Comput. Oper. Res. 2018, 89, 369–384. [Google Scholar] [CrossRef]
- Sazvar, Z.; Rahmani, M.; Govindan, K. A Sustainable Supply Chain for Organic, Conventional Agro-Food Products: The Role of Demand Substitution, Climate Change and Public Health. J. Clean. Prod. 2018, 194, 564–583. [Google Scholar] [CrossRef]
- Taghikhah, F.; Voinov, A.; Shukla, N.; Filatova, T.; Anufriev, M. Integrated Modeling of Extended Agro-Food Supply Chains: A Systems Approach. Eur. J. Oper. Res. 2021, 288, 852–868. [Google Scholar] [CrossRef]
- Rohmer, S.U.K.; Gerdessen, J.C.; Claassen, G.D.H. Sustainable Supply Chain Design in the Food System with Dietary Considerations: A Multi-Objective Analysis. Eur. J. Oper. Res. 2019, 273, 1149–1164. [Google Scholar] [CrossRef]
- Onggo, B.S.; Panadero, J.; Corlu, C.G.; Juan, A.A. Agri-Food Supply Chains with Stochastic Demands: A Multi-Period Inventory Routing Problem with Perishable Products. Simul. Model. Pract. Theory 2019, 97, 101970. [Google Scholar] [CrossRef]
- Fikry, I.; Gheith, M.; Eltawil, A. A New Formulation and Solution for the Crop Rotation Planning Problem. In Proceedings of the International Conference on Computers and Industrial Engineering, CIE, Beijing, China, 18–21 October 2019; Volume 2019. [Google Scholar]
- CBS Centraal Bureau Voor de Statistiek. Available online: https://www.cbs.nl/ (accessed on 12 February 2022).
- Asadi, M. Beet-Sugar Handbook; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Mandryk, M.; Reidsma, P.; Kanellopoulos, A.; Groot, J.C.J.; van Ittersum, M.K. The Role of Farmers’ Objectives in Current Farm Practices and Adaptation Preferences: A Case Study in Flevoland, the Netherlands. Reg. Environ. Chang. 2014, 14, 1463–1478. [Google Scholar] [CrossRef]
- Hardenburg, R.E.; Watada, A.E.; Wang, C. The Commercial Storage of Fruits, Vegetables, and Florist and Nursery Stocks; Agriculture Handbook No.66 Revis; US Department of Agriculture: Washington, DC, USA, 1986.
- Wolf, J.; Mandryk, M.; Kanellopoulos, A.; van Oort, P.A.J.; Schaap, B.F.; Reidsma, P.; van Ittersum, M.K. Methodologies for Analyzing Future Farming Systems in Flevoland as Applied within the AgriAdapt Project; Wageningen UR: Wageningen, The Netherlands, 2010. [Google Scholar]
- Kolfschoten, R.C.; Bruins, M.E.; Sanders, J.P.M. Opportunities for Small-Scale Biorefinery for Production of Sugar and Ethanol in the Netherlands. Biofuels Bioprod. Biorefining 2014, 8, 475–486. [Google Scholar] [CrossRef]
- Jonkman, J.; Bloemhof, J.M.; van der Vorst, J.G.A.J.; van der Padt, A. Selecting Food Process Designs from a Supply Chain Perspective. J. Food Eng. 2017, 195, 52–60. [Google Scholar] [CrossRef]
| Publication | Planning Level | AD | CR | Tr | Industrial Stage | Products | Se | Pe | Horizon | EI | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | T | O | P | St | Si | M | SP | MP | |||||||
| Accorsi et al., 2016 [11] | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| Allaoui et al., 2018 [29] | √ | √ | √ | √ | √ | √ | √ | ||||||||
| Sazvar et al., 2018 [30] | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| Banasik et al., 2019 [13] | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| Jonkman et al., 2019 [2] | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||
| Onggo et al., 2019 [33] | √ | √ | √ | √ | √ | √ | √ | ||||||||
| Rohmer et al., 2019 [32] | √ | √ | √ | √ | √ | √ | √ | ||||||||
| Sinha et.al, 2020 [24] | √ | √ | √ | √ | √ | ||||||||||
| Esteso et al., 2021 [16] | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||
| Fikry et al., 2021 [7] | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||||
| Hajimirzajan et al., 2021 [23] | √ | √ | √ | √ | √ | √ | √ | √ | √ | ||||||
| Liu et al., 2021 [28] | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| Taghikhah et al., 2021 [31] | √ | √ | √ | √ | √ | √ | √ | √ | |||||||
| This paper | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | √ | |||
| Publication | Objective Function | Modeling/Solution Approach | |
|---|---|---|---|
| Single | Multiple | ||
| Accorsi et al., 2016 [11] | √ | Linear programing/Gurobi | |
| Allaoui et al., 2018 [29] | √ | MILP/LP Solver | |
| Sazvar et al., 2018 [30] | √ | Mixed-integer non-linear programing/CPLEX | |
| Banasik et al., 2019 [13] | √ | Linear programing/Xpress-IVE | |
| Jonkman et al., 2019 [2] | √ | MILP/CPLEX | |
| Onggo et al., 2019 [33] | √ | MILP/hybrid method (heuristics and Monte Carlo simulation) using Java application | |
| Rohmer et al., 2019 [32] | √ | Linear programing/Xpress-IVE | |
| Sinha et.al, 2020 [24] | √ | Mathematical model/approximate method (improved bacteria foraging algorithm) | |
| Esteso et al., 2021 [16] | √ | MILP/Gurobi | |
| Fikry et al., 2021 [7] | √ | MILP/Gurobi | |
| Hajimirzajan et al., 2021 [23] | √ | MILP/CPLEX | |
| Liu et al., 2021 [28] | √ | Mixed-integer non-linear programing/YALMIP (MATLAB Toolbox) | |
| Taghikhah et al., 2021 [31] | √ | Hybrid simulation modeling/AnyLogic | |
| This paper | √ | MILP/Gurobi | |
| Obj. Function | THQ (tons) | TTQ (tons) | NTU | TCI (tons) | TPP (tons) | TPI (tons) | FD (tons) | LS (tons) | CW (tons) | PW (tons) |
|---|---|---|---|---|---|---|---|---|---|---|
| Eco. | 1200 | 1200 | 24 | 0 | 176 | 440 | 176 | 0 | 0 | 0 |
| Env. | 600 | 600 | 12 | 0 | 88 | 77 | 88 | 88 | 0 | 0 |
| Conf. | Env. Obj. (kg CO2-eq) | Eco. Obj. (EUR) | THQ (tons) | TTQ (tons) | NTU | TCI (tons) | TPP (tons) | TPI (tons) | FD (tons) | LS (tons) | CW (tons) | PW (tons) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 47,616 | 66,241 | 1200 | 1200 | 24 | 0 | 175 | 440 | 175 | 0 | 0 | 0 |
| 2 | 44,930 | 57,374 | 1100 | 1100 | 22 | 0 | 161 | 337 | 161 | 15 | 0 | 0 |
| 3 | 39,557 | 48,362 | 1000 | 1000 | 20 | 0 | 146 | 266 | 146 | 29 | 0 | 0 |
| 4 | 36,870 | 39,303 | 900 | 900 | 18 | 0 | 132 | 200 | 132 | 44 | 0 | 0 |
| 5 | 31,497 | 30,182 | 800 | 800 | 16 | 0 | 117 | 143 | 117 | 58 | 0 | 0 |
| 6 | 28,810 | 21,015 | 700 | 700 | 14 | 0 | 102 | 105 | 102 | 73 | 0 | 0 |
| 7 | 23,437 | 11,833 | 600 | 600 | 12 | 0 | 88 | 77 | 88 | 88 | 0 | 0 |
| Instance | I | J | K | T | V | P | F | Eco. Objective (EUR) | Env. Objective (kg CO2-eq) | Gap (%) | Computation Time (s) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 12 | 96 | 12 | 4 | 1 | 1 | 1 | 66,240.7 | 23,437 | 0 | 0.27 |
| 2 | 5 | 96 | 12 | 4 | 1 | 1 | 1 | 66,249.7 | 23,435 | 0 | 0.11 |
| 3 | 12 | 96 | 48 | 4 | 1 | 1 | 1 | 264,243 | 92,874 | 0 | 0.50 |
| 4 | 5 | 96 | 48 | 4 | 1 | 1 | 1 | 264,243 | 92,874 | 0 | 0.33 |
| 5 | 12 | 96 | 100 | 4 | 1 | 1 | 1 | 270,845 | 91,297 | 0 | 1.07 |
| 6 | 5 | 96 | 100 | 4 | 1 | 1 | 1 | 550,506 | 193,586 | 0 | 0.55 |
| 7 | 12 | 96 | 1000 | 4 | 1 | 1 | 1 | 281,381 | 87,422 | 0 | 14.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azab, R.; Mahmoud, R.S.; Elbehery, R.; Gheith, M. A Bi-Objective Mixed-Integer Linear Programming Model for a Sustainable Agro-Food Supply Chain with Product Perishability and Environmental Considerations. Logistics 2023, 7, 46. https://doi.org/10.3390/logistics7030046
Azab R, Mahmoud RS, Elbehery R, Gheith M. A Bi-Objective Mixed-Integer Linear Programming Model for a Sustainable Agro-Food Supply Chain with Product Perishability and Environmental Considerations. Logistics. 2023; 7(3):46. https://doi.org/10.3390/logistics7030046
Chicago/Turabian StyleAzab, Rana, Rana S. Mahmoud, Rahma Elbehery, and Mohamed Gheith. 2023. "A Bi-Objective Mixed-Integer Linear Programming Model for a Sustainable Agro-Food Supply Chain with Product Perishability and Environmental Considerations" Logistics 7, no. 3: 46. https://doi.org/10.3390/logistics7030046
APA StyleAzab, R., Mahmoud, R. S., Elbehery, R., & Gheith, M. (2023). A Bi-Objective Mixed-Integer Linear Programming Model for a Sustainable Agro-Food Supply Chain with Product Perishability and Environmental Considerations. Logistics, 7(3), 46. https://doi.org/10.3390/logistics7030046






