1. Introduction
In a CLSC, the emphasis on green, fewer emissions progressively came to researchers’ notice [
1]. CLSC may decrease emissions and energy consumption via long-term design, maintenance, reuse, re-manufacturing and recycling. A CLSC is not a means to cut costs, but progressively generates additional options for manufacturers to enhance the efficiency of utilizing resources, especially rare materials [
2]. A forward supply chain (SC) is a set of activities that satisfy consumer demands, including manufacturers, suppliers, warehouses, transporters, retailers and customers [
3]. The reverse SC may begin at any level, depending on the points of collecting old materials, garbage, end-of-life items and their components. However, it generally starts with the gathering of items used by end users, which are then utilized in the SC again or another SC [
4]. Second-hand materials may be returned to the SC via reuse, repair or re-manufacturing. Reverse logistics (RL) oversees all the reverse flows—a cost-effective technique for recovering and inventorying materials [
5]. Uncertainty is a state that cannot be represented with a specific quantity of knowledge [
6]. It is difficult to analyze or quantify the uncertainty—nevertheless, it is feasible to compute the risk, a portion of the uncertainty. If so, a portion of the uncertainty is feasible to anticipate, while a part fluctuates randomly.
Moreover, each possible case corresponds to a specific probability. Therefore, uncertainty is an inherent feature of a CLSC. This feature increases the complexity of CLSC management [
7]. Pokharel et al. examined the uncertainty in CLSC/RL. They analyzed the entire RL field [
8]. Govindan et al. conducted a review of CLSC published before 2013 [
4]. In reviewing the literature, CLSC uncertainty factors such as quantity, quality, the timing of scrapped goods, demand for recycled products and system costs are expressed in CLSC design and planning. Various parameters’ uncertainty is mainly considered random and vague [
9].
A comprehensive planning of the SC is required since there is a growing rivalry between businesses both internationally and domestically, as well as growing demands on the part of customers. In this kind of setting, the expansion of SCs amplifies the significance of potential disruptions and the geographical dispersion of supply system facilities [
10]. Even though various sectors have successfully cut SC costs by implementing a variety of strategies, these sectors are still vulnerable to disruptions [
11], such as Black Swans, which are unexpected events that cannot be predicted but have a significant impact on the economy of the entire world. These considerations point to the need of putting into action a complete strategy in order to properly handle all of the goals. Therefore, the best strategy would be to construct an SC that is both sustainable and robust [
12]. Companies may enhance their economic share in global marketplaces and retain their market value by paying attention to the rivalry that exists within their SCs [
11]. In addition, firms have been compelled to place a greater emphasis on equipping themselves with new methods for efficient SC management [
13] as a result of the competitive market. Demand risk, supply disruptions and other operational risks are the three primary types of SC risks. Demand risk is the most common kind of SC risk.
The important decisions that are made in the SCN include strategic decisions, such as facility location and tactical decisions, such as determining the transportation method, optimal allocation and vehicle routing. If these decisions are not adopted at the same time in the SCN, it can increase the costs of the SC, so that the incorrect location of the facilities leads to an increase in the transportation time between the levels of the SCN. In addition to increasing transportation costs, this leads to an increase in greenhouse gas emissions and ultimately increases transportation time. This issue also affects social aspects, including driver fatigue. Therefore, strategic and tactical decisions, if they are taken correctly, can help the better performance of the SCN.
In this paper, the location of the distribution/collection, production, supplier and destruction centers is performed, and the optimal flow allocation between the selected facilities is performed. The purpose of the optimal allocation is to determine the type of transportation of products between both levels of the SCN. Moreover, vehicle routing is performed between the two levels of the distribution/collection center and the customers. The reason for using vehicle routing between these two levels is to reduce transportation costs and greenhouse gas emissions.
One of the most important factors influencing the design of SCNs is decisions related to transportation planning. Transportation and optimal allocation of vehicles to material transfer routes are among the most important decisions to be addressed in the real world [
14]. The more accurate and realistic the transportation planning, the lower the costs incurred by the SCN. Moreover, with the reduction of transportation costs, the cost of the products is also reduced and leads to a reduction in the selling price. Therefore, transportation planning can be considered an important factor for product pricing, which leads to competitive advantage. The existence of different time periods in the supply networks adds to the transportation planning; therefore, due to the uncertainty of the transportation costs in different periods, the planning of these types of issues for transportation is difficult and requires control methods. It is suitable. Another factor that affects the costs of the total SCN is uncertainty in demand. The more uncertain this parameter is, the more difficult it is to plan the transportation of products. Uncertainty control methods, including the fuzzy-probabilistic robust method, should be used for more realistic work transportation planning.
The purpose of this research Is to provide a new solution for solving location-routing issues that arise in sustainable CLSC networks. The economic, social and environmental concerns of the future are concurrently taken into account by this network. This article’s major objective is to provide a response to the unpredictability of the demand placed by consumers in a variety of contexts in which the recently developed fuzzy-probabilistic robust approach is employed to estimate the precise demand. Several considerations, both strategic and tactical, such as the ideal flow allocation in the CLSC network, the routing of vehicles and the positioning of facilities, are also taken into consideration. This network takes into consideration features, such as queue systems in product distribution and time windows in product delivery, both of which contribute to the capabilities of the CLSC network.
The following outline describes the format of this article: The literature review is discussed in the second section. The final section discusses the ideal configuration for the network. The findings are dissected in the fourth section. The fifth and last portion is dedicated to the discussion of the conclusion.
3. Modelling Process and Methods
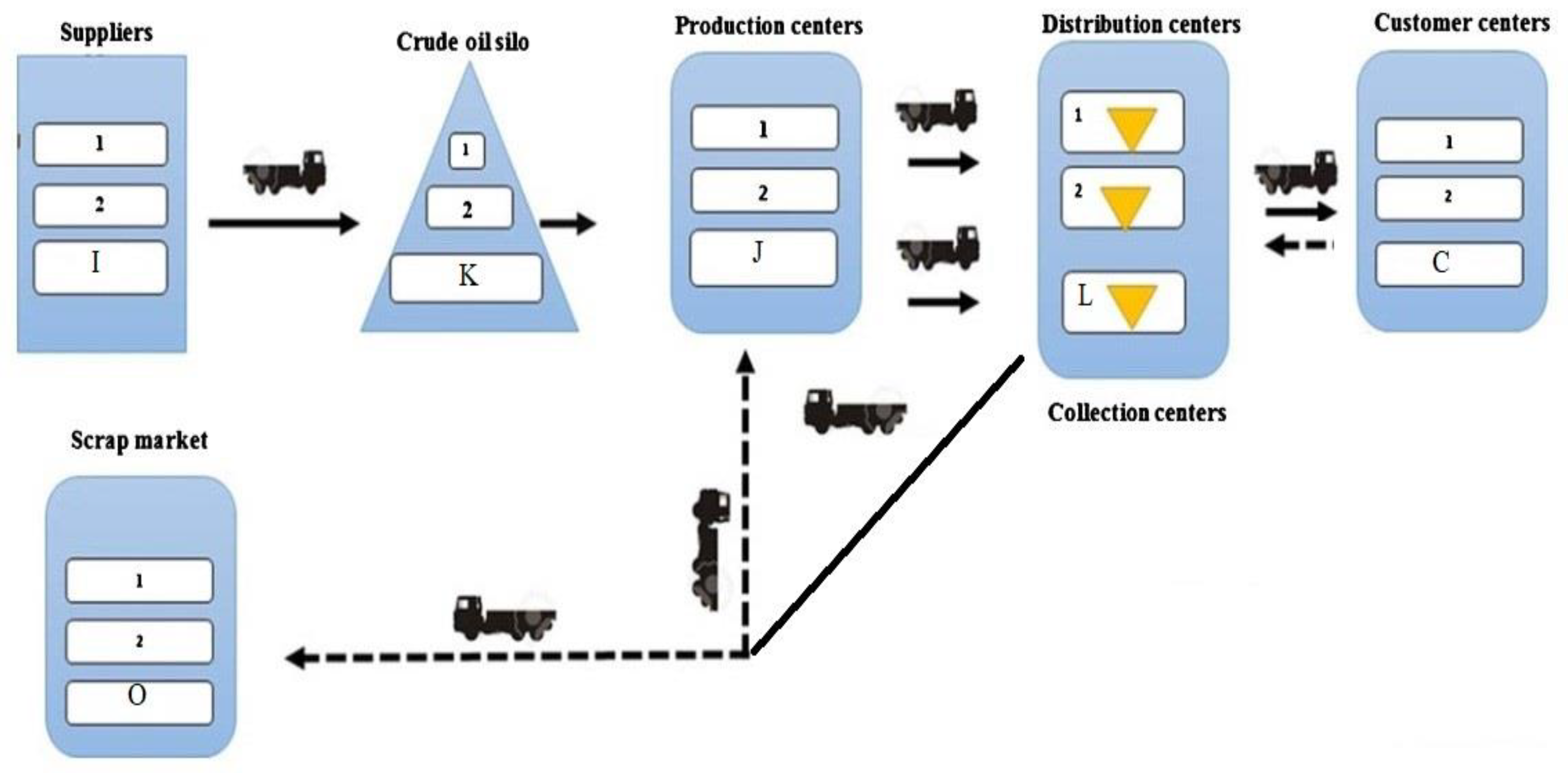
In this section, a CLSC problem is examined. In this model, according to
Figure 1, a 7-echelon SCN consisting of raw material suppliers, warehouses (silos), production centers, distribution centers, end customers, collection centers and disposal centers is considered. In this model, customers send their demand for different products to distribution centers. As a result, distribution/collection centers are responsible for the distribution of products and the collection of returned products from customers. This action is performed in the form of vehicle routing. That is, a vehicle collects the returned product at the same time as delivering the product to the customer and transfers it to the collection center. The production centers also produce the products needed by the distribution centers after receiving the raw materials from the warehouse and sending them to that center with different vehicles. Suppliers are also responsible for supplying raw materials and transporting them to warehouses. Moreover, in the reverse SC, after inspection, the collected products are either sent to the production center for reuse or sent to disposal centers for destruction. In addition, due to the limited number of vehicles, a queuing system has been considered in the distribution centers. So that the vehicles wait to receive the cargo in distribution centers. This issue is caused by the presence of uncertain demand in the SCN. Moreover, after receiving the cargo, the vehicles must deliver the products and pick them up within a specific time window. Otherwise, the penalty cost will be added to the objective function (OBF). The main goal of this network is to minimize the costs of the total SCN, including location, allocation and routing. In this problem, the parameters of the problem are considered uncertainty.
In the rest of this section, the definitions of symbols used in modeling are discussed. Due to the existence of uncertainty in the SCN, a non-deterministic model has been designed first. Then the equations related to the M/M/C queuing system in the distribution center have been added to the main model. Finally, the uncertainty parameters have been controlled using the robust-fuzzy-probabilistic method. In this way, each uncertainty parameter is first considered as fuzzy data in different scenarios and then the robust optimization method is used to justify the problem-solving space.
Sets
i Supplier (i = 1,2,…,I)
j Production center (j = 1,2,…,J)
k Candidate locations for crude oil silos (k = 1,2,…,K)
l Candidate locations for distribution/collection center (l = 1,2,…,L)
c Fixed locations of customer (c = 1,2,…,C)
n Collection/distribution centers and customers
(n,n’ = 1,2,…,L,L + 1,…,L + C)
o Fixed locations of disposal center (o = 1,2,…,O)
r Raw materials (crude oil) scrap product (r = 1,2,…,R)
p Final product (p = 1,2,…,P)
t Time period (t = 1,2,…,T)
v Transportation mode (v = 1,2,…,V)
s Scenario (s = 1,2,…,S)
Parameters
| Supplier selection cost i |
| Production center establishment cost j |
| Distribution/collection center Establishment cost l |
| Warehouse establishment cost k |
| Fixed cost of using the vehicle v |
| Product delivery amount p to customer c in period t under scenario s |
| Product pick up amount p from customer c in period t under scenario s |
| Vehicle capacity v |
| Maximum distribution center capacity l of product distribution p |
| Maximum supplier capacity i of raw material supply r |
| Maximum storage capacity k of raw material storage r |
| Maximum production center capacity p from the production of product p |
| Distance between nodes n and n’ |
| Transportation cost between nodes n and n’ with mode of transport v under scenario s |
| Transportation cost between node i and k with mode of transport v under scenario s |
| Transportation cost between nodes k and j with mode of transport v under scenario s |
| Transportation cost between nodes j and l with mode of transport v under scenario s |
| Transportation cost between nodes l and j with mode of transport v under scenario s |
| Transportation cost between node l and o with mode of transport v under scenario s |
| Transportation time between nodes n and n’ |
| Unloading and loading time of the vehicle in the node c |
| Distribution cost per unit of product p by the distribution center l |
| Soft time window for pick up delivery of customer products c |
| Penalty cost of soft time window |
| Product-dependent greenhouse gas emissions |
| Probability of occurrence of scenario s |
| Number of raw materials r used per unit of product p |
| Average fraction of product recycling p |
| Number of employees in the distribution center l |
| Waiting time cost to serve in the distribution center l |
| Distribution center service rate l (exponential distribution) |
| Upper limit of queue length for service in the distribution center l |
| High limit probability for excessive service queue length at the distribution center l |
Decision variables
| Product amount total p that can be distributed from the distribution center l by vehicle v under scenario s in period t |
| If distribution center l is established/selected, 1 and otherwise 0. |
| If the distribution center l is assigned to customer c and the vehicle v is assigned under scenario s in period t, 1 and otherwise 0. |
| If node n’ is visited after node n by vehicle v under scenario s in period t, 1 and otherwise 0. l, c ∈ L∪C. |
| Auxiliary variable for sub-tour deletion limit |
| Vehicle arrives time v at customer c and exits the distribution center l under scenario s in period t |
| Product amount p in the vehicle load v in the customer node c and out of the distribution center l under scenario s in period t |
| Time exceeds the vehicle time window v in customer node c under scenario s in period t |
| Maximum vehicle visit time vehicle v out of distribution center l under scenario s in time period t |
| Raw material amount r transferred from the supplier i to the warehouse (silo) k with the transportation mode v in period t under scenario s |
| Raw material amount r transferred from the warehouse (silo) k to the production center j with the transportation mode v in time period t under scenario s |
| Product amount p transferred from the production center j to the distribution collection center l with the transportation mode v in period t under scenario s |
| Raw material amount r transferred from the distribution/collection center l to the production center j with the transportation mode v in period t under scenario s |
| Raw material amount/scrap product r transferred from distribution center/collection l to disposal center o with the transportation mode v in period t under scenario s |
| If supplier i is selected to supply raw materials, 1 and otherwise 0. |
| If distribution/collection center l is constructed for product distribution/collection, 1 and otherwise 0. |
| If a warehouse (silo) k is constructed for the storage of raw materials, 1 and otherwise 0. |
| If the production center j is constructed to produce the product, 1 and otherwise 0. |
The overall expenses of the CLSC network can be reduced to their lowest possible level using Equation (1). These costs consist of the expenditures associated with the location, transportation and distribution, in addition to the costs associated with going over the allotted time window. The emission of greenhouse gases caused by the transportation of goods is reduced as much as possible by Equation (2). The maximum number of hours that drivers are allowed to work is cut down significantly by Equation (3). Equation (4) provides reassurance that just a single distribution center should be responsible for serving a given consumer. Because of Equation (5), we know that the total quantity of cargo that may be carried by the vehicle cannot exceed its carrying capacity.
In the process of vehicle routing, Equation (6) is known as the sub-tour elimination equation. Equation (7) ensures that every vehicle leaves after visiting a customer by requiring them to do so. Equation (8) ensures that each customer should have only one vehicle assigned to them. Based on Equation (9), it is clear that the vehicle must make its way back to the center after making its rounds to the various clients. The sum of all the products that were dispersed can be found in Equation (10). The solution to Equation (11) ensures that the distribution center can operate at its full capacity in the event that it is constructed. The quantities of merchandise delivered to each consumer by vehicle are shown by Equations (12) and (13), respectively.
The time that the car will arrive to each individual consumer is represented by Equations (14) and (15). The amount of time it takes for each truck to return to the distribution center is represented by Equations (16) and (17). The quantity of commodities that were moved from the production center to the distribution center is represented by Equation (19). It reveals the quantity of raw materials that were moved from the storage facility to the production center in order to facilitate the manufacturing of new goods. The quantity of items that were moved from the supplier to the warehouse is represented by Equation (21). (silo). The quantity of returned commodities in the reverse SC can be calculated using Equation (22). The quantities of commodities that were transported to the collecting center and the destruction facility, respectively, are accounted for by Equations (23) and (24). The limits associated with the capacity of the centers are represented by Equations (25)–(27). The constraint that is related to the length of the line in the middle of the distribution is represented by Equation (28). Equations (29) and (30) demonstrate the variables involved in decision making.
3.1. Jackson Network
In the SCN, goods are usually sent from distribution centers where parallel service providers are responsible for packing, loading, etc. The existence of different demands from customers makes it difficult to manage the distribution of goods. Therefore, a queue system is usually created in the distribution centers. Determining the number of servers can reduce the queue length while it can change the overall SCN costs. Therefore, in the optimization of SCN problems, it is very important to consider the queuing system in order to reduce costs and reduce queue length. The distribution centers chosen for research in
Figure 2 of the Jackson network and the suggested network equations are presented below [
67]:
In above the Equation,
and
are input rates and
is the output rate for
k center. Therefore, according to the values mentioned in the figure, the input rate to the distribution center is obtained as follows:
As a result, in the designed SCN, the queuing system in the distribution center is considered, whose entry rate includes the number of products sent from the production center for distribution to customers, and its exit rate is equal to all the products that are being is distributed. Therefore, due to uncertain demand, a queue system is formed as follows:
The model must be changed to a specific condition in order to satisfy Equation (28); therefore, this constraint is changed to a definite constraint using an M/M/C queue model. The input rate equal to
λ (Poisson distribution) and the service time are used in this model to construct the M/M/C queue for the distribution center
μ (exponential distribution). There are m servers with a constrained capacity
C in the queue model.
The first expression of Equation (34) shows that the likelihood that there are fewer than
n customers in the service queue of the distribution center
l with
of the server is less than
, and the second equation demonstrates that the total of all probabilities is equivalent to 1. The rate of service may be derived by doing the following:
By combining the above constraints
(the probability of selecting a node as the distribution center
l under scenario
s in period
t) is obtained as follows:
In the results, the probability of a robust condition for
n customers in the service queue of distribution center
l (Equation (28)) is as follows [
67,
68]:
Moreover, according to the above, the customer waiting time in the
l distribution center can be obtained, as described in Equation (39) as follows:
The amount of customer waiting time cost in the distribution center l, is also added to the first OBF as an additional cost.
3.2. Robust-Fuzzy-Probabilistic Method
Because of the unpredictable nature of a number of important factors (such as the costs of transportation and demand), which are not amenable to planning, as well as the unavailability and even the unavailability of historical data that is necessary during the design stage, these characteristics are largely dependent on points of view. Since the mental experiences of experts are also approximated, the previously described hazy parameters are given as uncertain data in the form of trapezoidal fuzzy numbers. It is essential to keep in mind that calculating the production facility’s capacity, demand and transportation costs for long-term decisions may be difficult, if not impossible. This is why it is crucial to keep this in mind. Even if it is possible to estimate a distribution function for these parameters, it is possible that they will not behave in the same manner as the data from earlier times. As a consequence of this, the data obtained from these variables, which change over an extended period of time, are considered to be fuzzy [
69].
Furthermore, uncertain (probable) restrictions are often handled using indefinite finite programming where uncertain data on the left or right side is equal. The notion of decision-making may accomplish the lowest degree of certainty as an acceptable safe margin for imposing any of these restrictions if this approach is utilized to regulate the confidence level in generating these indefinite limits. Two regularly used standard fuzzy method actions, with optimistic fuzzy and pessimistic fuzzy names, are utilized to accomplish this. It is noteworthy that the pessimistic fuzzy represents the pessimistic choice of the uncertain event, while the optimistic fuzzy reflects the degree of optimistic probability of the occurrence of an uncertain event, including unknown parameters. We presume that decision-making has a pessimistic and optimistic attitude while concurrently imposing indefinite limits; thus, we utilize a pessimistic-optimistic combination fuzzy; this is more cautious. Currently, the obvious counterpart of the original indefinite model can be stated using the ambiguous parameters mentioned above, the anticipated value for the OBF and the pessimistic-optimistic action for the indefinite constraints. To start, think about the model’s condensed version given in [
70] as follows:
,
,
F and
indicate the fixed cost of construction, variable cost (transportation), demand and facility capacity, respectively.
A and
E are coefficient matrices, while
and
are continuous variables, zero and one for scenario
s. In the given model, the vectors
and
are indeterminate parameters. The general form of uncertain restricted planning requires the anticipated value of the OBF and the pessimistic fuzzy to handle the OBF and indefinite constraint, respectively. The acronym’s pessimistic fuzzy basic model is as follows:
where
(pessimistic) decision-making controls the lowest degree of confidence of uncertain constraint. Equation (42) is given by the trapezoidal probability distribution for the following conditions [
69]:
Moreover, the general form of Uncertain limited planning, OBF expected value and the optimistic fuzzy to deal with the OBF and the uncertain constraint, respectively, are as follows:
The optimistic fuzzy’s pessimistic controls the indefinite constraint’s minimal degree of confidence. Equation (44) is given by the trapezoidal probability distribution for ambiguous parameters as follows [
59]:
According to the relationships expressed in this paper, a new pessimistic-optimistic fuzzy hybrid model has been used to control uncertain parameters. Therefore, the pessimistic-optimistic fuzzy base model is as follows:
In the pessimistic-optimistic fuzzy basic model and Equation (46),
is parameter zero and one; If
takes 1, the hybrid fuzzy model becomes an optimistic fuzzy model and if
takes 0, the hybrid fuzzy model becomes a pessimistic fuzzy model. Moreover, if
takes the value 0.5, the combined fuzzy model becomes the moderate fuzzy model, so to solve the final model in this paper,
will be defined as parameters with three values 0, 0.5 and 1. Finally, the main model for controlling uncertain parameters in hybrid fuzzy is as follows [
71]:
Decision preferences establish the lowest confidence level for unknown constraints in probabilistic models. The OBF in the suggested models is not sensitive to variation from its predicted value; hence, robust solutions in the base model are not guaranteed. In such instances, the excessive risk may affect decision-making in many practical scenarios, particularly strategic ones when solution consolidation is most important. To address this inefficiency, robust-stochastic uncertain planning is utilized. Robust and stochastic planning make this uncertainty planning technique stand out. The following suggested model is used for uncertainty planning in this study:
where M is a huge non-negative number and
,
and
can be expressed as follows:
The first equation in Equation (48)’s first OBF is the expected value using the model’s mean uncertain parameters. The cost of the penalty for deviating from the anticipated value of the first OBF is the second statement. The third phrase displays the overall demand deviation penalty cost (uncertain parameter). Thus, the OBF weight coefficient is
, and
the penalty for not predicting demand is 1. The coefficients of correction in fuzzy number surfaces should be between 0.5 and 1. The queuing system-controlled SCN model is [
72].
3.3. Psedou Code of Meta Heuristics Algorithm
In the designed SCN, there is a combination of different decisions, such as facility location, routing and optimal flow allocation under uncertainty. Therefore, the model can be called an Np-Hard problem [
73]. Because it is very hard and impossible to solve these problems with exact methods, and as the size of the problem increases, its calculation time also increases [
74]. For this reason, two non-dominated sorting genetic algorithms (NSGA II) and multi-objective particle swarm optimization (MOPSO) algorithms have been used in this research, and their pseudocodes are presented in
Figure 3 and
Figure 4.
4. Analysis of Results
In this part of the article, the issue is addressed according to
Table 2 in order to satisfy the requirements of a small sample according to
Table 3 and on the basis of random parameters. Because we do not have access to data taken from the actual world and because we are in the process of developing a mathematical model, we have been using random data that is based on the uniform distribution function.
The three-objective model is solved using the comprehensive multi-objective decision-making approach with the Baron solver in GAMS software once the issue has been designed and the problem range has been presented. Before attempting to solve the model, an exhaustive approach to making decisions that take into account several objectives is first described. When making decisions based on comprehensive criteria, it is necessary to do individual optimization in order to acquire the greatest possible value for each OBF. To put it another way, the program has to first determine the value of each OBF on its own without taking into account any of the other functions that will be utilized in the computations. The multi-objective decision-making process is represented as a complete one in Equation (88), which may be found below.
In the above relation,
the OBF of the
i th problem,
the best value of the OBF obtained from the individual optimization method and
is the weight assigned to each OBF. In this research, linear softness, i.e.,
and random weights based on the Monte Carlo method, have been used.
Table 4 shows the optimal value of each OBF by individual optimization methods.
From solving the small-size numerical example, 8 efficient solutions in 30 consecutive repetitions of the Monte Carlo method are obtained, which are shown in
Table 5.
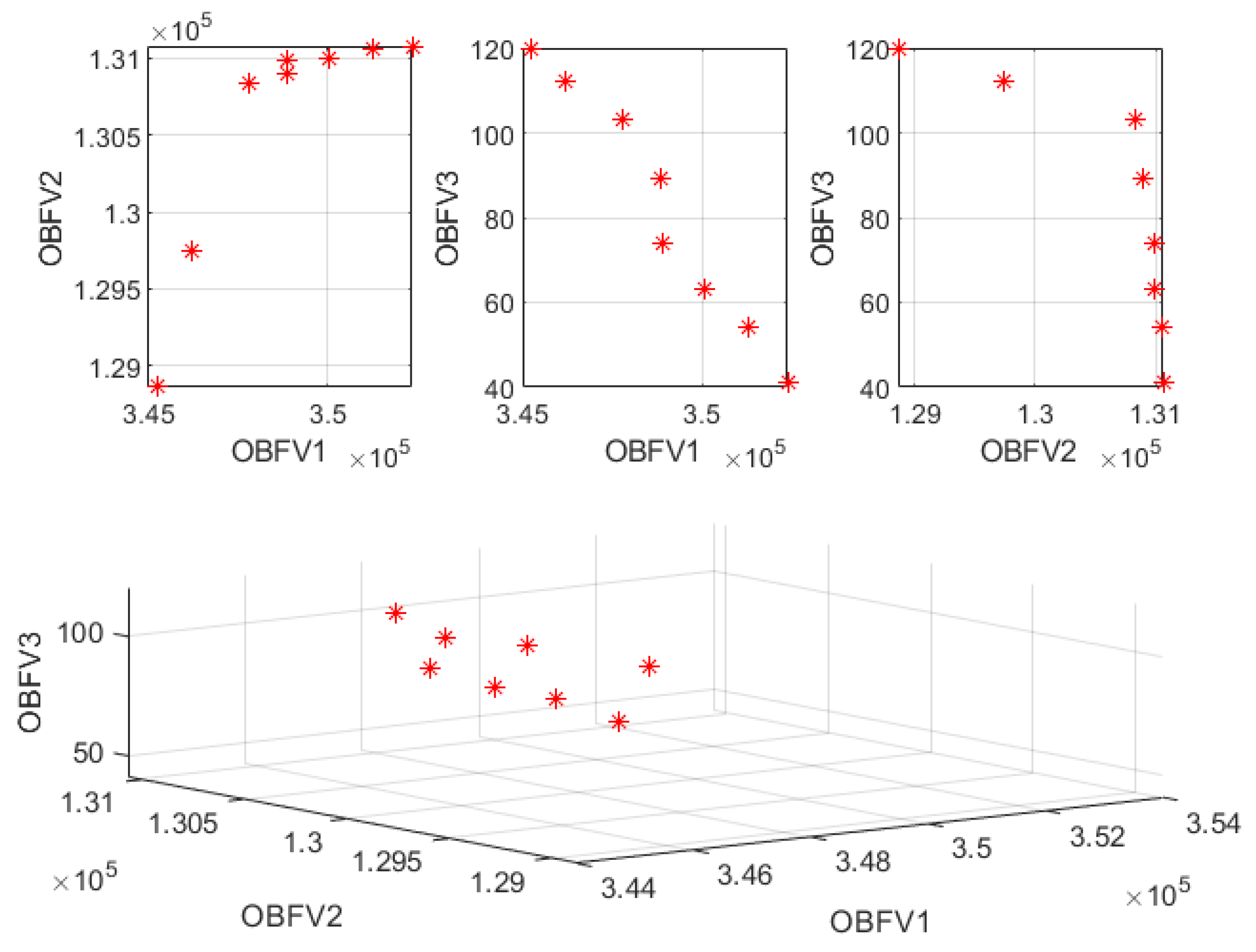
Figure 5 also shows the Pareto front created between different target functions.
According to
Table 5 and
Figure 5, vehicles with higher speeds and higher costs should be used, and the route of product transfer between centers should be changed to reduce the maximum traffic time of vehicles. This has led to an increase in shipping costs. According to this model, with the reduction of greenhouse gas emissions, transmission costs have also increased due to changes in the design of the network structure.
To examine the output variables of the problem, one of the efficient solutions (work solution number one out of the eight work solutions obtained) is examined to obtain changes in the problem decision variables. Based on the results of
Table 5, it can be seen that the efficient solutions have not reached their optimal value and have a relative difference from the best value of the OBF.
Table 6 shows the location and routing of the vehicle in the first efficient solution obtained.
The sensitivity of the issue that is being analyzed, as well as the influence of changes in some of the problem parameters on the values of the OBFs, will be examined in more detail in the following paragraphs. As a result, the total quantity of greenhouse gas emissions produced by the SCN has been analyzed, and the results show that these emissions are 30%, 20% and 10% lower than their base value, respectively. The changes that take place in the values of the problem’s goal functions as a result of shifts in the total quantity of greenhouse gas emissions is outlined in
Table 7, which may be found below.
According to
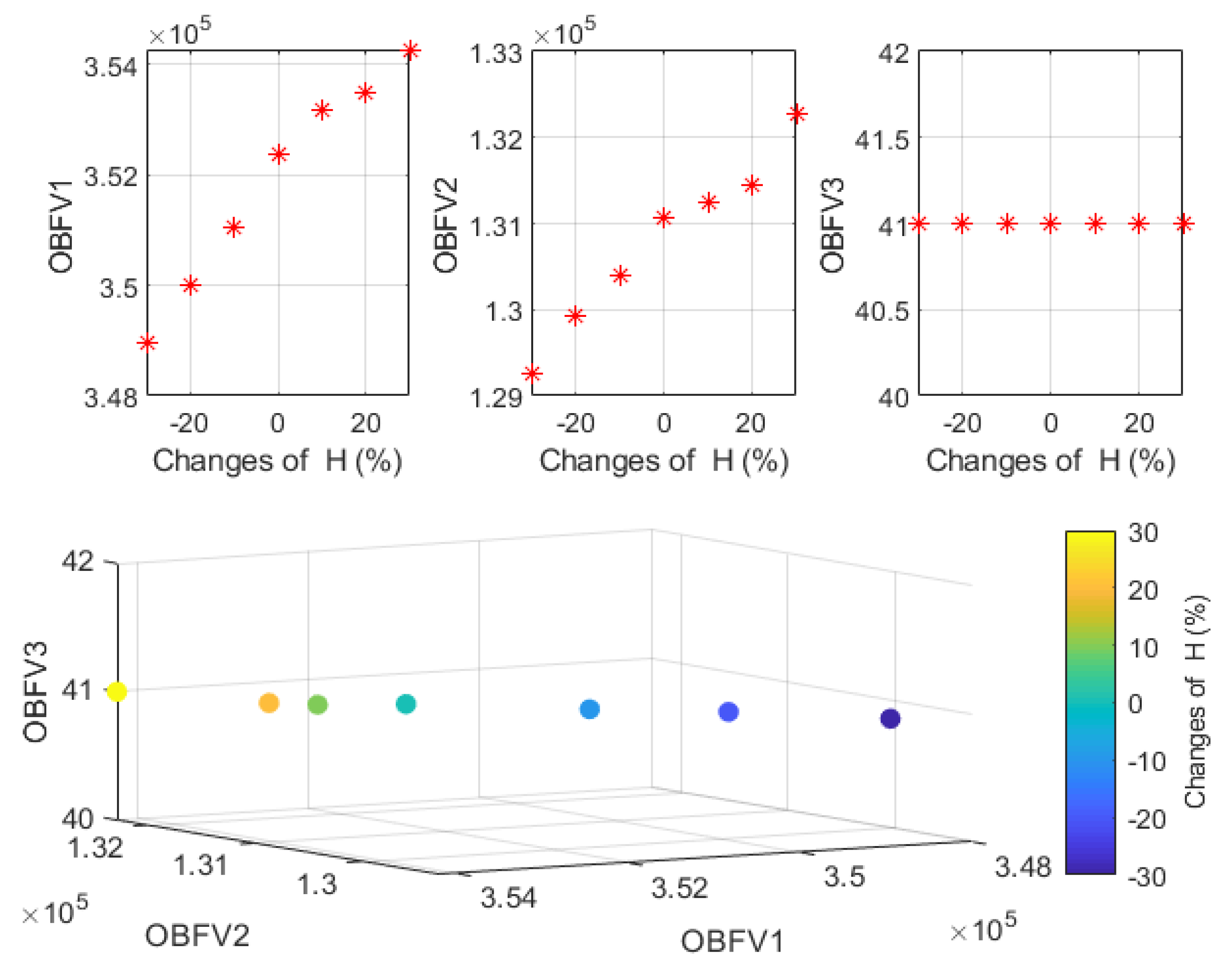
Table 7, it can be seen that the overall quantity of greenhouse gas emissions rose as a result of the direct influence that this parameter had on the second OBF of the issue. As a consequence of this, the total cost of the SCN design increased as well. despite the fact that the maximum amount of time spent in traffic did not change. The pattern of shifts in the values of the goal functions that occur in exchange for changes in the total quantity of greenhouse gas emissions is shown in
Figure 6.
In the following, the the fine due to exceeding the time window is examined and its amount is 30%, 20% and 10% less and more than its base amount.
Table 8 shows the change in the values of the OBFs of the problem in exchange for the change in the amount of the fine due to exceeding the time window.
According to
Table 8, it can be seen that the overall cost of network design, as well as the amount of greenhouse gas emissions, has grown with the growing fines that have resulted from going over the allotted time frame. In addition, because this parameter does not have any impact on the third OBF of the issue, the maximum amount of time spent in traffic caused by vehicles does not change.
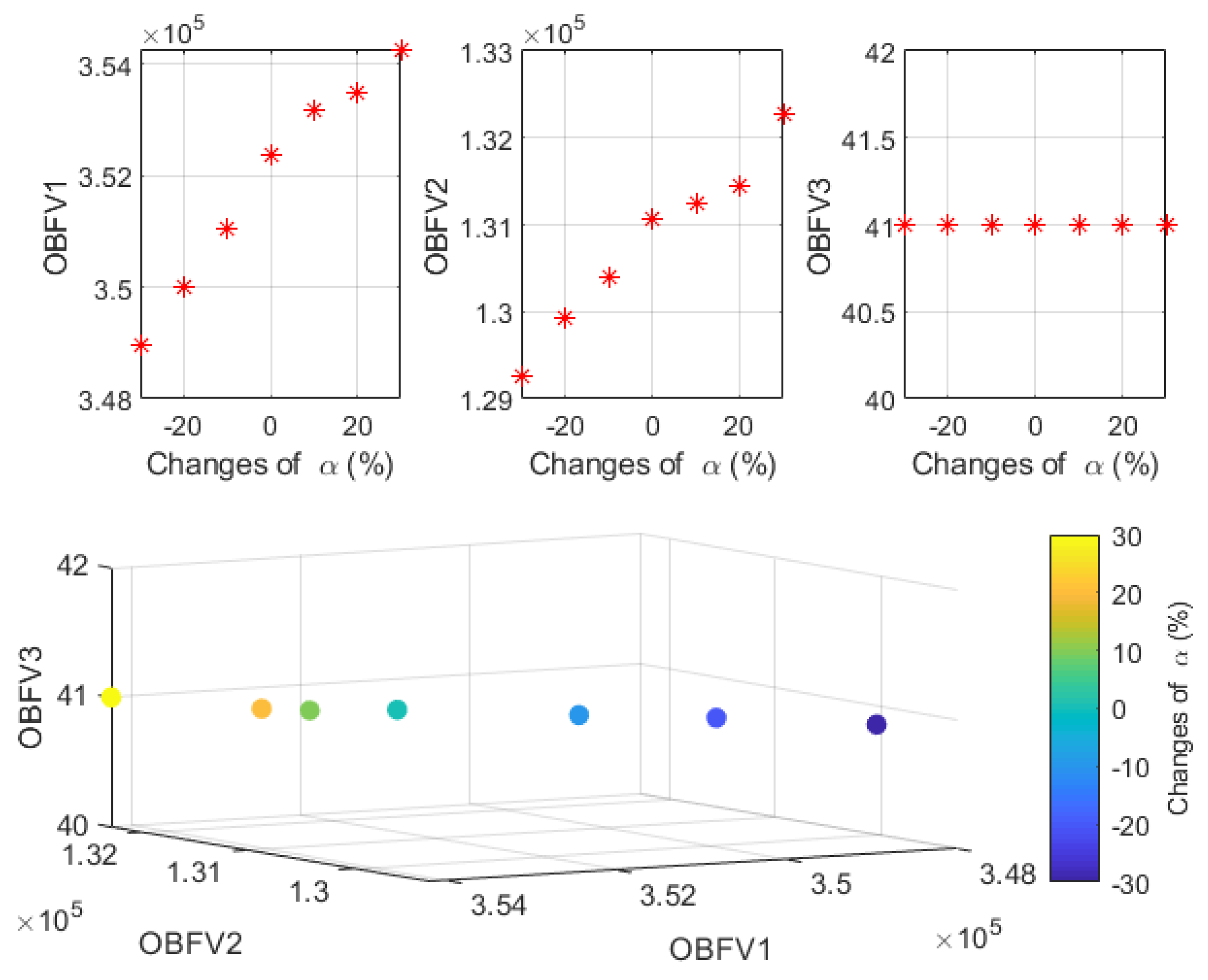
Figure 7 illustrates the pattern of how the values of the goal functions shift over time in response to alterations in the total amount of the time window penalty.
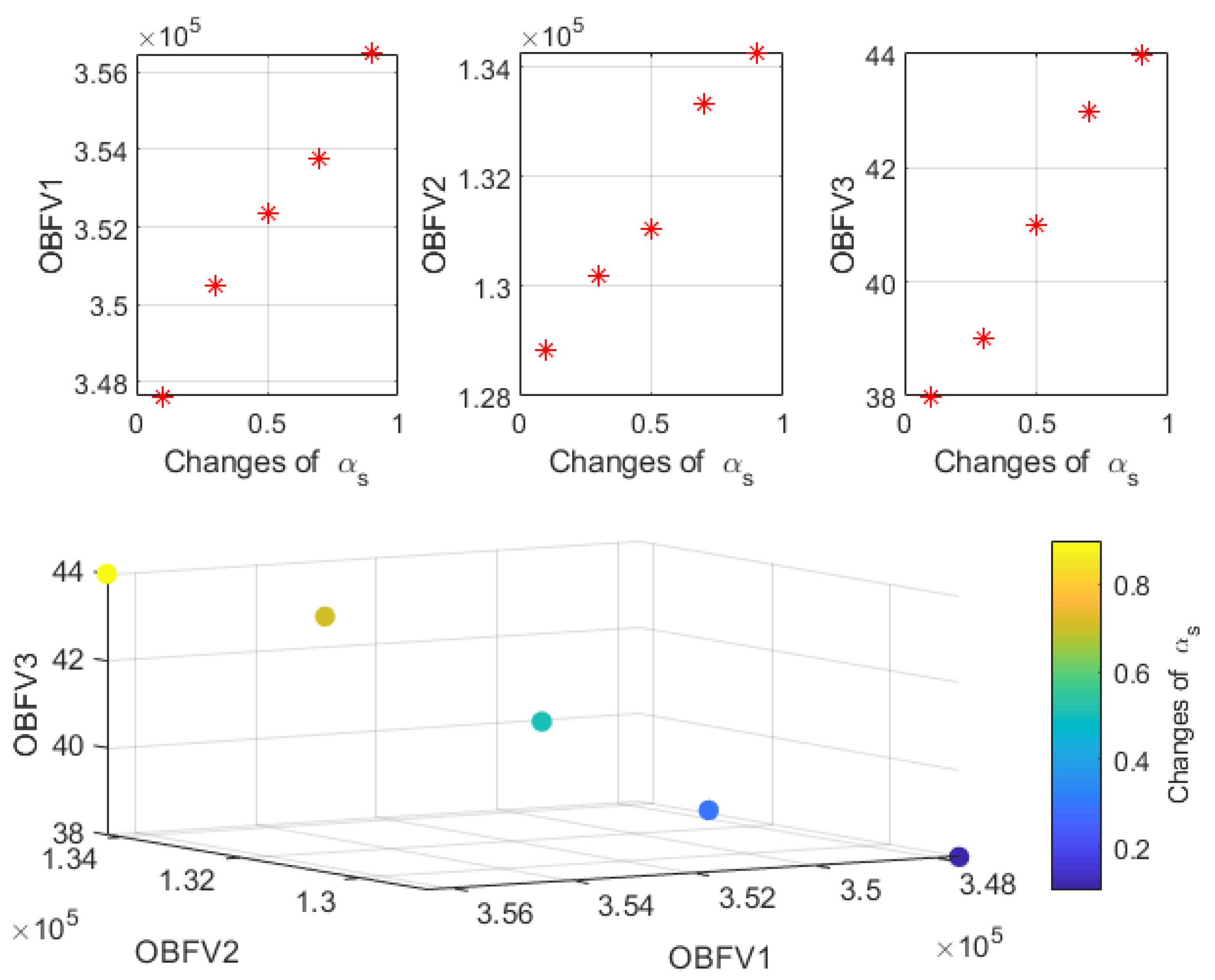
In the end, an investigation is carried out to determine the pattern of shifts that occur in the values of the OBFs of the issue in exchange for shifts in the rate of uncertainty in a number of different problem situations. The goal of this investigation is to determine how these shifts come about. In this section, the changes that take place in the values of the issue’s goal functions in exchange for the changes that take place in the uncertainty rate are presented. The values range from 0.1 to 0.9. These results are derived from an examination of the issues in question that was carried out with an uncertainty rate of 0.5.
Table 9 displays, for a variety of uncertainty rates, the pattern of shifts that take place in the values of OBFs as they go through their lifetimes.
According to
Table 9, it can be shown that the quantity of demand in the network grows with the rate of uncertainty. This, in turn, has a direct influence on the expenses of the whole network, the amount of greenhouse gas emissions and the maximum amount of time a vehicle spends in traffic.
Figure 8 also demonstrates the effects of the uncertainty rate on the values of the goal functions and explains how those changes occurred.
Following the completion of the analysis of the sample problem in its small size, the NSGA II and MOPSO are used to complete the solution of the sample issue in its big size. As a result, before attempting to solve the issue, the parameters of the algorithms that have been stated are first specified and then an initial solution to the problem is presented.
The Taguchi technique requires that first the important components be recognized, then the levels of each element be decided, and finally the suitable test design for these control factors must be defined. The Taguchi method was developed by Kaoru Taguchi.
After the test design has been decided upon, the tests are carried out and then examined to see which combination of factors produces the best results. According to
Table 10, there have been three degrees of consideration given to each aspect during the course of this study. The design of the experiment and the manner in which it is to be carried out for each algorithm are both defined by the number of factors and the number of levels each factor has. In light of the fact that the proposed model incorporates three different goal functions, it is necessary to begin by deriving the value of each experiment from Equation (89). In this regard, in the case of subtraction of the indicators used in the comparison of meta-heuristic algorithms, including (the average of the first to third OBF, number of efficient solutions, maximum expansion index, metric distance index and computational time), has been used. Specifically, the average of the first to third OBF. In order to conduct an analysis of the design of the Taguchi experiment, the first step is to determine the value of each experiment. Subsequently, the scaled value of each experiment (RPD) is determined using Equation (89).
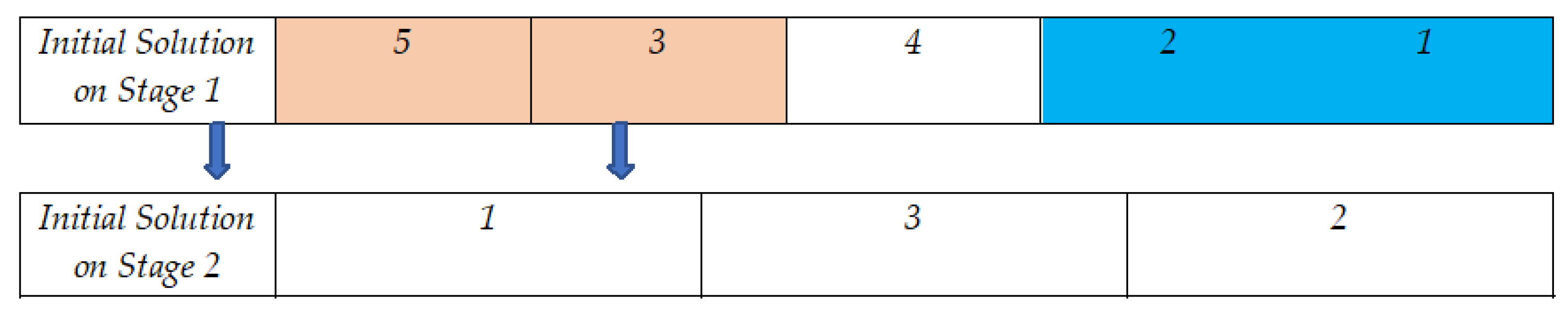
Based on the results of the Taguchi method in the parameterization of meta-heuristic algorithms, it is observed that the maximum number of iterations and also the number population in the two algorithms is equal to 200. After parameterizing the meta-heuristic algorithms, a primary chromosome is presented to solve the problem. Therefore, in this section, two different chromosomes are considered. The first part of the chromosome is related to the routing of the vehicle between the distribution centers and the customers, and the second part is related to the optimal location and the allocation of goods between other levels of the SC. Therefore, in the first part, assuming five customers and three distribution centers, the primary chromosome is presented according to
Figure 9. In this chromosome, in the first level of the SCN, the substitution of natural numbers is first produced for the total number of customers.
The next step in the design of the chromosome is to decide which clients will be assigned to which intermediary warehouses. Therefore, the entire number of clients is arbitrarily distributed among the total number of distribution centers, and the path that the vehicle takes is determined by the numbers generated in the first level of the chromosome’s initial solution.
Figure 8 demonstrates how customers are assigned to distribution locations, and
Figure 9 illustrates how chromosomes are used to determine truck routing.
According to
Figure 10, it is observed that customers 5 and 3 are allocated to distribution center 1, customer 4 is allocated to distribution center 3, and customers 2 and 1 are allocated to distribution center 2. Moreover, vehicle routing from distribution center 1 is
, vehicle routing from distribution center 2 is
. The second part of the chromosome discusses the location of the facility as well as the optimal allocation of flow between the selected facility. Hence another chromosome will be generated and decoded for each level of the SCN as follows. This encryption is based on a permutation of natural numbers to the number of nodes in each level of the two levels of the SCN.
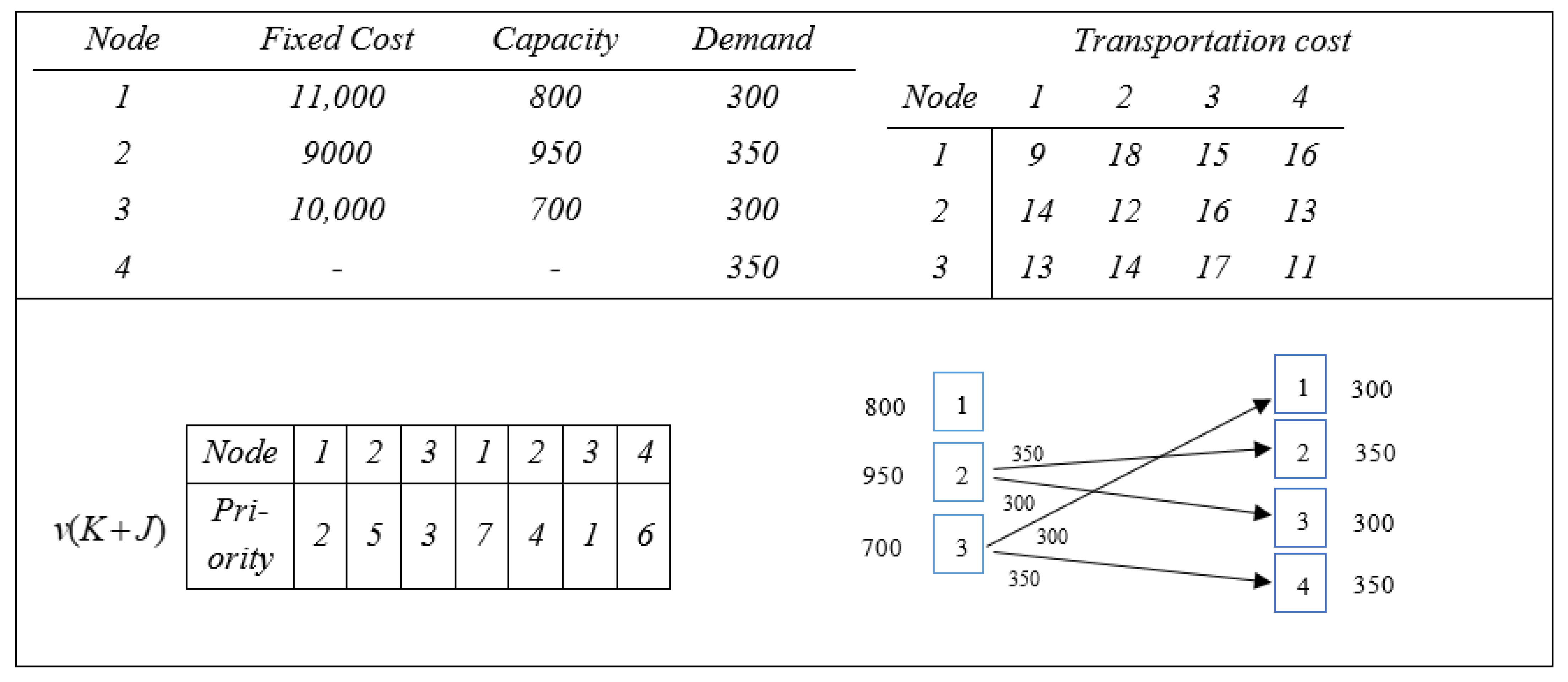
Figure 11 shows the priority-based encoding for one of the network levels with 3 major distribution centers and 4 fixed demand centers.
Encoding (6-1-4-7-3-5-2) that illustrates the priorities (7-4-1-6) for fixed demand centers and how (2-5-3) is connected to the distributor center is shown in
Figure 9. In order to successfully decode anything, you will need to complete the following two steps:
Step 1—To begin, the donor with the highest number (priority) from the selected major distribution centers (priority 5 for the second major distribution center), and if this donor can meet all of the demands of the customer centers, the priority of the other donation centers will be reduced to zero. Step 2—If this donor cannot meet all of the demands of the customer centers, the donor with the next highest number (priority) from the major distribution centers will.
Figure 11 presents an example in which the capacity of the main distribution center is shown to be two times 950; however, the total demand from the stationary client centers is shown to be 1300. In this instance, the distribution hub with the second greatest priority on the list is chosen to be the subsequent main one (priority 3 related to the third major distribution center). Now, the combined total capacity of the two main distribution centers, which is 1650, is more than the combined total demand of the client centers (amount 1300). In such a scenario, the priority of just the very first big distribution center will be lowered all the way to zero.
Step 2: The ideal allocation is established between the main distribution centers that have been chosen and the demand centers once it has been determined how many prospective major distribution centers there are and where they are located. In this stage, the highest priority is selected (priority 7, which is related to the first demand center), and the lowest transportation cost related to this customer is identified with the major distribution center that was selected from the first stage (the third donor center at a cost of 15), along with the distribution center’s minimum capacity. The ideal allocation amount is computed, and it is decided to go to the chosen major and the given consumer. After increasing the available capacity or satisfying any remaining unmet demand, the priority will be lowered to zero. The second step is performed several times until the values of all the priorities have been brought down to zero.
According to the findings for large sample (see
Table 10) presented in
Table 11,
Table 12 and
Table 13, it has been observed that the value of the first OBF all the way up to the third OBF has increased as the size of the problem has grown. This is because the number of customers has grown and estimates of their demand have been made. Moreover, as the size of the issue has grown, the amount of time required to solve the problem has risen exponentially, which is an indication of the rigidity of the model that has been provided. It has also been noticed that in terms of algorithm performance, NSGA II has a better average of the second and third OBFs, maximum spread index (MSI) and spacing metric (SM) index, when compared to MOPSO. These indices refer to maximum spread index and spacing metric, respectively.
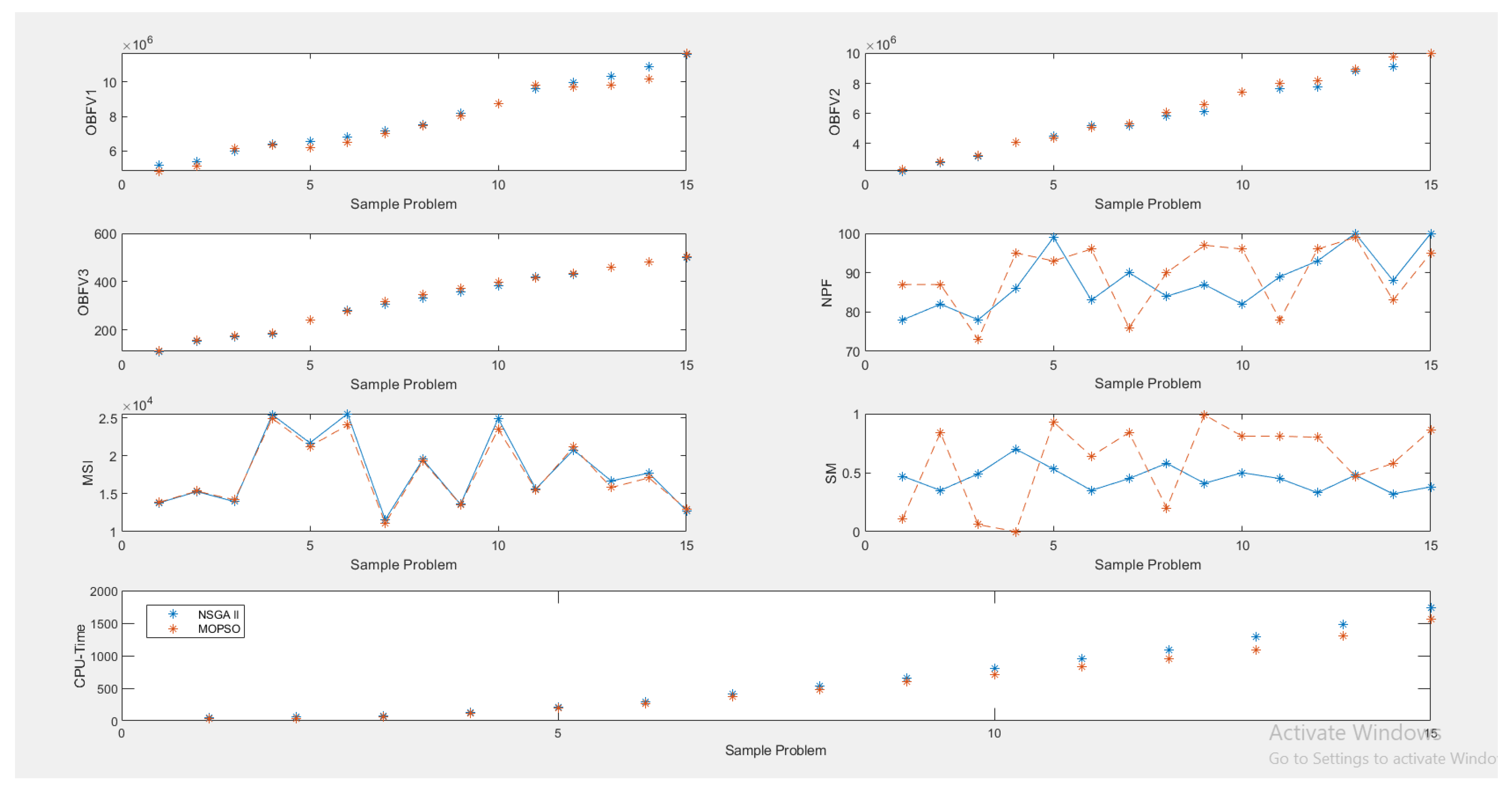
Figure 12 presents a comparison of the results that were achieved when large-scale numerical cases were solved using two different techniques.
According to the diagram in
Figure 12, it can be seen that as the size of the problem increases, the computational time increases exponentially, which is proof that the problem is NP-Hard. Moreover, with increasing the computational time, the mean of the OBFs has increased and the most significant increase has been in the changes of periods.
Since each of the algorithms has been successful in obtaining a specific index and the weighted average of the results has been close to each other. Therefore, a
t-test at a 95% confidence level was used to evaluate the significant difference between the mean results.
Table 14 summarizes these results.
According to the results of
Table 14 and the value of
p-value, it is observed that there is a significant difference between the means of the OBFs, the maximum expansion and computational time between the two algorithms, and therefore, it is not possible to prefer the algorithms to each other. Therefore, using the TOPSIS method, a more efficient algorithm has been selected (see
Table 15).
After the above analysis, the NSGA II with a gain weight of 0.6832 and the MOPSO with a gain weight of 0.3168, respectively, are recognized as the most efficient algorithm for solving the problem.
5. Conclusions
The ever-increasing growth of urbanization, as well as industries, particularly support sectors, has resulted in the movement of both people and things, which has led to an issue whose complexity is continually growing. The growth of cities has led to an increase in the demand placed on the transportation sector. This, in turn, has led to an increase in the number of challenges faced by cities and large industries, including an increase in the amount of time wasted traveling, an increase in the amount of fuel used and an increase in the value of vehicles. It is necessary to have a transportation system that is both well-equipped and efficient in order to alleviate traffic difficulties and the subsequent economic, social and environmental issues that they cause in big cities, manufacturing enterprises and service-oriented businesses. The transportation industry is both a substantial and crucial component of every nation’s economy, as well as one of the most important factors in determining the final price of completed goods. Because of the significance of product transfer, this investigation was undertaken to simulate and find a solution to a challenge posed by a CLSC operating in an unpredictable environment. The researchers took into account the queuing system, as well as simultaneous delivery and harvesting. In light of this, the study in question takes into account a seven-tiered SCN, which includes raw material suppliers, storage facilities (silos), production centers, distribution centers, end customers, collecting centers and destruction centers. In this scenario, the suppliers of raw materials provided to the warehouses the raw materials that are required for the production of the final goods (silos). At the next level of the SC network (SCN), production centers take the raw materials that they receive from silos and collection centers and use those commodities to make finished goods, which are then distributed to customers through distribution centers. After the items have been sorted into their appropriate categories, distribution facilities next send them on to clients via the appropriate method of transportation.
When it comes to the return chain, consumers end up throwing away a certain proportion of the things they purchase after using them. Following the collection and inspection of the products as well as their transformation into raw materials or scrap, the collection centers allocate a certain percentage of the products for reproduction to production centers and a certain percentage of the products for destruction centers. The primary objective of this network is to reduce overall SCN costs as much as possible. These costs include location, allocation and routing expenses. In order to address the issue, a simplified model was developed, and then that model was solved with the use of an all-encompassing multi-objective decision-making process. The end result was the production of eight effective solutions. After looking at the output variables of the problem, it was discovered that the value of the first and second OBFs has increased as the amount of the fine for exceeding the time window and the amount of greenhouse gas emissions have increased. This was one of the observations that were made after the examination of the output variables of the problem. Following that, NSGA II and MOPSO were used since the GAMS program proved to be ineffective. As a result, 15 different sample issues were devised and tested on bigger scales.
When the magnitude of the issue expanded, the amount of time needed to solve it also climbed exponentially. Therefore, the issue at hand is one that falls within the NP-Hard category of problems. The conclusion that could be drawn from the findings of the study that compared the two algorithms was that the NSGA II is more effective at finding solutions to problems. The findings that were acquired from the presentation of the mathematical model in this article may be of assistance to managers in cutting expenses and lowering the amount of dispersion that is brought about by the SC of manufacturing units. Within this model, a variety of efficient solutions have been presented, and as a result, managers may be able to improve their decision-making abilities, both in terms of the choices they make at the strategic and tactical levels. Additionally, the fact that the mathematical model has an uncertainty rate is of great assistance to the managers of production units in predicting the costs that are likely to be incurred on the SC under the most pessimistic and optimistic scenarios. It is proposed as a future study that the OBF of dependability in the distribution of goods to consumers and the problem of resilience in the CLSC network be both studied. Additionally, it is advised that the issue of resilience in the CLSC network be considered. Additionally, the optimization of one’s capacity to fulfill one’s societal duties has to be included in the mathematical model as well. In order to speed up the process of issue-solving, it has also been recommended that hybrid meta-heuristic algorithms be developed.