A Mixed-Integer Linear Formulation for a Dynamic Modified Stochastic p-Median Problem in a Competitive Supply Chain Network Design

Abstract

Background: The Dynamic Modified Stochastic p-Median Problem (DMS-p-MP) is an important problem in supply chain network design, as it deals with the optimal location of facilities and the allocation of demand in a dynamic and uncertain environment. Methods: In this research paper, we propose a mixed-integer linear formulation for the DMS-p-MP, which captures the key features of the problem and allows for efficient solution methods. The DMS-p-MP adds two key features to the classical problem: (1) it considers the dynamic nature of the problem, where the demand is uncertain and changes over time, and (2) it allows for the modification of the facility locations over time, subject to a fixed number of modifications. The proposed model uses robust optimization in order to address the uncertainty of demand by allowing for the optimization of solutions that are not overly sensitive to small changes in the data or parameters. To manage the computational challenges presented by large-scale DMS-p-MP networks, a Lagrangian relaxation (LR) algorithm is employed. Results: Our computational study in a real-life case study demonstrates the effectiveness of the proposed formulation in solving the DMS p-Median Problem. The results show that the number of opened and closed buildings remains unchanged as the time horizon increases due to the periodic nature of our demand. Conclusions: This formulation can be applied to real-world problems, providing decision-makers with an effective tool to optimize their supply chain network design in a dynamic and uncertain environment.

1. Introduction

Mobile grocery stores, also known as grocery trucks (GT) or pop-up grocery stores, have emerged as a new trend in the retail industry. GTs typically stock a wide variety of fresh fruits and vegetables, as well as other grocery items. They are usually equipped with refrigeration units to keep the food fresh and have a payment system in place for customers to buy the products.

These mobile stores bring convenience and accessibility to customers in under-served or rural areas, or in areas where traditional brick-and-mortar grocery stores are not present [1,2]. The trend of grocery trucks is expected to continue to grow in the coming years as more and more people look for ways to improve access to healthy food in their communities. In the U.S., the mobile food vendors market is valued at 1.16 billion dollars in 2021 and is predicted to grow at a rate of 6.4% annually from 2022 to 2030, driven by the increasing trend of culinary arts and the preference of young people for different dining experiences over the traditional dining in restaurants [3].

Another application of GTs is to provide food to people in emergency situations, such as natural disasters or power outages [4,5], as well as address food insecurity by increasing access to healthy food options. GTs are valuable resources for alleviating food insecurity, and these trucks are often operated by non-profit organizations, local governments, and community groups that want to address food insecurity and promote healthy eating [6].

Logistics for mobile grocery stores refer to the process of planning, coordinating, and controlling the movement and storage of goods, services and information from the point of origin to the point of consumption. This includes transportation, inventory management, warehousing, and distribution of products. In the case of mobile grocery stores, logistics also includes the planning and coordination of the routes and schedule of the mobile store, as well as the management of the supply chain and inventory. This includes sourcing products from suppliers, managing inventory levels and restocking the mobile store as needed, and coordinating delivery schedules [7,8]. Effective logistics management is crucial for the success of mobile grocery stores, as it can impact delivery times, cost, and overall customer satisfaction. By optimizing logistics, mobile grocery store owners and operators can improve their business by reducing costs and increasing efficiency, ultimately resulting in a better customer service [9,10].

The goal of this research is to address the challenges in the logistics management of mobile grocery stores by proposing a mixed-integer linear formulation for a Dynamic Modified Stochastic p-Median Problem (DMS-p-MP) in a supply chain. The aim is to enhance the robustness of the solution by considering the uncertainties and variabilities of the parameters in this problem. Additionally, this study aims to address the lack of consideration of the dynamic aspects in the existing literature of supply chain network design by incorporating the time-varying nature of the problem. The proposed mixed-integer linear programming (MILP) model will not only provide a robust solution to the mobile grocery store problem but also offer a framework that can be applied to other similar supply chain network design problems. In this regard, we first provide a comprehensive literature review of the proposed location-allocation models in the literature in Section 2 and then provide a mathematical formulation for our model considering the uncertainty of demand in Section 3. Section 4 and Section 5 show the application of our proposed model in the real-world mobile grocery location problem and provide managerial insights, respectively.

2. Literature Review

Supply chain management is the coordination and management of activities involved in the production and delivery of goods and services from the raw material stage to the end customer [11,12]. It involves the planning, design, execution, monitoring, and control of all processes involved in the flow of goods and services from the initial sourcing of raw materials to the delivery of the finished product to the end customer [13]. The principles of supply chain management can be applied in various industries, including healthcare [14,15], retail, manufacturing, and transportation, to optimize the flow of goods, information, and resources, thereby improving efficiency and reducing costs [16]. Location allocation is a critical aspect of supply chain management, particularly in distribution and service industries. The objective of location allocation is to determine the optimal number and placement of facilities to serve customers while minimizing costs. In this section, we discuss some of the most well-known location-allocation problems and characteristics of different models in the literature.

The maximal covering location problem (MCLP) is highly regarded as one of the most useful facility location models from both a theoretical and practical standpoint [17,18]. The goal of MCLP is to identify a set of facilities that maximizes the total weight of covered customers [19], who are considered covered if they are located within a specified distance from their nearest facility [20]. This problem was first introduced by [21], in which the search for an optimal solution was limited to nodes. The study by [22] later expanded the search to a dominant set of points and solved the problem through linear programming if the solution was an integer and through branch and bound if it was not.

The p-center problem is a well-studied optimization problem in the field of operations research and location allocation. It involves finding the optimal location of p facilities to serve a set of demand points in such a way as to minimize the maximum distance between a demand point and its nearest facility. A comprehensive survey of the p-center problem and its variants was conducted by [23]. The authors provide an overview of the different formulations and solution methods for the p-center problem and discuss extensions to the problem such as the p-median and p-center with capacities. In recent years, there have been several advances in the solution of the p-center problem using approximation algorithms and metaheuristics. A paper by [24] presents a memetic algorithm for the p-center problem and demonstrates its effectiveness through a set of computational experiments.

The p-median problem is another well-known location-allocation problem that involves determining the optimal number and location of facilities to minimize the total access cost [25]. It is a popular choice for various applications, including the allocation of mobile grocery stores. This problem is particularly well-suited for this application due to its focus on minimizing the access cost, which is crucial in determining the most cost-effective locations for the stores. By optimizing the number and location of stores, the p-median problem can help ensure that the stores are located in the areas where they can provide the most accessible and convenient service to customers while minimizing the access costs. This can result in increased efficiency and cost savings, making it a good choice for the allocation of mobile grocery stores.

The p-median problem is formulated as an integer programming model and can be solved using various algorithms, such as the primal-dual method or branch-and-bound algorithm. The work of Berge [26] initially explored the challenge of finding the minimum coverage in location problems. Later, Miehle et al. [27] introduced the well-known p-median problem, in which the objective is to select the optimal p facilities to open with the goal of minimizing the total transportation cost. Subsequently, Hakimi’s node optimality theorem [28,29] was developed to show that, in a continuous graph, the optimal solution for absolute median problems always lies on the graph’s vertices. This implies that many network problems can be transformed into their discrete versions without loss of optimality.

In the quest to tackle increasingly complex and realistic optimization problems, mixed-integer linear programming (MILP) emerged as a widely used method in the location optimization domain [30,31]. Early works such as [32,33] utilized MILP to solve various location problems including the uncapacitated facility location problem, the discrete p-median problem, and the covering-location problem. The deterministic model assumes that all parameters are known with certainty, but real-life scenarios always involve unpredictable elements. To address this issue, researchers have been exploring the combination of location models with stochastic programming methods. For example, Refs. [34,35] incorporate stochastic variables, such as customer demand, the cost of serving a customer from a specific location, and the cost of opening a facility, into the uncapacitated facility location and p-median problems. Ref. [36] considers the impact of stochastic customer demand on the capacitated facility location problem. Ref. [37] studies the uncertainty surrounding the number of facilities to open. Ref. [38] proposes a method to increase the number of facilities based on customer demand, while Ref. [39] considers the opposite scenario of closing existing facilities. Ref. [40] explores the impact of demand uncertainty on covering-type location problems. Zaferanieh et al. discuss a strategy to address traffic congestion caused by the high demand of clients in a bi-level p-facility network [41].

Machine learning has demonstrated its potential for solving a range of challenges across various industries by leveraging the power of large datasets to develop optimization and predictive models [42,43]. Wang et al. [44] introduce a novel solution to the uncapacitated p-median problem that utilizes reinforcement learning. The proposed method, which uses Multi-Talking-Heads Graph Attention Networks, outperforms traditional classical heuristics and meta-heuristics [45] in terms of both solution quality and computational efficiency.

The incorporation of time into location problems is a common characteristic in practical applications. These problems are classified as either single-period or static, where decisions are based on fixed parameters, or multi-period [46] or dynamic, where decisions vary over time [47]. Early works in this field include [48,49], which deal with the location and relocation of a single facility over a period of time. The concept was then expanded to cover multiple facilities, as seen in [50]. The integration of the Weber problem with the multi-period facility location problem was explored in [51], which aimed to determine the best facility to open at each time period. Other studies, such as [52,53,54,55], focus on dynamic uncapacitated facility location problems, location problems on networks, network p-median problems, and network center problems, respectively. The impact of facility opening and closing costs was studied in [51,56,57,58]. Additionally, dynamic location problems under uncertain environments were addressed in [59,60,61].

Despite the numerous studies on location allocation models, there remains a gap in the literature when it comes to considering both robustness and dynamic allocation. While robust optimization has been used to address uncertainty in the demand, cost, and other parameters, the majority of these models are static and do not take into consideration the dynamic aspect of the location problem. On the other hand, dynamic location models have been proposed to account for the changing nature of the location problem over time, but they do not address the uncertainty present in real-world scenarios. In light of these gaps, this study aims to fill the void by proposing a MILP model that incorporates both robustness and dynamic allocation. This model aims to provide a more comprehensive solution for real-world location problems that are subject to both uncertainties and changes over time.

3. Modeling Process and Methods

This section presents the development of a MILP model to address the research problem.

3.1. Notation List

Table 1. Notations used for mathematical modeling of DMS-p-MP.

Sets
T	Set of time periods in the planning horizon; $t\in \{1,2,\cdots ,|T\left|\right\}$
K	Set of categories (groups) in the area
B	Set of candidate locations; $i,j\in \{1,2,\cdots ,|B\left|\right\}$
	where, based on our problem, the candidate locations (j) are the same as demand nodes (i).
Parameters
$c_{ij}$	Unit cost of satisfying demand of location i from facility j
${\gamma }^o$	Mobile store’s opening cost in each location
${\gamma }^c$	Mobile store’s closing cost in each location
$d_{it}$	Demand of location i at day t
p	Available number of mobile stores in each day
$m_k$	Maximum number of stores allowed in group k
$n_k$	Minimum number of stores allowed in group k
Decision Variables
$x_{ijt}$	Fraction of demand of i that is supplied from j at day t
$y_{jt}$	Binary variables that is 1 if a mobile store is located at j at day t, and is 0 otherwise
$a_{jt}$	Auxiliary binary variables which 1 if a store is located in j
	at day t and will not be located in j at day $t+1$ (i.e., closing variable), and is 0 otherwise
$b_{jt}$	Auxiliary binary variable which is 1 if a store is not located in j
	at day t and will be located in j at day $t+1$ (i.e., opening variable), and is 0 otherwise

provides the notations used in the formulation of the model, including sets, parameters, and decision variables:

The set of all candidate locations (buildings) in group k is denoted by $F_k$. We know that $B=\cup {\left(F_k\right)}_{k\in \left[K\right]}$ means that each building should be at least in one group. Note that $\cap {\left(F_k\right)}_{k\in \left[K\right]}$ can be nonempty, meaning that one building can be a member of more than one group. Moreover, we do not need to define opening and closing costs ($a_{jt}$, $b_{jt}$) as binary variables since our minimization model and constraints force them to be 0 or 1. In order to have a feasible solution, we assume that p must satisfy the following inequalities:

$$\begin{array}{c}\hfill \sum _{k\in K}{n}_k\le p\le \sum _{k\in K}{m}_k,\end{array}$$

meaning that there is a solution that satisfies the model’s assumptions.

3.2. Mathematical Formulation

We defined all parameters and variables of our problem. The goal is to minimize the total cost of the system. We can model our problem as follows:

$$\begin{array}{cc}\hfill & Min\sum _{t\in T}\sum _{j\in B}\sum _{i\in B}{d}_{it}{c}_{ij}{x}_{ijt}+\sum _{t\in T\backslash \left\{\right|T\left|\right\}}\sum _{j\in B}({\gamma }^c{a}_{jt}+{\gamma }^o{b}_{jt})\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill \end{array}$$

(1)

$$\begin{array}{cccc}\hfill & \sum _{j\in B}{x}_{ijt}=1\hfill & \hfill & \forall i\in B,t\in T\hfill \end{array}$$

(2)

$$\begin{array}{cccc}\hfill & \sum _{j\in B}{y}_{jt}=p\hfill & \hfill & \forall t\in T\hfill \end{array}$$

(3)

$$\begin{array}{cccc}\hfill & x_{ijt}-y_{jt}\le 0\hfill & \hfill & \forall i,j\in B,t\in T\hfill \end{array}$$

(4)

$$\begin{array}{cccc}\hfill & y_{jt}-y_{j(t+1)}-a_{jt}\le 0\hfill & \hfill & \forall j\in B,t\in T\backslash \left\{\right|T\left|\right\}\hfill \end{array}$$

(5)

$$\begin{array}{cccc}\hfill & y_{j(t+1)}-y_{jt}-b_{jt}\le 0\hfill & \hfill & \forall j\in B,t\in T\backslash \left\{\right|T\left|\right\}\hfill \end{array}$$

(6)

$$\begin{array}{cccc}\hfill & \sum _{j\in F_k}{y}_{jt}\le m_k\hfill & \hfill & \forall k\in K,t\in T\hfill \end{array}$$

(7)

$$\begin{array}{cccc}\hfill & \sum _{j\in F_k}{y}_{jt}\ge n_k\hfill & \hfill & \forall k\in K,t\in T\hfill \end{array}$$

(8)

$$\begin{array}{cccc}\hfill & y_{jt}\in \{0,1\}\hfill & \hfill & \forall j\in B,t\in T\hfill \end{array}$$

(9)

$$\begin{array}{cccc}\hfill & a_{jt},b_{jt}\in \{0,1\}\hfill & \hfill & \forall j\in B,t\in T\hfill \end{array}$$

(10)

$$\begin{array}{cccc}\hfill & 0\le x_{ijt}\le 1\hfill & \hfill & \forall i,j\in B,t\in T\hfill \end{array}$$

(11)

where constraint (2) ensures the demand of all locations over the time horizon must be satisfied, constraint (3) ensures the number of mobile stores allocated in each day should be p, constraint (4) shows the relation between continuous and binary variables, i.e., if $x_{ijt}>0$, then $y_{jt}$ should be 1. Constraints (5) and (6) ensure that we consider the closing and opening costs, respectively. Constraints (7) and (8) ensure that we are following the policies regarding the limits on the number of stores in each group. Finally, constraint (9) and (10) are the binary constraints, and (11) is the non-negativity constraint.

3.3. Solution Approach

The problem at hand is a mixed-integer mathematical programming model that involves uncertainty. We will outline a state-of-the-art methodology to tackle these characteristics in the following manner:

3.3.1. Robust Optimization

In this section, an overview of the robust optimization approach proposed by [62] is presented. To do so, the following linear programming model is considered:

$$\begin{array}{cc}\hfill Mi{n}_{}& \sum _j^{}{c}_j{x}_j\hfill \\ \hfill s.t.& \sum _j^{}{\tilde{a}}_{ij}{x}_j\le b_i;\forall i\hfill \\ & x_j\ge 0;\forall j\hfill \end{array}$$

(12)

where the technological coefficients ${\tilde{a}}_{ij}$ are assumed to be uncertain. In other words, each coefficient ${\tilde{a}}_{ij}$ is regarded as an independent, symmetric, and bounded parameter, which can take values in $[a_{ij}-{\widehat{a}}_{ij},a_{ij}+{\widehat{a}}_{ij}]$, i.e., ${\tilde{a}}_{ij}\in [a_{ij}-{\widehat{a}}_{ij},a_{ij}+{\widehat{a}}_{ij}]$. In this definition, $a_{ij}$ and ${\widehat{a}}_{ij}$ denote the nominal value and the maximum deviation from the nominal value, respectively. Associated with each row i in problem (12) is $J_i$, which is defined as the set of all coefficients in row i that are subject to uncertainty. Furthermore, a scaled deviation ${\eta }_{ij}\in [-1,1]$ is defined for each uncertain coefficient ${\tilde{a}}_{ij}$ as ${\eta }_{ij}={\displaystyle \frac{{\tilde{a}}_{ij}-a_{ij}}{{\widehat{a}}_{ij}}}$ that represents the scaled perturbation of ${\tilde{a}}_{ij}$ from its nominal value $a_{ij}$.

Ref. [62] also introduced a parameter ${\Gamma }_i\in [0,|J_i\left|\right]$ as the budget of uncertainty for each constraint i, where $|J_i|$ denotes the number of elements of set $J_i$. In fact, ${\Gamma }_i$ is the maximum number of parameters that can really deviate from their nominal values for each constraint i. The parameter ${\Gamma }_i$ that bounds the total scaled deviation of uncertain parameters as ${\sum }_{j\in J_i}\left|{\eta }_{ij}\right|\le {\Gamma }_i$ adjusts the robustness of the proposed method against the level of solution conservatism. In particular, ${\Gamma }_i=0$ represents the nominal or deterministic formulation, whereas ${\Gamma }_i=\left|{\eta }_{ij}\right|$ relates to the worst-case formulation in which all uncertain parameters are fixed at their worst-case values from the uncertainty set. However, the decision maker can make a trade-off between the protection level of constraint i and the degree of conservatism of the solution if ${\Gamma }_i\in (0,|J_i\left|\right)$. Therefore, the budget of uncertainty ${\Gamma }_i$ that is an input to the robust optimization model can specify how risk-averse the decision-maker is [63].

Ref. [62] proposed a nonlinear programming model as follows, which is equivalent to the uncertain model (12):

$$\begin{array}{cc}\hfill Mi{n}_{}& \sum _j^{}{c}_j{x}_j\hfill \\ \hfill s.t.& \sum _j^{}{a}_{ij}{x}_j+\underset{\Omega }{max}\{\sum _{j\in S_i}^{}{\widehat{a}}_{ij}{x}_j+({\Gamma }_i-⌊{\Gamma }_i⌋){\widehat{a}}_{i{t}_i}{x}_j\}\le b_i;\forall i\hfill \\ & x_j\ge 0;\forall j\hfill \end{array}$$

(13)

where $\Omega =\{S_i\cup \left\{t_i\right\}|S_i\subseteq J_i,S_i=⌊{\Gamma }_i⌋,t_i\in J_i\backslash S_i\}$ is defined as the uncertainty set. For a given optimal solution $x^{*}$ of the problem (13), Bertsimas and Sim [62] demonstrated that the protection function for constraint i against uncertainty, which is ${\beta }_i(x^{*},{\Gamma }_i)=\underset{\Omega }{max}\{{\sum }_{j\in S_i}^{}{\widehat{a}}_{ij}{x}_j+({\Gamma }_i-⌊{\Gamma }_i⌋){\widehat{a}}_{i{t}_i}{x}_j\}$ can be formulated as the following linear programming problem:

$$\begin{array}{cc}\hfill {\beta }_i(x^{*},{\Gamma }_i)=Ma{x}_{}& \sum _{j\in J_i}{\widehat{a}}_{ij}\left|x_j^{*}\right|{\eta }_{ij}\hfill \\ \hfill s.t.& \sum _{j\in J_i}^{}{\eta }_{ij}\le {\Gamma }_i;\forall i\hfill \\ & 0\le {\eta }_{ij}\le 1;\forall i,j\hfill \end{array}$$

(14)

According to the theory of strong duality, since problem (14) is always feasible and bounded for all ${\Gamma }_i\in [0,|J_i\left|\right]$, its dual problem is feasible and bounded as well. Therefore, replacing the dual problem of the problem (14) into (13), Bertsimas and Sim (2004) derived the robust formulation of the uncertain linear programming problem (12) as follows:

$$\begin{array}{cc}\hfill Mi{n}_{}& \sum _j^{}{c}_j{x}_j\hfill \\ \hfill s.t.& \sum _j^{}{a}_{ij}{x}_j+{\beta }_i{\Gamma }_i+\sum _{j\in J_i}{\mu }_{ij}\le b_i;\forall i\hfill \\ \hfill & {\beta }_i+{\mu }_{ij}\ge {\widehat{a}}_{ij}{x}_j;\forall i,j\in J_i\hfill \\ \hfill & {\mu }_{ij}\ge 0;\forall i,j\in J_i\hfill \\ \hfill & {\beta }_i\ge 0;\forall i\hfill \\ & x_j\ge 0;\forall j\hfill \end{array}$$

(15)

where ${\beta }_i$ and ${\mu }_{ij}$ are dual variables associated with the first and second constraints in programming problem (14), respectively.

If the number of uncertain coefficients in constraint i that perturb from their respective nominal values is less than or equal to ${\Gamma }_i$, then the optimal solution from the robust problem (15) will always remain feasible. However, if more than ${\Gamma }_i$ coefficients deviate from their nominal values, then the probability of violating constraint i for an optimal solution $x_j^{*}$ is calculated as follows:

$$\begin{array}{c}\hfill Pr(\sum _j{\tilde{a}}_{ij}{x}_j^{*}<b_i)\le 1-\phi ({\displaystyle \frac{{\Gamma }_i-1}{\sqrt{|J_i|}}})\end{array}$$

(16)

where $\phi (.)$ is the cumulative distribution function of a standard normal random variable.

The robust optimization equivalent of the proposed problem (1) is:

$$\begin{array}{cc}\hfill \underset{x,y,a,b}{min}\underset{d\in \mathcal{U}}{max}& d{c}^{1}x+c^2(a+b)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(2\right)–\left(11\right)\hfill \end{array}$$

(17)

or equivalently:

$$\begin{array}{cc}\hfill \underset{x,y,a,b}{min}& \theta +c^2(a+b)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(2\right)–\left(11\right)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & \theta \ge \underset{d\in \mathcal{U}}{max}d{c}^{1}x\hfill \end{array}$$

(19)

where $\mathcal{U}$ is the uncertainty set for demand, and a, b are decision vectors for $a_{jt}$, $b_{jt}$, respectively. In robust decision-making, the goal is to make decisions that are not overly sensitive to small variations in the uncertain parameters, by taking into account a set of possible realizations (the uncertainty set) and seeking a solution that is feasible against all of them. This approach is often used in situations where the uncertainty is difficult or impossible to model precisely, and can lead to more robust solutions compared to approaches that only consider a single, most likely realization of the uncertainty [62,64].

In robust decision-making, there are different types of uncertainty sets that can be used to model the uncertain parameters, depending on the problem setting and the type of uncertainty that is being considered. The three main types of uncertainty sets are the box uncertainty set, the budget uncertainty set, and the conic uncertainty set. The box uncertainty set is a simple, rectangular set that bounds the uncertain parameters from above and below. The budget uncertainty set is a set of distributions that are considered "close" to a nominal distribution, where the notion of closeness is specified using a distance metric. The conic uncertainty set is defined using a combination of linear constraints and convex cones, and can be used to model more complex types of uncertainty, such as uncertainty in the mean and covariance of a random variable [65,66]. Among these, the budget uncertainty set is widely used, both due to its intuitive interpretation and tractability. The budget uncertainty set for the demand is:

$$\mathcal{U}=\{d\in {\mathbb{R}}^{\left|\mathcal{D}\right|\times \left|\mathcal{D}\right|}|d=\overline{d}+\delta \xi ,||\xi |{|}_{\infty }\le 1,\sum _{i,j\in \mathcal{D}}{\xi }_{it}\le \delta \}$$

where $\Gamma$ is the uncertainty budget. Using this definition, we have:

$$\begin{array}{cc}\hfill \underset{x,y,a,b}{min}& \theta +c^2(a+b)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(2\right)–\left(11\right)\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \underset{{\left|\right|\xi \left|\right|}_{\infty }\le {1,\left|\right|\xi \left|\right|}_1\le \Gamma }{max}\xi c^{1}x\le \theta -\overline{d}{c}^{1}x\hfill \end{array}$$

(21)

Let us focus on the left-hand-side of Equation (21):

$$\begin{array}{cc}\hfill & \underset{{\left|\right|\xi \left|\right|}_{\infty }\le {1,\left|\right|\xi \left|\right|}_1\le \Gamma }{max}\delta \xi c^{1}x\to \underset{\xi }{max}\delta \xi c^{1}x,s.t.:\sum _{i,t}\left|{\xi }_{it}\right|\le \Gamma ,-1\le {\xi }_{it}\le 1\hfill \end{array}$$

(22)

Letting $a_{it}=\left|{\xi }_{it}\right|$, then we have:

$$\begin{array}{cc}\hfill max& \delta \xi c^{1}x\hfill \end{array}$$

(23)

$$\begin{array}{cccc}\hfill \mathrm{s}.\mathrm{t}.& \sum _{i,t}{a}_{it}\le \Gamma \hfill & \hfill & \hfill \left[{\pi }^1\right]\end{array}$$

(24)

$$\begin{array}{cccc}\hfill & {\xi }_{it}\le 1\hfill & \hfill & \hfill \hspace{1em} \left[{\pi }_{it}^2\right]\end{array}$$

(25)

$$\begin{array}{cccc}\hfill & -{\xi }_{it}\le 1\hfill & \hfill & \hfill \hspace{1em} \left[{\pi }_{it}^3\right]\end{array}$$

(26)

$$\begin{array}{cccc}\hfill & {\xi }_{it}-a_{it}\le 0\hfill & \hfill & \hfill \hspace{1em}\left[{\pi }_{it}^4\right]\end{array}$$

(27)

$$\begin{array}{cccc}\hfill & -{\xi }_{it}-a_{it}\le 0\hfill & \hfill & \hfill \left[{\pi }_{it}^5\right]\end{array}$$

(28)

$$\begin{array}{ccc}\hfill & {\xi }_{it}\in \mathbb{R},a_{it}\in {\mathbb{R}}^{+}\hfill & \hfill \end{array}$$

(29)

Since the model is a minimization problem, we need to obtain the dual problem whose objective is also minimization: The dual problem is:

$$\begin{array}{cc}\hfill \underset{\pi }{min}& \Gamma {\pi }^1+\sum _{i,t\in \mathcal{D}}({\pi }_{it}^2+{\pi }_{it}^3)\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill \mathrm{s}.\mathrm{t}.& {\pi }^1\ge {\pi }_{it}^4+{\pi }_{it}^5\forall i,t\in \mathcal{D}\hfill & \end{array}$$

(31)

$$\begin{array}{cc}\hfill & \pi \in {\mathbb{R}}^{+}\hfill \end{array}$$

(32)

Finally, the DMS-p-MP reformulation of the problem becomes:

$$\begin{array}{cc}\hfill & \underset{x,y,a,b}{min}\theta +c^2(a+b)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left(2\right)–\left(11\right)\hfill \end{array}$$

(33)

$$\begin{array}{cccc}\hfill & \Gamma {\pi }^1+{\pi }_{it}^2+{\pi }_{it}^3+\overline{d}{c}^{1}x\le \theta \hfill & \hfill & \forall i,t\in \mathcal{D}\hfill \end{array}$$

(34)

$$\begin{array}{ccccc}\hfill & {\pi }^1\ge {\pi }_{it}^4+{\pi }_{it}^5\hfill & \hfill & \hfill & \hspace{1em}\hspace{1em}\forall i,t\in \mathcal{D}\hfill \end{array}$$

(35)

$$\begin{array}{cccc}\hfill & {\pi }_{it}^2-{\pi }_{it}^3+{\pi }_{it}^4-{\pi }_{it}^5={\delta }_{it}{c}_{it}^1{x}_{ijt}\hfill & \hfill & \forall i,t\in \mathcal{D},\forall j\in B\hfill \end{array}$$

(36)

$$\begin{array}{cccc}\hfill & {\pi }^1,{\pi }_{it}^2,{\pi }_{it}^3,{\pi }_{it}^4,{\pi }_{it}^5\ge 0\hfill & \hfill & \forall i,t\in \mathcal{D}\hfill \end{array}$$

(37)

3.3.2. Lagrangian Relaxation

In discrete location theory, one of the basic models is the p-median problem, and it is an NP-hard problem, as with most location problems [67]. The MILP model presented in Section 3 is typically solved in practice with numerous residence areas (demand points), potential facility locations, and time horizons. As a result of the large-scale property of the developed model, it presents substantial computational difficulty when applied to real problems, which cannot be addressed by commercial optimization software, such as Cplex, Xpress, or Gurobi. For supply chain optimization problems involving such computational complexity, Lagrangian relaxation (LR) is widely used [68,69,70,71,72] in the literature.

Therefore, this section develops an LR approach for solving the presented MILP problem. The LR method is an iterative algorithm that provides the upper and lower bounds of the optimal objective value as well as the estimation of the optimality gap of the feasible established solution in each iteration [20]. The LR method used in this paper includes the general steps as follows:

• Relax one of the constraints by multiplying it by a Lagrange multiplier and bringing the constraint into the objective function;
• Solve the model to find the optimal values of the relaxed problem;
• Find the feasible solution to the original problem by using the resulting decision variables found in step 2;
• Compute the lower bound using the solution obtained from the relaxed problem in step 2;
• Use the subgradient optimization method to modify the Lagrange multiplier assigned to the violated constraint and return to step 2 after finding the new multiplier(s) for the Lagrange variable.

The algorithm terminates whenever the lower bound is close enough to the upper bound.

Step 1. Solving the Relaxed Problem

In order to make the problem easier to solve, the constraints in this study are relaxed, even if this relaxation may lead to infeasibility [20]. Specifically, constraints (2) and (3) are relaxed, resulting in the following Lagrangian dual problem:

$$\begin{array}{cc}\hfill \underset{x,y,a,b}{min}& \theta +c^2(a+b)+\hfill \\ & \sum _{j\in B}\sum _{i\in B}\sum _{t\in T}{\lambda }_{bt}^1(x_{ijt}-1)+\hfill \\ \hfill & \sum _{j\in B}\sum _{t\in T}{\lambda }_t^2(y_{jt}-p)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \left(4\right)–\left(11\right),\left(34\right)–\left(37\right)\hfill \end{array}$$

(38)

The optimal value of the objective function in the Lagrangian dual problem above, which is defined using non-negative Lagrange multipliers (${\lambda }_{bt}^1$, ${\lambda }_t^2$), serves as a lower bound for the mixed-integer linear programming problem (38).

Step 2. Finding a Feasible Solution and an Upper Bound

In most situations, the solution to the Lagrangian dual problem is not feasible due to the relaxation of constraints (2) and (3). However, it is possible to obtain a feasible solution that provides an upper bound on the single objective MILP model by solving this model and setting the decision variables $x_{ijt}$, $y_{jt}$, $a_{jt}$, and $b_{jt}$ to the optimal values obtained from solving the Lagrangian dual problem.

Step 3. Finding a Lower Bound and Updating the Lagrange Multipliers

During each iteration of the Lagrangian procedure, the Lagrangian multipliers ${\lambda }_{bt}^1$, ${\lambda }_t^2$ are updated, and new lower and upper bounds are subsequently derived. There are various methods in the literature, such as cutting planes [73], sub-gradients [20], and bundling [74], that can be used for this purpose. In this paper, the sub-gradient approach is employed to update the Lagrangian multipliers because it is a widely recognized and commonly used method. According to the sub-gradient procedure [20], the Lagrange multipliers at the $(n+1)$ iteration are calculated as follows:

$$\begin{array}{cc}\hfill & {\left({\lambda }_{bt}^1\right)}^{n+1}=max\left\{0,{\left({\lambda }_{bt}^1\right)}^n-{\tau }_1^n(x_{ijt}-1)\right\}\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & {\left({\lambda }_t^2\right)}^{n+1}=max\left\{0,{\left({\lambda }_t^2\right)}^n-{\tau }_2^n(y_{jt}-p)\right\}\hfill \end{array}$$

(40)

The step sizes ${\tau }_1^n$, and ${\tau }_2^n$ in the algorithm are defined as follows:

$$\begin{array}{cc}\hfill & {\tau }_1^n=\frac{{\alpha }^n(UB-L{B}^n)}{{\sum }_{j\in B}{\sum }_{i\in B}{\sum }_{t\in T}{\lambda }_{bt}^1{(x_{ijt}-1)}^2}\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill & {\tau }_2^n=\frac{{\alpha }^n(UB-L{B}^n)}{{\sum }_{j\in B}{\sum }_{t\in T}{\lambda }_t^2{(y_{jt}-p)}^2}\hfill \end{array}$$

(42)

The term $\alpha$ is simply a constant that will be changed during each iteration of the algorithm as described above. $\alpha$ is initialized to 2. If the lower bound, $LB$, has not increased in an iteration, then its value will be halved. Additionally, let $UB$ be the best upper bound (the one with the smallest value) that has been discovered thus far, and $L{B}^n$ is the lower bound obtained at iteration n.

Step 4. Termination Criteria

The algorithm will stop when one of the following conditions is met [20]:

• A predetermined number of iterations have been completed;
• The lower bound is equal to the upper bound ($UB=L{B}^n$) or is close enough to the upper bound ($UB-L{B}^n<0.1$);
• The value of $\alpha$ becomes small.

4. Numerical Experiment

4.1. Case Description

In this section, we discuss a case in which a company wants to place some mobile grocery stores on the campus of the University of Waterloo. These self-service mobile stores can serve all students and staff. Figure 1 shows a sample picture of these stores. Specifically, the company wants to propose a plan to specify the optimal locations of stores needed on campus dynamically (every day) based on the demand variation on campus. They update their plan every month, i.e., they decide on all days at the beginning of each month. In this research, we aim to find the optimal locations of stores over the time horizon (one month). Based on Section 3, $\left|T\right|=28$, $\left|K\right|=6$, and $\left|B\right|=91$.

Figure 2 shows the University of Waterloo campus map. As per the legend associated with this figure, all buildings on campus are categorized into five groups: Service and Administrative Buildings, Academic Buildings, Residence Buildings, Research Park Buildings, and others. Considering the parking lots, the campus can be effectively divided into six distinct categories. The University of Waterloo asked the company to follow some rules regarding each group. Specifically, there are some limitations on the number of stores needed for each group for each day. More details and the list of buildings included in each group are provided in the following sections.

Each building has a specific demand on each day. Obviously, it is not (financially) feasible to place one store in each building. The company has only p stores, and in each period (day), they want to place all of them on campus. We consider a demand cost for students and staff in a building that does not have a store, and they need to go to other buildings. The goal is to place the stores to satisfy the demand of all buildings while minimizing the costs. There are two more costs in our problem: opening cost and closing cost. Although the stores are mobile, we need to consider an opening (closing) cost if we want to open (close) a store at the beginning of each day. In fact, we are capturing all transportation costs needed to change a store’s location. In our model, we assume that the cost of opening or closing a store is not related to the distance between different locations.

The demand of each building may change from day to day due to different reasons such as weekends, events, etc. Then, it is an excellent motivation for day-to-day decision-making following demand variation. In this research, we assume that our demand prediction is accurate. Then, we can finalize all decisions for each day of the month, once at the beginning of the month. This variability highlights the need for a more dynamic approach to decision-making, and robust optimization can provide a solution to this challenge.

We can model this problem as a DMS-p-MP. Generally, our problem has two modifications compared to the simple multi-period p-median problem. First, we are considering opening and closing costs over the time horizon. Second, there are some extra constraints raised from University of Waterloo policies.

4.2. Data Collection

We divide all of the University of Waterloo (UW)’s facilities according to their functionality into six different segments: Academic Buildings, Parking Spots, Student Residence Buildings, Research Park Buildings, Athletic Buildings, and University Plaza, respectively. The workspace is based on the UW’s official map, which includes 91 facilities, and we also make an assumption that the population in each facility within a segment is all equivalent. Segments indicated in

Table 2. The functional classification for all facilities in the workspace.

Segment	Buildings Included in the Segment (Building Id)
Academic Buildings	COG (1), COM (2), CPH (3), RA2 (4), M3 (5), ML (6), RAC (7), GSC (8), GH (9), BRH (10), SLC (11), OWE (12), HMN (13), MC (14), TC (15), KOC (16), C2 (17), EV3 (18), OPT (19), DC (20), SCH (21), FED (22), QNC (23), AL (24), HS (25), B2 (26), EV2 (27), REN (28), ESC (29), EV1 (30), STJ (31), EIT (32), HH (33), STP (34), Bl (35), PAS (36), CGR (37), E3 (38), EC3 (39), BMH (40), PHY (41), EC1 (42), LHI (43), NHI (44), EC2 (45), UC (46), LIB (47), ECH (48), ERC (49), E2 (50), ES (51), CSB (52), RCH (53), E6 (54).
Parking Lots	Parking CL (55), Parking A (56), Parking X (57), Parking C (58), Parking W (59), Parking OV (60), Parking V (61), Parking S (62), Parking K (63), Parking J (64), Parking R (65), Parking P (66), Parking T (67), Parking M (68), Parking L (69), Parking D (70), Parking EC (71), Parking HV (72), Parking N (73), Parking UWP (74).
Residence Buildings	CLN (75), CLV (76), MKV (77), V1 (78), REV (79), TH (80), MHR (81), UWP (82).
Research Park Buildings	445 (83), 375 (84), 340 (85), 275 (86), ACW (87), 300 (88).
Athletic Buildings	CLF (89), PAC (90).
University Plaza	Plaza (91).

are as follows,

We use Python’s OpenCV toolbox by [76] to determine facilities’ specific locations by fixing pixels’ coordinates in the workspace. Students and staff allow going through buildings, and it is likely for us to use Euclidean distance measurement

$$l_2=\sqrt{{(x-a)}^2+{(y-b)}^2}$$

to find the distance between the two pairs in the data set as follows in Figure 3.

From the UW’s website, we obtained the rough number of students and staff for each faculty, the rough number of students and staff for each university college, and the capacities of each residence. A general assumption is that 10% of university students will use one of two gyms (CIF and PAC).

Table 3. Descriptive Statistics for Academic Buildings.

Segment (1)	Population
Engineering Faculty	11,000
Mathematics Faculty	9260
Science Faculty	6000
Health Faculty	3643
Arts Faculty	3000
Environment Faculty	3000
Others	1200
Total population	37,103
Total facilities	54
Average per facility	687

,

Table 4. Descriptive Statistics for Parking Lots.

Segment (2)	Population
Campus parking	4000
Total population	4000
Total facilities	20
Average per facility	200

,

Table 5. Descriptive Statistics for Student Residence Buildings.

Segment (3)	Population
Columbia Lake Village—North	404
Columbia Lake Village—South	400
William Lyon Mackenzie King Village	320
Student Village 1	1381
Ron Eydt Village	960
Tutors’ Houses	100
Minota Hagey Residence	70
University of Waterloo Place	1650
Others	200
Total population	5285
Total facilities	8
Average per facility	660

,

Table 6. Descriptive Statistics for Research Parking Buildings.

Segment (4)	Population
David Johnson Research Park	4000
Others	100
Total population	4100
Total facilities	6
Average per facility	683

,

Table 7. Descriptive Statistics for Athletic Buildings.

Segment (5)	Population
Columbia Icefield	2100
Physical Activities Complex	2100
Others	100
Total population	4300
Total facilities	2
Average per facility	2150

and

Table 8. Descriptive Statistics for University Plaza.

Segment (6)	Population
University Shops Plaza	3200
Total population	3200
Total facilities	1
Average per facility	3200

below are the population of all classifications for each segment.

It was given in the previous section that the time horizon $T=28$ (approximately equivalent to a month), but it can also be separated into four periods (weeks). Based on the functionality of each segment, with time varying from Monday to Sunday, we may empirically define the facility in the different segments and the different days in utilization rate $U_{kt}$. For instance, the utilization rates for the academic buildings are 100 out of 100, but there are 30 out of 100 during the weekend. The complete estimated utilization rates for different functional buildings for each day over a week are as follows in

Table 9. The Estimated Utilization Rate for Different Functional Buildings for Each Day over a Week.

Functionality	Monday	Tuesday	Wednesday	Thursday	Friday	Saturday	Sunday
Academic Buildings	100	90	90	80	90	30	30
Parking Spots	100	100	100	100	100	20	20
Residence Buildings	50	50	50	50	60	100	100
Research Park Buildings	100	90	90	80	90	10	10
Athletic Buildings	50	50	50	60	50	100	100
University Plaza	100	100	70	80	90	50	50

:

Thus, the demand $d_{kt}$ of each building in segment k on day t, where $t\in \{1,\dots ,7\}$, in a week, is able to be defined as

$$d_{kt}=U_{kt}\times \frac{\mathrm{Total}\mathrm{Population}\left(k\right)}{\mathrm{Total}\mathrm{Facilities}\left(k\right)}.$$

As for having a unified standard, we calculate the lower bound of opening facilities in constraint (8) by taking a floor of 70% of the number of facilities in segment k over the total facilities in the workspace:

$$n_k=⌊p\times \frac{\mathrm{the}\mathrm{Number}\mathrm{of}\mathrm{Facilities}\mathrm{in}\mathrm{Segment}\left(k\right)}{91}\times 70\%⌋.$$

For example, $n_1=⌊18\times \frac{54}{91}\times 70\%⌋=⌊7.47⌋=7.$ Similarly, the upper bound of opening facilities in constraint (7) by taking a ceiling of 130% of the number of facilities in segment k over the total facilities in the workspace,

$$m_k=⌈p\times \frac{\mathrm{the}\mathrm{Number}\mathrm{of}\mathrm{Facilities}\mathrm{in}\mathrm{Segment}\left(k\right)}{91}\times 130\%⌉.$$

The following

Table 10. Bounds on the number of Robomarts.

Functionality	Min (${\mathit{n}}_{\mathit{k}}$)	Max (${\mathit{m}}_{\mathit{k}}$)
Academic Buildings	7	14
Parking Lots	2	6
Residence Buildings	1	3
Research Park Buildings	0	2
Athletic Buildings	0	1
University Plaza	0	1

is the maximum (minimum) number of Robomarts that are allowed in segment k,

4.3. Computational Experiments

In this section, we use all parameters discussed in the Section 4.2 Data Collection to solve our problem. All numerical experiments have been run on an Apple M1 processor, limited to 16 GB of RAM. Gurobi has access to 8 physical cores and 8 logical processors, using up to 8 threads. This model is MILP and has M (=239,512) variables and N (=239,694) constraints (excluding sign constraints). We use Gurobi version 9.5.1 by [77] to solve this optimization model. Since default settings in Gurobi generally work well, we are keeping all settings as default. Specifically, we use Gurobi’s API embedded in Python 3.11.2.

MILP models are generally solved using a linear-programming based branch-and-bound algorithm. The Gurobi provides advanced implementations of the latest MILP algorithms including deterministic parallel, nontraditional search, heuristics, solution improvement, cutting planes, and symmetry breaking.

Based on Section 5, the demand is weekly periodic. Then, we expect the model to make the same decision over the weeks.

Table 11. Results—Optimal Objective Value = 43,175.7, CPU Time = 12.99 s.

t	Id of Opened Buildings
1 (Monday)	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90
6 (Saturday)	0, 2, 3, 5, 10, 17, 27, 34, 40, 44, 48, 54, 63, 76, 77, 81, 89, 90
8 (Monday)	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90
13 (Saturday)	0, 2, 3, 5, 10, 17, 27, 34, 40, 44, 48, 54, 63, 76, 77, 81, 89, 90
15 (Monday)	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90
20 (Saturday)	0, 2, 3, 5, 10, 17, 27, 34, 40, 44, 48, 54, 63, 76, 77, 81, 89, 90
22 (Monday)	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90
27 (Saturday)	0, 2, 3, 5, 10, 17, 27, 34, 40, 44, 48, 54, 63, 76, 77, 81, 89, 90

shows what buildings are open during the planning horizon. We show the days that we change our decisions. For instance, the buildings that are open between day 1 and day 6 are the same.

Table 11 shows that we only open new buildings and close the current buildings over the weekend. We again change our decision on weekdays. It is expected because the utilization rates of some of our segments are significantly different during the weekend.

Specifically, we close buildings 12, 55, and 83 (that, based on Table 3, are Conrad Grebel university college, Parking lots, Research building 375, respectively) and open buildings 63, 77, and 81 (that are Parking P, Student Village, University of Waterloo Place, respectively). The interesting point is that all of the buildings 63, 77, and 81 are around students’ residences. Students are mostly in the residence area instead of the academic campus during the weekends. Then, it is worth closing some stores and opening new ones in students’ residences.

4.4. Sensitivity Analysis

In this section, we will change the parameters to see how variability can affect our results.

4.4.1. Time Horizon

First, we analyze the impact of the length of time horizon on our results.

Table 12. Sensitivity Analysis on Time Horizon.

T	Id of Opened Buildings	Id of Closed Buildings	Objective Value	CPU Time (S)
14	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 81)	63, 77, 81, (12, 55, 83)	21570.1	12.43
21	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 81)	63, 77, 81, (12, 55, 83)	32372.9	6.08
28	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 81)	63, 77, 81, (12, 55, 83)	43175.7	12.99
35	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 81)	63, 77, 81, (12, 55, 83)	53978.5	17.02
42	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 81)	63, 77, 81, (12, 55, 83)	64781.3	20.40

shows the results when we increase (decrease) the time horizon. For instance, as we increase the time horizon, it will take more time to find the optimal solution. In addition, our optimal objective value would increase since we are adding more positive terms to our cost.

Moreover, we see that the opened and closed buildings remain the same as we increase the time horizon. The reason is that our demand is periodic over the weeks. By increasing the number of weeks, the optimal decision to open and close some stores would be the same. Figure 4 shows the results, in which red line represents the objective value and the blue line represents CPU run time.

4.4.2. Number of Facilities to Be Located (P)

Now, we change parameter P and see how it affects our results. Variability of P is important since it would help the company to decide the number of stores they want to buy and create on the campus.

Note that we could also consider a fixed cost of buying each store in our model (i.e., we could add the $Price$ of each facility to the objective function). However, since in our optimization model P is fixed and given, we do not need to consider it. Figure 5 shows the results when we change P. First, it seems that the running time is not directly dependent on P. However, P is determining the complexity of the problem. In addition, the objective value is obviously decreasing as we increase P since we did not consider the price of each store.

In addition,

Table 13. Sensitivity Analysis on Parameter P.

P	Id of Opened Buildings	Id of Closed Buildings	Objective Value	CPU Time (S)
12	2, 5, 10, 17, 27, 35, 44, 54, 65, 76, 83, 90, (63, 89)	63, 89, (65, 83)	58,616.4	58.07
15	2, 3, 5, 10, 27, 35, 45, 48, 63, 66, 74, 76, 83, 89, 90 (81, 17, 61, 79)	81, 17, 61, 79, (83, 3, 66, 76)	49,402.9	7.79
18	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 81)	63, 77, 81, (12, 55, 83)	43,175.7	12.99
21	0, 2, 5, 7, 10, 12, 17, 23, 26, 34, 40, 44, 48, 53, 54, 55, 76, 83, 85, 89, 90, (64, 77, 81, 3, 79)	64, 77, 81, 3, 79, (7, 55, 83, 76, 85)	38,266.5	7.89
24	0, 2, 3, 5, 6, 10, 12, 17, 23, 34, 40, 44, 48, 53, 54, 61, 67, 76, 80, 81, 83, 87, 89, 90, (64, 78)	64, 78, (80, 87)	34,874.4	107.60

shows how our decision changes in different P. There is one interesting point in our decisions. Compare $P=12$ with $P=15$. In $P=15$, we do not use the same opened building we used in $P=12.$ This shows that, as we want to add one building, we may no longer need another building.

4.4.3. Cost Coefficients

Followed by two previous sections, we want to discuss the effects of changing the opening and closing costs together on our results.

Table 14. Sensitivity Analysis on Cost Coefficients (together).

${\mathit{\gamma }}^{\mathit{o}\left(\mathit{c}\right)}$	Id of Opened Buildings	Id of Closed Buildings	Objective Value	CPU Time (S)
0	0, 2, 3, 10, 12, 17, 26, 35, 45, 48, 54, 65, 76, 83, 86, 88, 90, (1, 4, 5, 23, 26, 27, 34, 40, 44, 56, 63, 81, 89)	4, 5, 27, 34, 40, 44, 56, 63, 81, 89, (23, 26, 35, 45, 65, 86, 88)	42,900	3.90
2.5	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 79, 81)	63, 77, 79, 81, (12, 55, 76, 83)	43,049.3	9.34
5	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (63, 77, 81)	63, 77, 81, (12, 55, 83)	43,175.7	12.99
10	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (80, 81)	80, 81, (12, 83)	43,382.3	58.45
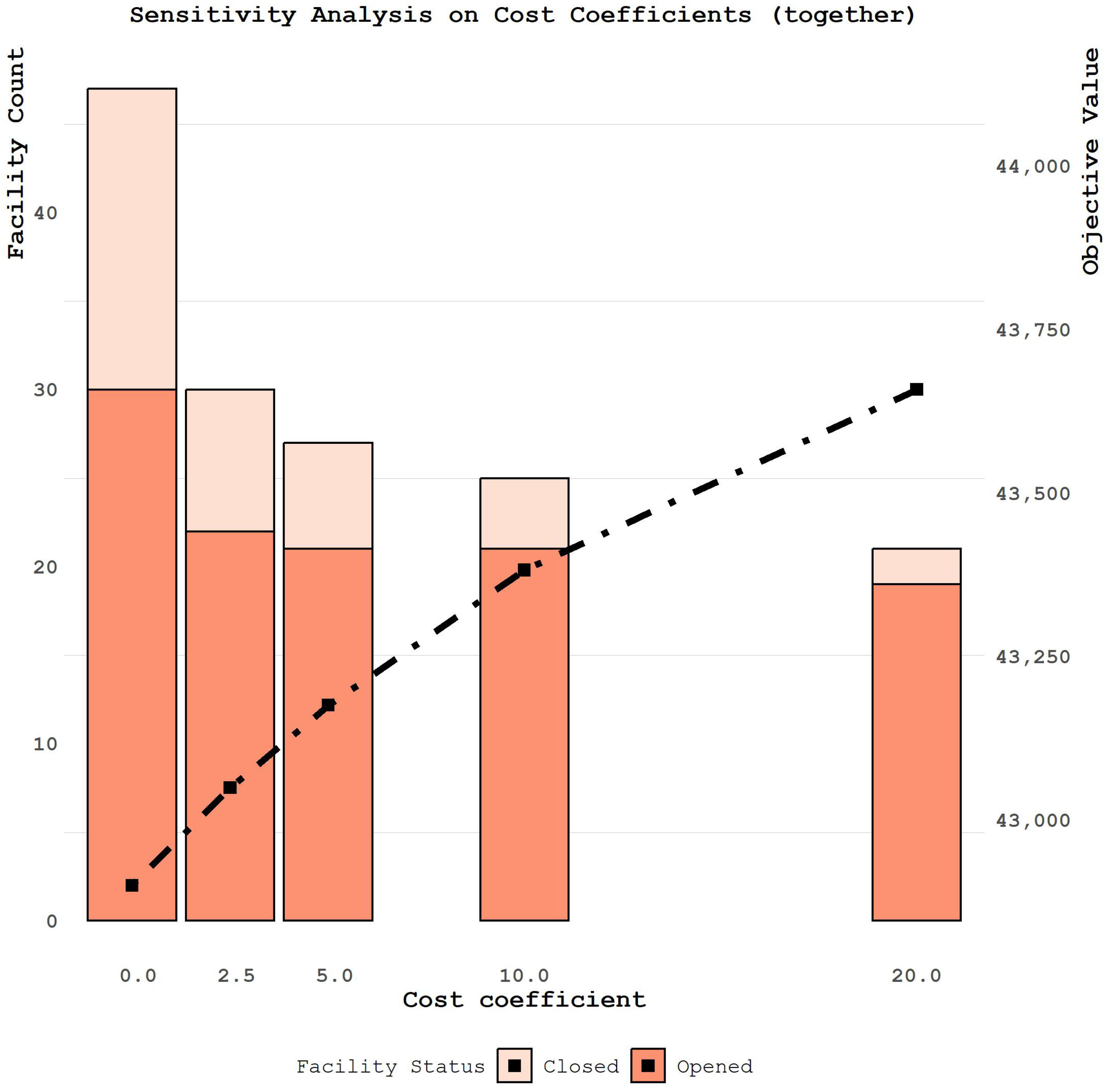
20	0, 2, 3, 5, 10, 12, 17, 27, 34, 40, 44, 48, 54, 55, 76, 83, 89, 90, (81)	81, (83)	43,658.2	82.58

shows the results when we increase (decrease) the cost coefficients. Considering the case in which costs are both zero, the model tries to open (and close) any building in each period. In other words, it does not care how many building it wants to open or close each day. Another noteworthy point is that running time increases as we increase the costs. It shows that the trade-off between keeping current buildings and opening (closing) other buildings is becoming important and challenging to the model.

Figure 6 shows that the initially opened buildings remain the same and start to dynamically be changed as we increase the opening/closing cost. Moreover, the objective value increases as we increase the opening cost. In addition, in the case of high opening costs, we prefer not to open new buildings (and close the current open buildings) since it would be costly.

5. Discussion

In this paper, we propose a mixed-integer linear formulation for the Dynamic Modified Stochastic p-Median Problem in a Competitive Supply Chain Network Design. The presented model takes into account the robust optimization and time horizon as a novel approach, which enables the decision-maker to consider uncertainty and short-term changes in the supply chain network design. The robust optimization approach used in this study allows for the consideration of different scenarios and uncertainty in demand and supply, which is crucial in real-world applications. Additionally, the time horizon approach allows for the dynamic nature of the problem to be captured, which is important in today’s fast-paced business environment.

The proposed model was tested using computational experiments, and the results demonstrate the effectiveness of the proposed approach in handling the dynamic and stochastic nature of the problem. The results also provide valuable insights for practitioners and researchers in the field of supply chain network design. The proposed model can be extended and applied to other similar problems in the field, such as facility location, transportation and logistics, and inventory management.

One of the main contributions of this study is the integration of robust optimization and time horizon in the mixed-integer linear formulation for the Dynamic Modified Stochastic p-Median Problem. The robust optimization approach allows for the consideration of different scenarios and uncertainty, while the time horizon approach allows for the dynamic nature of the problem to be captured. This integration provides a more realistic and practical solution to the problem, which can be useful for practitioners and researchers in the field.

Another important contribution of this study is the application of the proposed model to a competitive supply chain network design problem. This application is relevant and valuable as it provides insights into how the proposed model can be used in a real-world context. The results of the computational experiments demonstrate the effectiveness of the proposed model in handling the dynamic and stochastic nature of the problem and provide valuable insights for practitioners and researchers in the field. For instance, we can change over the problem definition to solve any other location problems. Covering location problems are valuable to investigate, such as trying to find the optimal number of Robomarts [75] that can serve all facilities in the workspace if the single Robomart can only serve facilities within a limited number of miles.

The results of the computational study demonstrate the effectiveness and robustness of the proposed formulation in solving the DMS-P-MP. The results show that the number of opened and closed buildings remains constant as the time horizon advances, even though the demand patterns change over time. This highlights the ability of the proposed formulation to adapt to changing demand patterns and ensure that the supply chain network is both cost-efficient and responsive to changes in demand. Moreover, the robustness of the solution is demonstrated by its ability to provide effective solutions even in the presence of uncertainty in demand patterns. The proposed formulation can be applied to real-world problems, providing decision-makers with an effective and robust tool to optimize their supply chain network design in a dynamic and uncertain environment. The ability of the formulation to take into account the periodic nature of demand and adapt to changing demand patterns makes it a valuable tool for decision-makers who are facing challenges in designing a cost-efficient and responsive supply chain network.

While the cost of opening or closing a store is currently considered as a constant parameter in the model, it is recognized that this cost could vary dynamically based on various factors such as the distance between different locations. This presents an exciting opportunity for further research, where the dynamic nature of opening and closing costs could be explored and incorporated into the model.

One limitation of this study is that the Robomart can only be located at specific facilities (nodes) in the proposed model. In reality, however, the Robomart can also be located somewhere on the route between two nodes (edges). This limitation may affect the validity and applicability of the proposed model in real-world scenarios. To address this limitation, it is possible to consider analogous absolute p-median problems to simulate reality. This approach would involve the inclusion of edge-based locations for the Robomart in the model, which would provide a more realistic representation of the problem. However, this would require additional mathematical development and computational resources, and would be a subject for future research.

Another potential area of future research is to make the problem an Adaptive Robust Optimization (ARO) problem [64]. In this approach, the number of trucks p would be determined in the first stage and other variables in the second stage. This would enable a more flexible and dynamic approach to supply chain network design, as the number of trucks can be adjusted in response to changes in demand and supply.

In summary, the proposed model in DMS-p-MP takes into account the robust optimization and time horizon as a novel approach, which enables the decision-maker to consider uncertainty and short-term changes in the supply chain network design. The results of the computational experiments demonstrate the effectiveness of the proposed model in handling the dynamic and stochastic nature of the problem and provide valuable insights for practitioners and researchers in the field. The proposed model can be extended and applied to other similar problems in the field of supply chain network design. The integration of robust optimization and time horizon in the proposed model provides a more realistic and practical solution to the problem, which can be useful for practitioners and researchers in the field.