Ant Colony Optimization for Multiple Pickup and Multiple Delivery Vehicle Routing Problem with Time Window and Heterogeneous Fleets
Abstract
1. Introduction
2. Mathematical Model
3. Solution Approach
3.1. Initialization of the Parameter
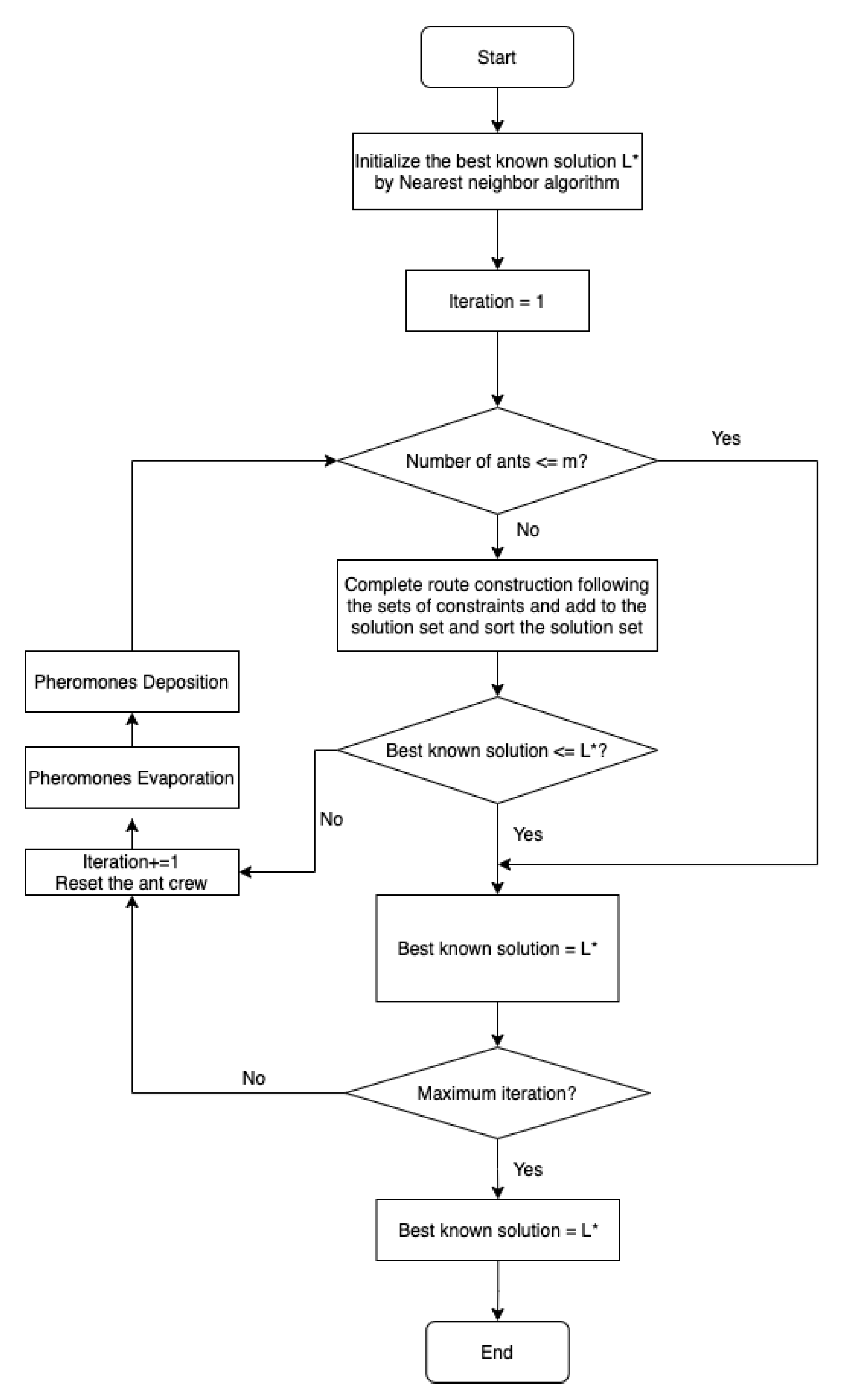
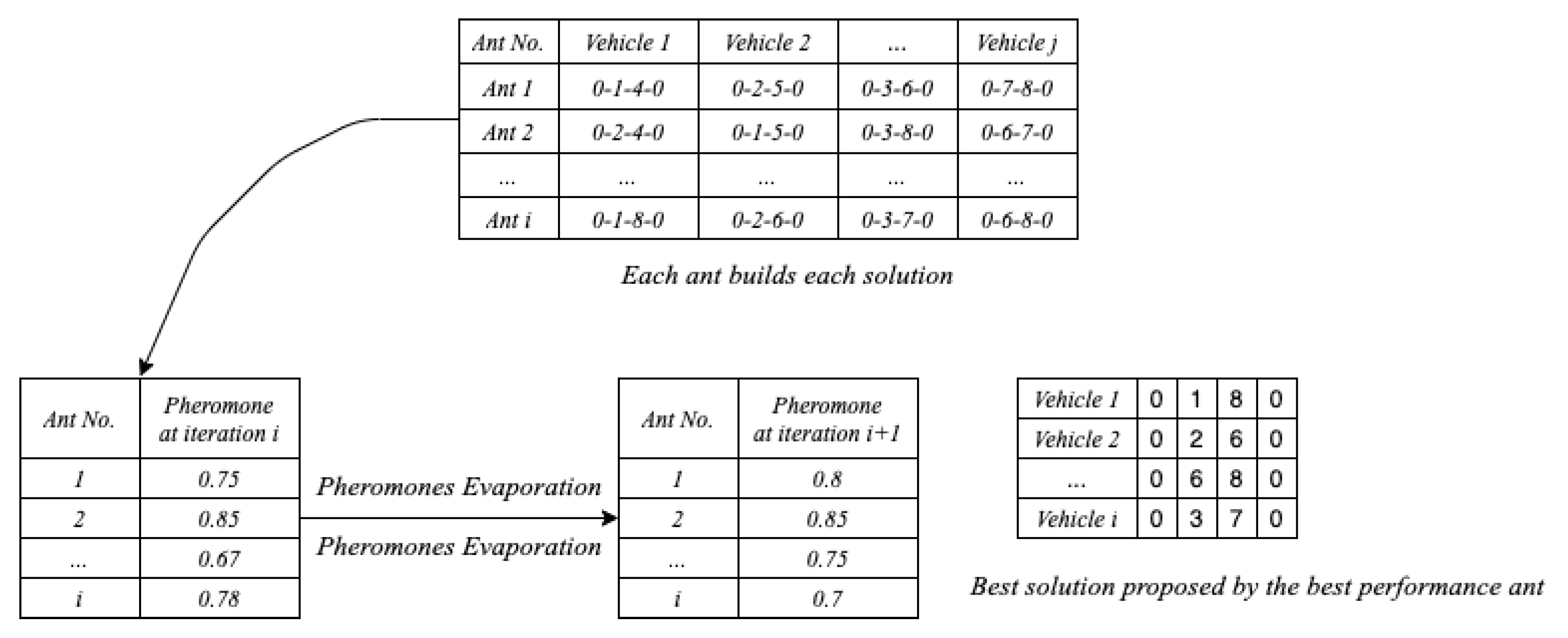
3.2. Solution Construction
| Algorithm 1: ACO for the MPMDVRPTWHF |
 |
4. Computational Results and Conclusion
4.1. Benchmark Description
4.2. Comparison with Exact Solution
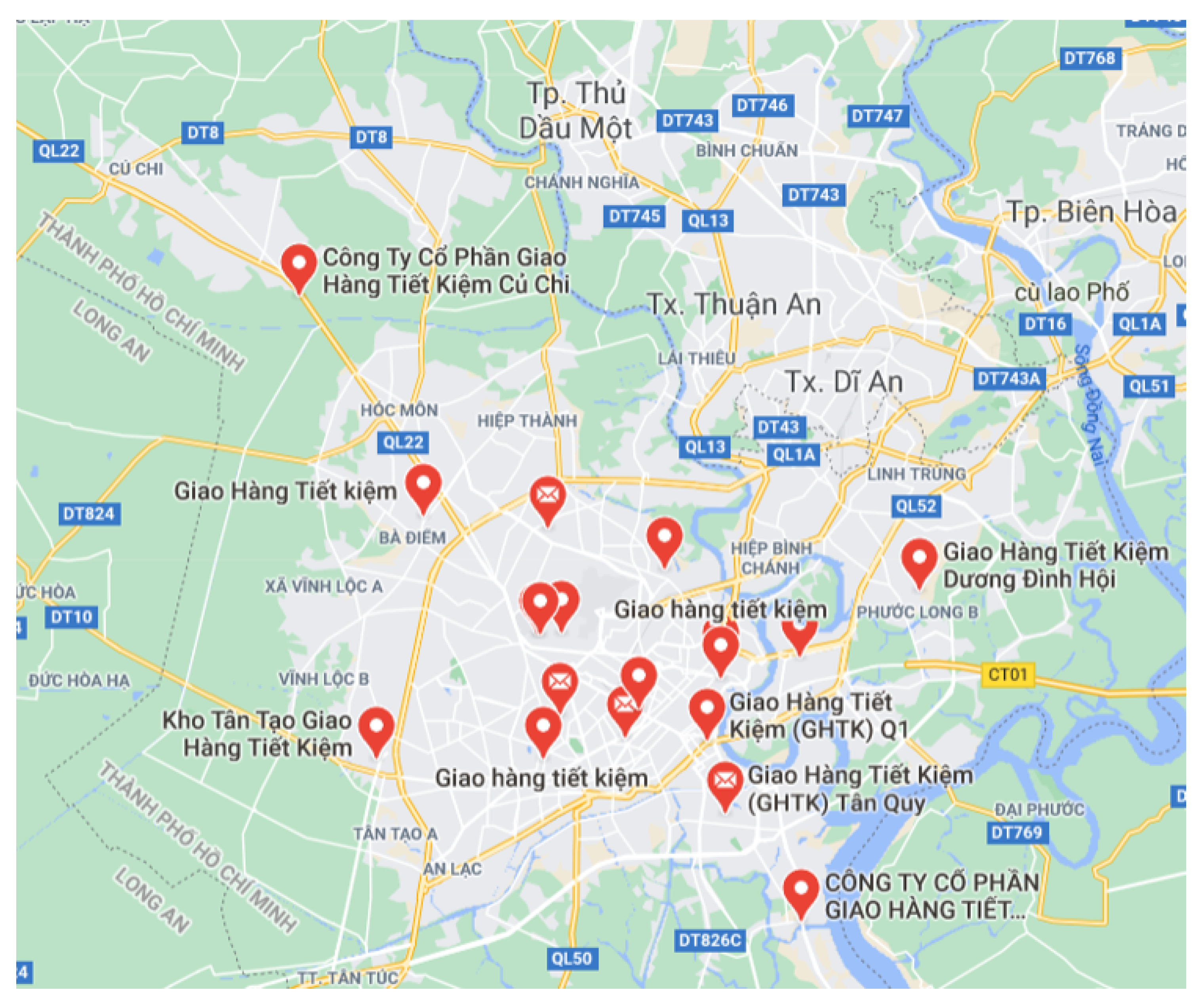
4.3. Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MPMDVRPTWHF | Multiple pickup and multiple delivery vehicle routing problem with time window and heterogeneous fleets |
| VRPTW | Vehicle Routing Problem with Time window |
| VRP | Vehicle Routing Problem |
| CVRP | Capacitated Vehicle Routing Problem |
| VRPB | Vehicle Routing Problem with Backhauls |
| VRPPD | Vehicle Routing Problem with Pickup and Delivery |
| Notations | |
| C | be the set of all nodes |
| be the set of nodes not including the starting depot, | |
| be the set of nodes not including the ending depot, | |
| K | be the set of vehicles |
| P | be the pickup set |
| D | be the delivery set |
| R | be the set of pair where i is the pick up point of j |
| be the pickup or delivery quantity of node i. if i is the pickup node, otherwise | |
| be the service time at node i | |
| be the earliest starting time at customer i | |
| be the latest starting time of customer i | |
| be the distance between node i and node j | |
| be the capacity of vehicle k | |
| be the cost per distance of vehicle k | |
| be the maximum working duration | |
| M | be the number of vehicles |
| be the traveling time from node i to node j | |
| binary parameter, if node is the pickup node of node otherwise, | |
| be the very large number | |
| Decision variable | |
| be the binary variable. if vehicle k travels directly from node i to node j, otherwise | |
| be the start time of service of vehicle k at node i | |
| be the load of vehicle k at node i | |
References
- Toth, P.; Vigo, D. The Vehicle Routing Problem, 1st ed.; Society for Industrial and Applied Mathematics: Philadelphia, PN, USA, 2002; pp. 385–386. [Google Scholar]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J.W. Scheduling of vehicles from a central depot to a number of delivery points. Oper. Res. 1964, 12, 568–584. [Google Scholar] [CrossRef]
- Montoya-Torres, J.R.; Lopez Franco, J.; Nieto Isaza, S.; Felizzola Jimenez, H.; Herazo-Padilla, N. A literature review on the vehicle routing problem with multiple depots. Comput. Ind. Eng. 2015, 79, 115–129. [Google Scholar] [CrossRef]
- Jian, L.; Li, Y.; Panos, M.P. Multiple-depot vehicle routing problem with time windows under shared depot resources. J. Comb. Optim. 2016, 31, 515–532. [Google Scholar]
- Solomon, M.M. Algorithms for the vehicle routing and scheduling problem with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Desaulniers, G.; Desrosiers, J.; Solomon, M.M.; Soumis, F. The VRP with time windows. In The Vehicle Routing Problem; Toth, P., Vigo, D., Eds.; SIAM Monograp: Philadenphia, PA, USA, 2002; pp. 157–186. [Google Scholar]
- Baldacci, R.; Bartolini, E.; Mingozzi, A. An exact algorithm for the pickup and delivery problem with time windows. Oper. Res. 2011, 59, 414–426. [Google Scholar] [CrossRef]
- Furtado, M.G.S.; Munari, P.; Morabito, R. Pickup and delivery problem with time windows: A new compact two-index formulation. Oper. Res. Lett. 2017, 45, 334–341. [Google Scholar] [CrossRef]
- Baldacci, R.; Toth, P.; Vigo, D. Exact algorithms for routing problems under vehicle capacity constraints. Ann. Oper. Res. 2010, 75, 213–245. [Google Scholar] [CrossRef]
- Desrochers, M.; Lenstra, J.K.; Savelsbrgh, M.W.P.; Soumis, F. Vehicle routing with time windows: Optimization and approximation. In Vehicle Routing: Methods and Studies; Golden, B.L., Assad, A.A., Eds.; Elsevier Science Publishers: Amsterdam, The Netherlands, 1988; pp. 65–82. [Google Scholar]
- Laporte, G. The vehicle routing problem: An overview of exact and approximate algorithms. Eur. J. Oper. Res. 1992, 59, 345–358. [Google Scholar] [CrossRef]
- Chen, X.; Kong, Y.; Dang, L.; Hou, Y.; Ye, X. Exact and metaheuristic approaches for a biobjective school bus scheduling problem. PLoS ONE 2015, 10, e0132600. [Google Scholar]
- Laporte, G.; Nobert, Y. Exact Algorithms for the Vehicle Routing Problem. N.-Holl. Math. Stud. 1987, 132, 147–184. [Google Scholar]
- Faiz, T.; Chrysafis, V.; Md Noor, E.A. A column generation algorithm for vehicle scheduling and routing problems. Comput. Ind. Eng. 2019, 130, 222–236. [Google Scholar] [CrossRef]
- Fisher, M.L. Optimal solution of vehicle routing problems using minimum K-trees. Oper. Res. 1987, 42, 626–642. [Google Scholar] [CrossRef]
- Ropke, S.; Cordeau, J.-F. Branch and cut and price for the pickup and delivery problem with time windows. Transp. Sci 2009, 43, 267–286. [Google Scholar] [CrossRef]
- Roeva, O.; Fidanova, S. Comparison of different metaheuristic algorithms based on InterCriteria analysis. J. Comp. App. Math. 2018, 340, 615–628. [Google Scholar] [CrossRef]
- Ho, S.C.; Haugland, D. A tabu search heuristic for the vehicle routing problem with time windows and split deliveries. Comput. Oper. Res. 2004, 31, 1947–1964. [Google Scholar] [CrossRef]
- Bowerman, R.L.; Calamai, P.H. The spacefilling curve with optimal partitioning heuristic for the vehicle routing problem. Eur. J. Oper. Res. 1994, 76, 128–142. [Google Scholar] [CrossRef]
- Dondo, R.; Cerda, J. A cluster-based optimization approach for the multi depot heterogeneous fleet vehicle routing problem with time windows. Eur. J. Oper. Res. 2007, 176, 478–1507. [Google Scholar] [CrossRef]
- Cordeau, J.F.; Gendreau, M.; Laporte, G.; Potvinand, J.Y.; Semet, F. A guide to vehicle routing heuristics. J. Oper. Res. Soc. 2002, 53, 512–522. [Google Scholar] [CrossRef]
- Szeto, W.Y.; Wu, Y.; Ho, S.C. An artificial bee colony algorithm for the capacitated vehicle routing problem. Eur. J. Oper. Res. 2011, 215, 126–135. [Google Scholar] [CrossRef]
- Dorigo, M.; Stutzle, T. Ant Colony Optimization, 1st ed.; MIT Press: Cambridge, MA, USA, 2004; pp. 305–315. [Google Scholar]
- Bullnheimer, B.; Hartl, R.F.; Strauss, C. Applying the ant system to the vehicle routing problem. In Meta-Heuristics: Advances and Trends in Local Search for Optimization; Voss, S., Martello, S., Osman, I.H., Roucairol, C., Eds.; Kluver Academic Publishers: Boston, MA, USA, 2012; pp. 285–296. [Google Scholar]
- Tan, W.F.; Lee, L.S.; Majid, Z.A.; Seow, H.V. Ant colony optimization for capacitated vehicle routing problem. J. Comput. Sci. 2012, 8, 846–852. [Google Scholar]
- Doerner, K.; Gronalt, M.; Hartl, R.F.; Reimann, M.; Strauss, C.; Stummer, M. Savings Ants for the vehicle routing problem. Lect. Notes Comput. Sci. 2002, 2279, 73–109. [Google Scholar]
- Ma, Y.; Han, J.; Kang, K.; Yan, F. An Improved ACO for the multi-depot vehicle routing problem with time windows. In Proceedings of the Tenth International Conference on Management Science and Engineering Management; Xu, J., Hajiyev, A., Nickel, S., Gen, M., Eds.; Springer: Singapore, 2018; pp. 1181–1189. [Google Scholar]
- Zhang, X.; Tang, L. A new hybrid ant colony optimization algorithm for the vehicle routing problem. Pattern Recognit. Lett. 2009, 30, 848–855. [Google Scholar] [CrossRef]
- Mazzeo, S.; Loiseau, I. An ant colony algorithm for the capacitated vehicle routing. Electron. Notes Discret. Math. 2004, 18, 181–186. [Google Scholar] [CrossRef]
- Yu, B.; Yang, Z.Z.; Yao, B.Z. An improved ant colony optimization for vehicle routing problem. Eur. J. Oper. Res. 2009, 196, 171–176. [Google Scholar] [CrossRef]
- Anh, P.T.; Cuong, P.T.; Ky Phuc, P.N. The vehicle routing problem with time windows: A case study of fresh food distribution center. In Proceedings of the 11th International Conference on Knowledge and Systems Engineering (KSE), Danang, Vietnam, 24–26 October 2019. [Google Scholar]
- Bullnheimer, B.; Hartl, R.F.; Strauss, C. An improved ant system for the vehicle routing problem. Ann. Oper. Res. 1999, 89, 319–328. [Google Scholar] [CrossRef]
| Computational Result | |||||
|---|---|---|---|---|---|
| Instance | ACO VRP | CPLEX | Gap | ||
| Min | Max | Average | |||
| c101c6 | 1319.98 | 1319.98 | 1319.98 | 1319.98 | 0.00% |
| c103c6 | 1153.75 | 1153.75 | 1153.75 | 1153.75 | 0.00% |
| c206c6 | 1338.86 | 1338.86 | 1338.86 | 1338.86 | 0.00% |
| c208c6 | 902.69 | 902.69 | 902.69 | 902.69 | 0.00% |
| r104c6 | 1029.47 | 1029.47 | 1029.47 | 1029.47 | 0.00% |
| r105c6 | 831.31 | 831.31 | 831.31 | 831.31 | 0.00% |
| r202c6 | 885.63 | 885.63 | 885.63 | 885.63 | 0.00% |
| r203c6 | 1126.40 | 1126.40 | 1126.40 | 1126.40 | 0.00% |
| rc105c6 | 1465.66 | 1465.66 | 1465.66 | 1465.66 | 0.00% |
| rc108c6 | 1352.30 | 1352.30 | 1352.30 | 1352.30 | 0.00% |
| rc204c6 | 954.15 | 954.15 | 954.15 | 954.15 | 0.00% |
| rc208c6 | 925.42 | 925.42 | 925.42 | 925.42 | 0.00% |
| c104c10 | 2029.37 | 2029.37 | 2029.37 | 2029.37 | 0.00% |
| c205c10 | 1822.89 | 1822.89 | 1822.89 | 1822.89 | 0.00% |
| r201c10 | 1766.95 | 1766.95 | 1766.95 | 1766.95 | 0.00% |
| r203c10 | 1385.67 | 1385.67 | 1385.67 | 1385.67 | 0.00% |
| rc108c10 | 1916.49 | 1916.49 | 1916.49 | 1916.49 | 0.00% |
| rc201c10 | 2050.08 | 2050.08 | 2050.08 | 2050.08 | 0.00% |
| rc205c10 | 2463.76 | 2463.76 | 2463.76 | 2463.76 | 0.00% |
| c101c12 | 2167.13 | 2172.13 | 2169.33 | 2155.75 | 0.63% |
| c202c12 | 1851.35 | 1878.35 | 1858.75 | 1833.35 | 1.39% |
| r102c12 | 1518.96 | 1535.96 | 1525.16 | 1503.66 | 1.43% |
| r103c12 | 1227.01 | 1247.01 | 1240.81 | 1225.71 | 1.23% |
| rc102c12 | 2038.62 | 2162.62 | 2100.62 | 2035.12 | 3.22% |
| c103c16 | 2283.20 | 2502.33 | 2327.03 | 2283.20 | 1.92% |
| c106c16 | 1671.41 | 1701.41 | 1686.41 | 1631.41 | 3.37% |
| c202c16 | 2294.32 | 2375.74 | 2335.03 | 2283.22 | 2.27% |
| c208c16 | 2283.21 | 2433.93 | 2358.57 | 2283.21 | 3.30% |
| r105c16 | 2296.32 | 2336.32 | 2316.32 | 2247.45 | 3.06% |
| r202c16 | 3343.71 | 3443.71 | 3393.71 | 3311.95 | 2.47% |
| r209c16 | 2392.01 | 2408.79 | 2400.40 | 2332.01 | 2.93% |
| rc103c16 | 2794.23 | 2894.23 | 2844.23 | 2774.23 | 2.52% |
| rc108c16 | 2993.06 | 3093.06 | 3043.06 | 2970.06 | 2.46% |
| rc202c16 | 2912.30 | 3087.30 | 2999.80 | 2892.67 | 3.70% |
| rc204c16 | 3533.47 | 3663.25 | 3598.36 | 3519.47 | 2.24% |
| r102c18 | 2848.34 | 2884.23 | 2866.29 | 2765.34 | 3.65% |
| Avg. | 1.16% | ||||
| Vehicle ID | Total Distance (m) | Total Time (h) | Capacity |
|---|---|---|---|
| 28 | 181,683 | 3.29482 | 0.039473684 |
| 37 | 146,620 | 2.95774 | 0.043274854 |
| 44 | 269,635 | 5.28208 | 0.048245614 |
| 48 | 278,462 | 5.44326 | 0.083333333 |
| 22 | 273,706 | 4.92704 | 0.078654971 |
| 29 | 252,486 | 5.35718 | 0.017836257 |
| 33 | 155,872 | 3.19608 | 0.029532164 |
| 35 | 282,634 | 5.59536 | 0.603216374 |
| 41 | 145,496 | 3.17976 | 0.013157895 |
| 45 | 216,041 | 4.09412 | 0.043859649 |
| 23 | 197,074 | 3.96682 | 0.046491228 |
| 27 | 227,014 | 4.84774 | 0.066374269 |
| 2 | 243,202 | 4.61812 | 0.958 |
| 30 | 149,347 | 3.44958 | 0.047953216 |
| 39 | 190,161 | 4.1299 | 0.092690058 |
| 40 | 184,611 | 3.35338 | 0.034795322 |
| 46 | 277,438 | 5.32206 | 0.040350877 |
| 47 | 263,489 | 4.7877 | 0.497076023 |
| 49 | 253,517 | 5.39702 | 0.007309942 |
| 51 | 237,076 | 4.90112 | 0.104093567 |
| 26 | 255,230 | 4.85868 | 0.114619883 |
| 32 | 138,889 | 2.63174 | 0.005847953 |
| 34 | 279,517 | 5.91702 | 0.061988304 |
| 4 | 237,012 | 5.06692 | 0.852555556 |
| 36 | 277,189 | 5.0947 | 0.566959064 |
| 6 | 193,887 | 3.5942 | 0.629111111 |
| 8 | 145,858 | 3.187 | 0,850222222 |
| 38 | 109,955 | 2.46894 | 0,707894737 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ky Phuc, P.N.; Phuong Thao, N.L. Ant Colony Optimization for Multiple Pickup and Multiple Delivery Vehicle Routing Problem with Time Window and Heterogeneous Fleets. Logistics 2021, 5, 28. https://doi.org/10.3390/logistics5020028
Ky Phuc PN, Phuong Thao NL. Ant Colony Optimization for Multiple Pickup and Multiple Delivery Vehicle Routing Problem with Time Window and Heterogeneous Fleets. Logistics. 2021; 5(2):28. https://doi.org/10.3390/logistics5020028
Chicago/Turabian StyleKy Phuc, Phan Nguyen, and Nguyen Le Phuong Thao. 2021. "Ant Colony Optimization for Multiple Pickup and Multiple Delivery Vehicle Routing Problem with Time Window and Heterogeneous Fleets" Logistics 5, no. 2: 28. https://doi.org/10.3390/logistics5020028
APA StyleKy Phuc, P. N., & Phuong Thao, N. L. (2021). Ant Colony Optimization for Multiple Pickup and Multiple Delivery Vehicle Routing Problem with Time Window and Heterogeneous Fleets. Logistics, 5(2), 28. https://doi.org/10.3390/logistics5020028






