Lashing Force Prediction Model with Multimodal Deep Learning and AutoML for Stowage Planning Automation in Containerships
Abstract
1. Introduction
1.1. Consideration of Stowage Planning
1.2. Literature Review
1.3. Lashing in Containership
1.4. Machine Learning in Lashing of Containership
2. Lashing Force Prediction with Multimodal Deep Learnings
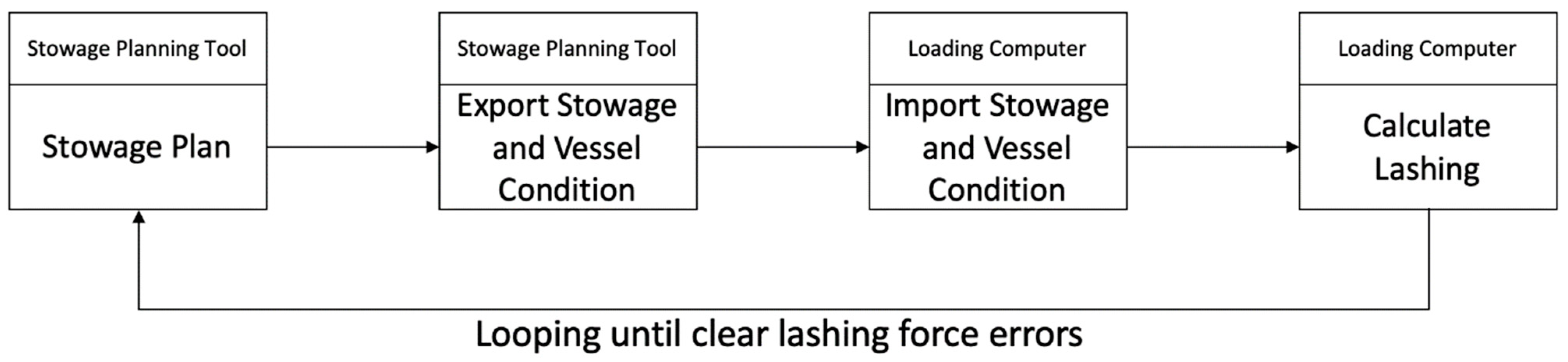
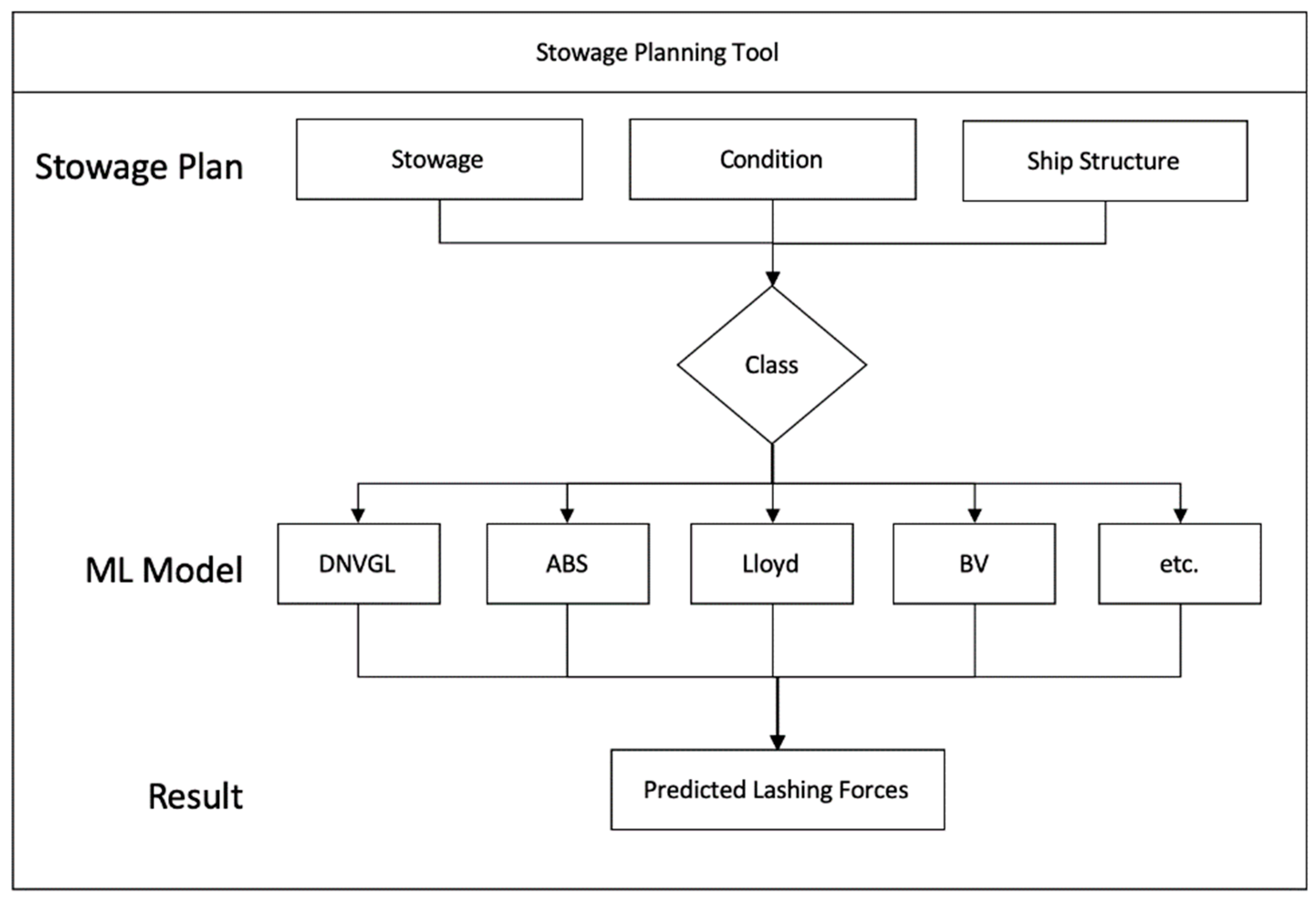
2.1. Idea and Process
- As part of auto stowage planning process, the stowage planning tool slots containers on deck.
- The conditions, as input parameters for lashing force prediction, are set from both the stability result (e.g., GM, Draft, Trim, etc.; subject to Class), calculated by the stowage planning tool and inputted values (e.g., Wind Speed, Roll Angle, etc.; subject to Class) by the stowage planner.
- The stowage system requests the lashing force result for one of the embedded lashing force prediction models, trained per each Class.
- The model returns the lashing force percentage for each lashing component.
- If any of the returned lashing force values is greater than 100%, the stowage planner or stowage planning tool changes the containers with lighter ones and repeats from step no. 2.
2.2. Feature Extraction and Engineering
2.2.1. Containership Structure
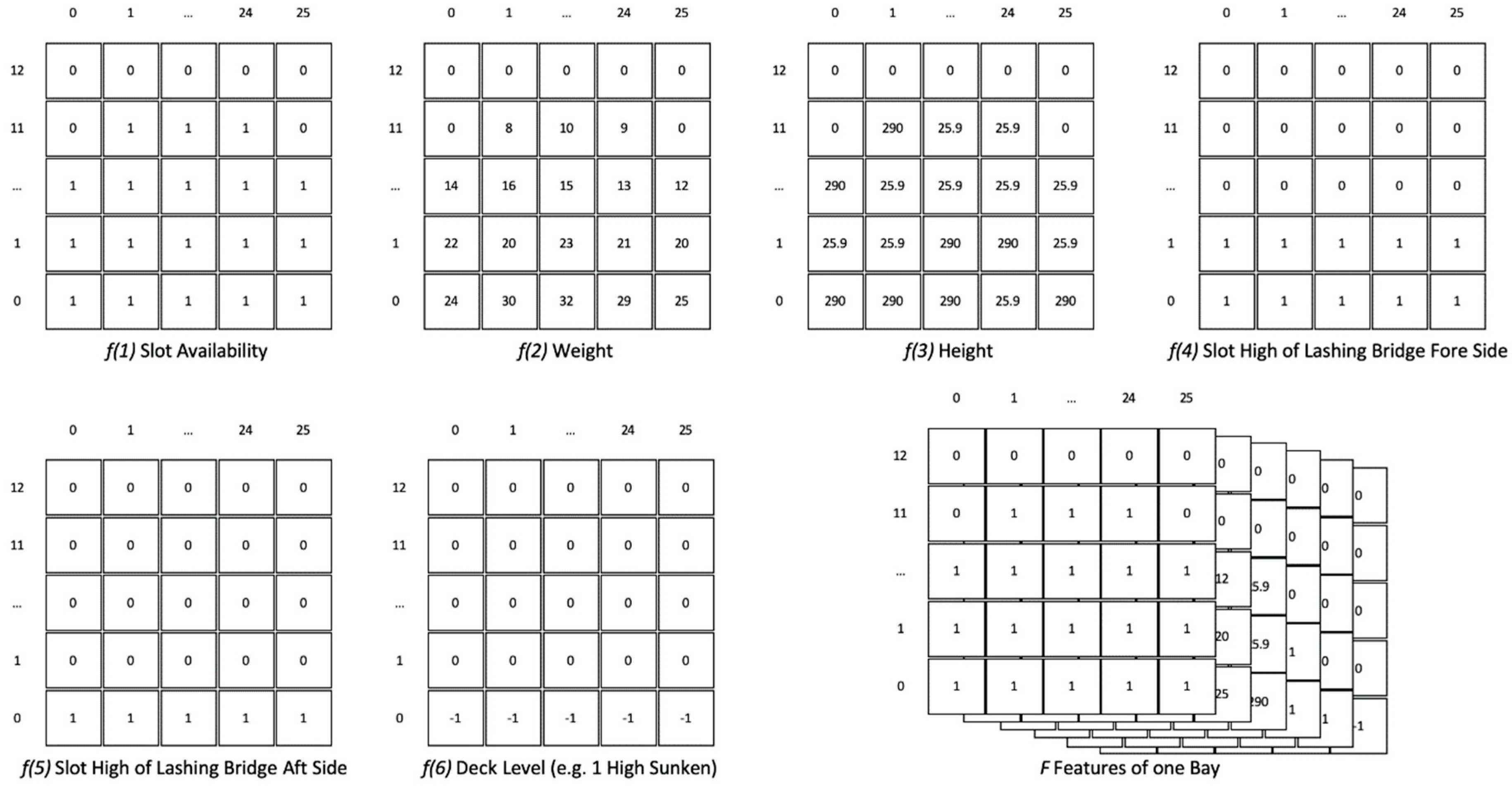
2.2.2. Features
- Physical slot availability in each slot, , from fixed maximum dimension. If available set 1, otherwise 0.
- Weight of container in each slot, . Generally heavier containers stack in lower slots to be stable.
- Height of container in each slot, . Generally a lower height is more stable.
- Slot Highof Lashing Bridge Fore Side. Higher lashing bridge gives a safer lashing force value in general.
- Slot High of Lashing Bridge Aft Side. Higher lashing bridge gives lower lashing force value in general.
- Deck Level where the deck starts as compared to other Bays. For example, the Sunken Bay has lower lashing force values because it is one level lower than other normal Bays.
- GM (Metacentric Height)—this is the result condition when stability is calculated.
- Wind Speed.
- Roll Angle.
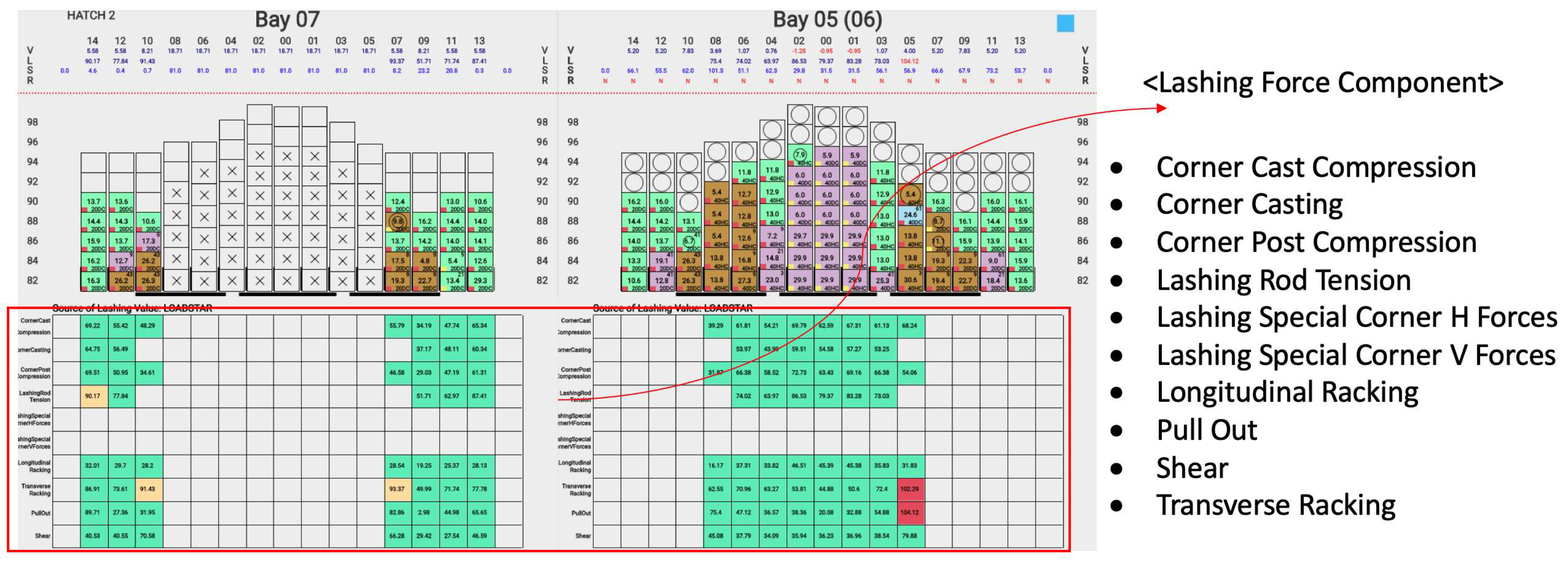
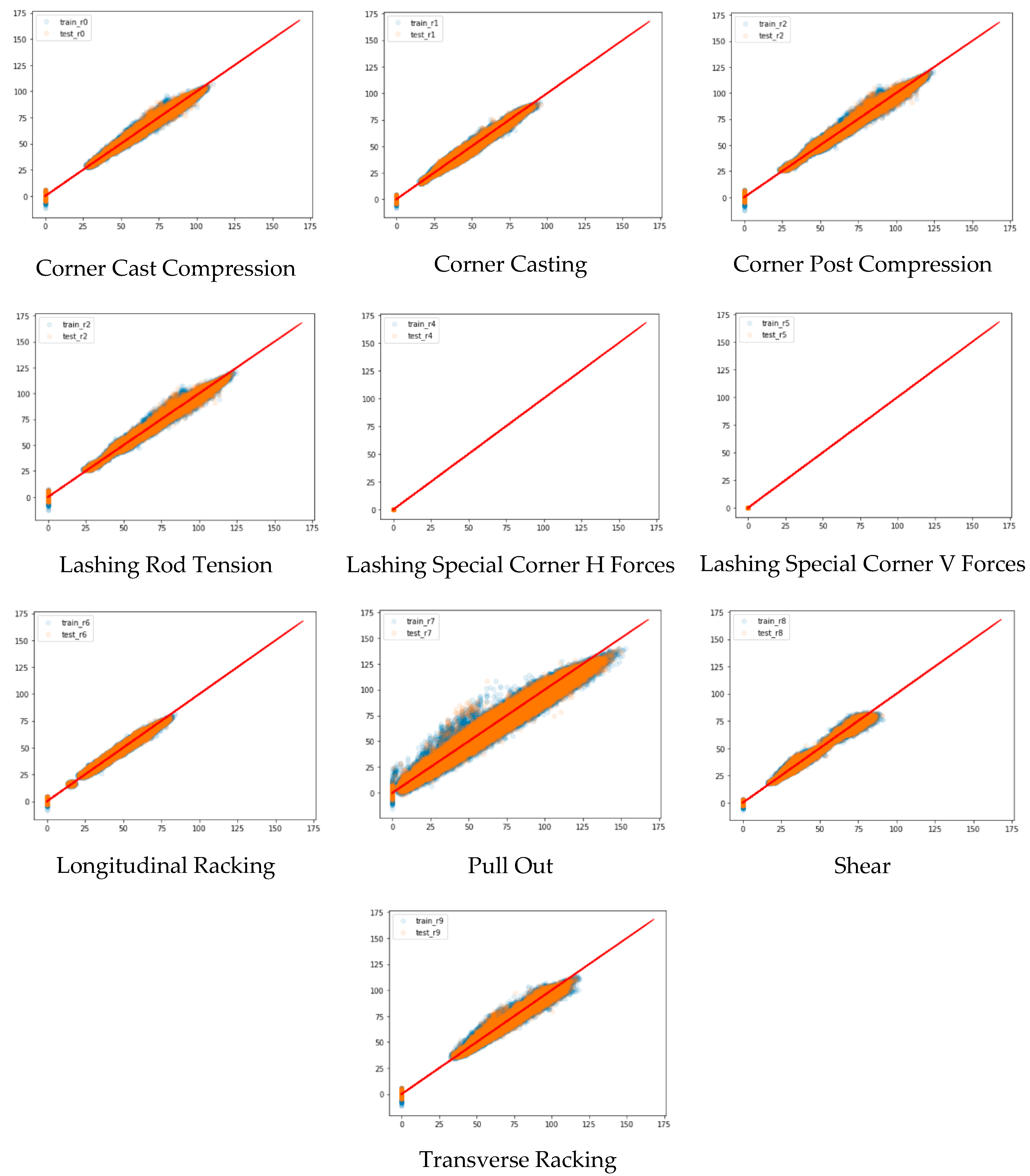
2.2.3. Lashing Force
- Corner Cast Compression;
- Corner Casting;
- Corner Post Compression;
- Lashing Rod Tension;
- Lashing Special Corner H Forces (not applicable for this ship);
- Lashing Special Corner V Forces (not applicable for this ship);
- Longitudinal Racking;
- Pull Out;
- Shear;
- Transverse Racking.
2.2.4. Dataset
- 11 different realistic vessel conditions;
- For each condition, random weight variance in 10%, 15% and 20% for each container onboard;
- A total of 21 different Hatches as the different stacking profile.
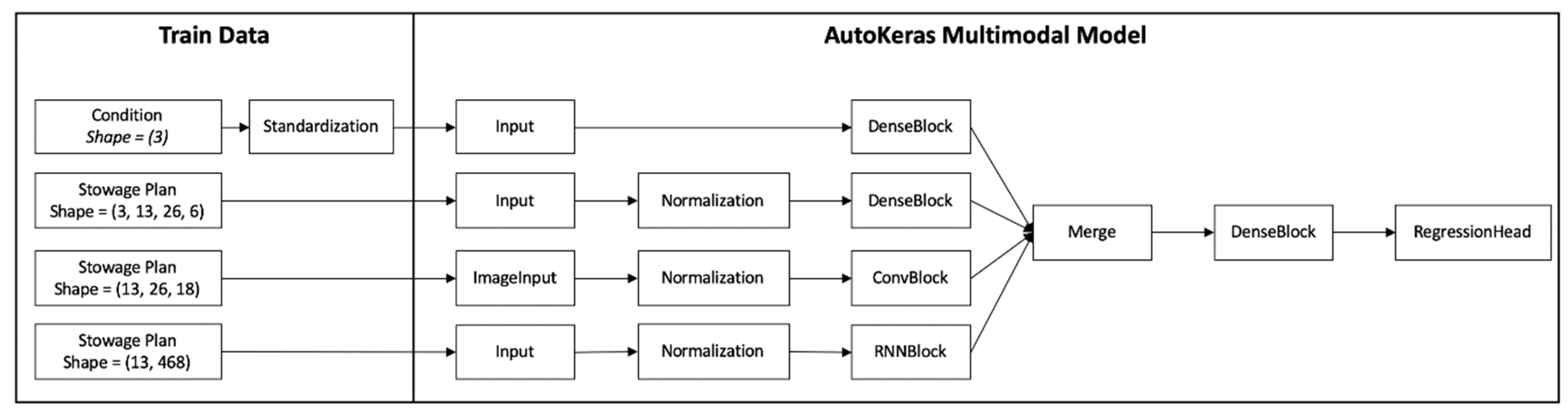
2.2.5. Modeling
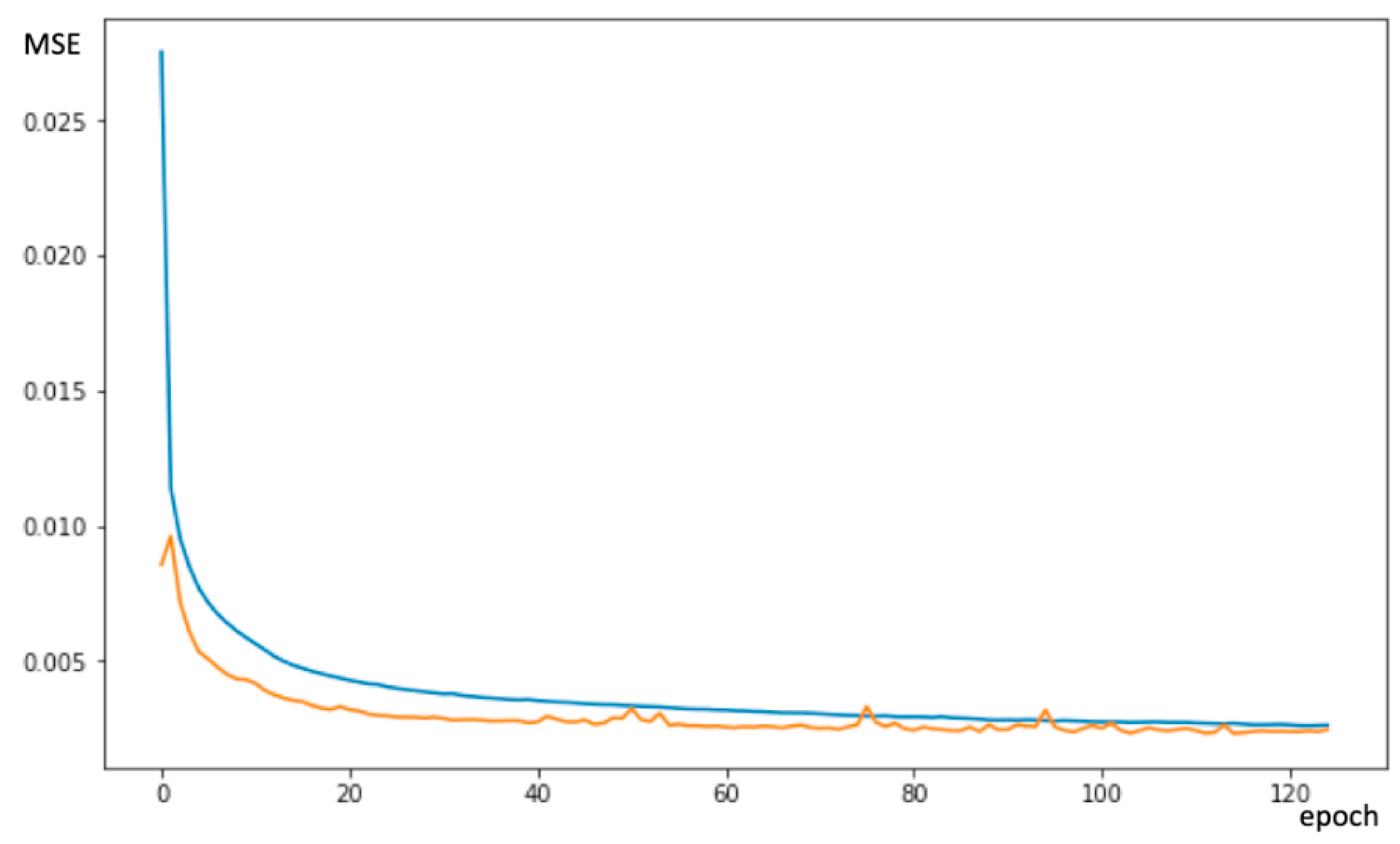
2.2.6. Training
- vCPU: 24 (Intel(R) Xeon(R) CPU E5-2690 v3 @ 2.60 GHz);
- RAM: 224 GiB System Memory;
- GPU: 4 (GK210GL (Tesla K80), NVIDIA Corporation).
2.2.7. Testing
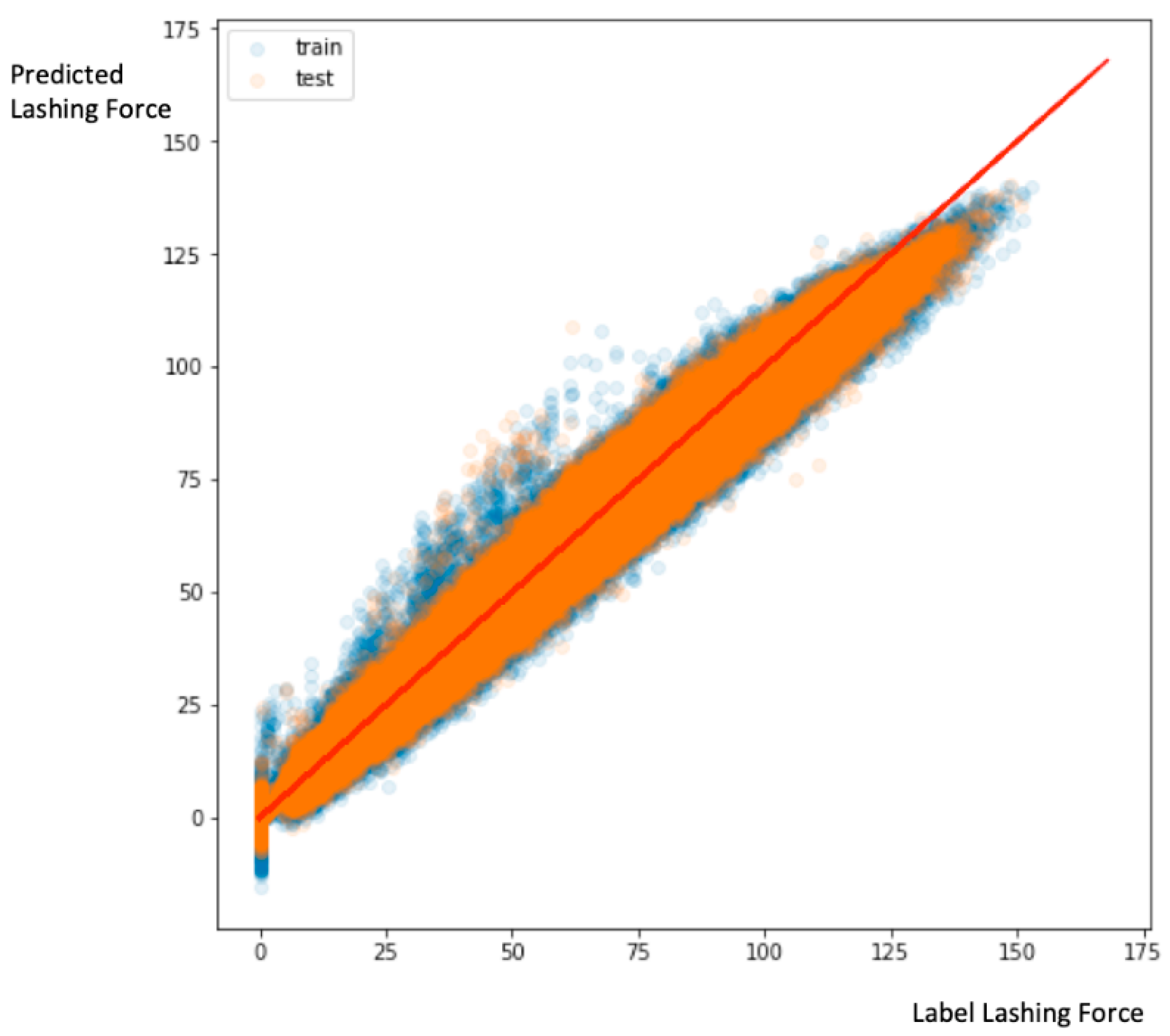
2.2.8. Result Evaluation
- Total number of predicted values: 969;
- Max difference: 12.23;
- Average: 0.66;
- Total number of identical: 320 (33.02%);
- Total number of greater than 10% difference: 4 (16.62%);
- Total number of greater than 5% difference: 16 (1.65%);
- Total number of greater than 1% difference: 161 (0.41%);
- Total number of less than 1% difference: 468 (48.30%).
3. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Ding, D.; Chou, M.C. Stowage planning for container ships: A heuristic algorithm to reduce the number of shifts. Eur. J. Oper. Res. 2015, 246, 242–249. [Google Scholar] [CrossRef]
- Avriel, M.; Penn, M.; Shpirer, N.; Witteboon, S. Stowage planning for container ships to reduce the number of shifts. Ann. Oper. Res. 1998, 76, 55–71. [Google Scholar] [CrossRef]
- Avriel, M.; Penn, M.; Shpirer, N. Container ship stowage problem: Complexity and connection to the coloring of circle graphs. Discret. Appl. Math. 2000, 103, 271–279. [Google Scholar] [CrossRef]
- Low, M.; Xiao, X.; Liu, F.; Huang, S.Y.; Hsu, W.J.; Li, Z. An automated stowage planning system for large containerships. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 17–19 March 2010; pp. 17–19. [Google Scholar]
- Ambrosino, D.; Sciomachen, A.; Tanfani, E. Stowing a containership: The master bay plan problem. Transp. Res. Part A Policy Pr. 2004, 38, 81–99. [Google Scholar] [CrossRef]
- Korach, A.; Brouer, B.D.; Jensen, R.M. Matheuristics for slot planning of container vessel bays. Eur. J. Oper. Res. 2020, 282, 873–885. [Google Scholar] [CrossRef]
- Rahsed, D.M.; Gheith, M.S.; Eltawil, A.B. A Rule-based Greedy Algorithm to Solve Stowage Planning Problem. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Macau, China, 16–19 December 2018; pp. 437–441. [Google Scholar]
- Shen, Y.; Zhao, N.; Xia, M.; Du, X. A Deep Q-Learning Network for Ship Stowage Planning Problem. Pol. Marit. Res. 2017, 24, 102–109. [Google Scholar] [CrossRef]
- Rathje, H.; Abt, D.; Wolf, V.; Schellin, T.E. Route-specific container stowage. In Proceedings of the PRADS 2013, Changwan City, Korea, 20 October 2013. [Google Scholar]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/List_of_largest_container_ships (accessed on 24 August 2020).
- Wolf, V.; Darie, I.; Rathje, H. Rule development for container stowage on deck. In Proceedings of the Third International Conference on Marine Structures—MARSTRUCT, Hamburg, Germany, 28–30 March 2011; Volume 1, pp. 715–722. [Google Scholar]
- World Shipping Council. Containers Lost at See—2017 Update. Available online: https://www.worldshipping.org/industry-issues/safety/Containers_Lost_at_Sea_-_2017_Update_FINAL_July_10.pdf (accessed on 24 August 2020).
- Ngiam, J.; Khosla, A.; Kim, M.; Nam, J.; Lee, H.; Ng, A.Y. Multimodal deep learning. In Proceedings of the 28th International Conference on Machine Learning, ICML 2011, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Gijsbers, P.; LeDell, E.; Thomas, J.; Poirier, S.; Bischl, B.; Vanschoren, J. An open source AutoML benchmark. arXiv 2019, arXiv:1907.00909. [Google Scholar]
- He, X.; Zhao, K.; Chu, X. AutoML: A survey of the state-of-the-art. Knowl.-Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Real, E.; Liang, C.; So, D.R.; Le, Q.V. Automl-zero: Evolving machine learning algorithms from scratch. arXiv 2020, arXiv:2003.03384. [Google Scholar]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning Spatiotemporal Features with 3D Convolutional Networks. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4489–4497. [Google Scholar]




| Condition | GM | Wind Speed | Roll Angle | 10% Variance | 15% Variance | 20% Variance | Total 104,786 |
|---|---|---|---|---|---|---|---|
| 1 | 2.00 | 30.00 | 22.00 | 4578 | 6636 | 2982 | 14,196 |
| 2 | 1.80 | 29.00 | 21.50 | 2520 | 2583 | 5796 | 10,899 |
| 3 | 2.10 | 28.00 | 21.00 | 2611 | 2708 | 2856 | 8175 |
| 4 | 2.40 | 27.00 | 20.50 | 2898 | 2580 | 2503 | 7981 |
| 5 | 2.70 | 26.00 | 20.00 | 3066 | 2646 | 4662 | 10,374 |
| 6 | 3.00 | 25.00 | 19.50 | 3141 | 2710 | 2559 | 8410 |
| 7 | 3.30 | 24.00 | 19.00 | 2594 | 3149 | 2581 | 8324 |
| 8 | 3.60 | 23.00 | 18.50 | 2541 | 2541 | 2552 | 7634 |
| 9 | 3.90 | 22.00 | 18.00 | 2568 | 2705 | 2734 | 8007 |
| 10 | 4.20 | 21.00 | 17.50 | 2566 | 2791 | 3799 | 9156 |
| 11 | 4.50 | 20.00 | 17.00 | 2478 | 3191 | 5961 | 11,630 |
| Category | Configuration | Value | Description |
|---|---|---|---|
| Model | trial | 50 | The maximum number of different Keras models to try |
| Fit | batch_size | 32 | Number of samples per gradient update |
| epochs | 1000 | The number of epochs to train each model during the search. It stops training if the validation loss stops improving for 10 epochs | |
| validation_split | 0.2 | The model will set apart this fraction of the training data, will not train on it, and will evaluate the loss and any model metrics on these data at the end of each epoch |
| Result | Value | Description |
|---|---|---|
| Validation loss MSE | 0.0023243355099111795 | Normalized MSE |
| Train and validation MSE | 0.8656454525367441 | Scaled MSE (original percentage unit) for training and validation |
| test MSE | 0.8769041770067165 | Scaled MSE (original percentage unit) for test |
| Hyperparameters | Value | |
|---|---|---|
| dense_block_2 | num_layers | 2 |
| use_batchnorm | False | |
| dropout | 0 | |
| units_0 | 32 | |
| units_1 | 32 | |
| conv_block_1 | kernel_size | 3 |
| num_blocks | 2 | |
| num_layers | 1 | |
| separable | False | |
| max_pooling | False | |
| dropout | 0 | |
| filters_0_0 | 64 | |
| filters_0_1 | 32 | |
| filters_1_0 | 32 | |
| filters_1_1 | 32 | |
| rnn_block_1 | bidirectional | True |
| layer_type | lstm | |
| num_layers | 1 | |
| dense_block_1 | num_layers | 2 |
| use_batchnorm | True | |
| dropout | 0.0 | |
| units_0 | 16 | |
| units_1 | 16 | |
| dense_block_3 | num_layers | 3 |
| use_batchnorm | True | |
| dropout | 0 | |
| units_0 | 32 | |
| units_1 | 32 | |
| units_2 | 128 | |
| regression_head_1 | dropout | 0 |
| optimizer | optimizer | adam |
| learning_rate | learning_rate | 0.001 |
| Bay | 16 | 14 | 12 | 10 | 08 | 06 | 04 | 02 | 00 | 01 | 03 | 05 | 07 | 09 | 11 | 13 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.00 | 0.01 | 0.01 | 0.00 | 0.00 | 0.11 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | 0.00 | 0.00 | 0.00 | 0.00 | 0.28 | 0.10 | 0.60 | 0.47 | 0.65 | 1.00 | 1.09 | 0.28 | 0.18 | 0.00 | 0.00 | 0.00 | 0.00 |
| 3 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.00 | 0.00 | 0.01 | 0.05 | 0.31 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 |
| 5 | 0.00 | 0.43 | 0.07 | 0.78 | 0.01 | 0.07 | 0.00 | 0.03 | 0.00 | 0.01 | 0.00 | 0.05 | 1.33 | 0.61 | 0.11 | 1.24 | 0.00 |
| 6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.66 | 0.03 | 0.70 | 0.41 | 1.70 | 0.38 | 0.02 | 2.15 | 0.00 | 0.17 | 0.10 | 0.00 | 0.00 |
| 7 | 0.00 | 1.05 | 1.86 | 0.74 | 0.00 | 0.06 | 0.03 | 0.03 | 0.00 | 0.00 | 0.05 | 0.00 | 0.83 | 0.24 | 1.45 | 0.59 | 0.00 |
| 9 | 0.00 | 1.16 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.11 | 0.00 | 0.00 | 0.15 | 0.00 | 0.00 | 0.00 |
| 10 | 2.46 | 0.07 | 0.47 | 1.03 | 1.40 | 1.16 | 0.08 | 0.19 | 0.83 | 0.29 | 0.87 | 0.57 | 0.30 | 0.90 | 0.17 | 0.66 | 4.56 |
| 11 | 0.00 | 1.04 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.00 | 0.00 | 0.12 | 0.00 | 0.00 | 0.00 |
| 13 | 0.00 | 0.79 | 0.72 | 0.15 | 0.00 | 0.00 | 0.00 | 0.02 | 0.01 | 0.00 | 0.07 | 0.00 | 0.00 | 0.23 | 0.06 | 0.98 | 0.00 |
| 14 | 1.62 | 3.23 | 0.00 | 4.42 | 0.83 | 0.37 | 1.00 | 1.13 | 0.16 | 0.88 | 0.34 | 0.48 | 1.68 | 1.51 | 0.80 | 1.16 | 0.72 |
| 15 | 0.00 | 0.65 | 0.16 | 0.10 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.07 | 0.00 | 0.05 | 0.11 | 0.08 | 2.05 | 0.00 |
| 17 | 0.00 | 0.23 | 0.65 | 0.24 | 0.00 | 0.08 | 0.00 | 0.00 | 0.00 | 0.00 | 0.12 | 0.07 | 0.22 | 0.01 | 0.20 | 0.65 | 0.00 |
| 18 | 2.64 | 0.27 | 1.75 | 1.29 | 0.49 | 0.65 | 0.05 | 1.43 | 0.49 | 0.31 | 1.91 | 0.30 | 0.79 | 0.23 | 0.82 | 0.89 | 2.48 |
| 19 | 0.00 | 0.49 | 0.62 | 0.46 | 0.00 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.10 | 0.12 | 0.29 | 0.17 | 0.22 | 0.62 | 0.00 |
| 21 | 0.00 | 2.11 | 1.27 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.05 | 0.00 | 0.00 | 0.00 | 0.00 | 0.74 | 0.00 |
| 22 | 0.62 | 0.71 | 0.94 | 1.92 | 1.20 | 0.91 | 0.20 | 0.14 | 0.29 | 0.81 | 0.61 | 0.28 | 0.11 | 0.74 | 0.87 | 5.36 | 0.91 |
| 23 | 0.00 | 1.40 | 2.03 | 0.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.02 | 0.01 | 0.05 | 2.85 | 0.00 |
| 25 | 0.00 | 0.05 | 0.00 | 0.09 | 0.00 | 0.20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.19 | 0.14 | 0.00 | 0.46 | 0.08 | 0.08 | 0.00 |
| 26 | 1.51 | 0.93 | 0.99 | 0.06 | 0.08 | 0.04 | 0.29 | 0.15 | 1.03 | 0.41 | 0.77 | 0.26 | 0.60 | 0.67 | 0.56 | 0.99 | 1.52 |
| 27 | 0.00 | 0.09 | 0.00 | 0.10 | 0.00 | 0.24 | 0.00 | 0.00 | 0.00 | 0.00 | 0.18 | 0.16 | 0.25 | 0.04 | 0.22 | 0.01 | 0.00 |
| 29 | 0.00 | 0.18 | 0.17 | 0.10 | 0.00 | 0.33 | 0.00 | 0.00 | 0.00 | 0.00 | 0.24 | 0.19 | 0.11 | 0.33 | 0.09 | 1.04 | 0.00 |
| 30 | 0.69 | 0.97 | 1.28 | 1.42 | 0.60 | 0.84 | 0.32 | 0.20 | 0.91 | 0.11 | 2.06 | 0.22 | 0.51 | 0.69 | 1.97 | 0.03 | 0.78 |
| 31 | 0.00 | 0.22 | 0.26 | 0.22 | 0.00 | 0.34 | 0.00 | 0.00 | 0.00 | 0.00 | 0.21 | 0.42 | 0.21 | 0.11 | 0.14 | 0.74 | 0.00 |
| 33 | 0.00 | 0.24 | 0.56 | 0.11 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 | 0.25 | 0.07 | 0.13 | 0.27 | 0.00 |
| 34 | 1.89 | 0.73 | 0.59 | 0.48 | 0.36 | 1.30 | 0.06 | 0.78 | 0.80 | 1.12 | 0.27 | 0.73 | 0.11 | 0.76 | 1.32 | 2.73 | 0.67 |
| 35 | 0.00 | 0.26 | 0.75 | 0.31 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.01 | 0.23 | 0.15 | 0.16 | 0.30 | 0.00 |
| 37 | 0.00 | 0.47 | 0.57 | 0.15 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.00 | 0.17 | 0.04 | 0.18 | 0.08 | 0.00 |
| 38 | 1.10 | 0.26 | 0.03 | 0.09 | 0.54 | 2.37 | 0.23 | 0.86 | 0.24 | 0.19 | 0.07 | 0.01 | 1.29 | 1.01 | 1.45 | 1.97 | 1.03 |
| 39 | 0.00 | 0.51 | 0.61 | 0.35 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.13 | 0.00 | 0.21 | 0.16 | 0.16 | 0.10 | 0.00 |
| 41 | 0.00 | 0.49 | 0.53 | 0.22 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.08 | 0.00 | 0.33 | 0.09 | 0.21 | 0.50 | 0.00 |
| 42 | 0.45 | 0.85 | 8.33 | 0.52 | 0.17 | 8.15 | 0.32 | 2.04 | 1.17 | 0.11 | 0.27 | 7.33 | 1.36 | 0.91 | 0.07 | 3.27 | 1.11 |
| 43 | 0.00 | 0.42 | 0.72 | 0.42 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.08 | 0.00 | 0.32 | 0.22 | 0.22 | 0.34 | 0.00 |
| 45 | 0.00 | 0.48 | 0.15 | 0.16 | 0.00 | 0.43 | 0.00 | 0.02 | 0.01 | 0.00 | 1.32 | 0.28 | 0.03 | 0.44 | 0.10 | 0.17 | 0.00 |
| 46 | 0.36 | 1.33 | 0.21 | 1.04 | 0.99 | 0.29 | 0.01 | 1.46 | 1.99 | 0.93 | 2.42 | 0.23 | 4.36 | 0.81 | 0.69 | 0.06 | 1.09 |
| 47 | 0.00 | 0.34 | 0.19 | 0.16 | 0.01 | 0.39 | 0.00 | 0.00 | 0.00 | 0.01 | 0.83 | 0.51 | 0.17 | 0.11 | 0.16 | 0.22 | 0.00 |
| 49 | 0.00 | 0.23 | 0.48 | 0.26 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.17 | 0.00 | 0.28 | 0.11 | 0.21 | 0.25 | 0.00 |
| 50 | 1.84 | 0.69 | 12.23 | 2.76 | 1.97 | 3.96 | 0.79 | 6.14 | 4.99 | 5.38 | 2.43 | 3.14 | 3.53 | 5.16 | 11.81 | 1.66 | 5.06 |
| 51 | 0.00 | 0.31 | 0.63 | 0.41 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.18 | 0.00 | 0.31 | 0.19 | 0.23 | 0.22 | 0.00 |
| 53 | 0.00 | 0.41 | 0.42 | 0.32 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.09 | 0.00 | 0.32 | 0.26 | 0.27 | 0.30 | 0.00 |
| 54 | 1.18 | 3.10 | 0.54 | 0.22 | 0.91 | 0.37 | 0.63 | 3.94 | 0.74 | 2.23 | 2.00 | 1.37 | 1.92 | 2.02 | 0.42 | 2.88 | 0.17 |
| 55 | 0.00 | 0.40 | 0.55 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.06 | 0.00 | 0.38 | 0.25 | 0.29 | 0.32 | 0.00 |
| 58 | 1.64 | 9.26 | 2.89 | 3.75 | 2.02 | 1.84 | 0.35 | 1.43 | 1.10 | 0.08 | 2.04 | 0.90 | 2.62 | 2.71 | 2.22 | 9.03 | 1.91 |
| 62 | 5.36 | 2.24 | 2.71 | 0.07 | 0.16 | 1.47 | 0.29 | 0.89 | 0.11 | 0.32 | 1.11 | 3.76 | 2.97 | 4.70 | 10.64 | 1.65 | 1.25 |
| 65 | 0.00 | 0.53 | 0.37 | 0.33 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.10 | 0.00 | 0.20 | 0.22 | 0.23 | 0.20 | 0.00 |
| 66 | 1.71 | 8.10 | 1.50 | 0.38 | 1.51 | 8.11 | 1.00 | 1.19 | 0.98 | 1.18 | 1.42 | 1.35 | 1.77 | 1.59 | 0.19 | 6.66 | 1.51 |
| 67 | 0.00 | 0.54 | 0.28 | 0.38 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 | 0.00 | 0.30 | 0.20 | 0.22 | 0.27 | 0.00 |
| 69 | 0.00 | 0.55 | 0.72 | 0.55 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.16 | 0.00 | 0.41 | 0.27 | 0.39 | 0.43 | 0.00 |
| 70 | 0.95 | 0.70 | 10.55 | 0.68 | 0.52 | 4.20 | 0.55 | 2.72 | 1.85 | 2.89 | 0.19 | 1.49 | 1.40 | 1.22 | 1.05 | 0.11 | 3.81 |
| 71 | 0.00 | 0.54 | 0.53 | 0.59 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.20 | 0.01 | 0.51 | 0.26 | 0.39 | 0.43 | 0.00 |
| 73 | 0.00 | 0.57 | 0.20 | 0.11 | 0.00 | 0.20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.20 | 0.10 | 0.16 | 0.37 | 0.08 | 0.19 | 0.00 |
| 74 | 5.73 | 2.73 | 1.02 | 1.22 | 2.70 | 4.70 | 3.70 | 2.56 | 0.19 | 3.04 | 3.90 | 0.93 | 2.49 | 3.02 | 1.82 | 3.04 | 1.12 |
| 75 | 0.00 | 0.42 | 0.29 | 0.28 | 0.00 | 0.26 | 0.00 | 0.00 | 0.00 | 0.00 | 0.20 | 0.22 | 0.22 | 0.13 | 0.12 | 0.22 | 0.00 |
| 77 | 0.00 | 0.50 | 0.36 | 0.23 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.00 | 0.11 | 0.00 | 0.19 | 0.21 | 0.19 | 0.19 | 0.00 |
| 78 | 0.43 | 6.73 | 0.10 | 0.28 | 0.75 | 0.83 | 2.35 | 2.17 | 0.73 | 2.64 | 2.93 | 0.85 | 1.80 | 1.59 | 0.96 | 4.87 | 1.24 |
| 79 | 0.00 | 0.52 | 0.57 | 0.35 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.12 | 0.00 | 0.26 | 0.19 | 0.21 | 0.22 | 0.00 |
| 82 | 2.48 | 3.04 | 1.09 | 0.19 | 0.64 | 1.50 | 2.23 | 2.62 | 1.19 | 0.65 | 1.91 | 0.30 | 1.07 | 2.33 | 1.49 | 2.71 | 0.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.; Lee, M.K.; Shin, J.Y. Lashing Force Prediction Model with Multimodal Deep Learning and AutoML for Stowage Planning Automation in Containerships. Logistics 2021, 5, 1. https://doi.org/10.3390/logistics5010001
Lee C, Lee MK, Shin JY. Lashing Force Prediction Model with Multimodal Deep Learning and AutoML for Stowage Planning Automation in Containerships. Logistics. 2021; 5(1):1. https://doi.org/10.3390/logistics5010001
Chicago/Turabian StyleLee, Chaemin, Mun Keong Lee, and Jae Young Shin. 2021. "Lashing Force Prediction Model with Multimodal Deep Learning and AutoML for Stowage Planning Automation in Containerships" Logistics 5, no. 1: 1. https://doi.org/10.3390/logistics5010001
APA StyleLee, C., Lee, M. K., & Shin, J. Y. (2021). Lashing Force Prediction Model with Multimodal Deep Learning and AutoML for Stowage Planning Automation in Containerships. Logistics, 5(1), 1. https://doi.org/10.3390/logistics5010001





