Optimizing Long-Lasting Insecticidal Nets Campaign in Ivory Coast

Abstract

This research supports the United Nations Children’s Fund’s (UNICEF) conceptualization, planning and implementation of a campaign for distribution of more than 12 million mosquito nets in Ivory Coast. Procured from four different suppliers in Asia, the nets were transported to the two ports in Ivory Coast before being pre-positioned at 71 Health Districts across the country, a mixed integer network flow model identifies optimal transport options. The process of modeling and the model developed in this paper brought a significant understanding of the problem and, consequently, a reduction in the overall procurement and logistics costs. The implications of using mathematical modeling by practitioners as a tool which contributes to solve humanitarian logistics problems are significant. Mathematical models, like linear programming, can greatly support overall decision-making within humanitarian organizations by helping to ensure that limited resources are used in the most cost-effective and efficient manner. However, it is important to ensure consultations with and involvement by on the ground practitioners to ensure developed solutions assessed to fit the operating context before being implemented.

1. Introduction

Despite major gains in life-saving interventions, malaria remains a major cause of death among children in developing countries; every two minutes, a child under the age of 5 dies of malaria. Children’s deaths account for 67% of all malaria deaths worldwide in 2018. 272,000 deaths occurred in sub-Saharan Africa, where approximately 24 million children were estimated to be infected with the deadliest form of malaria [1]. The disease is caused by five different species of parasites, all belonging to the genus Plasmodium: P. falciparum, P. ovale, P. knowlesi, P. malariae and P. vivax. Malaria caused by P. falciparum is the deadliest form and is present primarily in Africa [2].

The incidence rate of malaria declined globally between 2010 and 2015, from 72 to 59 cases per 1000 people at risk [3]. This represents an 18% reduction in the incidence rate over the period, and can be attributed to international initiatives to contain the disease. Between 2004 and 2014, more than 900 million insecticide-treated mosquito nets were delivered to malaria-endemic countries in sub-Saharan Africa, averting over 6.2 million malaria cases primarily of children under five years of age. Interventions aiming at the reduction of malaria related deaths have been an important contributor to achieving the Millennium Development Goal #6 (MDG 6)—“to reduce by two thirds the under-5 mortality rates between 1990 and 2015” [4]. Despite these positive impacts, the incidence rate of malaria remained unchanged from 2015 to 2017 [3]. Hence, fighting malaria is still a United Nations (UN) priority. In the UN Sustainable Development Goal (SDG) 3: Ensure healthy lives and promote well-being for all at all ages, target 3.3 envisions the end of the malaria epidemic by 2030 [5].

Malaria is a preventable and treatable disease. The World Health Organization recommends the properly implementation of four interventions: (i) vector control through the use of insecticide treated nets (ITNs), indoor residual spraying (IRS) and, larval control; (ii) chemoprevention for the most vulnerable populations, especially pregnant women and infants; (iii) confirmation of malaria diagnosis through microscopy or rapid diagnostic tests (RDTs) for every suspected case; and (iv) according to the parasite species and any documented drug resistance, timely treatment with appropriate antimalarial medicines [6].

Sleeping under ITN is the most effective way to prevent malaria transmission. It reduces child mortality from all causes by almost one-fifth compared to children sleeping without a net: severe malaria episodes reduced by more than 40% and uncomplicated cases of malaria were also reduced by almost one-half. The prevalence of P. falciparum is reduced by 17% [7].

Given the effectiveness of ITNs, humanitarian agencies and governments need to work together to strengthen and optimize supply chains to ensure universal coverage is achieved and every child is able to sleep under a net. Among the methods for increasing coverage, mass distribution of ITNs is a key strategy. Campaigns for distribution of ITNs require many months of planning and complex logistics, and for these reasons they are only planned every few years, either to increase coverage rapidly or to replace nets distributed in previous campaigns among a large part of a country’s population [8].

In this study, we develop a network flow model to minimize the costs associated with the procurement and distribution of ITNs to 71 Health Districts in Ivory Coast (CIV). To minimize these logistics costs, we have considered a number of variables, including: (i) the number and size of containers dispatched to each one of the Districts; (ii) the specific manufacturer (e.g., where the ITN was procured) and the source port used at origin; (iii) the port used at arrival in CIV; and, (iv) whether or not to use any CIV cities as prepositioning hubs before distributing to the different health districts.

The paper presents the development process of the logistics model and the constructive interaction between practitioners and academics. The work exemplifies the benefits of collaboration between academia and the humanitarian sector during the phases of planning for complex projects like the mass distribution in challenging operating environments. For humanitarian practitioners, a structured approach and the development of models promote better insight into the problem’s solution, which results in cost reduction and service level improvement. For academics, the feedback of practical application of modelling tools and the possible use in other humanitarian operations projects are valuable. Such collaborations and their results, spanning from costs savings, to service improvements, and increased efficiency, become ever more relevant especially given the limited availability of funds and the pleas for increased effectiveness and transparency of humanitarian operations.

1.1. Long-Lasting Insecticidal Nets (LLINs)

A long-lasting insecticide-treated net (LLIN) is a category of ITN treated with insecticide to kill and repel mosquitoes. LLINs are designed to remain effective at least three years under field conditions without retreatment [9]. As mentioned earlier, one of the most effective ways to prevent malaria transmission and reduce deaths among children is for them to sleep under a LLIN on a regular basis [10]. The World Malaria Report 2017 indicates that between 2014 and 2016, 582 million of LLINs were delivered globally, of which almost 505 million (87%) were delivered to countries in sub-Saharan Africa. This marks a substantial increase of LLINs delivered, but a fifth of households still do not have access to any nets in sub-Saharan Africa countries. For these countries, it is estimated that 54% of the population at risk slept under a net in 2016, however the proportion of households with sufficient LLINs, was only 43% [11]. Decreasing prices also have contributed to increase these numbers, with the average price falling from USD 6.27 to USD 4.36 per net between 2010 and 2014 [12].

At the beginning of 2014, UNICEF (United Nations Children’s Fund) planned to procure and deliver 36.5 million LLINs to 18 countries. Six of these countries: Chad, Ethiopia, Guinea Bissau, Ivory Coast (CIV), Sierra Leone and Sudan account for approximately 95% of the total demand. More than 900 million ITNs were delivered to malaria-endemic countries in sub-Saharan Africa between 2004 and 2014 [13].

As malaria is still considered a poverty related disease—affecting mainly children under five from poor families living in rural areas—it commands a strong moral obligation to prevent it. UNICEF estimates that child mortality can be reduced by up to 20%, when universal ITN coverage (defined as one ITN for every other person) is reached. But in addition to saving children’s lives, malaria prevention also yields other health and economic benefits as healthy children can go to school and healthy adults can continue to work. Between 2009 and 2014, UNICEF supported LLINs campaigns in over 30 countries in sub-Saharan Africa with the procurement and distribution of 120 million LLINs [14].

In 2011, within UNICEF’s “A promise Renewed” initiative, 50 out of 99 partner countries were on track to reduce the rates of malaria cases by 75% by 2015 [4].

Despite the advantages of the use of LLINs, there is still some resistance to their use. A study in eastern Rwanda [15] shows that 92 % households have at least one LLIN and 72% of household members use them. However, males were particularly less likely to use bed nets even when they are available.

1.2. Ivory Coast

Ivory Coast (CIV) is located in West Africa and it is surrounded by Liberia to the West, Ghana to the East, and Guinea, Mali and Burkina Faso to the North. CIV has access to the Atlantic Ocean in the South. The country has an area of 322,462 km², a population of approximately 20.6 million, and a Human Development Index (HDI) of 0.432, placing it in the 168th position among other countries. The capital city is Yamoussoukro and Abidjan is its largest city, also home to the main seaport in the country. In 2002, a civil war split the country between rebel-held North and government-controlled South; the presidential poll in 2000 led to further violence. In April 2013 voting for the location elections were quite peaceful. In 2016, CIV was targeted by Al Qaeda attack.

Malaria is still endemic in CIV and constitutes one of its key public health problems. Malaria is also included as one of the priorities of the National Sanitary Development Plan 2016–2020 [16]. CIV is one of the six countries that account for more than half of all malaria cases worldwide [17].

Among the children under 5, malaria is the leading cause of morbidity and mortality in Ivory Coast (CIV). Out of an estimated 128,000 deaths in children under 5 each year, 63,000 are directly related to malaria [18]. While the use of LLINs can effectively reduce child mortality, their utilization rate is still low. In 2006, only 26% of children under 5 received an appropriate malaria treatment. Since 2012, free malaria treatment has been made available in public health centers [16]. To further combat malaria, two main objectives were established: (i) the free distribution of around 30 million LLINs; (ii) intervention to increase the coverage of households in LLINs up to 95%. To address the first objective, a campaign was planned which would allow the replacement of LLINs previously distributed in 2011. The LLINs mass distribution campaign in CIV was part of the “Plan National De Developpement Sanitaire 2016–2020”. The plan was developed by the Ministry of Health in CIV and includes the health priorities for the country as well the international commitments as indicated in the Sustainable Development Goals [16],

“LLIN mass distribution strategies vary by country, each having its own objectives and challenges. Common to all, however, is the crucial requirement to plan mass distributions early, ensuring that all the details of the country’s strategy, objectives and specific situation are considered.”

[8]

1.3. United Nations Children’s Fund (UNICEF) and Global Fund

Timely procurement, strategic logistics arrangements, and adequate transport and storage solutions are critical to ensure a successful campaign. Because of its well-demonstrated capabilities and capacities for managing the procurement and the entire in-country logistics chain for the LLIN mass campaign [19], UNICEF was requested by stakeholders to coordinate the procurement, the transportation and the pre-positioning of the LLINs for the mass LLINs campaign in CIV. A model to optimize the costs of purchasing and pre-positioning 12 million bed-nets in Ivory Coast at district level was developed.

To model a realistic physical system of this kind requires a significant amount of data. Most of the data was obtained from two reliable sources: the Global Fund and UNICEF. “The Global Fund is a partnership designed to accelerate the end of AIDS, tuberculosis and malaria as epidemics” [20]. UNICEF promotes the rights and wellbeing of every child. Together with partners, UNICEF operates in 190 countries and territories with programmes targeting areas such as child survival and development (including vaccination and nutrition), education, child protection, advocacy and partnerships. Equity and reaching the most vulnerable and excluded children are a focus for UNICEF,

“The next steps of our journey will depend on our willingness to adapt to the changing world around us… to infuse equity throughout our programmes… and to find new ways to realize the rights—and brighten the futures—of the most disadvantaged children around the world”

Anthony Lake, Executive Director, UNICEF [21]

1.4. Campaign Outline

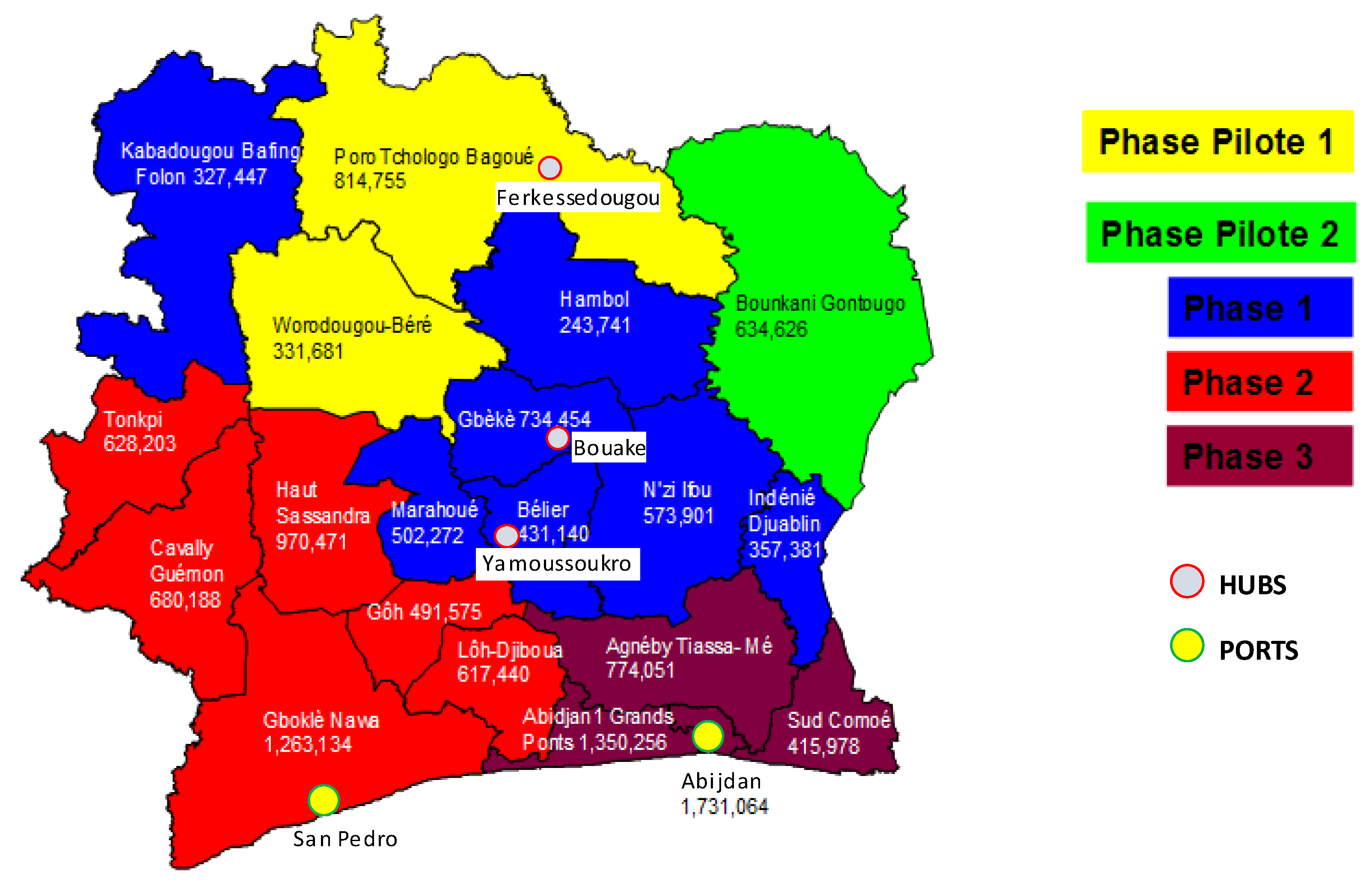
UNICEF’s campaign envisioned serving about 22 million beneficiaries through the distribution of 12 million LLINs to 71 Health Districts in 17 Regions of CIV. UNICEF purchased the LLINs from various Asian suppliers for delivery through their nearest regional ports, (e.g., Haiphong and Ho Chi Minh (Vietnam), Chennai (India), Bangkok (Thailand), Qingdao, Shanghai and Tianjin (China)). Receipt in CIV would take place either through the two main seaports (e.g., Abidjan and San Pedro), or three cities (e.g., Ferkessedougou, Yamoussoukro, and Bouake). The cities could be used as dry ports, that is, strategic hubs for the consolidation of containers. This optimization model considered all manufacturers, seven possible departure ports, five possible arrival ports (including the three dry ports) and the 71 Health Districts, before final distribution to different Distribution Centers. With the exception of the quantity of LLINs planned for the Abidjan region, the LLINs needed to be delivered to the Health Districts in containers. This allowed UNICEF to address one of the main challenges encountered during past campaigns in CIV: the lack of secure storage capacity at the Health District level.

The distribution took place from June to November. The distribution of LLINs for the campaign in CIV was planned to take place in 5 phases: the first 2 phases (called pilot phases) funded by a development bank and implemented by an international Non-Governmental Organization (NGO) through the distribution of 1.8 million LLINs to 9 Health Districts in 3 Regions. The remaining 3 phases were to be implemented by UNICEF funded by Global Funds.

Figure 1 illustrates the map of CIV with the ports, hubs, quantities of LLINs in each district, and the phases of the mass distribution campaign.

UNICEF was in charge of the entire supply chain for this LLINs campaign: from procurement of the LLINs, including freight, in-land transportation, pre-positioning at Health District level, up to distribution. UNICEF was also responsible for the headcount to confirm the quantity of LLINs required for each Health District, transporting the LLINs to the distribution centres, distributing the LLINs and organizing both the waste management and reverse logistics. The last mile distribution was carried out at a later stage according to guidelines from the Ministry of Health of the CIV.

As per WHO (World Health Organization) guidance,

“mass campaigns should be repeated normally at an interval of no more than three years unless there is reliable observational evidence that a longer interval could be appropriate. The lifespan of LLINs varies widely between individual nets and between settings, making it difficult to plan the rate or frequency at which replacement nets need to be procured and delivered. All medium and large-scale LLIN programmes should carry out durability monitoring using WHO guidance documents. In addition, there should be efforts to improve LLINs and/or behavior change interventions to improve net longevity and usage”

[22]

1.5. Problem Statement and Contribution

The optimization model presented in this paper is applied to a mass distribution campaign of 12 million LLINs in CIV. During previous campaigns the importance of ensuring that each Health District receives LLINs supplied exclusively by one supplier in order to prevent any kind of confusion during the distribution (by different packaging) was also noted. This requirement was reflected in the model as a constraint.

LLIN distributions are complex projects which require meticulous planning, careful monitoring throughout the phases, and a strong coordination among all stakeholders [23]. If one considers the mass campaign in CIV, the number of stakeholders involved was a significant potential challenge. Other possible challenges which could impact a campaign like this are: the environment where the project is to be implemented, factors out of the project team’s direct control and/or influence (e.g., delays in vessel arrival, inclement weather conditions, insecurity issues, etc.), budget constraints, changing of priorities within the organization, etc.

A very real constraint of campaigns such as this is the operating environment and in particular the challenging logistics infrastructure that may be present. The poor condition of roads in rural areas may make the use of larger trucks impractical and smaller more maneuverable trucks may have a higher per unit transportation cost. Also, the time required to reach deeply rural areas may be significantly longer. Fuel availability may be unreliable or limited potentially requiring trucks to carry their own for part of the journey. These are just a few of the examples of challenges faced by humanitarian organizations during campaigns.

WHO recommends 16 types of LLINs [24], which are manufactured in East Asia and Europe. The beneficiaries of these products are located mainly in sub-Saharan Africa and South America. In the literature, review articles about the subject [25,26,27] evaluated criteria and strategies for last mile distribution and delivery of bed nets from a distribution point located in the beneficiaries’ country. In this regard, the contribution of this paper is to extend the previous studies evaluating the supply chain, from the supplier to the distribution point in collaboration with practitioners and academics.

2. Literature Review

In this literature review we studied papers about modelling in humanitarian logistics and bed nets strategies for distribution during campaigns to present the characteristics and particularities of this kind of application. The increase in studies of quantitative research in the field of humanitarian logistics increased in last decade, but “actual applications is an open issue for mathematical modeling in humanitarian relief chain management to get a holistic analysis in the decision-making process [28].

As stated by Apte [29], disasters provide us with lessons for planning future humanitarian logistics operations. “One of the most important lessons learned is that money is not a panacea, as evidenced in the aftermath of the tsunami in Aceh, Indonesia”. During the response to the Tsunami in 2004, there was an enormous quantity of relief supplies sent to the affected areas, however many of these supplies did not reach the victims because there were no distribution channels in place and there was a lack of overall preparation. Improved decision-making models can help humanitarian organizations and first responders refine their strategy for planning, manage their operations for pre-positioning, storage and distribution, and sustain aid both during and after a crisis [29].

The most recent economic crisis has put enormous pressure on humanitarian organizations to show results and optimize the available resources. One effective way to optimize available resources is the use of modelling to strategically plan the supply chain of essential life-saving supplies. Based on an empirical survey investigating the practice of supply chain management (SCM) in humanitarian organizations, Blecken [30] learned that supply chain process modelling and optimization are still in their infancy in humanitarian organizations. Hence, there is a significant opportunity to improve ongoing operations through collaborative supply chain management implementations between academia and humanitarian organizations (HOs). Studying Vehicle Fleet Management, Pedraza Martinez et al. [31] characterize some of the complexities and particularities of humanitarian operations, identify a lack of academic understanding of real humanitarian operations, and a need for additional research on the topic due to the complexity and particularities of humanitarian operations.

Kumar et al. [32] assessed how NGOs manage their operations with limited resources in Africa. Although donors spend billions of dollars on humanitarian efforts, efficiency and effectiveness are not always on par with expected results. Supplies are frequently sourced from offshore sources and shipping is an expensive and significant part of the lead time.

A unique characteristic of humanitarian logistics is equity. Huang et al. [33] define equity as the extent to which all recipients receive comparable service. They explored how this concept of equity can influence the distribution of humanitarian resources, developing a model for last-mile distribution from a distribution centre to beneficiaries.

Geoffrion and Graves [34] first found the optimal location in a multi-commodity two-stage production-distribution system using benders decomposition. The problem was briefly defined as: “There are commodities produced at several plants with known production capacities and a demand that must be satisfied by sending through distribution centers”. The proposed model in this paper is similar to that of Geoffrion and Graves [34], with the exception of the fixed cost element. Geoffrion [35] states that: “The purpose of mathematical programming is insight, not numbers” and extended the concept of facility location with a comprehensive model considering interdependent decisions, possible changes and alternative decisions and policies [36]. These concepts are still very much applied to humanitarian logistics problems.

Melo et al. [37] conducted a literature review of facility location models in the context of supply chain management identifying basic features that models must capture in order to support decision in strategic supply chain planning. They presented that facility location decision making plays a critical role in the strategic design of supply chain networks, in particular, the integration of location.

An additional study, not directly applied to humanitarian logistics, but similar to this problem and relevant to consider is the study of Jula and Leachman [38], where the authors developed a model for optimizing supply chains of importers of waterborne containerized goods from Asia to the USA. The model determines the least-cost strategy for an importer, in terms of ports and inland transportation modes to be used, considering costs for transportation and handling. Dubke and Pizzolato [39] developed a model for a case defining ports for the export of soybeans in Brazil. The proposed model also considers service activities and the capacity of the maritime port. The difference between their model and this study is the flow direction of the material; one is facing the export and other the import.

Many operational research models have been developed to help the commercial sector find ways of becoming more cost efficient. However, much of this practice has not transferred to the humanitarian field [40]. The authors developed a mathematical trans-shipment multi-commodity supply-chain flow model to design an effective supply chain humanitarian relief operation.

In the case of disasters, the logistical problem for relief materials management is to move a from a number of origins to one or more destinations over a transportation network in a timely manner effectively and efficiently [41]. Their problem was a multi-commodity, multi-modal network flow problem with time windows. They also recommended that the model should be tested with real-world data rather than artificially generated data.

Two papers [42,43] conduct a review and evaluate the delivery system to achieve and to increase equity of coverage in the case of tropical diseases prevention. These studies evaluate the logistics and the methods and conclude that delivery is relatively complex and needs an external control. Another study [44] presented an evaluation of coverage across socioeconomic groups in Kenya. They state that funding is not the only way for mass campaigns achieve the target of 80% coverage. The distribution also requires careful planning.

Regarding humanitarian operations and LLIN distribution, Rancourt et al. [45] developed in a network flow model to distribution of food aid in Kenya. They presented location models to determine a set of distribution centers, where the food is directly distributed to the beneficiaries. They also considered rainy seasons, as in this paper. Research on logistics optimization to reduce malaria or tropical diseases mortality was developed by Rottkemper et al. [46] who proposed a trans-shipment model for distribution and inventory of artemisinin combination therapy (ACT) in Burundi to minimize the unsatisfied demand and overall cost during response phase to an outbreak of a malaria that resulted in a surge of demand for ACT. The situation required a rapid response and the model could lead to significantly better results in terms of unsatisfied demand without a significant increase in costs. All these papers highlight the need for strong coordination between the actors involved in assistance operations [47], and the need for collaborative relationships between humanitarian organizations [48] and share information during a campaign [49].Willey et al. [26] conducted a review in 32 papers about strategies for scaling up delivery of insecticide-treated nets to identify studies regarding the large-scale delivery of insecticide-treated nets (including LLINs) and presented an adapted strategy for the last mile distribution, without considering all the supply chain. Kilian et al. [25] also presented a review of delivery strategies for insecticide treated mosquito nets. They analyzed 174 papers and reports and concludes that campaign distributions that target the general population are best suited for the scale-up phase of universal access to LLIN.

Chanda et al. [50] found in a study to capture lessons learnt of a large-scale LLIN distribution in South Sudan that “while widespread access to insecticide-treated bednets has been advocated by the Roll Back Malaria Partnership, universal deployment of such nets still requires major financial, technical and operational inputs, particularly in post-conflict environments”. They also suggest the use of operational research to support the decision makers.

Beer et al. [51] evaluate the effectiveness of a mass distribution of LLINs in Tanzania. Their results show free mass distribution results in high and equitable bed net coverage among children under five and, to sustain high effective coverage, there is need for complimentary distribution strategies. Yukich et al. [27] also studied the Tanzania case and detected that the campaign successfully reached households with school-age children but left a substantial number of households that did not have school-enrolled children without sufficient ITNs. Webster et al. [52] also concludes that the bed nets should be distributed free of charge through the public sector.

Grabowsky et al. [53] studied the distribution of bed nets and states the logistical demands of transporting, distributing and monitoring the distribution of bed nets precluded the distribution. They suggest using the logistical infrastructure of measles campaign for the distribution of bed nets in order to achieve high and equitable coverage.

We found in the literature articles about criteria and strategies for last-mile distribution and delivery of bed nets from a distribution point to the beneficiaries. Papers evaluating the entire supply chain, from the suppliers to the distribution points were not found.

3. Model Development

Before elaborating the mathematical model, there was a need to understand the problem, mapping the actual situation and possible alternatives for cost savings and improvements in service level, in an interaction between UNICEF staff and academics. Interim models (called “status quo”) were built based on information available at the different stages of the project and show progressive improvements in planning due to the modelling exercise. They are briefly outlined below.

3.1. Interim Models

When the first interim model was developed (Status Quo 1). Five potential suppliers were chosen based on: (i) production capacity, (ii) cost of LLINs, and (iii) availability of LLINs. UNICEF also had to take into account other planned or ongoing LLINs distributions taking place elsewhere.

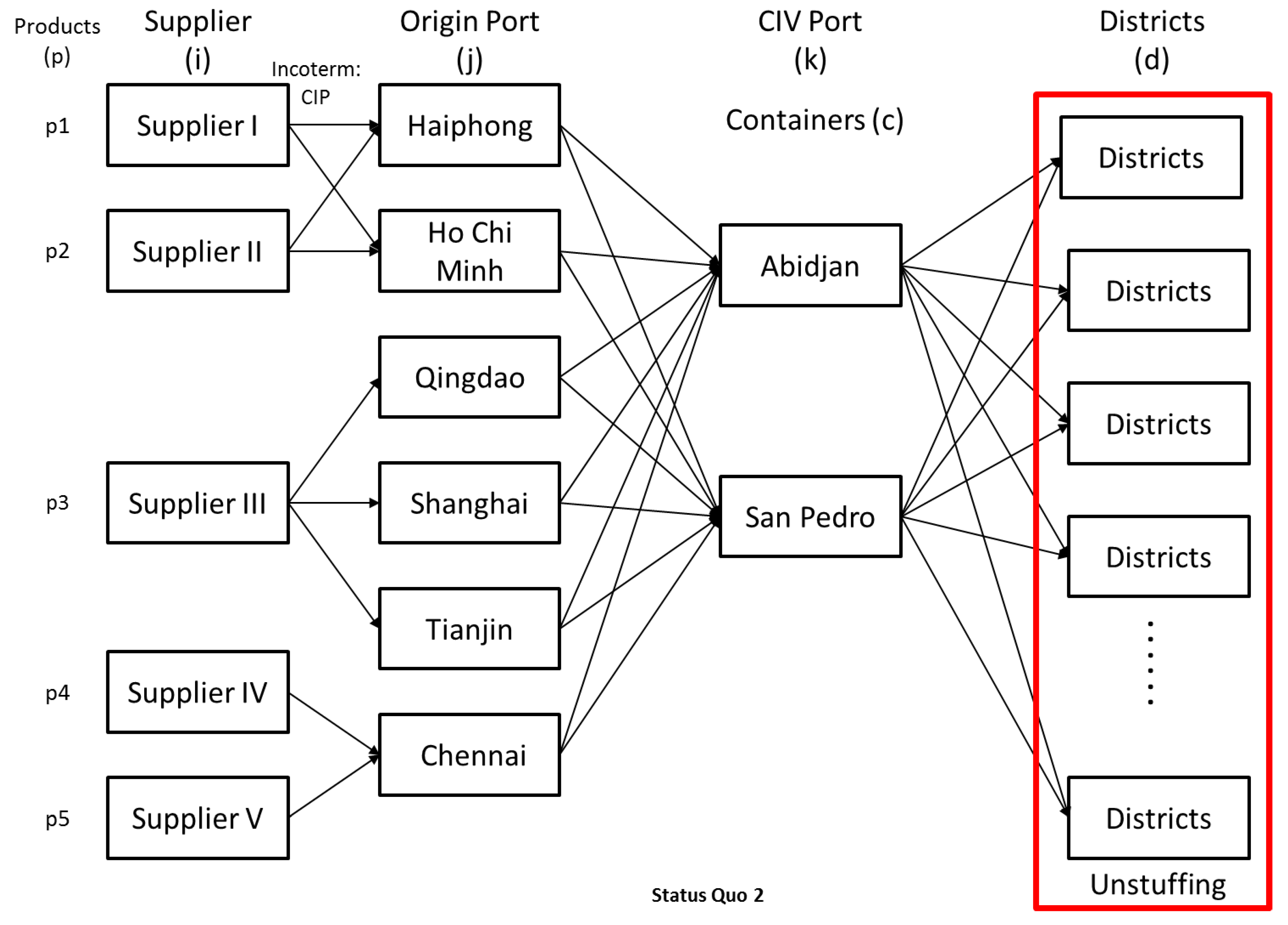
The benefit of this first model is that, by knowing which suppliers were to be used, and by knowing their respective locations, planning with Freight Forwarders could start for the procurement of the SOC (shipper-owned containers) based on requirements and availability in each one of the Asian ports.

The main limitation of this first model is the use of only one seaport in CIV: Abidjan. Using only one port could cause a serious bottleneck especially in consideration of the high number of containers (at the beginning of the project, estimated to be 538 containers) to be received in a short period of time. Additionally, there is the use of a limited number of ports in Asia which could preclude UNICEF from utilizing other shipping companies which might offer better rates, more frequent vessels departure, and from where available and cheaper SOC could be found. The flow shown in Figure 2 represents the possible options to procure and transport the LLINs from the suppliers and ports in Asia, the CIV port until to the Health Districts in CIV, defined in Status Quo 1.

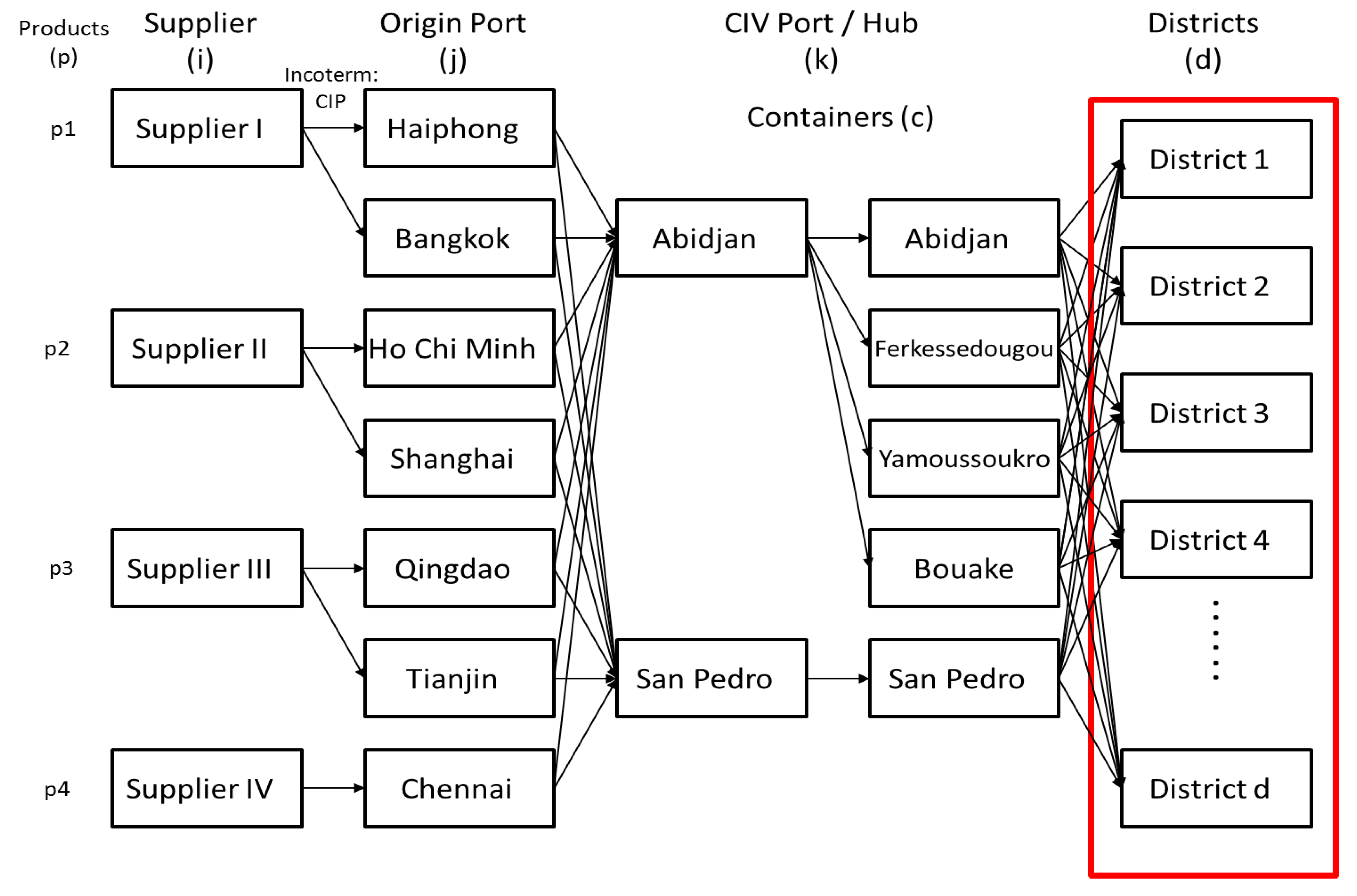
The second interim model (Status Quo 2) was further developed to include an additional port in CIV: San Pedro, which is closer to some of the Health Districts where UNICEF was to deliver the LLINs. San Pedro has a reasonable port infrastructure able to manage an annual volume of approximately 300,000 TEUs (twenty-feet container equivalent unit). San Pedro is port dedicated to exports. Through a mix of export commodities with different harvest times, the port is busy year-round: cashew exports are between February and September, coffee/cocoa exports are from June to August and September to December while the mango season runs from May to August. The export of wood is a year-round activity. In addition to the addition of a new destination seaport, the number of departure seaports in Asia increased to six to include all available options and to explore other solutions to procure the SOC. The limitation of this model is that still does not include the possibility of using the three hubs in CIV as consolidation points. The usage of the hubs was seen as a possible solution to overcome the constraint of limited availably of trucks with cranes (especially at Health District level). Cranes are required to offload the containers, which could potentially be used as storage solution before the LLINs are distributed to the beneficiaries. The flow showed in Figure 3 represents the possible options to procure and transport the LLINs from the suppliers and ports in Asia, the CIV port until to the Health Districts in CIV, defined in Status Quo 2.

3.2. The Network Flow Model

After the interim models, a mixed integer linear programming model (network flow) was developed to support UNICEF in planning the distribution of 12 million LLINs in 71 Health Districts during the mass LLINs campaign by identifying constrains and possible bottlenecks and to propose the most cost effective and efficient solution.

The departure ports are Haiphong and Ho Chi Minh (Vietnam), Chennai (India), Bangkok (Thailand), Qingdao, Shanghai and Tianjin (China). There are two main seaports in CIV (Abidjan and San Pedro) and three cities which could be used as strategic hubs for the consolidation of containers for such a campaign. The cities are: Ferkessedougou, Yamoussoukro and Bouake and, in the model, they are considered as possible destinations where the freight forwarder could deliver the containers of LLINs. From the ports of arrival (or from the three main hubs) the LLINs were to be transported to, and pre-positioned at the 71 Health Districts, before distribution takes place at the distribution centres level. With the exception of the quantity of LLINs planned for Abidjan region, the LLINs needed to be delivered to the Health Districts in containers to address one of the main challenges encountered during past campaigns: the lack of secure storage capacity at Health District level.

To develop the model, the actual cost of: (i) purchasing the LLINs and the shipper-owned container (SOC); (ii) freight; (iii) any additional charges at port of arrival in CIV were used. The freight costs obtained through market research and the in-land transportation costs calculated through linear regression are presented. The information related to packaging, dimensions, container stuffing capacity, etc. were obtained from public sources (UNICEF and Suppliers’ websites). The distances between CIV ports and the 71 Health Districts, as well as to/from the 3 hubs (i.e., Bouake, Yamoussoukro, and Ferkessédougou), were calculated using Google Maps and then using linear regression to estimate the transportation costs. Customs and ports charges in CIV were confirmed looking at the Customs Authority website and in-land transportation costs were calculated using linear regression based on historical data costs obtained from 3PL (Third Party Logistics) suppliers in CIV.

The information used for the model includes:

• Procurement cost of the LLINs;
• Number of UNICEF suppliers for LLINs;
• Number of ports at origin from where to ship the LLINs and purchase the SOC;
• Freight costs from suppliers to CIV ports;
• Number of LLINs which suppliers could stuff in each container size;
• Number, size and cost of SOC required by Health District;
• Number of LLINs required for each Health District;
• Number of Health Districts where the LLINs needed to be pre-positioned;
• Distance between the ports in CIV and the 71 Health Districts served by UNICEF;
• In-land transportation costs;
• Handling, demurrage, and customs costs.

A specific consideration for such a large-scale campaign is the production capacity of the suppliers. Suppliers may be required to serve multiple customers or multiple simultaneous LLINs campaigns. UNICEF had to apply a degree of judgement and market knowledge to ensure both economies of scale through sufficiently large order quantities but also risk management by spreading the procurement between suppliers in case of default or manufacturing delay.

The Incoterm used for the shipment of the nets was CIP: suppliers were responsible for delivering the LLINs in SOC up to the port of departure (in Asia). The SOC size could be of 20 ft, 40 ft and 40 ft HC (high-cube), depending on the total quantity of LLINs required for a specific Health District and based on supplier’s stuffing capacity, which varied significantly.

UNICEF ran the model using the freight costs to ship the containers from the Asian ports to the ports in CIV (and to the three hubs in CIV) obtained by the freight forwarders. Freight costs were obtained through market research and include local insurance in CIV, customs clearance and duties, port storage and offloading of containers at warehouse locations both at the CIV ports and the three hubs.

The transportation costs from the CIV ports (and from the three hubs) to the 71 Health Districts assigned to UNICEF, was calculated using simple linear regression based on the market research with a coefficient of determination R2 = 0.99, which takes into consideration the distance between CIV ports/hubs and the Health Districts, using historical pricing data from 3PL suppliers in CIV. The estimated regression (in USD) had a coefficient of 395.60 (USD) and the slope of 2.45 (USD/km).

Inland cost = 395.60 + 2.45 × distance

(1)

It is worth noting that suppliers had market differences in terms of:

• LLINs production capacity;
• Container stuffing capacity: some suppliers are able to fit double the quantity of nets in the same size container—this is primarily attributed to the different types of packaging used;
• Price of the LLINs.

The model takes these three factors into consideration and the quantity of LLINs that a container c of product p contains exactly reflects the stuffing capacity.

To meet the target of universal coverage, it is calculated that one LLIN should be distributed to every two people at risk of malaria. Specifically, WHO recommends an overall ratio of 1 LLIN for every 1.8 persons in the target population [22]. The model reflects this recommendation in the demand.

Security concerns, the rainy season and any increase in CIV export activities could have affected the transportation options. To address this potential bottleneck the model takes into consideration three binary parameters that indicate (according the season) if a route is available from supplier i to port of departure j, from port of departure j to CIV ports (or hubs) k, and from CIV ports (or hubs) k to Health Districts d. The big number auxiliary was set as 10⁷.

As the goal of the model was to optimize the procurement and logistics costs for the LLINs campaign, the following was considered:

(i)

The number and size of SOC to be used for the 71 Health Districts;

(ii)

The suppliers from whom the LLINS are purchased and their port of departure. This decision is also influenced by the availability and cost of SOC in each of the ports of departure;

(iii)

The port in CIV at which the containers should be received;

(iv)

The three hubs in CIV as consolidation points for the LLINs before they are transported to the 71 Health Districts.

Figure 4 illustrates the structure of the model and represents the possible options to procure and transport the LLINs from the suppliers in Asia to the Health Districts in CIV.

3.3. Model Details, Variables and Parameters

Index sets
P	Supplier products (LLINs) p ∈ P
C	Container type c ∈ C
I	Suppliers i ∈ I
J	Departure port in Asia j ∈ J
K	Port/hub in Ivory Coast k ∈ K
D	Health districts d ∈ D
Parameters and units (Supplementary Materials)
cspcij	Transportation cost (in USD/container) of a container c with LLINs p from supplier i to departure port j
copcjk	Shipping cost (in USD/container) of a container c with LLINs p from departure port j to Port/hub in Ivory Coast k.
cppckd	Transportation cost (in USD/container) of a container c with LLINs p from port/hub in Ivory Coast k to a health district d.
prp	Cost (in USD) of a LLIN p
cccj	Cost (in USD) of a container c at departure port j (USD).
dmd	LLINs demand at health district d.
sci	Supplier’s i capacity to manufacture LLIN p.
nqpc	Quantity of LLINs p that a container c fits.
aspij	Binary parameter indicating whether the route from supplier i to departure port j is available for LLIN p.
aopjk	Binary parameter indicating whether the route from departure port j to port/hub in Ivory Coast k is available for LLIN p.
appkd	Binary parameter indicating whether the route from port/hub in Ivory Coast k to a health district d is available for LLIN p.
bigM	Big number, to ensure that a health district is supplied by one LLIN only.
Decision variables
TSpcij	Number of containers c that transported LLINs p from supplier i to departure port j.
TOpcjk	Number of containers c that transported LLINs p from departure port j to port/hub in Ivory Coast k.
TPpckd	Number of containers c that transported LLINs p from port/hub in Ivory Coast k to Health District d.
Zpd	Binary auxiliary to ensure that a health district is supplied by only one LLIN p. Assumes 1 if a Health District is supplied by a LLIN p and 0 otherwise.

Objective function

$$\begin{array}{l}\min TC={\displaystyle \sum _p}{\displaystyle \sum _c}{\displaystyle \sum _i}{\displaystyle \sum _j}\left(c{s}_{pcij}\times T{S}_{pcij}\right)\\ +{\displaystyle \sum _p}{\displaystyle \sum _c}{\displaystyle \sum _j}{\displaystyle \sum _k}\left(c{o}_{pcjk}\times T{O}_{pcjk}\right)\\ +{\displaystyle \sum _p}{\displaystyle \sum _c}{\displaystyle \sum _k}{\displaystyle \sum _d}\left(c{p}_{pckd}\times T{P}_{pckd}\right)\\ +{\displaystyle \sum _p}{\displaystyle \sum _c}{\displaystyle \sum _i}{\displaystyle \sum _j}\left(n{q}_{pc}\times p{r}_p\times T{S}_{pcij}\right)\\ +{\displaystyle \sum _p}{\displaystyle \sum _c}{\displaystyle \sum _j}{\displaystyle \sum _k}\left(c{c}_{cj}\times T{O}_{pcjk}\right)\end{array}$$

(2)

The first term represents the transportation costs from suppliers to departure ports, the second refers to transportation costs from ports of departure to of CIV ports/hubs, the third term is transportation costs from Ivory Coast ports/hubs to the districts. The fourth term represents the purchase costs and the final term is the cost of the containers. To assure traceability of supplies throughout the chain until their delivery at district level, the index p is retained in all parts of the equation.

Subject to:

Flow conservation at j.

$${\displaystyle \sum }_{i}T{S}_{pcij}={\displaystyle \sum }_{k}T{O}_{pcjk } \forall p,c,j$$

(3)

Flow conservation at k.

$${\displaystyle \sum }_{j}T{O}_{pcjk}={\displaystyle \sum }_{d}T{P}_{pckd} \forall p,c,k$$

(4)

Assures that the demand at health district d is satisfied.

$${\displaystyle \sum }_p{\displaystyle \sum }_c{\displaystyle \sum }_k(T{P}_{pckd}\times n{q}_{pc})\ge d{m}_d \forall d$$

(5)

Capacity of supplier i produce LLINs p.

$${\displaystyle \sum }_c{\displaystyle \sum }_j\left(T{S}_{pcij}\times n{q}_{pc}\right)\le s{c}_{pi} \forall p,i$$

(6)

The following three constraints ensure the model proposes only the available routes from supplier i to departure port j due to insecurity, rainy season or increased port trade volume (due to agricultural harvest, etc.).

Ensure to use only available routes from supplier i to departure port j.

$$T{S}_{pcij}\times a{s}_{pij}\ge T{S}_{pcij} \forall p,c,i,j$$

(7)

Ensure to use only available routes from departure port j to Port/hub in Ivory Coast k.

$$T{O}_{pcjk}\times a{o}_{pjk}\ge T{O}_{pcjk} \forall p,c,j,k$$

(8)

Ensure to use only available routes from Port/hub in Ivory Coast k to district d.

$$T{P}_{pckd}\times a{p}_{pkd}\ge T{P}_{pckd} \forall p,c,k,d$$

(9)

The 3 next constraints ensure the specific feature of this problem, that a health district is supplied by only one LLIN p.

If TP_pckd > 0, Z_pd = 1 (but if TP_pcdk = 0, Z_pd could be 0 or 1).

$${\displaystyle \sum }_c{\displaystyle \sum }_{k}T{P}_{pckd}\le Z_{pd}\times bigM \forall p,d$$

(10)

If TP_pcdk = 0, z_pd = 0.

$${\displaystyle \sum }_c{\displaystyle \sum }_{k}T{P}_{pckd}\ge Z_{pd} \forall p,d$$

(11)

Ensure that a district is supplied by one product only.

$${\displaystyle \sum }_p{Z}_{pd}=1 \forall d$$

(12)

Integer variables.

$$T{S}_{pcij}, T{O}_{pcjk}, T{P}_{pckd}\in N$$

(13)

Binary variables.

$$Z_{pd}\in \left\{0,1\right\}$$

(14)

4. Results of the Model

The objectives of our research were to demonstrate the benefits of the implementation of a modelling process to optimize UNICEF supply chain, to support its decision-making process in complex malaria distribution campaigns, and to identify potential cost savings opportunities in the procurement, shipment, and distribution of LLINs in CIV.

4.1. Logistics Results

The model was run using the software AIMMS 3.13, CPLEX solver 12.5, processor Intel Core i7, 8 Gb RAM, 64-bit operating system Windows10^®. It took different times to solve the three phases of the campaign: 24′52″ (phase 1), 25′38″ (phase 2), and 13′15″ (phase 3). The model found the optimal solution more rapidly in phase 3 mainly because all Health Districts are located close to each other in that phase.

The model was run for all the three phases of the LLINs campaign and the result indicates, for each one of the 71 Health Districts, the following information: (i) from which supplier and from which port of departure to ship the LLINs; (ii) number and size of containers to be used to deliver the LLINs to the Health Districts; (iii) to which port and/or hub in CIV the LLINs should be delivered; (iv) from which port (and/or hub) in CIV the 71 Health Districts should receive the LLINs f; (v) total logistics and procurement costs.

Table 1. Results of the transport from suppliers to ports at destination.

Supplier		Supplier I			Supplier III			Supplier IV			Total
Departure Port		Haiphong			Chennai			Qingdao
CIV Port/Hub		40 ft	40 ft HC	20 ft	40 ft	40 ft HC	20 ft	40 ft	40 ft HC	20 ft
Abidjan	Phase 1	1	23			2		2	8	2	38
	Phase 2		4		1	24				1	30
	Phase 3	3	121	7				2	35	1	169
San Pedro	Phase 1		2		1	5		1	9		18
	Phase 2	1	68	5	5	30	1	4	41	1	156
	Phase 3										0
Yamoussoukro	Phase 1		14		3	12		2	9		40
	Phase 2						1				1
	Phase 3										0
Bouake	Phase 1		16	2	1	4		1	5	1	30
	Phase 2										0
	Phase 3										0
Ferkessdougou	Phase 1										0
	Phase 2										0
	Phase 3										0
Total		5	248	14	11	77	2	12	107	6	482

shows the number and the sizes of containers that each CIV port and/or hub would receive from each supplier and port of departure. This is indicated for all three phases.

Out of four suppliers, the model optimization process proposed that the procurement be done from three suppliers only (it excludes supplier II mainly due its high product price) and to use three ports of departure (Ho Chi Minh, Bangkok, Shanghai, and Tianjin were excluded mainly due to high freight costs). In most of the cases, the 40 ft HC is the container size which better optimizes the space and reduces the transportation costs. With the exception of Abidjan port, neither San Pedro nor the three hubs are utilized for all the three phases due to operations’ geographic characteristics. Ferkessdougou hub is not used at all (mainly due to fixed costs).

Among the three phases, phase 1 includes those Health Districts located quite far both from Abidjan and San Pedro port. For this phase the model proposes to use, as trans-shipment points: the Abidjan port, San Pedro port, Yamoussoukro hub, and Bouake hub. Phase 2 has only one container assigned by the model to arrive in Yamoussoukro. However, after evaluating this option, UNICEF decided not to use Yamoussoukro for phase 2 because the effort to manage just 1 container was simply not worth it.

Table 2. Number of districts supplied/served by CIV ports and/or hubs.

Port/Hub	Abidjan	San Pedro	Yamoussoukro	Bouake	Total Districts
Phase 1	9	4	9	6	28
Phase 2	4	20	1		25
Phase 3	21				21
Total Districts	34	24	10	6	74 *

* This value is higher than 71 because district could be supplied for more than 1 port/hub.

shows how many Health Districts each port/hub in CIV will supply for each phase of the campaign. It is noted that Abidjan is the port supplying more districts, especially in phase 3, which covers the Abidjan region. Phase 2 is primarily served by San Pedro and this reflects the geographical position of the districts in relation to the port.

The model suggested the use of consolidation points in CIV for three main reasons: (i) to reduce the last mile transportation distance and, therefore, the overall transport costs, (ii) to address a possible bottleneck represented by the specific equipment required to handle the containers at district level (i.e., trucks with crane or forklifts), and (iii) to allow the usage of smaller trucks to reach the most remote areas, especially during the raining season. Another relevant aspect to consider is the overall coordination of the supply chain. The availability of consolidation points can enhance coordination among stakeholders and can greatly facilitate a prompt response in case of unforeseen situations and bottlenecks which could occur during the implementation of the campaign. Additionally, not all Health Districts have sufficient space to accommodate the SOC: up to 30 containers in some of the Districts.

4.2. Total Costs and Comparison between Initial Situation and the Model Results

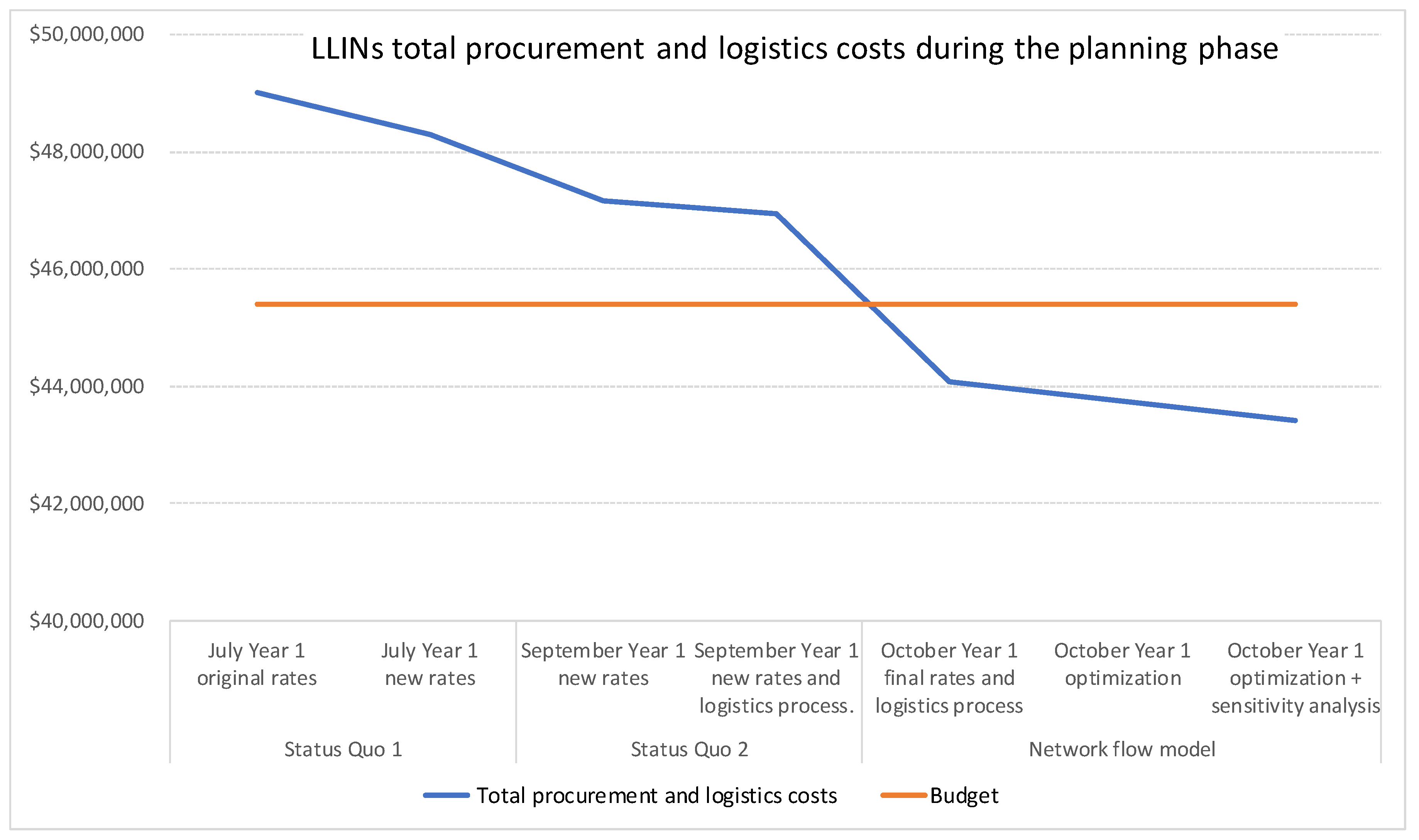
Comparing the results of the model with the initial budget and first supply and distribution plan there was a reduction of the total costs. Figure 5 shows the total procurement and logistics cost during the planning exercise and the budget promoting a significant achievement obtained in the cost reduction of the procurement and logistics elements for the LLIN mass campaign in CIV. This remarkable result was obtained due to a commitment by the UNICEF task force and academics to the development and refinement of the process from the interim models to the final model and promoted the need for the establishment of specific tools and guidances for campaigns.

The figure illustrates the total cost reduction due to the optimization process proposed and encouraged by this study. The original cost to consider is July (year 1) as the figures indicated this and the budget was drafted in May (year 1) before conducting any comprehensive costs analysis.

Table 3. Savings due to optimization.

	Budget May (Year 1)	Original Cost July (Year 1)	Optimized Cost July (Year 1)
Cost	$45,399,355.33	$49,018,368.12	$43,426,374.88
Savings due optimization	$1,972,980.45	$5,591,993.24
%	4.3%	11.4%

represents the savings (total and percentage) due the optimization comparing the optimized solution with the budget and original rates. This result was obtained despite some limitations regarding incomplete information related to suppliers’ production capacity and final in-land transportation costs.

The result obtained clearly demonstrates one of the main objectives of this research: how beneficial collaboration between academia and the humanitarian sector can be, especially when planning for complex projects like the mass distribution of LLINs in challenging operating environments. It also clearly shows the added value of using modelling to find the optimal solution when resources are limited. By adopting an academic approach and utilizing modelling tools to represent a complex humanitarian distribution, the bottlenecks and key interfaces for intervention/improvement can be more easily seen and ultimately addressed by feasible solutions. A more structured approach to complex distribution planning can result in greater efficiencies/cost reduction and improved service delivery. In turn, the benefit to academia is that through practical application of modelling tools, the model can be refined for replication on other similar projects and can be used for future research studies also related to the humanitarian sector. Finally, the fact that the model can be adapted and used again by both academia and UNICEF is important and indicative of a much greater value and impact than just this campaign.

4.3. Sensitivity Analysis

One critical piece of information, not fully available for this study, was the suppliers’ production availability. To demonstrate the criticality of this information in order to obtain an optimal solution, and to reinforce the importance of having a holistic approach when planning, the suppliers’ production availability was increased by 50% and the sensitivity analysis for parameter sci capacity of supplier i to produce LLINs was calculated. Overall, increased supplier production capacity leads to an additional cost savings of 0.7%, which represents 11.41% saving from the original costs.

This result is due to the difficulty of coordinating the procurement of humanitarian organizations. Campaigns conducted by these organizations in several countries are not distributed regularly over time, instead occurring according to the availability of funds. This “modus operandi” may result in high demand during some periods and low demand during others, hindering the suppliers’ ability to adequately manage their production capacities.

Table 4. Costs variation increasing 50% the suppliers’ availability.

	Logistics Costs	Container Costs	Purchase Costs	Total Costs
Phase 1	0.21%	−3.71%	−0.97%	−0.96%
Phase 2	0.53%	−2.89%	−0.88%	−0.82%
Phase 3	−0.74%	−2.40%	−0.35%	−0.47%

shows the impact of a 50% increase in supplies’ capacity on the campaign costs (e.g., cost variation). The results suggest that the increase in suppliers’ capacity, raises logistics costs for phase 1 and phase 2, but decreases procurement costs (both for the SOCand LLINs) leading to an overall reduction in cost for the campaign. For phase 3, the increase in capacity leads to a reduction in all costs, including logistics ones.

The main reason behind the decrease in costs due to an increase in suppliers’ capacity is due to the possibility of purchasing more items from those suppliers with lower prices. It is interesting to note that the total cost is close to the procurement cost of LLINs. This indicates that the procurement costs have the highest influence on the total costs for the supply chain of the CIV campaign.

Table 5. Level of utilization of suppliers’ availability.

		Supplier I	Supplier III	Supplier IV
Phase 1	Initial Solution	84.0%	97.2%	97.2%
	50% increase	35.8%	89.9%	97.0%
Phase 2	Initial Solution	77.9%	92.1%	96.6%
	50% increase	31.9%	91.8%	98.4%
Phase 3	Initial Solution	91.2%	0.0%	97.0%
	50% increase	67.5%	0.0%	99.2%

shows the utilization level of suppliers’ capacity and confirms that the lower the procurement costs the higher the supplier utilization.

The sensitivity analysis suggests that suppliers’ production availability capacity is the element with the highest influence on the optimal results. This is mainly due to LLIN prices contributing directly to procurement costs.

5. Conclusions and Implications for Future Research

The objectives of our research were threefold: (i) to demonstrate the benefits of the implementation of a modelling process to optimize UNICEF supply chain; (ii) to support UNICEF country offices with its decision-making process within complex malaria distribution campaigns; and (iii) to identify potential cost savings opportunities in the procurement, shipment, and distribution of LLINs.

The ability to save 11.4% of the total campaign cost is extremely relevant in the current global economic climate in which availability of funds are more limited. It is also critical as the commitment by UNICEF in supporting governments to strengthen and optimize their supply chains is increasing. The contribution of our study goes well beyond the development of an optimization model providing a feasible and optimal solution to UNICEF, more importantly, it includes building internal ability to confront complex distribution campaigns in a more structured way, informed by constructive discussions among the campaign stakeholders and academics.

Organizing the procurement, shipment, and distribution of 12 million LLINs requires a strong coordination among stakeholders and a meticulous supply chain plan, which must identify, monitor and mitigate key risks. Failure to do so in a timely manner could ultimately hamper the successful implementation of the campaign. UNICEF’s initial supply and distribution plan proposed to procure LLINS from 5 suppliers based in Asia, shipping from 4 ports of departure (contingent on suppliers’ locations), to purchase more than 500 40-feet containers, and to use Abidjan as the only port of arrival in CIV. UNICEF soon realized the importance of exploring additional options to ensure optimal planning for this massive campaign. After our intervention, UNICEF’s final supply and distribution plan procured LLINS from 3 Asian suppliers, shipping from 3 ports of departure, purchased over 482 containers of different sizes (e.g., 20 ft, 40 ft, and 40 ft HC), and distributed through 4 entry points in CIV (e.g., Abidjan port, San Pedro port, Yamoussoukro hub, and Bouake hub). UNICEF’s final supply and distribution plan highlighted a much more versatile and effective solution at a much lower cost. Finally, this research highlights the need to consolidate existing materials and available tools, to draw lessons learnt, and to develop a more structured and consistent planning approach. For many humanitarian organizations, the use of mathematical models to support decision-making represents a dramatic cultural and paradigmatic shift. It is important that sufficient time be allocated during the planning process for large-scale campaigns for model development and refinement in order to identify, review, and pursue the most flexible, robust, cost effective, and cost efficient options. As more integrated campaigns become common (where multiples commodities are distributed simultaneously), the benefits of using modelling can be even more substantial. While the mathematical model presented in this study focuses exclusively on the LLIN supply chain (from procurement to pre-positioning) the coordination of all actors involved in a complex distribution campaign requires management of multiple other aspects (e.g., funding, human resources, scheduling, etc.). Mathematical models that also address such aspects can be helpful and could be considered in future studies.