1. Introduction
Buchanan et al. [
1] demonstrated that replacing the global fleet of roof panels and container walls with aluminum would save
$28 billion in fuel and that a 20% reduction in the steel mass would result in a reduction of 17% in energy and lifecycle emissions, or 3.6 exajoule of the energy demand. Their results demonstrate the significant potential fuel savings and energy potential that could be achieved by lightening shipping containers. The strategies are based on reducing the weight of a vehicle and on the collection and development of a set of physics-based expressions to describe the effect of reducing vehicle mass on fuel consumption across transportation modes [
2]. A 10% reduction in vehicle weight (assuming a constant payload) would result in a 2% improvement in fuel consumption for trains and light, medium, and heavy trucks; 4% improvement for buses; and 7% improvement for airplanes [
2].
Obrecht and Knez [
3] studied the carbon and resource savings of different container designs. They indicated that a possible solution for more sustainable freight transport is the use of environmentally friendly containers manufactured according to eco-design principles. They are lighter, made of fewer materials, and have less impact on the environment throughout their lifecycle [
3]. Goh [
4] studied the impact of foldable sea containers on freight forwarders and carbon emissions. Their study examined the sender’s foldable shipping containers and prospects for sustainability. The viability of foldable containers as a carbon offset tool for the shipping industry was also explored [
4].
Sureeyatanapas et al. [
5] studied green initiatives for logistics service providers in a survey of background factors and contributions to business objectives. This study aimed to provide information on the launch of green policies in logistics companies by examining the important factors influencing the adoption of green practices, as well as the extent to which several green activities contribute to cost reduction and environmental protection. The results indicate that “green driving” and “vehicle routing” activities are more recognized and generally conducted in the industry [
5].
This research was undertaken to provide a global solution for reducing the energy demand of transportation, more specifically providing lightweight solutions for shipping containers. As the utilization of lightweight shipping containers has been an unexplored strategy, the reduction of both fuel consumption and the operational costs of transportation would become possible. This research presents the new design of a 40-foot container made of carbon fiber laminates. The curb weight of a 40-foot traditional shipping container is approximately 80% lower. Tests are also performed to explore the resistance and buckling problems of the new model. The analyses reveal that the composite shipping container is a highly promising candidate for reducing greenhouse gas (GHG) emissions, saving fuel, and thus reducing the operating costs of transportation.
The remainder of this paper is organized as follows.
Section 2 reviews the literature on light composite applications and vehicle mass concerns, as well as the eco-design of containers and need to develop better fuel efficiency in logistics.
Section 3 presents the materials and methods used to perform the complex design and analyses of the composite container design.
Section 4 describes the analyses and results.
Section 5 concludes the paper.
2. Literature Review
The prevailing research reflects the increasing amount of international literature on this area based on different viewpoints. For example, lightweight composite air cargo containers were studied by William et al. [
6]. They indicated that innovative concepts for the design and assembly of lightweight air cargo container construction configurations have been developed through light composite applications. The prototype of a typical airfreight container was constructed to assess the technical feasibility and economic viability of creating such a container from fiber-reinforced polymer composite materials [
6]. Ranta et al. [
7] studied the radio frequency identification and demonstration of composite container technology for the transportation of wood biomass logistics, finding a higher readability of Radio-frequency identification (RFID) tags with composite containers than with metal ones.
Lee and Song [
8] reviewed shipping container transport in global supply chains. They emphasized that the dynamic operations and uncertain activities of long-distance container shipping pose challenges to the quality of shipping services, as well as that shipping operations and performance are affected by increasing concerns about the social and environmental impacts. All these issues bring challenges to the container shipping industry [
8]. Rødseth et al. [
9] studied the impact of density savings in container handling operations on the time spent and ship emissions in ports using data provided by Norwegian container terminals. They indicated that Norwegian and European decision-makers are committed to improving the economic and environmental performance of the transport system.
Wu and Huang [
10] modeled the profitability of container transport lines. Their research contributes to the maritime literature by constructing a theoretical model to empirically examine the determinants of the profitability of container ships. Mantovani et al. [
11] researched the load planning problem for two-train intermodal trains and presented a methodology for solving this problem. Intermodal transport is an important component of a profitable freight transportation system, which is an essential part of a competitive economy, in which different modes of transport are linked to moving goods from a point of origin to a point of destination.
Notteboom and Vernimmen [
12] examined the effect of high fuel costs on the liner service configuration in container shipping. They indicated that for shipping activities, not least container shipping, bunker fuel is a considerable expense. Denac et al. [
13] studied the current and potential integration of eco-design in small- and medium-sized enterprises in the construction and related industries. The study found that the most frequently applied criteria were to maximize product life and ease of reuse, disassembly, and recycling. The highest level of eco-design implementation was observed in the “design for use” phase. Andriankaja et al. [
14] proposed a method for the eco-design of structural parts in the transport sector based on the management of the product lifecycle.
Acanfora et al. [
15] estimated design loads on container stacks due to excessive acceleration under adverse weather conditions. Majidian and Azarsina [
16] evaluated the cargo configuration effect on frontal wind loads by addressing the fuel consumed during ships’ propulsion. They found that the optimal stacking of containers reduces wind drag by 25%, which has a positive impact on fuel consumption. Khor et al. [
17] analyzed the optimal speed for large container ships and stated that innovations in design and a slowing speed are becoming more important. Their article also described in detail new software designed to facilitate the speed optimization process of large container ships.
Podeur et al. [
18] assessed fuel economy using the kite propulsion of a merchant ship. Malchow [
19] investigated the growth of ship sizes and found that transport costs would not significantly reduce by increasing them further. Their research demonstrated that increasing the size of container ships does not bring about any further benefits for the ports and their terminals, for the lines themselves, or for shippers.
Martin et al. [
20] studied international regulations for container construction and ISO standards and their suitability for its purpose. The growing adoption of terminal automation also calls for the greater standardization of container coding and marking. Their study demonstrated that the roles of the International Maritime Organization (IMO) and ISO in regulating and promoting standards for container design, dimensions, size, coding, marking, and strength are largely unknown. Abrasheva et al. [
21] researched shipping containers from a sustainable city perspective and found that the challenges of sustainable urban development are enormous. Abrasheva et al. [
22] explored shipping containers in a sustainable habitat, showing that the container construction industry has significant potential for sustainability.
Goulielmos [
23] studied the structural changes in the containership market after 2008 and their impact on industry policy. As large vessels are more competitive, smaller vessels are being abandoned and eventually scrapped. Their model showed that the containership market is oligopolistic or purely competitive, confirming the double-edged sword of containership markets that has long been debated by maritime economists. Kana and Harrison [
24] adopted a Monte Carlo approach to the vessel-centric Markov decision process to analyze the conversion of a containership to an Liquefied Natural Gas (LNG) carrier. A case study was used to show how uncertain parameter variations can significantly affect the optimal decision strategies.
Cariou et al. [
25] studied low carbon global supply chains and performed a multi-trade analysis to reduce emissions in container shipping. They also indicated that the IMO has agreed to reduce GHG emissions from international shipping, which should lower annual CO
2 emissions by at least 50% by 2050 compared with 2008. Patricksson and Erikstad [
26] assessed sulfur emissions to minimize total costs, with aggregated power requirements and emission regulations serving as constraints to the problem.
Priftis et al. [
27] performed a parametric design and multi-objective optimization of container ships. Fluctuations in fuel prices along with the shipping industry’s constant striving for economic growth have led the shipbuilding industry to explore new designs for various types of ships. Guven and Eliiyi [
28] modeled and optimized online container stacking under operational constraints. The objective of the container stacking problem is to minimize the number of reworkings, thereby increasing the efficiency of terminal operations. They also indicated that additional weight-related operational constraints increase the complexity of online stacking decisions.
Ding and Chou [
29] examined container docking planning by developing a heuristic algorithm to reduce the number of shifts. Their heuristic algorithm is capable of generating docking plans with a reasonable number of shifts. Parreño et al. [
30] proposed a Greedy Randomized Adaptive Search Procedure (GRASP) algorithm for the storage location planning problem. This work presented a generalization of the slot planning problem that arises when the liner shipping industry needs to plan the placement of containers within a vessel (stowage planning). Christensen and Pacino [
31] proposed a solution to the problem of cargo bulk blocking. They found that the demand for efficient and cheap transportation and fierce competition have resulted in lower transport rates, forcing carriers to use their vessels in the most efficient way [
31].
Lee et al. [
32] used archival data to research a decision support system for understanding vessel speed in marine logistics, which provides more than 70% of global transport. Optimizing the speed of liner ships has a significant economic and environmental impact in terms of reducing fuel costs and GHG emissions. In the same vein, Bal and Vleugel [
33] investigated container port calls with emissions at sea. They indicated that these emissions are a serious threat to the planet and the health of its species [
33]. Ammar [
34] provided an environmental and economic analysis of the use of methanol for a cellular containership, which can reduce NO
x, SO
x, CO, CO
2, and PM emissions by 76.8%, 89%, 55%, 18.1%, and 82.6%, respectively [
34].
Based on the foregoing, the present study contributes to the existing literature by using composite materials to design a shipping container. In particular, it provides a better theoretical understanding of a composite container made of carbon fiber laminates. Specifically, it differs from previous works in that it investigates the possibility of significantly reducing the weight of a marine container without compromising the functionality of a traditional steel-made shipping container.
3. Materials and Methods
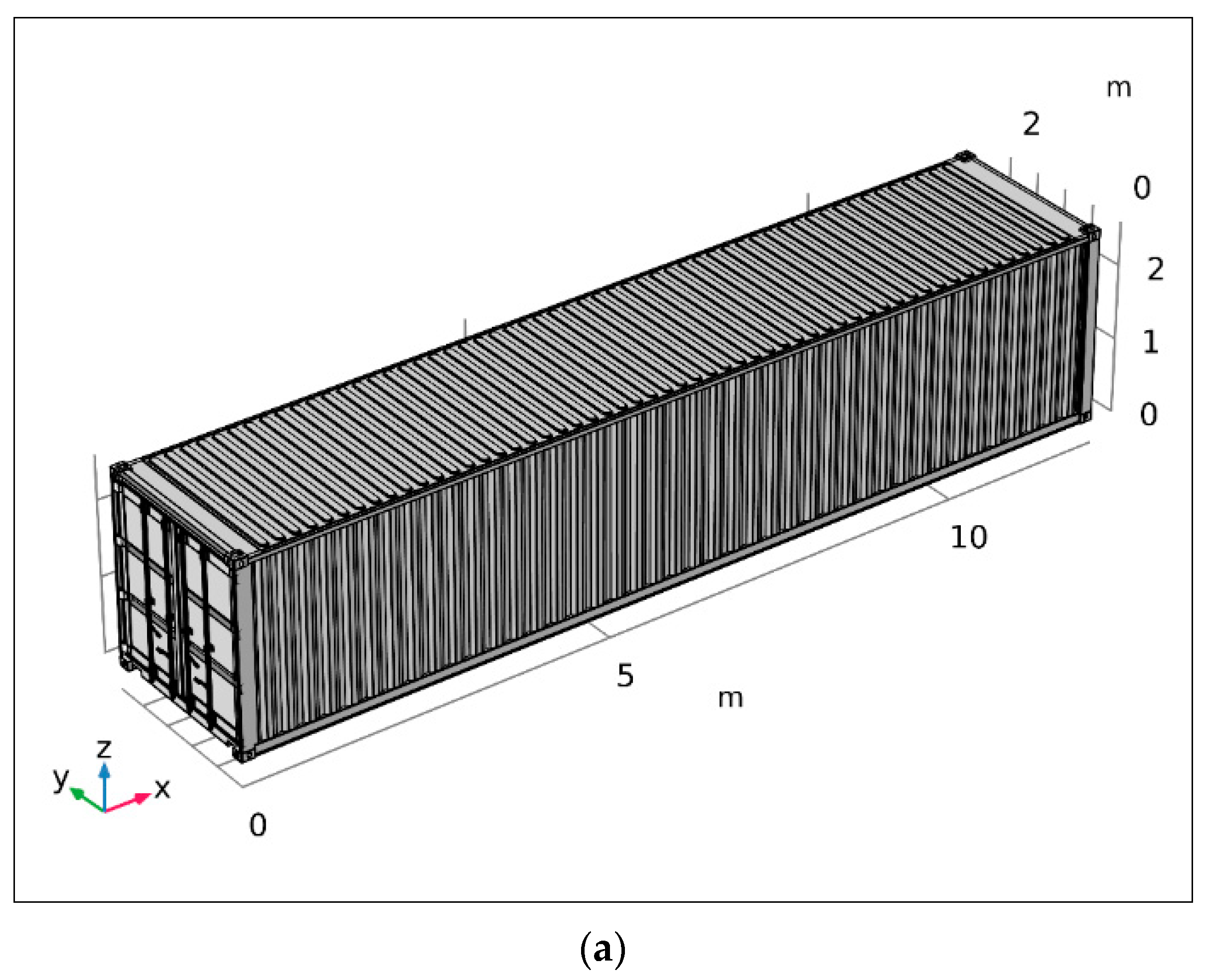
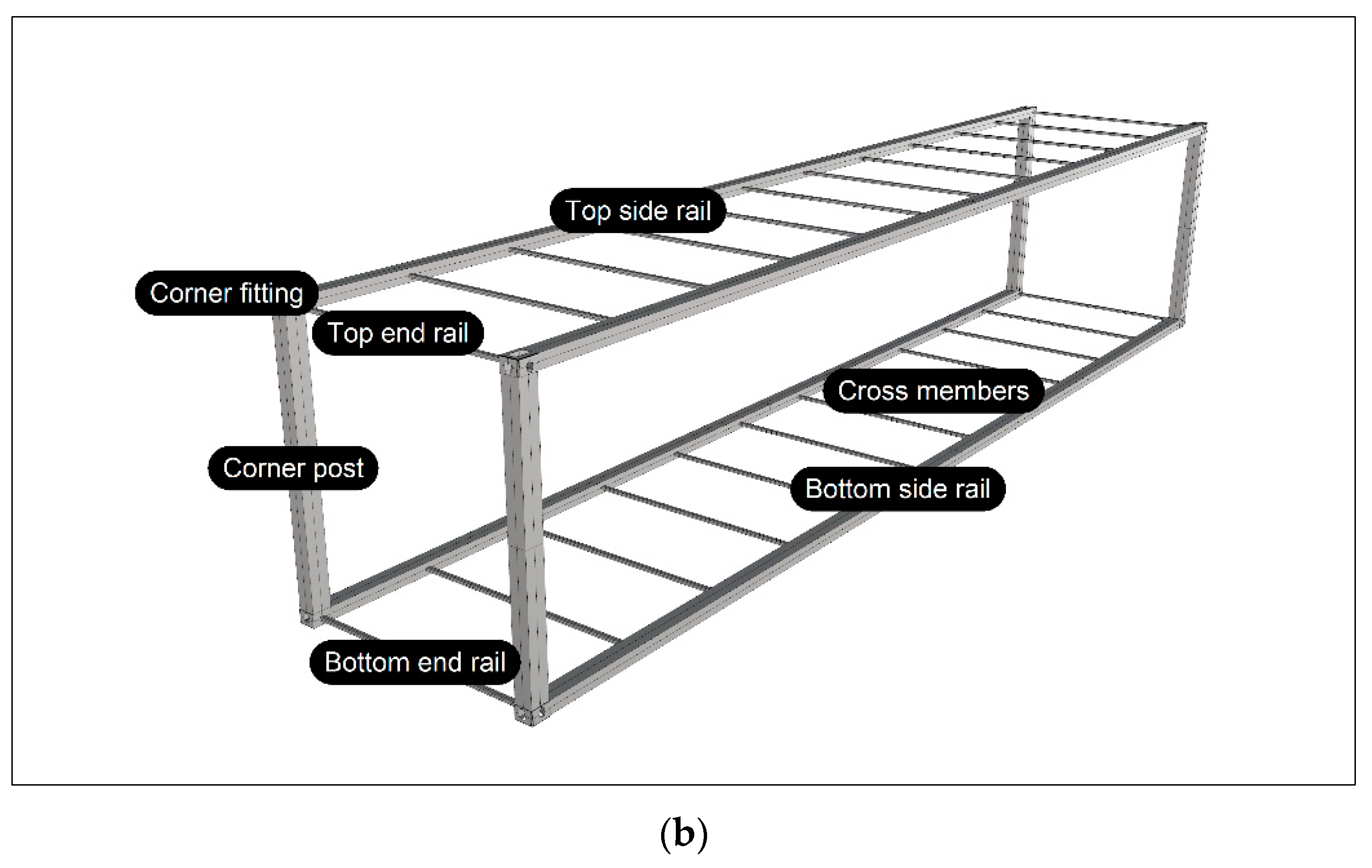
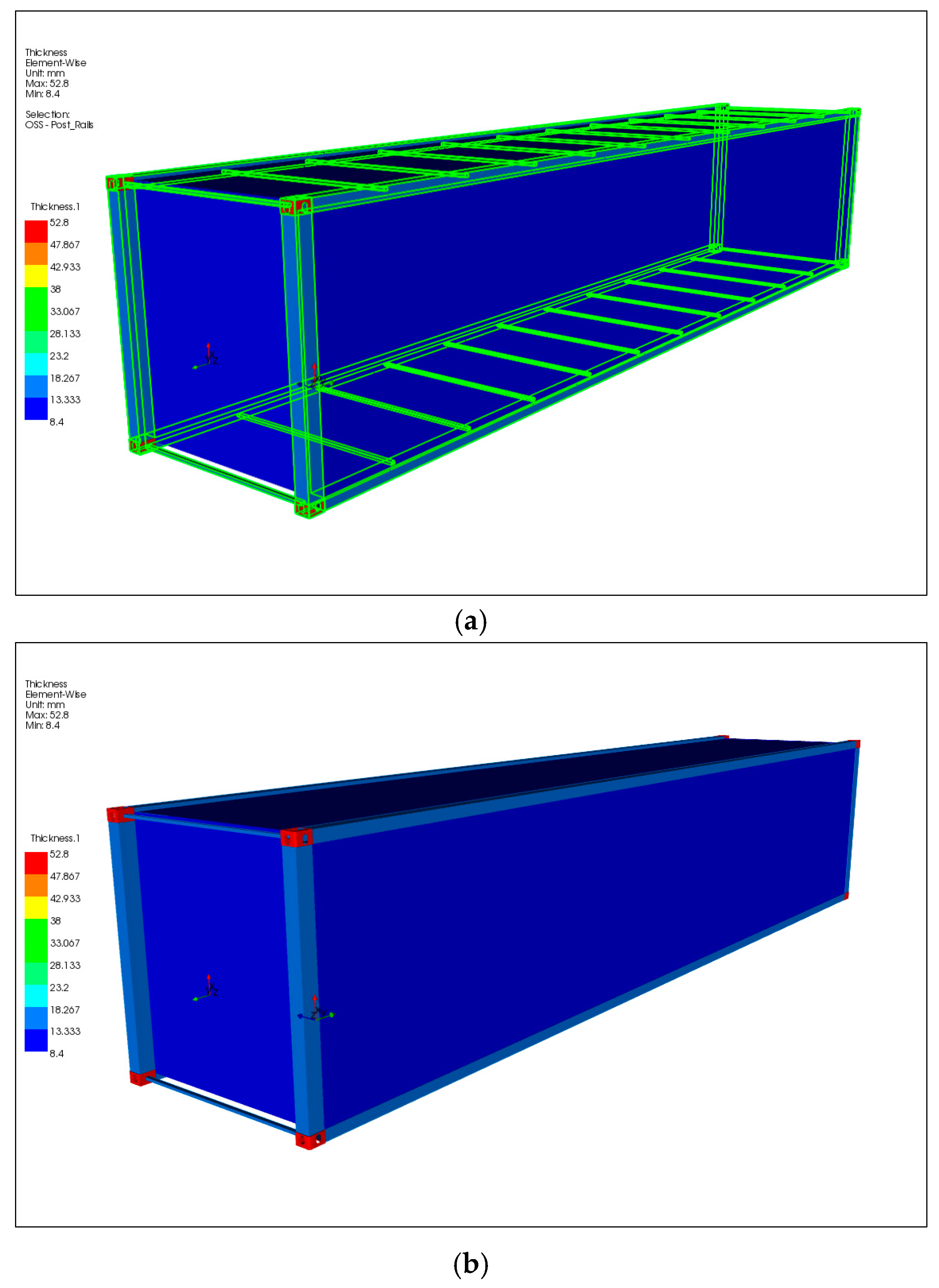
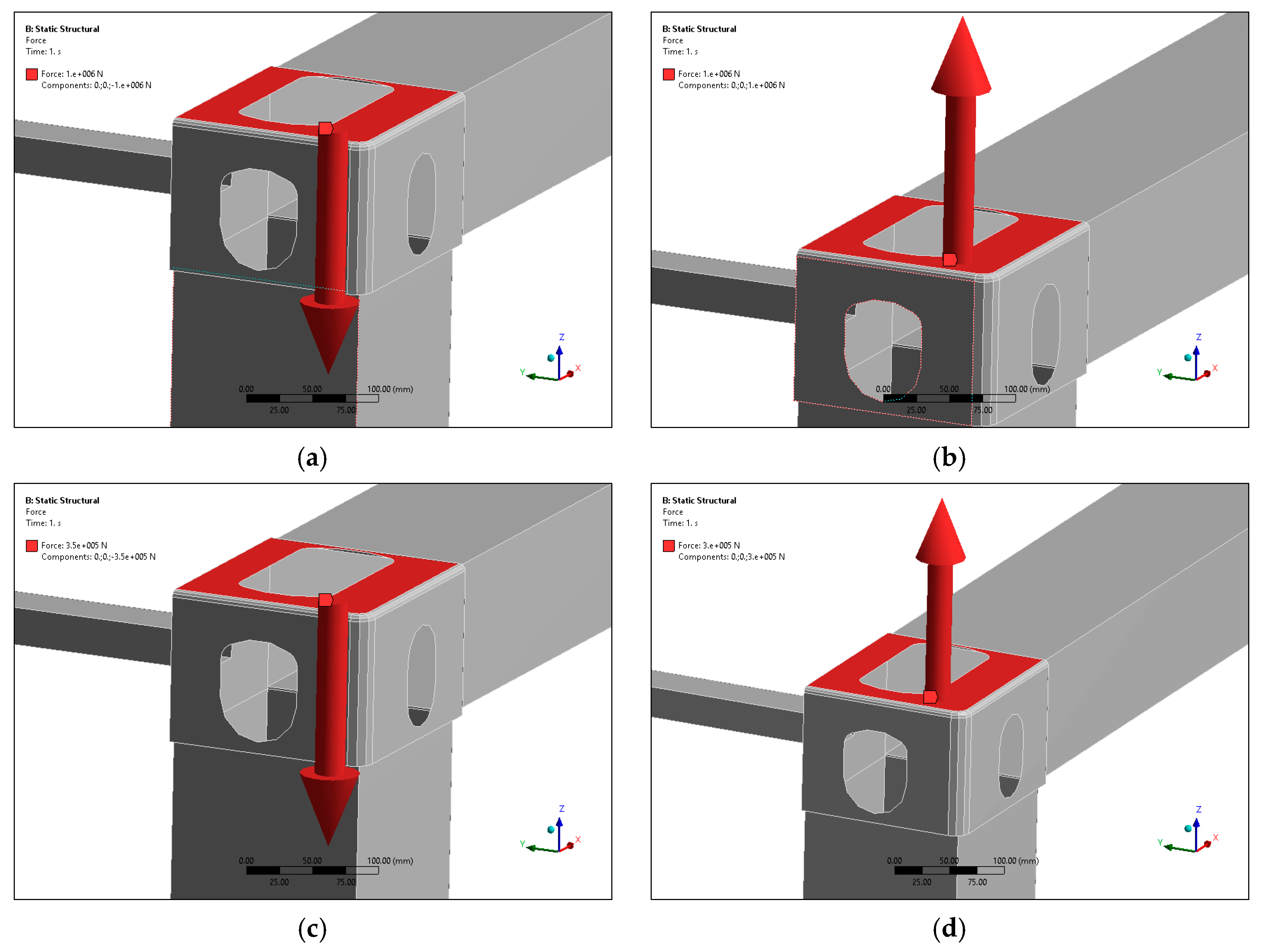
A standard ISO container is designed to support a weight of 192 tons stacked on its four corner posts. Since a container has four corner posts, each should be able to support at least
tons of weight. There is a total stack of 192,000 kg (192 t) on the bottom container, which is equivalent to eight containers of 24,000 kg (24 t). This means that a bottom container must support a stack of six fully-loaded 40-foot containers or eight fully-loaded 20-foot containers.
Table 1 provides more properties of standard shipping containers (see also
Table A1 and
Table A2 in the
Appendix A). Additionally, the standard ISO container is subjected to a dynamic G force of 1.8. Therefore, a composite container design must consider these basic values to be a viable replacement for a standard ISO container without compromising the current functionality; otherwise, it would collapse due to the stack weight (see
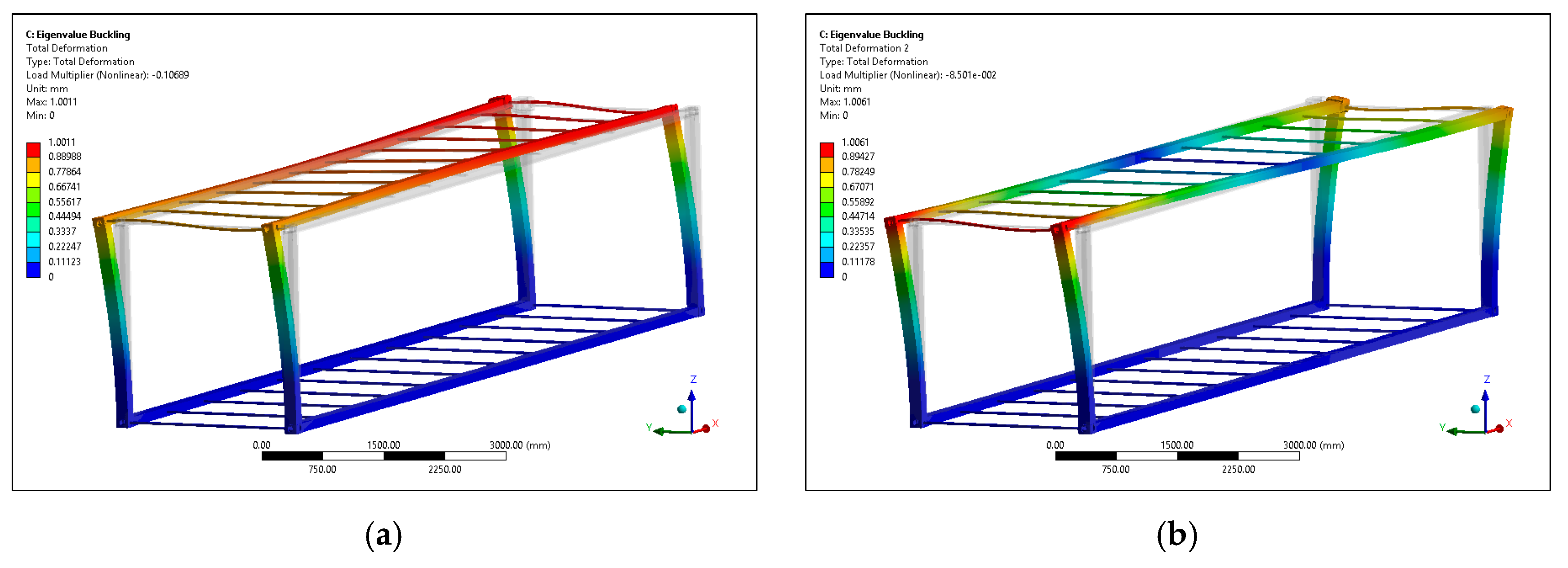
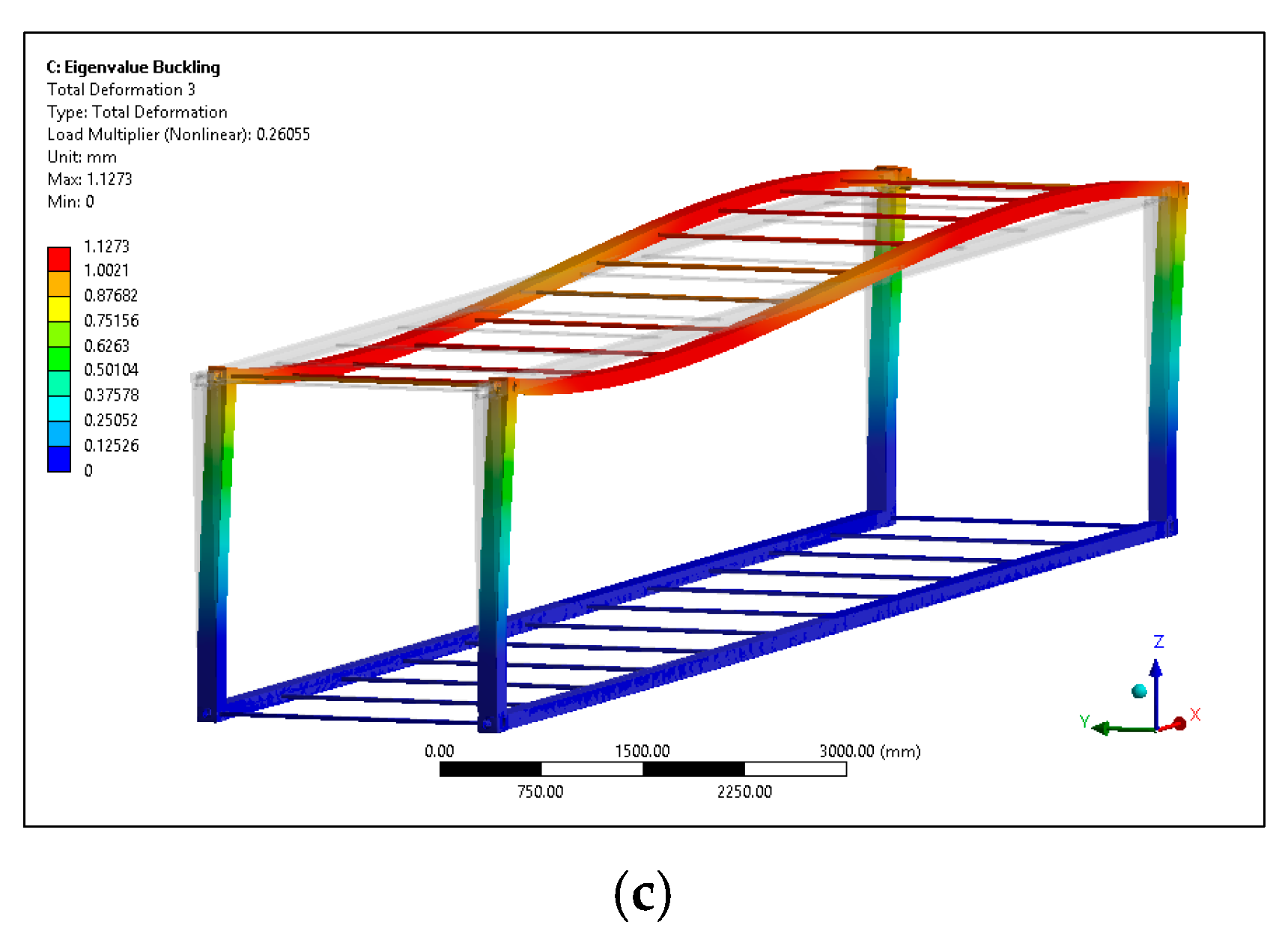
Figure 1a,b).
Composite materials are used to build the new generation of containers. The advantages and disadvantages of composites are explained by Campbell [
35]. The advantages of composites are numerous. They have a lighter weight; can adapt the installation to ensure an optimum strength and rigidity; show better fatigue resistance and corrosion resistance; and, with good design practices, can reduce the costs of assembly by lowering the number of parts and fasteners. The disadvantages of composites are their high raw material costs and generally high manufacturing and assembly costs; the adverse effects of temperature and humidity on them; their low resistance in the out-of-plane direction where the die supports the main load; their susceptibility to impact damage and the delamination or separation of layers; and the greater difficulty in repairing them compared with metal structures.
On the contrary, the corrosion resistance of composites can lead to significant savings in support costs [
35]. Carbon fiber composites cause the galvanic corrosion of aluminum if the fibers come into direct contact with the metal surface; however, the bonding of a layer of glass fabric electrical insulation to all interfaces in contact with the surface aluminum eliminates this problem.
This study first presents the composite materials and layers used in the design of the composite container. Then, a static structural analysis is performed to test if the composite design of the container can handle extreme conditions. Thereafter, a buckling analysis is performed to investigate the critical loads of the composite container. Finally, a statistical analysis is presented to explore the data generated by the composite container model.
The initial container model is drawn using Rhinoceros 5, which is computer-aided design software. The curves and surface objects drawn by the software are mathematically precise. It is a free-form surface modeler and utilizes non-uniform rational B-spline (NURBS) mathematical models. Then, the shell geometry of the container design model is loaded, developed, and analyzed using ANSYS ACP 2019. For the 3D static structural and buckling analyses of the composite container model, ANSYS Mechanical APDL 2019 is used as the simulation platform. Except in simple cases, the equations governing static structural and buckling analyses are generally not suitable for analytical solutions. Therefore, to perform the analyses of the composite container, the domains are divided into smaller subdomains (consisting of geometric primitives, such as hexahedra/tetrahedra in 3D and quadrilaterals/triangles in 2D). The governing equations are then discretized and resolved in each of these subdomains. The design and simulations are performed on an Intel i7-6700 with 8 cores, 3.4 GHz CPU, and 24 GB of RAM.
The analysis presented hereafter follows these main steps. Firstly, the composite materials and layers used in this study are presented. Then, the methods and static structural and buckling analyses of the composite container are described. Finally, the statistical analyses are performed and statistical significances are reported.
3.1. Composite Materials and Layers
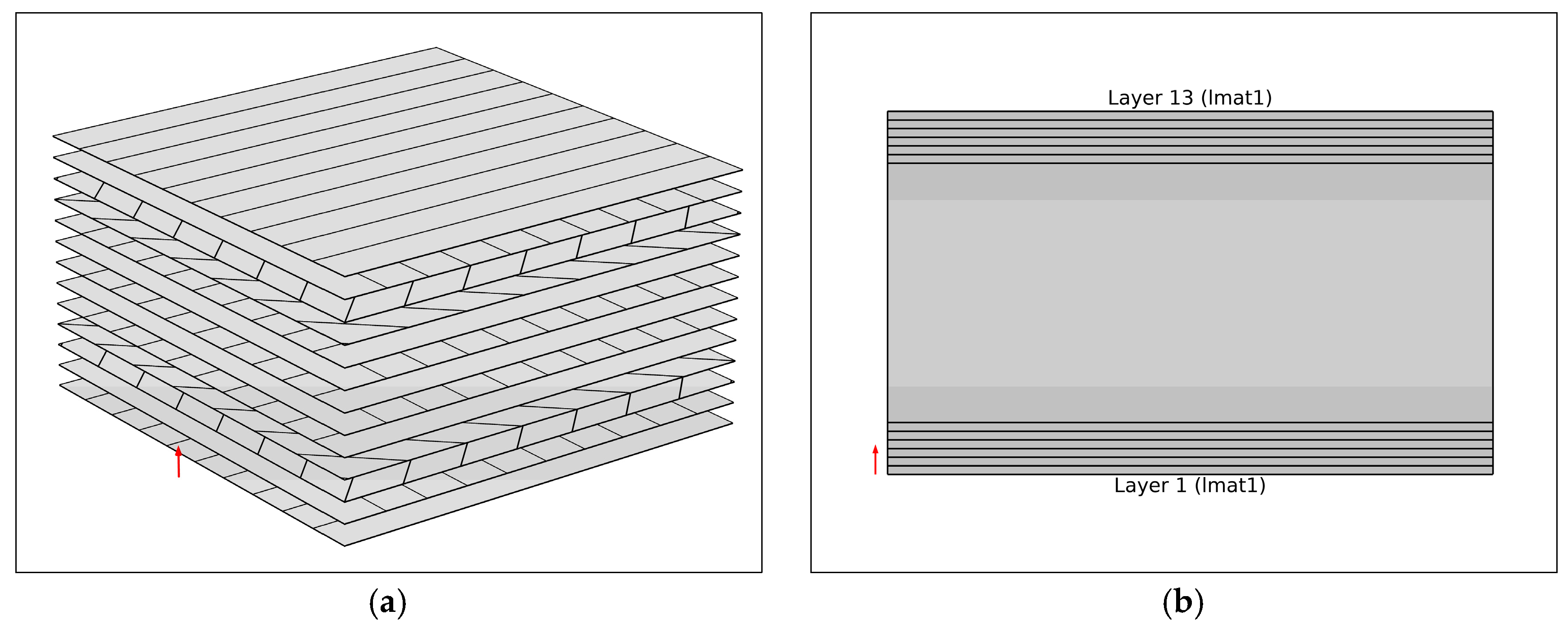
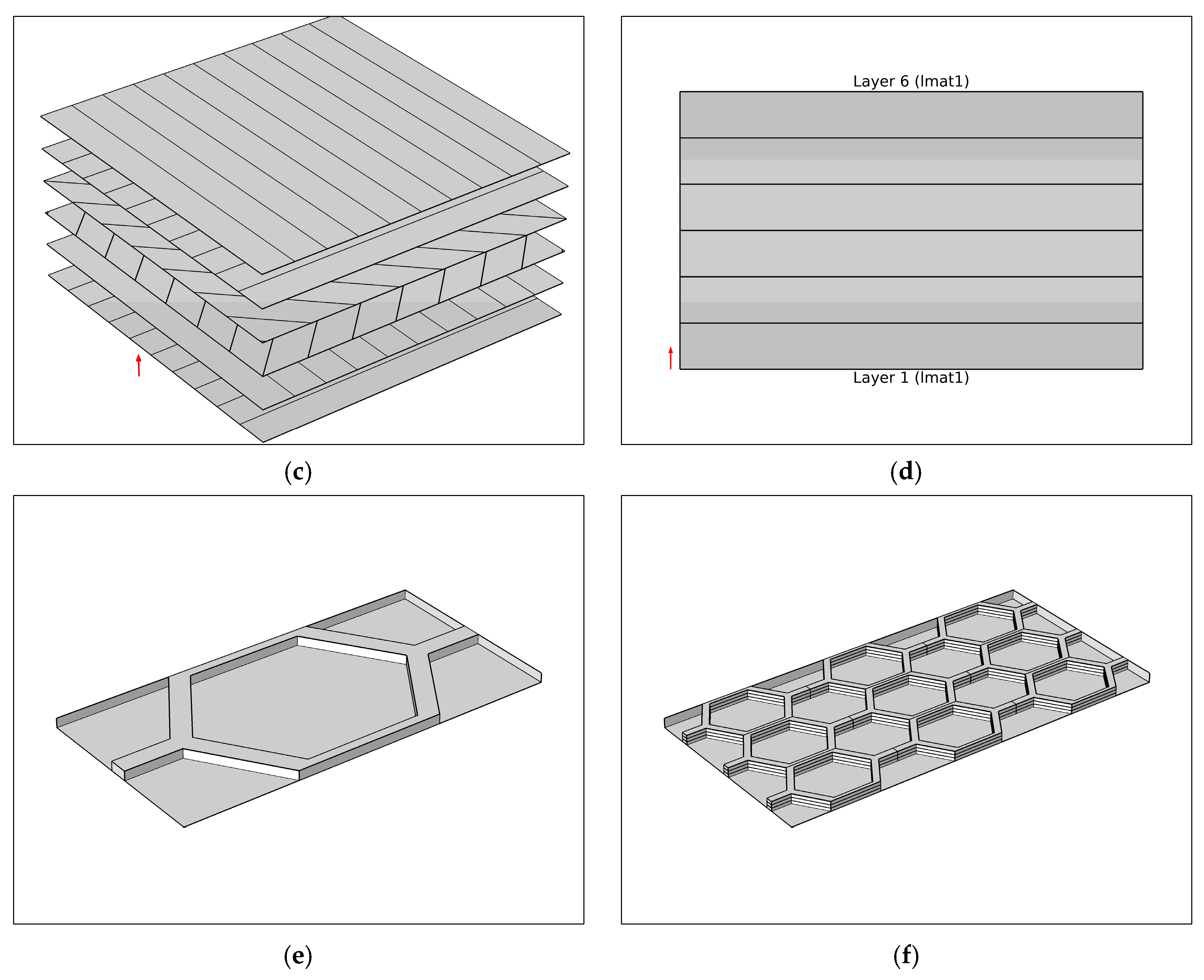
Two main types of composite laminates are used. These are the epoxy carbon unidirectional (UD) prepreg and honeycomb layer. A composite offers higher strength to weight and stiffness ratios than conventional materials [
36] (see
Figure 2). The sandwich construction, in particular the honeycomb construction, is extremely structurally effective, particularly in rigidity critical applications [
35]. Doubling the core thickness increases the rigidity by more than seven times with a weight gain of only 3%, while a quadruple core thickness increases the stiffness by more than 37 times with a weight gain of only 6% [
35].
Fiber composites can be viewed from two perspectives, namely micromechanics and macromechanics. Micromechanical analyses aim to explain the behavior of composites, typically those with UD fiber reinforcement, in terms of the fiber and matrix properties [
37]. Macro-mechanics is used to predict the strength and stiffness of composite structures, as well as other properties, such as distortion, based on the “average” properties of the UD material, namely the longitudinal modulus
, the transverse modulus
, the major Poisson’s ratio
, and the shear modulus in the
plane, as well as the appropriate resistance values [
37] (see
Figure 2).
In materials science, composite laminates are assemblies of layers of fibrous composite materials that can be joined to provide the required technical properties, particularly with respect to plane stiffness, flexural stiffness, strength, and expansion [
38]. A laminate is a stack of blades, as illustrated in
Figure 3, specifically oriented to achieve the desired result [
36]. The response of the laminate depends on the properties of each laminate, as well as the order in which the layers are stacked [
36].
In this research, quasi-isotropic and balanced laminates are used (see
Figure 3). The quasi-isotropic laminate is made up of six plies of identical materials. Quasi-isotropic laminates usually exhibit isotropic elastic behavior in the xy plane [
35]. In this research, a balanced and symmetric quasi-isotropic laminate is used (0°, 90°, 45°, –45°, –45°, 45°, 90°, 0°). When the ply configuration is made of equal numbers of plies at 0°, +45°, and 90°, the in-plane mechanical properties do not vary with loading direction and the composite is then said to be quasi-isotropic [
37]. A balanced laminate having equal numbers of plies in the 0°, +45°, –45°, and 90° directions is called a quasi-isotropic laminate because it carries equal loads in all four directions [
35]. For the additional properties of the epoxy carbon UD material, see
Table A3 in
Appendix A.
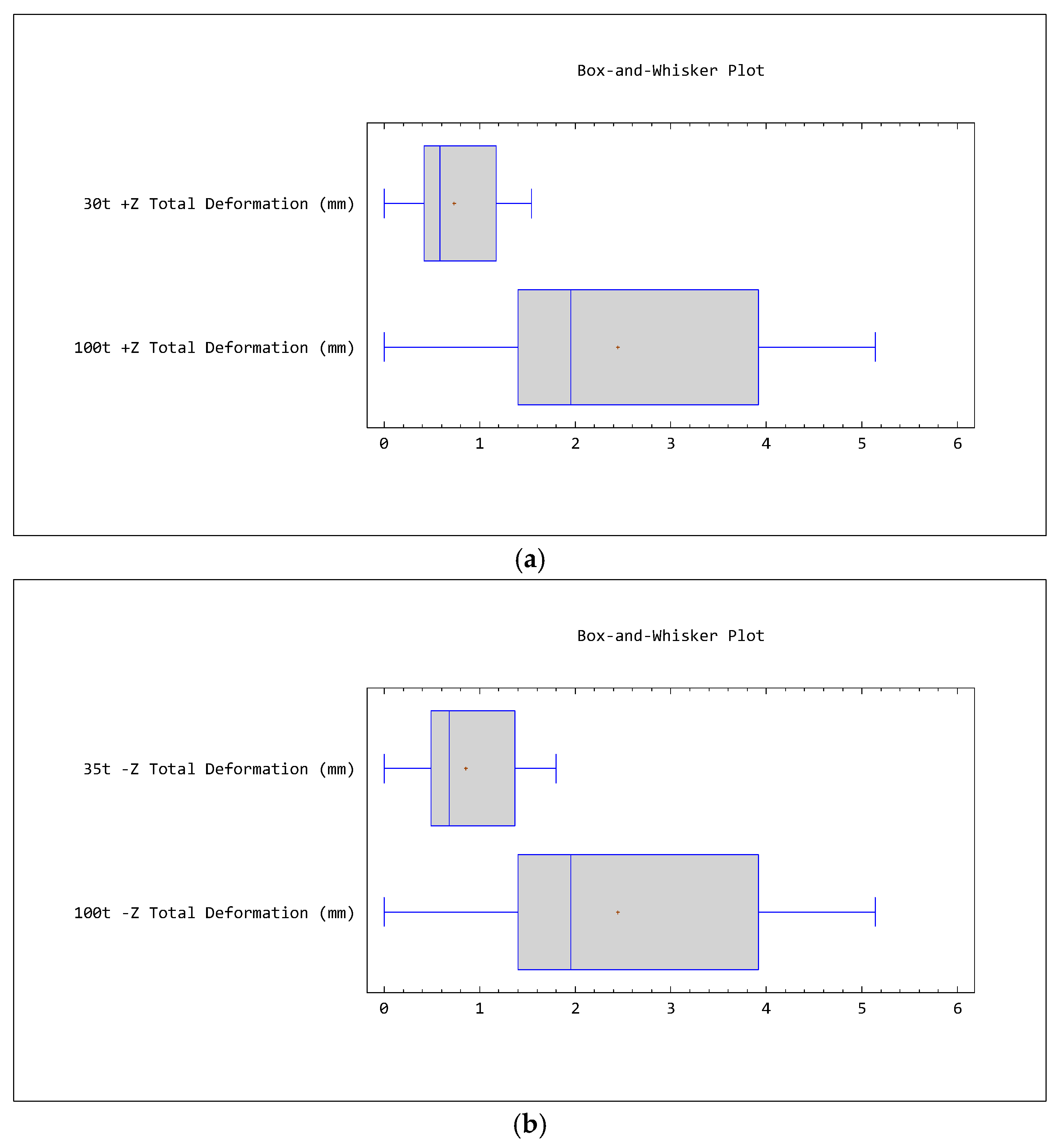
3.2. Static Structural Analysis
The static structural analysis is performed to observe the total deformation of the composite container. Structural analysis deals with stresses, strains, and deformations in engineering structures subjected to mechanical and thermal loads [
35]. In this analysis, only mechanical loads are tested. The analysis of composite structures is more complicated. Stress is associated with the strength of the material from which the body is made, while strain is a measure of the deformation of the body [
39]. Whenever a force is applied to a body, it will tend to change the body’s shape and size. These changes are referred to as deformation, and they may be either highly visible or practically unnoticeable [
39]. An increase in stress causes a proportionate increase in strain. This is known as Hooke’s law [
39], which may be expressed mathematically as
. Here,
represents the constant of proportionality, which is called the modulus of elasticity or Young’s modulus, while
is the strain [
39].
As the governing equations for a linear static analysis, the displacement vector is solved in the matrix equation as . Here, is a constant and is the stiffness matrix. In addition, small deflection theory is used and linear elastic material behavior is assumed. The vector represents the external forces statically applied when time-varying forces and inertial effects do not exist.
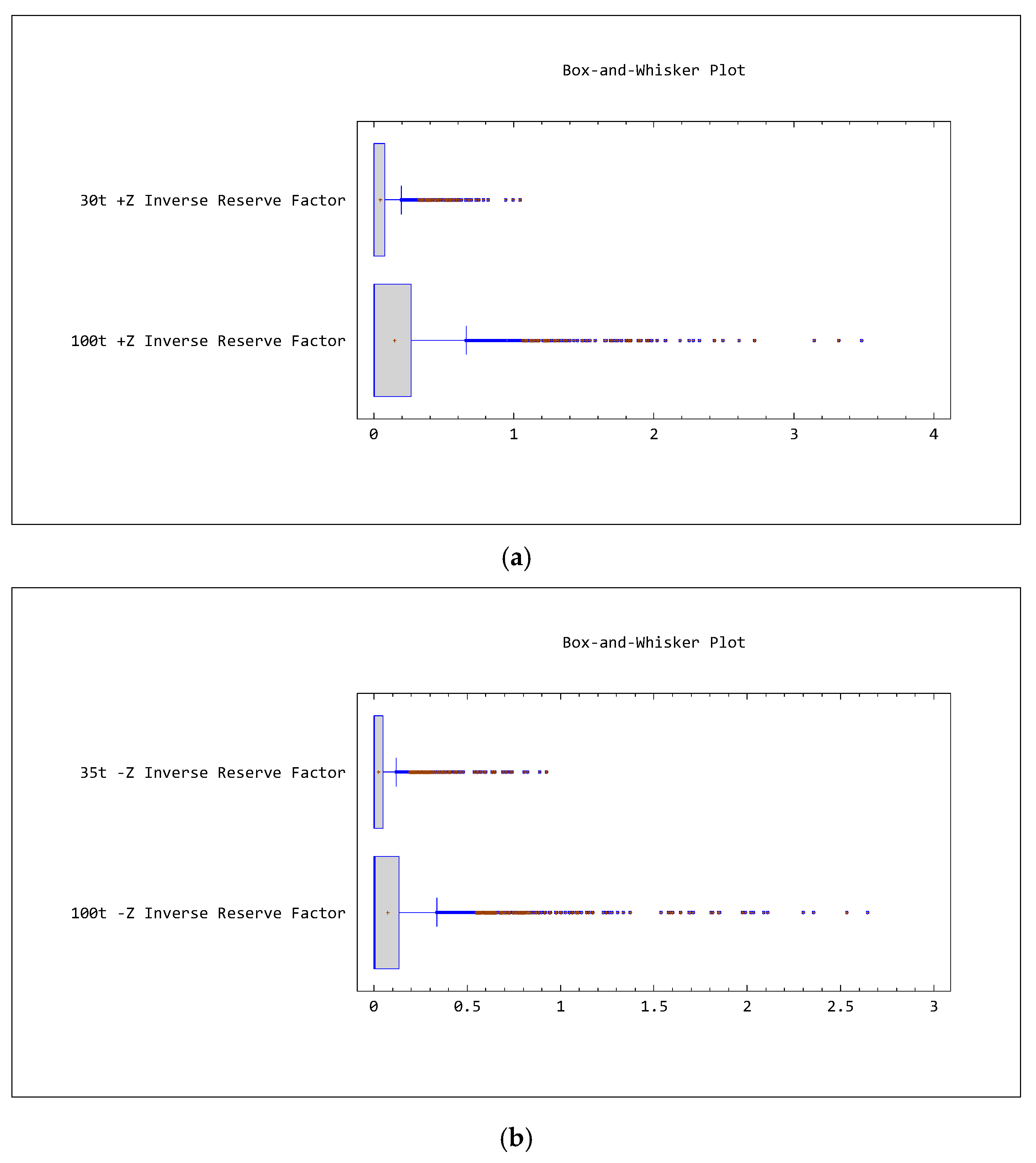
3.3. Buckling Analysis
The buckling analysis is performed to investigate the critical loads of the composite container. Long slender members subjected to an axial compressive force are called columns (here, the corner posts of the container) and the lateral deflection that occurs is called buckling. Because the buckling of a corner post can often lead to a sudden and dramatic failure of the composite structure, special attention must be paid to the design of corner posts so that they can safely support their intended loadings without buckling [
39].
As the governing equations are used to obtain the buckling load multiplier
, the eigenvalue problem for a linear buckling analysis is solved. The buckling mode
is defined as
. Here, the
and
matrices are constants. The assumption is that linear elastic material behavior exists, and nonlinearities are not included, as small deflection theory is used. Finally, the response based on the loading vector of
is a linear function of the buckling load multiplier
. The maximum axial load that a column can support when it is on the verge of buckling is called the critical load [
39]. The load multiplier is interpreted as
or
.
5. Conclusions
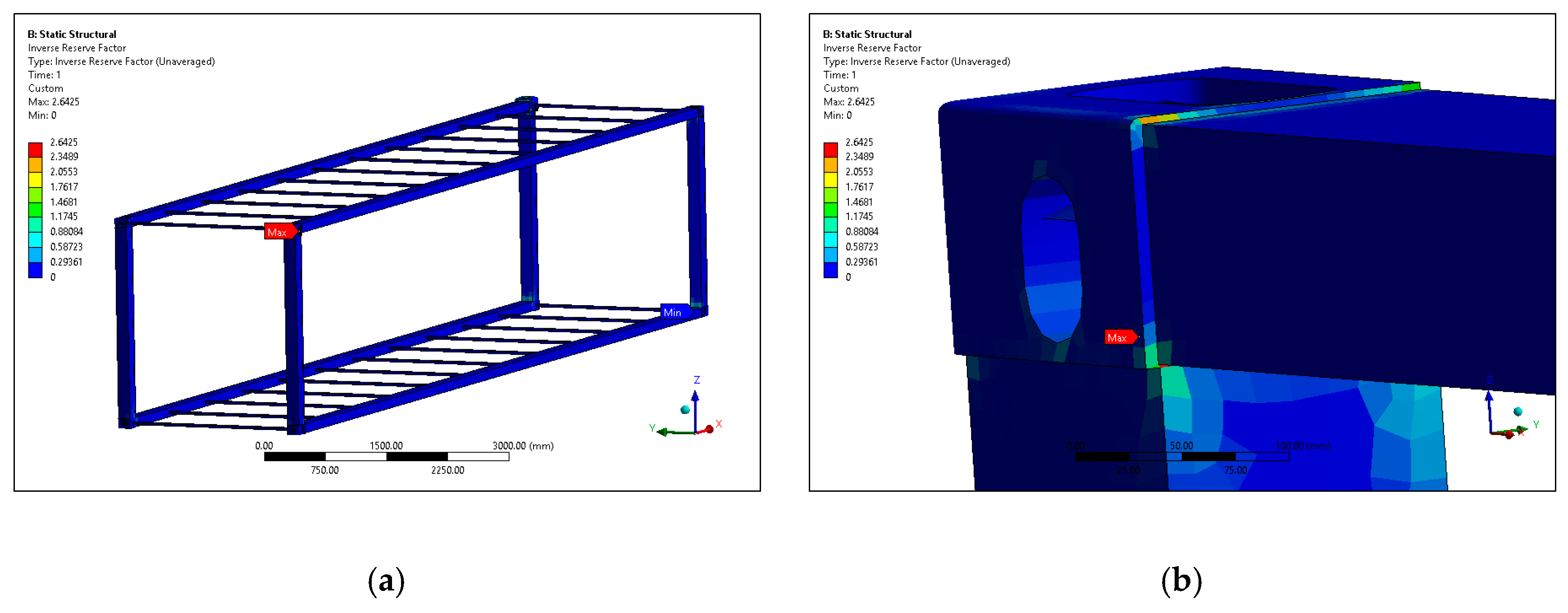
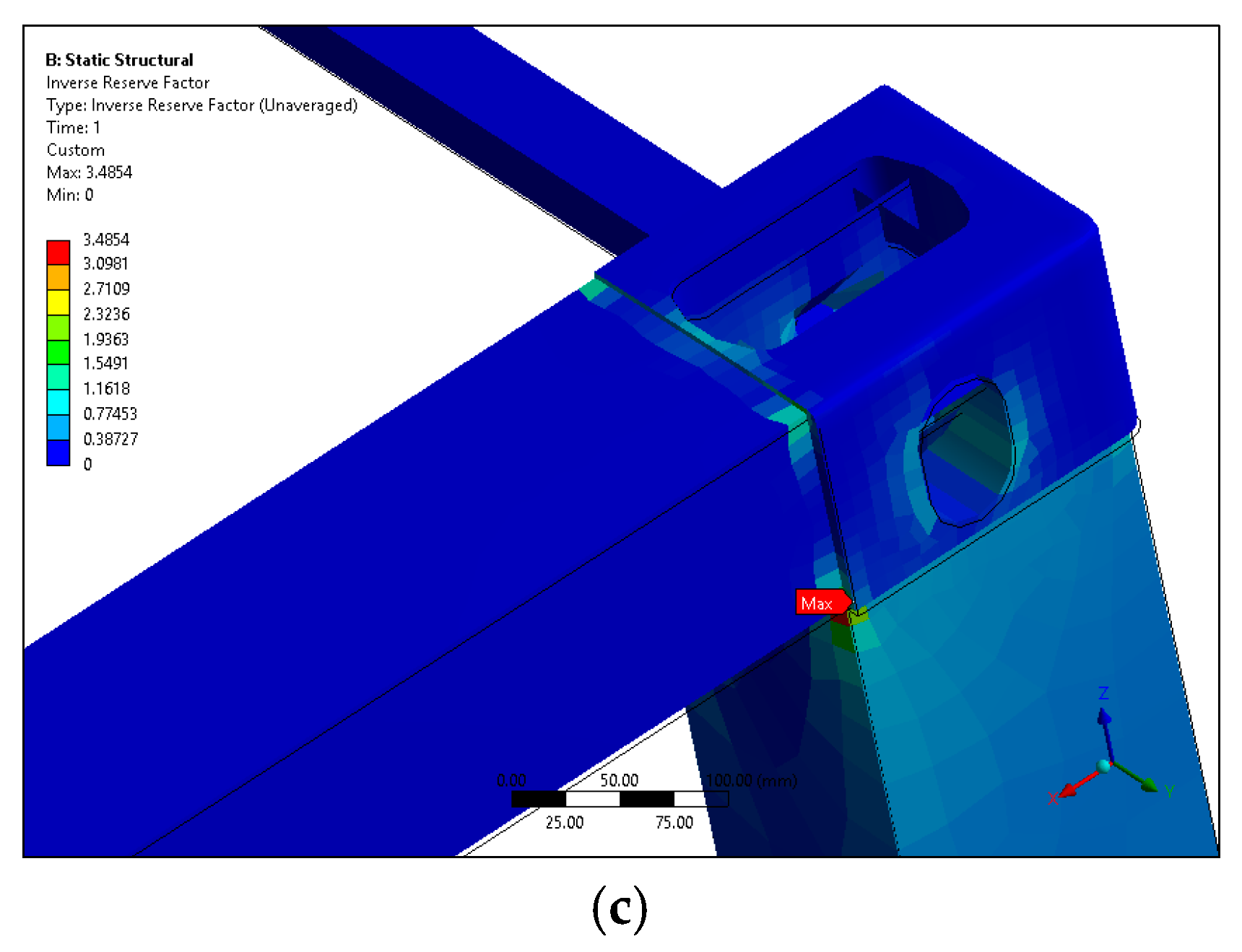
The presented modeling and simulations effectively demonstrated a promising new future for container transportation in the shipping and logistics industry. In this study, static structural and buckling analyses were used to test and verify the presented design, providing insight and inspiration for the replacement of traditional steel containers with composites. However, the analyses indicated that corner fittings should be further reinforced to handle the extreme conditions that occur when containers are lifted and stacked on top of each other.
The current research has limitations, as it only theoretically developed a composite container made of carbon fibers. In this research, optimization techniques are not utilized to significantly reduce the carbon fiber materials. However, a realistic composite container model is presented. On the contrary, the corner fittings of the composite container have emerged as an issue that must be addressed with a different approach. At corner fittings, numerous plies are needed to achieve the strength necessary not to compromise the strength of the traditional corner fittings of a steel container. The plies of the corner fittings should not be any thicker, which might prevent the fitting of twist locks. To overcome this issue, special carbon fiber layers with a significantly higher elastic modulus could be used to make fittings thinner.
Further research should be performed on the topologically optimized container to further reduce the composite materials used and thus the weight of the container. In addition, the panels of the composite shipping container could be replaced by cost-efficient glass fiber composite solutions such as E-Glass/S-Glass to reduce the unit cost. With aggressive optimization strategies for the container frame, weight reductions exceeding 80% over traditional steel containers might become possible. However, the optimized design must not compromise the strength, functionality, and structural integrity. Topology optimization might further complicate the composite container manufacturing process, which already involves complex challenges. Furthermore, composite material solutions in the manufacturing industry are highly labor intensive, which necessitates a qualified workforce along with the resulting high labor costs.