1. Introduction
In the modern world, technology plays an essential role in business management. One of the main reasons why many companies are poorly managed is because they do not utilize software effectively to manage their business operations. Regarding transportation, an increasing number of companies rely on commercial software to reduce the cost of transportation, as transport prices have increased exponentially over the decades (in Thailand, the logistic cost is currently 14% of the GDP (gross domestic product)). Despite the use of commercial software to attempt to reduce costs, this software is only applicable to certain businesses, as not all businesses have the same transportation needs. Many businesses that utilize commercial software that does not satisfy their business needs often underperform. Therefore, in order for businesses to perform effectively and efficiently, customized software can be integrated into the core of their business plan.
The process of software design comprises seven core steps. These include: (1) software identification and selection; (2) software initiating and planning; (3) analysis; (4) logical design; (5) physical design; (6) system implementation; and (7) system maintenance. The first four steps require the identification of the user’s needs and the discovery of effective solutions to construct a plan for an operative software that will be designed in the latter steps.
This research aims to find effective algorithms to solve a special case of the vehicle routing problem (VRP) (the first four steps of software design). This customized VRP has many attributes and functions in addition to already published algorithms or commercial software. The proposed case study is to design a customized operational software for a school bus pickup and delivery system with an annual budget of 10,619,250 baht to operate the entire system.
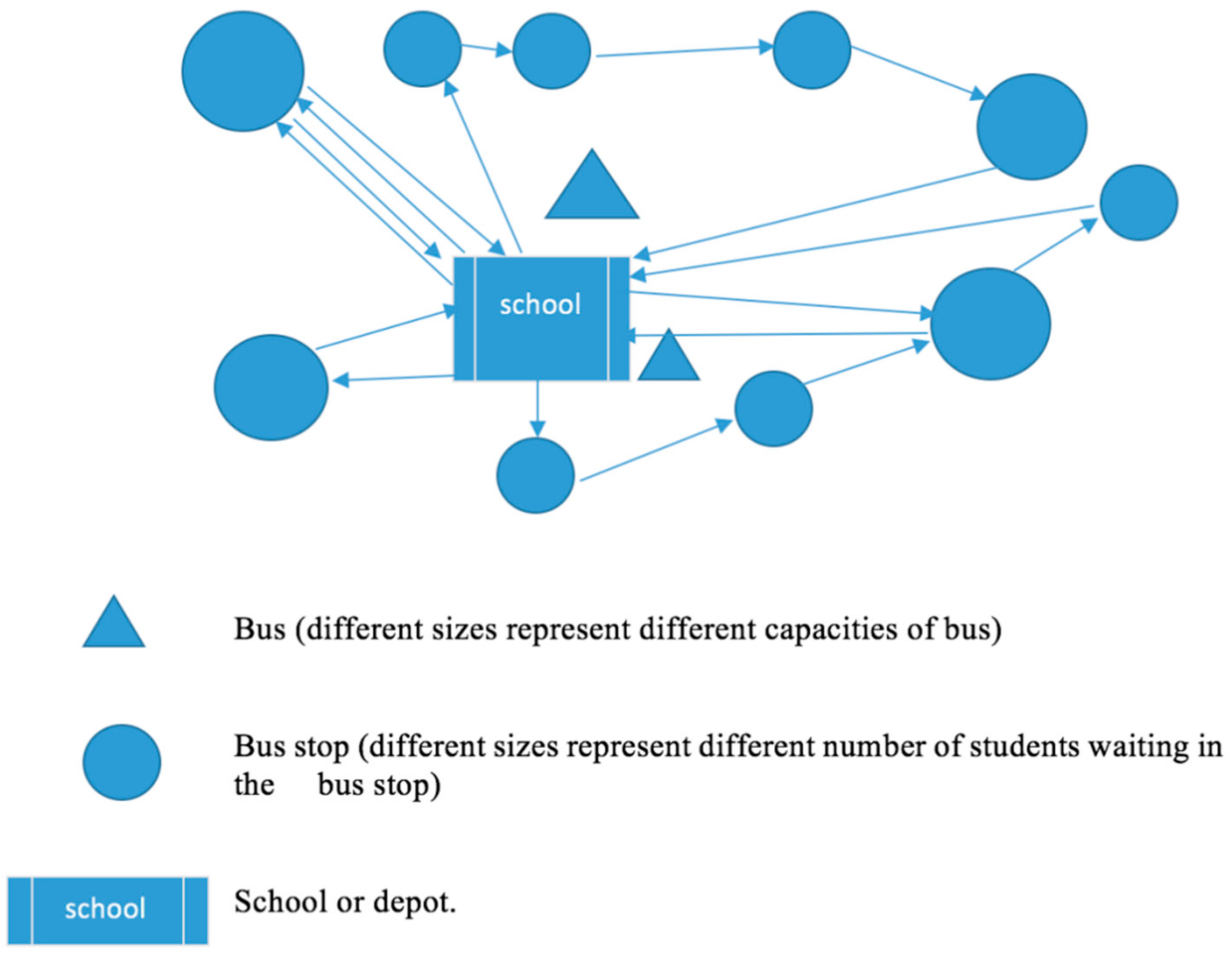
A school bus pickup and delivery system may seem to be an unproblematic system to manage. However, it is a complex system because it consists of many variables that need to be taken into account. Firstly, students need to be picked up from their nearest bus stops and delivered to school on time. Secondly, distances between students’ houses to bus stops must be of acceptable walking distances. Thirdly, the number of students assigned to a bus must not exceed its capacity. Lastly, the number of students assigned to a bus stop must not exceed its capacity. Once these variables are integrated into the simple VRP, the system becomes more complicated. Overall, the core rules that the system must satisfy are: (1) multiple fleets’ VRP; (2) exceed capacity at some pickup points (a bus stop can be visited by more than once); (3) longest time constraints; and (4) capacitated VRP. Despite these core rules, the service of the school bus needs to be good enough so that there would be no complaints from the parents.
The classical VRP was first introduced by Dantzig and Ramser [
1] in the article “Truck Dispatching Problem”. Using a specific customized algorithm, they determined how a fleet of homogeneous trucks could serve the demand of multiple gas stations from a central hub while minimizing the distance traveled. Current VRP models are immensely different from the one introduced by Dantzig and Ramser [
1], and Lenstra and Rinnooy [
2] asserted that VRP is an NP-hard problem.
Various types of VRP have been consecutively proposed after Dantzig and Ramser [
1], such as a VRP with time windows, a VRP with heterogeneous fleets, or the multiple depot heterogeneous vehicle routing problem with time windows [
3,
4,
5]. The studies by Braekers et al. [
6] and Braelers et al. [
7] give an overview of a scenario and its associated physical characteristics problems, extending the basic incapacitated VRPs that have been considered most often in review articles.
VRP is one type of network and communication problem; in the new era, many applications of network problems have been studied. The objective function can have a single objective, multiple cost terms, or multiobjectives. Tsiropoulou et al. [
8] and Tsiropoulou et al. [
9] presented a joint interest in the physical and energy-aware clustering and resource management framework of the of machine-to-machine (M2M)-driven Internet of Things (IoT). Lin and Gerla [
10] described a self-organizing, multi-hop, mobile radio network that relies on a code-division access scheme for multimedia support. Wu et al. presented a good survey of the communication area [
11]. The reader can find excellent reviews of vehicle routing problems in Kim et al. [
12], Karakatič and Podgorelec [
13], Gupta and Saini [
14], and Braekers et al. [
6].
The case study, the school bus pickup and delivery problem, is one special case of VRP. This problem focuses on the heterogeneous fleets’ vehicle routing problem excessive demand of the vehicle at the pickup point, and the longest time constraint (HFVRP-EXDE-LTC), which is not mentioned in the previous literature.
There have been many publications that have proposed methods to solve this problem, such as tabu search [
15], the evolutionary algorithm [
16], and the genetics algorithm [
17,
18]. Differential evolution (DE) algorithms are widely used to solve many problems, including VRPs such as Pitakaso [
19], Pitakaso and Sethanan [
20], López et al. [
21], Liao et al. [
22], and Liao et al. [
23]. Hou et al. [
24] presented a discrete DE with modified process operators. Dechampai et al. [
25], Akkararungruangkul, and Kaewman [
26] proposed a DE to solve the capacitated VRP with the flexibility of mixing pickup and delivery services and the maximum duration of a route in the poultry industry. Boon et al. [
27] uses DE to solve the capacitated vehicle routing problem by combining it with local search techniques. The DE is more effective if the local search is included, but it increases the computational time [
28]. The DE is modified by adding some more processes to the original version such as a recombination process, reborn process, and reincarnation process to get better solutions [
29,
30,
31,
32,
33]. These processes can improve the solution quality of the original DE due to it enhancing the search capability of the original system. From the computational result of the proposed DE, it outperformed all of the other heuristics while solving the same problem. Thus, DE was one of the heuristics selected to solve the case study in this article.
The adaptive large neighborhood search (ALNS) was introduced by Shaw [
34] for the capacitated vehicle routing problem (CVRP). Later on, ALNS was widely used in various problems, including Aksen [
35], which was a study of a selective and periodic inventory routing problem (SPIRP). Azi et al. [
36] proposed an ALNS for solving a VRP with multiple routes (VRPM). Emec et al. [
37] presented new removal, insertion, and vendor selection allocation mechanisms. Ribeiro and Laporte [
38] proposed an ALNS for solving the cumulative capacitated vehicle routing problem (CCVRP). Hemmelmayr et al. [
39] proposed an ALNS heuristic for the two-echelon vehicle routing problem (2E-VRP). The results of ALNS when applied to all of the problems outperformed the previously proposed algorithms, and thus, the ALNS was the second heuristic that we selected to solve the presented case study.
From the literature review, the DE has been proposed to solve various types of combinatorial problems, and it outperforms all of the previous algorithms due to it being fast and effective, as shown in Pitakaso [
19], Pitakaso and Sethanan [
20], López et al. [
21], Liao et al. [
22], Liao et al. [
23], and Hou et al. [
24]. ALNS has been developed to solve mostly network problems such as VRP, and it is very flexible when it comes to designing algorithms to solve the proposed problems, as shown in Aksen [
34] and Emec et al. [
37]. The proposed problem is the heterogeneous fleets vehicle routing problem with excessive demand of the vehicle at the pickup point, and the longest time constraint (HFVRP-EXDE-LTC), whereby the new, modified DE algorithm and ALNS were designed to solve this new class of VRP. We select these two algorithms due to their flexibility, easy modification, and use of only a few parameters. Moreover, these two metaheuristics have been successfully used in many combinatorial optimizations.
This paper covers five sections.
Section 1 is the introduction.
Section 2 is the definition of the problem and the best practices procedure that is currently used. The proposed heuristics are shown in
Section 3, while the computational results and the conclusion and outlook are shown in
Section 4 and
Section 5, respectively.
4. Computational Result and Framework
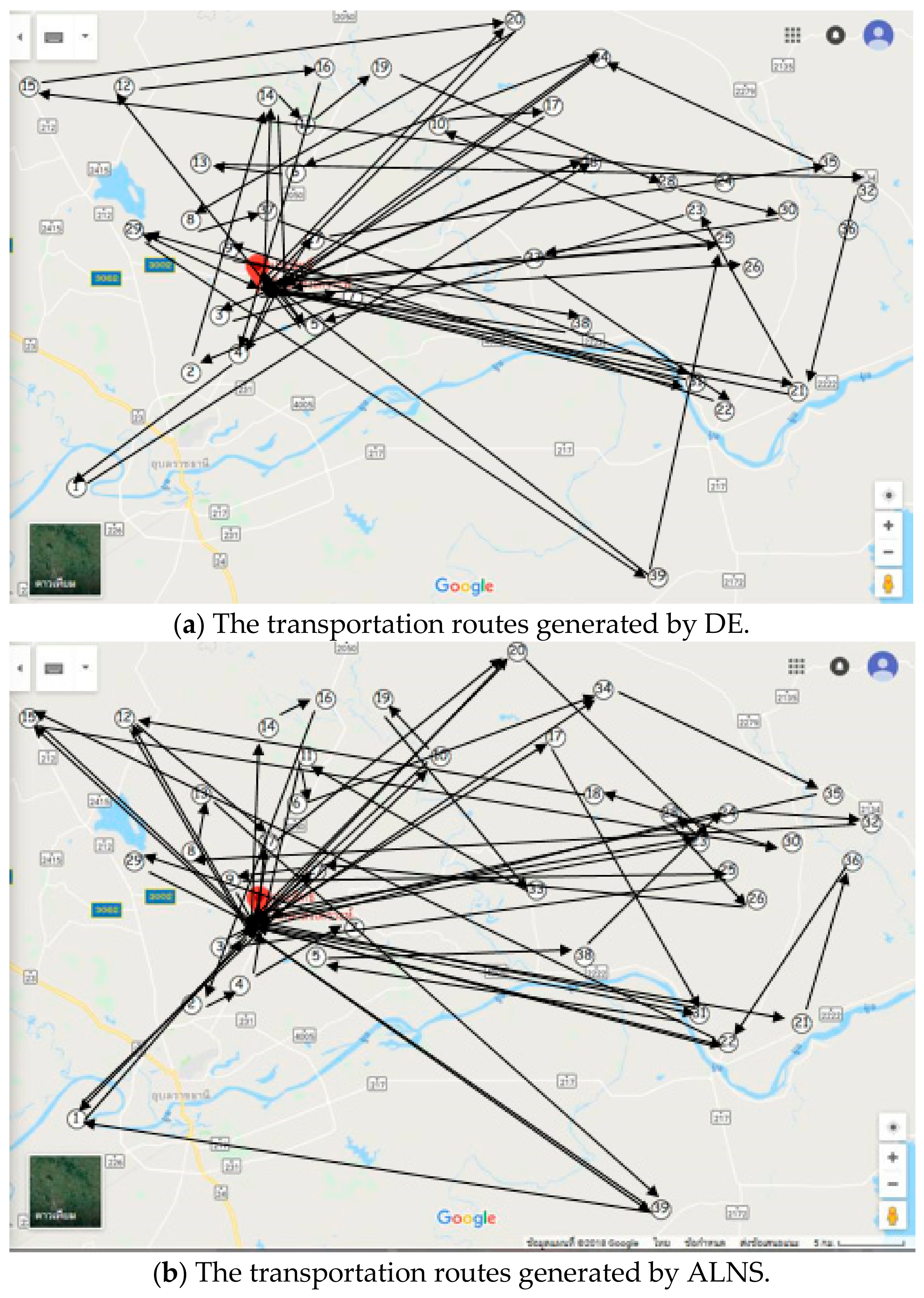
DE and ALNS were tested using 10 small instances and a single case study. The parameters of the test instances were randomly generated using uniform distribution. Distances between the bus stops were randomly generated from 5 km to 25 km. The capacity of the bus had three levels, which were 25 seats, 40 seats, and 60 seats. The number of available buses was set to have 30% of the total capacity of the buses. The number of students at each bus stop was set to be within the range of 10–100 students. The simulation was executed five times and the best solutions among all five results were drawn to be the representative of the algorithm. The simulation was conducted on a Computer Notebook Core™ i5-2467M CPU 1.6 GHz. The stopping criteria was the run time limitation, which was set to 10 min. The computational result of the 11 test instances is shown in
Table 6.
From
Table 6, we can see that in DE, there were three out of 11 instances that achieved the lowest cost, while ALNS could achieve the lowest cost in nine instances. We can see that the proposed heuristics achieved better solutions in all of the cases. Furthermore,
Table 7 shows the percentage difference (% diff) of each method. It is the difference between
H1 and
H2, and it can be calculated using Formula (6), where
H1 and
H2 are used in the current practice method, DE, and ALNS.
From
Table 7, we can see that the DE and ALNS generate 9.79% and 8.89%, respectively, lower costs than the current practice. When comparing the proposed heuristic DE to ALNS, we can see that ALNS has a lower cost than DE by 0.99%.
Table 8 represents the significance test of all of the heuristics, with a 95% level of confidence using the Wilcoxon signed rank test. The results shown in
Table 8 shows that the DE and ALNS results are significantly different from those of the current practice procedure. ALNS is also significantly different from that of DE.
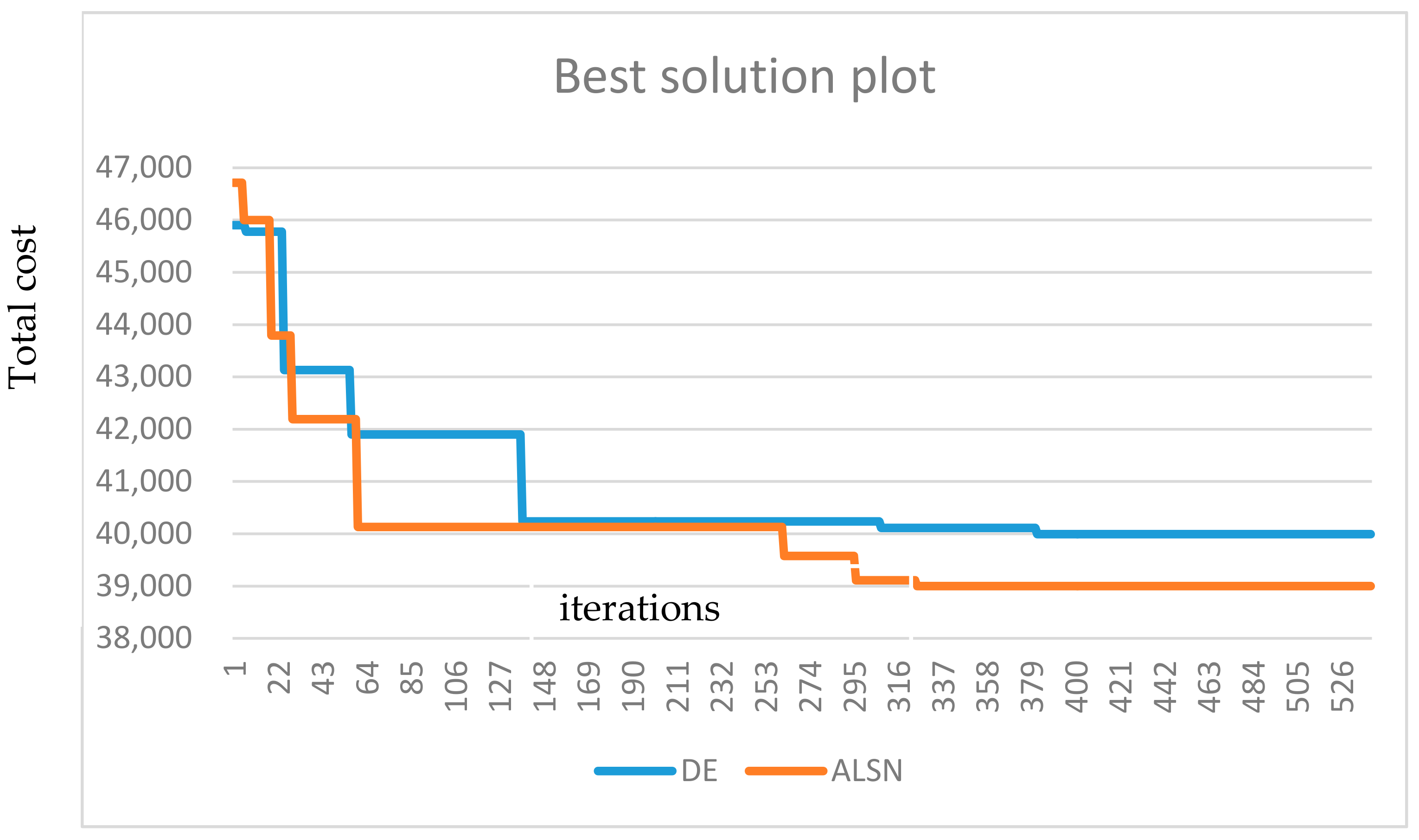
Figure 3 and
Figure 4 show the nature of DE and ALNS in finding the solution for the case study. We can see that DE was better at searching for a good solution during the simulation run, while ALNS was more effective at finding a good solution. When the iteration was high, DE seemed to stick to the same local optimal, but ALNS made changes to the solution, which means that it had a better way than DE to escape from the local optimal solution.
5. Conclusions and Outlook
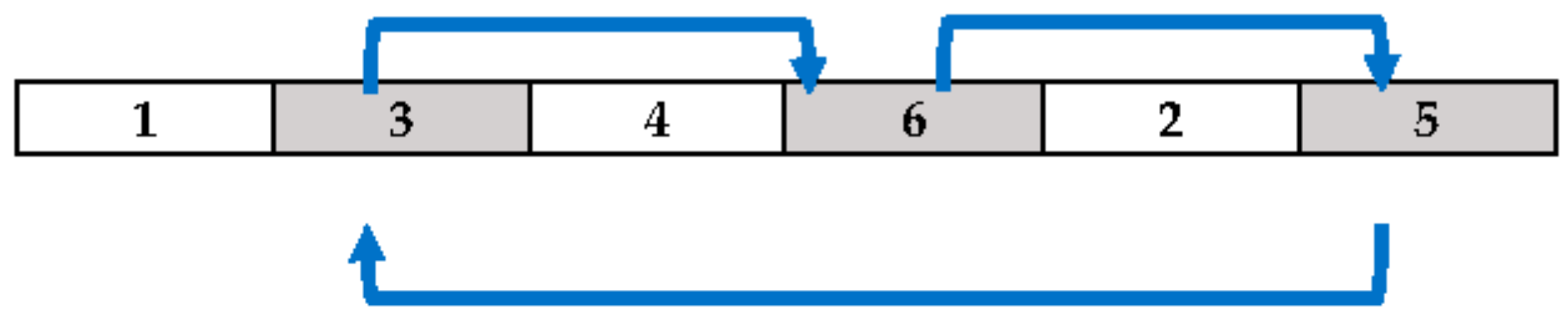
This paper presents a methodology to solve a special case of VRP, which makes simple VRP into a complex NP problem. We presented two metaheuristics, which were the differential evolution (DE) algorithm and the adaptive large neighborhood search (ALNS). DE was used to optimize the sequence of the bus stops that were assigned to buses that were randomly selected one at a time by roulette wheel selection. The attractiveness of the bus is the score of the bus, which is iteratively updated due to the quality of the solution contributed by the bus. In ALNS, six destroy methods and four repair methods were presented.
From the computational results, we can see that the proposed heuristics outperformed the best practices currently used in school systems. DE had an 8.89% lower cost than that of the current practice, while ALNS had 9.79% lower cost than that of the current practice. Calculations of the annual operational costs showed that DE could reduce the cost by 757,250 baht, while ALNS could reduce the cost by 906,750 baht from the current practice. When comparing the two proposed heuristics, ALNS had a lower cost than DE by 0.99% because ALNS had a mechanism that was better at escaping from the local optimal.
DE needs to add a local search or a restarting behavior so that it can find a better way to escape from the local optimal. ALNS may find a better solution if a variety of destroy and repair methods are applied.
The proposed heuristics are used as a tool in the development of effective and efficient user-friendly software. In addition to being effective and efficient, the software needs to be customized to satisfy customer needs. This is done by elucidating an effective algorithm to find solutions to satisfy customer needs. This research only shows the effectiveness of DE and ALNS in finding the most efficient solution. Future research should focus on satisfying customer needs. This may involve conducting primary research to identify what customers want and applying the findings to the algorithm.
Currently, the new emergent technology has been introduced to real-world situations regarding vehicle such as the driverless vehicle or the autonomous cars. It is composed of various up-to-date technologies such as radar, laser light, GPS, and computer vision. The advanced control system will be used to control the moving and routing of the car that is needed. The navigation system is necessary for this type of car to have the shortest, fastest, and cheapest route for the owner. Therefore, when the vehicle starts from the depot, without the driver, a good routing system will be calculated and used to control the car. When the car starts, it needs to move in such a way that the navigation system is shown, hence a fast and effective algorithm to show which route the vehicle have to travel is needed. Therefore, this research is applicable and suitable to install in the main brain of the driverless car so that it enhances the capability of the vehicle.