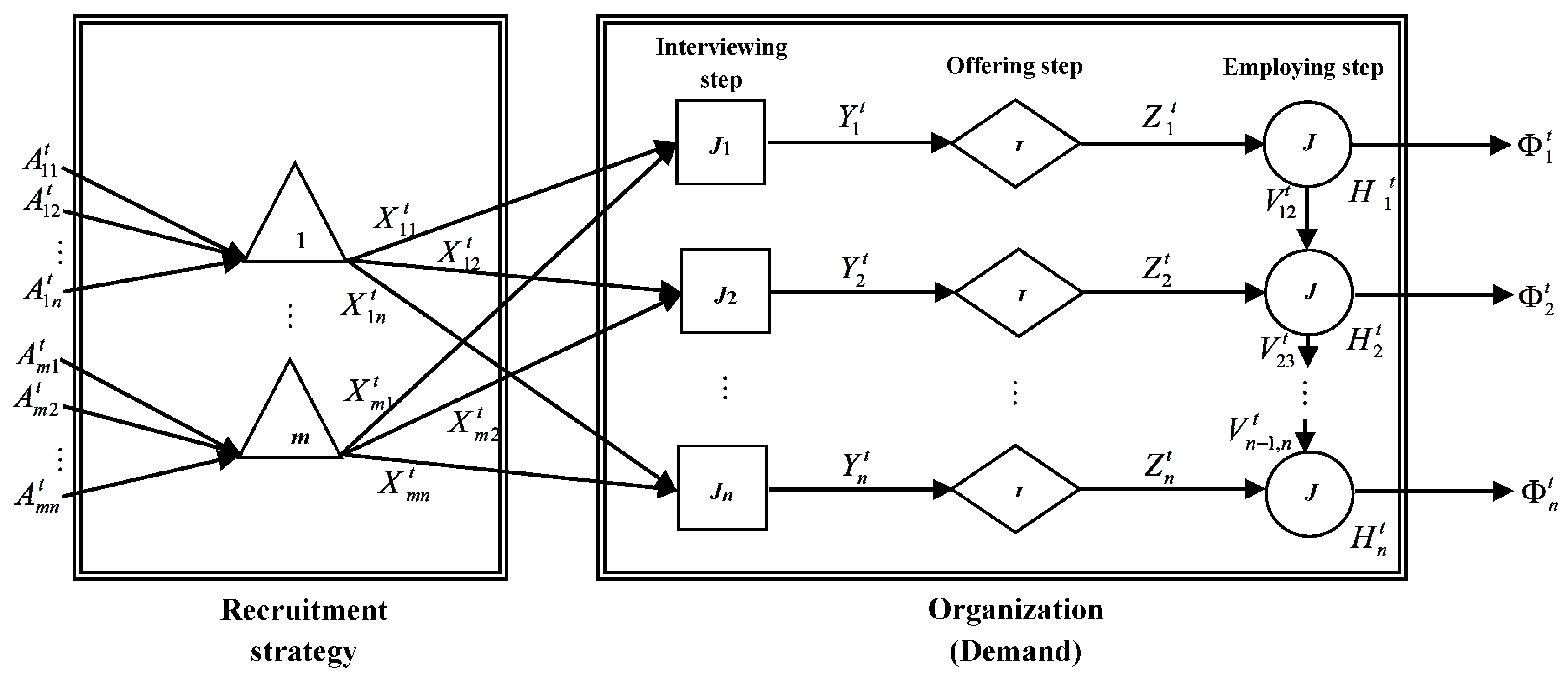
5.1. Linearization
The programming model developed in the preceding section is a multi-period mixed integer
nonlinear problem, which might arise hardships to be solved. To conquer any of such difficulties, we linearize nonlinear terms that are present in the objective function and constraints by some mathematical programming techniques [
39,
40] and obtain an equivalent mixed integer
linear programming (MILP) model.
The absolute term appeared in Objective Function (11), i.e., , can be eliminated from the model by substituting with a new integer variable and adding two constraints as and . Consequently, the integer decision variable is multiplied by binary variable in the last term of the objective function. Now, the product denoted by can be linearized by adding the following four constraints: , , and for . Such a linearization is authentic because if , then the first two constraints imply that , and if , then the last two constraints gives .
Another nonlinear term in the objective function is in which and are continuous and integer decision variables, respectively. Assuming with respect to Constraints (19) and (20), we determine a bound on as . In this case, the integer decision variable is characterized as follows: along with the constraint , where and for . Now, the abovementioned nonlinear term is rewritten as , which contains multiplication of the continuous variable by the binary variable . To handle the current nonlinearity, we substitute by , i.e., , and add the following four sets of linear constraints: , , and for . We also use the later procedure to eliminate the nonlinearity appeared in Constraint (12).
Using some arithmetic on Constraints (14)–(16), an upper bound for is derived as . Based on the current upper bound, the products , and in Constraints (13) and (14) can be linearized in the same way as described above. In this case, is rewritten as , where for and , and . Moreover, the following four sets of linear constraints are added: , , and where for and . To linearize the next quadratic term, we rewrite as and then include the following four sets of linear constraints: , , and where for and . Ultimately, we linearize the last quadratic term by rewriting it as and imposing the following four sets of constraints: , , and where for and .
Constraint (16) can be transformed into two separate constraints as and for . We can linearize the product terms , and in these separate constraints in same way as described before.
Constraint (17) seems more complicated to be linearized because it contains a product of one integer and two continuous decision variables. We first handle the product of two continuous decision variables, i.e., , and introduce two new continuous variables and , where , , and . In this case, we rewrite the product as a separable function . The quadratic terms of the current separable function are then piecewisely linearized using three breakpoints, which sounds a good approximation because the feasible intervals of the quadratic terms are not too wide. In this case, using three breakpoints of 0, 0.5 and 1, we obtain where , , , , , and . In the same way, using three breakpoints of −1/2, 0 and 1/2, we have where , , , , , and . Consequently, the term in Constraint (17) is transformed into with respect to all added constraints above. The later term contains products of continuous and integer variables and hence, as explained earlier, can be fully linearized. Assuming with lower and upper bounds of −0.25 and 1, respectively, we write as , then substitute with and finally add the following four sets of linear constraints: , , and for .
According to Constraint (16), an upper bound for is obtained as . Hence, in Constraint (18), we linearize the quadratic term by replacing it with where , , and . In addition, based on Constraints (13) and (16), and that , an upper bound for can be obtained as where . Therefore, we substitute the product in Constraint (18) with where , , and .
We rewrite the quadratic term in Constraint (23) as , replace by and add the following four sets of constraints: , and for .
Finally, we transform Constraint (24) to three usual linear constraints as: , and for .
5.2. Stochastic Constraints
According to the theory of CCP, it might be possible to convert the stochastic constraints to their deterministic equivalents for the predetermined confidence levels. Then, the deterministic programming problem is solved by typical solution approaches. Although this procedure seems relatively difficult to employ and only successful for special cases, we explain how it is effectively utilized along with Lemma 1 to deal with the stochastic Constraint (17) after being linearized. Nonetheless, we should use the stochastic simulation to encounter the stochastic Constraint (12), because the aforementioned conversion to obtain its deterministic equivalent after linearization is not easily applicable on it.
Lemma 1. Assuming , the deterministic equivalent of in CCP model is derived as , where and is the inverse of cumulative distribution function [
37].
In the preceding section, we linearized the stochastic Constraint (17) as
along with some additional constraints, which are avoided being rewritten here. Manipulating this linear constraint results in:
Regarding
and
as
and
ξ, respectively, we derive the following expression based on Constraint (10) in CCP theory and Lemma 1:
where
is the cumulative distribution function of
. The latter expression can be further simplified as:
Now, we substitute the stochastic Constraint (17) with Constraint (32), which is its deterministic equivalent, in the proposed mathematical programming model. We could even more simplify Expression (32) providing that the stochastic variable followed a well-defined distribution function with a closed form cumulative distribution function. However, the exact distribution function of that can be exploited to derive its cumulative distribution function is available in rare situations. Therefore, we should infer in many cases the distribution function of from the available historical data. In such circumstances, the most fitted distribution function to the available data is estimated using statistical methods such as Chi-square or Kolmogorov–Smirnov test.
In addition, we linearized the stochastic Constraint (12) in the former section as
(again, we avoid citing the additional constraints here). Now, according to Constraint (10) in the CCP theory, we impose confidence level
on this constraint and rewrite it as follows:
For a very special case in which and are two independent stochastic parameters following normal distributions as and respectively, we are able to derive a deterministic equivalent to stochastic Constraint (33). In this case, we can prove that follows a normal distribution with mean and variance of and , respectively. Now, we can follow a somewhat similar argument in Lemma 1 to derive a deterministic equivalent to Constraint (33) as , where and denotes the inverse of cumulative distribution function of a standard normal random variable. In this case, we substitute the stochastic Constraint (12) by the deterministic constraint in the developed programming model.
However, the aforementioned very special case restricts us to a couple of strict assumptions: having independent random variables
and
, and following the normal distributions. Based on the definitions of
and
in
Section 4, we might not be able to infer in every situation that these two random variables are naturally independent to each other. More importantly, there might be lots of cases in which these two random variables do not follow a normal distribution. In such conditions, it might be extremely arduous to extract deterministic equivalent to the recently added stochastic Constraint (33). Instead, it is recommended applying Monte Carlo stochastic simulation. In the literature, there are several studies suggesting Monte Carlo stochastic simulation incorporated with genetic algorithm (GA) for solving chance constrained programming [
41,
42,
43]. Meanwhile, we implement this kind of simulation in this paper using Lingo 16 optimization software [
44], which provides us with a very suitable facility to handle the stochastic Constraint (33). In this regard,
Appendix A, Part (a) presents the required built-in functions of Lingo 16 software to generally model a chance-constrained programming problem.