Integrating Cacao Physicochemical-Sensory Profiles via Gaussian Processes Crowd Learning and Localized Annotator Trustworthiness
Abstract
1. Introduction
- –
- Construction of the LUKER-CACAO database, aligning standardized physicochemical measurements with sensory annotations from multiple expert panelists.
- –
- Application of the MAR-CCGP framework to learn latent ground truth sensory scores and context-dependent annotator reliability through a shared latent factor model from noisy multiple annotator regression data.
- –
- Development of a localized annotator trust score, leveraging the model’s posterior distribution to assess reliability per annotator and per sample.
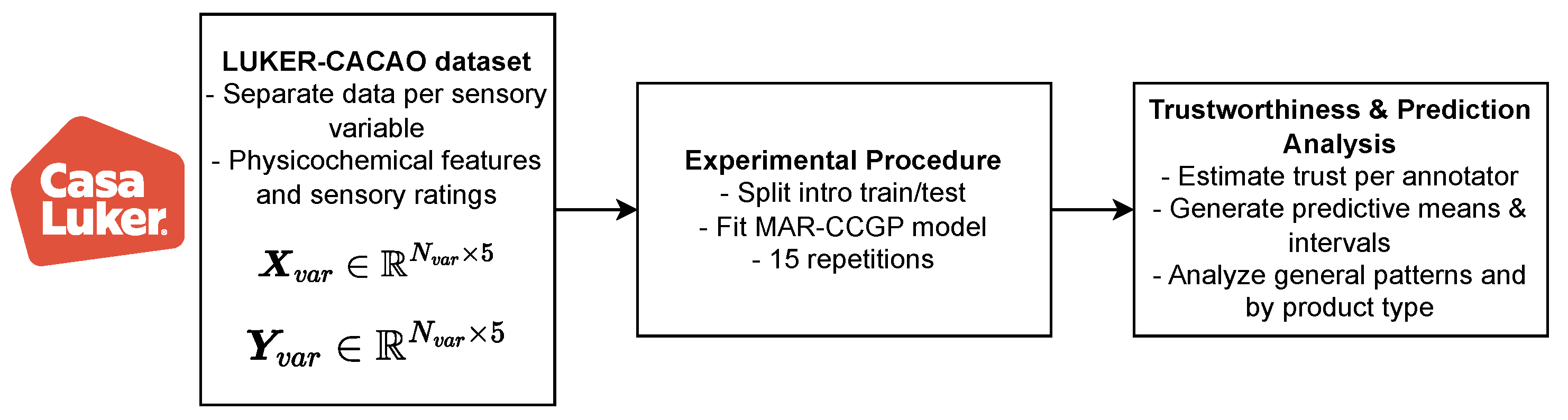
2. Materials and Methods
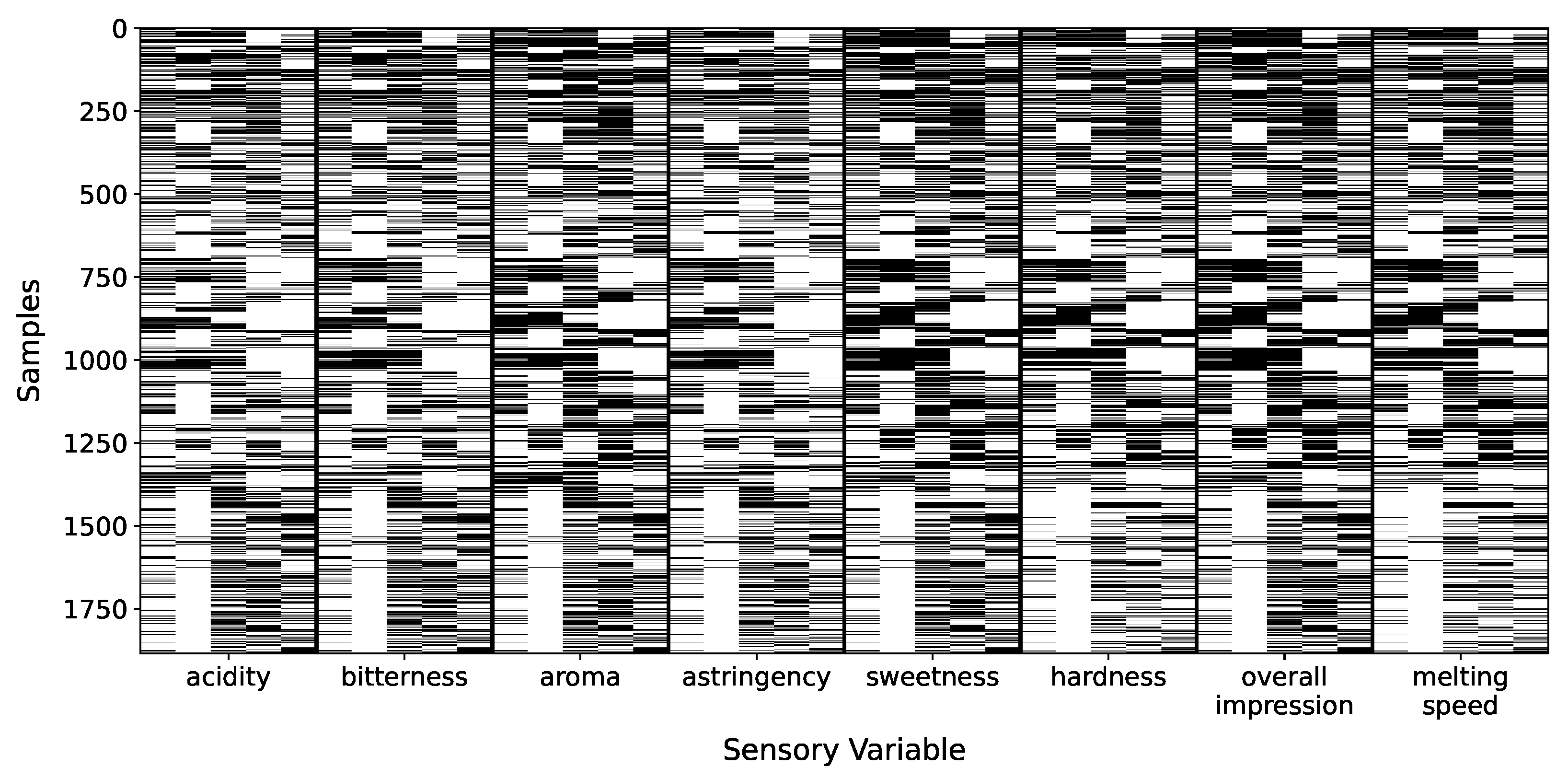
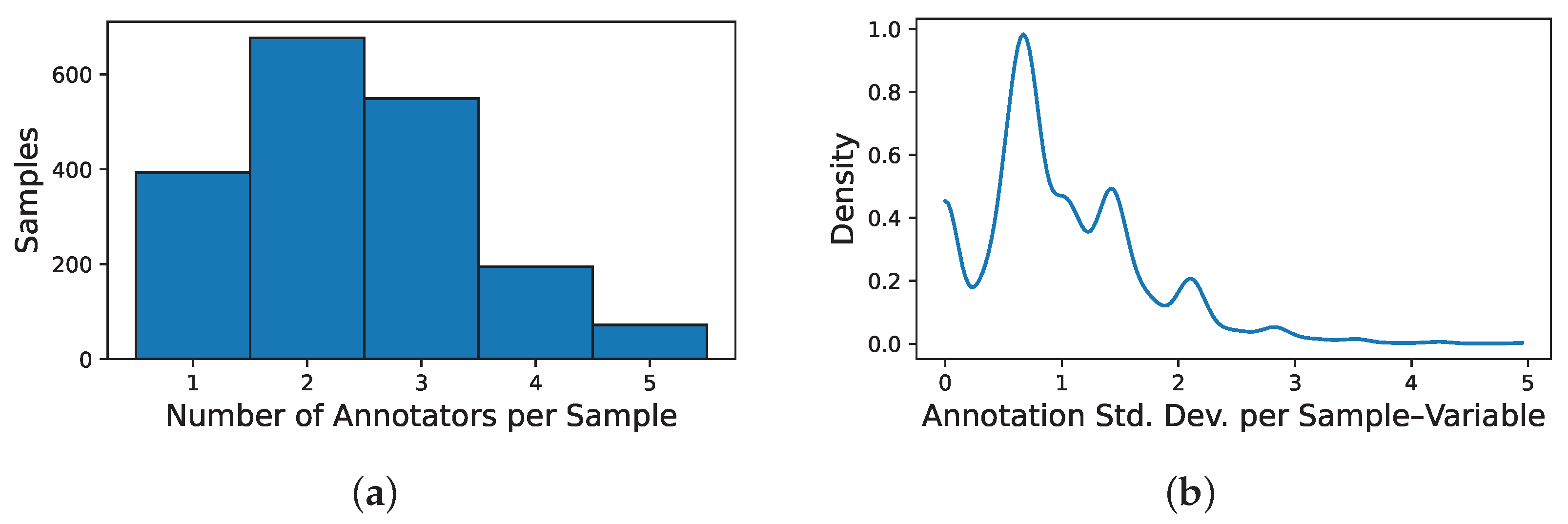
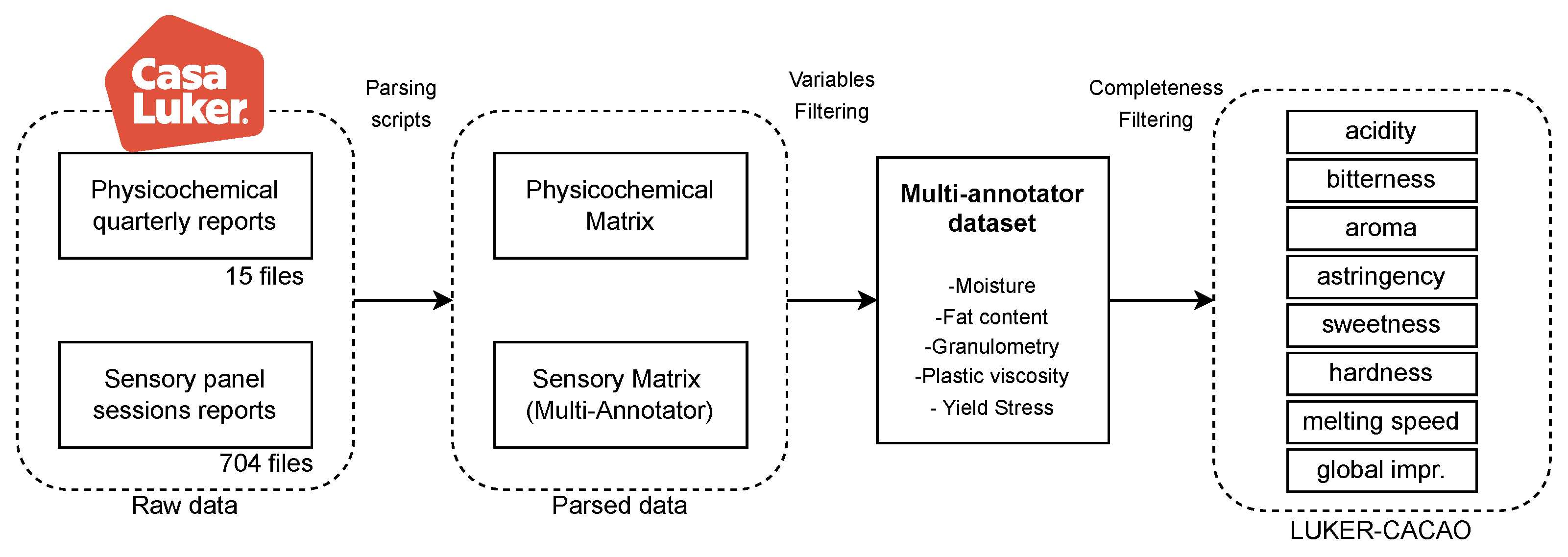
2.1. Casa Luker–Cacao Physicochemical-Sensory Dataset (LUKER-CACAO)
- –
- Moisture: It refers to the amount of water present in a cocoa-based product, expressed as a percentage of the product’s total weight (%). Moisture content significantly impacts physical attributes such as texture, shelf-life, and microbial stability. More critically, it modulates the release and perception of flavor compounds during consumption. Variations in moisture influence the volatilization of aroma molecules and alter the way flavors are experienced in the mouth, thereby reshaping the sensory profile in terms of intensity, balance, and mouthfeel [32]. In the dataset, moisture values—reported on a dry-basis—range from 0 to approximately 200%.
- –
- Fat content: It represents the proportion of lipids present in cocoa-based products, expressed as a percentage of total weight (%). Its modulation influences physical properties like viscosity, structure, and film formation capacity. These physical changes affect how the product interacts with the mouth during consumption, thereby altering the sensory profile by modifying lubrication, mouthfeel, and perception of flavor release [33]. In the dataset, values range from 0 to 60%.
- –
- Granulometry: It measures the size and distribution of solid particles in cocoa-based products, expressed in micrometers (m). Granulometry influences how particles interact and pack together, altering viscosity, flow behavior, and ultimately the perception of mouthfeel during consumption. Changes in granulometry reshape the sensory profile by modifying sensations like smoothness, thickness, and creaminess, which are critical for consumer acceptance [34]. Granulometry values range from 0 to 58 m.
- –
- Plastic viscosity: Measures the resistance of the product to flow after yielding has occurred, expressed in Pascal-seconds (Pa·s). It also reflects how easily the material continues to deform under applied shear during oral processing. Variations in plastic viscosity affect the sensory profile by altering the perceived thickness, smoothness, and creaminess during consumption. These changes shape the overall mouthfeel, influencing whether the product is experienced as rich, velvety, or fluid [34]. Observed values range from 0 to approximately 10.5 Pa·s.
- –
- Yield stress: Represents the minimum force required to initiate flow in the product, expressed in Pascals (Pa). It is closely related to the structural integrity of the product before deformation starts. Variations in yield stress affect the sensory profile by altering initial mouthfeel sensations such as firmness and body, shaping the consumer’s perception of texture at the start of consumption [34]. Yield stress values range from 0 to approximately 62 Pa.
- –
- Acidity: It refers to the perception of sourness resulting from organic acids formed during fermentation. When present at appropriate levels, acidity can enhance brightness and complexity; however, excessive acidity is considered a defect, particularly in fine chocolate [36].
- –
- Bitterness: It reflects the presence of alkaloids (primarily theobromine) and polyphenols, compounds inherent to cocoa. While some degree of bitterness is characteristic and desirable, excessive levels can disrupt sensory balance and negatively impact consumer acceptance [37].
- –
- Aroma: It encompasses volatile compounds responsible for cocoa’s characteristic smells (fruity, floral, roasted), highly influenced by fermentation and roasting [32].
- –
- Astringency: It refers to the drying, puckering sensation caused by interactions between polyphenols and salivary proteins. While moderate astringency can contribute positively to mouthfeel and complexity, excessive levels are perceived as unpleasant and may negatively impact sensory acceptance. [37].
- –
- Sweetness: It reflects sugar content, critical to balancing bitterness and acidity for overall flavor harmony.
- –
- Hardness: It describes the resistance during biting or deformation, influenced by fat content, tempering, and particle size.
- –
- Melting speed: It reflects how quickly the product liquefies in the mouth, depending on fat composition and tempering. Faster melting generally enhances flavor release and mouthfeel [35].
- –
- Global impresssion: It summarizes overall product quality, integrating flavor, aroma, and texture into a single judgment.
2.2. Correlated Chained Gaussian Processes (CCGPs)
2.3. CCGP-Based Crowd Learning and Localized Annotator Trustworthiness
3. Experimental Set-Up
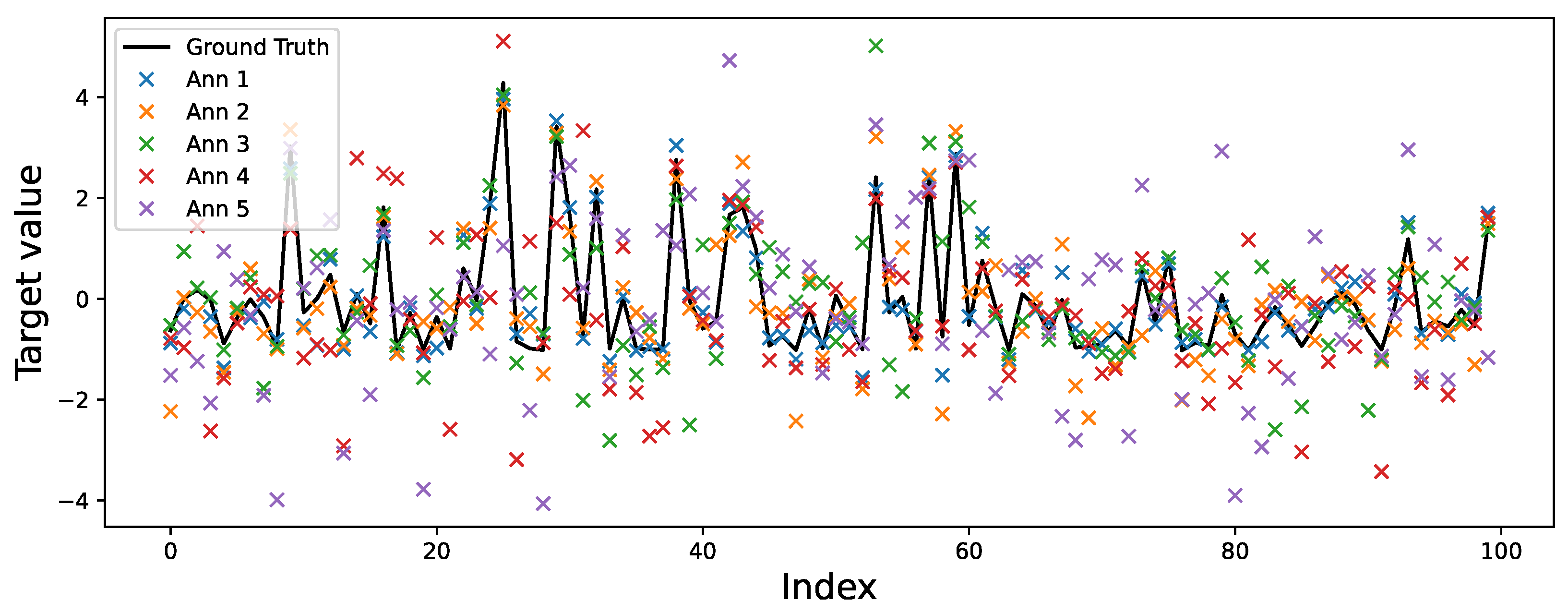
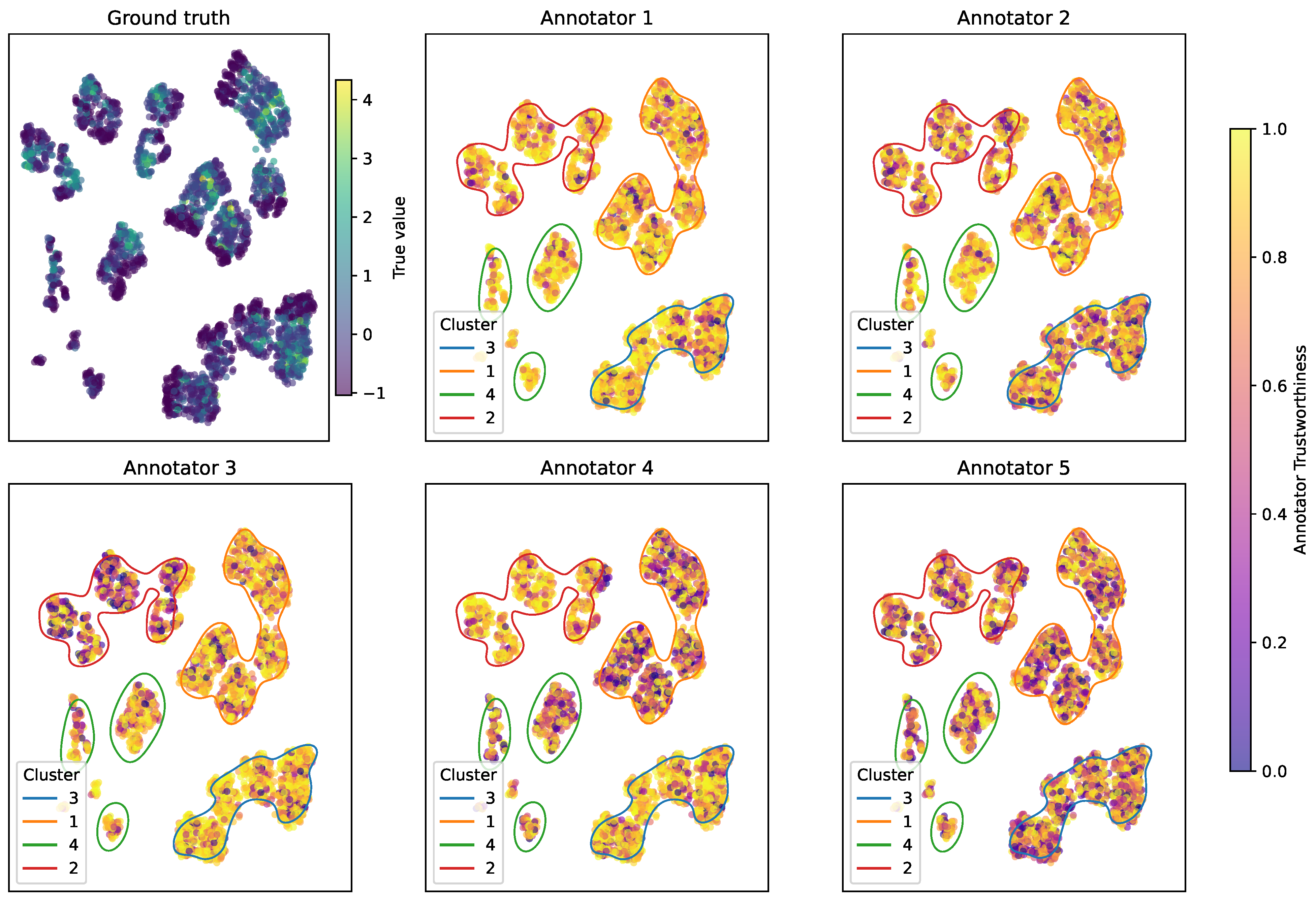
3.1. Semi-Synthetic Dataset Annotation Simulation
- –
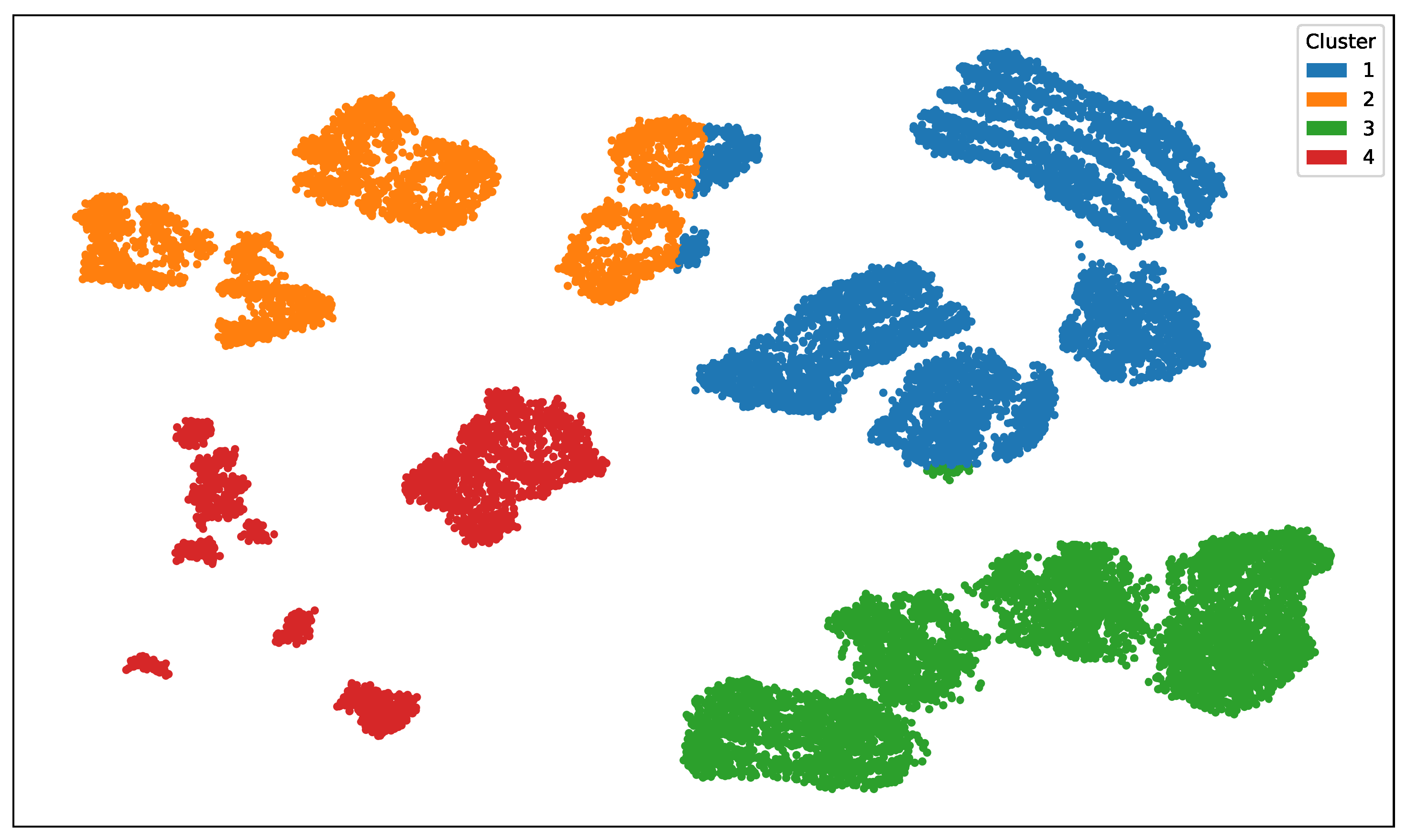
- The input data are standardized and then projected into a two-dimensional space using Uniform Manifold Approximation and Projection (UMAP) [50] to preserve local data structure by minimizing the cross-entropy between high-dimensional and low-dimensional fuzzy simplicial representations.
- –
- A K-means algorithm with C clusters is then applied to the UMAP projection to derive pseudo-contextual input space partitions [30] as latent indicators of instance-specific difficulty or domain shifts, used to modulate annotator behavior.
- –
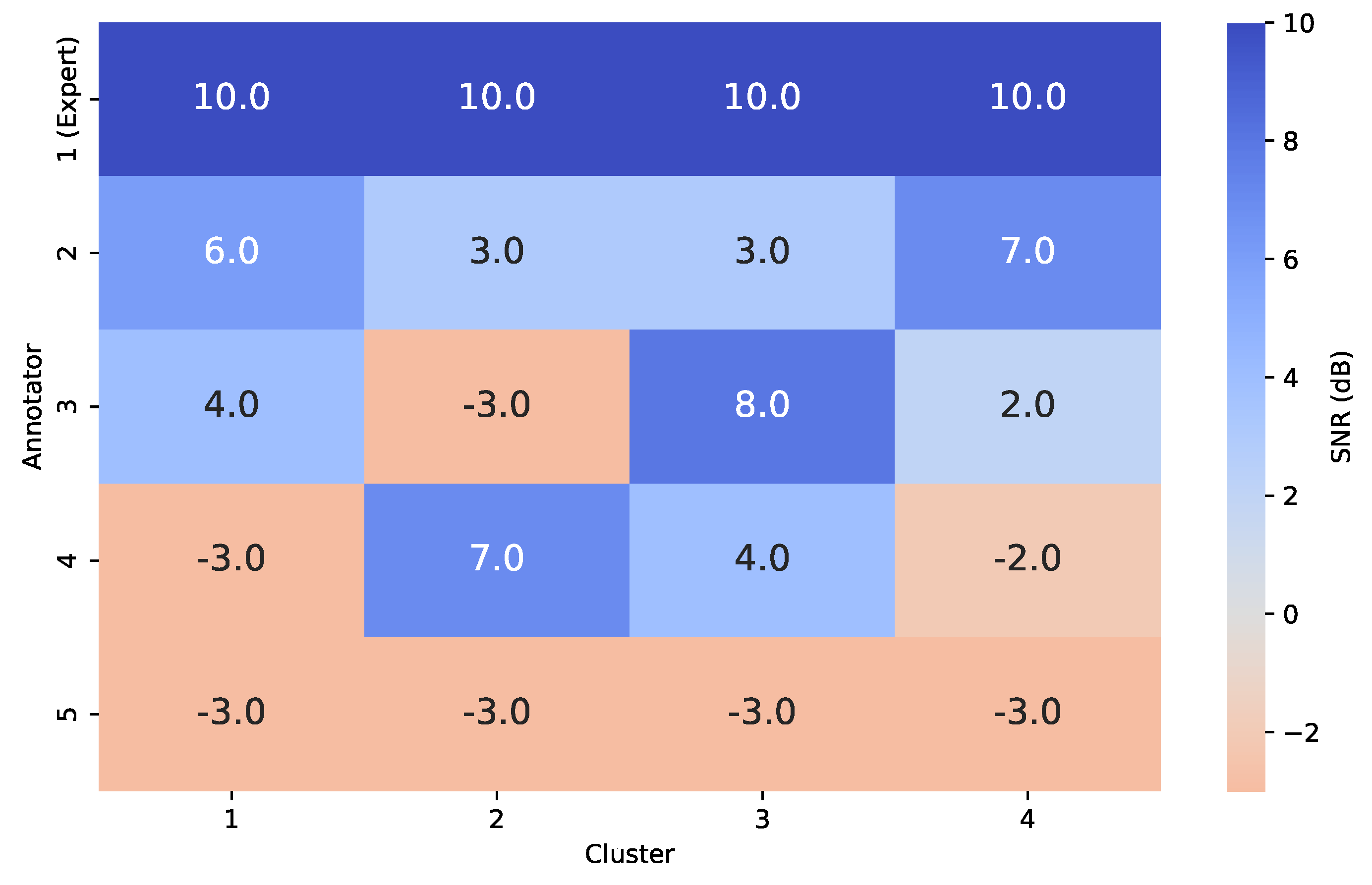
- Let denote the cluster assignment associated with the input , and let represent the corresponding ground-truth regression value. The simulated label assigned by annotator r to instance n is then generated as follows:where is the annotator-specific error variance for cluster . To ensure interpretability and reproducibility, each annotator’s variance profile across clusters is defined in terms of a fixed Signal-to-Noise Ratio (SNR) in dB. Then, the multiple annotator target matrix for regression tasks is built as in Equation (25).
3.2. Quality Assessment, Method Comparison, and Training Details
4. Results and Discussion
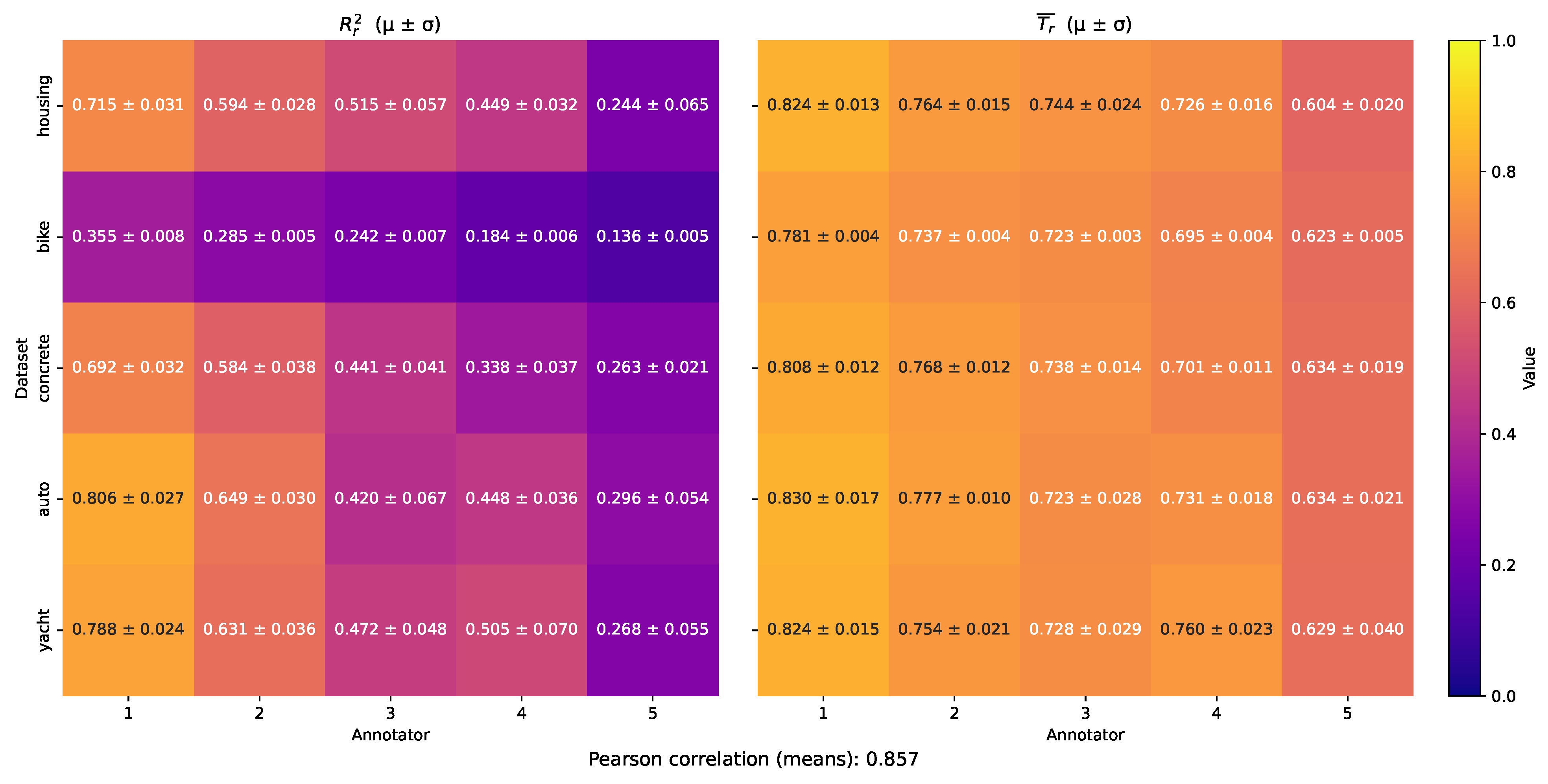
4.1. Semi-Synthetic Datasets Results
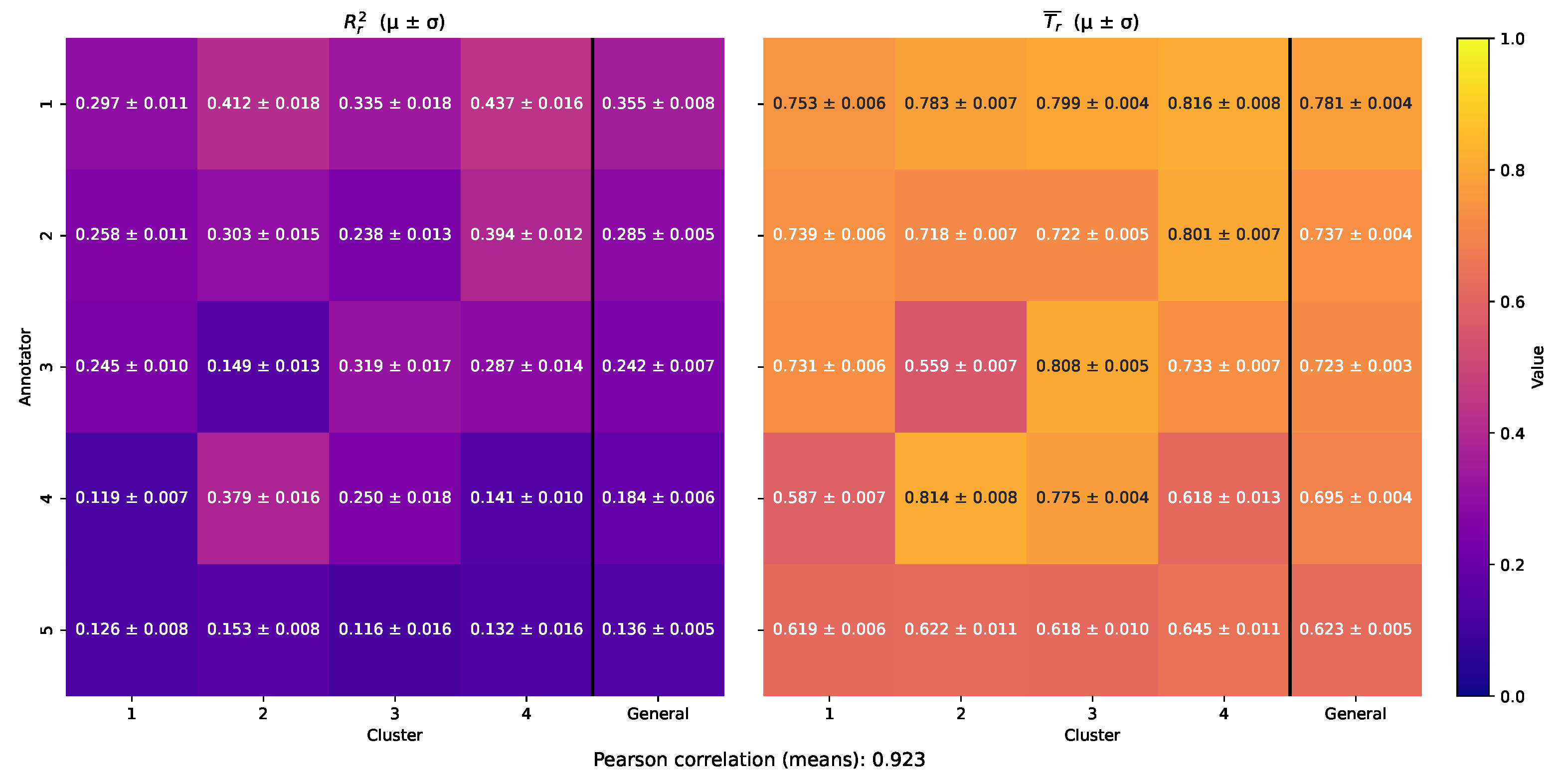
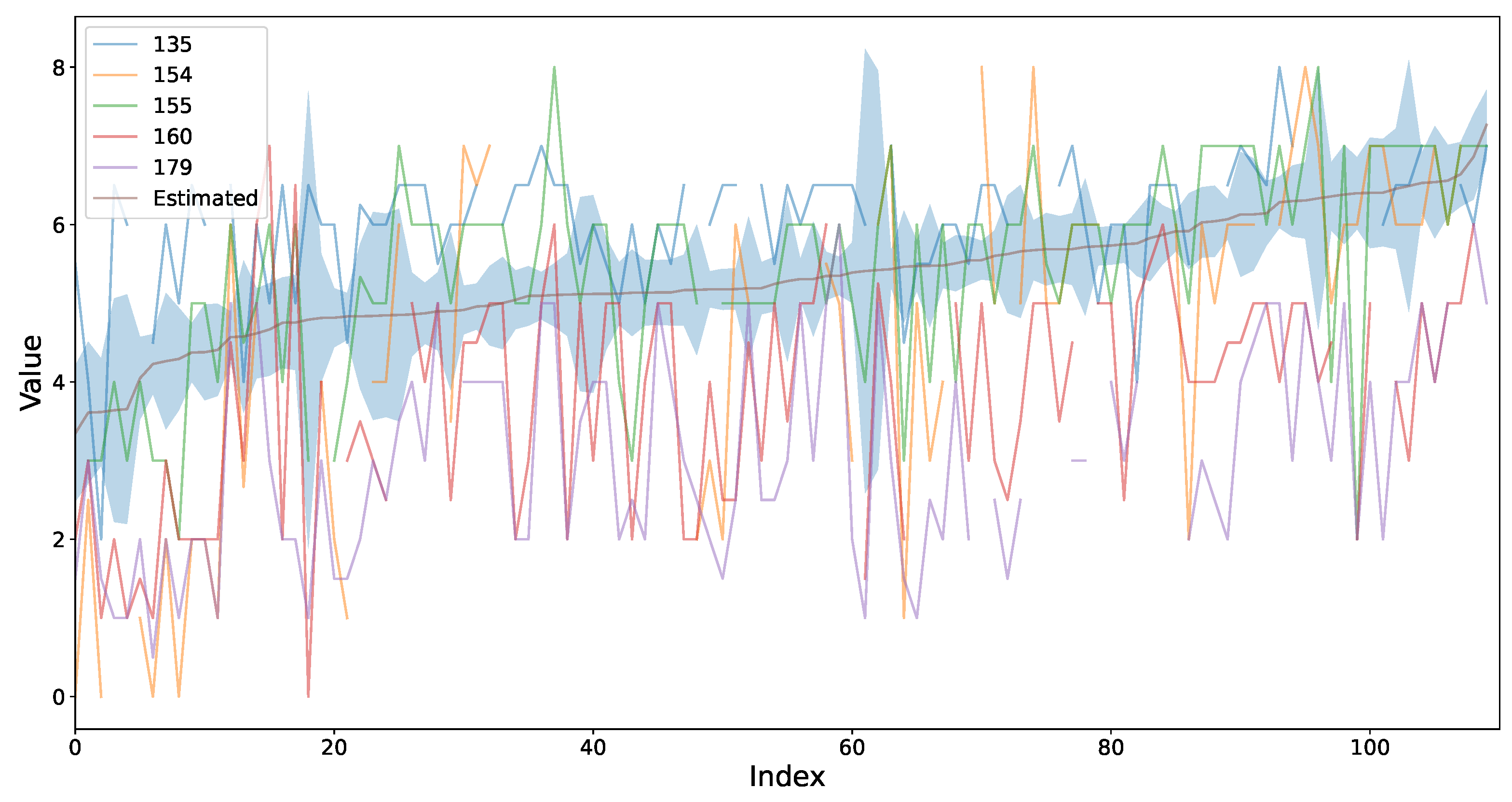
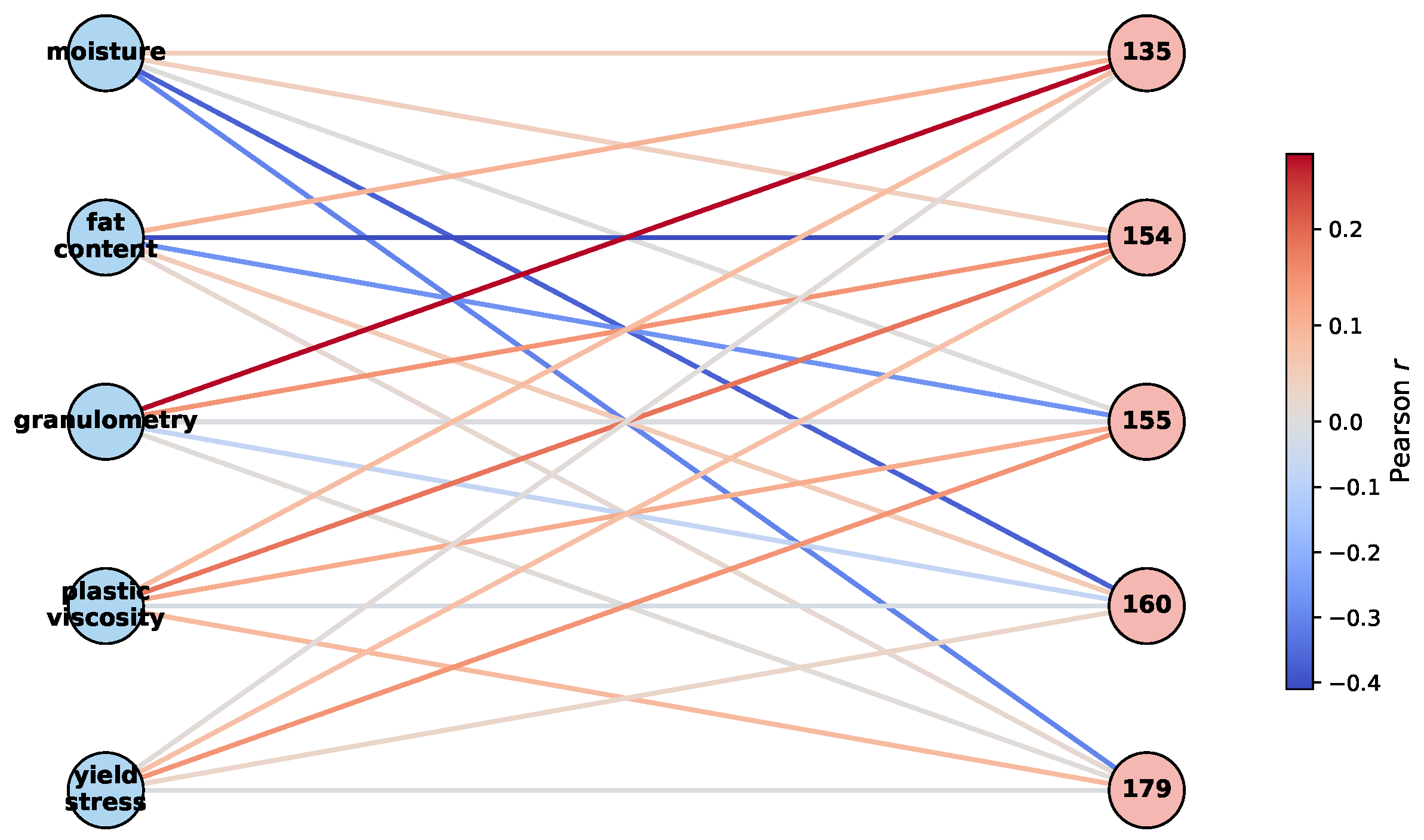
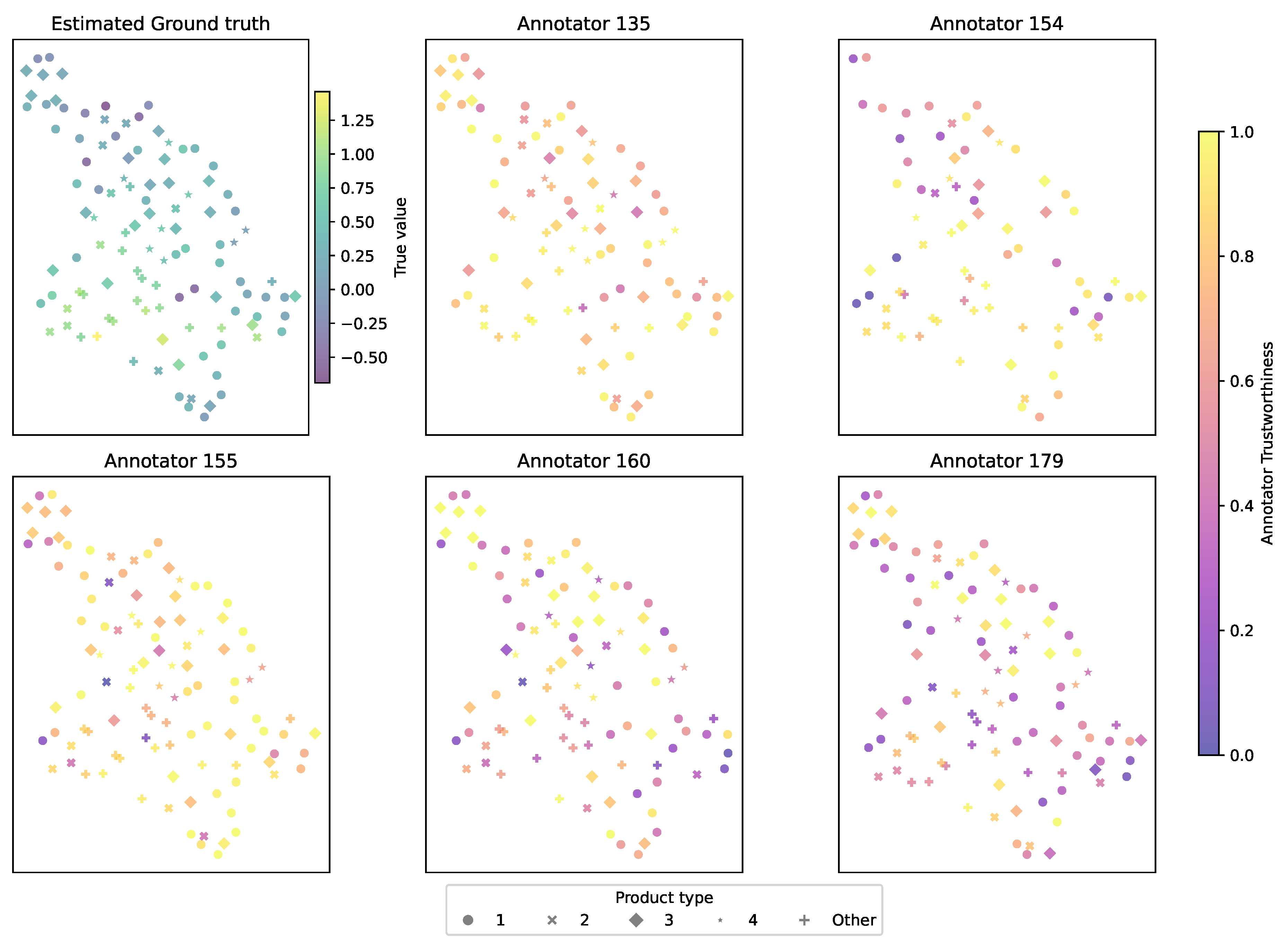
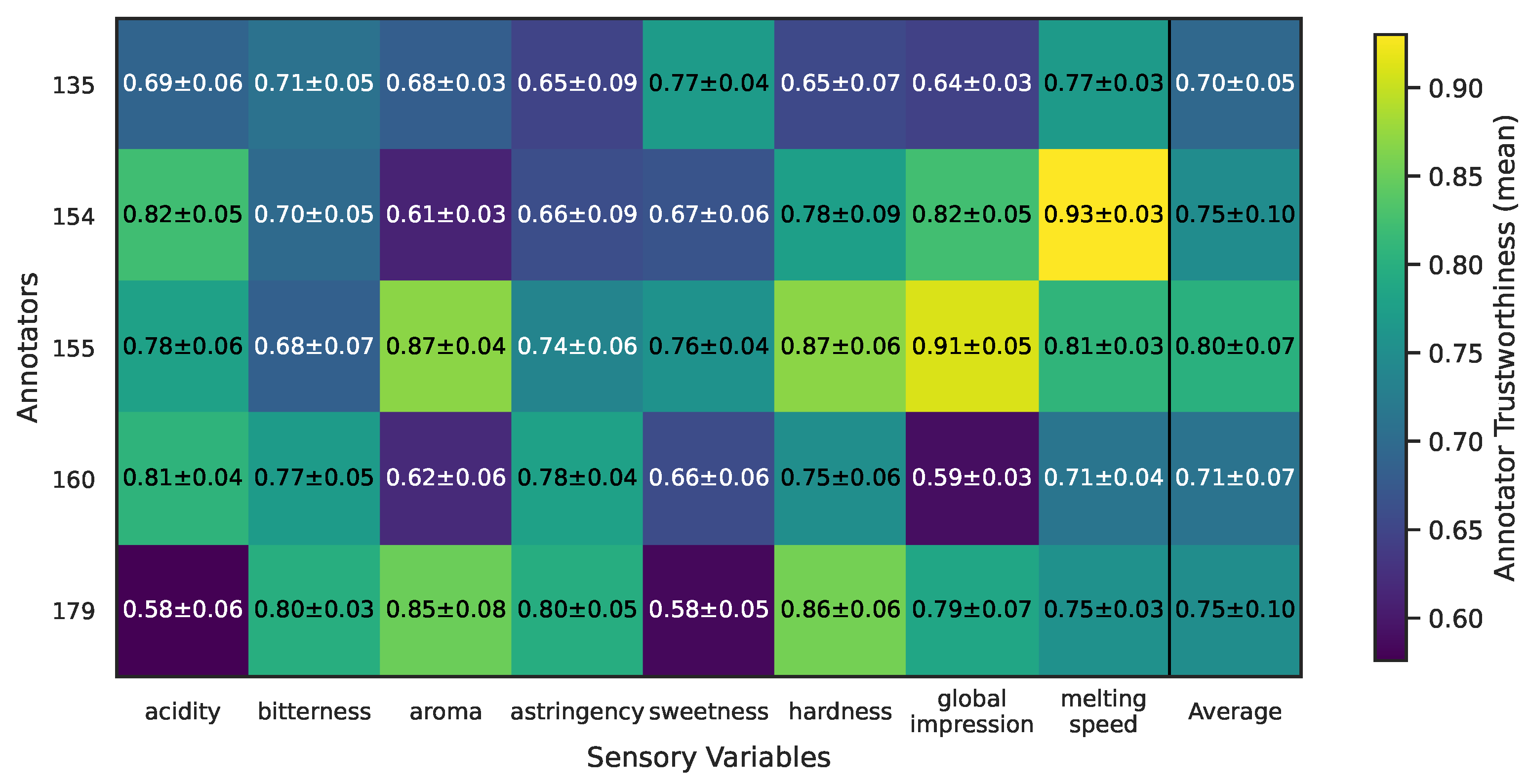
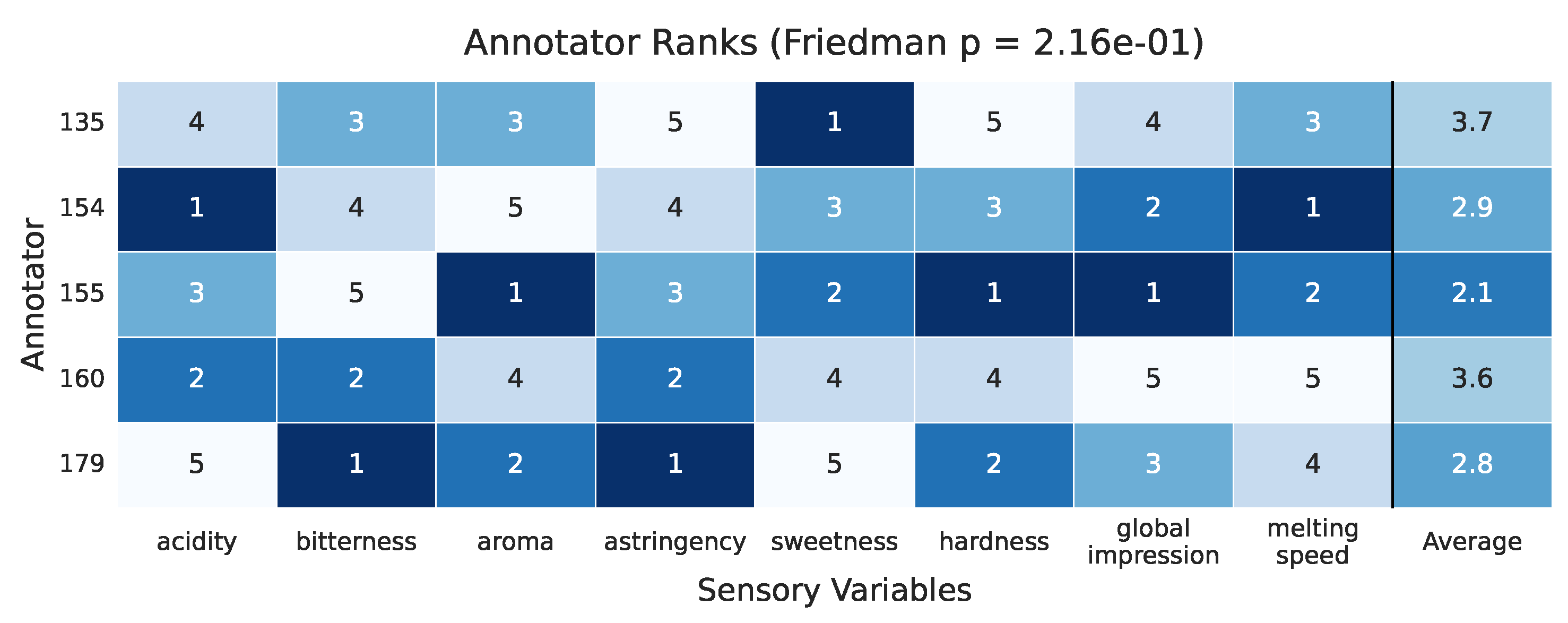
4.2. LUKER-CACAO Dataset Results
4.3. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Betancourt-Sambony, F.; Barrios-Rodríguez, Y.F.; Medina-Orjuela, M.E.; Amorocho Cruz, C.M.; Carranza, C.; Girón HernÁndez, L.J. Relationship between physicochemical properties of roasted cocoa beans and climate patterns: Quality and safety implications. LWT-Food Sci. Technol. 2025, 216, 117320. [Google Scholar] [CrossRef]
- Fanning, E.; Eyres, G.; Frew, R.; Kebede, B. Linking cocoa quality attributes to its origin using geographical indications. Food Control 2023, 151, 109825. [Google Scholar] [CrossRef]
- GonzÁlez-Orozco, C.E.; Porcel, M.; Yockteng, R.; Caro-Quintero, A.; Rodriguez-Medina, C.; Santander, M.; Zuluaga, M.; Soto, M.; Rodriguez Cortina, J.; Vaillant, F.E.; et al. Integrating new variables into a framework to support cacao denomination of origin: A case study in Southwest Colombia. J. Sci. Food Agric. 2024, 104, 1367–1381. [Google Scholar] [CrossRef]
- N. Suh, N.; F. Njimanted, G.; Thalut, N. Effect of farmers’ management practices on safety and quality standards of cocoa production: A structural equation modeling approach. Cogent Food Agric. 2020, 6, 1844848. [Google Scholar] [CrossRef]
- Dos Santos, R.M.; Silva, N.M.d.J.; Moura, F.G.; Lourenço, L.d.F.H.; Souza, J.N.S.d.; Sousa de Lima, C.L. Analysis of the sensory profile and physical and physicochemical characteristics of amazonian cocoa (Theobroma cacao L.) beans produced in different regions. Foods 2024, 13, 2171. [Google Scholar] [CrossRef]
- Palma-Morales, M.; Rune, C.J.B.; Castilla-Ortega, E.; Giacalone, D.; Rodríguez-Pérez, C. Factors affecting consumer perception and acceptability of chocolate beverages. LWT 2024, 201, 116257. [Google Scholar] [CrossRef]
- Spataro, F.; Rosso, F.; Peraino, A.; Arese, C.; Caligiani, A. Key molecular compounds for simultaneous origin discrimination and sensory prediction of cocoa: An UHPLC-HRMS sensomics approach. Food Chem. 2025, 463, 141201. [Google Scholar] [CrossRef] [PubMed]
- León-Inga, A.M.; VelÁsquez, S.; Quintero, M.; Taborda, N.; Cala, M.P. Effects of ultrafiltration membrane processing on the metabolic and sensory profiles of coffee extracts. Food Chem. 2024, 451, 139396. [Google Scholar] [CrossRef]
- Herrera-Rocha, F.; FernÁndez-Niño, M.; Duitama, J.; Cala, M.P.; Chica, M.J.; Wessjohann, L.A.; Davari, M.D.; Barrios, A.F.G. FlavorMiner: A machine learning platform for extracting molecular flavor profiles from structural data. J. Cheminformatics 2024, 16, 140. [Google Scholar] [CrossRef] [PubMed]
- Mota-Gutierrez, J.; Ferrocino, I.; Giordano, M.; Suarez-Quiroz, M.L.; Gonzalez-Ríos, O.; Cocolin, L. Influence of taxonomic and functional content of microbial communities on the quality of fermented cocoa pulp-bean mass. Appl. Environ. Microbiol. 2021, 87, e00425-21. [Google Scholar] [CrossRef]
- Cantini, C.; Salusti, P.; Romi, M.; Francini, A.; Sebastiani, L. Sensory profiling and consumer acceptability of new dark cocoa bars containing Tuscan autochthonous food products. Food Sci. Nutr. 2018, 6, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Collazos-Escobar, G.A.; Barrios-Rodríguez, Y.F.; Bahamón-Monje, A.F.; Gutiérrez-GuzmÁn, N. Mid-infrared spectroscopy and machine learning as a complementary tool for sensory quality assessment of roasted cocoa-based products. Infrared Phys. Technol. 2024, 141, 105482. [Google Scholar] [CrossRef]
- Yadav, S.; Singh, A.; Kumar, N. Electronic panel for sensory assessment of food: A review on technologies integration and their benefits. J. Food Sci. 2025, 90, e70128. [Google Scholar] [CrossRef] [PubMed]
- Putri, D.N.; De Steur, H.; Juvinal, J.G.; Gellynck, X.; Schouteten, J.J. Sensory attributes of fine flavor cocoa beans and chocolate: A systematic literature review. J. Food Sci. 2024, 89, 1917–1943. [Google Scholar] [CrossRef]
- An, J.; Lee, J. Consumers’ sensory perception homogeneity and liking of chocolate. Food Qual. Prefer. 2024, 118, 105178. [Google Scholar] [CrossRef]
- Shawky, E.; Zhu, W.; Tian, J.; Abu El-Khair, R.A.; Selim, D.A. Metabolomics-Driven Prediction of Vegetable Food Metabolite Patterns: Advances in Machine Learning Approaches. Food Rev. Int. 2025, 41, 1051–1080. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kazanskiy, N.L.; Oseledets, I.V.; Nikonorov, A.V.; Butt, M.A. Synergy between artificial intelligence and hyperspectral imagining—A review. Technologies 2024, 12, 163. [Google Scholar] [CrossRef]
- Mahanti, N.K.; Shivashankar, S.; Chhetri, K.B.; Kumar, A.; Rao, B.B.; Aravind, J.; Swami, D. Enhancing food authentication through E-nose and E-tongue technologies: Current trends and future directions. Trends Food Sci. Technol. 2024, 150, 104574. [Google Scholar] [CrossRef]
- Taheri, S.; Andrade, J.C.d.; Conte-Junior, C.A. Emerging perspectives on analytical techniques and machine learning for food metabolomics in the era of industry 4.0: A systematic review. Crit. Rev. Food Sci. Nutr. 2024, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Gil-GonzÁlez, J.; Daza-Santacoloma, G.; CÁrdenas-Peña, D.; Orozco-Gutiérrez, A.; Álvarez-Meza, A. Generalized cross-entropy for learning from crowds based on correlated chained Gaussian processes. Results Eng. 2025, 25, 103863. [Google Scholar] [CrossRef]
- Raykar, V.C.; Yu, S.; Zhao, L.H.; Valadez, G.H.; Florin, C.; Bogoni, L.; Moy, L. Learning from crowds. J. Mach. Learn. Res. 2010, 11, 1297–1322. [Google Scholar]
- Song, H.; Kim, M.; Park, D.; Shin, Y.; Lee, J.-G. Learning from noisy labels with deep neural networks: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 8135–8153. [Google Scholar] [CrossRef] [PubMed]
- Gil-Gonzalez, J.; Giraldo, J.J.; Orozco-Gutierrez, A. Correlated chained Gaussian processes for datasets with multiple annotators. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 4514–4528. [Google Scholar] [CrossRef]
- Rodrigues, F.; Pereira, F. Deep learning from crowds. In Proceedings of the AAAI, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zhang, Y.; Sheng, V.S. Learning from crowdsourced data with noise and annotation sparsity. In Proceedings of the IJCAI, New York, NY, USA, 9–15 July 2016. [Google Scholar]
- Zhang, Z.; Sabuncu, M.R. Generalized cross entropy loss for training deep neural networks with noisy labels. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Booth, B.M.; Narayanan, S.S. Fifty shades of green: Towards a robust measure of inter-annotator agreement for continuous signals. In Proceedings of the 2020 International Conference on Multimodal Interaction, Virtual Event, 25–29 October 2020; pp. 204–212. [Google Scholar]
- Schilling, M.; Scherr, T.; Münke, F.; Neumann, O. Automated annotator variability inspection for biomedical image segmentation. IEEE Access 2022, 10, 2753–2765. [Google Scholar] [CrossRef]
- Atcheson, M.; Sethu, V.; Epps, J. Demonstrating and Modelling Systematic Time-varying Annotator Disagreement in Continuous Emotion Annotation. In Proceedings of the Interspeech, Hyderabad, India, 2–6 September 2018. [Google Scholar]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Gil-Gonzalez, J.; Orozco-Gutierrez, A.; Álvarez-Meza, A. Learning from multiple inconsistent and dependent annotators to support classification tasks. Neurocomputing 2021, 423, 236–247. [Google Scholar] [CrossRef]
- Aprotosoaie, A.C.; Luca, S.V.; Miron, A. Flavor chemistry of cocoa and cocoa products—An overview. Compr. Rev. Food Sci. Food Saf. 2016, 15, 73–91. [Google Scholar] [CrossRef] [PubMed]
- Meza, B.E.; Carboni, A.D.; Peralta, J.M. Water adsorption and rheological properties of full-fat and low-fat cocoa-based confectionery coatings. Food Bioprod. Process. 2018, 110, 16–25. [Google Scholar] [CrossRef]
- Principato, L.; Carullo, D.; Gruppi, A.; Lambri, M.; Bassani, A.; Spigno, G. Correlation of rheology and oral tribology with sensory perception of commercial hazelnut and cocoa-based spreads. J. Texture Stud. 2024, 55, e12850. [Google Scholar] [CrossRef] [PubMed]
- Beckett, S.T.; Fowler, M.S.; Ziegler, G.R. Beckett’s Industrial Chocolate Manufacture and Use; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Afoakwa, E.O.; Paterson, A.; Fowler, M.; Ryan, A. Flavor formation and character in cocoa and chocolate: A critical review. Crit. Rev. Food Sci. Nutr. 2008, 48, 840–857. [Google Scholar] [CrossRef]
- Colonges, K.; Seguine, E.; Saltos, A.; Davrieux, F.; Minier, J.; Jimenez, J.C.; Lahon, M.C.; Calderon, D.; Subia, C.; Sotomayor, I.; et al. Diversity and determinants of bitterness, astringency, and fat content in cultivated Nacional and native Amazonian cocoa accessions from Ecuador. Plant Genome 2022, 15, e20218. [Google Scholar] [CrossRef]
- AOAC Official Method 963.15; Fat (Crude) in Cacao Products. AOAC International: Rockville, MD, USA, 2019.
- AOAC Official Method 931.04; Moisture in Cocoa Products. AOAC International: Rockville, MD, USA, 2019.
- ISO 13320:2020; Particle Size Analysis—Laser Diffraction Methods. International Organization for Standardization: Geneva, Switzerland, 2020.
- IOCCC Analytical Method 46; Viscosity of Cocoa and Chocolate. International Office of Cocoa, Chocolate and Confectionery: Hardricourt, France, 2000.
- NTC 3932; Sensory Analysis—Identification and Selection of Descriptors to Establish a Sensory Profile Using a Multidimensional Approach. ICONTEC: Bogotá, Colombia, 2004.
- Azur, M.J.; Stuart, E.A.; Frangakis, C.; Leaf, P.J. Multiple imputation by chained equations: What is it and how does it work? Int. J. Methods Psychiatr. Res. 2011, 20, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Williams, C.; Rasmussen, C. Gaussian processes for regression. Adv. Neural Inf. Process. Syst. 1995, 8, 514–520. [Google Scholar]
- Saul, A.D.; Hensman, J.; Vehtari, A.; Lawrence, N.D. Chained gaussian processes. In Proceedings of the Artificial Intelligence and Statistics, Cadiz, Spain, 9–11 May 2016; PMLR: London, UK, 2016; pp. 1431–1440. [Google Scholar]
- Titsias, M. Variational learning of inducing variables in sparse Gaussian processes. In Proceedings of the Artificial Intelligence and Statistics, Okinawa, Japan, 16–18 April 2019; PMLR: London, UK, 2009; pp. 567–574. [Google Scholar]
- Gal, Y.; van der Wilk, M. Variational Inference in Sparse Gaussian Process Regression and Latent Variable Models—A Gentle Tutorial. arXiv 2014, arXiv:1402.6842. [Google Scholar]
- Teh, Y.W.; Seeger, M.; Jordan, M.I. Semiparametric latent factor models. In Proceedings of the International Workshop on Artificial Intelligence and Statistics, Bridgetown, Christ Church Barbados, 6–8 January 2005; PMLR: London, UK, 2005; pp. 333–340. [Google Scholar]
- Rodrigues, F.; Lourenco, M.; Ribeiro, B.; Pereira, F.C. Learning supervised topic models for classification and regression from crowds. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2409–2422. [Google Scholar] [CrossRef]
- Healy, J.; McInnes, L. Uniform manifold approximation and projection. Nat. Rev. Methods Prim. 2024, 4, 82. [Google Scholar] [CrossRef]
- Wilson, A.G.; Hu, Z.; Salakhutdinov, R.; Xing, E.P. Deep kernel learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29, pp. 3703–3711. [Google Scholar]
- Salimbeni, H.; Deisenroth, M.P. Doubly stochastic variational inference for deep Gaussian processes. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30, pp. 4588–4599. [Google Scholar]
- Kutlu, M.; McDonnell, T.; Elsayed, T.; Lease, M. Annotator Rationales for Labeling Tasks in Crowdsourcing. J. Artif. Intell. Res. 2020, 69, 143–189. [Google Scholar] [CrossRef]
- Méndez Méndez, A.E.; Cartwright, M.; Bello, J.P.; Nov, O. Eliciting Confidence for Improving Crowdsourced Audio Annotations. Proc. ACM Hum.-Comput. Interact. 2022, 6, 88:1–88:25. [Google Scholar] [CrossRef]


| Variable | Analytical Method |
|---|---|
| Fat Content | AOAC Official Method 963.15 [38] |
| Moisture | AOAC Official Method 931.04 [39] |
| Granulometry | ISO 13320:2020 [40] |
| Plastic Viscosity | IOCCC Method 46 [41] |
| Yield Stress | IOCCC Method 46 [41] |
| Sensory Attributes | NTC 3932 [42] |
| Annotator | Acidity | Bitterness | Aroma | Astringency | Sweetness | Hardness | Global Impression | Melting Speed |
|---|---|---|---|---|---|---|---|---|
| 135 | 86.1 | 86.1 | 85.6 | 90.2 | 85.5 | 85.5 | 85.5 | 85.5 |
| 154 | 70.8 | 70.8 | 69.4 | 68.9 | 69.1 | 69.1 | 69.1 | 69.1 |
| 155 | 95.8 | 95.8 | 97.3 | 95.1 | 97.3 | 97.3 | 97.3 | 97.3 |
| 160 | 88.9 | 88.9 | 90.1 | 90.2 | 90.0 | 90.0 | 90.0 | 90.0 |
| 179 | 88.9 | 88.9 | 91.9 | 91.8 | 91.8 | 91.8 | 91.8 | 91.8 |
| Available samples | 72 | 72 | 111 | 61 | 110 | 110 | 110 | 110 |
| Physicochemical/ Sensory | Acidity | Bitterness | Aroma | Astringency | Sweetness | Hardness | Global Impression | Melting Speed |
|---|---|---|---|---|---|---|---|---|
| Moisture | 98.6 | 98.6 | 99.1 | 98.4 | 99.1 | 99.1 | 99.1 | 99.1 |
| Fat Content | 95.8 | 95.8 | 97.3 | 95.1 | 97.3 | 97.3 | 97.3 | 97.3 |
| Granulometry | 88.9 | 88.9 | 91.9 | 86.9 | 92.7 | 92.7 | 92.7 | 92.7 |
| Plastic viscosity | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| Yield stress | 97.2 | 97.2 | 98.2 | 96.7 | 98.2 | 98.2 | 98.2 | 98.2 |
| Available samples | 72 | 72 | 111 | 61 | 110 | 110 | 110 | 110 |
| Dataset | # Samples | # Features |
|---|---|---|
| Bike Sharing | 17,379 | 11 |
| Concrete Strength | 1030 | 8 |
| Boston Housing | 501 | 13 |
| Auto MPG | 392 | 7 |
| Yacht Hydrodynamics | 308 | 6 |
| Method | Acronym | Description |
|---|---|---|
| Gaussian Process on Ground Truth [30] | GPR-GT | Supervised GP regression trained on true outputs. Serves as an oracle upper bound and assumes full access to ground truth. Does not model annotators or uncertainty. |
| Gaussian Process on Average Annotations [23] | GPR-AVG | GP trained on the per-instance average of annotator targets. Assumes annotators are unbiased and neglects individual reliability. Serves as a baseline that models only the consensus. |
| Localized Kernel Alignment-based Annotator Relevance [31] | LKAAR | Jointly estimates annotator bias and variance, and embeds annotator consistency as a kernelized function over the input space. Provides localized reliability estimates. |
| Multi-Annotator Regression based on Correlated Chained Gaussian Process (ours) | MAR-CCGP | Proposed model. Captures latent inter-annotator correlations and input-dependent noise via correlated-chained latent functions and sparse variational GPs. Produces localized consistency-trustworthiness estimates. |
| Dataset | Method | MSE | MAE | MAPE | |
|---|---|---|---|---|---|
| Boston Housing | GPR-AVG | ||||
| GPR-GT | |||||
| LKAAR | |||||
| MAR-CCGP | |||||
| Bike Sharing | GPR-AVG | ||||
| GPR-GT | |||||
| LKAAR | |||||
| MAR-CCGP | |||||
| Concrete Strength | GPR-AVG | ||||
| GPR-GT | |||||
| LKAAR | |||||
| MAR-CCGP | |||||
| Auto MPG | GPR-AVG | ||||
| GPR-GT | |||||
| LKAAR | |||||
| MAR-CCGP | |||||
| Yacht Hydrodynamics | GPR-AVG | ||||
| GPR-GT | |||||
| LKAAR | |||||
| MAR-CCGP |
| Variable | Prod | Friedman (, p) | 135 | 154 | 155 | 160 | 179 |
|---|---|---|---|---|---|---|---|
| acidity | 1 | 42.35, 0.000 | 0.63 ± 0.09 b | 0.79 ± 0.06a | 0.74 ± 0.08 ab | 0.78 ± 0.07 a | 0.53 ± 0.08 c |
| 2 | 12.67, 0.013 | 0.82 ± 0.10 bc | 0.89 ± 0.08 ab | 0.88 ± 0.08 ab | 0.90 ± 0.05a | 0.79 ± 0.08 bc | |
| 3 | 24.33, 0.000 | 0.85 ± 0.14 ab | 0.79 ± 0.10 bc | 0.88 ± 0.11a | 0.74 ± 0.07 c | 0.83 ± 0.14 ab | |
| 4 | 9.37, 0.052 | 0.70 ± 0.20 c | 0.86 ± 0.09a | 0.72 ± 0.17 c | 0.83 ± 0.07 ab | 0.53 ± 0.12 d | |
| General | 43.73, 0.000 | 0.80 ± 0.19 b | 0.88 ± 0.10a | 0.84 ± 0.18 ab | 0.88 ± 0.09 a | 0.69 ± 0.20 c | |
| bitterness | 1 | 31.04, 0.000 | 0.70 ± 0.06 bc | 0.68 ± 0.06 c | 0.67 ± 0.08 c | 0.84 ± 0.06a | 0.83 ± 0.04 ab |
| 2 | 22.67, 0.000 | 0.59 ± 0.19 b | 0.47 ± 0.24 c | 0.56 ± 0.18 b | 0.48 ± 0.24 c | 0.67 ± 0.11a | |
| 3 | 10.47, 0.033 | 0.93 ± 0.04 a | 0.99 ± 0.01a | 0.85 ± 0.12 b | 0.52 ± 0.18 c | 0.53 ± 0.27 c | |
| 4 | 3.66, 0.454 | 0.73 ± 0.14 ab | 0.79 ± 0.19 a | 0.71 ± 0.19 ab | 0.71 ± 0.13 ab | 0.90 ± 0.06a | |
| General | 22.13, 0.000 | 0.75 ± 0.19 b | 0.77 ± 0.27a | 0.70 ± 0.23 bc | 0.62 ± 0.25 c | 0.66 ± 0.27 bc | |
| aroma | 1 | 48.75, 0.000 | 0.65 ± 0.05 b | 0.60 ± 0.05 c | 0.92 ± 0.04a | 0.69 ± 0.07 b | 0.84 ± 0.09 ab |
| 2 | 25.79, 0.000 | 0.63 ± 0.06 bc | 0.63 ± 0.12 bc | 0.79 ± 0.13 b | 0.65 ± 0.23 bc | 0.84 ± 0.18ab | |
| 3 | 42.24, 0.000 | 0.71 ± 0.06 b | 0.51 ± 0.12 c | 0.79 ± 0.06 b | 0.52 ± 0.14 c | 0.84 ± 0.12ab | |
| 4 | 26.31, 0.000 | 0.83 ± 0.14 a | 0.72 ± 0.01 b | 0.90 ± 0.17a | 0.29 ± 0.12 c | 0.73 ± 0.26 b | |
| General | 37.47, 0.000 | 0.73 ± 0.17 b | 0.66 ± 0.13 c | 0.86 ± 0.14a | 0.59 ± 0.25 bc | 0.86 ± 0.18 a | |
| astringency | 1 | 33.87, 0.000 | 0.65 ± 0.09 bc | 0.70 ± 0.08 b | 0.72 ± 0.06 b | 0.80 ± 0.06 ab | 0.84 ± 0.05a |
| 2 | 30.10, 0.000 | 0.62 ± 0.09 b | 0.56 ± 0.23 c | 0.70 ± 0.24 b | 0.46 ± 0.17 c | 0.85 ± 0.17a | |
| 3 | 16.00, 0.003 | 0.52 ± 0.11 c | 0.46 ± 0.11 d | 0.90 ± 0.06a | 0.83 ± 0.10 b | 0.97 ± 0.02 a | |
| 4 | 6.40, 0.171 | 0.71 ± 0.12 ab | 0.46 ± 0.14 c | 0.81 ± 0.15a | 0.79 ± 0.10 ab | 0.63 ± 0.20 b | |
| General | 27.52, 0.000 | 0.65 ± 0.15 bc | 0.53 ± 0.16 d | 0.77 ± 0.18a | 0.73 ± 0.20 b | 0.76 ± 0.28 b | |
| sweetness | 1 | 49.33, 0.000 | 0.80 ± 0.05 a | 0.55 ± 0.11 c | 0.82 ± 0.06a | 0.52 ± 0.07 c | 0.43 ± 0.06 d |
| 2 | 32.58, 0.000 | 0.72 ± 0.11 b | 0.61 ± 0.15 c | 0.52 ± 0.18 d | 0.70 ± 0.11 bc | 0.77 ± 0.15a | |
| 3 | 33.07, 0.000 | 0.73 ± 0.08 bc | 0.79 ± 0.12 b | 0.74 ± 0.06 bc | 0.93 ± 0.07a | 0.84 ± 0.08 ab | |
| 4 | 19.00, 0.001 | 0.84 ± 0.13 a | 0.88 ± 0.05a | 0.80 ± 0.13 ab | 0.62 ± 0.21 c | 0.52 ± 0.11 c | |
| General | 45.92, 0.000 | 0.76 ± 0.17 bc | 0.80 ± 0.16a | 0.72 ± 0.19 c | 0.69 ± 0.19 c | 0.66 ± 0.21 c | |
| hardness | 1 | 39.73, 0.000 | 0.61 ± 0.08 c | 0.87 ± 0.08 b | 0.87 ± 0.06 b | 0.73 ± 0.10 c | 0.88 ± 0.05a |
| 2 | 17.59, 0.001 | 0.62 ± 0.09 c | 0.85 ± 0.12 b | 0.84 ± 0.16 b | 0.77 ± 0.12 bc | 0.89 ± 0.14a | |
| 3 | 19.57, 0.001 | 0.67 ± 0.12 c | 0.77 ± 0.26 bc | 0.89 ± 0.07 b | 0.88 ± 0.09 b | 0.90 ± 0.07a | |
| 4 | 18.00, 0.001 | 0.70 ± 0.10 c | 0.87 ± 0.09 b | 0.94 ± 0.08a | 0.73 ± 0.12 c | 0.86 ± 0.10 b | |
| General | 38.13, 0.000 | 0.67 ± 0.21 c | 0.59 ± 0.34 d | 0.84 ± 0.21a | 0.70 ± 0.26 bc | 0.82 ± 0.22 b | |
| global impression | 1 | 41.17, 0.000 | 0.69 ± 0.06 b | 0.85 ± 0.08 ab | 0.91 ± 0.06a | 0.64 ± 0.06 b | 0.77 ± 0.09 ab |
| 2 | 22.98, 0.000 | 0.55 ± 0.07 c | 0.75 ± 0.20 b | 0.96 ± 0.07a | 0.55 ± 0.11 c | 0.83 ± 0.16 b | |
| 3 | 34.77, 0.000 | 0.65 ± 0.08 b | 0.81 ± 0.17 ab | 0.88 ± 0.11a | 0.52 ± 0.10 c | 0.86 ± 0.11 ab | |
| 4 | 25.60, 0.000 | 0.39 ± 0.11 d | 0.96 ± 0.08 a | 0.98 ± 0.02a | 0.42 ± 0.20 d | 0.50 ± 0.28 cd | |
| General | 53.49, 0.000 | 0.57 ± 0.21 c | 0.82 ± 0.16 b | 0.91 ± 0.18a | 0.58 ± 0.15 c | 0.78 ± 0.25 b | |
| melting speed | 1 | 36.96, 0.000 | 0.77 ± 0.05 bc | 0.97 ± 0.05a | 0.80 ± 0.05 b | 0.75 ± 0.06 c | 0.73 ± 0.04 c |
| 2 | 20.66, 0.000 | 0.88 ± 0.07 a | 0.89 ± 0.17 a | 0.89 ± 0.04 a | 0.61 ± 0.17 c | 0.77 ± 0.02 ab | |
| 3 | 36.00, 0.000 | 0.77 ± 0.07 c | 0.98 ± 0.03 ab | 0.75 ± 0.08 c | 0.72 ± 0.09 c | 0.78 ± 0.03a | |
| 4 | 28.30, 0.000 | 0.90 ± 0.08 b | 1.00 ± 0.01a | 0.94 ± 0.06 ab | 0.64 ± 0.10 c | 0.72 ± 0.03 bc | |
| General | 46.77, 0.000 | 0.77 ± 0.19 bc | 0.78 ± 0.27 bc | 0.81 ± 0.11a | 0.68 ± 0.21 c | 0.77 ± 0.06 bc |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lugo-Rojas, J.C.; Chica-Morales, M.J.; Florez-González, S.L.; Álvarez-Meza, A.M.; Castellanos-Dominguez, G. Integrating Cacao Physicochemical-Sensory Profiles via Gaussian Processes Crowd Learning and Localized Annotator Trustworthiness. Foods 2025, 14, 2961. https://doi.org/10.3390/foods14172961
Lugo-Rojas JC, Chica-Morales MJ, Florez-González SL, Álvarez-Meza AM, Castellanos-Dominguez G. Integrating Cacao Physicochemical-Sensory Profiles via Gaussian Processes Crowd Learning and Localized Annotator Trustworthiness. Foods. 2025; 14(17):2961. https://doi.org/10.3390/foods14172961
Chicago/Turabian StyleLugo-Rojas, Juan Camilo, Maria José Chica-Morales, Sergio Leonardo Florez-González, Andrés Marino Álvarez-Meza, and German Castellanos-Dominguez. 2025. "Integrating Cacao Physicochemical-Sensory Profiles via Gaussian Processes Crowd Learning and Localized Annotator Trustworthiness" Foods 14, no. 17: 2961. https://doi.org/10.3390/foods14172961
APA StyleLugo-Rojas, J. C., Chica-Morales, M. J., Florez-González, S. L., Álvarez-Meza, A. M., & Castellanos-Dominguez, G. (2025). Integrating Cacao Physicochemical-Sensory Profiles via Gaussian Processes Crowd Learning and Localized Annotator Trustworthiness. Foods, 14(17), 2961. https://doi.org/10.3390/foods14172961






