A Rice Hazards Risk Assessment Method for a Rice Processing Chain Based on a Multidimensional Trapezoidal Cloud Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Characteristics and Processing
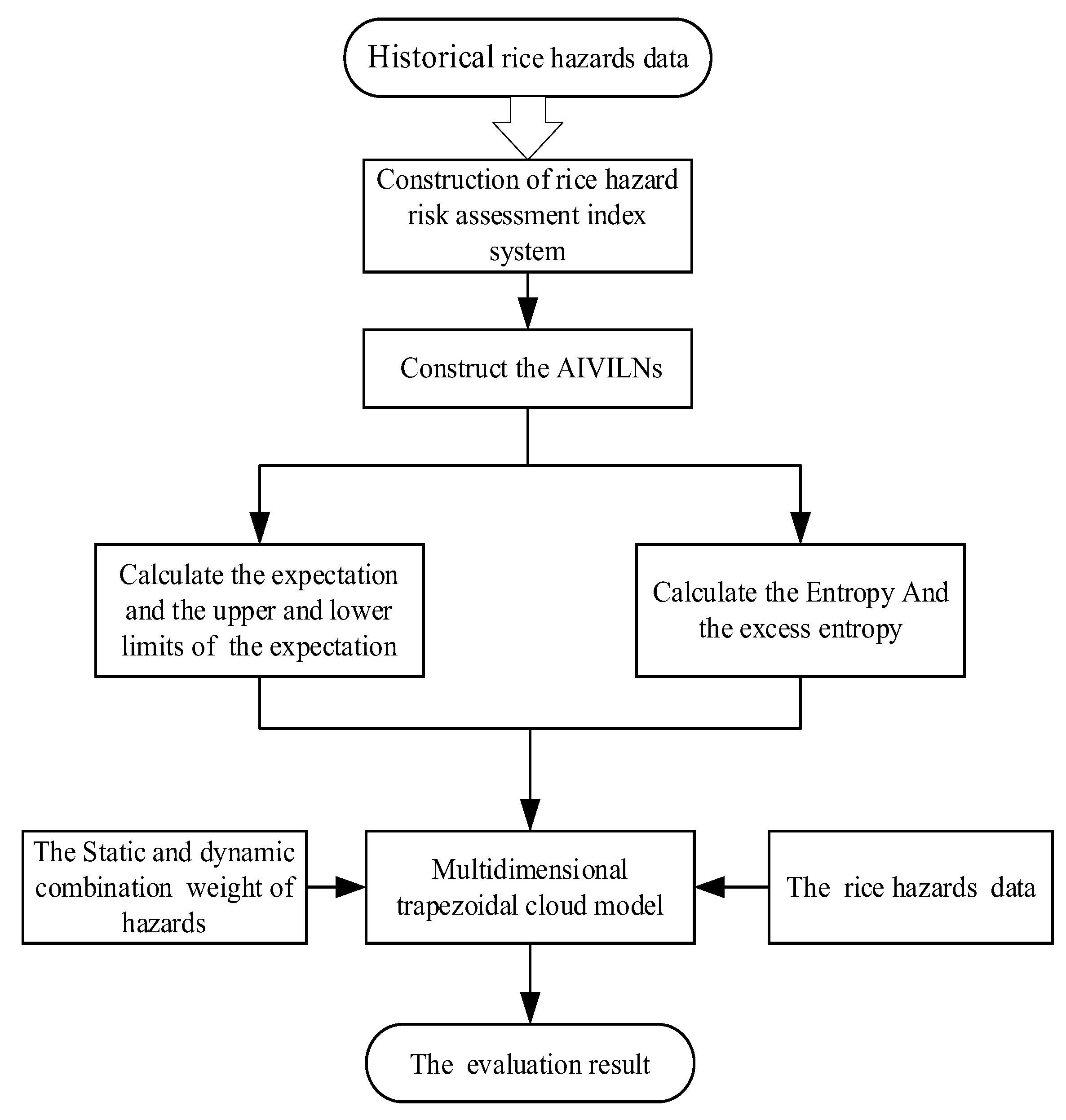
2.2. Risk Assessment Method of a Rice Processing Chain Based on a Multidimensional Trapezoidal Cloud Model
2.2.1. Construction of Risk Assessment Index System for Rice Hazards
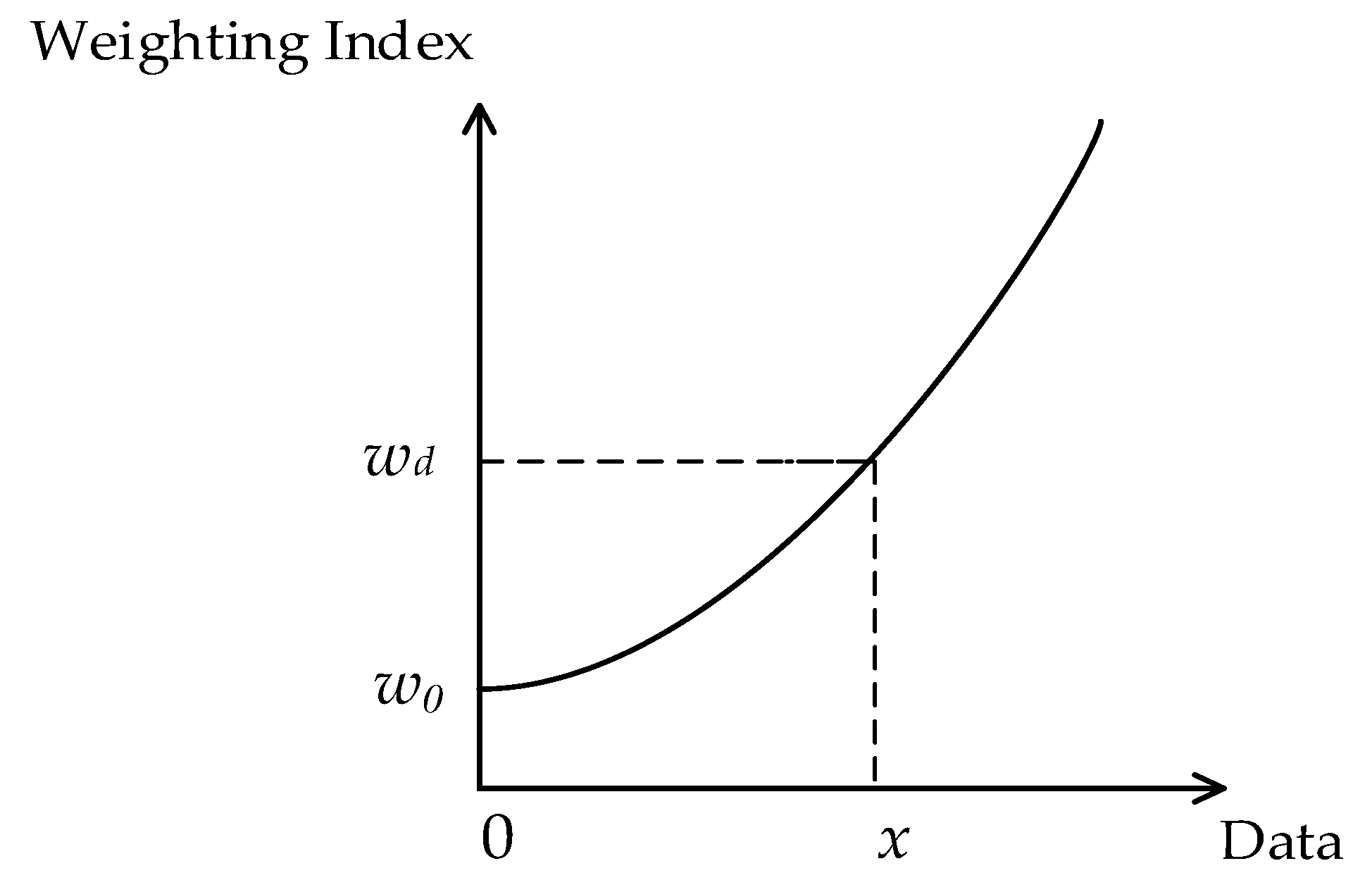
2.2.2. Weighting Method
2.2.3. Construction of the Evaluation Model of the Processing Chain
| Method flow | |
| Step 1 | if |
| Step 2 | μ = 1 |
| Step 3 | else |
| Step 4 | for i = 1:5 |
| Step 5 | if |
| Step 6 | |
| Step 7 | else if |
| Step 8 | |
| Step 9 | Else |
| Step 10 | |
| Step 11 | End |
| Step 12 | End |
| Step 13 | |
| Step 14 | End |
2.2.4. Construction of AIVILNs and the Evaluation Model Parameter Calculation
3. Experiments and Results
3.1. Risk Safety Evaluation in the Rice Processing Chain
3.2. Comparison Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, Q.; Zhao, Z.; Wang, X.; Xiong, K.; Shi, C. Microbiological predictive modeling and risk analysis based on the one-step kinetic integrated Wiener process. Innov. Food Sci. Emerg. 2022, 75, 102912. [Google Scholar] [CrossRef]
- Clayton, M.L.; Clegg Smith, K.; Neff, R.A.; Pollack, K.M.; Ensminger, M. Listening to food workers: Factors that impact proper health and hygiene practice in food service. Int. J. Occup. Environ. Health 2015, 21, 314–327. [Google Scholar] [CrossRef]
- Manning, L.; Soon, J.M. Mechanisms for assessing food safety risk. Br. Food J. 2013, 115, 460–484. [Google Scholar] [CrossRef]
- Muto, A.; Christofides, S.R.; Sirangelo, T.M.; Bartella, L.; Muller, C.; Di Donna, L.; Muzzalupo, I.; Bruno, L.; Ferrante, A.; Chiappetta, A.A.C.; et al. Fruitomics: The Importance of Combining Sensory and Chemical Analyses in Assessing Cold Storage Responses of Six Peach (Prunus persica L. Batsch) Cultivars. Foods 2022, 11, 2554. [Google Scholar] [CrossRef] [PubMed]
- Rosander, A.C. A Simple Method of Scoring and Interpreting Sequential Responses. J. Educ. Res. 1942, 36, 168–177. [Google Scholar] [CrossRef]
- Zickafoose, A.; Lu, P.; Baker, M. Forecasting Food Innovations with a Delphi Study. Foods 2022, 11, 3723. [Google Scholar] [CrossRef] [PubMed]
- López-Santiago, J.; García, A.I.G.; Gómez-Villarino, M.T. An Evaluation of Food Safety Performance in Wineries. Foods 2022, 11, 1249. [Google Scholar] [CrossRef]
- Du, Y.-W.; Chen, Q.; Sun, Y.-L.; Li, C.-H. Knowledge structure-based consensus-reaching method for large-scale multiattribute group decision-making. Knowl. Based Syst. 2021, 219, 106885. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Zou, M.; Wen, X.; Wang, Z.; Li, Y.; Zhang, Q. A Voting-Based Ensemble Deep Learning Method Focused on Multi-Step Prediction of Food Safety Risk Levels: Applications in Hazard Analysis of Heavy Metals in Grain Processing Products. Foods 2022, 11, 823. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Guo, A.; Bao, X.; Li, Q.; Liu, L.; Zhang, X.; Chen, X. Statistics and analyses of food safety inspection data and mining early warning information based on chemical hazards. LWT 2022, 165, 113746. [Google Scholar] [CrossRef]
- Wang, X.; Bouzembrak, Y.; Lansink, A.O.; van der Fels-Klerx, H.J. Application of machine learning to the monitoring and prediction of food safety: A review. Compr. Rev. Food Sci. Food Saf. 2022, 21, 416–434. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, R.M.; Nelson, D.R. The Use of Support Vector Machine to Analyze Food Security in a Region of Brazil. Appl. Artif. Intell. 2016, 30, 318–330. [Google Scholar] [CrossRef]
- Du, J.; Zhang, M.; Zhang, L.; Law, C.L.; Liu, K. Shelf-Life Prediction and Critical Value of Quality Index of Sichuan Sauerkraut Based on Kinetic Model and Principal Component Analysis. Foods 2022, 11, 1762. [Google Scholar] [CrossRef]
- Fang, S.; Guan, Z.; Su, C.; Zhang, W.; Zhu, J.; Zheng, Y.; Li, H.; Zhao, P.; Liu, X. Accurate fish-freshness prediction label based on red cabbage anthocyanins. Food Control 2022, 138, 109018. [Google Scholar] [CrossRef]
- Luo, T.; Wu, C.; Duan, L. Fishbone diagram and risk matrix analysis method and its application in safety assessment of natural gas spherical tank. J. Clean. Prod. 2018, 174, 296–304. [Google Scholar] [CrossRef]
- Ma, B.; Han, Y.; Cui, S.; Geng, Z.; Li, H.; Chu, C. Risk early warning and control of food safety based on an improved analytic hierarchy process integrating quality control analysis method. Food Control 2020, 108, 106824. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A review of fuzzy AHP methods for decision-making with subjective judgements. Expert Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Wang, J.; Peng, L.; Zhang, H.Y.; Chen, X.-h. Method of multi-criteria group decision-making based on cloud aggregation operators with linguistic information. Inf. Sci. 2014, 274, 177–191. [Google Scholar] [CrossRef]
- You, G.; Xu, B.; Su, H.; Zhang, S.; Pan, J.; Hou, X.; Li, J.; Ding, R. Evaluation of Aquaculture Water Quality Based on Improved Fuzzy Comprehensive Evaluation Method. Water 2021, 13, 1019. [Google Scholar] [CrossRef]
- Xu, Q.; Xu, K. Quality evaluation of Chinese red wine based on cloud model. J. Food Biochem. 2019, 43, e12787. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, G.; Fathollahi-Fard, A.; Wang, W.; Wu, P.; Li, Z. Interval-Valued Intuitionistic Uncertain Linguistic Cloud Petri Net and Its Application to Risk Assessment for Subway Fire Accident. IEEE Trans. Autom. Sci. Eng. 2020, 19, 1–15. [Google Scholar] [CrossRef]
- Wang, X.-K.; Wang, Y.-T.; Zhang, H.-Y.; Wang, J.-Q.; Li, L.; Goh, M. An asymmetric trapezoidal cloud-based linguistic group decision-making method under unbalanced linguistic distribution assessments. Comput. Ind. Eng. 2021, 160, 107457. [Google Scholar] [CrossRef]
- Papapostolou, A.; Karakosta, C.; Apostolidis, G.; Doukas, H. An AHP-SWOT-Fuzzy TOPSIS Approach for Achieving a Cross-Border RES Cooperation. Sustainability 2020, 12, 2886. [Google Scholar] [CrossRef]
- Niu, G.; Hu, Z.; Hu, D. Evaluation and prediction of production line health index based on matter element information entropy. Comput. Integr. Manuf. Syst. 2019, 25, 1639–1646. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.Y.; Li, G.H.; Liu, R.; Zhou, J. Assessment of satellite health state based on fuzzy variable weight theory. Syst. Eng. Electron. 2014, 36, 476–480. [Google Scholar]
- Zhao, Y.; Li, P.; Wang, T.; Kang, Y.; Zhao, Y.-B. Equipment Health Assessment Based on AHP-CRITIC Dynamic Weight. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 5841–5846. [Google Scholar] [CrossRef]
- Jia, Q.; Hu, J.; He, Q.; Zhang, W.; Safwat, E. A multicriteria group decision-making method based on AIVIFSs, Z-numbers, and trapezium clouds. Inf. Sci. 2021, 566, 38–56. [Google Scholar] [CrossRef]
- Yu, J.; Shen, Z.; Zhao, Z.; Wang, X.; Xu, J.; Sun, Q.; Wang, L.; Liu, G. Water eutrophication evaluation based on multidimensional trapezoidal cloud model. Soft Comput. 2021, 25, 2851–2861. [Google Scholar] [CrossRef]
- Jennifer HOLDAWAY, W.W. From Soil Pollution to ‘Cadmium Rice’; to Public Health Impacts: An Interdisciplinary Analysis of Influencing Factors and Possible Responses. J. Resour. Ecol. 2018, 9, 1–12. [Google Scholar] [CrossRef]
- Li, Y.; Qin, S.; Yang, Y.; Sun, H.; Qiao, X.; Li, J. Research Status of Mycotoxin Contamination in Grains in China. J. Chin. Cereals Oils Assoc. 2020, 35, 186–194. [Google Scholar]
- Chen, B.; Zheng, K.; Wang, J.; Ye, L.; Song, J. Content Characteristics and Health Risk Analysis of Mercury in Soilcrop System in Leizhou Peninsula. Ecol. Environ. Sci. 2022, 31, 572–582. [Google Scholar] [CrossRef]
- Rathore, R.; Thakkar, J.; Jha, J.K. A quantitative risk assessment methodology and evaluation of food supply chain. Int. J. Logist. Manag. 2017, 28, 1272–1293. [Google Scholar] [CrossRef]
- Wang, H.; Li, L. Comprehensive Evaluation of Probiotic Property, Hypoglycemic Ability and Antioxidant Activity of Lactic Acid Bacteria. Foods 2022, 11, 1363. [Google Scholar] [CrossRef]
- Zhao, Z.; Gu, J. Risk Evaluation of Mine-Water Inrush Based on Comprehensive Weight Method. Geotech. Geol. Eng. 2022, 41, 189–203. [Google Scholar] [CrossRef]
- Zhang, B.W.; Li, C.C.; Dong, Y.C.; Pedrycz, W. A Comparative Study Between Analytic Hierarchy Process and Its Fuzzy Variants: A Perspective Based on Two Linguistic Models. IEEE Trans. Fuzzy Syst. 2021, 29, 3270–3279. [Google Scholar] [CrossRef]
- Bougarne, L.; Ben Abbou, M.; El Haji, M.; Bouka, H. Consequences of surface water eutrophication: Remedy and environmental interest. Mater. Today Proc. 2019, 13, 654–662. [Google Scholar] [CrossRef]
- Yan, L.; Fan, X. Recursive integral proportional–integral control based on membership cloud for active power filter. IET Power Electron. 2014, 7, 2870–2876. [Google Scholar] [CrossRef]
- Bao, G.Y.; Lian, X.L.; He, M.; Wang, L.L. Improved two-tuple linguistic representation model based on new linguistic evaluation scale. Control Decis. 2010, 25, 780–784. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wang, P.; Wang, J.; Zhang, H.Y.; Chen, X.H. Atanassov’s Interval-Valued Intuitionistic Linguistic Multicriteria Group Decision-Making Method Based on the Trapezium Cloud Model. IEEE Trans. Fuzzy Syst. 2015, 23, 542–554. [Google Scholar] [CrossRef]


| Types of Evaluation Methods | Risk Assessment Methodology | Advantages | Disadvantages |
|---|---|---|---|
| Qualitative assessment methods | Index scoring method [5] | Clear quantitative metrics | Difficult to define indicator weights |
| Delphi [6] | Relatively simplified relationships between system elements | Complex and time-consuming for collecting expert opinions | |
| HACCP [6,7] | Multilevel and multi-indicator evaluation | Complex implementation | |
| Quantitative assessment methods | Random forest algorithm [11] | Simple calculation | Prone to overfitting |
| SVM [12] | High generalization ability | Unsuitable for classification of large data sets | |
| BP [13] | High nonlinear mapping capability | Prone to local miniaturization problems | |
| Qualitative and quantitative comprehensive analysis method | AHP [16] | A clear hierarchy of indicators and a wide range of applications | Reliance on the accuracy of expert assessment results |
| Fuzzy integrated evaluation [17] | Excellent evaluation results for fuzzy objects | Complex calculation and subjective determination of weights | |
| Cloud model [18] | Enables conversion of quantitative risk values to qualitative language sets | Difficulty in determining numerical characteristics |
| Province | Stage | Sampling Date | Hazards | ||||
|---|---|---|---|---|---|---|---|
| ZEA (μg/kg) | AFB1 (μg/kg) | Mercury (mg/kg) | Lead (mg/kg) | Chromium (mg/kg) | |||
| Anhui | Paddy rice | 20210304 | 30.756 | 0.671 | 0.009 | 0.137 | 1.300 |
| Anhui | Husking | 20210313 | 0.857 | 0.143 | 0.007 | 0.057 | 0.495 |
| Jiangsu | Paddy rice | 20210411 | 32.149 | 0.678 | 0.059 | 0.126 | 7.860 |
| Jiangsu | Polished rice | 20210413 | 0.517 | 0.200 | 0.008 | 0.051 | 0.156 |
| Heilongjiang | Polishing | 20211006 | 0.640 | 0.235 | 0.005 | 0.050 | 0.188 |
| Heilongjiang | Polished rice | 20211009 | 0.361 | 0.187 | 0.007 | 0.065 | 0.269 |
| Level | Evaluation Parameters | ||||
|---|---|---|---|---|---|
| ZEA (μg/kg) | AFB1 (μg/kg) | Mercury (mg/kg) | Lead (mg/kg) | Chromium (mg/kg) | |
| I | ≤12.0 | ≤2.0 | ≤0.004 | ≤0.04 | ≤0.2 |
| II | ≤24.0 | ≤4.0 | ≤0.008 | ≤0.08 | ≤0.4 |
| III | ≤36.0 | ≤6.0 | ≤0.012 | ≤0.12 | ≤0.6 |
| IV | ≤48.0 | ≤8.0 | ≤0.016 | ≤0.16 | ≤0.8 |
| V | ≤60.0 | ≤10.0 | ≤0.02 | ≤0.2 | ≤1.0 |
| VI | >64.0 | >10.0 | >0.02 | >0.2 | >1.0 |
| Number | Data | Comprehensive Weight Vector | Stage |
|---|---|---|---|
| (ZEA, AFB1, Mercury, Lead, Chromium) * | (ZEA, AFB1, Mercury, Lead, Chromium) * | ||
| 1 | (29.581, 0.691, 0.016, 0.159, 5.634) | (0.3635, 0.1796, 0.0988, 0.0437, 0.3414) | paddy rice |
| 2 | (15.231, 0.724, 0.009, 0.19, 6.112) | (0.3008, 0.1773, 0.0989, 0.0469, 0.3671) | paddy rice |
| 3 | (6.17, 0.577, 0.008, 0.074, 0.571) | (0.4251, 0.2176, 0.1341, 0.0817, 0.1145) | husking |
| 4 | (5.878, 3.514, 0.608, 0.048, 0.498) | (0.4176, 0.2761, 0.1286, 0.074, 0.1037) | husking |
| 5 | (0.713, 0.212, 0.008, 0.055, 0.513) | (0.3458, 0.2423, 0.1622, 0.1095, 0.1402) | polishing |
| 6 | (0.681, 3.179, 0.007, 1.352, 2.473) | (0.3075, 0.3004, 0.1295, 0.0851, 0.1775) | polishing |
| 7 | (0.512, 0.19, 0.007, 0.047, 0.226) | (0.3475, 0.2424, 0.1637, 0.1114, 0.1351) | polished rice |
| 8 | (0.113, 1.89, 0.007, 0.832, 0.226) | (0.3258, 0.2805, 0.1541, 0.1147, 0.1249) | polished rice |
| Stage | ZEA (μg/kg) | AFB1 (μg/kg) | Mercury (mg/kg) | Lead (mg/kg) | Chromium (mg/kg) |
|---|---|---|---|---|---|
| Paddy rice | 0.3635 | 0.1769 | 0.0988 | 0.0465 | 0.3144 |
| Husking | 0.4521 | 0.2176 | 0.1341 | 0.0817 | 0.1145 |
| Polishing | 0.3458 | 0.2423 | 0.1622 | 0.1095 | 0.1402 |
| Polished rice | 0.3475 | 0.2624 | 0.7771 | 0.1114 | 0.1351 |
| Level | AIVILNs | |||
|---|---|---|---|---|
| Paddy Rice | Husking | Polishing | Polished Rice | |
| I | ||||
| II | ||||
| III | ||||
| IV | ||||
| V | ||||
| VI | ||||
| Level | ZEA | AFB1 | Mercury | Lead | Chromium |
|---|---|---|---|---|---|
| I | (2.6, 2.9, 210/6, 4/18) | (0.43, 0.45, 158/6, 1/18) | (0.00087, 0.00088, 10/6, 0.01) | (0.0087, 0.0088, 6/6, 0.12) | (0.043, 0.045, 30/6, 0.03) |
| II | (16.56, 16.8, 178/6, 8/18) | (2.76, 2.8, 153/6, 1/18) | (0.0055, 0.0057, 10/6, 0.01) | (0.055, 0.057, 6/6, 0.03) | (0.276, 0.28, 28/6, 0.01) |
| III | (29.4, 30.6, 145/6, 15/18) | (4.9, 5.1, 147/6, 3/18) | (0.0098, 0.0102, 10/6, 0.002) | (0.098, 0.102, 6/6, 0.03) | (0.49, 0.51, 28/6, 0.01) |
| IV | (42.6, 44, 112/6, 12/18) | (7.09, 7.34, 142/6, 4/18) | (0.0142, 0.0147, 10/6, 0.03) | (0.142, 0.147, 6/6, 0.02) | (0.71, 0.73, 27/6, 0.02) |
| V | (55.8, 59.2, 110/6, 9/18) | (9.3, 9.8, 137/6, 2/18) | (0.0186, 0.0197, 10/6, 0.01) | (0.186, 0.197, 6/6, 0.10) | (0.93, 0.99, 27/6, 0.03) |
| VI | (6, 6.8, 2110/6, 5/18) | (10, 10.6, 135/6, 2/18) | (0.02, 0.028, 10/6, 0.01) | (0.2, 0.28, 6/6, 0.03) | (1, 1.04, 26/6, 0.01) |
| Stage | Membership Degrees | |||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | VI | |
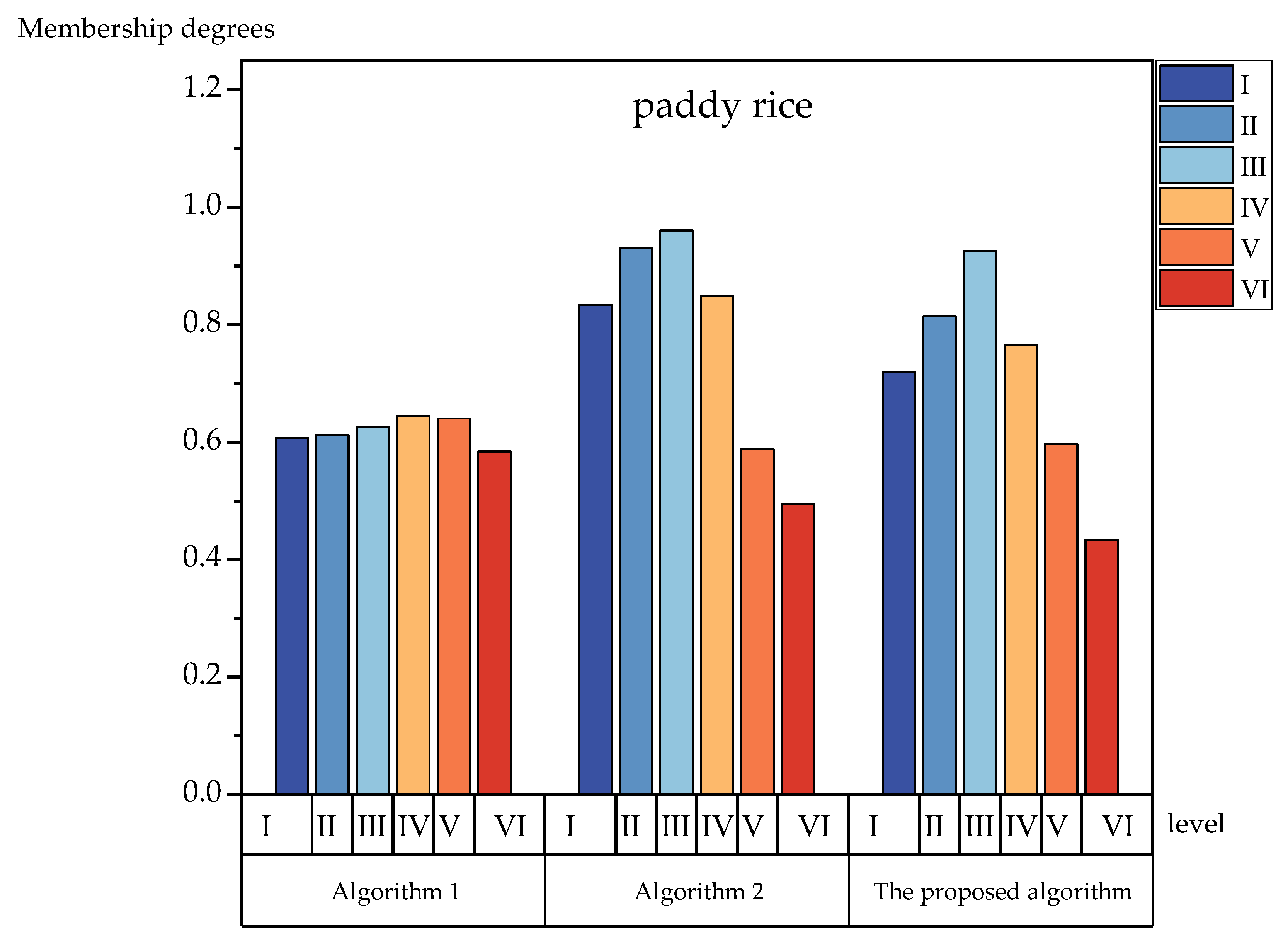
| paddy rice | 0.7389 | 0.8137 | 0.8456 | 0.7646 | 0.5965 | 0.5336 |
| husking | 0.9972 | 0.9635 | 0.8091 | 0.4200 | 0.1882 | 0.1405 |
| polishing | 0.9991 | 0.9957 | 0.7807 | 0.4143 | 0.2064 | 0.1611 |
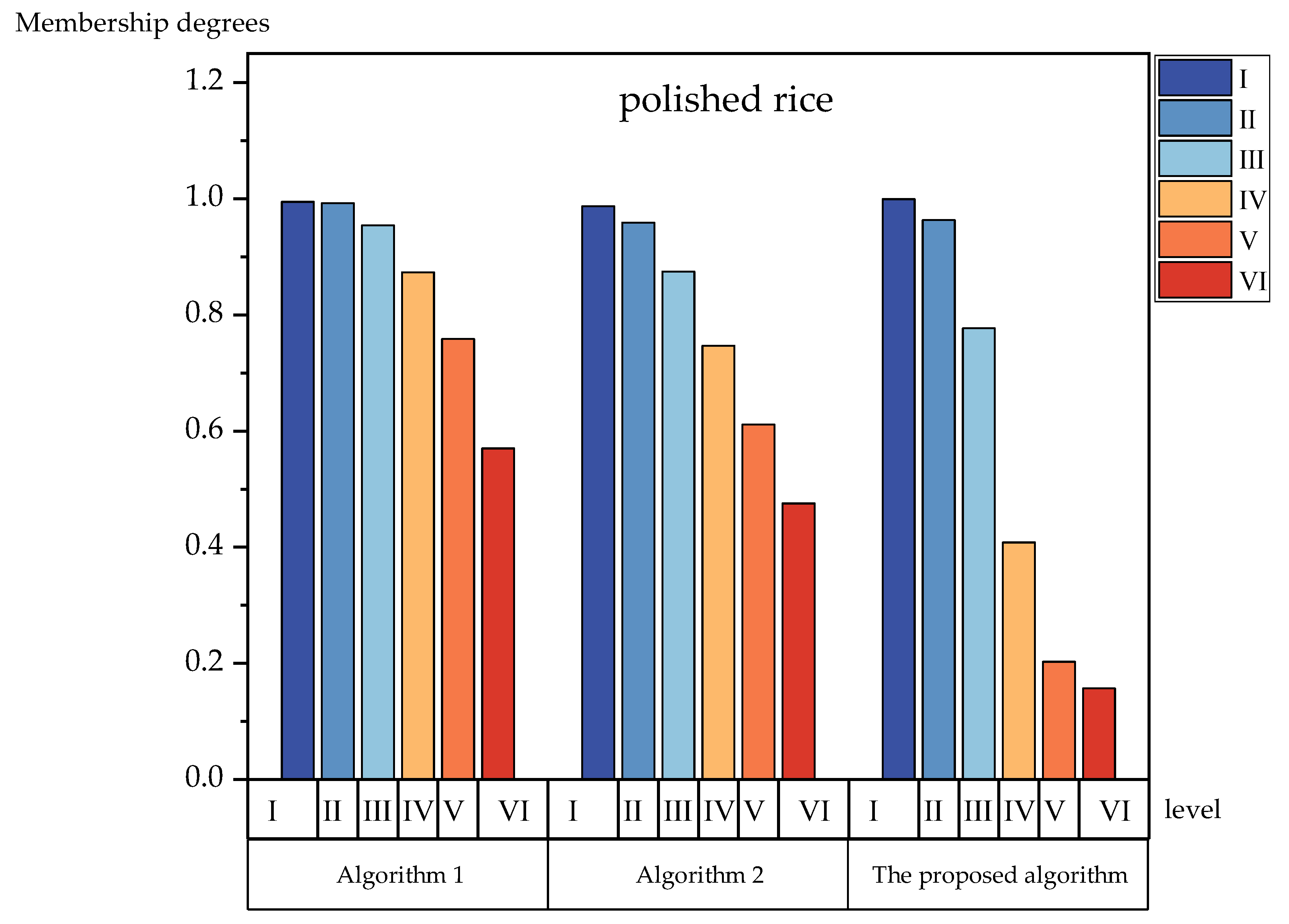
| polished rice | 0.9992 | 0.9632 | 0.7771 | 0.4083 | 0.2028 | 0.1570 |
| Algorithm | I | II | III | IV | V | VI | Evaluation Results |
|---|---|---|---|---|---|---|---|
| Algorithm 1 | 0.6067 | 0.6124 | 0.6262 | 0.6443 | 0.6401 | 0.5841 | IV |
| Algorithm 2 | 0.8337 | 0.9305 | 0.9606 | 0.8483 | 0.5877 | 0.4951 | III |
| The algorithm of the proposed method | 0.7189 | 0.8137 | 0.9256 | 0.7646 | 0.5965 | 0.4336 | III |
| Algorithm | I | II | III | IV | V | VI | Evaluation Results |
|---|---|---|---|---|---|---|---|
| Algorithm 1 | 0.9941 | 0.9961 | 0.9722 | 0.9109 | 0.8764 | 0.6298 | II |
| Algorithm 2 | 0.9975 | 0.9891 | 0.8542 | 0.8340 | 0.7036 | 0.6615 | I |
| The algorithm of the proposed method | 0.9972 | 0.9635 | 0.8091 | 0.4083 | 0.1882 | 0.1405 | I |
| Algorithm | I | II | III | IV | V | VI | Evaluation Results |
|---|---|---|---|---|---|---|---|
| Algorithm 1 | 0.9907 | 0.9919 | 0.9502 | 0.8799 | 0.7563 | 0.5871 | II |
| Algorithm 2 | 0.9912 | 0.9641 | 0.7833 | 0.7690 | 0.6438 | 0.6004 | I |
| The algorithm of the proposed method | 0.9991 | 0.9557 | 0.7807 | 0.4143 | 0.2064 | 0.1611 | I |
| Algorithm | I | II | III | IV | V | VI | Evaluation Results |
|---|---|---|---|---|---|---|---|
| Algorithm 1 | 0.9946 | 0.9923 | 0.9541 | 0.8735 | 0.7586 | 0.5703 | I |
| Algorithm 2 | 0.9871 | 0.9592 | 0.8746 | 0.7468 | 0.6111 | 0.4753 | I |
| The algorithm of the proposed method | 0.9992 | 0.9632 | 0.7771 | 0.4083 | 0.2028 | 0.1570 | I |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Chen, H.; Zhang, X.; Cui, X.; Zhao, Z. A Rice Hazards Risk Assessment Method for a Rice Processing Chain Based on a Multidimensional Trapezoidal Cloud Model. Foods 2023, 12, 1203. https://doi.org/10.3390/foods12061203
Yu J, Chen H, Zhang X, Cui X, Zhao Z. A Rice Hazards Risk Assessment Method for a Rice Processing Chain Based on a Multidimensional Trapezoidal Cloud Model. Foods. 2023; 12(6):1203. https://doi.org/10.3390/foods12061203
Chicago/Turabian StyleYu, Jiabin, Huimin Chen, Xin Zhang, Xiaoyu Cui, and Zhiyao Zhao. 2023. "A Rice Hazards Risk Assessment Method for a Rice Processing Chain Based on a Multidimensional Trapezoidal Cloud Model" Foods 12, no. 6: 1203. https://doi.org/10.3390/foods12061203
APA StyleYu, J., Chen, H., Zhang, X., Cui, X., & Zhao, Z. (2023). A Rice Hazards Risk Assessment Method for a Rice Processing Chain Based on a Multidimensional Trapezoidal Cloud Model. Foods, 12(6), 1203. https://doi.org/10.3390/foods12061203







