How Efficiently Do Elite US Universities Produce Highly Cited Papers?
Abstract
1. Introduction
2. Conceptual Framework
3. Methods
3.1. (Partial) Academic Production Frontier Analysis
3.1.1. Data Envelopment Analysis (DEA)
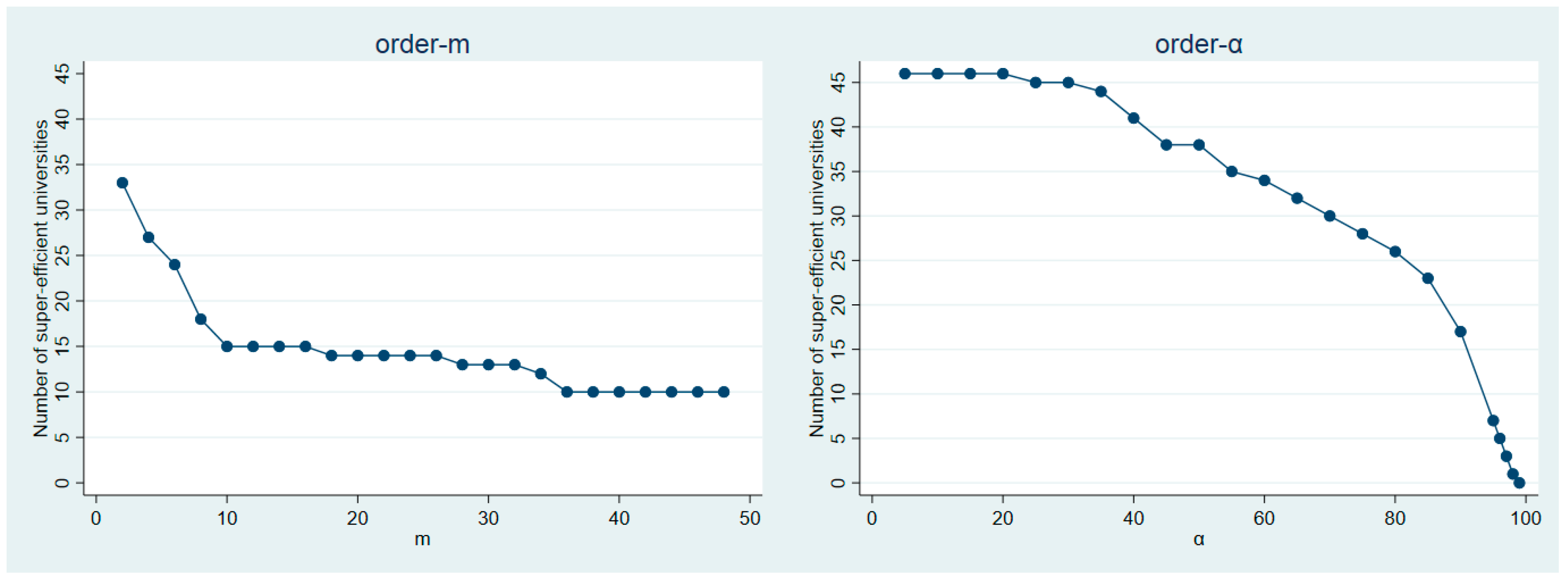
3.1.2. Order-m Efficiency
- Draw from a random sample of peer universities with replacement.
- A pseudo-FDH efficiency score ( is calculated using the artificially drawn data.
- Repeat steps 1 and 2 times.
- Order-m efficiency is calculated as the average of the pseudo-FDH scores
3.1.3. Order-α Efficiency
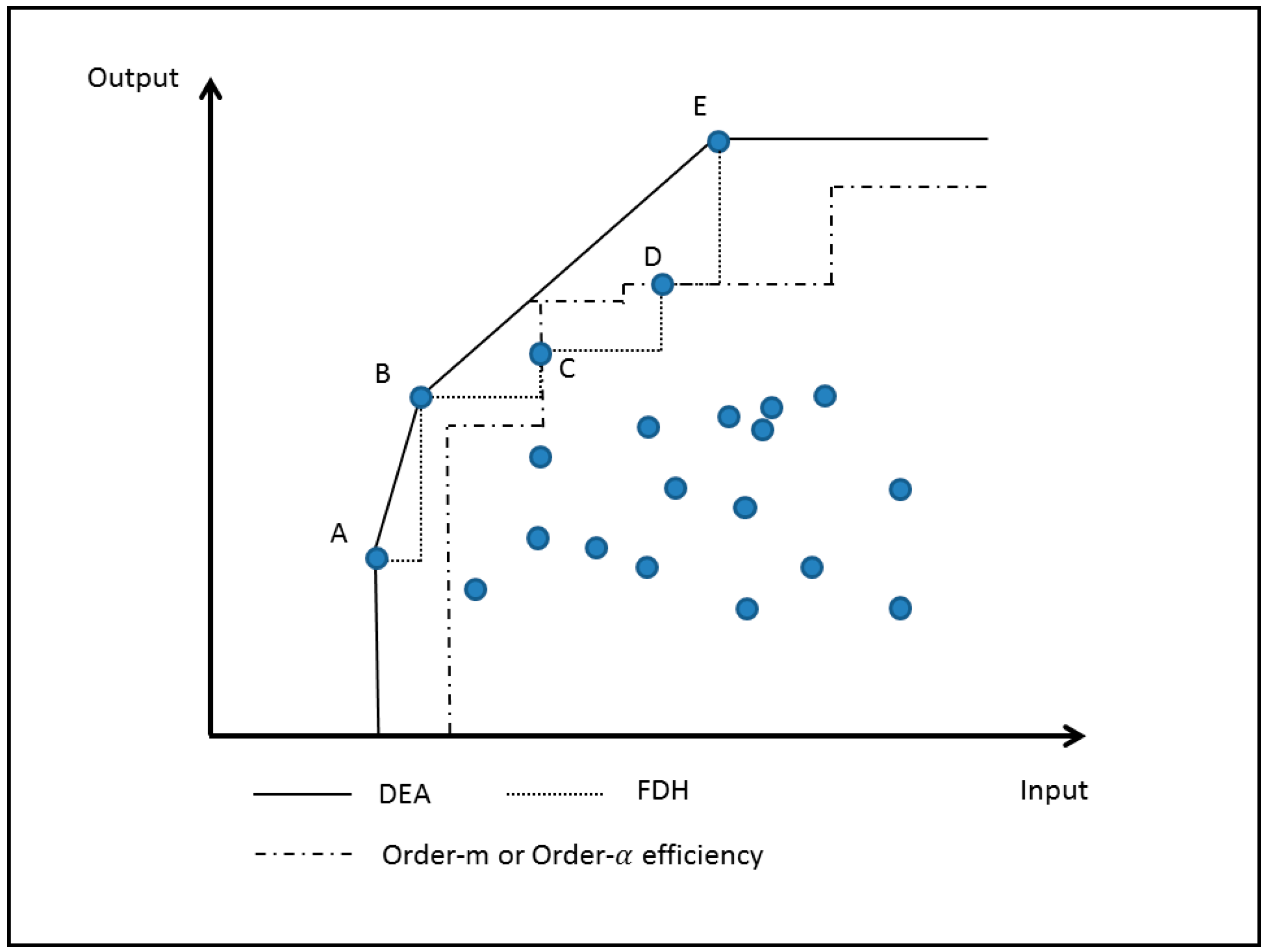
3.1.4. A Simple Example for Explaining the Approaches
3.1.5. Regression Analyses and Adjusted Efficiency Scores
3.2. Data
4. Results
4.1. Baseline Results
4.1.1. Results for 2013
4.1.2. Stability of the Results over Time
4.2. Adjusted Scores and Ranking Positions
4.2.1. Results for 2013
4.2.2. Stability of the Results over Time
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ziman, J. Real Science. What It Is, and What It Means; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bornmann, L. Scientific peer review. Annu. Rev. Inf. Sci. Technol. 2011, 45, 199–245. [Google Scholar] [CrossRef]
- Wilsdon, J.; Allen, L.; Belfiore, E.; Campbell, P.; Curry, S.; Hill, S.; Jones, R.; Kain, R.; Kerridge, S.; Thelwall, M.; et al. The Metric Tide: Report of the Independent Review of the Role of Metrics in Research Assessment and Management; Higher Education Funding Council for England (HEFCE): Bristol, UK, 2015. [Google Scholar]
- National Research Council. Furthering America’s Research Enterprise; The National Academies Press: Washington, DC, USA, 2014; p. 216. [Google Scholar]
- Tarango, J.; Hernandez-Gutierrez, P.Z.; Vazquez-Guzman, D. Evaluation of Scientific Production in Mexican State Public Universities (2007–2011) Using Principal Component Analysis. Prof. Inf. 2015, 24, 567–576. [Google Scholar] [CrossRef]
- Hazelkorn, E. Rankings and the Reshaping of Higher Education. The Battle for World-Class Excellence; Palgrave Macmillan: New York, NY, USA, 2011. [Google Scholar]
- Schmoch, U. The Informative Value of International University Rankings: Some Methodological Remarks. In Incentives and Performance; Welpe, I.M., Wollersheim, J., Ringelhan, S., Osterloh, M., Eds.; Springer International Publishing: New York, NY, USA, 2015; pp. 141–154. [Google Scholar]
- Daraio, C.; Bonaccorsi, A.; Simar, L. Rankings and university performance: A conditional multidimensional approach. Eur. J. Oper. Res. 2015, 244, 918–930. [Google Scholar] [CrossRef]
- Bornmann, L.; Stefaner, M.; de Moya Anegón, F.; Mutz, R. What is the effect of country-specific characteristics on the research performance of scientific institutions? Using multi-level statistical models to rank and map universities and research-focused institutions worldwide. J. Informetr. 2014, 8, 581–593. [Google Scholar] [CrossRef]
- Safón, V. What do global university rankings really measure? The search for the X factor and the X entity. Scientometrics 2013, 97, 223–244. [Google Scholar] [CrossRef]
- Moed, H.F.; Halevi, G. Multidimensional assessment of scholarly research impact. J. Assoc. Inf. Sci. Technol. 2015, 66, 1988–2002. [Google Scholar] [CrossRef]
- Abramo, G.; D’Angelo, C.A. A farewell to the MNCS and like size-independent indicators. J. Informetr. 2016, 10, 646–651. [Google Scholar] [CrossRef]
- Bornmann, L.; Haunschild, R. Efficiency of research performance and the glass researcher. J. Informetr. 2016, 10, 652–654. [Google Scholar] [CrossRef]
- Waltman, L.; van Eck, N.J.; Visser, M.; Wouters, P. The elephant in the room: The problem of quantifying productivity in evaluative scientometrics. J. Informetr. 2016, 10, 671–674. [Google Scholar] [CrossRef]
- Gralka, S.; Wohlrabe, K.; Bornmann, L. How to Measure Research Efficiency in Higher Education? Research Grants vs. Publication Output. J. High. Educ. Policy Manag. 2018, in press. [Google Scholar]
- Abramo, G.; D’Angelo, C. How do you define and measure research productivity? Scientometrics 2014, 101, 1129–1144. [Google Scholar] [CrossRef]
- Cazals, C.; Florens, J.P.; Simar, L. Nonparametric frontier estimation: A robust approach. J. Econom. 2002, 106, 1–25. [Google Scholar] [CrossRef]
- Aragon, Y.; Daouia, A.; Thomas-Agnan, C. Nonparametric frontier estimation: A conditional quantile-based approach. Econom. Theory 2005, 21, 358–389. [Google Scholar] [CrossRef]
- Lindsay, A.W. Institutional Performance in Higher-Education—The Efficiency Dimension. Rev. Educ. Res. 1982, 52, 175–199. [Google Scholar] [CrossRef]
- Bessent, A.M.; Bessent, E.W.; Charnes, A.; Cooper, W.W.; Thorogood, N.C. Evaluation of Educational-Program Proposals by Means of Dea. Educ. Adm. Q. 1983, 19, 82–107. [Google Scholar] [CrossRef]
- Worthington, A.C. An Empirical Survey of Frontier Efficiency Measurement Techniques in Education. Educ. Econ. 2001, 9, 245–268. [Google Scholar] [CrossRef]
- Rhaiem, M. Measurement and determinants of academic research efficiency: A systematic review of the evidence. Scientometrics 2017, 110, 581–615. [Google Scholar] [CrossRef]
- De Witte, K.; López-Torres, L. Efficiency in education: A review of literature and a way forward. J. Oper. Res. Soc. 2017, 68, 339–363. [Google Scholar] [CrossRef]
- Bonaccorsi, A.; Daraio, C.; Simar, L. Advanced indicators of productivity of universities. An application of robust nonparametric methods to Italian data. Scientometrics 2006, 66, 389–410. [Google Scholar] [CrossRef]
- Bonaccorsi, A.; Daraio, C.; Raty, T.; Simar, L. Efficiency and University Size: Discipline-Wise Evidence from European Universities; MPRA Paper 10265; University Library of Munich: Munich, Germany, 2007. [Google Scholar]
- De Witte, K.; Rogge, N.; Cherchye, L.; Van Puyenbroeck, T. Accounting for economies of scope in performance evaluations of university professors. J. Oper. Res. Soc. 2013, 64, 1595–1606. [Google Scholar] [CrossRef]
- Bruffaerts, C.; Rock, B.D.; Dehon, C. The Research Efficiency of US Universities: A Nonparametric Frontier Modelling Approach; Working Papers ECARES ECARES 2013-31; Universite Libre de Bruxelles: Bruxelles, Belgium, 2013. [Google Scholar]
- Gnewuch, M.; Wohlrabe, K. Super-efficiency of education institutions: An application to economics departments. Educ. Econ. 2018, in press. [Google Scholar] [CrossRef]
- Cohn, E.; Rhine, S.L.W.; Santos, M.C. Institutions of Higher-Education as Multi-Product Firms—Economies of Scale and Scope. Rev. Econ. Stat. 1989, 71, 284–290. [Google Scholar] [CrossRef]
- Harter, J.F.R.; Wade, J.A.; Watkins, T.G. An examination of costs at four-year public colleges and universities between 1989 and 1998. Rev. High. Educ. 2005, 28, 369–391. [Google Scholar] [CrossRef]
- Laband, D.N.; Lentz, B.F. Do costs differ between for-profit and not-for-profit producers of higher education? Res. High. Educ. 2004, 45, 429–441. [Google Scholar] [CrossRef]
- Sav, G.T. Stochastic Cost Inefficiency Estimates and Rankings of Public and Private Research and Doctoral Granting Universities. J. Knowl. Manag. Econ. Inf. Technol. 2012, 4, 11–29. [Google Scholar]
- Agasisti, T.; Johnes, G. Efficiency, costs, rankings and heterogeneity: The case of US higher education. Stud. High. Educ. 2015, 40, 60–82. [Google Scholar] [CrossRef]
- Titus, M.A.; Vamosiu, A.; McClure, K.R. Are Public Master’s Institutions Cost Efficient? A Stochastic Frontier and Spatial Analysis. Res. High. Educ. 2017, 58, 469–496. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the Efficiency of Decision-Making Units. Eur. J. Oper. Res. 1979, 3, 338–339. [Google Scholar] [CrossRef]
- Bogetoft, P.; Otto, L. Benchmarking with DEA, SFA and R; Springer: New York, NY, USA, 2011. [Google Scholar]
- Wilson, P.W.; Clemson, S.C. FEAR 2.0: A Software Package for Frontier Analysis with R; Department of Economics, Clemson University: Clemson, SC, USA, 2013. [Google Scholar]
- Deprins, D.; Simar, L.; Tulkens, H. Measuring Labor-Efficiency in Post Offices. In Public Goods, Environmental Externalities and Fiscal Competition; Chander, P., Drèze, J., Lovell, C.K., Mintz, J., Eds.; Springer US: Boston, MA, USA, 2006; pp. 285–309. [Google Scholar]
- Daraio, C.; Simar, L. Advanced Robust and Nonparametric Methods in Efficiency Analysis: Methodology and Applications; Springer: Heidelberg, Germany, 2007. [Google Scholar]
- Agasisti, T.; Wolszczak-Derlacz, J. Exploring efficiency differentials between Italian and Polish universities, 2001–2011. Sci. Public Policy 2015, 43, 128–142. [Google Scholar] [CrossRef]
- StataCorp. Stata Statistical Software: Release 14; Stata Corporation: College Station, TX, USA, 2015. [Google Scholar]
- Bornmann, L.; de Moya Anegón, F.; Mutz, R. Do universities or research institutions with a specific subject profile have an advantage or a disadvantage in institutional rankings? A latent class analysis with data from the SCImago ranking. J. Am. Soc. Inf. Sci. Technol. 2013, 64, 2310–2316. [Google Scholar] [CrossRef]
- Angeles, G.; Cronin, C.; Guilkey, D.K.; Lance, P.M.; Sullivan, B.A. Guide to Longitudinal Program Impact Evaluation; Measurement, Learning & Evaluation Project: Chapel Hill, NC, USA, 2014. [Google Scholar]
- Bonaccorsi, A. Knowledge, Diversity and Performance in Europe—An Higher Education: A Changing Landscape; Edvard Elgar: Cheltenham, UK, 2014. [Google Scholar]
- Eumida. Final Study Report: Feasibility Study for Creating a European University Data Collection; European Commission, Research Directorate-General C-European Research Area Universities and Researchers: Brussels, Belgium, 2009. [Google Scholar]
- Abramo, G.; D’Angelo, C.A.; Pugini, F. The measurement of Italian universities’ research productivity by a non parametric-bibliometric methodology. Scientometrics 2008, 76, 225–244. [Google Scholar] [CrossRef]
- Warning, S. Performance differences in German higher education: Empirical analysis of strategic groups. Rev. Ind. Organ. 2004, 24, 393–408. [Google Scholar] [CrossRef]
- Glänzel, W.; Schöpflin, U. A Bibliometric Study on Aging and Reception Processes of Scientific Literature. J. Inf. Sci. 1995, 21, 37–53. [Google Scholar] [CrossRef]
- Waltman, L.; van Eck, N.J. The need for contextualized scientometric analysis: An opinion paper. In Proceedings of the 21st International Conference on Science and Technology Indicator, Valencia, Spain, 14–16 September 2016; pp. 541–549. [Google Scholar]
- Glänzel, W.; Thijs, B.; Debackere, K. Productivity, performance, efficiency, impact—What do we measure anyway?: Some comments on the paper “A farewell to the MNCS and like size-independent indicators” by Abramo and D’Angelo. J. Informetr. 2016, 10, 658–660. [Google Scholar] [CrossRef]
- Aagaard, K.; Schneider, J.W. Research funding and national academic performance: Examination of a Danish success story. Sci. Public Policy 2016, 43, 518–531. [Google Scholar] [CrossRef]
| 1. | There are also parametric approaches available (e.g., the stochastic frontier analysis, SFA), which have several disadvantages too. One disadvantage is that they rely on distributional assumptions; a specific functional form is required. The potential endogeneity of inputs cannot be accounted for. |
| 2. | |
| 3. | The data are from http://nces.ed.gov/ipeds/datacenter/InstitutionProfile.aspx?unitid=adafaeb2afaf. The database provides also research staff figures, which could have been considered additionally in our study. However, the reported figures do not seem to be consistent. In some cases, the reported research staff were far too low compared to the overall staff of a university. For other universities, numbers varied substantially over time. |
| 4. | There are a few exceptions (n = 7) where the academic year differs slightly across years. We adjusted the figures accordingly. |
| 5. | See http://www.scimagoir.com. We preferred Scopus over Web of Science data as the coverage of the Scopus database is much broader. |
| 2011 | 2012 | 2013 | ||||
|---|---|---|---|---|---|---|
| Research Expenses | Ptop 1% | Research Expenses | Ptop 1% | Research Expenses | Ptop 1% | |
| Mean | 514 | 254 | 521 | 277 | 523 | 225 |
| Median | 482 | 213 | 483 | 228 | 477 | 197 |
| Standard Deviation | 289 | 160 | 298 | 182 | 303 | 151 |
| Minimum | 38 | 35 | 37 | 19 | 36 | 24 |
| Maximum | 1265 | 1002 | 1321 | 1198 | 1372 | 977 |
| DEA | FDH | Order-α | Order-m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| THE | University | Score | Rank | Score | Rank | Score | Rank | Score | Rank |
| 1 | California Institute of Technology | 0.680 | 6 | 1.000 | 1 | 1.264 | 6 | 1.059 | 5 |
| 2 | Harvard University | 1.000 | 1 | 1.000 | 1 | 1.000 | 8 | 1.000 | 11 |
| 3 | Stanford University | 0.382 | 28 | 0.765 | 20 | 0.765 | 30 | 0.765 | 23 |
| 4 | Massachusetts Institute of Technology | 0.268 | 43 | 0.619 | 31 | 0.619 | 38 | 0.619 | 35 |
| 5 | Princeton University | 0.473 | 15 | 0.614 | 32 | 0.866 | 24 | 0.704 | 29 |
| 6 | University of California, Berkeley | 0.414 | 23 | 1.000 | 1 | 1.000 | 8 | 1.000 | 9 |
| 7 | Yale University | 0.444 | 18 | 0.720 | 25 | 0.720 | 34 | 0.732 | 27 |
| 8 | University of Chicago | 0.577 | 11 | 1.000 | 1 | 1.077 | 7 | 1.023 | 6 |
| 9 | University of California, Los Angeles | 0.409 | 24 | 0.897 | 14 | 0.897 | 20 | 0.897 | 16 |
| 10 | Columbia University | 0.475 | 14 | 1.000 | 1 | 1.000 | 8 | 1.000 | 10 |
| 11 | Johns Hopkins University | 0.249 | 45 | 0.584 | 34 | 0.584 | 41 | 0.584 | 37 |
| 12 | University of Pennsylvania | 0.460 | 17 | 1.000 | 1 | 1.000 | 8 | 1.000 | 11 |
| 13 | University of Michigan, Ann Arbor | 0.359 | 32 | 0.794 | 17 | 0.794 | 27 | 0.794 | 19 |
| 14 | Duke University | 0.309 | 35 | 0.766 | 19 | 0.766 | 29 | 0.766 | 22 |
| 15 | Cornell University | 0.656 | 7 | 1.000 | 1 | 1.000 | 8 | 1.014 | 8 |
| 16 | North-western University, Evanston | 0.545 | 13 | 1.000 | 1 | 1.000 | 8 | 1.019 | 7 |
| 17 | Carnegie Mellon University | 0.381 | 29 | 0.486 | 40 | 0.892 | 21 | 0.639 | 34 |
| 18 | University of Washington | 0.354 | 33 | 0.749 | 23 | 0.749 | 33 | 0.749 | 25 |
| 19 | Georgia Institute of Technology | 0.208 | 49 | 0.361 | 48 | 0.456 | 47 | 0.389 | 49 |
| 20 | University of Texas, Austin | 0.313 | 34 | 0.476 | 42 | 0.602 | 39 | 0.507 | 42 |
| 21 | University of Illinois at Urbana-Champaign | 0.261 | 44 | 0.349 | 49 | 0.492 | 45 | 0.406 | 48 |
| 22 | University of Wisconsin, Madison | 0.225 | 48 | 0.402 | 46 | 0.402 | 50 | 0.413 | 47 |
| 23 | University of California, Santa Barbara | 0.618 | 8 | 0.902 | 13 | 1.000 | 8 | 0.974 | 14 |
| 24 | New York University | 0.273 | 41 | 0.472 | 43 | 0.472 | 46 | 0.484 | 43 |
| 25 | University of California, San Diego | 0.306 | 36 | 0.761 | 21 | 0.761 | 31 | 0.762 | 24 |
| 26 | Washington University in Saint Louis | 0.439 | 19 | 0.760 | 22 | 0.760 | 32 | 0.779 | 20 |
| 27 | University of Minnesota, Twin Cities | 0.240 | 46 | 0.416 | 44 | 0.448 | 48 | 0.425 | 46 |
| 28 | University of North Carolina, Chapel Hill | 0.364 | 31 | 0.594 | 33 | 0.594 | 40 | 0.605 | 36 |
| 29 | Brown University | 0.799 | 4 | 1.000 | 1 | 1.834 | 2 | 1.329 | 2 |
| 30 | University of California, Davis | 0.276 | 40 | 0.512 | 38 | 0.551 | 42 | 0.524 | 40 |
| 31 | Boston University | 0.782 | 5 | 1.000 | 1 | 1.410 | 3 | 1.156 | 3 |
| 32 | Pennsylvania State University | 0.192 | 50 | 0.329 | 50 | 0.416 | 49 | 0.354 | 50 |
| 33 | Ohio State University, Columbus | 0.386 | 26 | 0.713 | 26 | 0.879 | 22 | 0.738 | 26 |
| 34 | Rice University | 0.805 | 3 | 1.000 | 1 | 1.383 | 4 | 1.125 | 4 |
| 35 | University of Southern California | 0.468 | 16 | 0.742 | 24 | 0.939 | 18 | 0.799 | 18 |
| 36 | Michigan State University | 0.299 | 37 | 0.477 | 41 | 0.672 | 36 | 0.521 | 41 |
| 37 | University of Arizona | 0.283 | 39 | 0.388 | 47 | 0.547 | 43 | 0.450 | 44 |
| 38 | University of Notre Dame | 0.603 | 10 | 0.856 | 15 | 1.000 | 8 | 0.937 | 15 |
| 39 | Tufts University | 0.554 | 12 | 0.689 | 27 | 0.953 | 17 | 0.776 | 21 |
| 40 | University of California, Irvine | 0.414 | 22 | 0.578 | 35 | 0.815 | 25 | 0.680 | 30 |
| 41 | University of Pittsburgh | 0.289 | 38 | 0.534 | 37 | 0.658 | 37 | 0.554 | 38 |
| 42 | Emory University | 0.399 | 25 | 0.625 | 29 | 0.790 | 28 | 0.667 | 32 |
| 43 | Vanderbilt University | 0.431 | 21 | 0.793 | 18 | 0.977 | 16 | 0.818 | 17 |
| 44 | University of Colorado, Boulder | 0.432 | 20 | 0.572 | 36 | 0.806 | 26 | 0.657 | 33 |
| 45 | Purdue University | 0.383 | 27 | 0.661 | 28 | 0.932 | 19 | 0.721 | 28 |
| 46 | University of California, Santa Cruz | 0.618 | 9 | 0.826 | 16 | 1.368 | 5 | 0.982 | 13 |
| 47 | Case Western Reserve University | 0.272 | 42 | 0.495 | 39 | 0.698 | 35 | 0.544 | 39 |
| 48 | University of Rochester | 0.368 | 30 | 0.620 | 30 | 0.874 | 23 | 0.677 | 31 |
| 49 | Boston College | 1.000 | 1 | 1.000 | 1 | 3.018 | 1 | 1.856 | 1 |
| 50 | University of Florida | 0.237 | 47 | 0.405 | 45 | 0.511 | 44 | 0.435 | 45 |
| THE | DEA | FDH | order-α | order-m | |
|---|---|---|---|---|---|
| THE | 1.000 | ||||
| DEA | 0.073 | 1.000 | |||
| FDH | 0.299 | 0.840 | 1.000 | ||
| order-α | 0.035 | 0.927 | 0.890 | 1.000 | |
| order-m | 0.205 | 0.899 | 0.980 | 0.942 | 1.000 |
| DEA | FDH | ||||||
|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2011 | 2012 | 2013 | ||
| 2011 | 1.00 | 2011 | 1.00 | ||||
| 2012 | 0.95 | 1.00 | 2012 | 0.84 | 1.00 | ||
| 2013 | 0.93 | 0.96 | 1.00 | 2013 | 0.85 | 0.84 | 1.00 |
| order-α | order-m | ||||||
| 2011 | 1.00 | 2011 | 1.00 | ||||
| 2012 | 0.91 | 1.00 | 2012 | 0.86 | 1.00 | ||
| 2013 | 0.88 | 0.91 | 1.00 | 2013 | 0.87 | 0.89 | 1.00 |
| DEA | FDH | order-α | order-m | |
|---|---|---|---|---|
| Life sciences | −0.45 | −01.20 * | −00.46 | −00.99 |
| (−01.90) | (−02.41) | (−00.65) | (−01.83) | |
| Physical sciences | −01.43 * | −03.65 * | −01.39 | −02.99 |
| (−02.26) | (−02.52) | (−00.67) | (−01.91) | |
| Social sciences | −00.35 | −01.02 * | −00.17 | −00.74 |
| (−01.90) | (−02.36) | (−00.27) | (−01.54) | |
| Health sciences | −01.08 * | −02.60 * | −01.08 | −02.16 |
| (−02.51) | (−02.53) | (−00.73) | (−01.95) | |
| Private state | 0.18 *** | 0.14 | 0.33 ** | 0.21 * |
| (3.94) | (1.77) | (2.89) | (2.48) | |
| Constant | 0.34 *** | 0.63 *** | 0.69 *** | 0.65 *** |
| (10.36) | (10.38) | (7.65) | (8.82) | |
| Universities | 50 | 50 | 50 | 50 |
| University | DEA | DEA Adjust. | FDH | FDH Adjust. | order-α | order-α Adjust. | order-m | order-m Adjust. |
|---|---|---|---|---|---|---|---|---|
| Harvard University | 1 | 1 | 1 | 17 | 8 | 17 | 11 | 16 |
| Brown University | 4 | 2 | 1 | 6 | 2 | 1 | 2 | 1 |
| Rice University | 3 | 3 | 1 | 5 | 4 | 5 | 4 | 6 |
| Boston University | 5 | 4 | 1 | 9 | 3 | 6 | 3 | 8 |
| University of California, Santa Barbara | 8 | 5 | 13 | 3 | 8 | 11 | 14 | 7 |
| University of California, Santa Cruz | 9 | 6 | 16 | 14 | 5 | 3 | 13 | 3 |
| California Institute of Technology | 6 | 7 | 1 | 7 | 6 | 4 | 5 | 4 |
| Tufts University | 12 | 8 | 27 | 23 | 17 | 8 | 21 | 18 |
| Boston College | 1 | 9 | 1 | 19 | 1 | 2 | 1 | 2 |
| Cornell University | 7 | 10 | 1 | 8 | 8 | 22 | 8 | 14 |
| University of California, Los Angeles | 24 | 11 | 14 | 1 | 20 | 7 | 16 | 5 |
| Ohio State University, Columbus | 26 | 12 | 26 | 13 | 22 | 9 | 26 | 12 |
| University of California, Irvine | 22 | 13 | 35 | 31 | 25 | 14 | 30 | 21 |
| University of Michigan, Ann Arbor | 32 | 14 | 17 | 12 | 27 | 10 | 19 | 10 |
| Northwestern University, Evanston | 13 | 15 | 1 | 4 | 8 | 21 | 7 | 11 |
| University of North Carolina, Chapel Hill | 31 | 16 | 33 | 28 | 40 | 33 | 36 | 30 |
| University of Pittsburgh | 38 | 17 | 37 | 24 | 37 | 15 | 38 | 20 |
| Purdue University | 27 | 18 | 28 | 15 | 19 | 13 | 28 | 15 |
| University of Notre Dame | 10 | 19 | 15 | 11 | 8 | 47 | 15 | 23 |
| University of Colorado, Boulder | 20 | 20 | 36 | 35 | 26 | 26 | 33 | 34 |
| University of Chicago | 11 | 21 | 1 | 20 | 7 | 32 | 6 | 24 |
| University of Pennsylvania | 17 | 22 | 1 | 10 | 8 | 19 | 11 | 13 |
| University of Southern California | 16 | 23 | 24 | 22 | 18 | 30 | 18 | 27 |
| Washington University in Saint Louis | 19 | 24 | 22 | 29 | 32 | 28 | 20 | 25 |
| Vanderbilt University | 21 | 25 | 18 | 18 | 16 | 18 | 17 | 19 |
| University of California, Davis | 40 | 26 | 38 | 26 | 42 | 20 | 40 | 22 |
| Emory University | 25 | 27 | 29 | 34 | 28 | 25 | 32 | 33 |
| University of Arizona | 39 | 28 | 47 | 40 | 43 | 36 | 44 | 38 |
| University of California, Berkeley | 23 | 29 | 1 | 2 | 8 | 16 | 9 | 9 |
| Georgia Institute of Technology | 49 | 30 | 48 | 32 | 47 | 29 | 49 | 32 |
| University of Florida | 47 | 31 | 45 | 30 | 44 | 27 | 45 | 29 |
| University of California, San Diego | 36 | 32 | 21 | 21 | 31 | 12 | 24 | 17 |
| University of Minnesota, Twin Cities | 46 | 33 | 44 | 41 | 48 | 40 | 46 | 41 |
| University of Texas, Austin | 34 | 34 | 42 | 38 | 39 | 43 | 42 | 44 |
| University of Rochester | 30 | 35 | 30 | 36 | 23 | 23 | 31 | 35 |
| Columbia University | 14 | 36 | 1 | 16 | 8 | 37 | 10 | 28 |
| University of Washington | 33 | 37 | 23 | 25 | 33 | 31 | 25 | 26 |
| University of Wisconsin, Madison | 48 | 38 | 46 | 42 | 50 | 41 | 47 | 40 |
| Case Western Reserve University | 42 | 39 | 39 | 44 | 35 | 24 | 39 | 36 |
| Michigan State University | 37 | 40 | 41 | 33 | 36 | 42 | 41 | 43 |
| Yale University | 18 | 41 | 25 | 43 | 34 | 46 | 27 | 45 |
| University of Illinois at Urbana-Champaign | 44 | 42 | 49 | 46 | 45 | 45 | 48 | 46 |
| Carnegie Mellon University | 29 | 43 | 40 | 45 | 21 | 38 | 34 | 42 |
| Johns Hopkins University | 45 | 44 | 34 | 39 | 41 | 35 | 37 | 37 |
| Duke University | 35 | 45 | 19 | 27 | 29 | 34 | 22 | 31 |
| Stanford University | 28 | 46 | 20 | 37 | 30 | 39 | 23 | 39 |
| Princeton University | 15 | 47 | 32 | 48 | 24 | 48 | 29 | 48 |
| Pennsylvania State University | 50 | 48 | 50 | 47 | 49 | 49 | 50 | 49 |
| New York University | 41 | 49 | 43 | 50 | 46 | 50 | 43 | 50 |
| Massachusetts Institute of Technology | 43 | 50 | 31 | 49 | 38 | 44 | 35 | 47 |
| DEA | FDH | ||||||
|---|---|---|---|---|---|---|---|
| 2011 | 2012 | 2013 | 2011 | 2012 | 2013 | ||
| 2011 | 1.00 | 2011 | 1.00 | ||||
| 2012 | 0.92 | 1.00 | 2012 | 0.65 | 1.00 | ||
| 2013 | 0.91 | 0.93 | 1.000 | 2013 | 0.75 | 0.72 | 1.00 |
| order-α | order-m | ||||||
| 2011 | 1.00 | 2011 | 1.00 | ||||
| 2012 | 0.86 | 1.00 | 2012 | 0.76 | 1.00 | ||
| 2013 | 0.88 | 0.89 | 1.00 | 2013 | 0.82 | 0.82 | 1.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wohlrabe, K.; de Moya Anegon, F.; Bornmann, L. How Efficiently Do Elite US Universities Produce Highly Cited Papers? Publications 2019, 7, 4. https://doi.org/10.3390/publications7010004
Wohlrabe K, de Moya Anegon F, Bornmann L. How Efficiently Do Elite US Universities Produce Highly Cited Papers? Publications. 2019; 7(1):4. https://doi.org/10.3390/publications7010004
Chicago/Turabian StyleWohlrabe, Klaus, Félix de Moya Anegon, and Lutz Bornmann. 2019. "How Efficiently Do Elite US Universities Produce Highly Cited Papers?" Publications 7, no. 1: 4. https://doi.org/10.3390/publications7010004
APA StyleWohlrabe, K., de Moya Anegon, F., & Bornmann, L. (2019). How Efficiently Do Elite US Universities Produce Highly Cited Papers? Publications, 7(1), 4. https://doi.org/10.3390/publications7010004





