Abstract
In the second edition of The Selfish Gene, Richard Dawkins included a short bibliometric analysis of key papers instrumental to the sociobiological revolution, the intention of which was to support his proposal that ideas spread within a population in an epidemiological manner. In his analysis, Dawkins primarily discussed the influence of an article by British evolutionary biologist William Donald Hamilton which had introduced the concept of “inclusive fitness”, and he argued that citations to it were accumulating in a very different manner to two other seminal papers, demonstrating the appearance and spread of a new “meme” in academic circles. This paper re-examines Dawkins’ original analysis and the conclusions drawn from it, and updates those conclusions based on citation data accumulated in the intervening three decades since publication. This updated analysis shows that patterns of citation for the three papers, and Dawkins’ book itself, are actually remarkably similar and show no qualitative difference in citation growth. The data are well described by a two-phase exponential model of citation growth in which citations accumulate rapidly and then saturate at a slower level of growth dictated primarily by the general increase in scientific production. It is speculated that this two-phase exponential growth, with some modification to account for papers that are not immediately discovered, may be a signature that will help to reveal the emergence of genuinely novel ideas within the academic literature.
1. Introduction
The goal of this paper is to critically reappraise a well-known bibliometric study by Richard Dawkins [1] of several key papers from the field of sociobiology [2,3,4]. Bibliometrics is the quantitative study of publishing and citation patterns and a term first used by Otlet [5,6] and defined by Prichard [7] as “the application of mathematics and statistical methods to books and other media of communication.” From the development of the Science Citation Index, [8] through the pioneering work by Price [9] to the introduction of the Impact Factor [10] and into the modern era, bibliometric data has been used—and abused—in a variety of ways. It has been used as an administrative tool to optimise library resources [11], and it can also be of great use in separating fact from opinion in issues of research policy, such as in the ongoing debate regarding the Open Access “citation advantage” [12,13,14,15,16]. In the immediate future it is also likely to have a role to play in establishing the relevance, or otherwise, of web-based alternative metrics—or “altmetrics” [17]—for the evaluation of research outputs [18]. Bibliometrics can also be used to provide revealing insights into the global growth and development of science [19] and it has a potentially important role to play in the history of ideas, countering spurious revisionist claims regarding the development of various branches of science [20]. Worrying revisionist interpretations of the history of science are often driven by political and religious agendas [21] and the progress of science is occasionally hampered by the fact that scientists’ own rationalist worldview can often blind them to poor science that confirms their existing biases [22,23]. Bibliometrics can provide quantitative evidence to back up such claims.
One such claim regarding the development of an academic field can be found in an unexpected source: Richard Dawkins’ 1976 popular science book The Selfish Gene [24]. It is difficult to overestimate the cultural influence of this work. It popularised the gene-centric perspective of evolutionary theory, was in equal measure lauded and derided, and established Dawkins as something more than a scientist or a populariser of science: it made him a celebrity.
As Dawkins freely admitted in the preface to the second edition [1], there was relatively little material in The Selfish Gene which originated with him. Instead, it was a book written for a popular audience that presented in a simple and entertaining manner the highly original but sometimes rather dry and densely mathematical research of a select group of other scientists. The emerging field attempted to find biological, evolutionary explanations for social behaviours and became popularly known as ‘sociobiology’ thanks largely to E.O. Wilson’s book of the same name [25].
Not content with being at the vanguard of one intellectual movement, in his book Dawkins unintentionally founded a new field of study: memetics. In an attempt to demonstrate the applicability of some ideas of evolutionary theory beyond the confines of mere biology, he posited the existence of the “meme”—a unit of culture analogous to the biological unit of inheritance, the gene. Memes are ideas, tunes, concepts, symbols, etc. that are transmitted from mind to mind, thereby reproducing and occasionally mutating and giving rise to “endless forms most beautiful” [26]. His intention was to demonstrate that via cultural transmission of ideas and knowledge we can “rebel against the tyranny of the selfish replicators”, effectively saying that humans are no longer slaves to their genetic programming. As a field of study, memetics has not fared terribly well, perhaps representing an analogy too far for most scientists.
In the second edition of The Selfish Gene [1] an endnote was added (pp. 325–329) supporting the idea that ideas spread within a population in an epidemiological manner. In this endnote, Dawkins discussed the influence of an article by British evolutionary biologist William Donald Hamilton [2] which had been instrumental in the sociobiological revolution. Hamilton had proposed and mathematically described the concept of “inclusive fitness” as a basis for the evolution of altruism. Briefly, inclusive fitness is the theory that genes for altruistic (self-sacrificial) behaviours will be favoured by natural selection if the altruistic acts they encourage result in the survival and propagation of those same genes in the individual performing the altruistic act, or those individuals that survive or are aided by the altruistic act. In other words, a gene is “selfish” in that it acts to ensure its survival and reproduction not just in the individual that contains it, but in other related individuals that are also likely to carry it. In his endnote, Dawkins used bibliometric data from the Science Citation Index to chart the increase in citations to Hamilton’s paper, which he argues demonstrated the spread of the idea for inclusive fitness within the academic population.
Dawkins’ bibliometric analysis covered the years 1964 to 1985 and showed what he argued was an exponential increase in citations to Hamilton’s inclusive fitness paper. “Any growth process,” Dawkins argued, “where rate of growth is proportional to size already attained, is called exponential growth” and he went on to explain how epidemics demonstrate exponential growth as the number of people infected grows in proportion to the number already infected. Dawkins continues: “It is diagnostic of an exponential curve that it becomes a straight line when plotted on a logarithmic scale. If the spread of Hamilton’s meme was really like a gathering epidemic, the points on a cumulative logarithmic graph should fall on a single straight line.” This is not strictly true, as exponential curves only fit a straight line on semi-logarithmic plots where citations are plotted logarithmically whilst time is represented linearly, but Dawkins goes on to plot the cumulative citations to Hamilton [2] on a semi-logarithmic scale, where they do indeed fit a straight line with a steep gradient.
He compares this pattern of growth in citations to Hamilton [2] with several other influential works from evolutionary biology [3,4,27] which, although they show large and increasing numbers of citations, do not seem to show the straight line that he argues is diagnostic of explosive growth caused by the adoption of a new meme by the academic community. Instead, these other publications appear to show a decelerating curve: “Any cumulative curve would, of course, rise even if the rate of citations per year were constant. But on the logarithmic scale it would rise at a steadily slower rate: it would tail off.” Dawkins concludes from this analysis that there is “something special about the Hamilton meme”.
Curiously, this bibliometric analysis has not been updated in the editions produced for the thirtieth and fortieth anniversaries of The Selfish Gene [28,29]. This paper aims to examine Dawkins’ original analysis and the conclusions drawn from it and, if necessary to update those conclusions based on citation data accumulated in the intervening three decades since publication of the second edition of The Selfish Gene.
2. Materials and Methods
Data on citations to Hamilton [2] were obtained in November 2016 from the Web of Science™ Core Collection. Updated citation data was also obtained on the papers by Trivers [3] and Maynard Smith and Price [4] that were previously analysed by Dawkins. The other publication investigated by Dawkins was a book [27] and I analyse the pattern of citations to this book, and The Selfish Gene itself separately, as citations of books are likely to show different citation patterns as journal articles.
Data for yearly citations and cumulative citations showed a clear two-phase pattern of exponential growth (see Figure 1 and Figure 2) and were therefore fitted with a two-segment exponential curve where each segment of the curve was fitted with a least squares fit of an exponential curve of the form:
where c and b are constants and e is the base of the natural logarithm. The “knee-point” at which the data were split was ascertained by maximising the average of the R2 values for both segments. As a test of the appropriateness of this two-phase model, the cumulative citation data were also fit with a single power curve of the form:
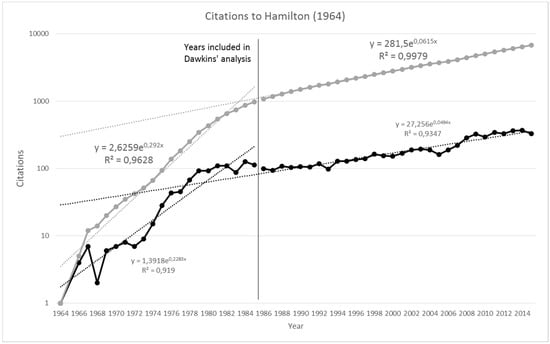
Figure 1.
Yearly citations (black) and cumulative citations (grey) to Hamilton (1964).
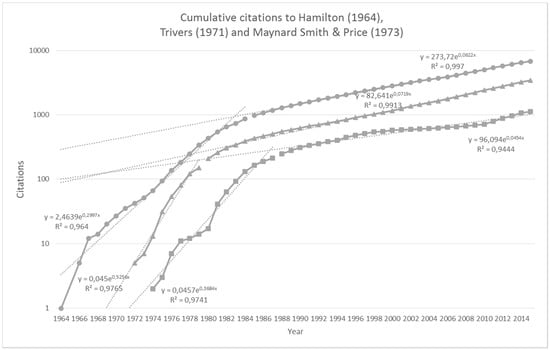
Figure 2.
Cumulative citations to Hamilton (circles), Trivers (triangles) and Smith and Price (squares).
3. Results
Citations per year for the Hamilton paper are presented in Figure 1 (black lines) and cumulative citations are presented in the same figure (grey lines). The data have been split into those years included in Dawkins’ analysis (1964–1985) and subsequent years (1986–2015) separated by the vertical line. The two-phase exponential model outlined in the previous section does a good job of fitting this data, but moving the knee-point from 1985–1986 to 1984–1985 (see Figure 2) increases the average R2 further (see Table 1).

Table 1.
R2 values for two-phase exponential fit and power fit. Best fits for each paper identified with an asterisk (*).
Due to the fact that Dawkins used the Science Citation Index available at the time and the database used in this study is the Web of Science™ Core Collection, which includes the Science Citation Index (Expanded) and various other scholarly databases, the data obtained for the years 1964–1985 are not identical to those produced by Dawkins. However, this dataset clearly replicates Dawkins’ analysis. Over the years covered by the original analysis, there was indeed an explosion of interest in Hamilton’s work, with citations to his paper increasing at a rate of almost 30% per year. The curve for cumulative citations over this initial period still shows up as a straight line indicating exponential growth, as it did in Dawkins’ initial study.
The first question we are concerned with here is whether this exponential growth has continued unchecked subsequent to the publication of this analysis in the second edition of The Selfish Gene [1]. Already in Dawkins’ data we can see a levelling off of the rate of citation in the last few years of his analysis, which might make one suspicious that citations to Hamilton’s paper were reaching a plateau.
This drop-off in the rate of citation growth beginning approximately around the year 1982 is also replicated here, and analysis of the citation data from the years 1986 to 2015 show that it reflects the growth in the number of citations slowing to a rate of around 6% per year. The curve for cumulative citations still fits a straight line, suggesting that the spread of the inclusive fitness idea continues to increases exponentially, albeit at a much slower rate.
Curiously, as can be seen in Figure 2, the papers on reciprocal altruism [3] and evolutionarily stable strategies [4] initially rejected by Dawkins as not demonstrating the sort of explosive growth shown by the Hamilton paper, seem here to show roughly the same pattern of citation. With the longer perspective available to us here, we can see that both of these papers also show an initial exponential growth in citations followed by a sudden convergence on a more modest rate of citation growth of around 5–7%. This convergence occurs around 1979–1980 for Trivers’ paper and around 1987–1988 for Smith and Price’s paper, the knee-point being determined by maximising the average R2 for both segments of the fit. The fact that the data is visibly noisier for the latter paper, as evidenced by the generally lower R2 values is almost certainly due to the smaller numbers of citations to this paper.
As a general test of the two-phase exponential model applied here, a power law fit was applied to the same data to determine whether this provided a better model of citation growth (see Section 2). As can be seen in Table 1, the two-phase exponential provided a better fit to the citation data for all three papers.
The same can be said for at least one of the two books under investigation. An analysis of the growth in citations in the Web of Science™ Core Collection to the various editions of The Selfish Gene shows a pattern very reminiscent of that shown by the journal articles discussed above, with the exception that the initial phase of citation is even more explosive than the articles it cites, with an exponent of around 1. This very steep initial phase means that the technique of identifying the knee-point by using the mean R2 of the two segments is derailed by the influence of the first segment, which converges rapidly on 1 when the number of datapoints is reduced. However, if the knee-point is identified in a more subjective manner (as I have done in Figure 3), then the growth in citations to The Selfish Gene seems to saturate at a very similar rate as the very papers it discusses, with an exponent of approximately 0.07.
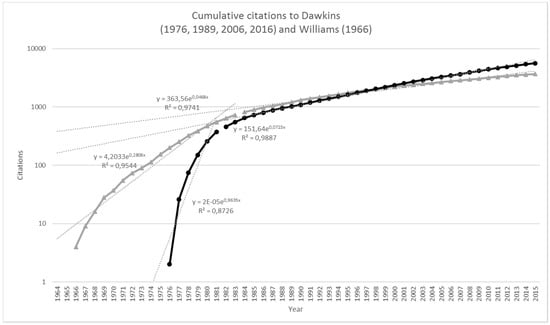
Figure 3.
Cumulative citations to the various editions of The Selfish Gene (black circles) and Adaptation and Natural Selection (grey triangles).
The pattern observed for citations to Williams [27], however, is somewhat different, with a cumulative citation curve that does not appear as a straight line, or even a combination of straight lines with a distinct knee-point. Instead, the increase in citations to Williams’ book follows a gentler curve, with the rate of citation growth gradually declining over the years. Indeed, unlike the three journal articles and The Selfish Gene, the data are better fit with a power function than with a two-phase exponent, as shown in Table 2.

Table 2.
R2 values for two-phase exponential fit and power fit. Best fits for each book identified with an asterisk (*).
4. Discussion
With the benefit of hindsight, we can see that the patterns of citation for the three journal articles discussed by Dawkins are actually remarkably similar. Dawkins distinguished between Hamilton’s paper [2] and the others [3,4] based on his observation that citations to these later papers had seemingly begun to level off. We can see now that citations to all three papers follow the same pattern, an initial steep exponential increase with citations increasing by 30–50% per year, followed by a second phase at which the increase in citations levels off at around 5–7%. Trivers’ paper simply reached this point earlier (around 1979–80, according to this analysis) and the levelling off in citations to Smith and Price’s paper observed by Dawkins looks to be actually be a temporary dip, perhaps caused by the fact that a generally smaller number of citations will naturally lead to noisier data. Citations to Dawkins’ book itself follow a very similar pattern, and although the two-exponent model does not fit the data for Williams’ book, citations to both books continue to increase at the 5–7% rate identified for the journal articles.
It is possible that a two-phase exponential pattern of citations reflects, firstly, the initial epidemic spread of new ideas, or “memes” to use Dawkins’ term, through the academic community and, secondly, the point at which those ideas reach saturation. A corollary to this saturation is the potential for an idea to reach a point at which researchers no longer feel the need to explicitly cite the original source, something that has been called variously “obliteration by incorporation” (OBI) [30] or “citation oblivion” [31]. Recent work on OBI by McCain [32] included a detailed investigated of one of the articles also investigated here: Smith and Price [4]. McCain showed that by the turn of the present century, 40% or more of the articles identified as being about evolutionarily stable strategies (ESS) did not actually cite either Smith and Price or one of the other appropriate articles by John Maynard Smith. This evidence that the ESS “meme” has to some extent reached an early level of citation obsolescence makes the continued exponential increase in citations observed here all the more surprising. The knee-point in the model presented here reflects the point at which the idea has pervaded the academic discourse to such an extent that those researchers who are likely to cite the paper, will do. This natural limit would be dictated by the size of the field and the numbers of researchers involved and their publication frequency. It may also reflect the spread of the idea to neighbouring fields. For example, Hamilton’s inclusive fitness idea, although originally proposed in the field of evolutionary biology and animal behaviour, rapidly spread to other fields where it is relevant, such as psychology. This spreading to neighbouring fields may provide a paper with a temporary ‘stay of execution’ before citing it finally becomes (in the minds of academics) obsolete.
Although citation growth saturates eventually, citations per year are still increasing at an exponential rate of 5–7% for all the works investigated here. They have neither slowed nor reached a plateau. A decrease in the rate of citation would be evidence of a discontinuation in the relevance of these ideas, and since they propose fundamental laws of biology and evolution it is not surprising that we do not see this. There is also another very good reason why we do not see a plateau. Scientific publication generally over the period under investigation here has shown exponential growth. Recent bibliometric analyses have suggested that global scientific output—measured indirectly in terms of the references cited in published papers—has increased at a rate of around 8–10% each year since the period between the World Wars [19,33]. This estimate rather exceeds the second (saturated) phase of citation growth of around 5–7% observed for the papers under investigation here, but other estimates of the growth in global scientific output based on published abstracts and articles are in this more moderate range. Price [34] established a growth estimate of 4.7% for the years 1907–1960 and recent work has suggested that this level of growth has been maintained in the period since 1960 with the caveat that growth is slowing in established scientific fields and increasing in newer fields [35]. Until global scientific production reaches a plateau, we will likely not see a similar plateau regarding citation rates to significant papers such as these.
Elucidating the rules that govern the time required for citation growth to saturate, and the level at which it saturates is a promising avenue for future work. Hamilton’s paper took 20 years to reach saturation, whilst Smith and Price’s took 14 years and Trivers’ took only 8 years. The remarkable similarity between the cumulative citation curves shown here is in marked contrast to the variation in curves shown in a study of Nobel-winning papers in physics [36]. Liu and Rousseau identified several different types of cumulative citation curve and argued that they reflect to some extent the dynamics of resistance to, and acceptance of, new ideas. Another hurdle to generalising this two-phase model is the fact that key papers can take varying time intervals to be discovered, the extreme example of this being so-called ‘sleeping beauties’ [37]. The two-phase model outlined here may need to be extended to incorporate a ‘dormant’ phase of varying duration before the initial exponential phase if it is to be generalised.
Dawkins’ analysis of these seminal papers was hampered by the paucity of data he had available at the time. He was observing citations to Hamilton’s paper during the initial explosive phase of citation growth and concluded that the relatively superficial difference in citation patterns between Hamilton’s paper and the others was due to a qualitative difference between the introduction of a paradigm-shifting “meme” into academic circles and what he identified as perhaps less ground-breaking, more incremental research. The updated analysis of citations presented here suggests that they all had significant influence and the ideas proposed in them spread quickly throughout the field. A systematic investigation of citation growth patterns for papers presenting more incremental, methodologically-focused research, rather than the theoretical advances such as those presented here, may show that different rules govern their spread within the academic community—and Dawkins’ original hypothesis may be rescued. It is tantalising to think that some variant of the two-phase exponential pattern of citation growth identified here may be a signature that will help to reveal the emergence of genuinely novel ideas amongst the quagmire that is modern science.
Conflicts of Interest
The author declares no conflict of interest.
References
- Dawkins, R. The Selfish Gene, 2nd ed.; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Hamilton, W.D. Genetical Evolution of Social Behaviour I. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef]
- Trivers, R.L. Evolution of Reciprocal Altruism. Q. Rev. Biol. 1971, 46, 35–57. [Google Scholar] [CrossRef]
- Smith, J.M.; Price, G.R. Logic of Animal Conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Otlet, P. Traité De Documentation: Le Livre Sur Le Livre, Théorie Et Pratique; Editiones Mundaneum: Mons, Belgium, 1934. [Google Scholar]
- Rousseau, Ronald. Library Science: Forgotten Founder of Bibliometrics. Nature 2014, 510, 218. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, A. Statistical Bibliography or Bibliometrics? J. Doc. 1969, 25, 348–349. [Google Scholar]
- Garfield, E. Citation Indexes for Science—New Dimension in Documentation through Association of Ideas. Science 1955, 122, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Price, D.J.D. Networks of Scientific Papers. Science 1965, 149, 510–515. [Google Scholar] [CrossRef] [PubMed]
- Garfield, E. Citation Analysis as a Tool in Journal Evaluation—Journals Can Be Ranked by Frequency and Impact of Citations for Science Policy Studies. Science 1972, 178, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Christopher, W.B.; Kaske, N.K. Using Bibliometrics to Demonstrate the Value of Library Journal Collections. Coll. Res. Libr. 2016, 77, 410–422. [Google Scholar]
- Antelman, K. Do Open-Access Articles Have a Greater Research Impact? Coll. Res. Libr. 2004, 65, 372–382. [Google Scholar] [CrossRef]
- Wray, K.B. No New Evidence for a Citation Benefit for Author-Pay Open Access Publications in the Social Sciences and Humanities. Scientometrics 2016, 106, 1031–1035. [Google Scholar] [CrossRef]
- Wray, K.B. Still No New Evidence: Author-Pay Open Access in the Social Sciences and Humanities. Scientometrics 2016, 107, 1527–1529. [Google Scholar] [CrossRef]
- Polonioli, A. Debunking Unwarranted Defenses of the Status Quo in the Humanities and Social Sciences. Scientometrics 2016, 107, 1519–1522. [Google Scholar] [CrossRef]
- Polonioli, A. Metrics, Flawed Indicators, and the Case of Philosophy Journals. Scientometrics 2016, 108, 987–994. [Google Scholar] [CrossRef]
- Priem, J.; Taraborelli, D.; Groth, P.; Neylon, C. Altmetrics: A Manifesto. Available online: http://altmetrics.org/manifesto (accessed on 10 May 2017).
- Aaen-Stockdale, C.R. Altmetrics: A Practical Guide for Librarians, Researchers and Academics. Coll. Res. Libr. 2017, 78, 114–116. [Google Scholar] [CrossRef]
- Bornmann, L.; Rüdiger, M. Growth Rates of Modern Science: A Bibliometric Analysis Based on the Number of Publications and Cited References. J. Assoc. Inf. Sci. Technol. 2015, 66, 2215–2222. [Google Scholar] [CrossRef]
- Aaen-Stockdale, C.R. Ibn Al-Haytham and Psychophysics. Perception 2008, 37, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Adrian, C.B. Presentism and Diversity in the History of Psychology. Psychol. Stud. 2015, 60, 373–379. [Google Scholar]
- Aaen-Stockdale, C.R. Neuroscience for the Soul. Psychologist 2012, 25, 520–523. [Google Scholar]
- Aaen-Stockdale, C.R. Throwing the Soul out with the Bathwater. Psychologist 2012, 25, 642–643. [Google Scholar]
- Dawkins, R. The Selfish Gene, 1st ed.; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- Wilson, E.O. Sociobiology: The New Synthesis; Cambridge, M.A., Ed.; Harvard University Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Darwin, C. On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life, 1st ed.; Murray: London, UK, 1859. [Google Scholar]
- Williams, G.C. Adaptation and Natural Selection; Princeton, N.J., Ed.; Princeton University Press: Princeton, NJ, USA, 1966. [Google Scholar]
- Dawkins, R. The Selfish Gene: 30th Anniversary Edition, 3rd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Dawkins, R. The Selfish Gene: 40th Anniversary Edition, 4th ed.; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Merton, R.K. The Matthew Effect in Science, II: Cumulative Advantage and the Symbolism of Intellectual Property. Isis 1988, 79, 606–623. [Google Scholar] [CrossRef]
- Tanzila, A.; Johnson, B.; Oppenheim, C.; Peck, C. Highly Cited Old Papers and the Reasons Why They Continue to Be Cited. Part II., the 1953 Watson and Crick Article on the Structure of DNA. Scientometrics 2004, 61, 147–156. [Google Scholar]
- Katherine, W.M. Assessing Obliteration by Incorporation: Issues and Caveats. J. Am. Soc. Inf. Sci. Technol. 2012, 63, 2129–2139. [Google Scholar]
- Van Raan, A.F.J. On Growth, Ageing, and Fractal Differentiation of Science. Scientometrics 2000, 47, 347–362. [Google Scholar] [CrossRef]
- Price, D.J.D. Little Science, Big Science; Columbia University Press: New York, NY, USA, 1963. [Google Scholar]
- Larsen, P.O.; von Ins, M. The Rate of Growth in Scientific Publication and the Decline in Coverage Provided by Science Citation Index. Scientometrics 2010, 84, 575–603. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Rousseau, R. Citation Analysis and the Development of Science: A Case Study Using Articles by Some Nobel Prize Winners. J. Assoc. Inf. Sci. Technol. 2014, 65, 281–289. [Google Scholar] [CrossRef]
- Van Raan Anthony, F.J. Sleeping Beauties in Science. Scientometrics 2004, 59, 467–472. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).