The Scientific Productivity of Collective Subjects Based on the Time-Weighted PageRank Method with Citation Intensity
Abstract
1. Introduction
- -
- Description of components used in the combined Time-Weighted PageRank method with citation intensity. Solving the problems of calculating the intensity of scientific publications citations and the problem of weighting the coefficients of the PageRank method over time;
- -
- Description of Time-Weighted application possibilities of the PageRank method with citation intensity for evaluating the scientific productivity of collective subjects.
2. Methods and Data
2.1. Basic Terms and Concepts
2.2. The Assessment of Scientific Productivity
3. Results
3.1. Collection of Data on Citations of Scientific Publications of Collective Subjects
3.2. The Results of the Calculation of Estimates of the Scientific Productivity of Collective Subjects
4. Discussion
4.1. Findings
4.2. Limitations and Future Research Lines
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Collective Subjects | Years | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | |
| IBM Thomas J, Watson RC, New York | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.995 | 0.944 | 0.893 | 0.855 | 0.854 |
| Carnegie-Mellon University Pittsburgh, PA | 0.600 | 0.625 | 0.644 | 0.658 | 0.677 | 0.680 | 0.695 | 0.711 | 0.732 | 0.749 | 0.772 | 0.791 | 0.813 | 0.839 | 0.858 | 0.887 | 0.912 | 0.951 | 0.933 | 0.919 | 0.913 | 0.913 |
| Stanford Univ., Stanford, CA | 0.570 | 0.595 | 0.616 | 0.645 | 0.668 | 0.677 | 0.692 | 0.711 | 0.730 | 0.755 | 0.778 | 0.798 | 0.825 | 0.850 | 0.874 | 0.909 | 0.944 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Massachusetts Institute of Technology, Cambridge | 0.540 | 0.554 | 0.562 | 0.574 | 0.584 | 0.583 | 0.581 | 0.587 | 0.592 | 0.601 | 0.615 | 0.626 | 0.639 | 0.653 | 0.665 | 0.685 | 0.702 | 0.730 | 0.716 | 0.708 | 0.702 | 0.701 |
| Bell Labs Research, Murray Hill, NJ | 0.490 | 0.501 | 0.510 | 0.510 | 0.502 | 0.478 | 0.459 | 0.442 | 0.423 | 0.408 | 0.392 | 0.375 | 0.361 | 0.349 | 0.343 | 0.335 | 0.330 | 0.320 | 0.300 | 0.281 | 0.268 | 0.267 |
| University of California at Berkeley | 0.420 | 0.438 | 0.464 | 0.503 | 0.557 | 0.593 | 0.635 | 0.669 | 0.683 | 0.700 | 0.720 | 0.730 | 0.749 | 0.769 | 0.788 | 0.816 | 0.841 | 0.880 | 0.865 | 0.852 | 0.837 | 0.837 |
| PARC (Palo Alto Research Center) | 0.290 | 0.294 | 0.302 | 0.305 | 0.310 | 0.301 | 0.289 | 0.278 | 0.268 | 0.259 | 0.249 | 0.240 | 0.234 | 0.229 | 0.225 | 0.220 | 0.215 | 0.208 | 0.191 | 0.175 | 0.163 | 0.163 |
| University of Illinois at Urbana-Champaign, USA | 0.280 | 0.289 | 0.288 | 0.289 | 0.293 | 0.294 | 0.305 | 0.313 | 0.324 | 0.342 | 0.359 | 0.377 | 0.394 | 0.410 | 0.424 | 0.442 | 0.456 | 0.475 | 0.467 | 0.458 | 0.450 | 0.450 |
| Cornell Univ., Ithaca, NY | 0.280 | 0.295 | 0.302 | 0.309 | 0.312 | 0.305 | 0.299 | 0.295 | 0.292 | 0.296 | 0.298 | 0.298 | 0.302 | 0.306 | 0.312 | 0.327 | 0.342 | 0.355 | 0.344 | 0.329 | 0.316 | 0.316 |
| University of Washington | 0.220 | 0.234 | 0.240 | 0.248 | 0.254 | 0.255 | 0.261 | 0.266 | 0.273 | 0.282 | 0.291 | 0.296 | 0.305 | 0.315 | 0.322 | 0.332 | 0.340 | 0.351 | 0.343 | 0.340 | 0.339 | 0.339 |
| Jagiellonian University, Krakow, Poland | 0.010 | 0.012 | 0.015 | 0.016 | 0.019 | 0.021 | 0.024 | 0.026 | 0.028 | 0.030 | 0.033 | 0.035 | 0.037 | 0.038 | 0.040 | 0.042 | 0.043 | 0.045 | 0.044 | 0.044 | 0.044 | 0.044 |
| Aalborg University, Aalborg, Denmark | 0.010 | 0.012 | 0.014 | 0.017 | 0.019 | 0.020 | 0.023 | 0.025 | 0.027 | 0.030 | 0.033 | 0.036 | 0.039 | 0.041 | 0.043 | 0.045 | 0.047 | 0.051 | 0.052 | 0.053 | 0.053 | 0.053 |
| Naval Postgraduate School | 0.010 | 0.010 | 0.011 | 0.011 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.011 | 0.011 | 0.011 | 0.012 | 0.012 | 0.012 | 0.013 | 0.012 | 0.012 | 0.011 | 0.011 |
| University of Warwick | 0.010 | 0.010 | 0.011 | 0.011 | 0.012 | 0.013 | 0.013 | 0.013 | 0.013 | 0.014 | 0.014 | 0.015 | 0.015 | 0.016 | 0.017 | 0.018 | 0.019 | 0.020 | 0.020 | 0.021 | 0.022 | 0.022 |
| Lockheed Palo Alto Res. Lab., California, USA | 0.010 | 0.010 | 0.009 | 0.009 | 0.008 | 0.007 | 0.007 | 0.006 | 0.006 | 0.006 | 0.005 | 0.005 | 0.005 | 0.005 | 0.004 | 0.004 | 0.004 | 0.004 | 0.004 | 0.003 | 0.003 | 0.003 |
| Colorado State University, Fort Collins, Colorado | 0.010 | 0.010 | 0.011 | 0.011 | 0.012 | 0.013 | 0.014 | 0.016 | 0.018 | 0.020 | 0.021 | 0.022 | 0.023 | 0.024 | 0.025 | 0.026 | 0.027 | 0.028 | 0.028 | 0.028 | 0.028 | 0.028 |
| University of Kentucky | 0.010 | 0.010 | 0.010 | 0.011 | 0.011 | 0.011 | 0.012 | 0.013 | 0.015 | 0.017 | 0.019 | 0.020 | 0.022 | 0.023 | 0.024 | 0.025 | 0.025 | 0.026 | 0.025 | 0.025 | 0.025 | 0.025 |
| Washington State University | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.011 | 0.011 | 0.011 | 0.012 | 0.012 | 0.013 | 0.014 | 0.015 | 0.016 | 0.017 | 0.018 | 0.018 | 0.019 | 0.020 | 0.020 |
| ENSICAEN, France | 0.010 | 0.009 | 0.009 | 0.009 | 0.008 | 0.007 | 0.007 | 0.006 | 0.006 | 0.005 | 0.005 | 0.005 | 0.005 | 0.004 | 0.004 | 0.004 | 0.004 | 0.004 | 0.003 | 0.003 | 0.003 | 0.003 |
| University of Connecticut, Farmington, Connecticut | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.010 | 0.011 | 0.012 | 0.013 | 0.015 | 0.017 | 0.019 | 0.021 | 0.022 | 0.023 | 0.024 | 0.026 | 0.028 | 0.028 | 0.028 | 0.028 | 0.028 |
| Facebook, Menlo Park, CA, USA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.003 | 0.006 | 0.010 | 0.014 | 0.019 | 0.024 | 0.038 | 0.054 | 0.079 | 0.108 | 0.108 |
| DeepMind Technologies Ltd, London, UK | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.004 | 0.017 | 0.031 | 0.049 | 0.069 | 0.069 |
| Beijing University of Posts and Tel., Beijing, China | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.001 | 0.002 | 0.003 | 0.004 | 0.005 | 0.007 | 0.010 | 0.013 | 0.019 | 0.026 | 0.034 | 0.041 | 0.041 |
| CTO of Baseband SoC at Huawei Technol., Plano, TX | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.002 | 0.003 | 0.005 | 0.008 | 0.013 | 0.019 | 0.024 | 0.028 | 0.028 |
| Aalto University, Espoo, Finland | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.002 | 0.003 | 0.004 | 0.006 | 0.009 | 0.014 | 0.018 | 0.022 | 0.025 | 0.025 |
| Disney Research, Pittsburgh PA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.002 | 0.004 | 0.006 | 0.008 | 0.010 | 0.015 | 0.017 | 0.020 | 0.021 | 0.021 |
| Max Planck Institute for Intelligent Systems, Germany | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.002 | 0.004 | 0.006 | 0.009 | 0.013 | 0.017 | 0.021 | 0.021 |
| Rice Univ. & Max Planck Institute | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.002 | 0.004 | 0.006 | 0.009 | 0.012 | 0.013 | 0.015 | 0.017 | 0.019 | 0.020 | 0.020 | 0.020 | 0.020 |
| Institute for Infocomm Research, A*STAR, Singapore | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.002 | 0.004 | 0.005 | 0.006 | 0.007 | 0.009 | 0.011 | 0.015 | 0.017 | 0.019 | 0.020 | 0.020 |
| University of Lugano, Lugano, Switzerland | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.002 | 0.002 | 0.003 | 0.005 | 0.007 | 0.009 | 0.010 | 0.012 | 0.013 | 0.015 | 0.017 | 0.019 | 0.020 | 0.020 |
| Collective Subjects | Years | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | |
| IBM Thomas J, Watson RC, New York | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.947 | 0.898 | 0.826 | 0.769 | 0.717 | 0.677 | 0.677 |
| Carnegie-Mellon University Pittsburgh, PA | 0.602 | 0.645 | 0.688 | 0.713 | 0.748 | 0.731 | 0.748 | 0.770 | 0.800 | 0.825 | 0.857 | 0.884 | 0.914 | 0.949 | 0.979 | 0.971 | 0.956 | 0.934 | 0.907 | 0.889 | 0.881 | 0.881 |
| Stanford Univ., Stanford, CA | 0.573 | 0.617 | 0.666 | 0.729 | 0.763 | 0.748 | 0.759 | 0.781 | 0.802 | 0.839 | 0.868 | 0.893 | 0.928 | 0.961 | 0.999 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Massachusetts Institute of Technology, Cambridge | 0.544 | 0.566 | 0.583 | 0.609 | 0.625 | 0.606 | 0.595 | 0.603 | 0.609 | 0.627 | 0.650 | 0.665 | 0.685 | 0.705 | 0.726 | 0.721 | 0.710 | 0.695 | 0.679 | 0.672 | 0.667 | 0.667 |
| Bell Labs Research, Murray Hill, NJ | 0.491 | 0.507 | 0.526 | 0.511 | 0.476 | 0.418 | 0.386 | 0.362 | 0.336 | 0.320 | 0.302 | 0.284 | 0.269 | 0.257 | 0.252 | 0.235 | 0.223 | 0.205 | 0.194 | 0.184 | 0.175 | 0.175 |
| University of California at Berkeley | 0.416 | 0.458 | 0.516 | 0.606 | 0.711 | 0.740 | 0.784 | 0.813 | 0.807 | 0.815 | 0.831 | 0.833 | 0.853 | 0.877 | 0.905 | 0.897 | 0.885 | 0.869 | 0.847 | 0.829 | 0.808 | 0.808 |
| PARC (Palo Alto Research Center) | 0.289 | 0.297 | 0.314 | 0.309 | 0.312 | 0.284 | 0.258 | 0.244 | 0.229 | 0.220 | 0.208 | 0.200 | 0.195 | 0.189 | 0.185 | 0.170 | 0.157 | 0.138 | 0.123 | 0.110 | 0.099 | 0.099 |
| University of Illinois at Urbana-Champaign, USA | 0.284 | 0.294 | 0.295 | 0.297 | 0.307 | 0.308 | 0.329 | 0.342 | 0.358 | 0.388 | 0.413 | 0.440 | 0.463 | 0.486 | 0.506 | 0.505 | 0.499 | 0.482 | 0.468 | 0.452 | 0.441 | 0.441 |
| Cornell Univ., Ithaca, NY | 0.283 | 0.307 | 0.328 | 0.342 | 0.343 | 0.319 | 0.307 | 0.299 | 0.295 | 0.307 | 0.312 | 0.313 | 0.320 | 0.328 | 0.343 | 0.353 | 0.358 | 0.350 | 0.334 | 0.311 | 0.292 | 0.292 |
| University of Washington | 0.223 | 0.243 | 0.259 | 0.279 | 0.287 | 0.279 | 0.284 | 0.291 | 0.300 | 0.313 | 0.325 | 0.331 | 0.345 | 0.357 | 0.369 | 0.363 | 0.355 | 0.341 | 0.330 | 0.327 | 0.328 | 0.328 |
| Jagiellonian University, Krakow, Poland | 0.010 | 0.014 | 0.020 | 0.024 | 0.029 | 0.032 | 0.035 | 0.037 | 0.040 | 0.043 | 0.046 | 0.048 | 0.050 | 0.052 | 0.053 | 0.053 | 0.051 | 0.049 | 0.048 | 0.047 | 0.047 | 0.047 |
| Aalborg University, Aalborg, Denmark | 0.010 | 0.014 | 0.019 | 0.031 | 0.032 | 0.030 | 0.033 | 0.036 | 0.040 | 0.044 | 0.048 | 0.051 | 0.054 | 0.058 | 0.060 | 0.060 | 0.059 | 0.059 | 0.059 | 0.060 | 0.059 | 0.059 |
| Naval Postgraduate School | 0.010 | 0.010 | 0.011 | 0.011 | 0.010 | 0.010 | 0.009 | 0.009 | 0.009 | 0.010 | 0.011 | 0.011 | 0.012 | 0.013 | 0.014 | 0.013 | 0.013 | 0.012 | 0.012 | 0.011 | 0.010 | 0.010 |
| University of Warwick | 0.010 | 0.011 | 0.012 | 0.013 | 0.014 | 0.016 | 0.016 | 0.015 | 0.015 | 0.016 | 0.017 | 0.018 | 0.019 | 0.020 | 0.021 | 0.021 | 0.021 | 0.022 | 0.022 | 0.023 | 0.025 | 0.025 |
| Lockheed Palo Alto Res. Lab., California, USA | 0.010 | 0.009 | 0.008 | 0.007 | 0.006 | 0.005 | 0.004 | 0.004 | 0.004 | 0.004 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | 0.002 |
| Colorado State University, Fort Collins, Colorado | 0.010 | 0.011 | 0.012 | 0.013 | 0.014 | 0.017 | 0.019 | 0.021 | 0.025 | 0.028 | 0.028 | 0.029 | 0.030 | 0.030 | 0.032 | 0.032 | 0.031 | 0.030 | 0.030 | 0.030 | 0.029 | 0.029 |
| University of Kentucky | 0.010 | 0.011 | 0.011 | 0.012 | 0.013 | 0.013 | 0.014 | 0.015 | 0.020 | 0.023 | 0.025 | 0.028 | 0.030 | 0.030 | 0.032 | 0.031 | 0.030 | 0.029 | 0.027 | 0.026 | 0.026 | 0.026 |
| Washington State University | 0.010 | 0.010 | 0.010 | 0.010 | 0.012 | 0.011 | 0.012 | 0.012 | 0.013 | 0.013 | 0.014 | 0.014 | 0.016 | 0.017 | 0.018 | 0.019 | 0.020 | 0.020 | 0.021 | 0.022 | 0.023 | 0.023 |
| ENSICAEN, France | 0.010 | 0.009 | 0.008 | 0.007 | 0.006 | 0.005 | 0.005 | 0.004 | 0.004 | 0.004 | 0.003 | 0.003 | 0.003 | 0.003 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | 0.001 | 0.001 | 0.001 |
| University of Connecticut, Farmington, Connecticut | 0.010 | 0.010 | 0.010 | 0.011 | 0.010 | 0.011 | 0.014 | 0.015 | 0.017 | 0.020 | 0.024 | 0.026 | 0.029 | 0.030 | 0.031 | 0.032 | 0.033 | 0.032 | 0.032 | 0.032 | 0.031 | 0.031 |
| Facebook, Menlo Park, CA, USA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.003 | 0.006 | 0.011 | 0.019 | 0.025 | 0.033 | 0.039 | 0.057 | 0.081 | 0.117 | 0.161 | 0.161 |
| DeepMind Technologies Ltd, London, UK | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0 | 0 | 0.001 | 0.007 | 0.028 | 0.051 | 0.078 | 0.108 | 0.108 |
| Beijing University of Posts and Tel., Beijing, China | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.001 | 0.002 | 0.003 | 0.004 | 0.006 | 0.008 | 0.010 | 0.013 | 0.018 | 0.023 | 0.031 | 0.043 | 0.053 | 0.064 | 0.064 |
| CTO of Baseband SoC at Huawei Technol., Plano, TX | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.003 | 0.004 | 0.006 | 0.009 | 0.013 | 0.021 | 0.029 | 0.036 | 0.042 | 0.042 |
| Aalto University, Espoo, Finland | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.002 | 0.003 | 0.006 | 0.008 | 0.012 | 0.016 | 0.022 | 0.027 | 0.032 | 0.036 | 0.036 |
| Disney Research, Pittsburgh PA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.004 | 0.007 | 0.011 | 0.015 | 0.017 | 0.023 | 0.026 | 0.028 | 0.029 | 0.029 |
| Max Planck Institute for Intelligent Systems, Germany | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.002 | 0.004 | 0.007 | 0.010 | 0.014 | 0.020 | 0.026 | 0.031 | 0.031 |
| Rice Univ. & Max Planck Institute | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.001 | 0.003 | 0.005 | 0.007 | 0.009 | 0.011 | 0.013 | 0.016 | 0.019 | 0.022 | 0.025 | 0.027 | 0.029 | 0.029 |
| Institute for Infocomm Research, A*STAR, Singapore | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.001 | 0.003 | 0.005 | 0.007 | 0.009 | 0.011 | 0.013 | 0.016 | 0.019 | 0.022 | 0.025 | 0.027 | 0.029 | 0.029 |
| University of Lugano, Lugano, Switzerland | 0 | 0 | 0 | 0 | 0.001 | 0.001 | 0.001 | 0.002 | 0.003 | 0.004 | 0.006 | 0.009 | 0.012 | 0.015 | 0.017 | 0.019 | 0.020 | 0.022 | 0.023 | 0.024 | 0.026 | 0.026 |
| Collective Subjects | Years | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | |
| IBM Thomas J, Watson RC, New York | 0.998 | 0.996 | 0.994 | 0.993 | 0.992 | 0.992 | 0.991 | 0.991 | 0.991 | 0.990 | 0.990 | 0.990 | 0.989 | 0.989 | 0.989 | 0.938 | 0.891 | 0.822 | 0.769 | 0.719 | 0.680 | 0.680 |
| Carnegie-Mellon University Pittsburgh, PA | 0.620 | 0.660 | 0.698 | 0.721 | 0.753 | 0.737 | 0.753 | 0.773 | 0.801 | 0.825 | 0.855 | 0.881 | 0.909 | 0.942 | 0.970 | 0.963 | 0.948 | 0.927 | 0.902 | 0.885 | 0.877 | 0.876 |
| Stanford Univ., Stanford, CA | 0.592 | 0.633 | 0.678 | 0.737 | 0.769 | 0.754 | 0.764 | 0.785 | 0.805 | 0.840 | 0.867 | 0.891 | 0.924 | 0.955 | 0.991 | 0.993 | 0.993 | 0.993 | 0.993 | 0.993 | 0.993 | 0.993 |
| Massachusetts Institute of Technology, Cambridge | 0.565 | 0.584 | 0.598 | 0.623 | 0.637 | 0.618 | 0.608 | 0.615 | 0.620 | 0.637 | 0.659 | 0.673 | 0.692 | 0.711 | 0.730 | 0.726 | 0.715 | 0.700 | 0.685 | 0.678 | 0.673 | 0.673 |
| Bell Labs Research, Murray Hill, NJ | 0.514 | 0.527 | 0.543 | 0.528 | 0.494 | 0.439 | 0.408 | 0.384 | 0.360 | 0.344 | 0.327 | 0.309 | 0.295 | 0.283 | 0.279 | 0.262 | 0.250 | 0.233 | 0.223 | 0.212 | 0.204 | 0.203 |
| University of California at Berkeley | 0.444 | 0.482 | 0.536 | 0.621 | 0.720 | 0.747 | 0.789 | 0.817 | 0.811 | 0.819 | 0.834 | 0.835 | 0.854 | 0.877 | 0.903 | 0.895 | 0.884 | 0.869 | 0.847 | 0.830 | 0.810 | 0.810 |
| PARC (Palo Alto Research Center) | 0.324 | 0.330 | 0.345 | 0.340 | 0.343 | 0.316 | 0.291 | 0.278 | 0.263 | 0.255 | 0.243 | 0.235 | 0.230 | 0.224 | 0.220 | 0.206 | 0.193 | 0.175 | 0.161 | 0.148 | 0.138 | 0.137 |
| University of Illinois at Urbana-Champaign, USA | 0.317 | 0.325 | 0.323 | 0.323 | 0.331 | 0.331 | 0.350 | 0.362 | 0.377 | 0.406 | 0.430 | 0.455 | 0.477 | 0.499 | 0.518 | 0.517 | 0.511 | 0.495 | 0.482 | 0.467 | 0.456 | 0.456 |
| Cornell Univ., Ithaca, NY | 0.260 | 0.277 | 0.291 | 0.309 | 0.315 | 0.307 | 0.312 | 0.318 | 0.327 | 0.339 | 0.350 | 0.355 | 0.368 | 0.380 | 0.391 | 0.385 | 0.377 | 0.364 | 0.354 | 0.351 | 0.351 | 0.351 |
| University of Washington | 0.255 | 0.281 | 0.319 | 0.358 | 0.391 | 0.395 | 0.403 | 0.412 | 0.419 | 0.428 | 0.442 | 0.455 | 0.469 | 0.487 | 0.500 | 0.494 | 0.484 | 0.475 | 0.468 | 0.471 | 0.471 | 0.471 |
| Jagiellonian University, Krakow, Poland | 0.054 | 0.054 | 0.056 | 0.057 | 0.060 | 0.060 | 0.061 | 0.062 | 0.065 | 0.067 | 0.069 | 0.071 | 0.074 | 0.075 | 0.077 | 0.077 | 0.075 | 0.073 | 0.072 | 0.071 | 0.071 | 0.070 |
| Aalborg University, Aalborg, Denmark | 0.054 | 0.053 | 0.054 | 0.064 | 0.064 | 0.061 | 0.063 | 0.065 | 0.068 | 0.072 | 0.076 | 0.079 | 0.081 | 0.084 | 0.085 | 0.084 | 0.083 | 0.082 | 0.083 | 0.083 | 0.083 | 0.082 |
| Naval Postgraduate School | 0.053 | 0.049 | 0.047 | 0.044 | 0.040 | 0.037 | 0.035 | 0.034 | 0.032 | 0.033 | 0.033 | 0.033 | 0.033 | 0.034 | 0.035 | 0.034 | 0.034 | 0.033 | 0.032 | 0.031 | 0.030 | 0.029 |
| University of Warwick | 0.052 | 0.047 | 0.044 | 0.042 | 0.041 | 0.041 | 0.041 | 0.039 | 0.038 | 0.038 | 0.037 | 0.038 | 0.039 | 0.039 | 0.040 | 0.040 | 0.039 | 0.039 | 0.040 | 0.041 | 0.043 | 0.042 |
| Lockheed Palo Alto Res. Lab., California, USA | 0.036 | 0.026 | 0.023 | 0.025 | 0.027 | 0.028 | 0.027 | 0.029 | 0.032 | 0.036 | 0.040 | 0.047 | 0.053 | 0.059 | 0.064 | 0.066 | 0.069 | 0.071 | 0.070 | 0.067 | 0.064 | 0.064 |
| Colorado State University, Fort Collins, Colorado | 0.052 | 0.047 | 0.044 | 0.042 | 0.042 | 0.043 | 0.046 | 0.048 | 0.052 | 0.055 | 0.056 | 0.057 | 0.057 | 0.057 | 0.058 | 0.058 | 0.057 | 0.056 | 0.056 | 0.056 | 0.055 | 0.054 |
| University of Kentucky | 0.052 | 0.047 | 0.044 | 0.042 | 0.042 | 0.043 | 0.046 | 0.048 | 0.052 | 0.055 | 0.056 | 0.057 | 0.057 | 0.057 | 0.058 | 0.058 | 0.057 | 0.056 | 0.056 | 0.056 | 0.055 | 0.054 |
| Washington State University | 0.052 | 0.047 | 0.042 | 0.039 | 0.039 | 0.037 | 0.036 | 0.037 | 0.037 | 0.037 | 0.037 | 0.038 | 0.039 | 0.041 | 0.043 | 0.044 | 0.044 | 0.044 | 0.045 | 0.047 | 0.048 | 0.048 |
| ENSICAEN, France | 0.057 | 0.054 | 0.050 | 0.049 | 0.047 | 0.044 | 0.044 | 0.042 | 0.0041 | 0.040 | 0.040 | 0.039 | 0.038 | 0.037 | 0.036 | 0.035 | 0.034 | 0.034 | 0.033 | 0.032 | 0.032 | 0.031 |
| University of Connecticut, Farmington, Connecticut | 0.052 | 0.046 | 0.040 | 0.037 | 0.033 | 0.033 | 0.035 | 0.035 | 0.037 | 0.041 | 0.046 | 0.048 | 0.051 | 0.052 | 0.054 | 0.054 | 0.055 | 0.055 | 0.056 | 0.055 | 0.054 | 0.054 |
| Facebook, Menlo Park, CA, USA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.030 | 0.030 | 0.040 | 0.045 | 0.051 | 0.059 | 0.065 | 0.073 | 0.079 | 0.096 | 0.120 | 0.155 | 0.197 | 0.197 |
| DeepMind Technologies Ltd, London, UK | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.047 | 0.046 | 0.039 | 0.032 | 0.050 | 0.075 | 0.095 | 0.122 | 0.150 | 0.151 |
| Beijing University of Posts and Tel., Beijing, China | 0 | 0 | 0 | 0 | 0.009 | 0.010 | 0.007 | 0.007 | 0.008 | 0.010 | 0.012 | 0.015 | 0.018 | 0.021 | 0.025 | 0.031 | 0.036 | 0.046 | 0.060 | 0.071 | 0.083 | 0.083 |
| CTO of Baseband SoC at Huawei Technol., Plano, TX | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.007 | 0.011 | 0.014 | 0.016 | 0.019 | 0.022 | 0.025 | 0.028 | 0.034 | 0.045 | 0.055 | 0.063 | 0.069 | 0.068 |
| Aalto University, Espoo, Finland | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.031 | 0.035 | 0.010 | 0.013 | 0.017 | 0.021 | 0.025 | 0.030 | 0.036 | 0.045 | 0.051 | 0.057 | 0.061 | 0.060 |
| Disney Research, Pittsburgh PA | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.008 | 0.010 | 0.028 | 0.036 | 0.042 | 0.048 | 0.052 | 0.056 | 0.062 | 0.066 | 0.068 | 0.070 | 0.069 |
| Max Planck Institute for Intelligent Systems, Germany | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.031 | 0.019 | 0.021 | 0.027 | 0.033 | 0.040 | 0.046 | 0.052 | 0.060 | 0.067 | 0.072 | 0.072 |
| Rice Univ. & Max Planck Institute | 0 | 0 | 0 | 0 | 0 | 0 | 0.037 | 0.046 | 0.046 | 0.049 | 0.053 | 0.056 | 0.061 | 0.064 | 0.066 | 0.067 | 0.068 | 0.068 | 0.067 | 0.066 | 0.065 | 0.065 |
| Institute for Infocomm Research, A*STAR, Singapore | 0 | 0 | 0 | 0 | 0 | 0 | 0.014 | 0.014 | 0.015 | 0.019 | 0.023 | 0.027 | 0.031 | 0.034 | 0.036 | 0.038 | 0.043 | 0.048 | 0.053 | 0.055 | 0.058 | 0.057 |
| University of Lugano, Lugano, Switzerland | 0 | 0 | 0 | 0 | 0.035 | 0.025 | 0.022 | 0.022 | 0.022 | 0.023 | 0.026 | 0.030 | 0.035 | 0.039 | 0.041 | 0.045 | 0.046 | 0.048 | 0.051 | 0.053 | 0.054 | 0.054 |
References
- Hirsch, J.E. An index to quantify an individual’s scientific research output. Proc. Natl. Acad. Sci. USA 2005, 102, 16569–16572. [Google Scholar] [CrossRef] [PubMed]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Net. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Leskovec, J.; Rajaraman, A.; Ullman, J.D. Mining of Massive Datasets; Stanford University Press: Palo Alto, CA, USA, 2014; p. 513. [Google Scholar]
- Biloshchytskyi, A.; Kuchansky, A.; Andrashko, Y.; Omirbayev, S.; Mukhatayev, A.; Faizullin, A.; Toxanov, S. Development of the set models and a method to form information spaces of scientific activity subjects for the steady development of higher education establishments. East.-Eur. J. Enterp. Technol. 2021, 3, 6–14. [Google Scholar] [CrossRef]
- Zhao, H.; Xu, X.; Song, Y.; Lee, D.L.; Chen, Z.; Gao, H. Ranking Users in Social Networks with Higher-Order Structures. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Bianchini, M.; Gori, M.; Scarselli, F. Inside pagerank. ACM Trans. Internet Technol. 2005, 5, 92–128. [Google Scholar] [CrossRef]
- Assessing Universities and Other Research-Focused Institutions. Scimago Journal & Country Rank. Available online: https://www.scimagoir.com/ (accessed on 10 August 2022).
- Bergstrom, C. Eigenfactor: Measuring the value and prestige of scholarly journals. Coll. Res. Libr. News 2007, 68, 314–316. [Google Scholar] [CrossRef]
- Zhang, F. Evaluating journal impact based on weighted citations. Scientometrics 2017, 113, 1155–1169. [Google Scholar] [CrossRef]
- Lages, J.; Patt, A.; Shepelyansky, D. Wikipedia ranking of world universities. Eur. Phys. J. B 2016, 89, 69. [Google Scholar] [CrossRef][Green Version]
- Maleki, A.; Abbaspour, G.; Jowkar, A.; Sotudeh, H. The Relationship between Textbooks’ Teaching Ranks in World Top Universities and Citation, PageRank and HITS Indicators. Scientometr. Res. J. 2019, 5, 221–240. [Google Scholar]
- Ding, Y.; Yan, E.; Frazho, A.; Caverlee, J. Pagerank for ranking authors in co-citation networks. J. Am. Soc. Inf. Sci. Technol. 2009, 60, 2229–2243. [Google Scholar] [CrossRef]
- Massucci, F.A.; Docampo, D. Measuring the academic reputation through citation networks via PageRank. J. Informetr. 2019, 13, 185–201. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X. Citation Oriented AuthorRank for Scientific Publication Ranking. Appl. Sci. 2022, 12, 4345. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, A.; Fan, Y.; Di, Z. Ranking scientific publications considering the aging characteristics of citations. Scientometrics 2019, 120, 155–166. [Google Scholar] [CrossRef]
- Fiala, D.; Tutoky, G.; Koncz, P.; Paralič, J. Ageing of Edges in Collaboration Networks and its Effect on Author Rankings. Acta Polytech. Hung. 2015, 12, 149–160. [Google Scholar]
- Xing, W.; Ghorbani, A. Weighted PageRank algorithm. In Proceedings of the Second Annual Conference on Communication Networks and Services Research, Fredericton, NB, Canada, 19–21 May 2004; pp. 305–314. [Google Scholar]
- Manaskasemsak, B.; Rungsawang, A.; Yamana, H. Time-weighted web authoritative ranking. Inf. Retr. 2011, 14, 133–157. [Google Scholar] [CrossRef]
- Aminer. Citation Network Dataset: DBLP + Citation, ACM Citation Network. Available online: https://www.aminer.org/citation (accessed on 10 August 2022).
- Tang, J.; Zhang, J.; Yao, L.; Li, J.; Zhang, L.; Su, Z. ArnetMiner: Extraction and Mining of Academic Social Networks. In Proceedings of the Fourteenth International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 14–18 August 2008; pp. 990–998. [Google Scholar]
- DBLP. Computer Science Bibliography. Available online: https://dblp.org/ (accessed on 10 August 2022).
- Association for Computing Machinery. Available online: https://www.acm.org/ (accessed on 10 August 2022).
- Microsoft Academic Graph. Available online: https://www.microsoft.com/en-us/research/project/microsoft-academic-graph/ (accessed on 10 August 2022).
- Biloshchytskyi, A.; Kuchansky, A.; Andrashko, Y.; Biloshchytska, S.; Kuzka, O.; Terentyev, O. Evaluation methods of the results of scientific research activity of scientists based on the analysis of publication citations. East.-Eur. J. Enterp. Technol. 2017, 3, 4–10. [Google Scholar] [CrossRef][Green Version]
- Biloshchytskyi, A.; Kuchansky, A.; Andrashko, Y.; Biloshchytska, S. Use of the link ranking method to evaluate scientific activities of scientific space subjects. Sci. J. Astana IT Univ. 2020, 1, 12–20. [Google Scholar] [CrossRef]
- Biloshchytskyi, A.; Kuchansky, A.; Andrashko, Y.; Biloshchytska, S.; Kuzka, O.; Shabala, Y.; Lyashchenko, T. A method for the identification of scientists’ research areas based on a cluster analysis of scientific publications. East.-Eur. J. Enterp. Technol. 2017, 5, 4–11. [Google Scholar] [CrossRef]
- Gephi. The Open Graph Viz Platform. Available online: https://gephi.org/ (accessed on 10 August 2022).

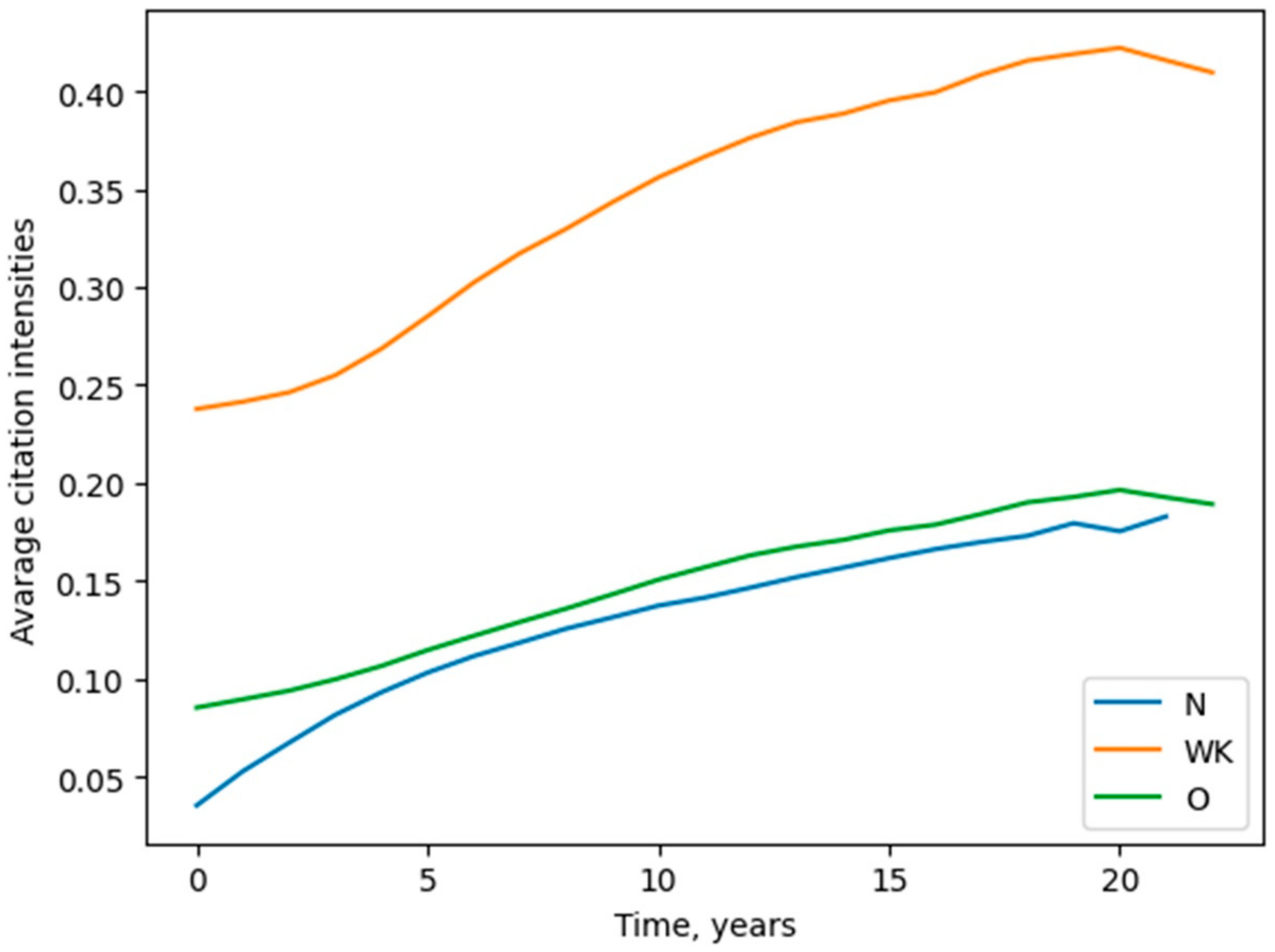
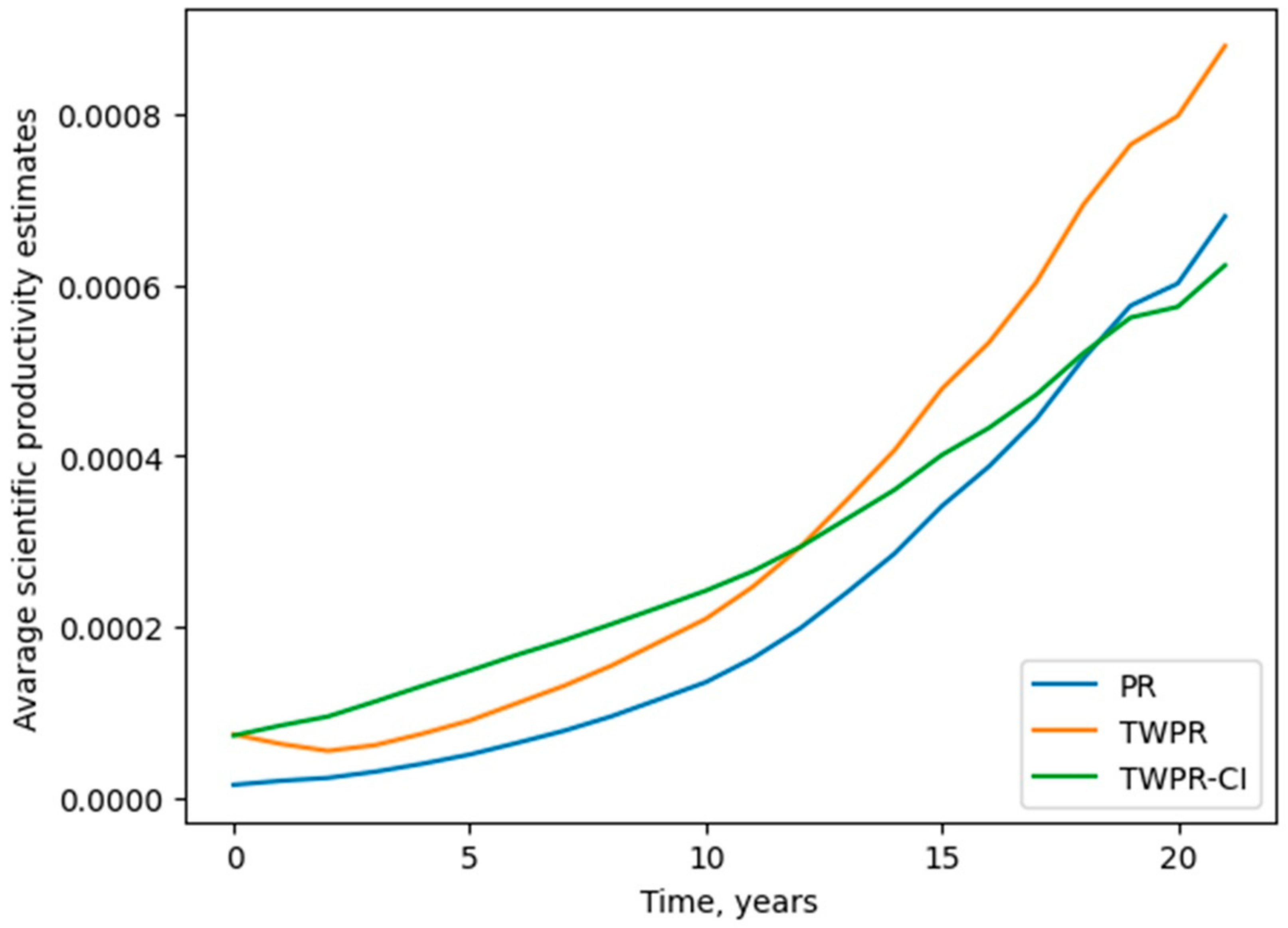
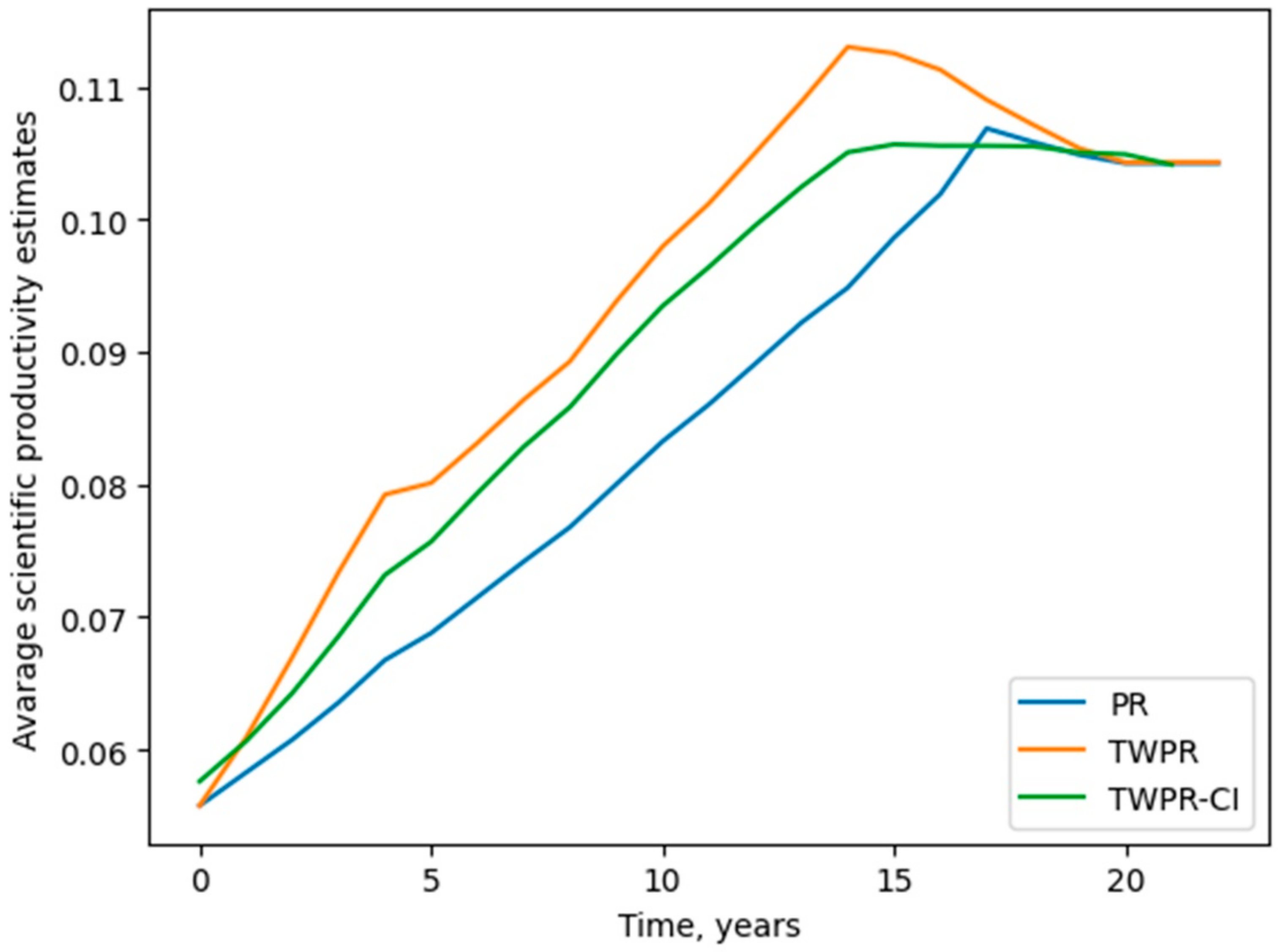

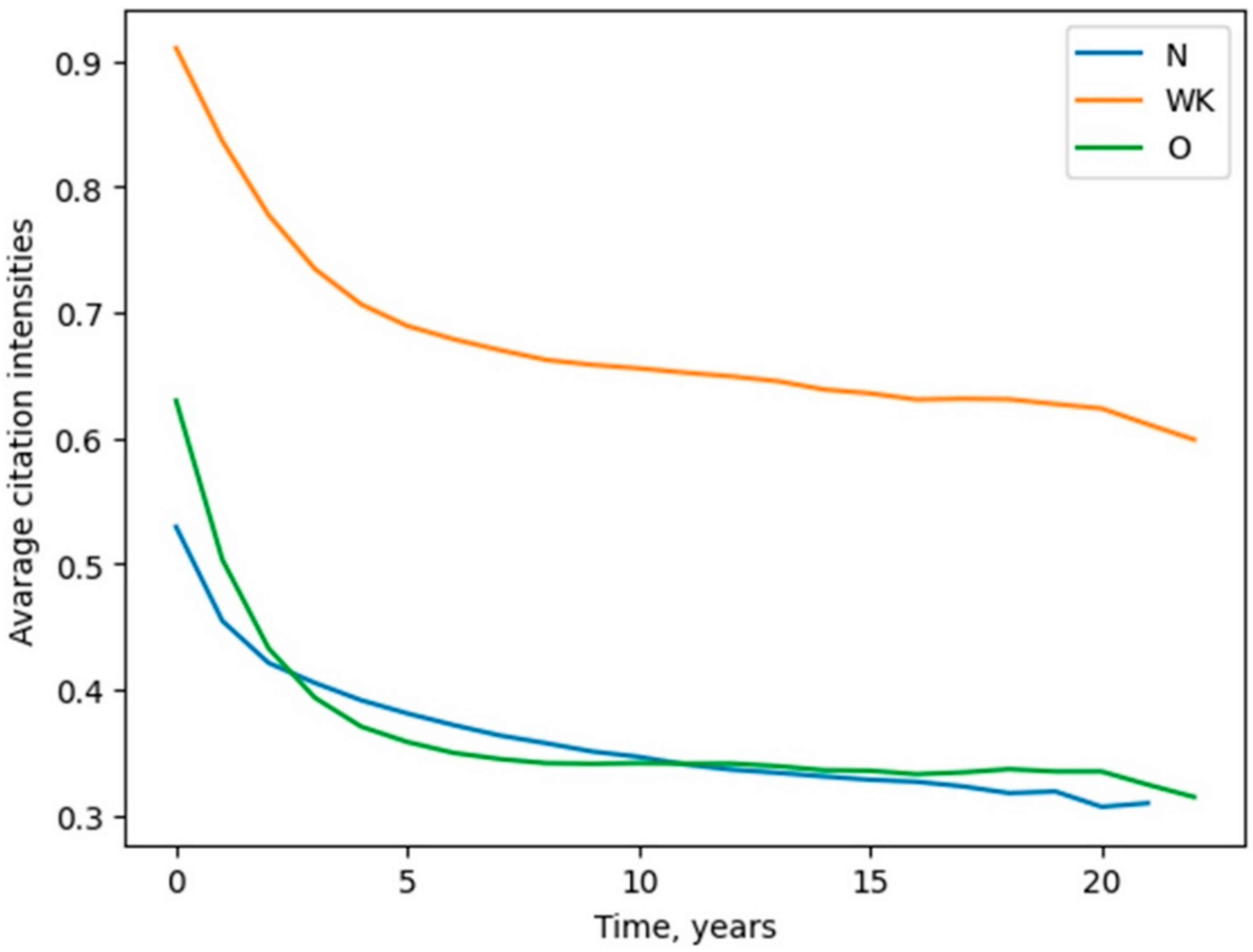
| Class | Number of Collective Subjects |
|---|---|
| N | 16,544 |
| WK | 236 |
| O | 4928 |
| NC | 5791 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuchansky, A.; Biloshchytskyi, A.; Andrashko, Y.; Biloshchytska, S.; Faizullin, A. The Scientific Productivity of Collective Subjects Based on the Time-Weighted PageRank Method with Citation Intensity. Publications 2022, 10, 40. https://doi.org/10.3390/publications10040040
Kuchansky A, Biloshchytskyi A, Andrashko Y, Biloshchytska S, Faizullin A. The Scientific Productivity of Collective Subjects Based on the Time-Weighted PageRank Method with Citation Intensity. Publications. 2022; 10(4):40. https://doi.org/10.3390/publications10040040
Chicago/Turabian StyleKuchansky, Alexander, Andrii Biloshchytskyi, Yurii Andrashko, Svitlana Biloshchytska, and Adil Faizullin. 2022. "The Scientific Productivity of Collective Subjects Based on the Time-Weighted PageRank Method with Citation Intensity" Publications 10, no. 4: 40. https://doi.org/10.3390/publications10040040
APA StyleKuchansky, A., Biloshchytskyi, A., Andrashko, Y., Biloshchytska, S., & Faizullin, A. (2022). The Scientific Productivity of Collective Subjects Based on the Time-Weighted PageRank Method with Citation Intensity. Publications, 10(4), 40. https://doi.org/10.3390/publications10040040






