Abstract
Information resulting from a comprehensive investigation into the intrinsic strengths of hydrated divalent magnesium clusters is useful for elucidating the role of aqueous solvents on the Mg2+ ion, which can be related to those in bulk aqueous solution. However, the intrinsic Mg–O and intermolecular hydrogen bond interactions of hydrated magnesium ion clusters have yet to be quantitatively measured. In this work, we investigated a set of 17 hydrated divalent magnesium clusters by means of local vibrational mode force constants calculated at the B97X-D/6-311++G(d,p) level of theory, where the nature of the ion–solvent and solvent–solvent interactions were interpreted from topological electron density analysis and natural population analysis. We found the intrinsic strength of inner shell Mg–O interactions for [Mg(H2O)n]2+ (n = 1–6) clusters to relate to the electron density at the bond critical point in Mg–O bonds. From the application of a secondary hydration shell to [Mg(H2O)n]2+ (n = 5–6) clusters, stronger Mg–O interactions were observed to correspond to larger instances of charge transfer between the lp(O) orbitals of the inner hydration shell and the unfilled valence shell of Mg. As the charge transfer between water molecules of the first and second solvent shell increased, so did the strength of their intermolecular hydrogen bonds (HBs). Cumulative local vibrational mode force constants of explicitly solvated Mg2+, having an outer hydration shell, reveal a CN of 5, rather than a CN of 6, to yield slightly more stable configurations in some instances. However, the cumulative local mode stretching force constants of implicitly solvated Mg2+ show the six-coordinated cluster to be the most stable. These results show that such intrinsic bond strength measures for Mg–O and HBs offer an effective way for determining the coordination number of hydrated magnesium ion clusters.
1. Introduction
Magnesium, being the eighth most abundant element and second most abundant alkaline earth metal, accounts for 2% of the Earth’s crust [1]. As a result, magnesium (Mg2+) is heavily prevalent in ground water and sea water as a result of rock and mineral dissolution (i.e., calcium magnesium carbonate CaMg(CO3)3). Chemical [2,3,4], automotive/aircraft [5,6,7,8,9], agricultural [10], and energy storage [11,12,13] industries have also contributed to the presence of magnesium in water. As the production and application of magnesium increase, the amount of magnesium waste increases [14], having been noted to pose dangerous environmental effects [15]. High concentrations of such mineral-based ions have resulted in hard water where the hydration of the Mg2+ ion yields insoluble precipitates.
The structure and reactivity of hydrated divalent magnesium (i.e., Mg2+) has been a topic of notable investigation, as such information is useful for understanding the role a solvent has on such physical properties. The determination of the coordination number (CN) has been highly sought after to understand the nature of hydrated magnesium ion clusters, where such information can be related to the bulk form of the metal cation in an aqueous solvent. The CN is based upon the number of inner shell water molecules (n) bounded to the Mg2+ ion by the formation of Mg–O bonds ([Mg(H2O)n]2+); the Mg–O interactions are primarily electrostatic, where the dipole of these interactions are pointed from the water molecules towards the metal ion [16]. Experimental work based on X-ray diffraction (XRD) [17,18], Raman spectroscopy [19,20] X-ray Raman scattering (XRS) spectroscopy [21], infrared action spectroscopy [22], small angle X-ray scattering (SAXS) [21], black body infrared radiative dissociation (BIRD) [23], and neutron diffraction [24] have proposed a CN of 6 (i.e., [Mg(H2O)6]2+), in an octahedral arrangement (O), for hydrated divalent magnesium ion clusters; and the BIRD experiments showed that two constitutional isomers of [Mg(H2O)6]2+ ([Mg(H2O)5]2+–HO and [Mg(H2O)6]2+) may exist [23]. The XRS and SAXS work of Waluyo and co-workers estimated the Mg–O distances for the [Mg(H2O)6]2+ cluster to be 2.1 Å, approximately [21]. Moreover, the Infrared Action Spectroscopy work of Bush et al. [22] and the High-Pressure Mass Spectrometry work of Peschke et al. [25] reported that the inner shell holds up to a maximum of six water molecules with additional water molecules moving towards outer shells. On the other hand, the XRD work of Albright and co-workers, involving hydrated divalent magnesium clusters in concentrated chloride solutions, reported a CN of 6.8 [26]. It is widely recognized that the second hydration shell of hydrated Mg2+ clusters accommodates up to 12 water molecules [18,27,28,29], where, determined via X-ray diffraction, the bond distance between the metal ion and water molecules of the second solvent shell range from 4.10 to 4.28 Å and the bond distance between the inner and outer solvent shell falls between 2.75 and 2.81 Å [18,29]. The X-ray absorption spectra of 2 and 4 M concentrations of the Mg2+ cation in chloride solution, generated by Cappa et al., revealed that a large amount of charge transfer occurs between the water molecules of the first solvent shell and the Mg2+ ion [30].
Numerous solid-state structures of inorganic composites have validated the existence of the six-coordinated structure ([Mg(H2O)6]2+) [31]. Theoretical investigations into the solvation of Mg2+ span across molecular dynamic (MD) simulations [20,32,33,34,35], Monte Carlo simulations [32,36,37,38], Car Parrinello molecular dynamic simulations (CPMD) [39], effective fragment potential (EFP) calculations [40], ab initio molecular dynamics (AIMD) [28,41,42,43], density functional theory (DFT) [41,44,45,46,47,48,49,50], Møller–Plesset second-order perturbation theory (MP2) [41,44,47,49], coupled cluster theory with singles, double, and perturbative triples (CCSD(T)) [47,49], and Born–Oppenheimer molecular dynamics (BOMD) [51]; among these studies, a CN of 6 has been reported. However, the DFT study of Pavlov and co-workers has suggested that the Mg2+ ion forms stable configurations when coordinated to seven water molecules [52]. The recent work of Lynes et al. observed CN values of 5 and 6 to be present 0.35% and 99.65% of the time with average inner Mg–O bond lengths between 2.13 and 2.14 Å [42]. The calculated binding enthalpies for [Mg(H2O)n]2+ (n = 18) clusters, obtained by Markham and co-workers via MP2 and DFT, affirmed that the complete occupancy of the first shell for [Mg(H2O)n]2+ (n = 5 and 6) clusters lead to more stable configurations in contrast to configurations where the water molecules were spread across multiple solvation shells and that the [Mg(H2O)6]2+ cluster is lower in energy than its constitutional isomer [Mg(H2O)5]2+–HO [16]. Examined via natural bond orbital analysis (NBO), Rao et al. and Bai et al. observed Mg–O bond lengths stretching and the charge of the metal ion to decrease steadily as the CN increased [41,47]; Bai et al. also reported that the first hydration shell influences the charge transfer between the divalent magnesium cation and outer solvent shells [41]. Furthermore, the work of Neela et al. noted that as inner shell ion–solvent bond lengths (i.e., Mg–O) increased, the charge transfer between the inner shell water molecules and the magnesium di-cation also increased [44]. Even though numerous experimental and computational analysis have been conducted, details regarding the intrinsic strengths of the ion–solvent (i.e., Mg–O) and solvent–solvent (i.e., hydrogen bonding between solvent shells) interactions within hydrated magnesium clusters remain unexplored due to a lack of reliant measures for the intrinsic bond strength.
The binding energy (BE) is a thermodynamic measure that provides structural and energetic information for molecular systems and their chemical reactions (e.g., hydrated divalent magnesium clusters). BE values are based upon the energy difference between the hydrated magnesium cluster and their fragments (i.e., Mg2+, H2O), where all systems are at a local minima. However, the BE is notably tainted with electron reorganizations and the geometrical relaxation of the fragments, causing the measure to be short of ideally describing intrinsic bond strength [53,54,55,56,57]. In this work, we used local mode stretching force constants, obtained from the local mode analysis (LMA) of Konkoli and Cremer [58,59,60,61], to directly assess the strength of a particular bond [62,63]. The local stretching force constant (), characteristic of the stretching vibration of a bond, preserves the geometry and electronic structure to precisely expresses the intrinsic bond strength. The local stretching force constant has had success in describing covalent bonds [63,64,65,66,67,68] and noncovalent interactions such as tetrel bonds [69], pnicogen bonds [70], chalcogen bonds [71], halogen bonds [72,73,74], and hydrogen bonds [75,76,77,78,79,80].
Acquiring quantitative explanations for the ion–solvent and solvent–solvent interactions of hydrated Mg2+ clusters would provide a comprehensive understanding of the hydration of divalent Mg ions and the interactions that are involved in stabilizing such clusters. In this work, we quantified, for the first time, the bond strength of the electrostatic interactions for the hydrated magnesium clusters, being Mg–O interactions (ion–solvent) and hydrogen bonds (solvent–solvent), via the local mode stretching force constants of Konkoli and Cremer [58]. The main goals of this work were: (i) to assess the intrinsic bond strengths of the ion–solvent interactions (Mg–O) and their variation as the CN, of the first hydration shell, expands from 1 to 6 ([Mg(H2O)n]2+, where n = 1–6); (ii) to establish how the addition of a secondary hydration shell affects the intrinsic bond strength of inner ion–solvent (Mg–O) interactions ([Mg(H2O)n]2+–m(HO) with n = 5 and 6, m = 1–5 with n + m = 6–10 and where m = 12, where m represents the number of water molecules in the second hydration shell); and (iii) to quantitatively measure the intermolecular hydrogen bonding established between inner and outer solvent shells.
2. Computational Methods
Minimum geometries and normal vibrational modes of 17 hydrated magnesium clusters and reference molecules R1–R5 were obtained using the B97X-D functional [81,82,83] in combination with the Pople’s 6-311++G(d,p) basis set of triple- quality [84,85,86]. The B97X-D functional was used as it is well known for accurately describing clusters dictated by non-covalent interactions (NCIs) [43,86,87] such as hydrogen bond interactions [88,89,90]. To account for the solvation effects of the outer hydration shells, clusters 1–6 and reference molecules R1 and R2 were recalculated, at the same level of theory, using the implicit conductor-like polarizable continuum model (CPCM). The implicit CPCM model was utilized as it has been demonstrated to comprehensively account for solvent effects [43,91,92]. The initial configurations of clusters 1–6 were extracted from the work of Rao et al. [47] and those of clusters 7–17 were based off the work of Bai et al. [41]. Following geometry optimization and frequency calculations, the LMA of Konkoli and Cremer [58,59,60,61] was employed to quantify the intrinsic strength of Mg–O and HB interactions. Because a comprehensive background on LMA has been elaborated in Ref. [93], we summarize only the main essence of LMA below.
Vibrational spectroscopy provides a comprehensive overview on the electronic structure and bonding of a molecule in the form of normal vibrational modes. However, normal modes tend to delocalize over the molecule due to the presence of electronic and kinematic (mass) coupling, hampering the direct description of the intrinsic strength of chemical bonds. The fundamental equation of vibrational spectroscopy (Wilson’s secular equation of molecular vibration) is used to eliminate the electronic coupling resulting from the off-diagonal elements of the force constant matrix (F):
where F is expressed in Cartesian coordinates and M depicts the mass matrix. The L matrix accumulates the 3N normal mode vibrational eigenvectors I and is a diagonal matrix consisting of vibrational eigenvalues . From = 4 (c = speed of light) normal mode vibrational frequencies (i.e., ) are retrieved. To solve the equation, the force constant matrix F undergoes diagonalization which requires that Cartesian coordinates be transformed into normal coordinates Q to yield in:
where the force constant matrix K is expressed by Q. The electronic decoupling of vibrational modes is a general procedure for the derivation of harmonic vibrational frequencies where the mass coupling between the resultant normal modes remains.
The remaining kinematic (mass) coupling can be eliminated by using a mass-decoupled equivalent of the Euler–Lagrange equation, as demonstrated by Konkoli and Cremer [58,59,60,61]. The proceeding local vibrational modes () are liberated from all mode–mode coupling ():
where the local mode vector corresponding to the n-th internal coordinate is represented by . Each local mode a corresponds to a distinct local mode force constant and local vibrational frequency through:
and:
where is the mass of the local mode a which is a diagonal element out of the Wilson G matrix. Hereafter, is used instead of (i.e., = ).
Via an adiabatic connection scheme (ACS), a one-to-one relation between local and normal vibrational modes is established [61,62]. Unlike normal modes, the local modes do not depend on the kind of coordinates used to describe a molecular system. Because the local mode force constants only rely upon electronic structure change, as they are independent of atomic masses, they capture pure electronic effects and adequately describe chemical bond strength. The measures of bond strength order can be acquired from local mode force constants through the generalized Badger rule [94]:
From the values of two reference compounds of known bond orders, constants a and b can be obtained following the specification that BSO n = 0 when = 0. For the Mg–O interactions, reference molecules MgH2 (R1) and Mg=O (R2) were used alongside BSO n values of 1.0 and 2.0, respectively. Using R1 and R2, the a and b, constants values of 0.7074 and 0.7968 were obtained. For HBs, references molecules F−H (R3) and [H···F···H]− (R4) were utilized and assigned BSO n values of 1.0 and 0.5, respectively. Using R3 and R4, the a and b constants of 0.5293 and 0.2781 were derived. The HB of the water dimer (R5) was also included as to assess the magnitude of intrinsic HB strengths.
All DFT calculations were carried out using the Gaussian 16 Rev. A.03 program package [95]. Geometry optimizations were conducted using a superfine grid integration and a tight convergence criterion for the forces and displacements. The local force constants were calculated using the LModeA program [93,96]. The NBO6 program was utilized to obtain natural population charges and second order perturbation stabilization energy () values through natural bond orbital (NBO) analysis [97,98]. values correspond to the stabilization energy resulting from intermolecular charge transfer events (i.e., orbital interactions). Electron densities () and energy densities () at Mg–O and O···H bond critical points were determined using the AIMAll program [99]. The nature of the Mg–O and HB interactions were distinguished following the Cremer–Kraka criteria where a negative (stabilizing) value of the energy density ( < 0) at the bond critical point (BCP) denotes the covalent bonding while a positive value (i.e., > 0) indicates electrostatic interaction [100,101,102].
3. Results and Discussion
First hydration shell.Table 1 collects the bond distances (R), local vibrational frequencies (), local mode force constants (), bond strength orders (BSO ), electron densities (), energy densities (), and energy density ratios (/) taken at the Mg–O bond critical points , all values were taken as averages over all Mg–O bonds of clusters 1–17. Optimized geometries, point groups, and the natural bond orbital (NBO) charge of the Mg atom are depicted in Figure 1. The water molecules of the first and second hydration shells are distinctly notated by [Mg(H2O)n]2+–m(HO), where n refers to the amount of water molecules in the first hydration shell and m is the amount in the second hydration shell. Regarding the plots, [Mg(H2O)n]2+ clusters (1–6) are depicted by red points and [Mg(H2O)n]2+–m(H2O) clusters (7–17) by blue points. Though a CN of 6 has been suggested to result in the most stable configurations for hydrated magnesium clusters, for the sake of completeness, we investigated clusters where the CN ranges from 1 through 7. It is noted that the optimization of [Mg(H2O)7]2+ results in the migration of a single water molecule from the first hydration shell to the second hydration shell, as observed in previous theoretical works [41,45,50]. Note that the initial coordinates in Ref. [45] were taken from X-ray crystallographic studies. In addition, as mentioned earlier, the experimental work of Peschke et al. and Bush et al. showed that a CN of 7 for hydrated magnesium clusters was unstable leading to a CN of 6 [22,25].

Table 1.
Bond distances (R), local mode frequencies (), local mode force constants (), bond strength orders (BSO n), electron densities (), energy densities (), and the energy density ratios () of Mg–O interactions for clusters 1–17 and reference molecules R1–R2, calculated at the B97X-D/6-311++G(d,p) level of theory .
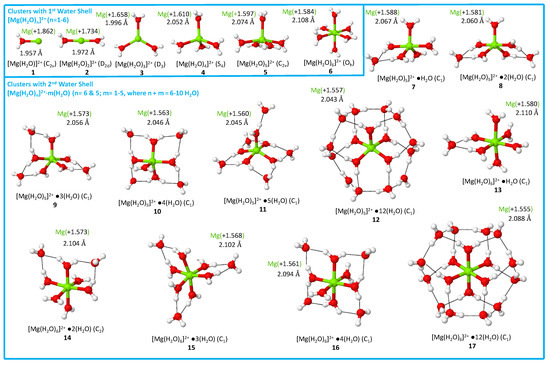
Figure 1.
A summary of the natural bond orbital (NBO) charges of the Mg atom alongside average Mg–O bond distances for clusters 1–17 obtained at the B97X-D/6-311++G(d,p) level of theory.
As the cluster size increases from 1–6, the Mg–O bond distance increases from 1.957 Å (1) to 2.108 Å (6). These results agree with the previous literature as the Mg–O bond length increases as n within the [Mg(H2O)n]2+ clusters increases from 1 to 6 [41,47]. We note that the Mg–O bond distances for clusters 1–6 (1.96 to 2.11 Å) agree well with experimentally determined lengths which range from 2.10 to 2.12 Å [17,18,19,20,24,26,103]. As verified by the Cremer–Kraka criterion [100,101,102], all Mg–O interactions have an electrostatic character, reflected by positive values.
Figure 2 shows the average BSO n values for the Mg–O bonds of clusters 1–6. The average BSO n (MgO) values vary from 1.104 to 0.546 units; decreasing in parallel to an increase in the CN for hydrated magnesium clusters. Furthermore, the Mg–O bonds within clusters 3–6 become weaker, where the MgO bond strengths of clusters 5 and 6 are notably weaker in contrast to the MgH bond within MgH2 (i.e., R1). Stabilization energies , based upon the second order perturbation analysis of the Fock matrix, show that the charge transfers between the lp orbital (i.e., unfilled valence-shell) of the the Mg ion and the (O–H) orbitals of inner shell water molecules cause the NBO charges of Mg and O atoms to decrease. The charges of Mg and O atoms steadily decline alongside a rise in the CN due to larger charge transfers occuring from lp(Mg) →(O–H) orbitals (see Figures S1 and S2, Supporting Information), inferring that the electrostatic interactions between Mg and O atoms become weaker alongside an increase in the CN. Furthermore, as shown in Figure 3, there exists a correlation between the electron density at the Mg–O bond critical point and the Mg–O bond strength, where a decrease in the electron density corresponds to a weakening of the Mg–O interaction.
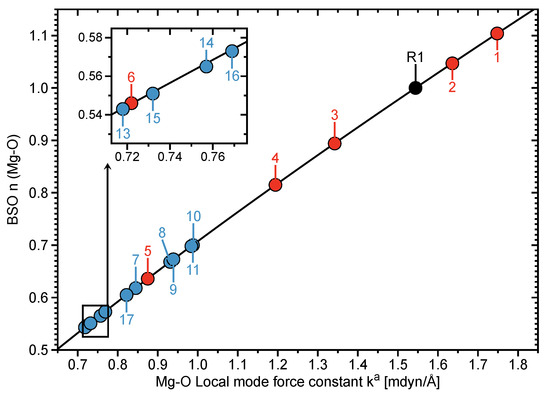
Figure 2.
BSO n (Mg–O) values and Mg–O force constants for clusters 1–17 and R1 calculated at the B97X-D/6-311++G(d,p) level of theory. BSO n (Mg–O) values were calculated via Equation (6). R2 was excluded from the plot to improve the visibility of the data. Clusters 1–6 are represented by red points, clusters 7–17 are depicted by blue points, and the black point portrays the Mg–O molecule (R1).
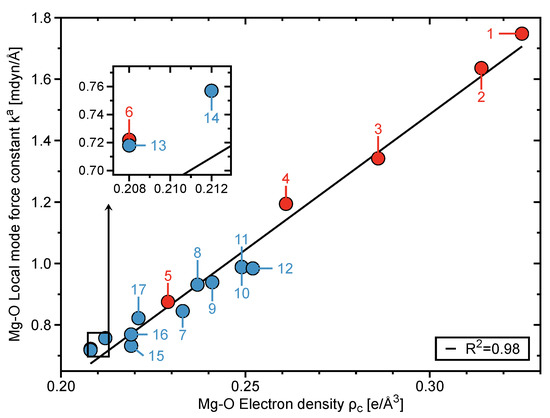
Figure 3.
The Mg–O force constants versus the Mg–O electron densities for clusters 1–17 calculated at the B97X-D/6-311++G(d,p) level of theory. Clusters 1–6 are represented by red points and clusters 7–17 are depicted by blue points.
Second hydration shell.Table 2 compiles the HB distances (R), local vibrational frequencies (), local mode force constants (), bond strength orders (BSO ), electron densities (), energy densities (), and their ratio (/), taken as averages over all HBs, for clusters 7–17. Both ion–solvent (Mg–O interactions) and solvent–solvent interactions (i.e., hydrogen bonds, O···H) are prevalent for clusters 7–17. As exhibited via dashed lines within clusters of Figure 1, HBs occur between hydrogen bond donor atoms (H atoms) in the first hydration shell and hydrogen bond acceptor atom (O atoms) in the second hydration shell. For clusters 7–17, the distance of inner Mg–O bonds varies between 2.043 and 2.110 Å (see Table 1). These results are in line with the work of Bai et al., which suggests that the inner Mg–O bond lengths, for clusters of similar configurations to 7–17, range between 2.045 and 2.109 Å [41]. As well, the HB distances between the solvent shells within [Mg(H2O)n]2+–m(HO) clusters vary, on average, between 1.806 and 1.928 Å; experimental values obtained by Vanhouteghem et al., via neutron diffraction analysis, were reported within the range of 1.815 to 2.008 Å, respectively [104]. In the following, we evaluated clusters 7–17 to assess how the intermolecular hydrogen bonding occurring between first and second hydration shells modulates the strength of inner Mg–O interactions. NBO charges can be found for clusters 7–17 in Figures S3–S8 of the Supporting Information.

Table 2.
Bond distances (R), local mode frequencies (), local mode force constants (), bond strength orders (BSO n), electron densities (), energy densities (), and the energy density ratios () for the hydrogen bonds (O···H) of clusters 7–17 and reference molecules R3–R5, calculated at the B97X-D/6-311++G(d,p) level of theory .
Cluster 7 involves five water molecules in the first hydration shell and one water molecule in the second hydration shell ([Mg(H2O)5]2+–HO). Two HBs (i.e., O–H···O) are established between the first and second water shell (see Figure 1), where the average BSO n is 0.337 ( = 0.197 mdyn/Å). Following the Cremer–Kraka criterion [100,101,102], the HBs of cluster 7 are primarily electrostatic in nature. The inner Mg–O bond length for cluster 7, on average, is shorter and weaker by 0.007 Å and 0.030 mdyn/Å in comparison to cluster 5. Moreover, the Mg–O bonds within 7, on average, are the weakest among secondly hydrated clusters with a CN of 5 (7–12).
Cluster 8 has five inner shell water molecules interacting with two outer shell water molecules ([Mg(H2O)5]2+–2(HO)) to form four HBs with a BSO n average of 0.330, respectively. The strength and length of the HBs of cluster 8 are weaker and longer than those of 7 (see Table 2). As demonstrated in the work of Tao et al., the orbital interaction occurring between the oxygen lone pair (i.e., lp(O)) of the acceptor water molecule and the anti-bonding orbital of the donor water molecule (i.e., (O–H)) plays an instrumental role behind HB stabilization; the HB strength is determined by push–pull effects which are interpreted from augmented charge transfer events [105]. As the magnitude of HB charge transfer becomes greater, the HB interaction becomes stronger [105]. Average stabilization energy values (), which represent the extent of charge transfer happening between the lp(O) of the second hydration shell and (O–H) of the first hydration shell, unveil that cluster the 8 obtains weaker HBs in contrast to cluster 7 due to smaller charge transfers (average = 15.27 (7); 14.77 kcal/mol (8)). Cluster 8 obtains, on average, shorter and stronger MgO bonds in contrast to those of 7 (see Table 1). The Mg–O bonds of 8 possess larger electrostatic contributions due to more charge being transferred from the lp(O) of inner shell H2O molecules to the lp(Mg) orbital (lp represents unfilled valence shell) ( = 137.93 (7); 141.83 kcal/mol (8)).
Cluster 9 contains five water molecules in the first shell and three water molecules in the second shell ([Mg(H2O)5]2+–3(HO)), and the six HBs that form between the two solvent shells (see Figure 1) have an average BSO n value of 0.318 ( = 0.162 mdyn/Å). The HBs of 9 are longer and weaker in contrast to the HBs of clusters 7 and 8 (See Table 2) due to a smaller amount of stabilization energy resulting from the charge transfer between outer →(O–H) and inner shell orbitals (average = 13.398 kcal/mol (9)). Similarly to cluster 8, cluster 9, in comparison to cluster 7, involves a greater amount of electron charge transfer from inner lp(O) → lp(Mg) ( = 146.92 kcal/mol (9)) which increases the electrostatic interactions between the Mg ion and the inner water shell within 9; this strengthening of the electrostatic interactions causes the Mg–O bonds of 9 to be shorter and stronger than those of 8 (see Table 1).
Cluster 10 is composed of five water molecules in the first hydration shell and four water molecules in the second hydration shell ([Mg(H2O)5]2+–4(HO)), and eight HBs are formed between the two hydration shells where the average BSO n is 0.297 ( = 0.125 mdyn/Å). In contrast to clusters 7–9, the HBs of 10 are weaker due to a smaller amount of charge transfer occurring between the two hydration shells (average = 11.350 kcal/mol (10)). Furthermore, 10 possesses the weakest HBs (see Table 1). As a consequence, the strength of the electrostatic interactions between the Mg ion and inner water molecules of cluster 10 increases and in turn strengthens and shortens the Mg–O bonds beyond that of clusters 6, 7, 8, and 9 (see Table 1). Cluster 11 has a total of ten water molecules across both hydration shells ([Mg(H2O)5]2+–5(HO)), and nine HBs were detected between the inner and outer hydration shell where the average BSO n value is 0.309 ( = 0.153 mdyn/Å). The HBs of 11 are stronger than those of 10 because of a greater charge transfer from the outer lp(O) to the inner (O–H) orbitals (average = 12.427 kcal/mol (11)). In comparison to cluster 10, the Mg–O bond length and the strength of 11, on average, are shorter and stronger (see Table 1). Furthermore, in comparison to cluster 10, the based off the charge transfer between inner lp(O) and the lp(Mg) orbital is slightly larger for cluster 11 ( = 154.29 (10, 154.53 kcal/mol (11)).
Cluster 12 is a five-coordinated structure that is surrounded by a second solvent shell composed of 12 water molecules ([Mg(H2O)5]2+–12(HO)), and 22 HBs are established between the two solvent shells having an average (HB) value greater than that of the water dimer by 0.010 mdyn/Å (R5). Moreover, the HBs within cluster 12 are the strongest HBs amongst all clusters having a secondary hydration shell (7–17) (see Table 1), the amount of charge delocalization occurring between both hydration shells is the largest for 12 (average = 14.672 kcal/mol (12)). Thus, for cluster 12, the electrostatic interactions between the Mg ion and inner H2O molecules become stronger and enable the charge transfer between the inner lp(O) orbitals and the lp(Mg) orbital to be greater in magnitude in comparison to clusters 6–11 ( = 557.56 kcal/mol (12)). This large amount of charge transfer between the Mg2+ ion and inner shell water molecules of 12 yields Mg–O bond distances that are smaller than those of clusters 6–11 (see Table 1).
Cluster 13 has six water molecules within the first solvent shell and one water molecule in the second solvent shell ([Mg(H2O)6]2+–HO); two HBs form between the two solvent shells with an average BSO n value of 0.323 ( = 0.169 mdyn/Å). The HB interactions of 13 are the weakest amongst [Mg(H2O)6]2+–m(HO) clusters (13–17). In comparison to cluster 6, the inner Mg–O interactions of 13 elongate and weaken slightly (See Table 1). The Mg ion within cluster 14 is coordinated to six inner shell water molecules and has a outer hydration shell holding two water molecules ([Mg(H2O)6]2+–2(HO)), and four HBs form between the hydration shells with an average BSO n value of 0.319. The HBs of 14 are weaker than those of 13 due to smaller charge transfers between outer lp(O) orbitals and inner shell (O–H) orbitals (average = 13.96 (13), 12.35 kcal/mol (14)). In comparison to clusters 6 and 13–16, the inner Mg–O interactions of 14 are shorter and stronger (see Table 1). The Mg–O bonds of 14 are stronger than those of 13 due to stronger electrostatic interactions as shown from the larger stabilization energy value stemming from the charge transfer between inner shell lp(O) to the lp(Mg) orbital ( = 144.35 (13), 148.58 kcal/mol (14)).
Cluster 15 ([Mg(H2O)6]2+–3(H2O)) acquires six HBs which are formed between the two water shells, with an average BSO n (HB) value of 0.330. The HB bond strengths between the inner and outer hydration shells of cluster 15 are in the closest proximity to that of the water dimer with regard to [Mg(H2O)6]2+–m(H2O) clusters (m = 1–4; 13–16) (see Table 2). The average HB strength within 15 is stronger than that of 14 due to a greater electronic charge transfer between the outer shell lp(O) orbitals and the inner shell (O–H) orbitals (average = 12.535 kcal/mol (15)). As a result, the decrease in the electrostatic interaction between the Mg ion and O atoms of the inner hydration shell slightly strengthen and shorten the Mg–O bonds of 15 with respect to that of 14 (see Table 1). Cluster 16 has six water molecules in the first shell and four water molecules in the second shell ([Mg(H2O)6]2+–4(H2O)); the two shells form nine HBs where the average BSO n value is 0.317 ( = 0.159 mdyn/Å). The HBs for 16 are the weakest with regard to clusters 13–15 and 17. The weaker HBs of 16 yield stronger Mg–O interactions, on average, for cluster 16 in comparison to clusters 13–15) and 17. The Mg–O interactions are stronger within cluster 16 than those of clusters 13–15 and 17 due to a smaller amount of charge transfer from the lp(O) of the inner shell to the lp(Mg) orbital ( = kcal/mol (16)).
Cluster 17 is a six-coordinated structure that is surrounded by a secondary shell comprised of 12 water molecules ([Mg(H2O)6]2+–12(H2O)); a HB network involving 24 HBs between the inner and outer hydration shell are established where the BSO n is nearly exact to that of the water dimer (R5) (see Table 1). Furthermore, cluster 17 has the second strongest HBs amongst clusters with a secondary hydration shell (see Table 1), where the magnitude of charge transfer between the two hydration shells is smaller in comparison to that of cluster 12 (average = 14.672 (12), 13.587 kcal/mol (17). In comparison to clusters 6 and 13–16, the Mg–O bonds are shorter and stronger (see Table 1) due to an increase in the electrostatic interactions between the Mg ion and inner shell water molecules. The values resulting from charge transfers from lp(O) → lp(Mg) are the largest for 17 with regard to clusters 13–16 ( = 652.16 kcal/mol (17)).
Utilizing cumulative local mode force constants to determine the CN for hydrated magnesium clusters. The cumulative local mode force constant , which is the sum of the local mode force constants for targeted bonds (i.e., multiple bonds) of a system, can be used to understand the stability of a molecule (i.e., cluster) in retrospect to a complementary set of molecules. In this work, the cumulative local mode force constants for clusters 1–17 are based upon the sum of all accompanying ion–solvent (i.e., Mg–O) and solvent–solvent (i.e., HBs) local mode stretching force constants. As demonstrated in Table 3, the values of explicitly solvated clusters 1–6 indicate a CN of 5 to acquire a slightly greater amount of stabilization in comparison to a CN of 6. In addition, the values for clusters 7–17, which contain explicitly modeled secondary hydration shells, demonstrate that the application of a second hydration shell to [Mg(H2O)n]2+ clusters (n = 5 and 6) further stabilizes the Mg–O interactions due to HB interactions between first and second hydration shells. Weighted BE values can be found in Table S1 of the Supporting Information.

Table 3.
The cumulative local mode force constants and binding energies (BE) for clusters 1–17 at the B97X-D/6-311++G(d,p) level of theory.
Moreover, the values of 6 (i.e., [Mg(H2O)6]2+) and 7 (i.e., [Mg(H2O)5]2+–H2O) suggest that cluster 7 acquires a greater stability than 6 (see Table 3), being in opposite viewpoint to the results disclosed by Markhem et al. (see Figure 4) [16]. It is mentioned that the values of 7 ([Mg(H2O)5]2+–H2O) and 13 ([Mg(H2O)6]2+–H2O) suggest the six-coordinated structure to be preferred over the five-coordinated structure ( = 4.617 (7), 4.644 mdyn/Å (13)).
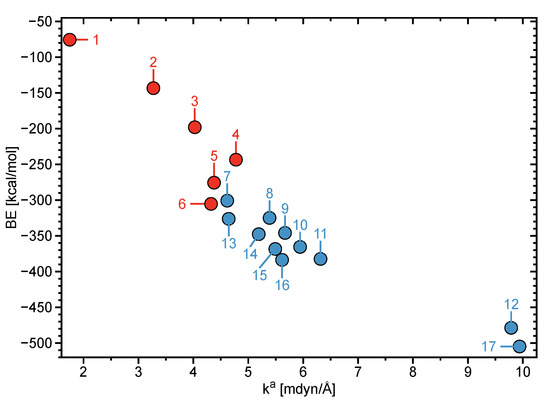
Figure 4.
The binding energy (BE) and the corresponding cumulative local mode force constants of the clusters 1–17 calculated at the B97X-D/6-311++G(d,p) level of theory. Clusters 1–6 are represented by red points and clusters 7–17 are depicted by blue points.
The values for 8 (i.e., [Mg(H2O)5]2+–2(H2O)) are larger than those for 14 (i.e., [Mg(H2O)6]2+–2(H2O)), revealing that, in the case where two water molecules comprise the second hydration shell, a CN of five results in a more stable configuration in contrast to a CN of 6 (see Table 3). Moreover, by comparing the values of cluster 9 (i.e., [Mg(H2O)5]2+–3(H2O)) and 10 (i.e., [Mg(H2O)5]2+–4(H2O)) to clusters 15 (i.e., [Mg(H2O)6]2+–3(H2O)) and 16 (i.e., [Mg(H2O)6]2+–4(H2O)) (see Table 3), a CN of 5, with respect to a CN of 6, is observed to result in more stable configurations. It is noted that current ab initio molecular dynamics simulations conducted by Lynes and co-workers revealed a small percentage of the CN for Mg2+ to be 5 [42]. Because 9–11 ([Mg(H2O)5]2+–m(H2O), m = 2–4) clusters possess larger values than 14–16 clusters ([Mg(H2O)6]2+–m(H2O), m = 2–4), it is inferred that clusters 9–11 are more likely to be present.
However, a CN of 6 is shown to be preferred over a CN of 5 when a single water molecules occupies the second hydration shell (see values for clusters 7 and 13 in Table 3). In agreement with the results from implicit solvation and previous studies on [Mg(H2O)n]2+–12(H2O) (n = 5 and 6) clusters [41], the values for the explicit model of [Mg(H2O)6]2+–12(H2O) (17), in which the second hydration shell holds the maximum of 12 water molecules, reveal that cluster 17 acquires the strongest bond stabilizations in comparison to all other explicitly modeled clusters (7–16). We note that clusters [Mg(H2O)5]2+–12(H2O) (12) have the second largest bond stabilizations (see Table 3 and Figure 4). Each of the six inner shell water molecules of cluster 17 form two HBs with water molecules of the second hydration shell and that second shell water molecules form a total of 12 HBs among themselves (see Figure 1) as demonstrated in previous works [16,41].
The implicit hydration of clusters 1–6 was assessed through the application of the CPCM solvation model as to determine the CN, here the water molecules of the first hydration shell were modeled explicitly while outer hydration shells are represented by a dielectric continuum. We derived values, via local mode analysis, for these clusters in order to establish the key element responsible for their chemical stability. From the values of the implicitly solvated clusters, as shown in Table 4, we observed the implicit addition of outer shells to [Mg(H2O)n]2+ (n = 1–6) clusters to increase in stability alongside increasing CN, the results revealing a CN of 6 to result in the most stable configuration due to the Mg–O and HB interactions. The CN of 6, as suggested from local mode analysis, agrees with recent experimental [16,19,21,22,24] and computational works [20,32,34,39,41,42,43,44,46,47,49,51].

Table 4.
The cumulative local mode force constants and binding energies (BE) for clusters 1–6 at the B97X-D/6-311++G(d,p) level of theory using the implicit CPCM solvation model.
Overall, the local mode analysis of explicitly solvated [Mg(H2O)5]2+–12(H2O) (15) and [Mg(H2O)5]2+–12(H2O) (16) is in agreement with our results from the implicitly solvated [Mg(H2O)5]2+ and [Mg(H2O)6]2+ clusters showing that a CN of 6, surrounded by a fully occupied second hydration shell, yielded the strongest bond stabilizations among the clusters investigated in this work.
Comparison of hydrated Mg2+ clusters with hydrated Ca2+ clusters.
In this work, via the utilization of cumulative local mode stretching force constants , we observed the divalent Mg ion to coordinate with up to six water molecules, whereas in our previous work regarding hydrated calcium clusters, the divalent Ca ion was observed to undergo coordination with up to eight water molecules [106].
The more restricted CN of the Mg2+ has previously been attributed to the smaller ion size [39,107,108], whereas the larger size of the Ca2+ ion has been linked to weaker inner ion–solvent interactions in retrospect to that of the hydrated Mg2+ ion [51]. As shown by Table 3 and Table 5, the values of explicitly hydrated systems, based upon inner ion–solvent interactions, are larger for [Mg(H2O)n]2+ (n = 1–6) (1–6) clusters in comparison to that of their Ca2+ counterparts by differences of 0.601 to 1.341 mdyn/Å (i.e., 1a–6a in Table 5) [106]; where the value for [Mg(H2O)6]2+ (6) is larger than that of [Ca(H2O)6]2+ (6a) by 0.788 mdyn/Å.

Table 5.
Cumulative local mode force constants for the implicit and explicit solvation of [Ca(H2O)n]2+ (n = 1–6) (1a–6a), calculated at the B97X-D/6-311++G(d,p) level of theory, from the work of Delgado et al. [106].
From the addition of explicitly modeled secondary solvation shells, we observed that the same amount of HBs form between the inner and outer solvent shell for both [Mg(H2O)6]2+–3(H2O) (15) and [Ca(H2O)6]2+–3(H2O) and for both [Mg(H2O)6]2+–4(H2O) (16) and [Ca(H2O)6]2+–4(H2O) [106], from values, which consider all Mg–O/Ca–O and HB interactions, we found that larger values are obtained for clusters [Mg(H2O)6]2+–3(H2O) (15) and [Mg(H2O)6]2+–4(H2O) (16) in contrast to their Ca2+ equivalents ( = 5.202 for [Ca(H2O)6]2+–3(H2O) and 4.822 mdyn/Å for [Ca(H2O)6]2+–4(H2O)) [106] (see Table 3). We note that the HB interactions, on average, are bigger for [Ca(H2O)6]2+–3(H2O) ((HB) = 0.196 mdyn/Å) and [Ca(H2O)6]2+–4(H2O) ((HB) = 0.173 mdyn/Å) clusters in comparison to their Mg2+ analogs [106] (see HB values for 15 and 16 in Table 2). Therefore, the hydrated magnesium clusters, 15 and 16, acquire a greater stability than their Ca2+ counterparts primarily due to stronger ion–solvent interactions between the first solvent shell and the Mg2+ ion.
4. Conclusions
Herein, 17 hydrated divalent magnesium clusters were investigated at the B97X-D/6-311++G(d,p) level of theory to reveal how electronic effects influence the intrinsic strengths of the ion–solvent and solvent–solvent interactions. Local mode analysis was employed to obtain local stretching force constants as an intrinsic bond strength measure, where the results were complemented with NBO charges, electron and energy densities, and stabilization energies. In such a way, a deeper understanding about the nature of Mg–O and HB interactions was acquired.
- For inner Mg–O bonds within [Mg(H2O)n]2+ (n = 1–6) clusters, the average intrinsic bond strength becomes weaker as the CN increases. As the size of the hydration shell becomes larger, the intrinsic Mg–O bond strength decreases alongside a weakening of the electrostatic interaction between the divalent Mg ion and O atoms by means of a decrease in the electron density allocated at the Mg–O bond critical point region caused by increased electron transfer between lp(O) and lp(Mg).
- The strength of HB interactions occurring between the first and second hydration shell within [Mg(H2O)n]2+–m(H2O) (n = 6–8, m = 1–4, n + m = 9 to 10, and where m = 12) clusters increase due to a greater extent of electron transfer occurring between the inner hydration shell HB donors and the HB acceptors of the outer hydration shell. The HB bonds of [Mg(H2O)n]2+–m(H2O) (n = 6–8, m = 1–4, n + m = 9 to 10, and where m = 12) clusters were observed, on average, to be weaker than that of the water dimer by as much as 0.086, and stronger, on average, by as much as 0.010 mydn/Å.
- An increase in the NBO charges of O atoms belonging to the first hydration shell is due to a greater magnitude of charge transfer between the inner and outer hydration shell and leads to a strengthening of the ion–solvent interactions (i.e., Mg–O bonds). The ion–solvent interactions, for clusters with a secondary hydration shell, are strengthened from a larger amount of charge transfer between lp(O) → lp(Mg) orbitals.
- From the explicit and implicit solvation of the Mg2+ ion, cumulative local mode force constants , which consider both Mg–O and HB interactions, were derived and suggested a CN of 5 and 6 to be prevalent among the clusters investigated, where a CN of 6 is primarily preferred in the instance where the second shell allocates 1 and 12 water molecules.
Understanding the structure and reactivity of hydrated divalent magnesium clusters is key to elucidating the effect of aqueous solvents on the Mg2+ ion. Shedding light upon the nature underlying Mg–O and HB intrinsic bond strengths is essential for elucidating such effects. The cumulative stretching force constant considers the strength of multiple bonds within a system, allowing one to assess the bond properties of a cluster by a single value. From values, one can obtain an immediate answer about the preferred CN among isomeric structures of hydrated divalent magnesium ion clusters.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/inorganics9050031/s1, Atomic Cartesian coordinates (in units Å) for the explicitly solvated clusters 1–17, calculated at the B97X-D/6-311++G(d,p) level of theory. Table S1: Weighted BE values for explicitly solvated clusters 1–17. Figures S1–S8: The natural bond orbital charges of explicitly solvated clusters 1–17.
Author Contributions
Conceptualization, D.S. and E.K.; methodology, E.K.; validation, A.A.A.D., D.S. and E.K.; formal analysis, A.A.A.D.; investigation, A.A.A.D.; resources, E.K.; data curation, A.A.A.D.; writing—original draft preparation, A.A.A.D.; writing—review and editing, D.S. and E.K.; visualization, A.A.A.D.; supervision, D.S. and E.K.; project administration, E.K.; funding acquisition, E.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation, Grant CHE 1464906.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Atomic cartesian coordinates (in units Å) for the explicitly solvated clusters 1–17, calculated at the B97X-D/6-311++G(d,p) level of theory, are listed. The natural bond orbital charges of explicitly solvated clusters 1–17 are shown in Figures S1–S8.
Acknowledgments
This work was supported by supported by the National Science Foundation, Grant CHE 1464906. The authors thank SMU and HPC for providing generous computational resources.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fröhlich, P.; Lorenz, T.; Martin, G.; Brett, B.; Bertau, M. Valuable Metals-Recovery Processes, Current Trends, and Recycling Strategies. Angew. Chem. Int. 2017, 56, 2544–2580. [Google Scholar] [CrossRef]
- Casetta, M.; Michaux, G.; Ohl, B.; Duquesne, S.; Bourbigot, S. Key Role of Magnesium Hydroxide Surface Treatment in the Flame Retardancy of Glass Fiber Reinforced Polyamide 6. Polym. Degrad. Stab. 2018, 148, 95–103. [Google Scholar] [CrossRef]
- Yam, B.J.; Le, D.K.; Do, N.H.; Nguyen, P.T.; Thai, Q.B.; Phan-Thien, N.; Duong, H.M. Recycling of Magnesium Waste into Magnesium Hydroxide Aerogels. J. Environ. Chem. Eng. 2020, 8, 104101. [Google Scholar] [CrossRef]
- Nguyen, Q.B.; Nai, M.L.S.; Nguyen, A.S.; Seetharaman, S.; Leong, E.W.W.; Gupta, M. Synthesis and Properties of Light Weight Magnesium–Cenosphere Composite. Mater. Sci. Technol. 2016, 32, 923–929. [Google Scholar] [CrossRef]
- Powell, B.; Krajewski, P.; Luo, A. Magnesium Alloys for Lightweight Powertrains and Automotive Structures. In Materials, Design and Manufacturing for Lightweight Vehicles; Elsevier: Amsterdam, The Netherlands, 2021; pp. 125–186. [Google Scholar]
- Kurtuluş, E.; Tekin, G. Conversion of Aluminum Front Bumper System to Magnesium Material by Using Design of Experiment Method. Int. J. Automot. Technol. 2021, 5, 34–42. [Google Scholar] [CrossRef]
- Dziubińska, A.; Gontarz, A.; Dziubiński, M.; Barszcz, M. The Forming of Magnesium Alloy Forgings for Aircraft and Automotive Applications. Adv. Sci. Technol. Res. 2016, 10, 158–168. [Google Scholar] [CrossRef]
- Dvorsky, D.; Kubasek, J.; Vojtech, D.; Minarik, P. Novel Aircraft Mg-Y-Gd-Ca Alloys with High Ignition Temperature and Suppressed Flammability. Mater. Lett. 2020, 264, 127313. [Google Scholar] [CrossRef]
- Kulekci, M.K. Magnesium and its Alloys Applications in Automotive Industry. Int. J. Adv. Manuf. Technol. 2007, 39, 851–865. [Google Scholar] [CrossRef]
- Wang, Z.; Hassan, M.U.; Nadeem, F.; Wu, L.; Zhang, F.; Li, X. Magnesium Fertilization Improves Crop Yield in Most Production Systems: A Meta-Analysis. Front. Plant Sci. 2020, 10, 1727. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zhao, S.; Li, T.; Su, D.; Guo, S.; Wang, G. Recent Advances in Rechargeable Magnesium-Based Batteries for High-Efficiency Energy Storage. Adv. Energy Mater. 2020, 10, 1903591. [Google Scholar] [CrossRef]
- Nakatsugawa, I.; Chino, Y.; Nakano, H. Discharge Behavior of Water-Activated Magnesium Battery. In Magnesium Alloys—Selected Issue; IntechOpen: Rijeka, Croatia, 2018; pp. 1–23. [Google Scholar]
- Shao, H.; He, L.; Lin, H.; Li, H.W. Progress and Trends in Magnesium-Based Materials for Energy-Storage Research: A Review. Energy Technol. 2017, 6, 445–458. [Google Scholar] [CrossRef]
- Wang, X.; Yan, X.; Li, X. Environmental Risks for Application of Magnesium Slag to Soils in China. J. Integr. Agric. 2020, 19, 1671–1679. [Google Scholar] [CrossRef]
- Koltun, P.; Tharumarajah, A.; Ramakrishnan, S. Life Cycle Environmental Impact of Magnesium Automotive Components. In Essential Readings in Magnesium Technology; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 175–180. [Google Scholar]
- Markham, G.D.; Glusker, J.P.; Bock, C.W. The Arrangement of First- and Second-Sphere Water Molecules in Divalent Magnesium Complexes: Results from Molecular Orbital and Density Functional Theory and from Structural Crystallography. J. Phys. Chem. B 2002, 106, 5118–5134. [Google Scholar] [CrossRef]
- Caminiti, R.; Licheri, G.; Piccaluga, G.; Pinna, G. X-ray Diffraction Study of MgCl2 Aqueous Solutions. J. Appl. Crystallogr. 1979, 12, 34–38. [Google Scholar] [CrossRef]
- Caminiti, R.; Licheri, G.; Piccaluga, G.; Pinna, G. Diffraction of X-rays and Hydration Phenomena in Aqueous Solutions of Mg(NO3)2. Chem. Phys. Lett. 1979, 61, 45–49. [Google Scholar] [CrossRef]
- Marques, M.A.; Cabaco, M.I.; de Barros Marques, M.I.; Gaspar, A.M. Intermediate-range Order in Aqueous Solutions of Salts Constituted of Divalent Ions Combined with Monovalent Counter-ions. J. Phys. Condens. Matter 2002, 14, 7427–7448. [Google Scholar] [CrossRef]
- Callahan, K.M.; Casillas-Ituarte, N.N.; Roeselová, M.; Allen, H.C.; Tobias, D.J. Solvation of Magnesium Dication: Molecular Dynamics Simulation and Vibrational Spectroscopic Study of Magnesium Chloride in Aqueous Solutions. J. Phys. Chem. A 2010, 114, 5141–5148. [Google Scholar] [CrossRef] [PubMed]
- Waluyo, I.; Huang, C.; Nordlund, D.; Bergmann, U.; Weiss, T.M.; Pettersson, L.G.M.; Nilsson, A. The Structure of Water in the Hydration Shell of Cations from X-ray Raman and Small Angle X-ray Scattering Measurements. J. Chem. Phys. 2011, 134, 064513. [Google Scholar] [CrossRef] [PubMed]
- Bush, M.F.; O’Brien, J.T.; Prell, J.S.; Wu, C.C.; Saykally, R.J.; Williams, E.R. Hydration of Alkaline Earth Metal Dications: Effects of Metal Ion Size Determined Using Infrared Action Spectroscopy. J. Am. Chem. Soc. 2009, 131, 13270–13277. [Google Scholar] [CrossRef]
- Rodriguez-Cruz, S.E.; Jockusch, R.A.; Williams, E.R. Hydration Energies and Structures of Alkaline Earth Metal Ions, M2+(H2O)n, n = 5–7, M = Mg, Ca, Sr, and Ba. J. Am. Chem. Soc. 1999, 121, 8898–8906. [Google Scholar] [CrossRef]
- Bruni, F.; Imberti, S.; Mancinelli, R.; Ricci, M.A. Aqueous Solutions of Divalent Chlorides: Ions Hydration Shell and Water Structure. J. Chem. Phys. 2012, 136, 064520. [Google Scholar] [CrossRef]
- Peschke, M.; Blades, A.T.; Kebarle, P. Hydration Energies and Entropies for Mg2+, Ca2+, Sr2+, and Ba2+ from Gas-Phase Ion-Water Molecule Equilibria Determinations. J. Phys. Chem. A 1998, 102, 9978–9985. [Google Scholar] [CrossRef]
- Albright, J.N. X-ray Diffraction Studies of Aqueous Alkaline-Earth Chloride Solutions. J. Chem. Phys. 1972, 56, 3783–3786. [Google Scholar] [CrossRef]
- Cowan, J. Magnesium Activation of Nuclease Enzymes-The Importance of Water. Inorg. Chim. Acta 1998, 275–276, 24–27. [Google Scholar] [CrossRef]
- Martínez, J.M.; Pappalardo, R.R.; Marcos, E.S. First-Principles Ion-Water Interaction Potentials for Highly Charged Monatomic Cations. Computer Simulations of Al3+, Mg2+, and Be2+ in Water. J. Am. Chem. Soc. 1999, 121, 3175–3184. [Google Scholar] [CrossRef]
- Ohtaki, H.; Radnai, T. Structure and Dynamics of Hydrated Ions. Chem. Rev. 1993, 93, 1157–1204. [Google Scholar] [CrossRef]
- Cappa, C.D.; Smith, J.D.; Messer, B.M.; Cohen, R.C.; Saykally, R.J. Effects of Cations on the Hydrogen Bond Network of Liquid Water: New Results from X-ray Absorption Spectroscopy of Liquid Microjets. J. Phys. Chem. B 2006, 110, 5301–5309. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. B 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Lightstone, F.C.; Schwegler, E.; Hood, R.Q.; Gygi, F.; Galli, G. A First Principles Molecular Dynamics Simulation of the Hydrated Magnesium Ion. Chem. Phys. Lett. 2001, 343, 549–555. [Google Scholar] [CrossRef]
- Larentzos, J.P.; Criscenti, L.J. A Molecular Dynamics Study of Alkaline Earth Metal-Chloride Complexation in Aqueous Solution. J. Phys. Chem. B 2008, 112, 14243–14250. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A.; Dixit, M.K.; Tembe, B.L. Solvation Structures and Dynamics of the Magnesium Chloride (Mg2+–Cl−) Ion Pair in Water-Ethanol Mixtures. J. Phys. Chem. A 2013, 117, 8703–8709. [Google Scholar] [CrossRef]
- Piquemal, J.P.; Perera, L.; Cisneros, G.A.; Ren, P.; Pedersen, L.G.; Darden, T.A. Towards Accurate Solvation Dynamics of Divalent Cations in Water Using the Polarizable Amoeba Force Field: From Energetics to Structure. J. Chem. Phys. 2006, 125, 054511. [Google Scholar] [CrossRef]
- Tongraar, A.; Rode, B.M. Structural Arrangement and Dynamics of the Hydrated Mg2+: An Ab Initio QM/MM Molecular Dynamics Simulation. Chem. Phys. Lett. 2005, 409, 304–309. [Google Scholar] [CrossRef]
- Tongraar, A.; Rode, B.M. The Role of Non-Additive Contributions on the Hydration Shell Structure of Mg2+ Studied by Born-Oppenheimer Ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation. Chem. Phys. Lett. 2001, 346, 485–491. [Google Scholar] [CrossRef]
- Krekeler, C.; Delle, L.S. Solvation of Positive Ions in Water: The Dominant Role of Water-Water Interaction. J. Phys. Cond. Matt. 2007, 19, 192101. [Google Scholar] [CrossRef]
- Ikeda, T.; Boero, M.; Terakura, K. Hydration Properties of Magnesium and Calcium Ions from Constrained First Principles Molecular Dynamics. J. Chem. Phys. 2007, 127, 074503. [Google Scholar] [CrossRef]
- Merrill, G.N.; Webb, S.P.; Bivin, D.B. Formation of Alkali Metal/Alkaline Earth Cation Water Clusters, M(H2O)1–6, M = Li+, Na+, K+, Mg2+, and Ca2+: An Effective Fragment Potential (EFP) Case Study. J. Phys. Chem. A 2003, 107, 386–396. [Google Scholar] [CrossRef]
- Bai, G.; Yi, H.B.; Li, H.J.; Xu, J.J. Hydration Characteristics of Ca2+ and Mg2+: A Density Functional Theory, Polarized Continuum Model and Molecular Dynamics Investigation. Mol. Phys. 2013, 111, 553–568. [Google Scholar] [CrossRef]
- Lynes, O.; Austin, J.; Kerridge, A. Ab Initio Molecular Dynamics Studies of Hydroxide Coordination of Alkaline Earth Metals and Uranyl. Phys. Chem. Chem. Phys. 2019, 21, 13809–13820. [Google Scholar] [CrossRef]
- Wang, X.; Toroz, D.; Kim, S.; Clegg, S.L.; Park, G.S.; Tommaso, D.D. Density Functional Theory based Molecular Dynamics Study of Solution Composition Effects on the Solvation Shell of Metal Ions. Phys. Chem. Chem. Phys. 2020, 22, 16301–16313. [Google Scholar] [CrossRef]
- Neela, Y.I.; Mahadevi, A.S.; Sastry, G.N. Analyzing Coordination Preferences of Mg2+ Complexes: Insights from Computational and Database Study. Struct. Chem. 2012, 24, 637–650. [Google Scholar] [CrossRef]
- Bock, C.W.; Kaufman, A.; Glusker, J.P. Coordination of Water to Magnesium Cations. Inorg. Chem. 1994, 33, 419–427. [Google Scholar] [CrossRef]
- Bock, C.W.; Markham, G.D.; Katz, A.K.; Glusker, J.P. The Arrangement of First- and Second-shell Water Molecules Around Metal Ions: Effects of Charge and Size. Theor. Chem. Acc. 2006, 115, 100–112. [Google Scholar] [CrossRef]
- Rao, J.S.; Dinadayalane, T.C.; Leszczynski, J.; Sastry, G.N. Comprehensive Study on the Solvation of Mono- and Divalent Metal Cations: Li+, Na+, K+, Be2+, Mg2+ and Ca2+. J. Phys. Chem. A 2008, 112, 12944–12953. [Google Scholar] [CrossRef]
- Adrian-Scotto, M.; Mallet, G.; Vasilescu, D. Hydration of Mg++: A Quantum DFT and Ab Initio HF Study. J. Mol. Struc. THEOCHEM 2005, 728, 231–242. [Google Scholar] [CrossRef]
- Gonzalez, J.D.; Florez, E.; Romero, J.; Reyes, A.; Restrepo, A. Microsolvation of Mg2+, Ca2+: Strong Influence of Formal Charges in Hydrogen Bond Networks. J. Mol. Model. 2013, 19, 1763–1777. [Google Scholar] [CrossRef] [PubMed]
- Tunell, I.; Lim, C. Factors Governing the Metal Coordination Number in Isolated Group IA and IIA Metal Hydrates. Inorg. Chem. 2006, 45, 4811–4819. [Google Scholar] [CrossRef] [PubMed]
- León-Pimentel, C.I.; Amaro-Estrada, J.I.; Hernández-Cobos, J.; Saint-Martin, H.; Ramírez-Solís, A. Aqueous Solvation of Mg(ii) and Ca(ii): A Born-Oppenheimer Molecular Dynamics Study of Microhydrated Gas Phase Clusters. J. Chem. Phys. 2018, 148, 144307. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, M.; Siegbahn, P.E.M.; Sandstrŏm, M. Hydration of Beryllium, Magnesium, Calcium, and Zinc Ions Using Density Functional Theory. J. Phys. Chem. A 1998, 102, 219–228. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. From Molecular Vibrations to Bonding, Chemical Reactions, and Reaction Mechanism. Curr. Org. Chem. 2010, 14, 1524–1560. [Google Scholar] [CrossRef]
- Setiawan, D.; Sethio, D.; Cremer, D.; Kraka, E. From Strong to Weak NF Bonds: On the Design of a New Class of Fluorinating Agents. Phys. Chem. Chem. Phys. 2018, 20, 23913–23927. [Google Scholar] [CrossRef]
- Tao, Y.; Tian, C.; Verma, N.; Zou, W.; Wang, C.; Cremer, D.; Kraka, E. Recovering Intrinsic Fragmental Vibrations Using the Generalized Subsystem Vibrational Analysis. J. Chem. Theory Comput. 2018, 14, 2558–2569. [Google Scholar] [CrossRef]
- Krapp, A.; Bickelhaupt, F.M.; Frenking, G. Orbital Overlap and Chemical Bonding. Chem. Eur. J. 2006, 12, 9196–9216. [Google Scholar] [CrossRef]
- Zhao, L.; Hermann, M.; Schwarz, W.H.E.; Frenking, G. The Lewis Electron-Pair Bonding Model: Modern Energy Decomposition Analysis. Nat. Rev. Chem. 2019, 3, 48–63. [Google Scholar] [CrossRef]
- Konkoli, Z.; Cremer, D. A New Way of Analyzing Vibrational Spectra. I. Derivation of Adiabatic Internal Modes. Int. J. Quantum Chem. 1998, 67, 1–9. [Google Scholar] [CrossRef]
- Konkoli, Z.; Larsson, J.A.; Cremer, D. A New Way of Analyzing Vibrational Spectra. II. Comparison of Internal Mode Frequencies. Int. J. Quantum Chem. 1998, 67, 11–27. [Google Scholar] [CrossRef]
- Konkoli, Z.; Cremer, D. A New Way of Analyzing Vibrational Spectra. III. Characterization of Normal Vibrational Modes in terms of Internal Vibrational Modes. Int. J. Quantum Chem. 1998, 67, 29–40. [Google Scholar] [CrossRef]
- Konkoli, Z.; Larsson, J.A.; Cremer, D. A New Way of Analyzing Vibrational Spectra. IV. Application and Testing of Adiabatic Modes within the Concept of the Characterization of Normal Modes. Int. J. Quantum Chem. 1998, 67, 41–55. [Google Scholar] [CrossRef]
- Zou, W.; Kalescky, R.; Kraka, E.; Cremer, D. Relating Normal Vibrational Modes to Local Vibrational Modes with the Help of an Adiabatic Connection Scheme. J. Chem. Phys. 2012, 137, 084114. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Identification of the Strongest Bonds in Chemistry. J. Phys. Chem. A 2013, 117, 8981–8995. [Google Scholar] [CrossRef]
- Kalescky, R.; Zou, W.; Kraka, E.; Cremer, D. Quantitative Assessment of the Multiplicity of Carbon-Halogen Bonds: Carbenium and Halonium Ions with F, Cl, Br, and I. J. Phys. Chem. A 2014, 118, 1948–1963. [Google Scholar] [CrossRef] [PubMed]
- Kraka, E.; Cremer, D. Characterization of CF Bonds with Multiple-Bond Character: Bond Lengths, Stretching Force Constants, and Bond Dissociation Energies. ChemPhysChem 2009, 10, 686–698. [Google Scholar] [CrossRef]
- Humason, A.; Zou, W.; Cremer, D. 11,11-Dimethyl-1,6-methano[10]annulene-An Annulene with an Ultralong CC Bond or a Fluxional Molecule? J. Phys. Chem. A 2014, 119, 1666–1682. [Google Scholar] [CrossRef] [PubMed]
- Sethio, D.; Lawson Daku, L.M.; Hagemann, H.; Kraka, E. Quantitative Assessment of B–B–B, B–Hb–B, and B–Ht Bonds: From BH3 to B12H122−. ChemPhysChem 2019, 20, 1967–1977. [Google Scholar] [CrossRef] [PubMed]
- Makoś, M.Z.; Freindorf, M.; Sethio, D.; Kraka, E. New Insights into Fe–H2 and Fe–H− Bonding of a [NiFe] Hydrogenase Mimic—A Local Vibrational Mode Study. Theor. Chem. Acc. 2019, 138, 76. [Google Scholar] [CrossRef]
- Sethio, D.; Oliveira, V.; Kraka, E. Quantitative Assessment of Tetrel Bonding Utilizing Vibrational Spectroscopy. Molecules 2018, 23, 2763. [Google Scholar] [CrossRef]
- Setiawan, D.; Kraka, E.; Cremer, D. Description of Pnicogen Bonding with the help of Vibrational Spectroscopy—The Missing Link Between Theory and Experiment. Chem. Phys. Lett. 2014, 614, 136–142. [Google Scholar] [CrossRef]
- Oliveira, V.; Cremer, D.; Kraka, E. The Many Facets of Chalcogen Bonding: Described by Vibrational Spectroscopy. J. Phys. Chem. A 2017, 121, 6845–6862. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. The Intrinsic Strength of the Halogen Bond: Electrostatic and Covalent Contributions Described by Coupled Cluster Theory. Phys. Chem. Chem. Phys. 2016, 18, 33031–33046. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. Quantitative Assessment of Halogen Bonding Utilizing Vibrational Spectroscopy. Inorg. Chem. 2016, 56, 488–502. [Google Scholar] [CrossRef]
- Oliveira, V.; Cremer, D. Transition from Metal-Ligand Bonding to Halogen Bonding Involving a Metal as Halogen Acceptor: A Study of Cu, Ag, Au, Pt, and Hg Complexes. Chem. Phys. Lett. 2017, 681, 56–63. [Google Scholar] [CrossRef]
- Yannacone, S.; Sethio, D.; Kraka, E. Quantitative Assessment of Intramolecular Hydrogen Bonds in Neutral Histidine. Theor. Chem. Acc. 2020, 139, 125. [Google Scholar] [CrossRef]
- Martins, J.; Quintino, R.P.; Politi, J.R.S.; Sethio, D.; Gargano, R.; Kraka, E. Computational Analysis of Vibrational Frequencies and Rovibrational Spectroscopic Constants of Hydrogen Sulfide Dimer using MP2 and CCSD(T). Spectrochim. Acta A 2020, 239, 118540. [Google Scholar] [CrossRef]
- Freindorf, M.; Kraka, E.; Cremer, D. A Comprehensive Analysis of Hydrogen Bond Interactions Based on Local Vibrational Modes. Int. J. Quantum Chem. 2012, 112, 3174–3187. [Google Scholar] [CrossRef]
- Kalescky, R.; Zou, W.; Kraka, E.; Cremer, D. Local Vibrational Modes of the Water Dimer—Comparison of Theory and Experiment. Chem. Phys. Lett. 2012, 554, 243–247. [Google Scholar] [CrossRef]
- Kalescky, R.; Kraka, E.; Cremer, D. Local Vibrational Modes of the Formic Acid Dimer—The Strength of the Double H-Bond. Mol. Phys. 2013, 111, 1497–1510. [Google Scholar] [CrossRef]
- Tao, Y.; Zou, W.; Jia, J.; Li, W.; Cremer, D. Different Ways of Hydrogen Bonding in Water—Why Does Warm Water Freeze Faster than Cold Water? J. Chem. Theory Comput. 2017, 13, 55–76. [Google Scholar] [CrossRef]
- Thanthiriwatte, K.S.; Hohenstein, E.G.; Burns, L.A.; Sherrill, C.D. Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions. J. Chem. Theory Comput. 2010, 7, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.D.; Head-Gordon, M. Systematic Optimization of Long-Range Corrected Hybrid Density Functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Hariharan, P.C.; Pople, J.A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar] [CrossRef]
- Taxer, T.; Ončák, M.; Barwa, E.; van der Linde, C.; Beyer, M.K. Electronic Spectroscopy and Nanocalorimetry of Hydrated Magnesium Ions [Mg(H2O)n]2+, n = 20–70: Spontaneous Formation of a Hydrated Electron? Faraday Discuss. 2019, 217, 584–600. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Wategaonkar, S. ZEKE Photoelectron Spectroscopy of p-Fluorophenol···H2S/H2O Complexes and Dissociation Energy Measurement Using the Birge-Sponer Extrapolation Method. J. Phys. Chem. A 2014, 118, 9386–9396. [Google Scholar] [CrossRef]
- Da Costa, L.M.; Stoyanov, S.R.; Gusarov, S.; Tan, X.; Gray, M.R.; Stryker, J.M.; Tykwinski, R.; de M. Carneiro, J.W.; Seidl, P.R.; Kovalenko, A. Density Functional Theory Investigation of the Contributions of π–π Stacking and Hydrogen-Bonding Interactions to the Aggregation of Model Asphaltene Compounds. Energy Fuels 2012, 26, 2727–2735. [Google Scholar] [CrossRef]
- Domagała, M.; Palusiak, M. The Influence of Substituent Effect on Noncovalent Interactions in Ternary Complexes Stabilized by Hydrogen-Bonding and Halogen-Bonding. Comput. Theor. Chem. 2014, 1027, 173–178. [Google Scholar] [CrossRef]
- Sutradhar, D.; Chandra, A.K.; Zeegers-Huyskens, T. Theoretical Study of the Interaction of Fluorinated Dimethyl Ethers and the ClF and HF Molecules. Comparison Between Halogen and Hydrogen Bonds. Int. J. Quantum Chem. 2016, 116, 670–680. [Google Scholar] [CrossRef]
- Takano, Y.; Houk, K.N. Benchmarking the Conductor-like Polarizable Continuum Model (CPCM) for Aqueous Solvation Free Energies of Neutral and Ionic Organic Molecules. J. Chem. Theory Comput. 2004, 1, 70–77. [Google Scholar] [CrossRef]
- Jesus, A.J.L.; Tomé, L.I.N.; Eusébio, M.E.S.; Rosado, M.T.S.; Redinha, J.S. Hydration of Cyclohexylamines: CPCM Calculation of Hydration Gibbs Energy of the Conformers. J. Phys. Chem. A 2007, 111, 3432–3437. [Google Scholar] [CrossRef] [PubMed]
- Kraka, E.; Zou, W.; Tao, Y. Decoding Chemical Information from Vibrational Spectroscopy Data: Local Vibrational Mode Theory. WIREs Comput. Mol. Sci. 2020, 10, 1480. [Google Scholar] [CrossRef]
- Kraka, E.; Larsson, J.A.; Cremer, D. Generalization of the Badger Rule Based on the Use of Adiabatic Vibrational Modes. In Computational Spectroscopy; Grunenberg, J., Ed.; Wiley: New York, NY, USA, 2010; pp. 105–149. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zou, W.; Tao, Y.; Freindorf, M.; Makoś, M.Z.; Verma, N.; Kraka, E. Local Vibrational Mode Analysis (LModeA. Computational and Theoretical Chemistry Group (CATCO); Southern Methodist University: Dallas, TX, USA, 2020. [Google Scholar]
- Weinhold, F.; Landis, C.R. Valency and Bonding: A Natural Bond Orbital Donor—Acceptor Perspective; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular Interactions From a Natural Bond Orbital, Donor-Acceptor Viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Keith, T.A. AIMall version 17.01.25; TK Gristmill Software: Overland Park, KS, USA, 2019; Available online: aim.tkgristmill.com (accessed on 21 April 2021).
- Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density? Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. 1984, 23, 627–628. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
- Kraka, E.; Cremer, D. Chemical Implication of Local Features of the Electron Density Distribution. In Theoretical Models of Chemical Bonding. The Concept of the Chemical Bond; Maksic, Z.B., Ed.; Springer: Heidelberg, Germany, 1990; Volume 2, pp. 453–542. [Google Scholar]
- Bol, W.; Gerrits, G.J.A.; van Panthaleon Eck, C.L. The Hydration of Divalent Cations in Aqueous Solution. An X-ray Investigation with Isomorphous Replacement. J. Appl. Crystallogr. 1970, 3, 486–492. [Google Scholar] [CrossRef]
- Vanhouteghem, F.; Lenstra, A.T.H.; Schweiss, P. Magnesium Bis(hydrogen maleate) Hexahydrate, [Mg(C4H3O4)2]·6H2O, Studied by Elastic Neutron Diffraction and Ab Initio Calculations. Acta Crystallogr. B Struct. Sci. Cryst. 1987, 43, 523–528. [Google Scholar] [CrossRef]
- Tao, Y.; Zou, W.; Kraka, E. Strengthening of Hydrogen Bonding With the Push-Pull Effect. Chem. Phys. Lett. 2017, 685, 251–258. [Google Scholar] [CrossRef]
- Delgado, A.A.A.; Sethio, D.; Munar, I.; Aviyente, V.; Kraka, E. Local Vibrational Mode Analysis of Ion–Solvent and Solvent–Solvent Interactions for Hydrated Ca2+ Clusters. J. Chem. Phys. 2020, 153, 224303. [Google Scholar] [CrossRef]
- Richens. Chemistry of Aqua Ions; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Carl, D.R.; Armentrout, P.B. Threshold Collision-Induced Dissociation of Hydrated Magnesium: Experimental and Theoretical Investigation of the Binding Energies for Mg2+(H2O)x Complexes (x = 2–10). ChemPhysChem 2012, 14, 681–697. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).