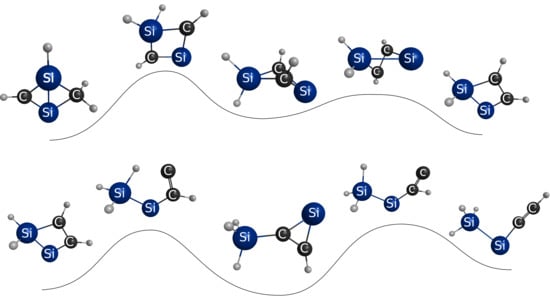
The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations
Abstract
1. Introduction
2. Computational Methods
3. Results
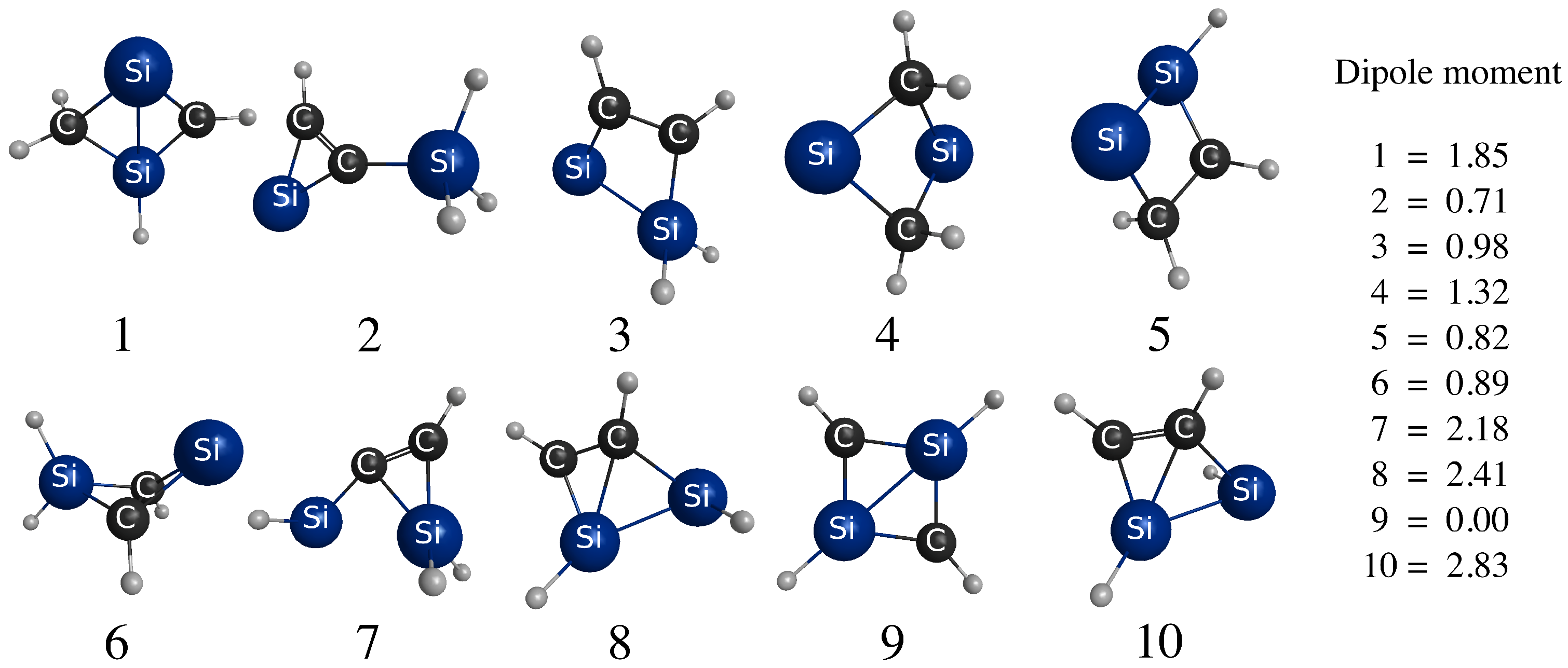
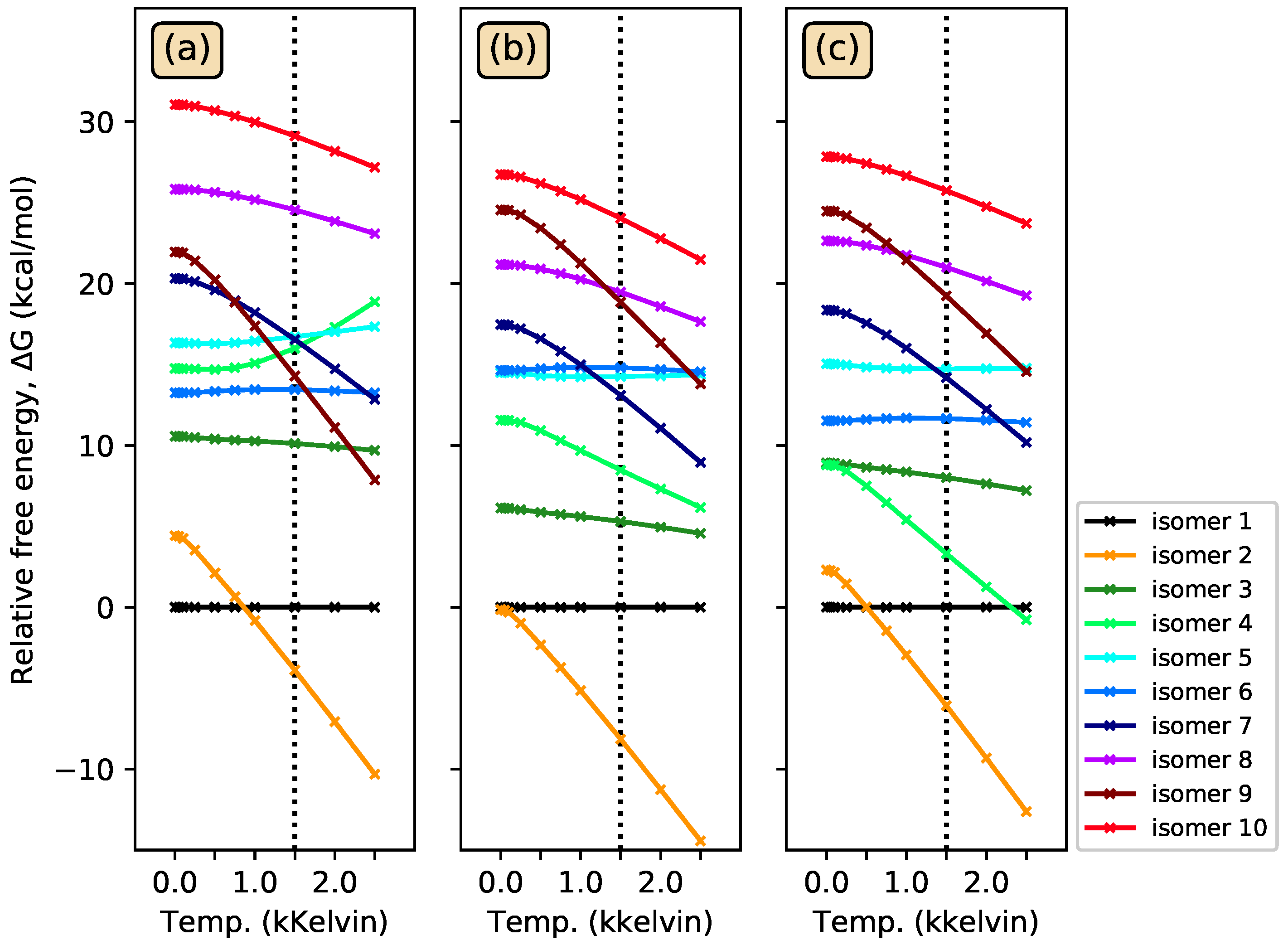
3.1. Energy-Ordering CSiH Isomers
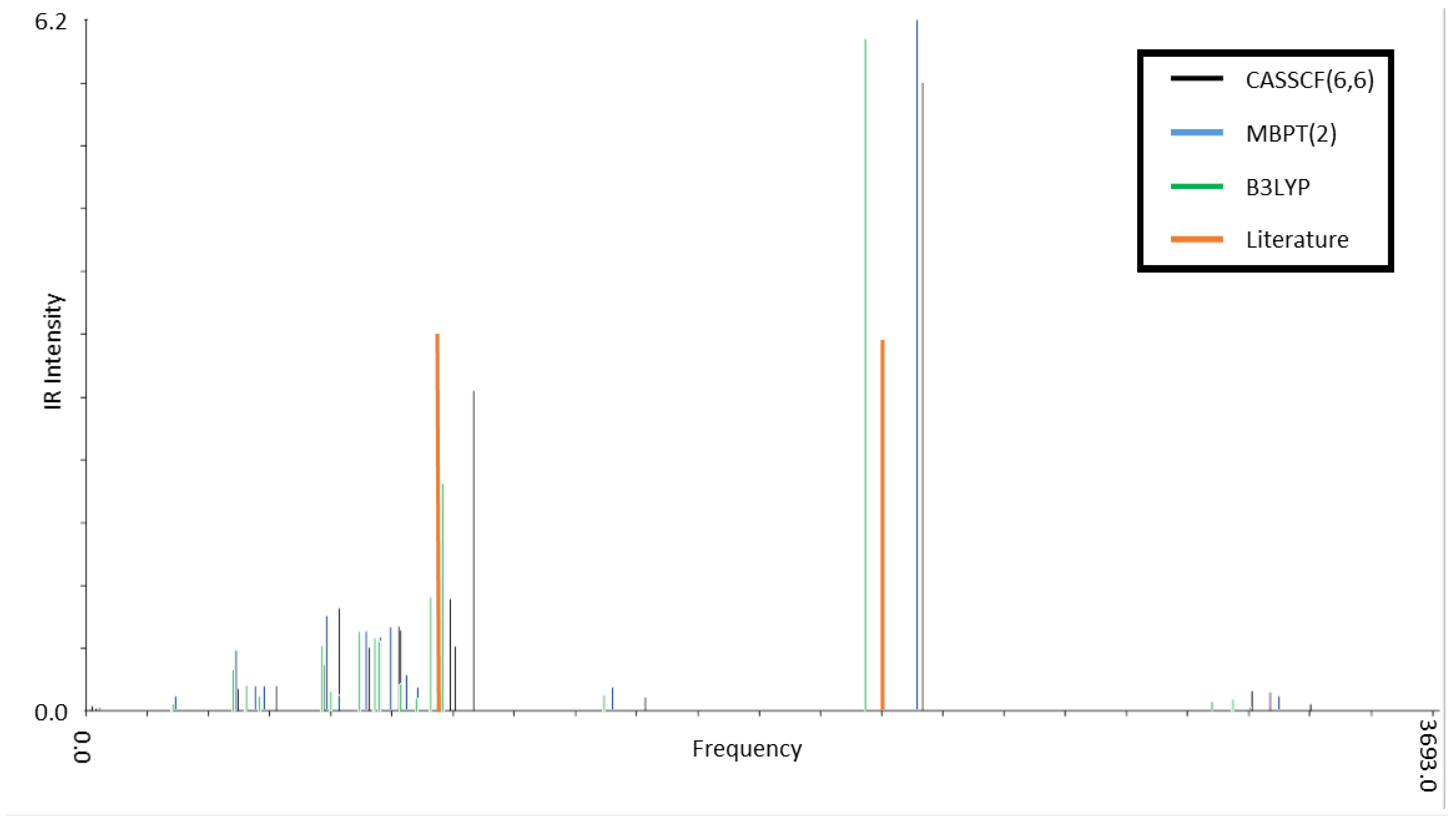
3.2. Infrared Spectroscopy of Low-Lying CSiH Isomers
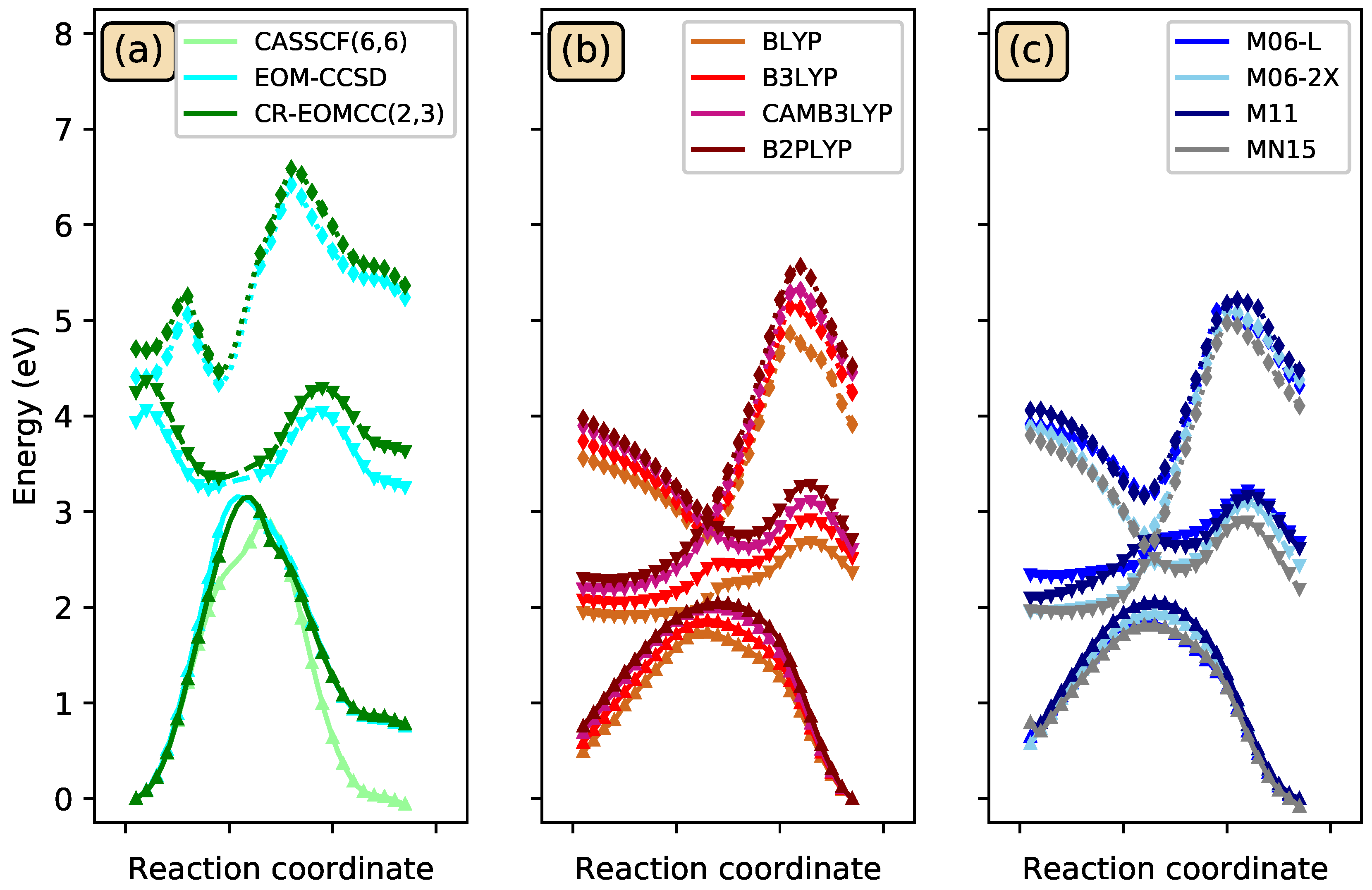
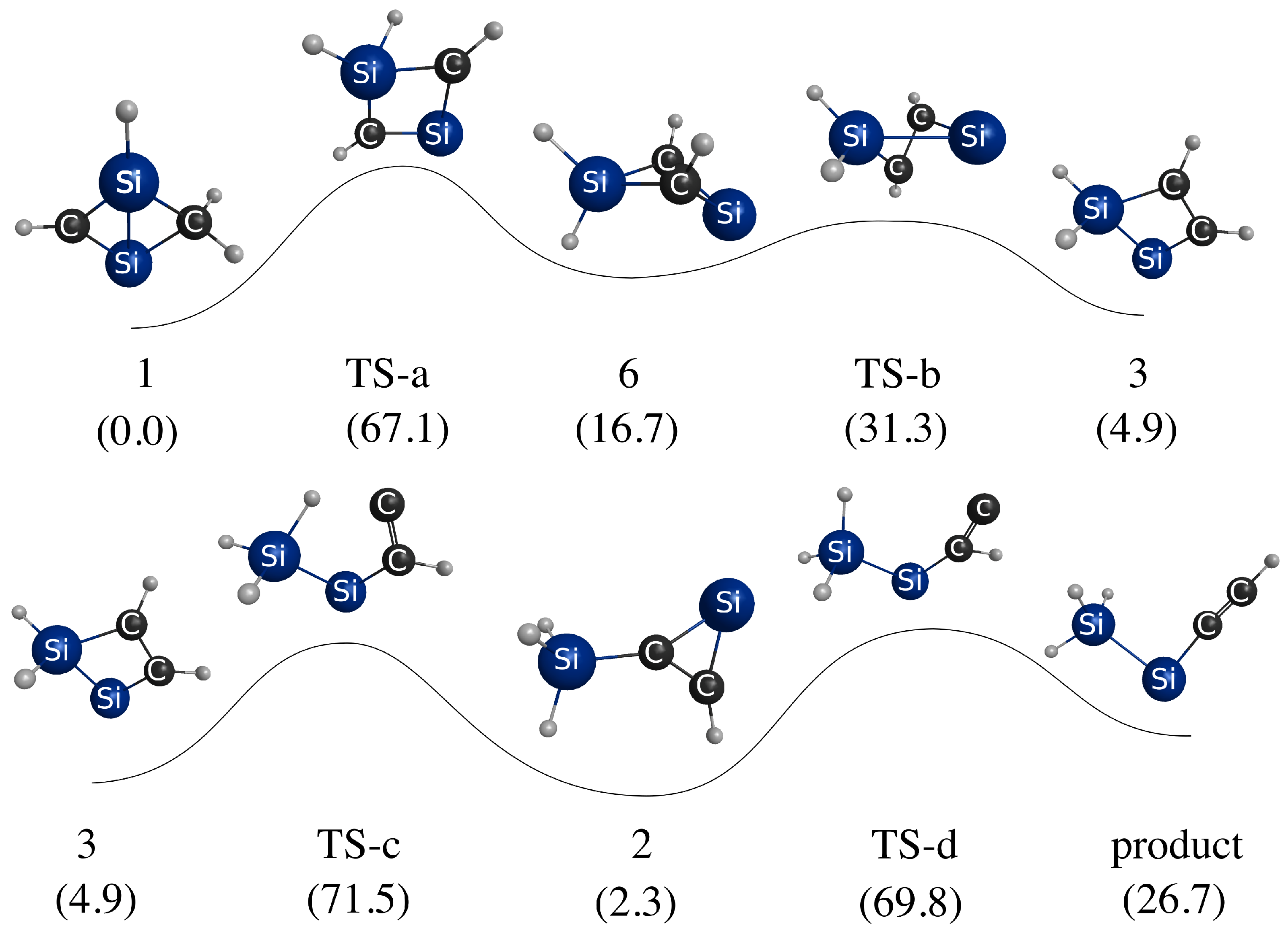
3.3. Photoisomerization of Low-Lying CSiH Isomers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DFT | Density functional theory |
| KS | Kohn-Sham |
| SCF | Self-consistent field |
| HF | Hartree-Fock |
| XCF | Exchange-correlation functional |
| LYP | Lee Yang Parr |
| PBE | Perdew Berke Ernzerhof |
| DH | Double-hybrid |
| MBPT | Many-body perturbation theory |
| DSD | Dispersion corrected, Spin-component scaled, Double-hybrid |
| TD | Time-dependent |
| CC | Coupled-cluster |
| CCSD | Coupled-cluster with singles and doubles |
| CR | Completely renormalized |
| EOM | Equation-of-motion |
| IR | Infrared |
| CBS | Complete basis set |
| CAS | Complete active space |
| ZPVE | Zero-point vibrational energy |
| MSE | Mean signed error |
| MUE | Mean unsigned error |
| IRC | Internal reaction coordinate |
| VEE | Vertical excitation energies |
References
- Holme, T.A.; Gordon, M.S.; Yabushita, S.; Schmidt, M.W. Theoretical studies of cyclic C2Si2H4 molecules. Organometallics 1984, 3, 583–586. [Google Scholar] [CrossRef]
- Maier, G.; Reisenauer, H.P.; Meudt, A. Silylenes of the Elemental Composition C2H4Si2: Generation and Matrix-Spectroscopic Identification. Eur. J. Org. Chem. 1998, 1998, 1291. [Google Scholar] [CrossRef]
- Casida, M.E. Time-Dependent Density Functional Response Theory for Molecules. In Recent Advances in Density Functional Methods; World Scientific: Singapore, 1995; pp. 155–192. [Google Scholar] [CrossRef]
- Casida, M.E. Jacob’s Ladder for Time-Dependent Density-Functional Theory: Some Rungs on the Way to Photochemical Heaven. In ACS Symposium Series; American Chemical Society: Washington, DC, USA, 2002; pp. 199–220. [Google Scholar] [CrossRef]
- Maitra, N.T. Fundamental aspects of time-dependent density functional theory. J. Chem. Phys. 2016, 144, 220901. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. B 1964, 136, 864. [Google Scholar] [CrossRef]
- Zhang, I.Y.; Wu, J.; Xu, X. Extending the reliability and applicability of B3LYP. Chem. Commun. 2010, 46, 3057–3070. [Google Scholar] [CrossRef] [PubMed]
- Kruse, H.; Goerigk, L.; Grimme, S. Why the Standard B3LYP/6-31G* Model Chemistry Should Not Be Used in DFT Calculations of Molecular Thermochemistry: Understanding and Correcting the Problem. J. Org. Chem. 2012, 77, 10824–10834. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. J. Phys. Chem. Lett. 2011, 2, 2810–2817. [Google Scholar] [CrossRef]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. How Accurate are the Minnesota Density Functionals for Noncovalent Interactions, Isomerization Energies, Thermochemistry, and Barrier Heights Involving Molecules Comprised of Main-Group Elements. J. Chem. Theory Comput. 2016, 12, 4303–4325. [Google Scholar] [CrossRef]
- Perdew, J.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. In Density Functional Theory and Its Applications to Materials; Doren, V.V., Alsenoy, K.V., Geerlings, P., Eds.; AIP Conference Proceedings: Melville, NY, USA, 2001; Volume 577, pp. 1–20. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Tao, J.; Staroverov, V.N.; Scuseria, G.E.; Csonka, G.I. Prescription for the design and selection of density functional approximations: More constraint satisfaction with fewer fits. J. Chem. Phys. 2005, 123, 062201. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, X.; Goddard, W.A. Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics. Proc. Natl. Acad. Sci. USA 2009, 106, 4963–4968. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. Double-hybrid density functionals. WIREs Comput. Mol. Sci. 2014, 4, 576–600. [Google Scholar] [CrossRef]
- Coester, F. Bound states of a many-particle system. Nucl. Phys. 1958, 7, 421. [Google Scholar] [CrossRef]
- Coester, F.; Kümmel, H. Short-range correlations in nuclear wave functions. Nucl. Phys. 1960, 17, 477. [Google Scholar] [CrossRef]
- Čížek, J. On the correlation problem in atomic and molecular systems. Calculation of wavefunction components in Ursell-type expansion using quantum-field theoretical methods. J. Chem. Phys. 1966, 45, 4256. [Google Scholar] [CrossRef]
- Čížek, J. On the use of the cluster expansion and the technique of diagrams in calculations of correlation effects in atoms and molecules. Adv. Chem. Phys. 1969, 14, 35. [Google Scholar]
- Čížek, J.; Paldus, J. Correlation problmes in atomic and molecular systems. III. Rederivation of the coupled-pair many-electron theory using the traditional quantum chemical methods. Int. J. Quantum Chem. 1971, 5, 359. [Google Scholar] [CrossRef]
- Paldus, J.; Čížek, J.; Shavitt, I. Correlation problems in atomic and molecular systems. IV. Extended coupled-pair many-electron theory and its application to the BH3 molecule. Phys. Rev. A 1972, 5, 50. [Google Scholar] [CrossRef]
- Margraf, J.T.; Perera, A.; Lutz, J.J.; Bartlett, R.J. Single-reference coupled cluster theory for multi-reference problems. J. Chem. Phys. 2017, 147, 184101. [Google Scholar] [CrossRef]
- Piecuch, P.; Włoch, M. Renormalized coupled-cluster methods exploiting left eigenstates of the similarity-transformed Hamiltonian. J. Chem. Phys. 2005, 123, 224105. [Google Scholar] [CrossRef]
- Piecuch, P.; Włoch, M.; Gour, J.R.; Kinal, A. Single-reference, size-extensive, non-iterative coupled-cluster approaches to bond breaking and biradicals. Chem. Phys. Lett. 2006, 418, 467. [Google Scholar] [CrossRef]
- Włoch, M.; Lodriguito, M.D.; Piecuch, P.; Gour, J.R. Two new classes of non-iterative coupled-cluster methods derived from the method of moments of coupled-cluster equations. Mol. Phys. 2006, 104, 2149–2172. [Google Scholar]
- Włoch, M.; Gour, J.R.; Piecuch, P. Extension of the renormalized coupled-cluster methods exploiting left eigenstates of the similarity-transformed Hamiltonian to open-shell systems: A benchmark study. J. Phys. Chem. 2007, A111, 11359. [Google Scholar] [CrossRef]
- Lutz, J.J.; Piecuch, P. Performance of the completely renormalized equation-of-motion coupled-cluster method in calculations of excited-state potential cuts of water. Comput. Theor. Chem. 2014, 1040–1041, 20–34. [Google Scholar] [CrossRef]
- Kornobis, K.; Kumar, N.; Lodowski, P.; Jaworska, M.; Piecuch, P.; Lutz, J.J.; Wong, B.M.; Kozlowski, P.M. Electronic Structure of the S1 State in Methylcobalamin: Insight from CASSCF/MC-XQDPT2, EOM-CCSD, and TD-DFT Calculations. J. Comp. Chem. 2013, 34, 987–1004. [Google Scholar] [CrossRef]
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef]
- Lutz, J.J.; Nooijen, M.; Perera, A.; Bartlett, R.J. Reference dependence of the two-determinant coupled-cluster method for triplet and open-shell singlet states of biradical molecules. J. Chem. Phys. 2018, 148, 164102. [Google Scholar] [CrossRef]
- Zhao, Y.; Tishchenko, O.; Gour, J.R.; Li, W.; Lutz, J.J.; Piecuch, P.; Truhlar, D.G. Thermochemical kinetics for multireference systems: Addition reactions of ozone. J. Phys. Chem. A 2009, 113, 5786–5799. [Google Scholar] [CrossRef] [PubMed]
- Lutz, J.J.; Hutson, J.M. Reactions between cold methyl halide molecules and alkali-metal atoms. J. Chem. Phys. 2014, 140, 014303. [Google Scholar] [CrossRef] [PubMed]
- Emrich, K. An extension of the coupled cluster formalism to excited-states (I). Nucl. Phys. A 1981, 351, 379–396. [Google Scholar] [CrossRef]
- Geertsen, J.; Rittby, M.; Bartlett, R.J. The equation-of-motion coupled-cluster method: Excitation energies of Be and CO. Chem. Phys. Lett. 1989, 164, 57–62. [Google Scholar] [CrossRef]
- Comeau, D.C.; Bartlett, R.J. The equation-of-motion coupled-cluster method. Applications to open- and closed-shell reference states. Chem. Phys. Lett. 1993, 207, 414–423. [Google Scholar] [CrossRef]
- Christiansen, O.; Koch, H.; Jørgensen, P.; Olsen, J. Excitation energies of H2O, N2 and C2 in full configuration interaction and coupled cluster theory. Chem. Phys. Lett. 1996, 256, 185–194. [Google Scholar] [CrossRef]
- Piecuch, P.; Włoch, M.; Lodriguito, M.; Gour, J.R. Noniterative coupled-cluster methods for excited electronic states. In Recent Advances in the Theory of Chemical and Physical Systems, Progress in Theoretical Chemistry and Physics; Wilson, S., Julien, J.P., Maruani, J., Brändas, E., Delgado-Barrio, G., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 15, pp. 45–106. [Google Scholar]
- Piecuch, P.; Gour, J.R.; Włoch, M. Left-eigenstate completely renormalized equation-of-motion coupled-cluster methods: Review of key concepts, extension to excited states of open-shell systems, and comparison with electron-attached and ionized approaches. Int. J. Quantum Chem. 2009, 109, 3268–3304. [Google Scholar] [CrossRef]
- Fradelos, G.; Lutz, J.J.; Wesołowski, T.A.; Piecuch, P.; Włoch, M. Embedding vs supermolecular strategies in evaluating the hydrogen-bonding-induced shifts of excitation energies. J. Chem. Theory Comput. 2011, 7, 1647–1666. [Google Scholar] [CrossRef]
- Fradelos, G.; Lutz, J.J.; Wesołowski, T.A.; Piecuch, P.; Włoch, M. Shifts in excitation energies induced by hydrogen bonding: A comparison of the embedding and supermolecular time-dependent density functional theory calculations with the equation-of-motion coupled-cluster results. In Advances in the Theory of Quantum Systems in Chemistry and Physics, Progress in Theoretical Chemistry and Physics; Hoggan, P.E., Brändas, E.J., Maruani, J., Piecuch, P., Delgado-Barrio, G., Eds.; Springer: Dordrecht, The Netherlands, 2012; Volume 22, pp. 219–248. [Google Scholar]
- Lutz, J.J.; Piecuch, P. Extrapolating Potential Energy Surfaces by Scaling Electron Correlation: Isomerization of Bicyclobutane to Butadiene. J. Chem. Phys. 2008, 128, 154116. [Google Scholar] [CrossRef]
- Magoon, G.R.; Aguilera-Iparraguirre, J.; Green, W.H.; Lutz, J.J.; Piecuch, P.; Oluwole, O.O.; Wong, H.W. Detailed Chemical Modeling of JP-10 (exo-tetrahydrodicyclopentadiene) High Temperature Oxidation: Exploring the Role of Biradical Species in Initial Decomposition Steps. Int. J. Chem. Kinet. 2012, 44, 179–193. [Google Scholar] [CrossRef]
- Gobrecht, D.; Crstallo, S.; Piersanti, L.; Bromley, S.T. Nucleation of Small Silicon Carbide Dust Clusters in AGB Stars. Astrophys. J. 2017, 840, 117. [Google Scholar] [CrossRef]
- Mohapatra, C.; Kundu, S.; Paesch, A.N.; Herbst-Irmer, R.; Stalke, D.; Andrada, D.M.; Frenking, G.; Roesky, H.W. The Structure of the Carbene Stabilized Si2H2 May Be Equally Well Described with Coordinate Bonds as with Classical Double Bonds. J. Am. Chem. Soc. 2016, 138, 10429–10432. [Google Scholar] [CrossRef]
- Pecher, L.; Tonner, R. Bond Insertion at Distorted Si(001) Subsurface Atoms. Inorganics 2018, 6, 17. [Google Scholar] [CrossRef]
- Lutz, J.J.; Duan, X.F.; Burggraf, L.W. Semiconductor color-center structure and excitation spectra: Equation-of-motion coupled-cluster description of vacancy and transition-metal defect photoluminescence. Phys. Rev. B 2018, 97, 115108. [Google Scholar] [CrossRef]
- Byrd, J.N.; Lutz, J.J.; Jin, Y.; Ranasinghe, D.S.; Montgomery, J.A., Jr.; Perera, A.; Duan, X.F.; Burggraf, L.W.; Sanders, B.A.; Bartlett, R.J. Predictive coupled-cluster isomer orderings for some SinCm (m, n ≤ 12) clusters: A pragmatic comparison between DFT and complete basis limit coupled-cluster benchmarks. J. Chem. Phys. 2016, 145, 024312. [Google Scholar] [CrossRef]
- Lutz, J.J.; Duan, X.F.; Ranasinghe, D.S.; Jin, Y.; Margraf, J.T.; Perera, A.; Burggraf, L.W.; Bartlett, R.J. Valence and charge-transfer optical properties for some SinCm (m, n ≤ 12) clusters: Comparing TD-DFT, complete-basis-limit EOMCC, and benchmarks from spectroscopy. J. Chem. Phys. 2018, 148, 174309. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.J.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Gordon, M.S.; Schmidt, M.W. Advances in electronic structure theory: GAMESS a decade later. In Theory and Applications of Computational Chemistry, the First Forty Years; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 1167–1189. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian~16 Revision B.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView Version 6; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Bode, B.M.; Gordon, M.S. MacMolPlt: A graphical user interface for GAMESS. J. Mol. Graph. Model. 1998, 16, 133–138. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals—Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291–309. [Google Scholar] [CrossRef]
- Neto, A.C.; Muniz, E.P.; Centoducatte, R.; Jorge, F.E. Gaussian basis sets for correlated wave functions. Hydrogen, helium, first- and second-row atoms. J. Mol. Struct. 2005, 718, 219–224. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Helgaker, T.; Klopper, W.; Koch, H.; Noga, J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997, 106, 9639–9646. [Google Scholar] [CrossRef]
- Hansen, J.A.; Piecuch, P.; Lutz, J.J.; Gour, J.R. Geometries and adiabatic excitation energies of the low-lying valence states of CNC, C2N, N3 and NCO studied with the electron-attached and ionized equation-of-motion coupled-cluster methodologies. Phys. Scr. 2011, 84, 028110. [Google Scholar] [CrossRef]
- Ehara, M.; Piecuch, P.; Lutz, J.J.; Gour, J.R. Symmetry-Adapted-Cluster Configuration- Interaction and Equation-of-Motion Coupled-Cluster Studies of Electronically Excited States of Copper Tetrachloride and Copper Tetrabromide Dianions. Chem. Phys. 2012, 399, 94–110. [Google Scholar] [CrossRef]
- Piecuch, P.; Kowalski, K.; Pimienta, I.S.O.; McGuire, M.J. Recent advances in electronic structure theory: Method of moments of coupled-cluster equations and renormalized coupled-cluster approaches. Int. Rev. Phys. Chem. 2002, 21, 527–655. [Google Scholar] [CrossRef]
- Leigh, G.J.; Favre, H.A.; Metanomski, W.V. Principles of Chemical Nomenclature: A Guide to IUPAC Recommendations, 2011 Edition ed; Blackwell Science: Oxford, UK, 2011. [Google Scholar] [CrossRef][Green Version]
| Ref. [1] | CCSD(T) | |||
|---|---|---|---|---|
| Def2-TZVP | Def2-TZVPD | Def2-QZVP | CBS | |
| 11.6 | 0.0 | −1.8 | −2.8 | −3.4 |
| Isomer | Ref. [1] | MBPT(2) | MBPT(3) | MBPT(4) | CCSD | CCSD(T) | Benchmark | |
|---|---|---|---|---|---|---|---|---|
| 2 | −11.6 | 4.4 | 1.9 | 0.4 | 0.1 | 2.8 | 3.4 | |
| 3 | −2.3 | 10.6 | 7.7 | 6.7 | 6.5 | 7.5 | 7.9 | |
| 4 | 17.0 | 14.7 | 10.6 | 9.7 | 9.3 | 11.2 | 11.3 | |
| 5 | 20.0 | 13.3 | 13.3 | 12.1 | 12.0 | 13.7 | 14.0 | |
| 6 | - | 16.3 | 16.4 | 16.2 | 16.4 | 15.1 | 15.4 | |
| 7 | 26.7 | 20.3 | 20.1 | 19.0 | 19.2 | 19.2 | 19.5 | |
| 8 | - | 25.8 | 24.4 | 23.4 | 23.5 | 23.5 | 23.6 | |
| 9 | 31.1 | 22.0 | 23.3 | 23.5 | 23.4 | 24.4 | 23.9 | |
| 10 | 38.1 | 31.1 | 29.2 | 28.4 | 28.5 | 28.7 | 28.8 | |
| MSE | - | 1.1 | 0.1 | −0.6 | −0.6 | −0.1 | 0.0 | |
| MUE | - | 1.7 | 0.5 | 0.8 | 0.8 | 0.2 | 0.0 |
| Functional | MSE | MUE |
|---|---|---|
| BLYP | 2.6 | 3.3 |
| B3LYP | −0.9 | 1.2 |
| B3LYP+D3 | −0.8 | 1.4 |
| B2-PLYP+D3 | 0.2 | 0.6 |
| PBE0 | −1.0 | 1.0 |
| PBE0+D3 | −1.1 | 1.1 |
| DSDPBEP86 | −0.1 | 0.4 |
| M06L | −2.3 | 3.6 |
| MN15L | −1.3 | 3.0 |
| M06-2X | −1.2 | 1.3 |
| MN15 | −0.1 | 1.3 |
| Isomer 1 | Isomer 2 | Exp. (Ref. [2]) | ||||
|---|---|---|---|---|---|---|
| Computational Method | Computational Method | |||||
| CASSCF(6,6) | MBPT(2) | B3LYP | CASSCF(6,6) | MBPT(2) | B3LYP | |
| 2300 (1.0) | 2230 (1.0) | 2140 (1.0) | 2300 (0.4) | 2280 (0.3) | 2210 (0.4) | 2190 |
| 1010 (0.1) | 960 (0.3) | 980 (0.3) | 1030 (0.3) | 970 (0.3) | 950 (0.4) | 950 (0.2) |
| 1000 (0.2) | 950 (0.3) | 950 (0.2) | 1020 (1.0) | 950 (1.0) | 930 (1.0) | 920 (1.0) |
| 860 (0.1) | 820 (0.1) | 810 (0.1) | 880 (0.2) | 860 (0.1) | 840 (0.2) | 840 (0.2) |
| 780 (0.1) | 790 (0.1) | 750 (0.1) | 820 (0.2) | 770 (0.1) | 750 (0.1) | 720 (0.1) |
| 690 (0.1) | 760 (0.1) | 670 (0.1) | 720 (0.2) | 680 (0.2) | 670 (0.1) | 670 (0.1) |
| 660 (0.1) | 650 (0.1) | 650 (0.1) | 700 (0.1) | 670 (0.1) | 650 (0.1) | 650 (0.2) |
| 1660 (1.0) | 1600 (1.0) | 1550 (1.0) | 1650 (0.5) | 1630 (0.4) | 1580 (0.5) | 1600 |
| 850 (0.8) | 820 (0.5) | 830 (0.5) | 850 (1.0) | 820 (0.6) | 810 (0.8) | 800 (0.6) |
| 780 (0.3) | 710 (0.3) | 720 (0.2) | 760 (1.0) | 710 (1.0) | 700 (1.0) | 690 (1.0) |
| 620 (0.1) | 550 (0.2) | 540 (0.1) | 560 (0.3) | 530 (0.2) | 520 (0.3) | 520 (0.1) |
| Method | Structures | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | TS-a | 6 | TS-b | 3 | TS-c | 2 | TS-d | Prod | |
| B3LYP | 0.0 | 67.1 | 16.7 | 31.3 | 4.9 | 71.5 | 2.9 | 69.8 | 26.8 |
| CCSD | 0.0 | 70.4 | 14.1 | 70.2 | 2.7 | 71.3 | −0.3 | 65.8 | 23.8 |
| CR-CC(2,3) | 0.0 | 66.9 | 14.8 | 69.4 | 3.1 | 71.0 | 1.1 | 67.3 | 25.4 |
| EOM-CCSD | 71.6 | 20.3 | 85.9 | 32.1 | 62.6 | 51.4 | 90.8 | 47.7 | 43.6 |
| CR-EOMCC(2,3) | 78.9 | 28.0 | 93.9 | 38.3 | 71.1 | 60.4 | 98.0 | 56.4 | 51.6 |
| -CR-EOMCC(2,3) | 64.3 | 9.9 | 80.0 | 22.9 | 56.9 | 45.5 | 84.8 | 43.4 | 38.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lutz, J.J.; Burggraf, L.W. The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations. Inorganics 2019, 7, 51. https://doi.org/10.3390/inorganics7040051
Lutz JJ, Burggraf LW. The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations. Inorganics. 2019; 7(4):51. https://doi.org/10.3390/inorganics7040051
Chicago/Turabian StyleLutz, Jesse J., and Larry W. Burggraf. 2019. "The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations" Inorganics 7, no. 4: 51. https://doi.org/10.3390/inorganics7040051
APA StyleLutz, J. J., & Burggraf, L. W. (2019). The Lowest-Energy Isomer of C2Si2H4 Is a Bridged Ring: Reinterpretation of the Spectroscopic Data Based on DFT and Coupled-Cluster Calculations. Inorganics, 7(4), 51. https://doi.org/10.3390/inorganics7040051