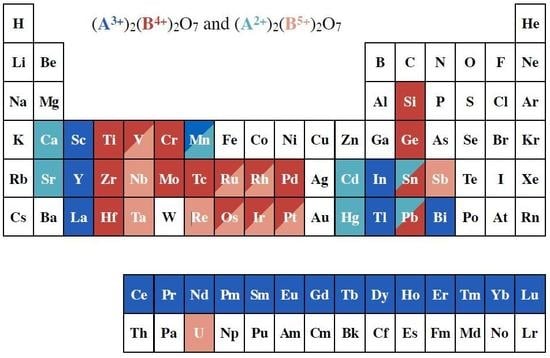
High-Pressure Routes to New Pyrochlores and Novel Magnetism
Abstract
:1. Introduction
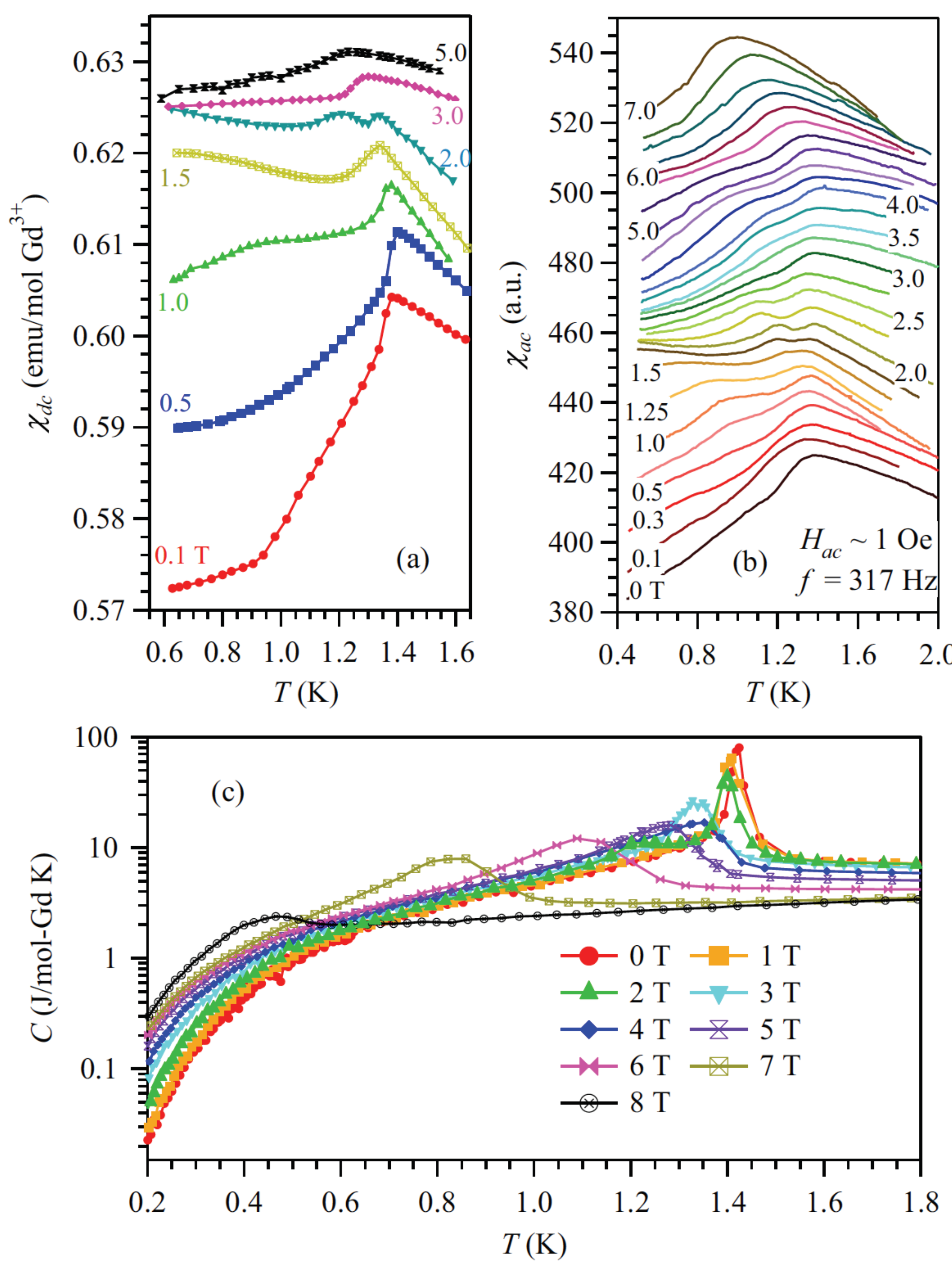
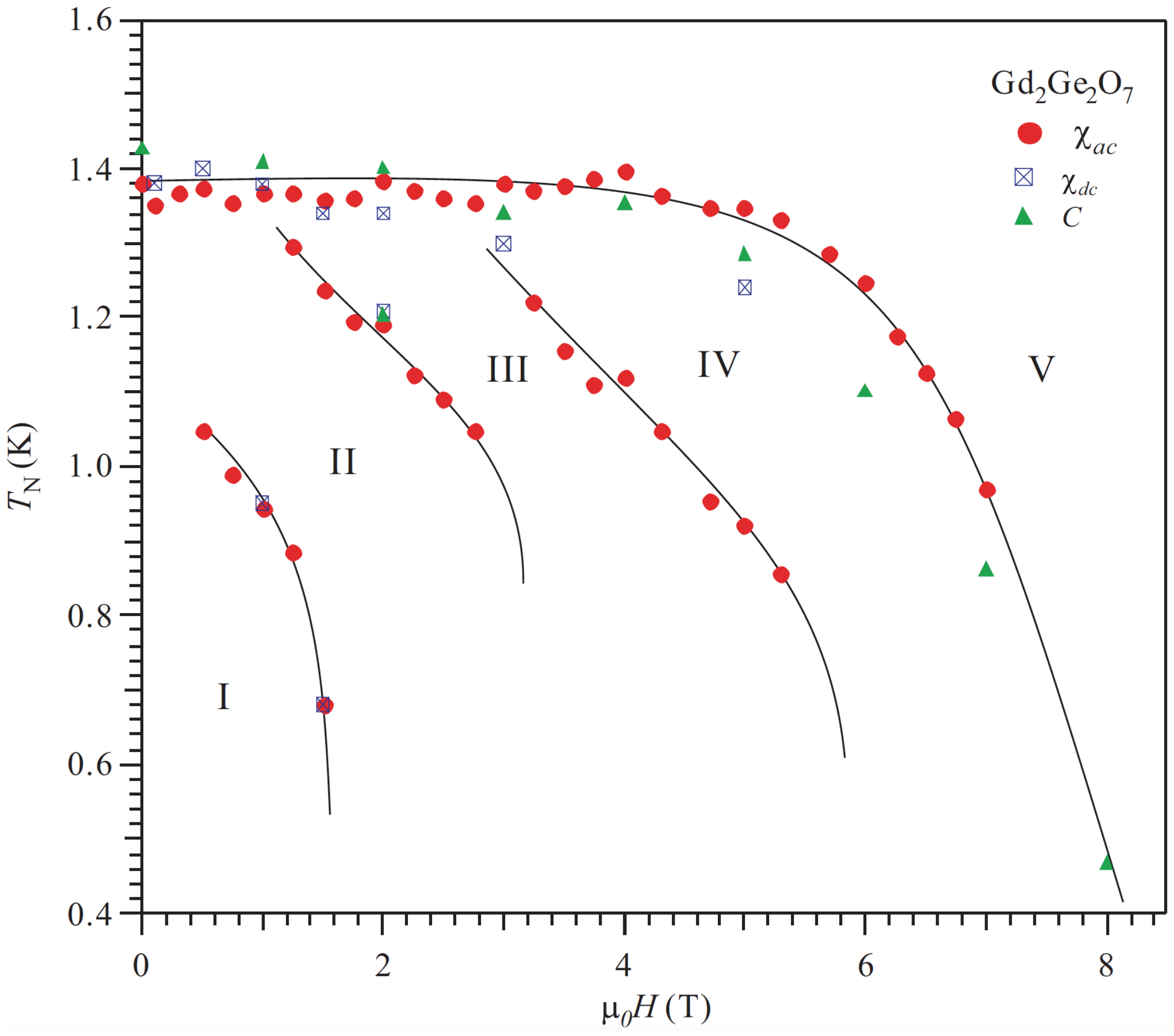
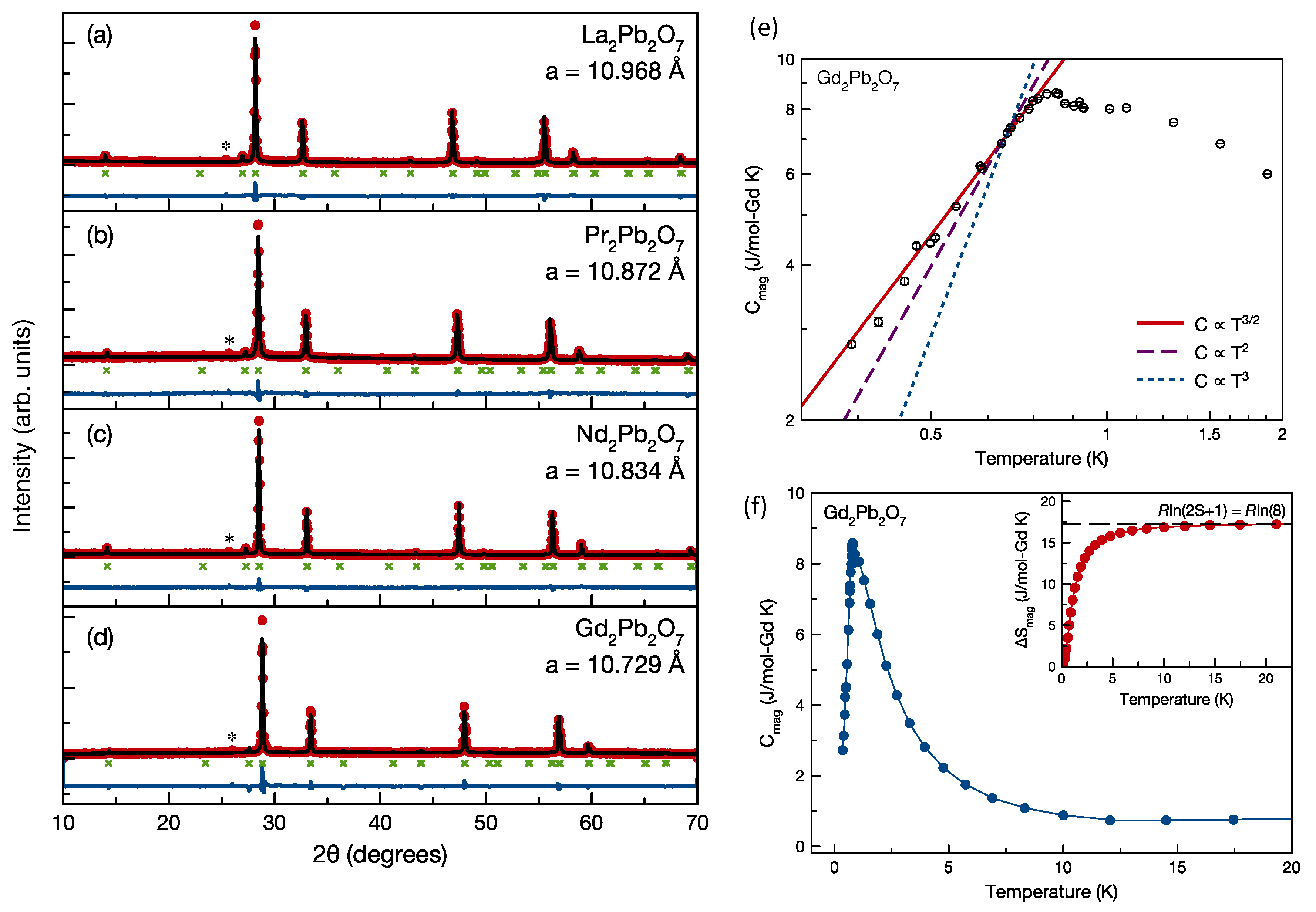
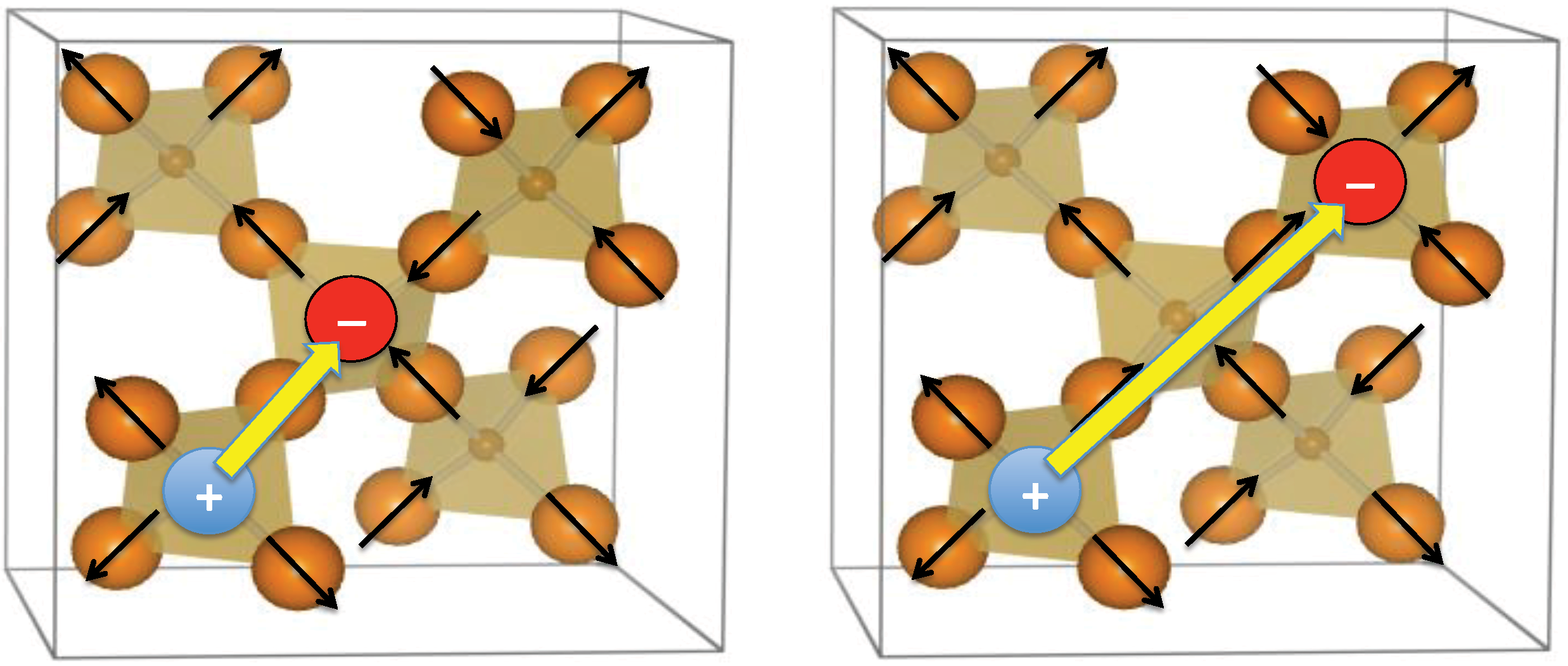
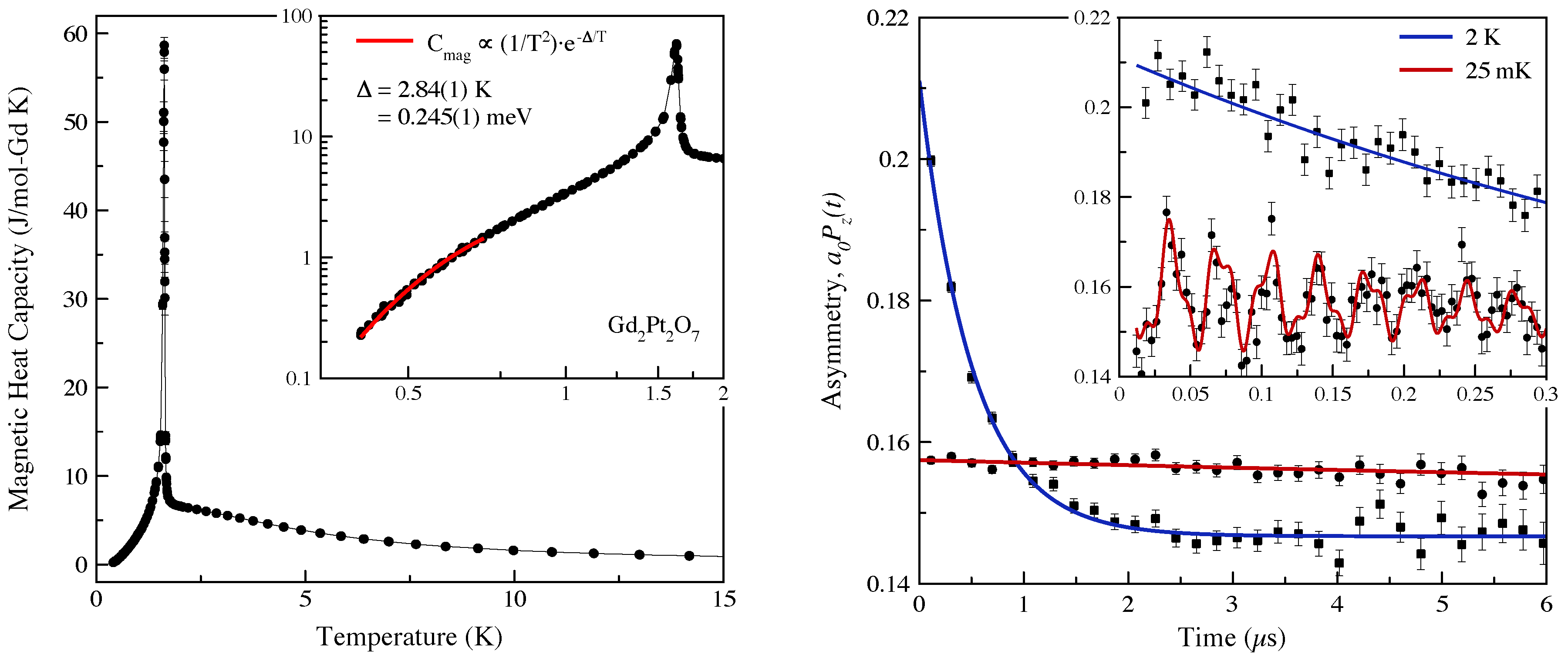
2. Heisenberg Spin Cases: Gd2Ge2O7 and Gd2Pb2O7
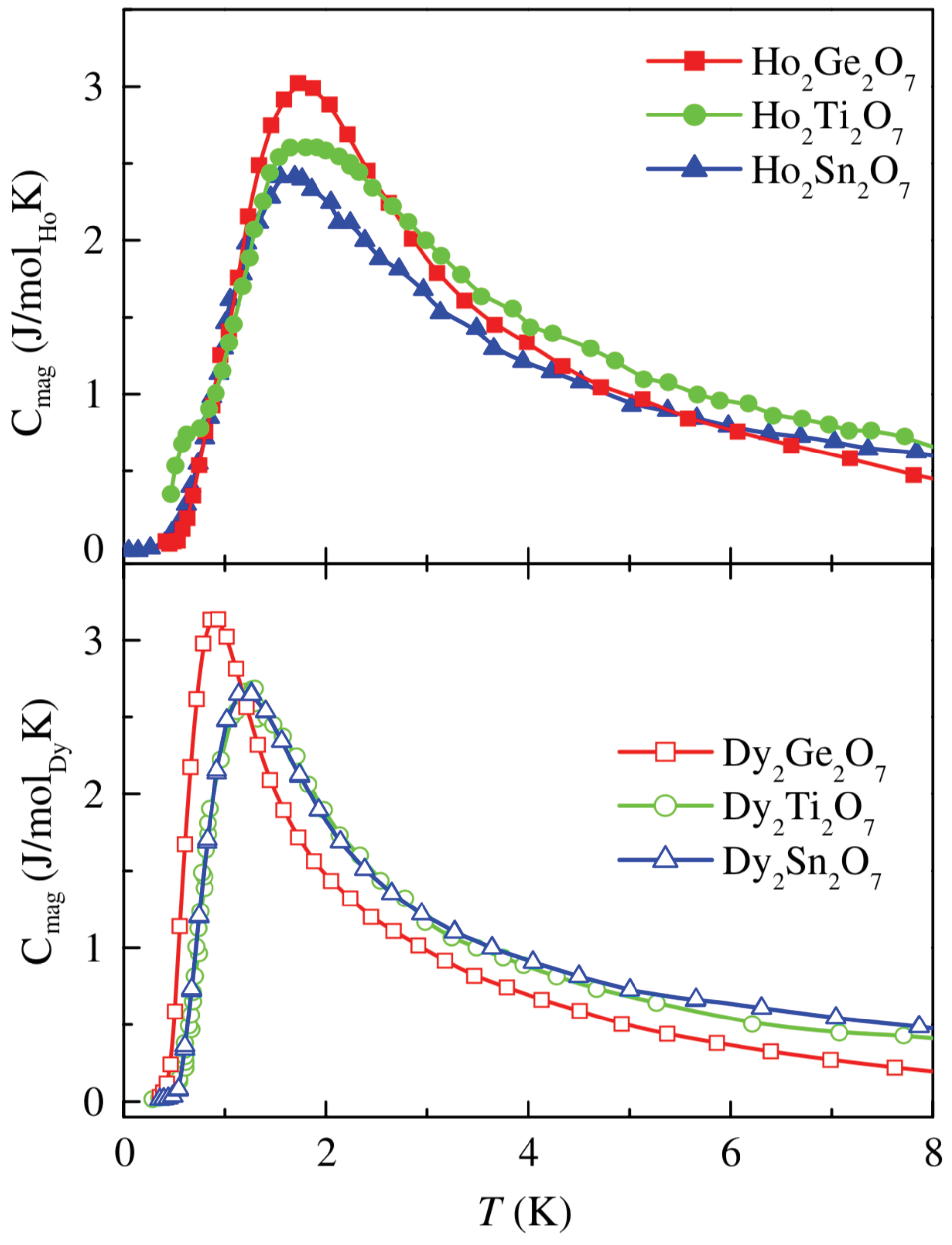
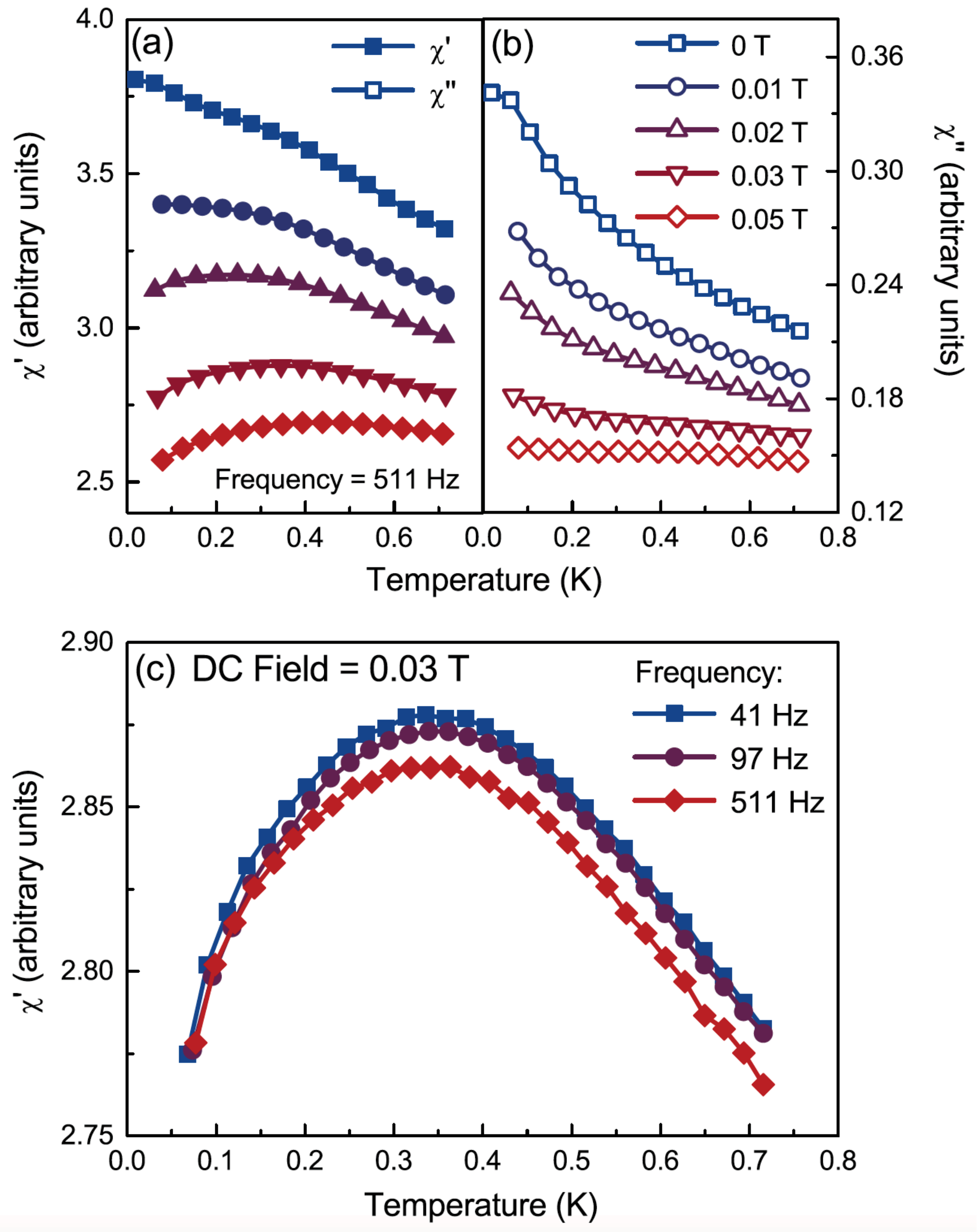
3. Ising spin ices: Ho2Ge2O7, Dy2Ge2O7
4. Ising Spin Liquid: Tb2Ge2O7
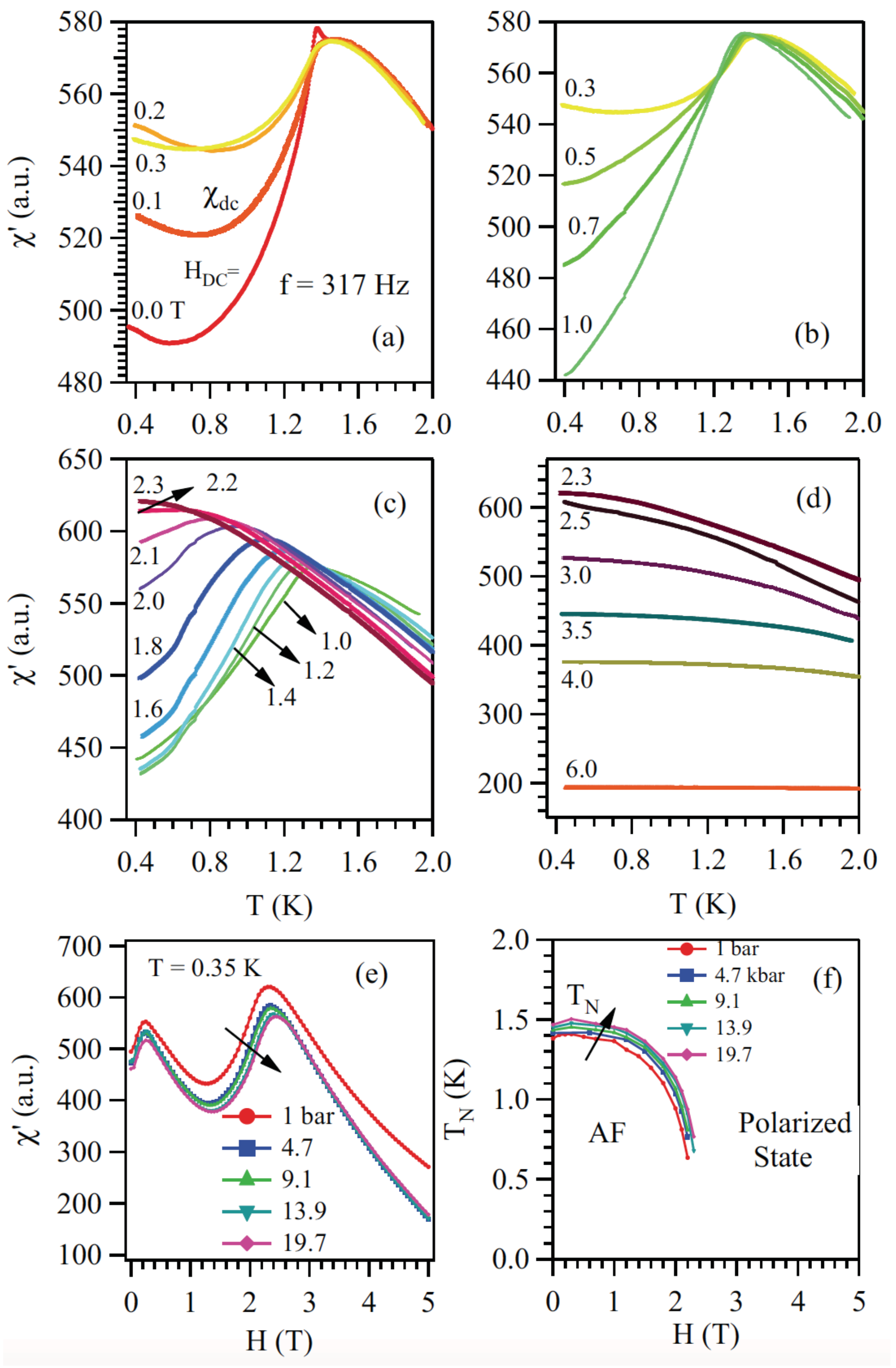
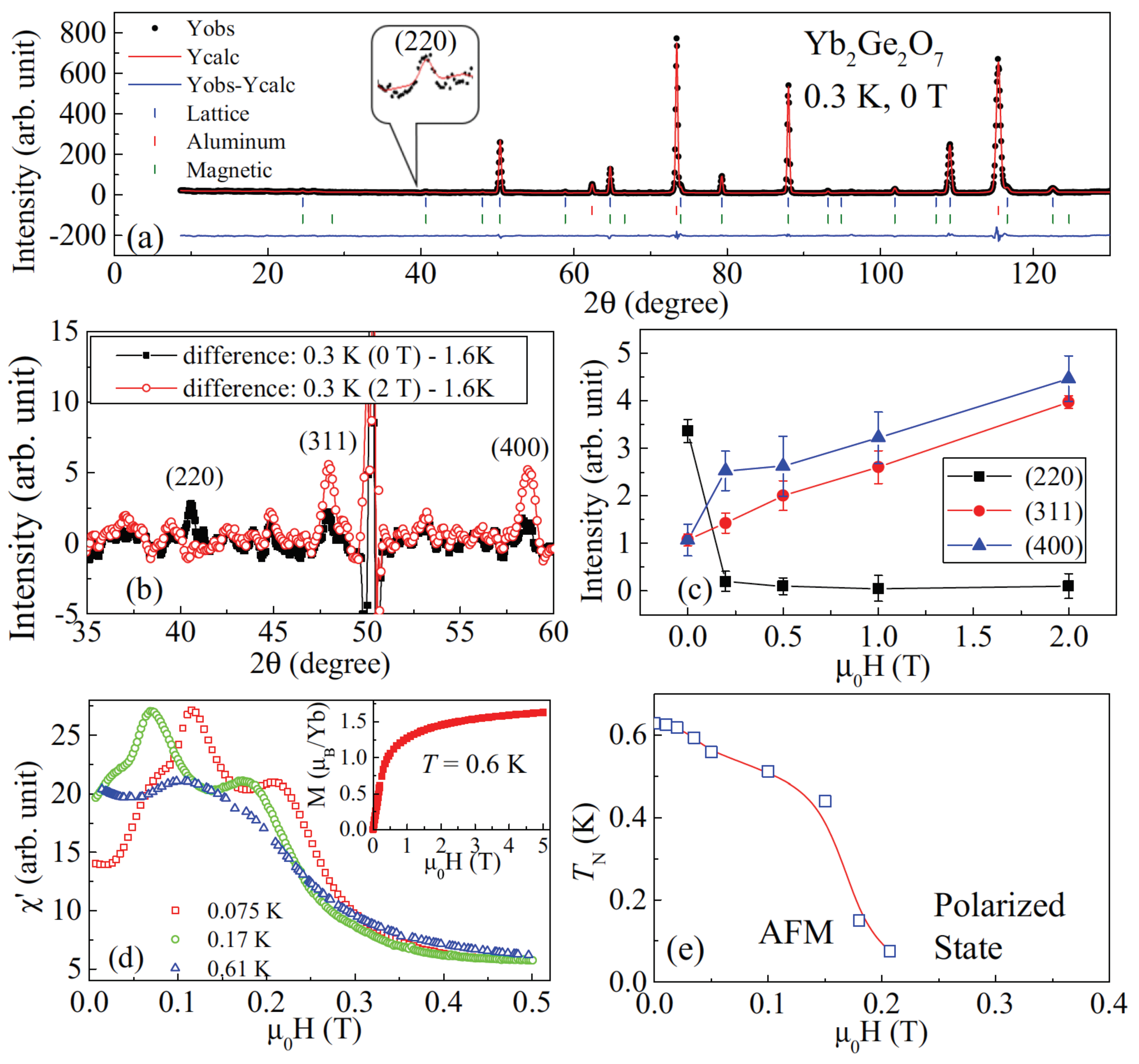
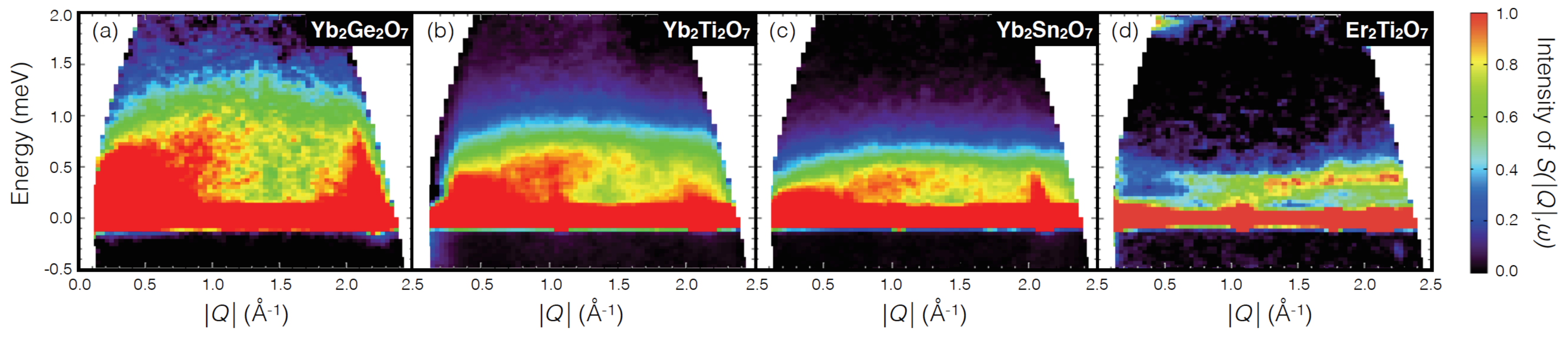
5. XY Spin Case: Er2Ge2O7/Yb2Ge2O7
6. The Future of High-Pressure Pyrochlore Research: 4d and 5d Transition Metal Phases
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Subramanian, M.A.; Aravamudan, G.; Rao, G.V.S. Oxide Pyrochlores: A Review. Prog. Solid State Chem. 1983, 15, 55–143. [Google Scholar] [CrossRef]
- Barthelmy, D. Pyrochlore Mineral Data. Available online: webmineral.com (accessed on 3 February 2015).
- Gardner, J.S.; Gingras, M.J.P.; Greedan, J.E. Magnetic Pyrochlore Oxides. Rev. Mod. Phys. 2010, 82, 53. [Google Scholar] [CrossRef]
- Hallas, A.M.; Wiebe, C.R. Frustration under pressure: Exotic magnetism in new pyrochlore oxides. APL Mater. 2015, 3, 041519. [Google Scholar] [Green Version]
- Morosan, E.; Fleitman, J.A.; Huang, Q.; Lynn, J.W.; Chen, Y.; Ke, X.; Dahlberg, M.L.; Schiffer, P.; Craley, C.R.; Cava, R.J. Structure and magnetic properties of the Ho2Ge2O7 pyrogermanate. Phys. Rev. B 2008, 77, 224423. [Google Scholar] [CrossRef]
- Walker, D.; Carpenter, M.A.; Hitch, C.M. Some simplifications to multianvil devices for high pressure experiment. Am. Minerol. 1990, 75, 1020–1028. [Google Scholar]
- Schmehr, J.L.; Wilson, S.D. Active crystal growth techniques for quantum materials. Ann. Rev. Mater. Res. 2017, 47, 153–174. [Google Scholar] [CrossRef]
- Ross, K.A.; Proffen, T.; Dabkowska, H.A.; Quilliam, J.A.; Yaraskavitch, L.R.; Kycia, J.B.; Gaulin, B.D. Lightly stuffed pyrochlore structure of single-crystalline Yb2Ti2O7 grown by the optical floating zone technique. Phys. Rev. B 2012, 86, 174424. [Google Scholar] [CrossRef]
- Kermarrec, E.; Gaudet, D.D.M.J.; Fritsch, K.; Pomaranski, D.; Kycia, J.B.; Qiu, Y.; Copley, J.R.D.; Couchman, M.M.P.; Morningstar, A.O.R.; Dabkowska, H.A.; et al. Gapped and gapless short-range-ordered magnetic states with (1/2, 1/2, 1/2) wave vectors in the pyrochlore magnet Tb2+xTi2−xO7+δ. Phys. Rev. B 2015, 92, 245114. [Google Scholar] [CrossRef]
- Blanchard, P.E.R.; Clements, R.; Kennedy, B.J.; Ling, C.D.; Reynolds, E.; Avdeev, M.; Stampfl, A.P.J.; Zhang, Z.; Jang, L.Y. Does local disorder occur in the pyrochlore zirconates? Inorg. Chem. 2012, 51, 13237–13244. [Google Scholar] [CrossRef] [PubMed]
- Wiebe, C.R.; Gardner, J.S.; Kim, S.-J.; Luke, G.M.; Wills, A.S.; Greedan, J.E.; Swainson, I.; Qiu, Y.; Jones, C. Magnetic ordering in the spin ice candidate Ho2Ru2O7. Phys. Rev. Lett. 2004, 93, 076403. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cai, Y.Q.; Cui, Q.; Jin, C.L.; Dun, Z.L.; Matsubayashi, K.; Uwatoko, Y.; Sato, Y.; Kawae, T.; Lv, S.J.; et al. Long-range magnetic order in the Heisenberg pyrochlore antiferromagnets Gd2Ge2O7 and Gd2Pt2O7 synthesized under high pressure. Phys. Rev. B 2016, 94, 214429. [Google Scholar] [CrossRef]
- Stewart, J.R.; Gardner, J.S.; Qiu, Y.; Ehlers, G. Collective dynamics in the Heisenberg pyrochlore antiferromagnet Gd2Sn2O7. Phys. Rev. B 2008, 78, 132410. [Google Scholar] [CrossRef]
- Freitas, R.S.; Gardner, J.S. The magnetic phase diagram of Gd2Sn2O7. J. Phys. Condens. Matter 2011, 23, 164215. [Google Scholar] [CrossRef]
- Bonville, P.; Hodges, J.A.; Ocio, M.; Sanchez, J.P.; Vulliet, P.; Sosin, S.; Braithwaite, D. Low temperature magnetic properties of geometrically frustrated Gd2Sn2O7. J. Phys. Condens. Matter 1003, 15, 7777. [Google Scholar] [CrossRef]
- Wills, A.S.; Zhitomirsky, M.E.; Canals, B.; Sanchez, J.P.; Bonville, P.; de Reotier, P.D.; Yaouanc, A. Magnetic ordering in Gd2Sn2O7: The archetypal Heisenberg pyrochlore antiferromagnet. J. Phys. Condens. Matter 2006, 18, L37. [Google Scholar] [CrossRef]
- Palmer, S.E.; Chalker, J.T. Order induced by dipolar interactions in a geometrically frustrated antiferromagnet. Phys. Rev. B 2000, 62, 488. [Google Scholar] [CrossRef]
- Raju, N.P.; Dion, M.; Gingras, M.J.P.; Mason, T.E.; Greedan, J.E. Transition to long-range magnetic order in the highly frustrated insulating pyrochlore antiferromagnet Gd2Ti2O7. Phys. Rev. B 1999, 59, 14489. [Google Scholar] [CrossRef]
- Stewart, J.R.; Ehlers, G.; Wills, A.S.; Bramwell, S.T.; Gardner, J.S. Phase transitions, partial disorder and multi-k structures in Gd2Ti2O7. J. Phys. Condens. Matter 2004, 16, L321. [Google Scholar] [CrossRef]
- Paddison, J.A.M.; Cairns, A.B.; Khalyavin, D.D.; Manuel, P.; Daoud-Aladine, A.; Ehlers, G.; Petrenko, O.A.; Gardner, J.S.; Zhou, H.D.; Goodwin, A.L.; et al. Nature of Partial Magnetic Order in the Frustrated Antiferromagnet Gd2Ti2O7. Available online: https://arxiv.org/abs/1506.05045 (accessed on 15 February 2019).
- Sleight, A. New Ternary Oxides of Tetravalent Platinum and Palladium with the Pyrochlore Structure. Mater. Res. Bull. 1968, 3, 699–704. [Google Scholar] [CrossRef]
- Hallas, A.M.; Arevalo-Lopez, A.M.; Sharma, A.Z.; Munsie, T.; Attfield, J.P.; Wiebe, C.R.; Luke, G.M. Magnetic frustration in lead pyrochlores. Phys. Rev. B 2015, 91, 104417. [Google Scholar] [CrossRef]
- Matsuhira, K.; Hinatsu, Y.; Tenya, K.; Sakakihara, T. Low temperature magnetic properties of frustrated pyrochlore ferromagnets Ho2Sn2O7 and Ho2Ti2O7. J. Phys. Condens. Matter 2000, 12, 649. [Google Scholar] [CrossRef]
- Ehlers, G.; Cornelius, A.L.; Fennell, T.; Koza, M.; Bramwell, S.T.; Gardner, J.S. Evidence for two distinct spin relaxation mechanisms in ”hot” spin ice Ho2Ti2O7. J. Phys. Condens. Matter 2004, 16, 635. [Google Scholar] [CrossRef]
- Zhou, H.D.; Cheng, J.G.; Hallas, A.M.; Wiebe, C.R.; Li, G.; Balicas, L.; Zhou, J.S.; Goodenough, J.B.; Gardner, J.S.; Choi, E.S. Chemical Pressure Effects on Pyrochlore Spin Ice. Phys. Rev. Lett. 2012, 18, 207206. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.D.; Bramwell, S.T.; Cheng, J.G.; Wiebe, C.R.; Li, G.; Balicas, L.; Bloxsom, J.A.; Silverstein, H.J.; Zhou, J.S.; Goodenough, J.B.; et al. High pressure route to generate magnetic monopole dimers in spin ice. Nat. Commun. 2011, 2, 478. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Den Hertog, B.C.; Gingras, M.J.P. Dipolar Interactions and Origin of Spin Ice in Ising Pyrochlore Magnets. Phys. Rev. Lett. 2000, 84, 3430. [Google Scholar] [CrossRef]
- Melko, R.G.; Gingras, M.J.P. Monte Carlo studies of the dipolar spin ice model. J. Phys. Condens. Matter 2004, 16, R1277. [Google Scholar] [CrossRef]
- Hallas, A.M.; Paddison, J.A.M.; Silverstein, H.J.; Goodwin, A.L.; Stewart, J.R.; Wildes, A.R.; Cheng, J.G.; Zhou, J.S.; Goodenough, J.B.; Choi, E.S.; et al. Statics and dynamics of the highly correlated spin ice Ho2Ge2O7. Phys. Rev. B 2012, 86, 134431. [Google Scholar] [CrossRef]
- Prando, G.; Carretta, P.; Giblin, S.R.; Lago, J.; Pin, S.; Ghigna, P. Dilution effects in Ho2−xYxSn2O7: From the spin ice to the single-ion magnet. J. Phys. Conf. Ser. 2009, 145, 012033. [Google Scholar] [CrossRef]
- Bramwell, S.T.; Harris, M.J.; den Hertog, B.C.; Gingras, M.J.P.; Gardner, J.S.; McMorrow, D.F.; Wildes, A.R.; Cornelius, A.L.; Champion, J.D.M.; Melko, R.G.; et al. Spin Correlations in Ho2Ti2O7: A Dipolar Spin Ice System. Phys. Rev. Lett. 2001, 87, 047205. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, A.P.; Hayashi, A.; Cava, R.J.; Siddharthan, R.; Shastry, B.S. Zero-point entropy in “spin ice”. Nature 1999, 399, 333. [Google Scholar] [CrossRef]
- Hallas, A.M.; Cheng, J.G.; Arevalo-Lopez, A.M.; Silverstein, H.J.; Su, Y.; Sarte, P.M.; Zhou, H.D.; Choi, E.S.; Attfield, J.P.; Luke, G.M.; et al. Incipient Ferromagnetism in Tb2Ge2O7: Application of Chemical Pressure to the Enigmatic Spin-Liquid Compound Tb2Ti2O7. Phys. Rev. Lett. 2014, 113, 267205. [Google Scholar] [CrossRef] [PubMed]
- Gingras, M.J.P.; den Hertog, B.C.; Faucher, M.; Gardner, J.S.; Dunsiger, S.R.; Chang, L.J.; Gaulin, B.D.; Raju, N.P.; Greedan, J.E. Thermodynamic and single-ion properties of Tb3+ within the collective paramagnetic-spin liquid state of the frustrated pyrochlore antiferromagnet Tb2Ti2O7. Phys. Rev. B 2000, 62, 6496. [Google Scholar] [CrossRef]
- Molavian, H.R.; Gingras, M.J.P.; Canals, B. Dynamically Induced Frustration as a Route to a Quantum Spin Ice State in Tb2Ti2O7 via Virtual Crystal Field Excitations and Quantum Many-Body Effects. Phys. Rev. Lett. 2007, 98, 157204. [Google Scholar] [CrossRef]
- Onoda, S.; Tanaka, Y. Quantum Melting of Spin Ice: Emergent Cooperative Quadrupole and Chirality. Phys. Rev. Lett. 2010, 105, 047201. [Google Scholar] [CrossRef] [PubMed]
- Fennell, T.; Kenzelmann, M.; Roessli, B.; Haas, M.K.; Cava, R.J. Power-Law Spin Correlations in the Pyrochlore Antiferromagnet Tb2Ti2O7. Phys. Rev. Lett. 2012, 109, 017201. [Google Scholar] [CrossRef]
- Yin, L.; Xia, J.S.; Takano, Y.; Sullivan, N.S.; Li, Q.J.; Sun, X.F. Low-Temperature Low-Field Phases of the Pyrochlore Quantum Magnet Tb2Ti2O7. Phys. Rev. Lett. 2013, 110, 137201. [Google Scholar] [CrossRef]
- Fritsch, K.; Ross, K.A.; Qiu, Y.; Copley, J.R.D.; Guidi, T.; Bewley, R.I.; Dabkowska, H.A.; Gaulin, B.D. Antiferromagnetic spin ice correlations at (1/2, 1/2, 1/2) in the ground state of the pyrochlore magnet Tb2Ti2O7. Phys. Rev. B 2013, 87, 094410. [Google Scholar] [CrossRef]
- Hallas, A.M.; Gaulin, B.D. Magnetic ordering in the spin liquid candidate Tb2Ge2O7. Phys. Rev. Lett. Pending Submitted.
- Hallas, A.M.; Gaudet, J.; Gaulin, B.D. Experimental insights into ground-state selection of quantum XY pyrochlores. Annu. Rev. Condens. Matter Phys. 2017, 9, 105–124. [Google Scholar] [CrossRef]
- Li, X.; Li, W.M.; Matsubayashi, K.; Sato, Y.; Jin, C.Q.; Uwatoko, Y.; Kawae, T.; Hallas, A.M.; Wiebe, C.R.; Arevalo-Lopez, A.M.; et al. Long-range antiferromagnetic order in the frustrated XY pyrochlore antiferromagnet Er2Ge2O7. Phys. Rev. B 2014, 89, 064409. [Google Scholar] [CrossRef]
- Dun, Z.L.; Li, X.; Freitas, R.S.; Arrighi, E.; Cruz, C.R.D.; Lee, M.; Choi, E.S.; Cao, H.B.; Silverstein, H.J.; Wiebe, C.R.; et al. Antiferromagnetic order in the pyrochlores R2Ge2O7 (R = Er, Yb). Phys. Rev. B 2015, 92, 140407. [Google Scholar] [CrossRef]
- Champion, J.D.M.; Harris, M.J.; Holdsworth, P.C.W.; Wills, A.S.; Balakrishnan, G.; Bramwell, S.T.; Cizmar, E.; Fennell, T.; Gardner, J.S.; Lago, J.; et al. Er2Ti2O7: Evidence of quantum order by disorder in a frustrated antiferromagnet. Phys. Rev. B 2003, 68, 020401(R). [Google Scholar] [CrossRef]
- Poole, A.; Wills, A.S.; Lelievre-Berna, E. Magnetic ordering in the XY pyrochlore antiferromagnet Er2Ti2O7 a spherical neutron polarimetry study. J. Phys. Condens. Matter 2007, 19, 452201. [Google Scholar] [CrossRef]
- Dun, Z.L.; Lee, M.; Choi, E.S.; Hallas, A.M.; Wiebe, C.R.; Gardner, J.S.; Arrighi, E.; Freitas, R.S.; Arevalo-Lopez, A.M.; Attfield, J.P.; et al. Chemical pressure effects on magnetism in the quantum spin liquid candidates Yb2X2O7 (X = Sn, Ti, Ge). Phys. Rev. B 2014, 89, 064401. [Google Scholar] [CrossRef]
- Hallas, A.M.; Gaudet, J.; Wilson, M.N.; Munsie, T.J.; Aczel, A.A.; Stone, M.B.; Freitas, R.S.; Arevalo-Lopez, A.M.; Attfield, J.P.; Tachibana, M.; et al. Antiferromagnetic ground state in the effective S = 1/2 pyrochlore Yb2Ge2O7. Phys. Rev. B 2016, 93, 104405. [Google Scholar] [CrossRef]
- Guitteny, S.; Petit, S.; Lhotel, E.; Robert, J.; Bonville, P.; Forget, A.; Mirebeau, I. Palmer-Chalker correlations in the XY pyrochlore antiferromagnet Er2Sn2O7. Phys. Rev. B 2013, 88, 134408. [Google Scholar] [CrossRef]
- Petit, S.; Lhotel, E.; Damay, F.; Boutrouille, P.; Forget, A.; Colson, D. Long range order in the dipolar XY antiferromagnet Er2Sn2O7. Phys. Rev. Lett. 2017, 119, 187202. [Google Scholar] [CrossRef]
- De Reotier, P.D.; Yaouanc, A.; Chapuis, Y.; Curnoe, S.H.; Grenier, B.; Ressouche, E.; Marin, C.; Lago, J.; Baines, C.; Giblin, S.R. Magnetic order, magnetic correlations, and spin dynamics in the pyrochlore antiferromagnet Er2Ti2O7. Phys. Rev. B 2012, 86, 104424. [Google Scholar] [CrossRef]
- Yaouanc, A.; de Reotier, P.D.; Bonville, P.; Hodges, J.A.; Glazkov, V.; Keller, L.; Sikolenko, V.; Bartkowiak, M.; Amato, A.; Baines, C.; et al. Dynamical Splayed Ferromagnetic Ground State in the Quantum Spin Ice Yb2Sn2O7. Phys. Rev. Lett. 2013, 110, 127207. [Google Scholar] [CrossRef]
- Hodges, J.A.; Bonville, P.; Forget, A.; Yaouanc, A.; de Reotier, P.D.; Andre, G.; Rams, M.; Krolas, K.; Ritter, C.; Gubbens, P.C.M.; et al. First Order Transition in the Spin Dynamics of Geometrically Frustrated Yb2Ti2O7. Phys. Rev. Lett. 2002, 88, 077204. [Google Scholar] [CrossRef]
- Chang, L.J.; Onoda, S.; Su, Y.; Kao, Y.J.; Tsuei, K.D.; Yasui, Y.; Kakurai, K.; Lees, M.R. Higgs transition from a magnetic Coulomb liquid to a ferromagnet in Yb2Ti2O7. Nat. Commun. 2012, 3, 992. [Google Scholar] [CrossRef] [PubMed]
- Savary, L.; Balents, L. Disorder-Induced Entanglement in Spin Ice Pyrochlores. Phys. Rev. Lett. 2012, 108, 037202. [Google Scholar] [CrossRef] [PubMed]
- Wong, A.W.C.; Hao, Z.; Gingras, M.J.P. Ground State Phase Diagram of Generic XY Pyrochlore Magnets with Quantum Fluctuations. Phys. Rev. B 2013, 88, 144402. [Google Scholar] [CrossRef]
- Hallas, A.M.; Gaudet, J.; Butch, N.P.; Tachibana, M.; Freitas, R.S.; Luke, G.M.; Wiebe, C.R.; Gaulin, B.D. Universal Dynamic Magnetism in Yb-Pyrochlores with Disparate Ground States. Phys. Rev. B 2016, 93, 100403. [Google Scholar] [CrossRef]
- Stoter, T.; Antlauf, M.; Opherden, L.; Gottschall, T.; Honung, J.; Gronemann, J.; Herrmannsdorfer, T.; Granovsky, S.; Schwartz, M.; Doerr, M.; et al. Tuning Interactions in the Spin-Ice Materials Dy2Ge2−xSixO7 by Silicon Substitution. Available online: https://arxiv.org/abs/1809.01480 (accessed on 15 February 2019).
- Hallas, A.M.; Sharma, A.Z.; Mauws, C.; Chen, Q.; Zhou, H.D.; Ding, C.; Gong, Z.; Tachibana, M.; Sarte, P.M.; Attfield, J.P.; et al. Coexistence of metallic and nonmetallic properties in the pyrochlore Lu2Rh2O7. NPJ Quantum Mater. 2019, 4, 9. [Google Scholar] [CrossRef]
- Hallas, A.M.; Sharma, A.Z.; Cai, Y.; Munsie, T.J.; Wilson, M.N.; Tachibana, M.; Wiebe, C.R.; Luke, G.M. Relief of Frustration in the Heisenberg Pyrochlore Antiferromagnet Gd2Pt2O7. Phys. Rev. B 2016, 94, 134417. [Google Scholar] [CrossRef]
- Hallas, A.M.; Gaudet, J.; Butch, N.P.; Xu, G.Y.; Tachibana, M.; Wiebe, C.R.; Luke, G.M.; Gaulin, B.D. Phase Competition in the Palmer-Chalker XY Pyrochlore Er2Pt2O7. Phys. Rev. Lett. 2017, 119, 187201. [Google Scholar] [CrossRef]
- Cai, Y.Q.; Jiao, Y.Y.; Cui, Q.; Li, Y.; Wang, B.S.; Fernandez-Diaz, M.T.; McGuire, M.A.; Yan, J.-Q.; Alonso, J.A.; Cheng, J.-G. Giant reversible magnetocaloric effect in the pyrochlore Er2Mn2O7 due to a cooperative two-sublattice ferromagnetic order. Phys. Rev. Mater. 2017, 6, 064408. [Google Scholar] [CrossRef]
- Klein, R.A.; Walsh, J.P.S.; Clarke, S.M.; Guo, Y.S.; Bi, W.L.; Fabbris, G.; Meng, Y.; Haskel, D.; Alp, E.E.; van Duyne, R.P.; et al. Impact of magnetic order in Jarosite. J. Am. Chem. Soc. 2018, 140, 12001–12009. [Google Scholar] [CrossRef]
- Somayazulu, M.; Ahart, M.; Mishra, A.K.; Geballe, Z.M.; Baldini, M.; Meng, Y.; Struzhkin, V.V.; Hemley, R.J. Evidence for Superconductivity above 260 K in Lanthanum Superhydride at Megabar Pressures. Phys. Rev. Lett. 2019, 122, 027001. [Google Scholar] [CrossRef] [PubMed]
- Greedan, J.E.; Gout, D.; Lozano-Gorrin, A.D.; Derahkshan, S.; Proffen, T.; Kim, H.-J.; Bozin, E.; Billinge, S.J.L. Local and average structures of the spin-glass pyrochlore Y2Mo2O7 from neutron diffraction and neutron pair distribution function analysis. Phys. Rev. B 2009, 79, 014427. [Google Scholar] [CrossRef]
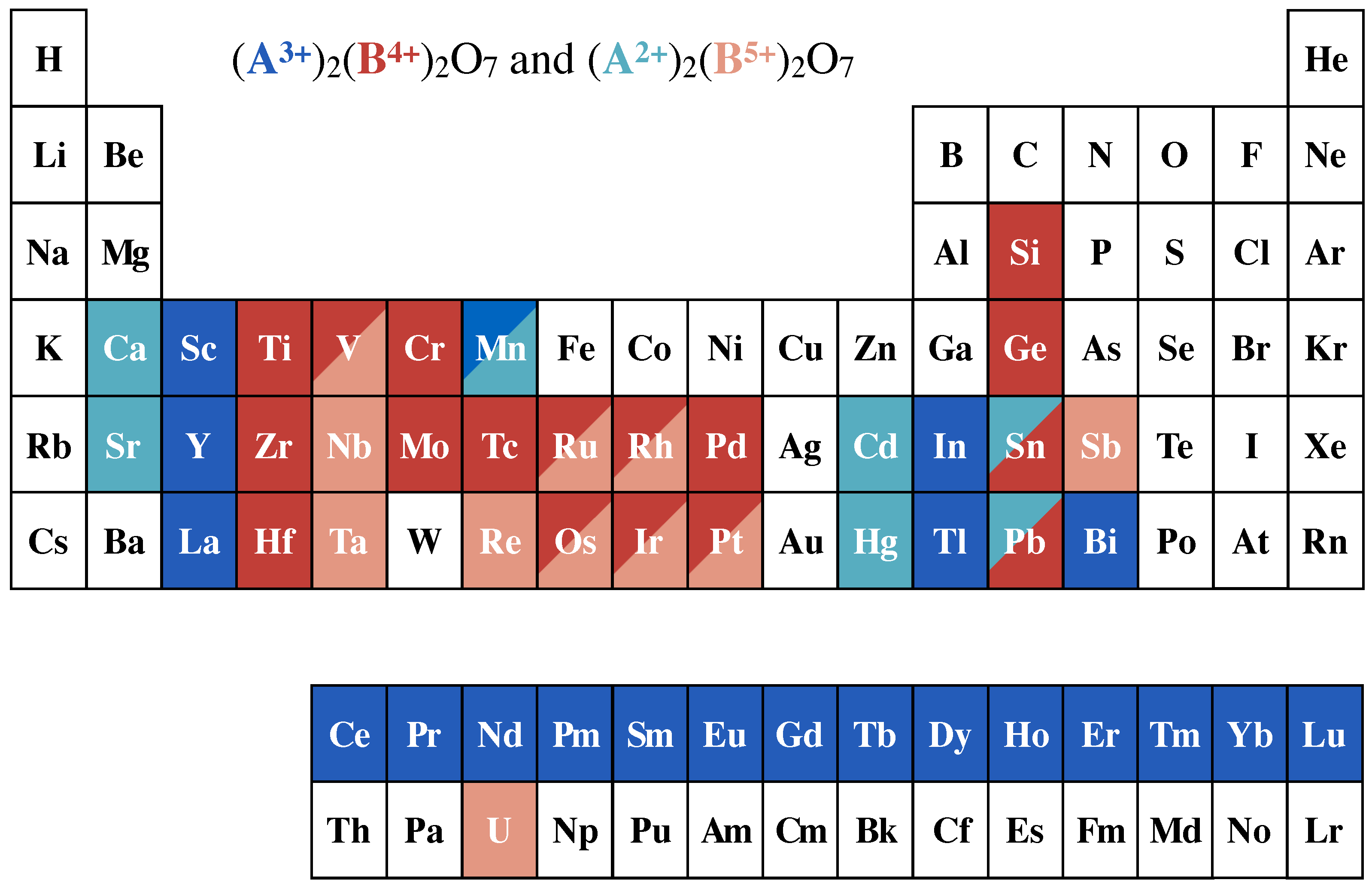



| Er2X2O7 | Yb2X2O7 | |||||
|---|---|---|---|---|---|---|
| X site ion | Sn | Ti | Ge | Sn | Ti | Ge |
| IR(X)(Å) | 0.69 | 0.605 | 0.53 | 0.69 | 0.605 | 0.53 |
| a (Å) | 10.35 | 10.07 | 9.88 | 10.28 | 10.03 | 9.83 |
| (K) | −14 | −15.9 | −21.9 | 0.53 | 0.75 | 0.9 |
| 0.1 | 1.17 | 1.41 | 0.15 | 0.24 | 0.62 | |
| Order type | ∼(AFM) | AFM | AFM | FM | FM | AFM |
| Reference | [48,49] | [50] | [42] | [51] | [52] | [46] |
| Spin state | ∼(PC) | SF | SF | |||
| Reference | [49] | [45] | [43] | [51] | [53] | [43] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Wiebe, C.R. High-Pressure Routes to New Pyrochlores and Novel Magnetism. Inorganics 2019, 7, 49. https://doi.org/10.3390/inorganics7040049
Zhou H, Wiebe CR. High-Pressure Routes to New Pyrochlores and Novel Magnetism. Inorganics. 2019; 7(4):49. https://doi.org/10.3390/inorganics7040049
Chicago/Turabian StyleZhou, Haidong, and Christopher R. Wiebe. 2019. "High-Pressure Routes to New Pyrochlores and Novel Magnetism" Inorganics 7, no. 4: 49. https://doi.org/10.3390/inorganics7040049
APA StyleZhou, H., & Wiebe, C. R. (2019). High-Pressure Routes to New Pyrochlores and Novel Magnetism. Inorganics, 7(4), 49. https://doi.org/10.3390/inorganics7040049