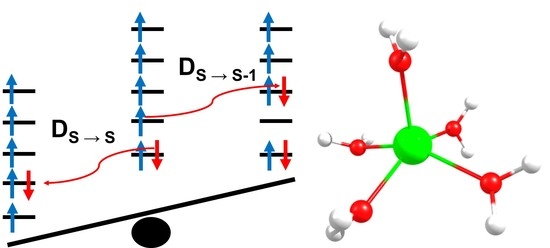
Effect of Low Spin Excited States for Magnetic Anisotropy of Transition Metal Mononuclear Single Molecule Magnets

Abstract

Rational, fine tuning of magnetic anisotropy is critical to obtain new coordination compounds with enhanced single molecule magnet properties. For mononuclear transition metal complexes, the largest contribution to zero-field splitting is usually related to the excited states of the same spin as the ground level. Thus, the contribution of lower multiplicity roots tends to be overlooked due to its lower magnitude. In this article, we explore the role of lower multiplicity excited states in zero-field splitting parameters in model structures of Fe(II) and Co(II). Model aquo complexes with coordination numbers ranging from 2 to 6 were constructed. The magnetic anisotropy was calculated by state of the art ab initio methodologies, including spin-orbit coupling effects. For non-degenerate ground states, contributions to the zero-field splitting parameter (D) from highest and lower multiplicity roots were of the same sign. In addition, their relative magnitude was in a relatively narrow range, irrespective of the coordination geometry. For degenerate ground states, the contribution from lower multiplicity roots was significantly smaller. Results are rationalized in terms of general expressions for D and are expected to be reasonably transferable to real molecular systems.

1. Introduction

The discovery of mononuclear single molecule magnets [1] (also known as single ion magnets) led to new opportunities for the interplay of theoretical methods in this field. Concretely, complete active space self-consistent field (CASSCF) calculations permitted the direct calculation of magnetic anisotropy, which is the physical phenomenon responsible for the development of an energy barrier blocking magnetic relaxation. Nowadays, CASSCF calculations are widely applied for the rationalization of magnetic properties of mononuclear single molecule magnets based on transition metal ions and lanthanides [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. Besides energies and wave functions, ab initio calculations can be analyzed in terms of Spin-Hamiltonian and ligand field parameters [19,20,21]. In this way, experimentally derived parameters as zero-field splitting D and E, effective g-factors, and Racah and ligand field parameters can be directly compared with their calculated counterparts. In many cases, data from magnetic measurements is not enough to fit a consistent parameter set in a univocal way, which can be estimated by electronic structure methods [22,23,24].

One of the critical parameters to optimize in the quest for single molecule magnets operating at higher temperatures is the height of the demagnetization barrier. In the double well model for magnetic moment inversion [25], the demagnetization barrier (U) is proportional to the zero-field splitting parameter D. Concretely, $U==D{S}^2$ and $U=D{S}^2-1/4$ for integer and half-integer systems, respectively. Although magnetic relaxation depends on several mechanisms [26,27,28,29], the fine tuning of magnetic anisotropy remains critical to improve the performance of single molecule magnets.

Concerning transition metal single molecule magnets, the relation between molecular structure and zero-field splitting has been explored [13,30,31,32,33,34]. These studies are useful to rationalize magnetic relaxation properties of new examples of single molecule magnets and to spot simple design rules to synthesize new systems with enhanced properties.

In most cases, magnetic anisotropy can be understood from the contributions of excited states of the same spin (S→S) as the ground level, which are mixed by the spin-orbit coupling (SOC) operator. Understandably, excited states of other multiplicities (S→S ± 1) are often not considered due to their lower contribution to D. An exception to the prevalence of S→S contributions are, of course, high-spin Fe(III) complexes, where magnetic anisotropy stems from sextet-quartet excitations. There are some examples of multireference ab initio studies on magnetic anisotropy of d⁵ systems [35,36,37] and one example of a mononuclear single molecule magnet featuring a high spin Fe(III) center [38]. Thus, it is interesting to explore the role of S→S − 1 contributions in the magnetic anisotropy of transition metal single molecule magnets, as they will be always present and could be beneficial or detrimental for magnetization relaxation properties.

In this article, we investigate the effect of S→S − 1 contributions to the magnetic anisotropy of high spin Fe(II) and Co(II) mononuclear complexes in various model geometries. The choice of these two ions is justified by the existence of a considerable number of single molecule magnets based on these metal centers [14,39,40,41,42,43,44,45,46,47,48,49,50,51]. Idealized structures of aquo complexes were built with the following coordination geometries: linear, trigonal planar, square planar, tetrahedral, trigonal bipyramidal, square pyramidal, and octahedral. Energies and wave functions for all models were obtained by CASSCF calculations, including the effect of SOC. Zero-field splitting parameters were decomposed in contributions from S→S and S→S − 1 excited states. For non-degenerate ground states, S→S and S→S − 1 contributions were of the same sign, and lower multiplicity states were responsible for 5–10% of the total magnetic anisotropy. This trend was observed for several coordination geometries and can be related to fundamental expressions for D. Then, the observed enhancement of magnetic anisotropy due to lower energy excited states should be encountered in real systems. In the case of degenerate ground states, the effect of S − 1 excited states in the value of D is minor (<2%).

2. Results and Discussion

2.1. d-Orbital Splitting

As mentioned earlier, several studies have established connections between molecular structure and magnetic anisotropy in mononuclear complexes based on transition metal ions. Thus, it is reasonable to consider the d-orbital splitting as the starting point for the discussion. Figure 1 shows the energy splitting of all of the studied geometries based on ab initio ligand field theory (AILFT) [19] energies for the d-orbitals (see Materials and Methods section for further information). Figure 2 presents molecular geometries for model complexes.

It is important to stress that zero-field splitting parameters are obtained by a perturbative treatment of ground state interaction with excited levels due to the spin-orbit coupling operator. In this way, the ground state must be energetically isolated to allow for the treatment. For orbitally degenerate ground states, D is undefined and ad hoc spin Hamiltonians must be developed for the case of interest.

In a strict sense, molecular complexes with high symmetry are scarce, as they require very simple ligands (monoatomic/linear) and the absence of distortions such as Jahn–Teller or crystal packing effects. In practice, complexes are described by reference shapes (e.g., square planar, octahedral) based on a similarity criterium for the metal center and donor atom positions. In most cases, many of the symmetry operations of the reference geometry are not present in the real compound. For the presented models, we always have a lower degree of symmetry due to the hydrogen atoms of the aquo ligands. A second set of geometries was constructed to analyze the effect of Jahn–Teller distortions. In some models, orbital degeneracy of the ground state is broken substantially by the geometric distortions, permitting the use of zero-field splitting parameters. Other examples develop a small energy splitting, which is insufficient for a perturbative treatment, and D cannot be used as a valid parameter.

Models with a unique metal-oxygen distance are analyzed first. In the case of linear coordination, d-orbitals order in three blocks as expected. The most stable orbitals are $d_{xy}$ and $d_{x^2-y^2}$, which are separated by less than 20 cm⁻¹ in all cases. The next block includes $d_{xz}$ and $d_{yz}$, which are significantly split by the lower symmetry due to hydrogen positions of the water ligands (ca. 1000–1500 cm⁻¹). The highest energy is associated to the $d_{z^2}$ orbital. CASSCF energies indicate both Fe(II) and Co(II) models present degenerate ground states. Thus, their low energy spectrum cannot be described by the standard zero-field splitting parameters. In the case of Fe(II), the d-orbital splitting is consistent with the observed degeneracy, as the $d_{xy}^2{d}_{x^2-y^2}^1{d}_{xz}^1{d}_{yz}^1{d}_{z^2}^1$ and $d_{xy}^1{d}_{x^2-y^2}^2{d}_{xz}^1{d}_{yz}^1{d}_{z^2}^1$ configurations will be the most stable. In the case of Co(II), the interplay of interelectronic repulsion and ligand field splitting yields a doubly degenerate ground state, which wave functions present significant contributions from $d_{xy}^2{d}_{x^2-y^2}^1{d}_{xz}^2{d}_{yz}^1{d}_{z^2}^1$, $d_{xy}^2{d}_{x^2-y^2}^1{d}_{xz}^1{d}_{yz}^2{d}_{z^2}^1$, $d_{xy}^1{d}_{x^2-y^2}^2{d}_{xz}^2{d}_{yz}^1{d}_{z^2}^1$ and $d_{xy}^1{d}_{x^2-y^2}^2{d}_{xz}^1{d}_{yz}^2{d}_{z^2}^1$ configurations.

Trigonal planar geometry leads again to three orbital blocks: $(d_{z^2}),(d_{xz},d_{yz}),(d_{xy},d_{x^2-y^2})$. The first three orbitals are close in energy. In the case of Fe(II), $d_{z^2}$ is the most stable where for Co(II) $d_{xz}$ and $d_{yz}$ are lower in energy. CASSCF energies show that the Fe(II) ground state is close to triply degenerate while the Co(II) first excited state appears at 1408.2 cm⁻¹ (CASSCF). In this way, the Fe(II) low energy spectrum cannot de described by D and E while Co(II) is probably suitable for this kind of description. Formally, the ground state of Co(II) in a trigonal planar environment is orbitally degenerate, but the symmetry lowering due to hydrogen positions of aquo ligands breaks this symmetry.

Square planar geometry follows the text book ordering, with $(d_{xz},d_{yz})$ as the lowest to orbitals, followed by $d_{z^2}$, $d_{xy}$ and $d_{x^2-y^2}$. The existence of two d-orbitals with the lowest energy leads again to a degenerate ground state for Fe(II), given its d⁶ configuration, as the first excited state has an energy of 70 cm⁻¹. For Co(II), the first excited state is at 1000–1200 cm⁻¹. Thus, the ground state is non-degenerate, but there are low energy excited states. In this regime, zero-field splitting parameters are expected to be qualitatively able to describe magnetic anisotropy, but their values will be dependent of the method of choice (second-order perturbation theory or effective Hamiltonian) and largely sensitive to small changes in state energies (for instance, by N-electron valence state perturbation theory (NEVPT2) correction). Thus, we are in a borderline situation where D values can be informative but must be analyzed with caution.

Tetrahedral coordination shows the characteristic e, t₂ splitting, with some splitting inside each block due to hydrogen positions. The splitting of the t₂ block is larger than the energy separation for the e levels, due to the antibonding nature of the t₂ orbitals. As mentioned earlier, having a set of two d-orbitals as the most stable will lead to a degenerate ground state for high spin d⁶ (Fe(II)), but not for d⁷ (Co(II)). In this way, the first excited state for the iron model is at ca. 200 cm⁻¹, while Co(II) presents an energy gap over 2000 cm⁻¹, allowing the use of D to describe its magnetic anisotropy.

Square pyramid coordination shows a slightly differing behavior, according to AILFT orbitals. In the case of Fe(II), $d_{xy}$, $d_{xz}$ and $d_{yz}$ appear close in energy and significantly mixed. For Co(II), the splitting between these orbitals is larger. In both cases, highest energy orbitals are $d_{z^2}$ and $d_{x^2-y^2}$. As three d-orbitals are close to be the lowest in energy, several configurations can be stabilized and several CASSCF states appear close to the ground state, although the ground state is still non-degenerate for both ions. First excitation energies are 526.2 cm⁻¹ (Fe(II), CASSCF) and 664.5 cm⁻¹ (Co(II), CASSCF). NEVPT2 results are qualitatively similar and are presented in Table S1. Under such small energy gap, the ability of D values to represent the low energy spectrum of the system is limited, and other spin Hamiltonian parameters such as effective g-values of each Kramers’ doublet can be especially useful for the description of the system.

Trigonal bipyramid spitting leads to three blocks of orbitals. The most stable orbitals are $(d_{xz},d_{yz})$, followed by $(d_{xy},d_{x^2-y^2})$ and finally $d_{z^2}$. Both $(d_{xz},d_{yz})$ and $(d_{xy},d_{x^2-y^2})$ are significantly split by symmetry lowering from hydrogen atoms (between 400–600 cm⁻¹). Low energy excitations are in the same range as the observed for 5-SPY geometry. For instance, first excited states for CASSCF appear at 638.0 cm⁻¹ for Fe(II) and 588.4 cm⁻¹ for Co(II). Similar to the case of square pyramid coordination, D will be in an intermediate range between the perturbative regime and a degenerate ground state.

Finally, octahedral geometry shows the typical t_2g, e_g splitting. In the case of Co(II), orbital blocks are essentially degenerate while Fe(II) shows a larger splitting. As expected when three d-orbitals are close to be the lowest in energy, both models will present low excitation energies consistent with a degenerate ground state. From CASSCF energies, Fe(II) has a state at 299.3 cm⁻¹ and Co(II) at 4.2 cm⁻¹. Therefore, D will not be suitable to describe these systems.

2.2. Effect of Jahn–Teller Distortion

In the development of single molecule magnets, Jahn–Teller distortions are often an unwanted effect, since they lift orbital degeneracies which favor the development of unquenched orbital angular momentum in the ground state, associated with magnetic anisotropy. To obtain a set of models including Jahn–Teller distortion, we repeated all optimizations, allowing for the relaxation of metal-oxygen distances, but constraining O–M–O angles to remain representative of the reference geometry.

Orbital splitting was affected to a varying degree by the inclusion of Jahn–Teller distortion. Of course, linear systems remain unaffected, although a small energy difference is observed due to the change in metal-oxygen distances. In terms of CASSCF energies, it is clear how first excitation energies are raised due to Jahn–Teller distortion (See

Table 1. First excitation energy (cm⁻¹) for CASSCF calculations, including all roots for all multiplicities stemming from for d⁶ (Fe^II) and d⁷ (Co^II) configurations. Geometries including and excluding Jahn–Teller distortion are labeled as “JT” and “noJT”, respectively. Geometries with fixed (noJT) and relaxed (JT) metal-oxygen distances are presented as Supporting Information.

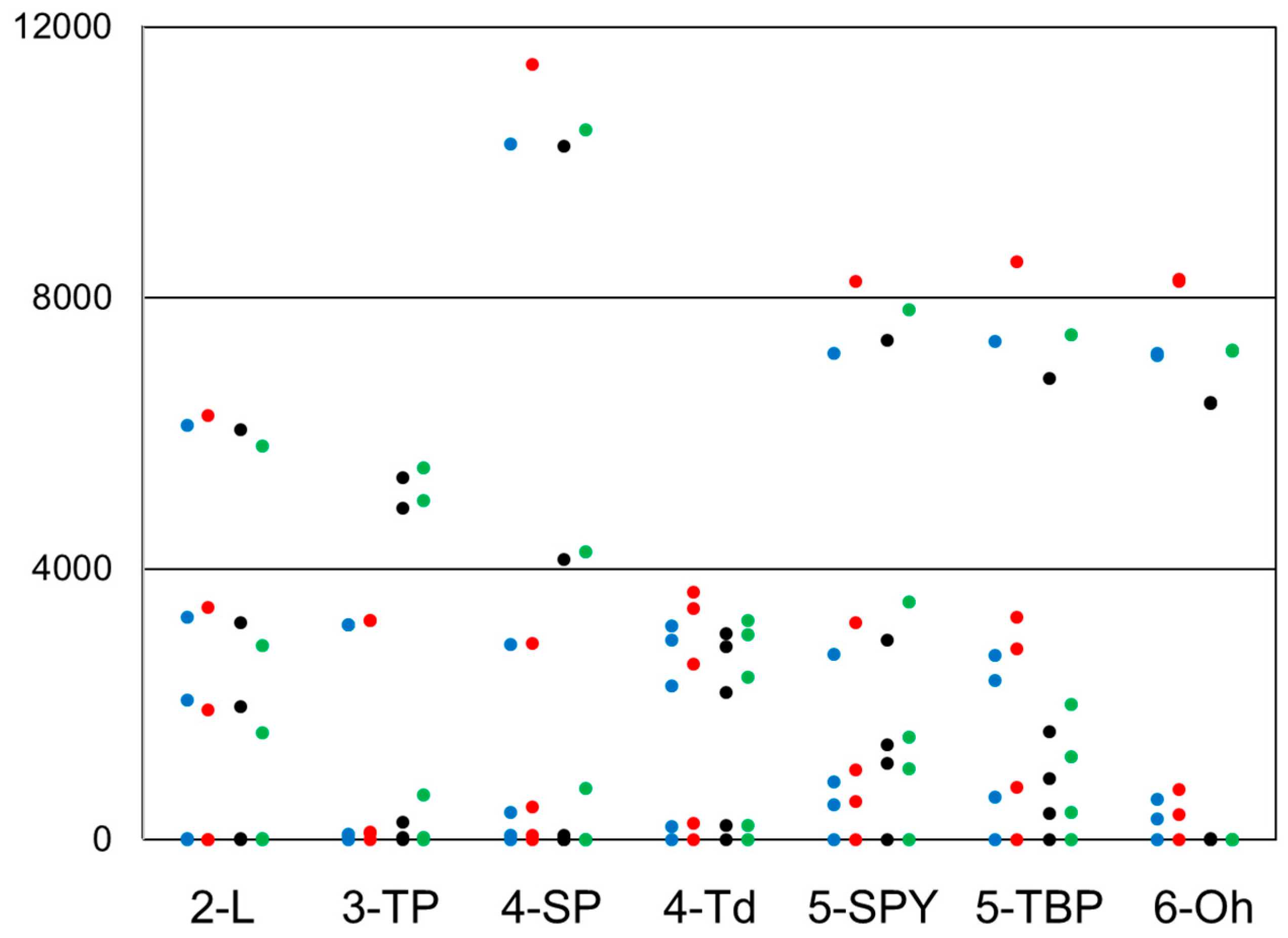
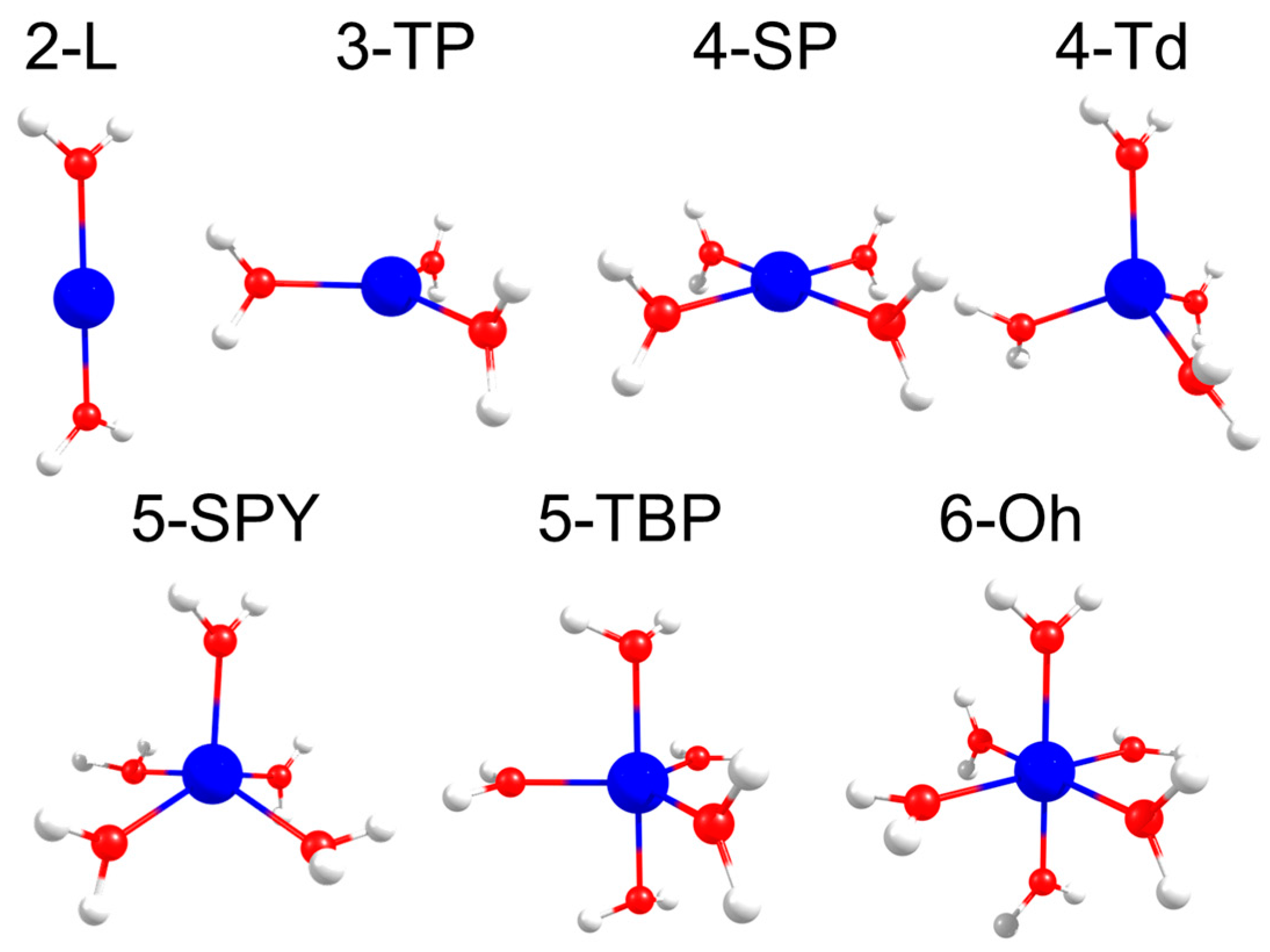
Geometry	Fe(II)		Co(II)
	noJT	JT	noJT	JT
2-L	8.9	26.3	7.3	3.8
3-TP	63.7	609	1408.2	2217.8
4-SP	68.8	565.1	1000.5	1195.9
4-Td	203.4	304.3	2268.5	3016.5
5-SPY	526.2	970.9	664.5	1155.2
5-TBP	638	913.8	588.4	2196.3
6-Oh	299.3	461.6	4.2	394.7

). Thus, zero-field splitting parameters for these geometries will be closer to the perturbational regime than undistorted models.

2.3. Adequacy of Zero-Field Splitting Parameters

As discussed earlier, D and E parameters are adequate to describe magnetic anisotropy as long as the ground state is isolated enough in energy. When the ground state is degenerate or exhibits low energy excited states, D is not a sensible parameter anymore and ad hoc spin Hamiltonians should be constructed for each case. Expectedly, calculated D values under these circumstances are not robust, yielding unphysical values which are strongly sensitive to the method and source energies (CASSCF or NEVPT2).

Table 2. D (cm⁻¹) and E/D parameters calculated for all models using second-order perturbation theory (2PT) and effective Hamiltonian (H_eff) approaches. CASSCF calculation including all roots for every possible multiplicity stemming from d-orbital configurations.

		Fe(II)				Co(II)
		D2PT	DHeff	E/D2PT	E/DHeff	D2PT	DHeff	E/D2PT	E/DHeff
noJT	2-L	−4799.7	−83.1	0.00	0.01	−36459.3	−239.8	0.00	0.00
	3-TP	475.9	21.4	0.05	0.02	133.8	79.1	0.02	0.02
	4-SP	−438.4	−37.7	0.03	0.26	160.2	87.0	0.00	0.00
	4-Td	−10.1	−4.9	0.10	0.06	−18.6	−14.6	0.25	0.24
	5-SPY	−22.1	18.0	0.28	0.31	−185.3	−117.9	0.17	0.21
	5-TBP	−11.1	−10.1	0.24	0.15	83.7	62.7	0.02	0.15
	6-Oh	−33.0	25.8	0.23	0.24	15175.6	175.0	0.03	0.02
JT	2-L	−1602.8	−82.5	0.00	0.00	−64329.6	−236.0	0.00	0.00
	3-TP	−49.0	−33.4	0.09	0.00	86.6	64.5	0.00	0.00
	4-SP	−54.6	−38.0	0.02	0.04	134.5	82.9	0.00	0.00
	4-Td	−8.1	−5.0	0.02	0.09	−15.7	−13.4	0.24	0.24
	5-SPY	−7.5	−6.1	0.30	0.27	−82.2	−66.6	0.26	0.26
	5-TBP	7.8	−6.7	0.29	0.32	50.7	42.0	0.02	0.02
	6-Oh	22.1	21.9	0.28	0.16	143.5	116.4	0.01	0.00

presents D values obtained for all model systems employing the second-order perturbation theory and effective Hamiltonian approaches. All roots of all multiplicities were included. It is clear that robust results are obtained only when the ground state is isolated enough to permit the perturbative regime defining the zero-field splitting parameters.

In the case of Co(II), zero-field splitting parameters are clearly unsuitable for linear and octahedral geometry, as evidenced by the unphysical values obtained by second-order perturbation theory (2PT) and the strongly dissimilar values provided by the effective Hamiltonian (H_eff) approach. For the remaining geometries, D_Heff values tend to be significantly smaller than D_2PT results, although E/D parameters are generally consistent between both approaches. This shows the existence of a regime where the ground state is non-degenerate but there are important low energy excited states. As expected, Jahn–Teller distorted geometries show smaller changes between D_2PT and D_Heff.

For Fe(II), reasonable geometries to analyze D are 5-SPY and 5-TBP. The sign change of D observed for 5-SPY geometry may suggest that this coordination is not fulfilling the requirements for the calculation of D. However, the high rhombic component of the system dilutes the meaning of the sign of D (considering CASSCF results, E/D is 0.28 and 0.31 for 2PT and H_eff methods, respectively). In the case of Jahn–Teller distorted geometries, we find that most geometries (except linear) show similar values for D_2PT and D_Heff.

As the objective of this article is to study the contributions of the same and different spin excitations to magnetic anisotropy, we want to keep as many cases as possible to draw the most general conclusions. In this way, only strongly differing cases in terms of D_2PT and D_Heff will be discarded due to the inapplicability of zero-field splitting parameters in orbitally degenerate ground states. To give a clear selection criterium, we chose D_Heff/D_2PT > 0.5 as the condition to accept a geometry. Of course, if the ratio between both D values is close to 0.5, predictions about energy splitting and magnetic anisotropy will be significantly dependent on the method chosen to calculate the zero-field splitting parameters and conclusions should be drawn carefully.

2.4. Inclusion of Lower Multiplicity Roots

The effect of lower multiplicity roots in magnetic anisotropy will be analyzed for the geometries with non-degenerate ground states. In the next section, cases with degenerate ground states will be analyzed separately.

Table 3. D (cm⁻¹) and E/D values for selected models of Fe(II) and Co(II). Parameters correspond to CASSCF (n,5) calculations including highest multiplicity roots (HS index) or all roots for every possible multiplicity stemming from d-orbital configurations (All index).

			CASSCF					NEVPT2
			DAll	E/DAll	DHS	E/DHS	DAll		E/DAll	DHS	E/DHS
Fe(II)	noJT	5-SPY	−22.1	0.28	−21.0	0.29	−19.9		0.25	−19.0	0.27
	noJT	5-TBP	−11.1	0.24	−11.5	0.14	−8.8		0.27	−9.4	0.15
	JT	3-TP	−49.0	0.09	−48.1	0.09	−44.6		0.07	−32.5	0.01
	JT	4-SP	−54.6	0.02	−53.1	0.02	−54.2		0.00	−36.5	0.02
	JT	4-Td	−8.1	0.02	−6.2	0.15	−7.7		0.04	−3.8	0.06
	JT	5-SPY	−7.5	0.30	−6.2	0.29	7.0		0.32	−5.6	0.22
	JT	5-TBP	7.8	0.29	−7.3	0.25	6.7		0.26	−7.1	0.19
	JT	6-Oh	22.1	0.28	21.6	0.23	18.1		0.32	21.8	0.13
Co(II)	noJT	3-TP	133.8	0.02	125.9	0.02	108.3		0.03	102.9	0.03
	noJT	4-SP	160.2	0.00	151.4	0.00	135.5		0.00	127.3	0.00
	noJT	4-Td	−18.6	0.25	−17.4	0.24	−14.8		0.27	−13.9	0.27
	noJT	5-SPY	−185.3	0.17	−177.8	0.15	−147.7		0.17	−145.9	0.15
	noJT	5-TBP	83.7	0.02	76.4	0.02	69.4		0.01	63.4	0.01
	JT	3-TP	86.6	0.00	78.4	0.00	73.3		0.00	58.2	0.00
	JT	4-SP	134.5	0.00	124.7	0.00	109.3		0.00	77.1	0.00
	JT	4-Td	−15.7	0.24	−14.4	0.23	−13.1		0.25	−12.3	0.23
	JT	5-SPY	−82.2	0.26	−78.9	0.23	−62.0		0.28	−64.4	0.24
	JT	5-TBP	50.7	0.02	43.5	0.02	42.3		0.02	36.2	0.02

presents the values for D and E/D, considering only the highest multiplicity roots or all roots in the CASSCF calculation. We only show results for the second-order perturbation theory method. Effective Hamiltonian values are presented in Table S2.

In general, the inclusion of all roots resulted in a rise in the magnitude of D. For CASSCF calculations, the majority of cases clustered around 5% to 10%. There are some exceptions, such as Fe(II)-5-TBP (noJT), where D_All is slightly lower than D_HS. Three models presented a rise exceeding 10%. In most cases, NEVPT2 calculations also show a rise in D upon the inclusion of roots from all multiplicities, with a broader range for the D_All/D_HS ratio. This change is not related to differences in the orbital optimization from the CASSCF calculation, as D and E/D values are not changing when the configuration interaction is performed with the orbitals optimized for all roots or only the highest multiplicity roots (see Table S3).

Table 4. D (cm⁻¹) for selected geometries under different choices of the multiplicity of included roots. D values in the “All” section correspond to CASSCF calculations including all roots. D_All is the total value, which is decomposed in contributions from highest multiplicity (D_High) and lower multiplicity roots (D_Low). The calculation considering only higher multiplicity roots is in the section HS. Results for the second-order perturbation theory method for the calculation of zero-field splitting parameters are presented.

			CASSCF				NEVPT2
			DAll	DHigh	DLow	DHS	DAll	DHigh	DLow	DHS
Fe(II)	noJT	5-SPY	−22.1	−20.3	−1.8	−21.0	−19.9	−18.0	−1.9	−19.0
	noJT	5-TBP	−11.1	−11.1	0.0	−11.5	−8.8	−8.6	−0.2	−9.4
	JT	3-TP	−49.0	−46.9	−2.1	−48.1	−44.6	−42.4	−2.2	−32.5
	JT	4-SP	−54.6	−52.1	−2.6	−53.1	−54.2	−51.4	−2.8	−36.5
	JT	4-Td	−8.1	−6.2	−1.9	−6.2	−7.7	−5.8	−1.9	−3.8
	JT	5-SPY	−7.5	−5.8	−1.8	−6.2	7.0	5.3	1.7	−5.6
	JT	5-TBP	7.8	6.3	1.5	−7.3	6.7	5.1	1.6	−7.1
	JT	6-Oh	22.1	21.2	1.0	21.6	18.1	17.1	1.0	21.8
Co(II)	noJT	3-TP	133.8	125.2	8.6	125.9	108.3	99.5	8.8	102.9
	noJT	4-SP	160.2	149.9	10.3	151.4	135.5	123.8	11.7	127.3
	noJT	4-Td	−18.6	−17.5	−1.2	−17.4	−14.8	−13.6	−1.2	−13.9
	noJT	5-SPY	−185.3	−180.0	−5.4	−177.8	−147.7	−142.1	−5.7	−145.9
	noJT	5-TBP	83.7	76.1	7.6	76.4	69.4	61.5	7.9	63.4
	JT	3-TP	86.6	77.8	8.8	78.4	73.3	64.3	9.0	58.2
	JT	4-SP	134.5	123.1	11.4	124.7	109.3	95.6	13.7	77.1
	JT	4-Td	−15.7	−14.4	−1.3	−14.4	−13.1	−11.7	−1.3	−12.3
	JT	5-SPY	−82.2	−79.2	−3.1	−78.9	−62.0	−58.6	−3.4	−64.4
	JT	5-TBP	50.7	43.2	7.5	43.5	42.3	34.5	7.8	36.2

shows the decomposition of the zero-field splitting parameter (D_All) in contributions from the highest multiplicity (D_High) and lower multiplicity roots (D_Low). These values are compared to the calculation including only the highest multiplicity roots (named “D_HS” in Table 4). In general, D_HS tends to be closer to D_High than D_All, indicating that the contribution from same spin excitation remains similar, independent of the roots included in the CASSCF. In this way, the differences between D_HS and D_All can be mainly attributed to excitations between states of different multiplicities. It is interesting to see that D_High and D_Low are of the same sign in all studied cases, and their relative weight is in many cases in the range between 5–10%. There are some cases where the contributions of D_Low represent a larger fraction of D_All, such as in Co(II)-5-TBP (JT), Fe(II)-4-Td, 5-SPY, and 5-TBP (JT).

The contribution of lower multiplicity roots to zero-field splitting parameters was always of the same sign of the total value. Moreover, it always led to a rise in magnetic anisotropy. As mentioned, the contribution of different-spin excitations to D was of a similar order in most cases, around 5–10% of the total value. To understand this behavior, it is instructive to recall the expression for the zero-field splitting parameter for excitations between states of the same spin ($D_{KL}^{SOC-(0)}$) and when the spin is lowered by one unit ($D_{KL}^{SOC-(-1)}$) [52,53].

$$D_{KL}^{SOC-(0)}=-\frac{1}{S^2}{\displaystyle \sum _{I\prime (S\prime =S)}{\Delta }_{J\prime }^{-1}\langle {\Psi }_0^{SS}|{\displaystyle \sum _i{\widehat{z}}_K(i){\widehat{s}}_0(i)}}|{\Psi }_{J\prime }^{SS}\rangle \langle {\Psi }_{J\prime }^{SS}|{\displaystyle \sum _i{\widehat{z}}_L(i){\widehat{s}}_0(i)}|{\Psi }_0^{SS}\rangle$$

(1)

$$D_{KL}^{SOC-(-1)}=-\frac{1}{S(2S-1)}{\displaystyle \sum _{I\prime (S\prime =S-1)}{\Delta }_{J\prime }^{-1}\langle {\Psi }_0^{SS}|{\displaystyle \sum _i{\widehat{z}}_K(i){\widehat{s}}_{+1}(i)}}|{\Psi }_{J\prime }^{S-1S-1}\rangle \langle {\Psi }_{J\prime }^{S-1S-1}|{\displaystyle \sum _i{\widehat{z}}_L(i){\widehat{s}}_{-1}(i)}|{\Psi }_0^{SS}\rangle$$

(2)

where S is the spin, K, L are cartesian components (x, y or z). ${\Delta }_{J\prime }^{-1}$ is the reciprocal of the energy difference between the ground state (${\Psi }_0^{SS}$) and the excited state of interest (${\Psi }_{J\prime }^{SS}$). ${\widehat{z}}_L(i)$ is part of the spin-orbit coupling operator ${\widehat{z}}_L(i){\widehat{s}}_L(i)$ for electron i, with respect to the L cartesian component. ${\widehat{s}}_{0,\pm 1}(i)$ are the components of the spin vector operator.

To simplify the problem, we will assume that states can be expressed in terms of single determinants. Thus, ${\widehat{z}}_L(i)$ is decomposed in the product of an effective SOC constant (${\xi }_{eff}$) and the corresponding angular momentum operator (${\widehat{l}}_{K,ba}(i)$), connecting the initial ($d_b$) and final ($d_a$) orbitals describing the excited electron. The matrix elements appearing in Equations (1) and (2) will be expressed as:

$${\xi }_{eff}\langle d_{a,i}|{\displaystyle \sum _i{\widehat{l}}_{K,ba}(i){\widehat{s}}_m(i)}|d_{b,i}\rangle$$

(3)

where m = −1, 0, 1. Considering ${\widehat{l}}_{K,ba}(i)$ is imaginary and ${\widehat{l}}_{K,ba}(i)=-{\widehat{l}}_{K,ab}(i)$, it is easy to see that $D_{KK}^{SOC-(0)}$ will be negative and $D_{KK}^{SOC-(-1)}$ will be positive. As D_High and D_Low tended to show the same sign, the largest component in absolute value for D_High must be the smallest for D_Low. This is indeed corroborated in CASSCF calculations (see Table S4). This relation will only hold for xx, yy, and zz components D. Mixed components for $D_{KL}^{SOC-(-1)}$ can be positive or negative, potentially leading to a different behavior. At least in our models, diagonal elements of the D tensor tended to dominate over non-diagonal values, yielding overall positive contributions to $D_{}^{SOC-(-1)}$.

The d⁶ system is taken as example. For a negative value of D, $D_{zz}<1/2(D_{xx}+D_{yy})$. Then, the most important contribution to D is associated with orbitals connected by the z component of the angular momentum operator. For $D_{KK}^{SOC-(0)}$, the excitation will correspond to the promotion of the only beta electron from the doubly occupied orbital in the ground state to a singly occupied orbital. Initial and final orbitals will be called ‘1’ and ‘2’, and the matrix element will be $l_{z,12}$. In the case of $D_{KK}^{SOC-(-1)}$, the electron must promote to an excited d-orbital and spin flip. Thus, the final orbital must be initially empty in order to accommodate the electron. For each S = S’ excitation (e.g., 21111 → 12111), there will be three lower multiplicity determinants contributing to $D_{KL}^{SOC-(-1)}$ (i.e., 22110, 22101, 22011). The relevant matrix elements will be $l_{K,23}$, $l_{K,24}$ and $l_{K,25}$. If “1” and “2” are already connected by the z component, it is likely that “2” is connected to “3”, “4”, and “5” by the x or y components. In this way, $D_{zz}^{SOC-(-1)}$ will be smaller than $D_{xx}^{SOC-(-1)}$ and $D_{yy}^{SOC-(-1)}$, in accordance with calculations.

2.5. Degenerate Ground States

As zero-field splitting parameters are not directly applicable for these systems, the influence of lower multiplicity roots will be analyzed in terms of state energies after the inclusion of spin-orbit coupling.

Table 5. State energies (cm⁻¹) after the inclusion of spin-orbit coupling effects (QDPT) for selected geometries (CASSCF calculations). Due to Kramers’ degeneracy, all states are doubly degenerate for Co(II), so we only show each energy once.

		All	HS		All	HS
Fe(II)	2-L (noJT)	0.0	0.0	4-Td (noJT)	0.0	0.0
		0.0	0.0		1.2	0.7
		193.8	190.9		14.8	10.2
		193.8	190.9		15.7	14.0
		388.0	385.1		20.5	16.0
	3-TP (noJT)	0.0	0.0	6-Oh (noJT)	0.0	0.0
		19.0	18.7		5.9	6.3
		21.0	21.2		39.8	37.7
		84.8	84.7		101.9	101.2
		84.8	84.8		110.6	108.9
	4-SP (noJT)	0.0	0.0	2-L (JT)	0.0	0.0
		0.6	0.6		0.0	0.0
		104.5	102.3		195.8	192.9
		113.7	111.5		196.0	193.0
		195.5	194.1		381.5	379.3
Co(II)	2-L (noJT)	0.0	0.0	2-L (JT)	0.0	0.0
		479.6	470.9		472.0	464.2
		960.9	954.7		941.7	937.5
		1444.5	1451.2		1423.3	1433.3
	6-Oh (noJT)	0.0	0.0	6-Oh (JT)	0.0	0.0
		350.3	350.1		232.9	234.4
		353.0	352.8		512.5	512.2
		933.8	947.7		960.8	969.7

presents the lowest energy levels for the geometries not considered in the previous section. As one of the key properties in single molecule magnet research is the excitation energy to overcome the top of the energy barrier produced by the splitting of the M_s components of the ground state, we consider this energy as the parameter to evaluate the effect of the inclusion of excitations to lower multiplicity states. In the case of Fe(II), it corresponds to the fifth state, and for Co(II) it is the second Kramers’ doublet. In the majority of cases, energy barrier energies are modified less than 2% upon the inclusion of lower multiplicity roots. This is significantly smaller than the observed changes in D parameters and is expected since the dominant contribution for magnetic anisotropy in degenerate systems comes from the interaction within the ground state levels. Thus, contributions from higher excited states will be of minor importance. The exception from this behavior is Fe(II)-4-Td, which exhibits a very low energy barrier (c.a. 20 cm⁻¹), and small changes in energy give large percentage modifications.

3. Materials and Methods

Computational Details

All calculations were performed using the ORCA 4.0.1.2 software package [54]. Model structures were constructed using ideal geometries for the MO_n fragment, while hydrogen positions were fully optimized for all cases. Metal-oxygen distances were set to the average of unconstrained optimizations for high spin hexa-aquo complexes of iron(II) (2.151 Å) and cobalt(II) (2.113 Å). To discuss the effect of Jahn–Teller bond elongation/compression, a second set of molecules was optimized without restrictions on metal-oxygen bond distances. The BP86 density functional [55,56] and the Def2-TZVP basis set [57,58] were employed in all geometry optimizations. We considered a CASSCF [59] active space involving the five 3d orbitals, following common practice in single-molecule magnet research. N-electron valence state perturbation theory (NEVPT2) [60,61] energy correction was also included. Converged CASSCF wave functions served as a basis to build the state interaction matrix of the spin-orbit coupling (SOC) operator (quasi degenerate perturbation theory (QDPT) approach). Zero-field splitting parameters (D and E) obtained by second-order perturbation theory and effective Hamiltonian approaches were compared, and d-orbital splitting was analyzed in terms of ab initio ligand field theory (AILFT) [19]. In all cases, CASSCF and NEVPT2 ground states corresponded to the highest multiplicity computed (quintet for Fe(II) and quartet for Co(II)).

4. Conclusions

The effect of lower multiplicity roots in zero-field splitting parameters was evaluated for model structures of d⁶ (Fe(II)) and d⁷ (Co(II)) complexes. When the ground state was energetically isolated, lower multiplicity states increased the total D value by ca. 5–10% in most cases. This trend should be observed in general and is related to the sign of the contributions of same spin and different spin excitations. In the case of degenerate ground states, the effect of high energy roots was less important, with contributions under 2%. This behavior is expected since spin-orbit coupling between levels of the ground state will greatly dominate the magnetic anisotropy. Conclusions drawn for model systems are expected to hold in real molecular systems given the correspondence of the observed trend with the basic equations describing zero-field splitting parameters.