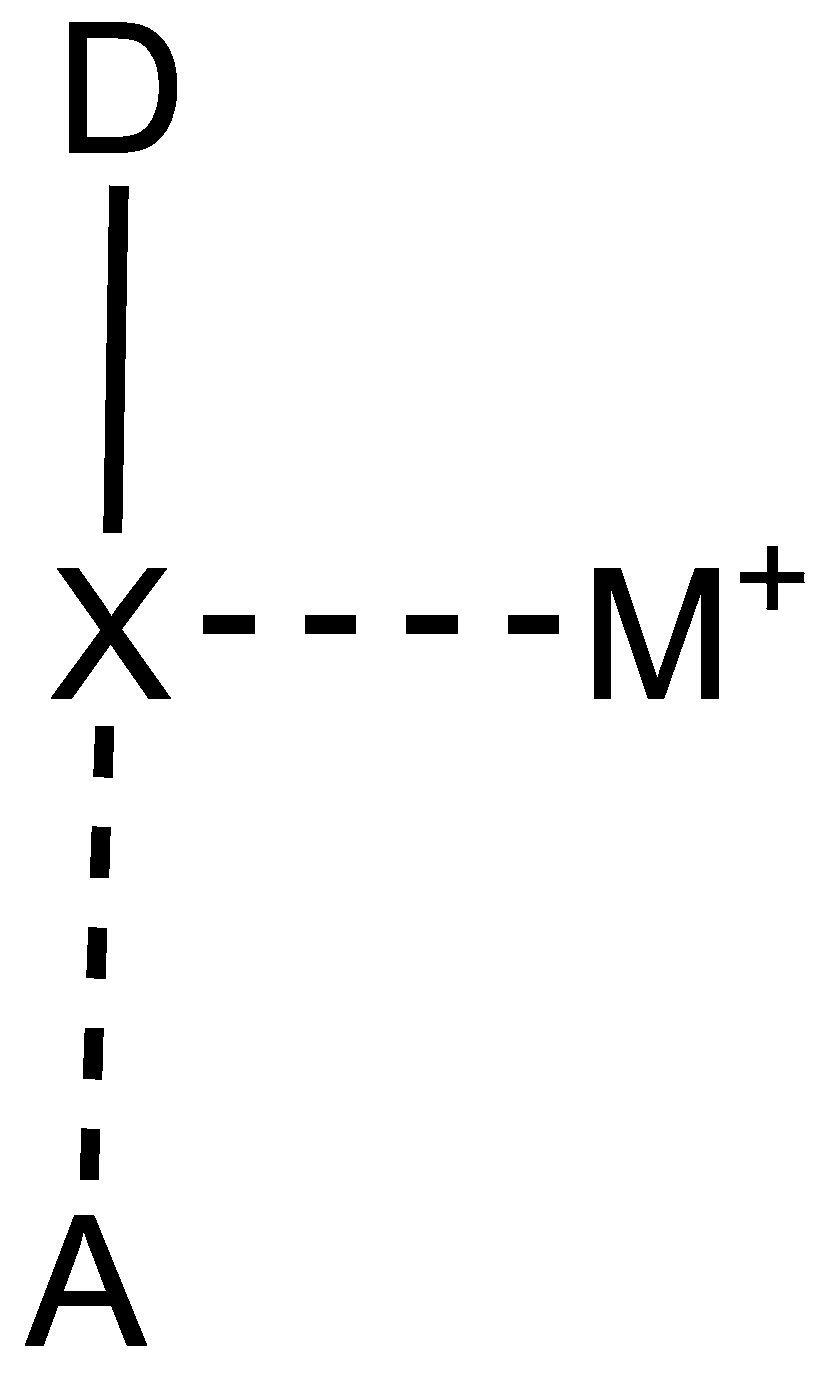Next Article in Journal
Limited Domain SnSb@N-PC Composite Material as a High-Performance Anode for Sodium Ion Batteries
Previous Article in Journal
Physicochemical and Toxicological Screening of Silver Nanoparticle Biosynthesis from Punica granatum Peel Extract
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 12
Issue 6
10.3390/inorganics12060161
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Alkali Metal-Ion Binding by a Model Macrocycle Containing a C-I···N Halogen Bonded Network: A DFT Study of C-I···M+ and N···M+ Binding Interactions, M+ = Li+, Na+, K+, and Rb+

by
Rubén D. Parra
Department of Chemistry and Biochemistry, DePaul University, Chicago, IL 60614, USA
Inorganics 2024, 12(6), 161; https://doi.org/10.3390/inorganics12060161
Submission received: 16 May 2024 / Revised: 31 May 2024 / Accepted: 4 June 2024 / Published: 6 June 2024
(This article belongs to the Special Issue Studies on Metal-Ion Binding by Halogen-Bonded Structures)
Browse Figures
Versions Notes

Abstract

:
The complexation of an alkali metal ion by a model macrocycle is examined using the M05-2X/DGDZVP DFT method. The macrocycle is built by connecting three cyclopenta[b]pyrrole motifs with alternating acetylene and ethylene linkages. Replacing one of the C-H bonds in each motif with a C-I bond allows for the formation of three intramolecular C-I···N halogen bonds. Two distinct binding modes were found for the complexation of each metal ion. In one mode, the binding of the ion occurs solely by the iodine atoms, via I···M+ interactions, while maintaining the integrity of the halogen bonds. The complexation energies are in the range −66 to −35 kcal/mol. In the other mode, the binding of the ion includes one nitrogen atom as well, with binding energies in the range of −71 to −38 kcal/mol. In this binding mode, the halogen bond network is weakened. The presence and strength of the interactions are further examined using AIM and NBO calculations. Lastly, the geometries for the transition state structures linking the less stable to the more stable metal ion complexes were obtained, and their calculated Gibbs free energy barriers were found in the range of 1.6 to 1.9 kcal/mol.

Graphical Abstract

1. Introduction

Materials with the ability to complex metal ions, usually known as ligands, are paramount in certain chemical and biochemical processes. Natural ionophores, for example, have the ability not only to complex metal ions but also to transport them across lipid membranes [1,2,3]. Moreover, the importance of metal ions in the activity of many enzymes has long been recognized [4,5,6]. To form a complex, a ligand must be endowed with one or more electron-rich sites that can interact favorably with the electron-deficient metal cation [7]. Indeed, the interaction between a metal ion and a ligand can be thought of as a Lewis acid–base interaction between an electron-rich species, the ligand as the Lewis base, and an electron-deficient species, the metal ion as the Lewis acid. Regions of high electron density in a ligand can emerge from a variety of contributors, most commonly lone pairs of atoms such as those in oxygen or in nitrogen atoms [8,9]. Other sources of electron density come from isolated double or triple bonds, and even from aromatic rings [10,11]. In the purposeful design of ligands for selectively binding metal ions, factors such as the size and charge of the metal ion and the relative ability of the ligand to donate electron density are to be considered judiciously [12,13,14,15,16]. For a polydentate ligand, one with multiple binding sites, the spatial orientation of the binding sites must be considered as well. Using polydentate ligands is known to result in metal ion complexes that are more stable than those obtained using an equivalent number of monodentate ligands; this is referred to as the chelate effect [17,18,19]. Similarly, the use of macrocyclic ligands generally results in more stable metal ion complexes than those from open-chain ligands possessing an equivalent number of binding sites; this is the macrocyclic effect [20,21,22]. Cyclic polyethers or crown ethers represent prime examples of the successful use of the macrocyclic effect [23,24]. That is, cyclic polyethers can form complexes with alkali metal ions that are orders of magnitude more stable than those of their linear counterparts. Moreover, the stability of these complexes could be fine-tuned by controlling the size of the macrocycle’s cavity to fit better the radius of the metal ion of interest, hence making the crown ether more selective by design [25,26]. The realization of the macrocyclic effect through the crown ethers in the early 1960s led scientists, especially inorganic chemists, to devote more attention to the coordination chemistry of the alkali metal ions [27,28].
The importance of alkali metal ions in chemical and biological processes can hardly be overestimated [29,30,31,32,33,34,35,36]. For example, lithium salts find medical use for the treatment of bipolar disorders [37]. Lithium-containing compounds have also found industrial applications in several areas, including ceramics, lubricants, and lithium-ion batteries [38]. The physiology of the Na+/K+ pump has been amply investigated [39,40,41]. It has even been suggested that Na+/K+ pumps display information-processing roles in some neurons [42]. Interest in the technological development and application of Na+/K+-based batteries as a cost-effective alternative to Li+-based analogs has increased significantly over the last decade [43]. The use of catalysts containing alkali-metal ions is common in many branches of chemistry [44,45,46]. Although less commonly encountered, the two heaviest stable alkaline cations, Rb+ and Cs+, have also been the subject of systematic fundamental and practical studies [47,48,49,50,51,52].
Because of the widespread importance of alkali metal ions, it remains of great research interest to design and develop ligands that can bind and selectively transport these metal ions; that is, novel ligands that can expand the horizon of metal ion complexation beyond well-established ligands such as polyethers, crown ethers, and cryptands. In the work presented here, a novel macrocycle is proposed and examined in terms of its ability to bind alkali metal ions. Specifically, the proposed macrocycle contains a cyclic sequence of three intramolecular, C-I···N, halogen-bonding interactions. It is worth noting that a halogen atom, X, exhibits a distinctive charge anisotropy when it is covalently bonded to another atom or group of atoms, D. On the one hand, the halogen atom shows a region of positive electrostatic potential, known as a σ-hole, opposite to the covalent bond, D-X. On the other hand, the halogen atom shows a region of negative electrostatic potential perpendicular to D-X, which is due to the lone pairs of the halogen atom. Accordingly, a halogen bond, D-X···A, can result from the interaction of an electron-rich species, A, with the σ-hole in D-X. Similarly, the negative electrostatic potential perpendicular to the halogen bond can potentially interact with an electron-poor species such as a metal ion, M+. Thus, this amphoteric character of the halogen atom enables it to act as an electrophile in one direction, and as a nucleophile in the orthogonal direction, as shown in Scheme 1.
Specifically, the halogen atom in the halogen bond can act as a Lewis acid, receiving electron density from the nitrogen lone pair acting as the Lewis base. Because of its amphoteric character, the halogen atom can also act as a Lewis base, donating electron density via its lone pairs of electrons to an electron-deficient or Lewis acid species like the metal ion indicated in Scheme 1. Not much research, however, has gone into examining or realizing the potential for binding metal cations through halogen atoms participating in halogen bonding [53,54,55,56,57,58,59]. In previous work, the author has specifically investigated the potential of intermolecular and intramolecular halogen-bonded systems to bind metal cations [60,61,62,63,64,65]. In this work, attention is given to perhaps the smallest number of intramolecular halogen bonds that can form a macrocyclic cavity. The addition of a metal ion to a halogen bond-containing system may result in disruption of the bond by competing for the electrons of the halogen-bond acceptor. The strength of the halogen bond correlates with the size of the halogen atom for a given halogen bond acceptor, hence the choice of the iodine atom as the halogen bond donor. Also, the larger the charge of the metal ion, the more likely it is for the metal ion to compromise the integrity of the halogen bond network. Accordingly, the spherical, monovalent alkali metal ions are chosen to examine the binding ability of the proposed halogen-bonded macrocyclic ligand.

2. Results and Discussion

2.1. Model Intramolecular Halogen-Bonded Macrocycle

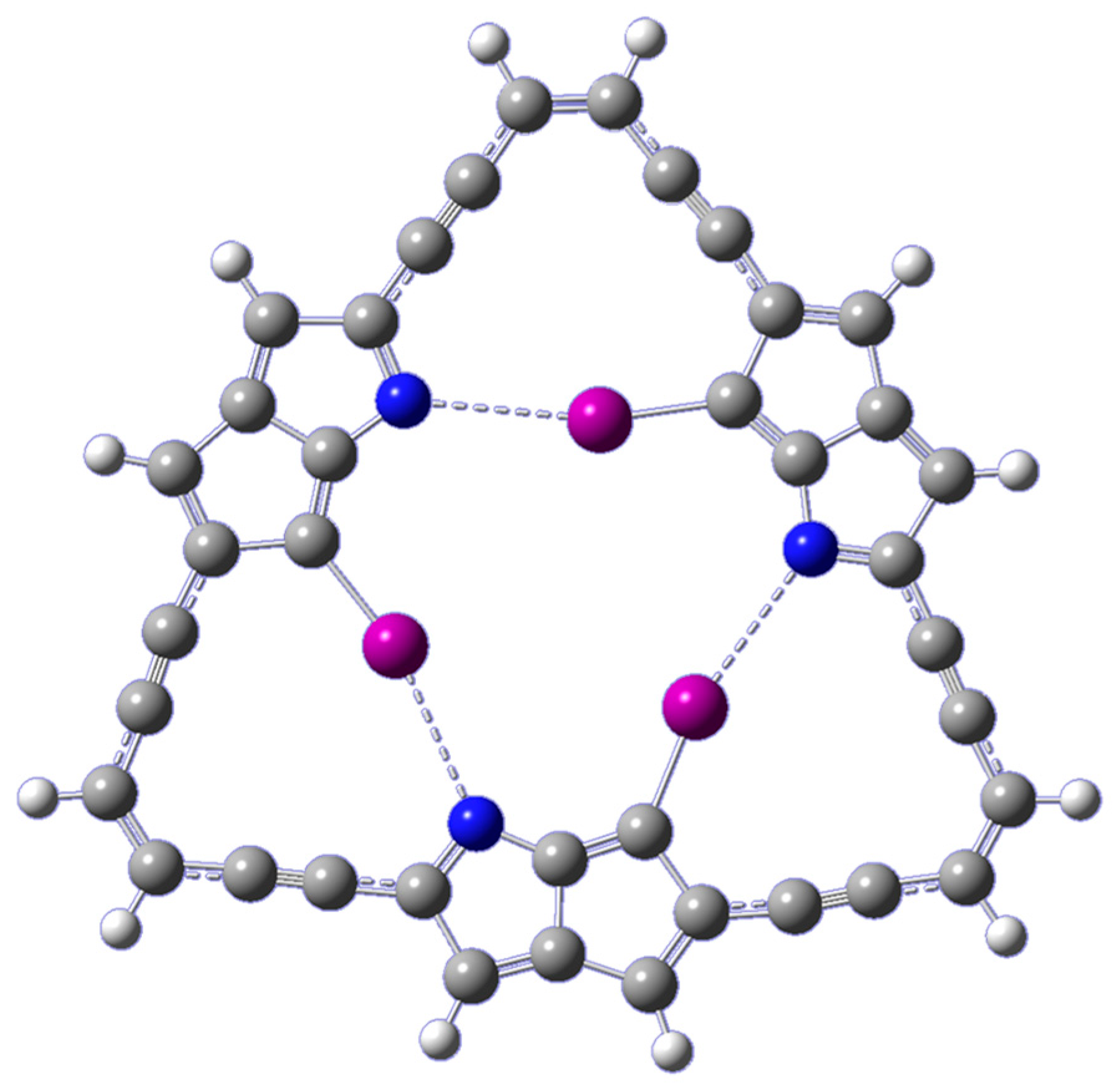
A macrocycle containing a network of three intramolecular halogen bonds is proposed as a potential host for binding a metal cation. As shown in Figure 1, the model system is built by connecting three cyclopenta[b]pyrrole motifs through an alternating sequence of acetylene and ethylene linkages. Replacing one of the C-H bonds in each motif with a C-I bond allows for the formation of an intramolecular network of three C-I···N halogen bonds. The optimization of the macrocyclic ligand results in a planar geometry of symmetry C3h. It should be noted that no symmetry was imposed for geometry optimization. In fact, starting with twisted geometries, C-I bonds away from the N atoms, optimization always converged to the same final C3h structure shown in Figure 1. Frequency calculations on the fully optimized geometry confirm the nature of the macrocycle as an energy minimum with no imaginary frequencies.
The existence of the halogen bond is evinced geometrically by an I···N distance (2.99 Å) that is much smaller than the sum of the van der Waals radii of the I and N atoms (3.53 Å), and a quasilinear C-I···N angle of 166.0°. Additional indicators of halogen bond presence and relative strength include electron densities at bond-critical points from AIM analyses and the amount of electron charge transfer and concomitant second-order stabilization energies from NBO analyses. Accordingly, the existence of the intramolecular C-I···N halogen bonds was further examined using topological analyses, within the framework of the AIM theory, and using delocalization energy analyses, within the framework of the NBO method. Specifically, the second-order NBO delocalization energies E2, associated with the charge transfer from the halogen bond acceptor lone pair into the antibonding orbital of the halogen bond donor (nN → σ*C–I), is calculated to be 5.51 kcal/mol. Moreover, AIM calculations reveal the existence of a critical point along the C-I···N path with an electron density, ρc, of 0.0186 a.u.
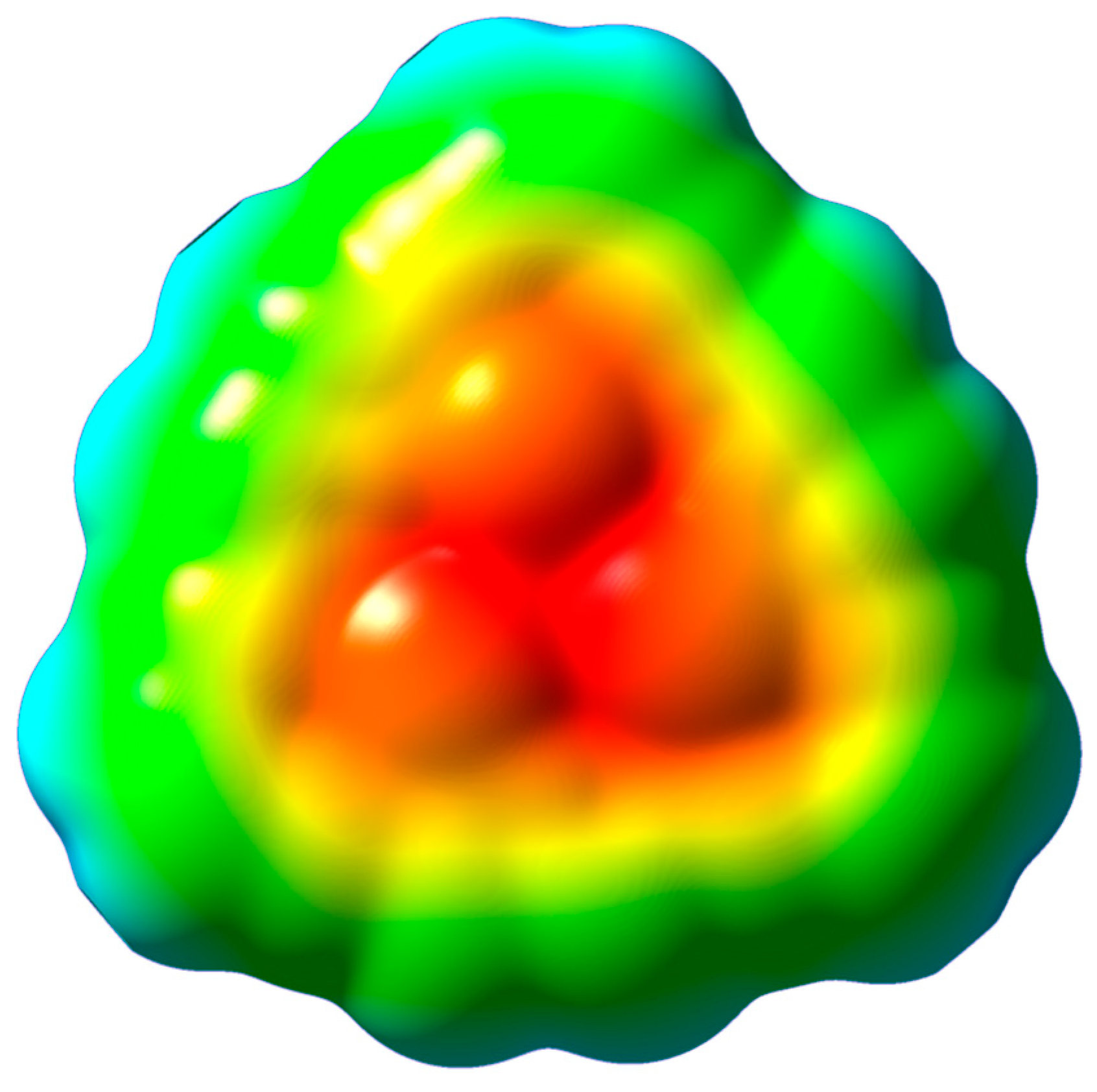
Having demonstrated the existence of the halogen bonds in the model macrocycle shown in Figure 1, it would be important to investigate their ability to bind a metal cation. For this purpose, the molecular electrostatic potential was calculated first for the optimized macrocycle ligand. The results, displayed in Figure 2, show the presence of a distinctive negative electrostatic potential region around the central cavity of the macrocycle. Consequently, a metal cation can, in principle, be attracted to this negative potential at the central cavity of the ligand. A sense of the ligand’s cavity can be gleaned from the I···I separations, which are about 4.65 Å. The specific geometries and energetics of the alkali metal ions (Li+, Na+, K+, and Rb+) are examined in the next section.

2.2. Alkali Metal Cation Binding via I···M+ Interactions

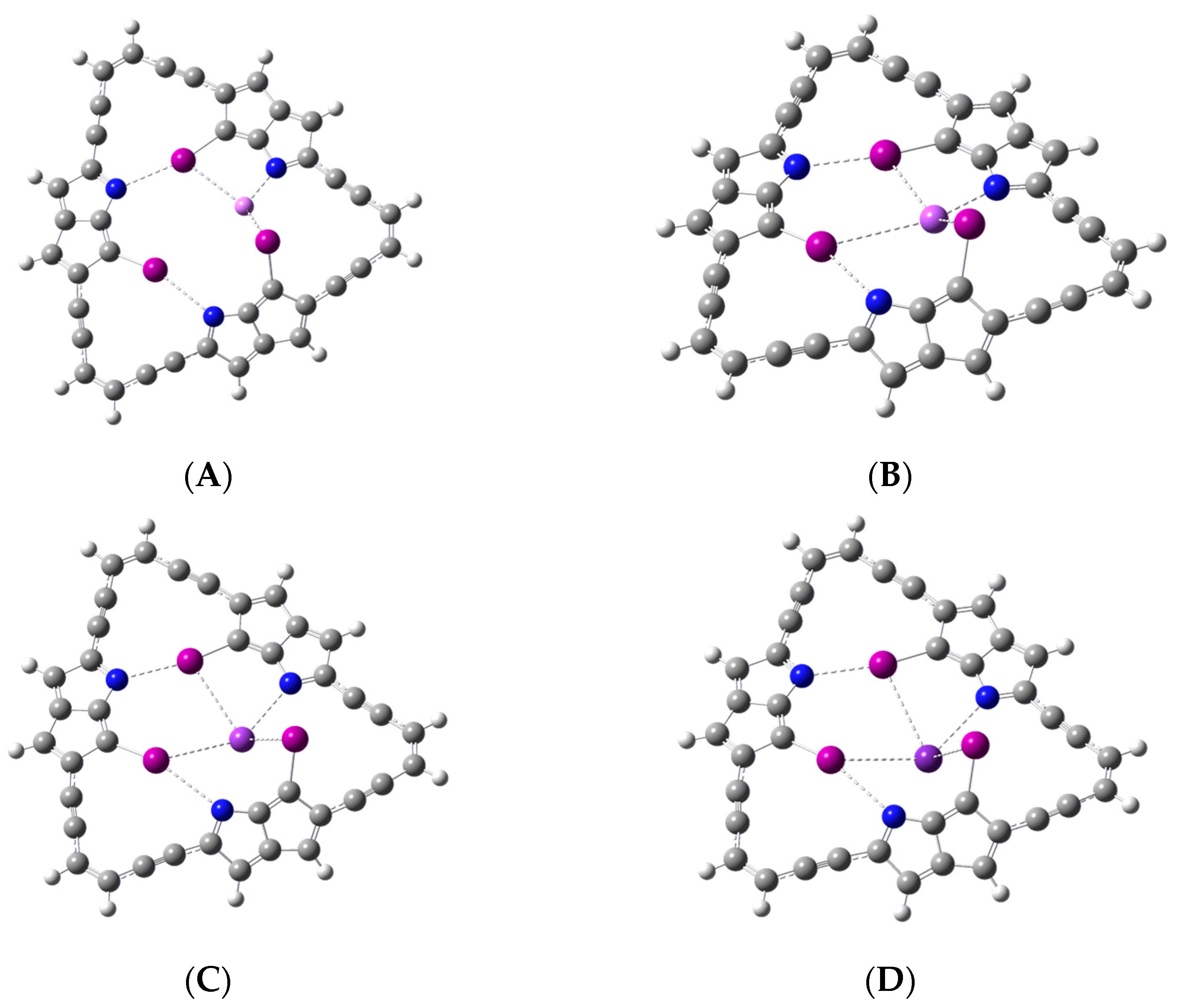
Geometry optimization shows that the model macrocycle binds Li+ at the center of symmetry of the macrocycle. That is, Li+ is found in the middle of the central cavity upon complexation, as shown in Figure 3A,B. For the larger metal cations (Na+, K+, and Rb+), the binding occurs, however, above the center of symmetry or plane of the macrocyclic ligand, as shown in Figure 3C,D for Rb+. In all cases, the complexation of the metal occurs primarily through the interaction between the metal ion and the iodine atoms. Frequency calculations confirm that the optimized complexes are indeed minimum energy structures with no imaginary frequencies.
The binding of the metal ion brings about changes in the geometrical parameters of the host. For example, the halogen bond distances, dC-I…N, and angles, AC-I…N, are listed in Table 1. Comparison with the halogen bond distances and angles of the free macrocycle, discussed in the previous section, reveals a shortening of the distances along with a widening of the angles upon metal ion complexation. These geometrical changes indicate that the complexation of the metal ion strengthens rather than weakens each of the halogen bonds in the macrocycle. It is noteworthy that the magnitude of the geometrical changes in the C-I···N halogen bonds decreases as the size of the metal ion increases. Table 1 also shows that the smallest distance from the metal ion to each of the iodine atoms, dI···M+, occurs for Li+. In fact, this distance is small enough to allow the metal ion to sit in the middle of the plane formed by the three halogen atoms. For the larger metal ions, the dI···M+ values are too large, however, for the metal ions to fit inside the cavity; hence, they sit above the center of the plane. As expected, the larger the metal ion, the larger the distance to the center of the plane, dc…M+, as shown in Table 1.
The complementarity between the Lewis acid, the metal ion, the Lewis bases, and the halogen atoms, results in a favorable metal-ion-binding interaction. A straightforward approach to gauge the relative strength of these binding interactions is to calculate the corresponding complexation energies, particularly after accounting for basis set superposition error, BSSE. The BSSE-corrected metal ion complexation energies, CE, are listed in Table 2. The complexation energies are calculated as the difference between the total energy of the complex and the sum of the energies of both the metal ion and the macrocyclic ligand with the geometry the ligand has in the complex. Because it sits in the middle of the plane formed by the halogen atoms, Li+ seems to experience more effectively the combined lone pair electron density of all the halogen atoms involved in its binding. The more effective favorable interaction for Li+ is shown in Table 2 as the most negative complexation energy of all the metal ions considered. In addition to the complementarity of the binding sites of the ligand to the metal ion, it is important to consider the extent to which the ligand changes its geometry to accommodate the metal ion guest. Energetically, the cost for the geometrical change of the ligand upon complexation can be seen in the deformation energy, ∆Edef, calculated as the difference between the energy of the ligand with the geometry adopted in the complex and the energy of the optimized free ligand. Table 2 reveals that the deformation energies are small, with values that are within 4% of the complexation energies: 2.7% for Li+, 3.9% for Na+ and K+, and 4.0% for Rb+. The relatively small deformation energies suggest that the macrocycle is preorganized, requiring little conformation or geometrical change to arrange its binding sites to maximize the favorable interaction with the metal ions while minimizing any unfavorable interactions, such as those among the binding sites themselves.
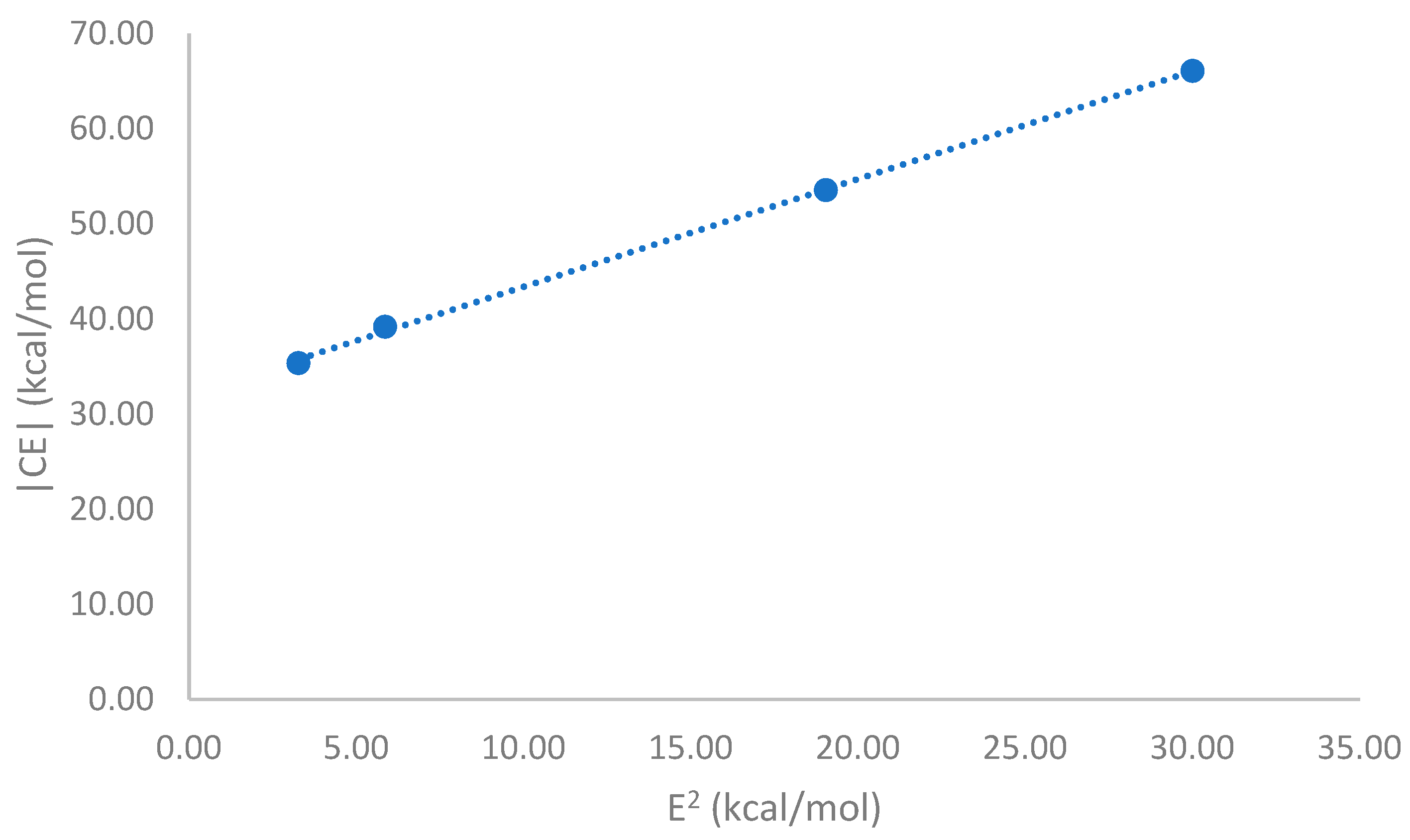
A steady decline of the magnitude of the complexation energies, |CE|, with the distance between the metal ion and the halogen atom, dI…M+, is represented graphically in Figure 4A. Likewise, a constant decline is seen in Figure 4B of |CE| with the distance of the metal ion to the center of the plane made by the three halogen atoms, dc…M+. In both cases, the goodness of fit for the linear equations has R2 values close to 1.0.
Table 3 lists the second-order NBO delocalization energies, E2, associated with both the intramolecular halogen bonds, C-I···N, and the intermolecular interaction between the halogen atoms of the ligand and the metal ion, C-I···M+. Comparison with the E2 value for the halogen bond in the free ligand (5.51 kcal/mol) shows that the corresponding E2 values are consistently larger upon metal ion complexation. This result is consistent with the notion that metal ion complexation strengthens the intramolecular halogen bonds suggested previously on geometrical grounds. The E2 values associated with the C-I···M+ interactions listed in Table 3 refer to the charge transfer from the halogen atom lone pairs into the anti-lone pair orbital of M+, nI → lp*M+. Interestingly, changes in these delocalization energies with respect to the size of the metal ion follow the same trend as the changes in the pertinent halogen bonds in the macrocyclic ligand. That is, as the size of the metal ion increases, the E2 value decreases, albeit the changes are much more substantial for the delocalization energies related to the halogen-metal ion interactions.
The E2 values associated with the C-I···M+ interactions are also found to correlate with the complexation energies. Specifically, the E2 values for these interactions become increasingly larger with the increasing magnitude of the metal ion complexation energies. Figure 5 explicitly displays this linear relationship with an R2 value of 1.00.
The specific interactions between the metal ion and the macrocyclic ligand are made apparent by the existence of a critical point along the path between the metal ion and each of the halogen atoms participating in its complexation. The electron density at each of these bond critical points, ρC-I…M+, are listed in Table 4. Except for Li+, the ρC-I…M+, value decreases steadily with increasing size of the metal ion. This trend in ρC-I…M+ correlates with the decline of the magnitude of the related complexation energies as the metal ion becomes larger. The exception shown for Li+, which shows a ρC-I…Li+ smaller than that for Na+, ρC-I…Na+, seems counterintuitive, given that the magnitude of Li+ complexation energy is over 12 kcal/mol larger than that for Na+. It should be noted, however, that the use of the electron density at the bond critical point to compare bond interactions involving different nuclei, say I···Li+ and I···Na+, provides just an estimate of their relative strength. This estimate becomes more meaningful when the nuclei participating in the bond are the same and within a similar chemical environment [66]. Thus, it is important to examine the strength of these binding interactions using indicators other than just the electron density. For example, the second-order delocalization energy, E2, as discussed earlier, is a commonly used indicator of bond strength. Other approaches to examine noncovalent bond strength include interaction energy decomposition analysis, EDA [67], and interacting quantum fragment analysis, IQF [68].
In addition to the halogen-metal ion interaction critical point densities, Table 4 shows the electron density at each of the halogen bond critical points, ρC-I…N. The strengthening of these intramolecular halogen bond interactions, C-I···N, upon metal ion complexation is evident in the increase of the electron density value at the halogen bond critical point, ρC-I…N, when compared with those in the free ligand (ρC-I…N = 0.0186 a.u.). In accord with the geometrical and the NBO results, the strengthening of the C-I···N halogen bonds revealed by the AIM results tends to decrease with the size of the metal ion being complexed by the macrocyclic ligand.

2.3. Alkali Metal Cation Binding via I···M+ and N···M+ Interactions

In the preceding section, the binding of the metal ion was discussed in terms of the I···M+ interactions that take place without disrupting or weakening any of the three C-I···N halogen bonds in the ligand. An alternative mode of binding the metal ion is considered in this section. Here, the binding of the metal ion includes the participation of the lone pair of one of the nitrogen atoms. 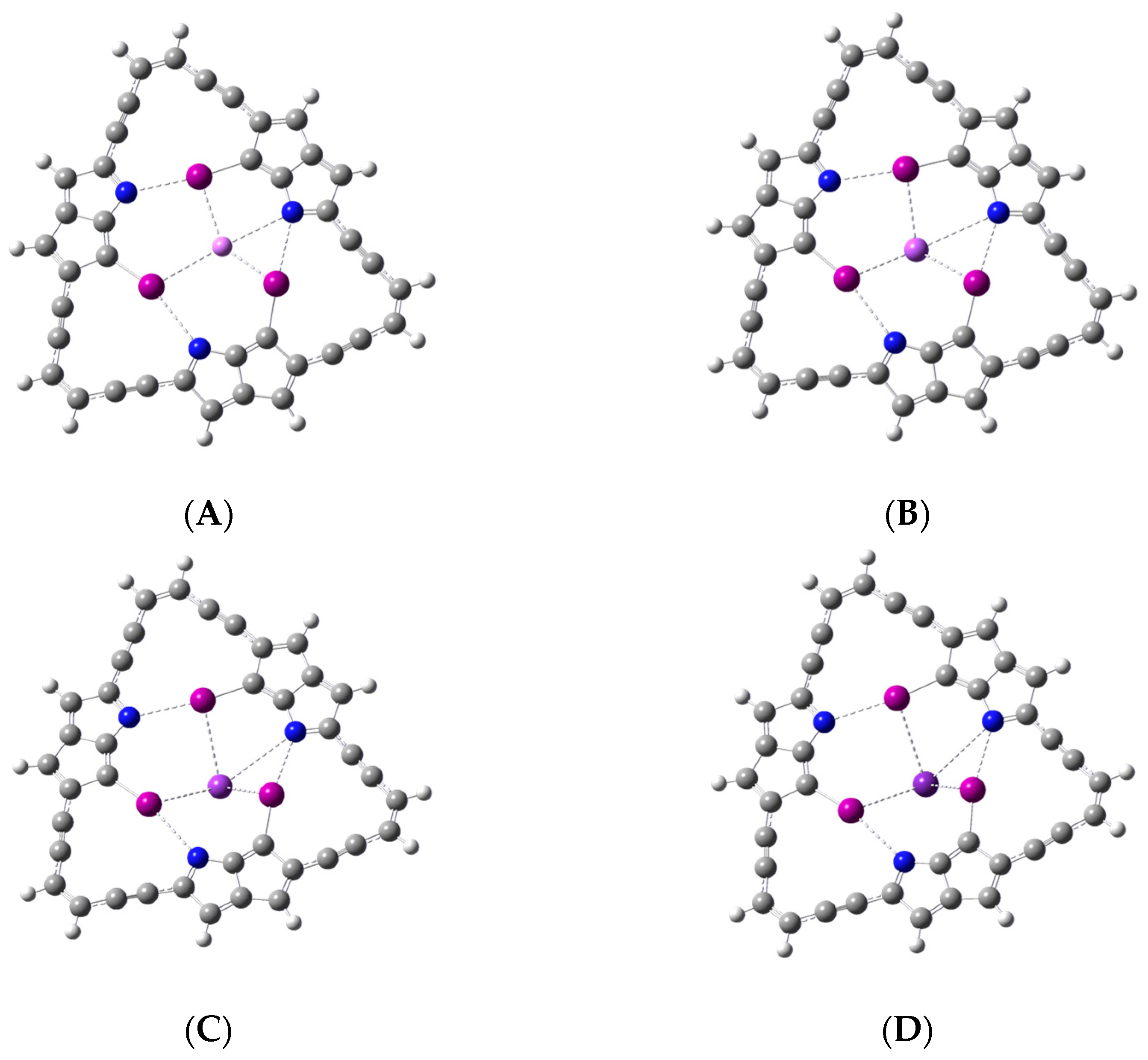This N···M+ interaction occurs by sacrificing one of the C-I···N halogen bonds in the macrocyclic ligand. The optimized geometries for each of the metal ion complexes, including I···M+ and N···M+ interactions, are displayed in Figure 6A–D. In all cases, the complexation of the metal ion includes the interaction between the metal ion and one of the nitrogen atoms. Binding of the metal ion, also including the three halogen atoms, seems to occur only for the larger Na+, K+, and Rb+ ions. For the smallest Li+ ion, one of the iodine atoms appears too far to contribute significantly to the binding of this metal ion. Figure 6A–D makes it apparent that one of the C-I···N halogen bonds in the ligand is effectively removed to enable the formation of the N···M+ interaction. Frequency calculations confirm that all the optimized complexes are indeed minimum energy structures with no imaginary frequencies.
Table 5 displays the halogen bond distances, dC-I…N, and angles, AC-I…N, as well as the distances from the metal ion to iodine, dI…M+, and nitrogen, dN…M+, respectively. These geometrical parameters are listed in Figure 6, reading counterclockwise and starting at the uppermost halogen bond. Comparison with the halogen bond distances and angles of the complexes discussed in the previous section reveals the complete disruption of one of the halogen bonds with halogen bond distances that are substantially larger and well beyond the sum of the N and I van der Waals radii. The related C-I···N angles are also significantly reduced. The other two halogen bonds remain with minor perturbations, as reflected in small changes in distances and angles. With respect to the metal-ion-to-nitrogen distance, dN…M+, Table 5 shows that only one nitrogen atom is effectively binding the metal ion, while the other two nitrogen atoms appear too far away from the metal ion. Similarly, one of the iodine atoms, the one opposite to the nitrogen binding the metal ion, appears substantially far away from the metal ion, suggesting that its contribution to complex formation is relatively small or even negligible when compared with the other two iodine atoms. Interestingly, the smallest dI…M+ values involve the iodine for which the halogen bond interaction was severely disrupted.
The BSSE-corrected metal ion complexation energies, CE, are listed in Table 6. The I···M+ and N···M+ interactions result in complexation energies that are between 9.33 and 10.36 kcal/mol more negative than those involving only I···M+ interactions (see Table 2). More specifically, the percent change in the CE listed in Table 6 relative to those listed in Table 2 tends to increase with the size of the metal ion, as 14% < 17% < 25% < 26%. These percent changes get much smaller, however, when the deformation energies, ΔEdef, are factored in. Indeed, a reduction by a factor of two or more is seen in these percent changes with a similar qualitative trend: 7% < 8% < 10% < 11% for Li+, Na+, Rb+, and K+, respectively. These values correspond to interaction energies that are 4.88, 4.45, 4.21, and 3.63 kcal/mol more negative than those listed in Table 2, respectively. Although the complexation energies are more favorable, these results underscore the large geometrical deformation that the macrocyclic ligand needs to undergo to facilitate the participation of a nitrogen atom lone pair in the binding of the metal ion. For comparison, the deformation energies calculated for the complexes formed via only I···M+ interactions were much smaller (see Table 2). These smaller deformation energies are consistent with the preorganized geometry of the macrocyclic ligand for the binding of the metal ion via the iodine atoms.
Table 7 lists the second-order NBO delocalization energies, E2, associated with both the intramolecular halogen bonds, C-I···N, and the intermolecular interaction between the halogen atoms of the ligand and the metal ion, I···M+; also listed are the NBO delocalization energies associated with the charge transfer from the nitrogen atom lone pair into the anti-lone pair orbital of the metal ion, nN → lp*M+. Specifically, regarding the E2 values of the N···M+ interactions, Table 7 reveals the involvement of primarily one of the three nitrogen atoms in the ligand. The participation of the other two nitrogen atoms tends to increase with the size of the metal ion, which brings about a reduction in the corresponding N···M+ distances. Accordingly, the percent contribution to the total E2 of the N···M+ interactions for the most involved nitrogen decreases as 100% < 93% < 76% < 72% for Li+, Na+, K+, and Rb+, respectively. Upon comparison with the E2 values for each of the three halogen bonds in Table 3, it is immediately apparent that one of them has vanished (E2 values of 0.00 kcal/mol). Of the two C-I···N halogen bonds remaining, one has been strengthened while the other has been weakened significantly. It is worth noting that the weakening of the halogen bond occurs to a larger extent than the strengthening of the other halogen bond. The actual difference depends on the metal ion. Accordingly, the largest difference is seen for Li+, with an E2 increase of about 6% in one of the halogen bonds and a decrease of about 47% for the other one. The smallest difference is seen for Na+, with an increase of about 44% and a decrease of 47% for the pertinent halogen bonds. The results for K+ and Rb+ are more similar, with respective increases in E2 of 28% and 23%. The corresponding decreases in E2 for K+ and Rb+ are 49% and 47%, respectively. Thus, these results indicate that the participation of the nitrogen atom in binding the metal ion produces an overall weakening of the halogen-bonded network, though the effect is different for each of the three C-I···N interactions in the network. Regarding the I···M+ interactions, the respective E2 values are smaller than those listed in Table 3 for Li+ and Na+. That is, the participation of the nitrogen atoms in binding the metal ion also tends to weaken these I···M+ interactions. The extent of the weakening effect, however, varies with the metal ion. For example, for Li+, the E2 value involving the iodine atom that no longer participates in halogen bonding is reduced by about 13%, while the E2 values for the I···M+ interactions involving the other two iodine atoms are reduced substantially, by 47% and 94%, respectively. In the case of Na+, the largest reduction of the E2 values is about 60%, while the smaller reductions are about 17% and 18%, respectively. In contrast, for the larger metal ions, K+ and Rb+, Table 7 shows E2 values for their I···M+ interactions that are consistently larger than those listed in Table 3. The percent increase of these E2 values for K+ follows the order of 5% < 12% < 34%. The percent changes are even more pronounced in the largest of the metal ions considered, Rb+, following the increasing sequence 36% < 47% < 71%.
Table 8 lists the electron density value at each of the bond critical points along the path between the metal ion and each of the halogen and nitrogen atoms participating in its complexation. Based solely on bond critical points, Table 8 reveals that just one of the three nitrogen atoms is involved in the binding of the metal ion, as no critical points were found connecting either of the other two nitrogen atoms to the metal ion. This contrasts with the NBO analysis that led to some minor contributions to the second-order delocalization energies by the other two nitrogen atoms in the ligand. It is also apparent that the ρN…M+ value declines with the size of the metal ion. Relative to Li+, the magnitude of the decline in ρN…M+ increases as 19% < 44% < 46% for Na+, K+, and Rb+, respectively. Regarding the interactions of the metal ion with each of the iodine atoms, the electron densities at each of these bond critical points, ρC-I…M+, shown in Table 8, are generally smaller than those listed in Table 4 for the complex involving only this type of metal ion binding interactions. That is, the participation of the nitrogen atoms in binding the metal ion weakens the I···M+ interactions, as already made evident by the NBO analysis. The weakening of the I···M+ interactions is not uniform, however. For example, the I···M+ interaction involving the iodine atom displaced by the metal ion and no longer participating in the halogen bond to any significant extent is the least affected. The most affected I···M+ interaction involves the iodine atom participating in the C-I···N halogen bond that is opposite to the N···M+ metal binding interaction.
In addition to the bond critical point densities associated with the halogen-metal ion and nitrogen-metal ion interactions, Table 8 shows the bond critical point densities at each of the three halogen bonds in the macrocycle. A comparison with the ρC-I…N values for each of these three halogen bonds in Table 4 makes it clear that one of them has vanished or severely weakened (with negligible ρC-I…N values). Of the two C-I···N halogen bonds remaining, one has been strengthened, while the other has been weakened significantly. These results mirror those found based on the E2 values for each of the three halogen bonds discussed previously. For example, the weakening of the halogen bond seems larger than the strengthening of the other halogen bond, as also indicated based on the trends in the related changes of E2 values. Thus, these results support the notion that the participation of the nitrogen atom in binding the metal ion brings about an overall weakening of the halogen-bonded network.

2.4. Transition State Geometries and Barrier Heights

The ability of the macrocyclic ligand to bind an alkali metal ion in at least two different modes makes it relevant to find the transition state structure that links these binding modes. Once the optimized geometries of the transition state structures are found, the corresponding energy barriers that need to be overcome for the metal ion complex to transition from one binding mode to the other can be readily calculated. Accordingly, a geometry optimization was conducted to find the transition state structure linking the two binding modes for each of the alkali metal ions considered. The optimized geometries of the transition state structures are shown in Figure 7A–D. The presence of a single imaginary frequency in each case confirms their nature as saddle points of the first order. One striking feature in Figure 7 is the closeness between the metal ion and one of the nitrogen atoms in the macrocycle (seen by the dashed lines). It also appears that the interactions of each iodine atom with the metal ion are still present in the transition structures (shown as dashed lines). Figure 7 shows how, as expected, the metal ion is gradually further away from the center of the macrocycle cavity as the metal ion size increases.
The energy cost associated with the complex structure transition from one mode of binding to the other is examined by calculating the Gibbs free energies of the three pertinent structures: the more stable complex binding the metal ion via both I···M+ and N···M+ interactions, the less stable complex binding the metal ion solely through the I···M+ interactions, and the transition state structure linking these two stable complexes. The Gibbs free energy barrier, in kcal/mol, was calculated for each metal ion relative to the more stable complex (ΔG1ǂ), and relative to the less stable complex (ΔG2ǂ). In terms of the metal ion, the results shown in Table 9 indicate that the largest ΔG1ǂ occurs for Li+ (8.36 kcal/mol), while for the larger metal ions, the ΔG1ǂ values are closer to one another, between 6.1 and 7.0 kcal/mol. With respect to ΔG2ǂ, all values are much smaller than their ΔG1ǂ counterparts, and in the 1.6 to 1.9 kcal/mol range. The difference between ΔG1ǂ and ΔG1ǂ provides a convenient way to determine the relative Gibbs free energy between the complexes representing the two different modes of binding the metal ion. The results in Table 9 show that the Gibbs free difference between these two types of complexes are not too large, in fact standing between 4.46 kcal/mol for the Rb+ complexes and 6.46 kcal/mol for Li+ complexes.
Table 10 displays relevant geometrical parameters for all the transition state structures: the halogen bond distances, dC-I…N, and angles, AC-I…N, as well as the distances from the metal ion to iodine, dI…M+, and nitrogen, dN…M+, respectively. These geometrical parameters are listed in Figure 7, reading counterclockwise and starting at the uppermost halogen bond. Cross-examination with the parameters listed in Table 1, for the less stable complexes, shows that the halogen bond distances in the transition state structures become, on average, slightly longer. These halogen bond elongations are in tandem with small reductions in the halogen bond angles. Thus, the weakening of the halogen bonds as the complex transition from the less stable binding mode to the more stable one appears to be emerging, though still far from what is noted in the more stable complex. It is also found that, on average, the dI…M+ values in the transition state structures remain close to those in the less stable complex. These results are consistent with the transition state structures lying much closer in energy to the less stable complex, implying that their geometries are also not too far from one another. Further evidence that the transition state geometries are closer to those of the less stable complexes rather than to those of the more stable ones can be seen by cross-comparison of the dN…M+ values with those in Table 5. Regarding the nitrogen atom most responsible for M+ binding, the dN…M+ values in the transition state structures, for example, are still much longer than those in their more stable counterparts. The percent difference in dN…M+ declines with the size of the metal ion as 46% < 39% < 32% < 30% for Li+, Na+, K+, and Rb+, respectively.

3. Computational Methods

All calculations were performed with the M05-2X/DGDZVP model using the Gaussian 16 program [69]. The DFT model employed here has been shown to be adequate and cost-effective for studying intermolecular interactions, especially the halogen bonding of relatively large systems [70,71,72,73,74,75]. The geometries for all systems were fully optimized and their nature as minima or transition state structures was determined by the absence or presence of imaginary frequencies resulting from the corresponding frequency calculations. Calculated binding energies for all complexes were corrected for basis set superposition error (BSSE) [76]. Additional insight into the strength of the halogen bond interactions and the various metal ion-ligand interactions was gained by carrying out analyses based on the theory of atoms in molecules, AIM [77,78,79,80], and natural bond orbital, NBO, analysis [81]. Gibbs free energy barriers were calculated for the transition from the less stable to the more stable metal ion complexes using the optimized geometries of the minima and related transition state structures. The calculations in this study are for all the systems in the gas phase. Thus, the insights gained pertain solely to the intrinsic interactions between the metal ion and the macrocyclic ligand in the absence of any solvent molecules or counterions.

4. Summary and Future Perspectives

In this study, the ability of a model macrocycle to host an alkali metal cation in two different modes was demonstrated computationally. The proposed macrocycle is a planar molecule of C3h symmetry possessing a central cavity enclosed by a network of three C-I···N halogen bonds. In one mode, the metal ion is attracted to the electron-rich region generated by the lone pair of each halogen atom. Here, Li+ sits at the center of the host’s cavity, while the larger ions sit above it. The magnitudes of the complexation energies are significant and decline with increasing size of the metal ion. Interestingly, the halogen bonds are not only retained but also strengthened upon binding the metal ion in this mode. In the other mode, the metal ion disrupts one of the C-I···N halogen bonds effectively to replace it with a direct interaction of the metal ion and the lone pair of the nitrogen atom, N···M+. The other two halogen bonds are somewhat weakened though not destroyed. In this mode, both N···M+ and I···M+ interactions are responsible for binding the metal ion. Moreover, the magnitudes of the complexation energies are just a few kcal/mol larger than those involving only the I···M+ binding interaction mode. Lastly, the geometries for the transition state structures linking the less stable to the more stable metal ion complexes were obtained, and their calculated Gibbs free energy barriers were found in the range of 1.6 to 1.9 kcal/mol. Also, the calculated Gibbs free energy differences between the two types of metal ion complexes were found in the range of 4.5 to 6.5 kcal/mol.
The results presented here are expected to spark interest in the scientific community, particularly in the field of supramolecular chemistry, to further validate and generalize the results through relevant experimental work and additional computational studies. At the fundamental level, for example, it would be of interest to examine in more detail the relative strength and nature of both the N···M+ and the I···M+ interactions responsible for binding the metal ion by the proposed macrocycle. That is, in addition to the electron density at bond critical points and the NBO second-order delocalization energies presented here, future work should include a more in-depth analysis such as breaking down the interaction energies into various components, as done in the energy decomposition analysis approach or the interacting quantum fragment approach [67,68]. A comprehensive investigation of the conformational space of the macrocycle ligand would be important to determine whether a stable conformation that could bind the metal ion with two or even all three nitrogen atoms exists. The examination of solvent effects on the metal ion binding geometries and energies is likewise an area of future research work that should be undertaken. For example, the effect of solvent polarity on the free energies of solvation of both the cation and the macrocyclic ligand should be explored. Moreover, the explicit presence of a counterion is to be examined in terms of its interactions with the solvent and the metal ion, and the impact on the binding ability of the ligand. Similarly, the use of a different structural motif to build the macrocycle ligand should also be examined. One possibility would be to replace the cyclopenta[b]pyrrole motif [82,83] with benzimidazole, which will change the cyclopentadiene ring with a benzene ring [84,85], or with azapentalene, which will retain the notion of two fused 5-membered rings with the potential for increasing the number of nitrogen atoms [86,87]. Lastly, considering stronger N-I···N halogen bonds for the intramolecular halogen-bonded network in the host remains the subject of future work.

Funding

This research received no external funding.

Data Availability Statement

Data are contained within the article.

Acknowledgments

The author is grateful to the Department of Chemistry and Biochemistry at DePaul University for its continuing support.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Dembitsky, V.M. Natural polyether ionophores and their pharmacological profile. Mar. Drugs 2022, 20, 292. [Google Scholar] [CrossRef] [PubMed]
  2. Tsukube, H. Cation binding by natural and modified ionophores: From natural ionophore to synthetic ionophore. In Cation Binding by Macrocycles; Routledge: London, UK, 2018; pp. 497–522. [Google Scholar]
  3. Chock, P.B.; Titus, E.O. Alkali metal ion transport and biochemical activity. In Current Research Topics in Bioinorganic Chemistry; John Wiley and Sons: Hoboken, NJ, USA, 2009; Volume 18, pp. 287–370. [Google Scholar]
  4. Lehninger, A.L. Role of metal ions in enzyme systems. Physiol. Rev. 1950, 30, 393–429. [Google Scholar] [CrossRef] [PubMed]
  5. Milan, V.; Schnabl, J. Sodium and potassium ions in proteins and enzyme catalysis. In The Alkali Metal Ions: Their Role for Life; Springer Nature: Berlin/Heidelberg, Germany, 2016; pp. 259–290. [Google Scholar]
  6. Andreini, C.; Bertini, I.; Cavallaro, G.; Holliday, G.L.; Thornton, J.M. Metal ions in biological catalysis: From enzyme databases to general principles. J. Biol. Inorg. Chem. 2008, 13, 1205–1218. [Google Scholar] [CrossRef] [PubMed]
  7. Lumetta, G.J.; Rapko, B.M.; Garza, P.A.; Hay, B.P.; Gilbertson, R.D.; Weakley, T.J.R.; Hutchison, J.E. Deliberate design of ligand architecture yields dramatic enhancement of metal ion affinity. J. Am. Chem. Soc. 2002, 124, 5644–5645. [Google Scholar] [CrossRef] [PubMed]
  8. Burk, P.; Sults, M.L.; Tammiku-Taul, J. Comparative calculations of alkali metal cation basicities of some Lewis bases. Proc. Est. Acad. Sci. Chem. 2007, 56, 107–121. [Google Scholar] [CrossRef]
  9. McMahon, T.B.; Ohanessian, G.A. An experimental and ab initio study of the nature of the binding in gas-phase complexes of sodium ions. Chem. Eur. J. 2000, 6, 2931–2941. [Google Scholar] [CrossRef] [PubMed]
  10. Dougherty, D.A. The cation-π interaction. Acc. Chem. Res. 2013, 46, 885–893. [Google Scholar] [CrossRef] [PubMed]
  11. Gokel, G.W.; Negin, S. The Supramolecular Alkali Metal Cation–p Interaction. In Comprehensive Supramolecular Chemistry II; Elsevier: Amsterdam, The Netherlands, 2017; pp. 103–120. [Google Scholar]
  12. Steed, J.W.; Atwood, J.L. Supramolecular Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
  13. Istemi, K.; Krummenacher, I.; Meyer, J.; Armbruster, F.; Breher, F. Multidentate ligand systems featuring dual functionality. Dalton Trans. 2008, 43, 5836–5865. [Google Scholar]
  14. Guedes, I.A.; de Magalhães, C.S.; Dardenne, L.E. Receptor–ligand molecular docking. Biophys. Rev. 2014, 6, 75–87. [Google Scholar] [CrossRef]
  15. Ali, S.M.; Maity, D.K.; De, S.; Shenoi, M.R.K. Ligands for selective metal ion extraction: A molecular modeling approach. Desalination 2008, 232, 181–190. [Google Scholar] [CrossRef]
  16. Hancock, R.D.; Wade, P.W.; Ngwenya, M.P.; De Sousa, A.S.; Damu, K.V. Ligand design for complexation in aqueous solution. 2. Chelate ring size as a basis for control of size-based selectivity for metal ions. Inorg. Chem. 1990, 29, 1968–1974. [Google Scholar] [CrossRef]
  17. Lynn, S.E. More on the chelate effect. J. Chem. Educ. 1979, 56, 578–579. [Google Scholar]
  18. Frausto da Silva, J.J.R. The chelate effect redefined. J. Chem. Educ. 1983, 60, 390–392. [Google Scholar] [CrossRef]
  19. Arkajyoti, S.; Seitz, A.; Merz Jr, K.M. Simulating the chelate effect. J. Am. Chem. Soc. 2018, 140, 15166–15169. [Google Scholar]
  20. Hancock, R.D.; Martell, A.E. The chelate, cryptate and macrocyclic effects. Comments Inorg. Chem. 1988, 6, 237–284. [Google Scholar] [CrossRef]
  21. Bhake, A.B.; Shastri, S.S.; Limaye, N.M. A review on macrocyclic complexes. Chem. Sci. Rev. Lett. 2014, 2, 449–455. [Google Scholar]
  22. Varnek, A.; Wipff, G.; Solov’e, V.P.; Solotnov, A.F. Assessment of the macrocyclic effect for the complexation of crown-ethers with alkali cations using the substructural molecular fragments method. J. Chem. Inf. Comput. Sci. 2002, 42, 812–829. [Google Scholar] [CrossRef] [PubMed]
  23. Pedersen, C.J. The discovery of crown ethers (Noble Lecture). Angew. Chem. Int. Ed. Engl. 1988, 27, 1021–1027. [Google Scholar] [CrossRef]
  24. Bradshaw, J.S.; Izatt, R.M. Crown ethers: The search for selective ion ligating agents. Acc. Chem. Res. 1997, 30, 338–345. [Google Scholar] [CrossRef]
  25. Iklima, O.; Tamm, S.; Herrmann, C.; Abetz, V. Lithium selectivity of crown ethers: The effect of heteroatoms and cavity size. Sep. Purif. Technol. 2022, 294, 121142. [Google Scholar]
  26. Al-Kahtani, A.A.; Al-Jallal, N.A.; El-Azhary, A.A. Conformational and vibrational analysis of 18-crown-6–alkali metal cation complexes. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2014, 132, 70–83. [Google Scholar] [CrossRef]
  27. Fabbrizzi, L. The origins of the coordination chemistry of alkali metal ions. ChemTexts 2020, 6, 10. [Google Scholar] [CrossRef]
  28. Poonia, N.; Bajaj, A. Coordination chemistry of alkali and alkaline earth cations. Chem. Rev. 1979, 79, 389–445. [Google Scholar] [CrossRef]
  29. Kim, Y.; Nguyen, T.T.T.; Churchill, D.G. Bioinorganic chemistry of the alkali metal ions. In The Alkali Metal Ions: Their Role for Life. Metal Ions in Life Sciences; Sigel, A., Sigel, H., Sigel, R., Eds.; Springer Nature: Berlin/Heidelberg, Germany, 2016; Volume 16, pp. 1–10. [Google Scholar]
  30. Gang, W.; Zhu, J. NMR studies of alkali metal ions in organic and biological solids. Prog. Nucl. Magn. Reson. Spectrosc. 2012, 61, 1–70. [Google Scholar]
  31. Takashi, N.; Masaoka, T.; Yoshikawa, Y.; Sadakane, K.; Kenmotsu, T.; Schiessel, H.; Yoshikawa, K. Markedly Different Effects of Monovalent Cations on the Efficiency of Gene Expression. Adv. Biol. 2023, 7, 2200164. [Google Scholar]
  32. Thomas, G.X.; Mulvey, R.E. Alkali—Metal Mediation: Diversity of Applications in Main—Group Organometallic Chemistry. Angew. Chem. Int. Ed. 2021, 60, 9247–9262. [Google Scholar]
  33. Smith, J.D. Phosphanides of the Heavier Alkali Metals. Angew. Chem. Int. Ed. 1998, 37, 2071–2073. [Google Scholar] [CrossRef]
  34. Davison, N.; Erli, L. The quest for organo-alkali metal monomers: Unscrambling the structure–reactivity relationship. Dalton Trans. 2023, 52, 8172–8192. [Google Scholar] [CrossRef]
  35. Truter, M.R. Structures of organic complexes with alkali metal ions. In Alkali Metal Complexes with Organic Ligands; Springer: Berlin/Heidelberg, Germany, 2005; pp. 71–111. [Google Scholar]
  36. Li, S.; Wang, C.; Luo, Z.; Zhu, X. Investigation on the catalytic behavior of alkali metals and alkaline earth metals on the biomass pyrolysis assisted with real-time monitoring. Eng. Fuels 2020, 34, 12654–12664. [Google Scholar] [CrossRef]
  37. Ochoa, E.L.M. Lithium as a neuroprotective agent for bipolar disorder: An overview. Cell. Mol. Neurobiol. 2022, 42, 85–97. [Google Scholar] [CrossRef]
  38. Kudryavtsev, P. Lithium in nature, application, methods of extraction. Sci. Isr. Technol. Advant. 2016, 18, 63–83. [Google Scholar]
  39. Arkady, P.S.; Calahorro, F.; Walker, R.J. Na+/K+-pump and neurotransmitter membrane receptors. Invertebr. Neurosci. 2019, 19, 1. [Google Scholar]
  40. Shrivastava, A.N.; Triller, A.; Melki, R. Cell biology and dynamics of Neuronal Na+/K+-ATPase in health and diseases. Neuropharmacology 2020, 169, 107461. [Google Scholar] [CrossRef] [PubMed]
  41. Jiří, B.; Spiwok, V.; Kmoníčková, E.; Rimpelová, S. Na+/K+-ATPase revisited: On its mechanism of action, role in cancer, and activity modulation. Molecules 2021, 26, 1905. [Google Scholar] [CrossRef] [PubMed]
  42. Forrest, M.D. The sodium-potassium pump is an information processing element in brain computation. Front. Physiol. 2014, 5, 117222. [Google Scholar] [CrossRef] [PubMed]
  43. Xiao, S.; Li, X.; Li, T.S.; Xiang, Y.; Chen, J.S. Practical strategies for enhanced performance of anode materials in Na+/K+-ion batteries. J. Mater. Chem. A 2021, 9, 7317–7335. [Google Scholar] [CrossRef]
  44. Ik-Hwan, U.; Cho, H.-J.; Kim, M.-Y.; Buncel, E. Alkali-Metal Ion Catalysis and Inhibition in SNAr Displacement: Relative Stabilization of Ground State and Transition State Determines Catalysis and Inhibition in SNAr Reactivity. Chem. Eur. J. 2014, 20, 13337–13344. [Google Scholar]
  45. Shokoufeh, R.; Santos, K.T.; Angelucci, C.A.; Wittstock, G. Catalytic activity of alkali metal cations for the chemical oxygen reduction reaction in a biphasic liquid system probed by scanning electrochemical microscopy. Chem. Eur. J. 2020, 26, 10882–10890. [Google Scholar]
  46. Patel, C.K.; Banerjee, S.; Kant, K.; Sengupta, R.; Aljaar, N.; Malakar, C.C. Roles of Alkali Metals tert-Butoxide as Catalysts and Activators in Organic Transformations. Asian J. Org. Chem. 2023, 12, e202300311. [Google Scholar] [CrossRef]
  47. Li, J.; Stoumpos, C.C.; Trimarchi, G.G.; Chung, I.; Mao, L.; Chen, M.; Wasielewski, M.R.; Wang, L.; Kanatzidis, M.G. Air-stable direct bandgap perovskite semiconductors: All-inorganic tin-based heteroleptic halides AxSnClyIz (A = Cs, Rb). Chem. Mater. 2018, 30, 4847–4856. [Google Scholar] [CrossRef]
  48. Zhang, Y.; Wang, X.; Luo, B.; Xia, Y. Density functional theory study of the bis-3-benzo-crown ethers and their complexes with alkali metal cations Na+, K+, Rb+ and Cs+. J. Phys. Org. Chem. 2012, 25, 222–229. [Google Scholar] [CrossRef]
  49. Friedrich, D.; Byun, H.R.; Hao, S.; Patel, S.; Wolverton, C.; Jang, J.I.; Kanatzidis, M.G. Layered and Cubic Semiconductors A Ga M′ Q 4 (A+ = K+, Rb+, Cs+, Tl+; M′ 4+ = Ge4+, Sn4+; Q2– = S2–, Se2–) and High Third-Harmonic Generation. J. Am. Chem. Soc. 2020, 142, 17730–17742. [Google Scholar] [CrossRef] [PubMed]
  50. Suhang, H.; Huang, B.; Xiao, B.; Chang, S.; Podalko, M.; Nau, W.M. Stabilization of Guest Molecules inside Cation-Lidded Cucurbiturils Reveals that Hydration of Receptor Sites Can Impede Binding. Angew. Chem. Int. Ed. 2023, 62, e202313864. [Google Scholar]
  51. Messiha, F.S. Lithium, rubidium and cesium: Cerebral pharmacokinetics and alcohol interactions. Pharmacol. Biochem. Behav. 1984, 21, 87–92. [Google Scholar] [CrossRef] [PubMed]
  52. Bondarev, N.V. Computer analysis of stability of cation complexes with ionophore antibiotics. Russ. J. Gen. Chem. 2020, 90, 1474–1482. [Google Scholar] [CrossRef]
  53. Berger, G.; Frangville, P.; Meyer, F. Halogen bonding for molecular recognition: New developments in materials and biological sciences. Chem. Commun. 2020, 56, 4970–4981. [Google Scholar] [CrossRef] [PubMed]
  54. Shan, H.; Zhou, L.; Ji, W.; Zhao, A. Flexible Alkali–Halogen Bonding in Two Dimensional Alkali-Metal Organic Frameworks. J. Phys. Chem. Lett. 2021, 12, 10808–10814. [Google Scholar] [CrossRef] [PubMed]
  55. Carreras, L.; Benet-Buchholz, J.; Franconetti, A.; Frontera, A.; van Leeuwen, P.W.; Vidal-Ferran, A. Halogen bonding effects on the outcome of reactions at metal centres. Chem. Commun. 2019, 55, 2380–2383. [Google Scholar] [CrossRef] [PubMed]
  56. Zheng, B.; Zhou, F.; Liu, Y.; Wang, Z.; Liu, Y.; Ding, X. Halogen bonds and metal bonds involving superalkalies M2OCN/M2NCO (M = Li, Na) complexes. Struct. Chem. 2019, 30, 965–977. [Google Scholar] [CrossRef]
  57. Zarina, B.M.; Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Bokach, N.A.; Kukushkin, V.Y. Electrophilic–nucleophilic dualism of nickel (II) toward Ni··· I noncovalent interactions: Semicoordination of iodine centers via electron belt and halogen bonding via σ-hole. Inorg. Chem. 2017, 56, 13562–13578. [Google Scholar]
  58. Lev, Z.E.; Eliseeva, A.A.; Baykov, S.V.; Suslonov, V.V.; Galmés, B.; Frontera, A.; Kukushkin, V.Y.; Ivanov, D.M.; Bokach, N.A. Electron belt-to-σ-hole switch of noncovalently bound iodine (I) atoms in dithiocarbamate metal complexes. Inorg. Chem. Front. 2021, 8, 2505–2517. [Google Scholar]
  59. Frenio, A.R.; Kropman, A.; Müller, C.; Zewge, S.E.; Beckers, H.; Paulus, B.; Riedel, S. Theoretical investigation of the structures, stabilities and vibrational properties of triatomic interhalide ions and their alkali ion pairs. J. Fluor. Chem. 2018, 216, 81–88. [Google Scholar]
  60. Parra, R.D. Concerted halogen bonding and orthogonal metal-halogen interactions in dimers of lithium formamidinate and halogenated formamidines: An ab Initio study. Molecules 2014, 19, 1069–1084. [Google Scholar] [CrossRef] [PubMed]
  61. Parra, R.D. Metal–ion binding by cyclic halogen-bonded structures: A theoretical study using M–(BrZ)4 clusters (Z = F or NH2; M = Li+, Na+, or Mg2+). Chem. Phys. Lett. 2015, 637, 177–181. [Google Scholar] [CrossRef]
  62. Parra, R.D. Metal-ion binding via a cyclic network of intramolecular halogen-bonded interactions: A theoretical study. Mol. Phys. 2016, 114, 1485–1493. [Google Scholar] [CrossRef]
  63. Parra, R.D.; Castillo, A. Cyclic networks of halogen-bonding interactions in molecular self-assemblies: A theoretical N—X· · · N versus C—X· · · N investigation. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2017, 73, 179–187. [Google Scholar] [CrossRef] [PubMed]
  64. Parra, R.D. Halogen-Bonded Driven Tetra-Substituted Benzene Dimers and Trimers: Potential Hosts for Metal Ions. Sci 2022, 4, 9. [Google Scholar] [CrossRef]
  65. Parra, R.D. A Model Halogen-Bonded Network as a Potential Tube-like Host for Li+: A DFT Study. Inorganics 2023, 12, 16. [Google Scholar] [CrossRef]
  66. Popelier, P. Atoms in Molecules: An Introduction; Prentice Hall: Manchester, UK, 2000. [Google Scholar]
  67. Zhao, L.; von Hopffgarten, M.; Andrada, D.M.; Frenking, G. Energy decomposition analysis. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1345. [Google Scholar] [CrossRef]
  68. Popelier, P. Non-covalent interactions from a Quantum Chemical Topology perspective. J. Mol. Model. 2022, 28, 276. [Google Scholar] [CrossRef]
  69. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  70. Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theor. Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef] [PubMed]
  71. Zhao, Y.; Truhlar, D.G. Density functionals for noncovalent interaction energies of biological importance. J. Chem. Theor. Comput. 2007, 3, 289–300. [Google Scholar] [CrossRef] [PubMed]
  72. Hohenstein, E.G.; Chill, S.T.; Sherrill, C.D. Assessment of the Performance of the M05−2X and M06−2X Exchange-Correlation Functionals for Noncovalent Interactions in Biomolecules. J. Chem. Theor. Comput. 2008, 4, 1996–2000. [Google Scholar] [CrossRef] [PubMed]
  73. Zhang, Y.; Ma, N.; Wang, W. Assessment of the performance of the M05-class and M06-class functionals for the structure and geometry of the hydrogen-bonded and halogen-bonded complexes. J. Theor. Comput. Chem. 2012, 11, 1165–1173. [Google Scholar] [CrossRef]
  74. Siiskonen, A.; Priimagi, A. Benchmarking DFT methods with small basis sets for the calculation of halogen-bond strengths. J. Mol. Model. 2017, 23, 50. [Google Scholar] [CrossRef] [PubMed]
  75. Elric, E.; Reinhard, D.; Huber, S.M. Is There a Single Ideal Parameter for Halogen-Bonding-Based Lewis Acidity? Chem. Eur. J. 2020, 26, 3843–3861. [Google Scholar]
  76. Boys, S.F.; Bernardi, F. Calculation of small molecular interactions by differences of separate total energies—Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
  77. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  78. Zou, J.-W.; Lu, Y.-X.; Yu, Q.-S.; Zhang, H.-X.; Jiang, Y.-J. Halogen bonding: An AIM analysis of the weak interactions. Chin. J. Chem. 2006, 24, 1709–1715. [Google Scholar] [CrossRef]
  79. Biegler-König, F.; Schönbohm, J.; Bayles, D. AIM2000—A program to analyze and visualize atoms in molecules. J. Comput. Chem. 2001, 22, 545–554. [Google Scholar]
  80. Keith, T.A. AIMAll, Version 13.11.04; TK Gristmill Software: Overland Park, KS, USA, 2013. [Google Scholar]
  81. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor–acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  82. Yang, X.; Wu, K.; Wu, P.; Chen, J.; Sun, C.; Yu, Z. Brønsted Acid-Mediated Annulation of a-Oxo Ketene Dithioacetals with Pyrroles: Efficient Synthesis of Structurally Diverse Cyclopenta[b]pyrroles. Chem. Eur. J. 2015, 21, 9323–9327. [Google Scholar] [CrossRef] [PubMed]
  83. Heffernan, M.L.; Fang, Q.K.; Foglesong, R.J.; Hopkins, S.C.; Ogbu, C.O.; Soukri, M.; Spear, K.L. Preparation of Fused Pyrrole Derivatives as Inhibitors of D-Amino acid Oxidase. U.S. Patent 7,902,252, 8 March 2011. [Google Scholar]
  84. Mohd, F.; Rathaur, A.; Pandey, A.; Singh, V.K.; Tiwari, A.K. A review on the modern synthetic approach of benzimidazole candidate. ChemistrySelect 2020, 5, 3981–3994. [Google Scholar]
  85. Hernández-López, H.; Tejada-Rodríguez, C.J.; Leyva-Ramos, S. A panoramic review of benzimidazole derivatives and their potential biological activity. Mini-Rev. Med. Chem. 2022, 22, 1268–1280. [Google Scholar] [CrossRef]
  86. Reyhangul, A.; Kerim, A. A study on the aromaticity and magnetotropicity of 10π-electron azapentalene derivatives. Chem. Phys. Lett. 2012, 546, 144–149. [Google Scholar]
  87. Chandana, P.; Barik, P.; Ali, S.A.; Nayak, D.S.; Ikbal, M.; Mandal, A.; Jana, R.; Giri, S.; Samanta, S. Recent synthetic journey on pyrrole-fused compounds. New J. Chem. 2023, 47, 6476–6527. [Google Scholar]
Inorganics 12 00161 sch001
Scheme 1. Graphical representation of the ability of a halogen atom, X, in a covalent bond D-X, to act both as an electrophile receiving electron density from a halogen bond acceptor, A, and as a nucleophile providing perpendicularly electron density to an electron-deficient species like a metal ion, M+.
Scheme 1. Graphical representation of the ability of a halogen atom, X, in a covalent bond D-X, to act both as an electrophile receiving electron density from a halogen bond acceptor, A, and as a nucleophile providing perpendicularly electron density to an electron-deficient species like a metal ion, M+.
Inorganics 12 00161 sch001
Inorganics 12 00161 g001
Figure 1. Optimized geometry of the structure of the model intramolecular halogen-bonded macrocycle with C3h symmetry. Dashed lines represent C-I···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), and purple (I).
Figure 1. Optimized geometry of the structure of the model intramolecular halogen-bonded macrocycle with C3h symmetry. Dashed lines represent C-I···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), and purple (I).
Inorganics 12 00161 g001
Inorganics 12 00161 g002aInorganics 12 00161 g002b
Figure 2. Solid (top) and transparent (bottom) views of the M05-2X/DGDZVP molecular electrostatic potential at the 0.001-au molecular surface of the model macrocycle ligand. Red areas represent the most negative potential and blue areas the most positive ones. Dashed lines (bottom view) represent C-I···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), and purple (I).
Figure 2. Solid (top) and transparent (bottom) views of the M05-2X/DGDZVP molecular electrostatic potential at the 0.001-au molecular surface of the model macrocycle ligand. Red areas represent the most negative potential and blue areas the most positive ones. Dashed lines (bottom view) represent C-I···N halogen bonds. The color representation is as follows: white (H), gray (C), blue (N), and purple (I).
Inorganics 12 00161 g002aInorganics 12 00161 g002b
Inorganics 12 00161 g003
Figure 3. Top view (A) and side view (B) of the optimized geometries of the Li+ complex with the macrocycle ligand showing the metal ion sitting at the center of symmetry of the ligand. The corresponding geometries of the complexes with the larger alkali metal ions, Na+, K+, and Rb+ ions show the metal ions sitting off the plane of the ligand, as seen for the Rb+ top (C) and side view (D). Dashed lines represent C-I···N halogen bonds and I···M+ binding interactions. The color representation is as follows: white (H), gray (C), blue (N), light pink (Li+), dark pink (I), and purple (Rb+).
Figure 3. Top view (A) and side view (B) of the optimized geometries of the Li+ complex with the macrocycle ligand showing the metal ion sitting at the center of symmetry of the ligand. The corresponding geometries of the complexes with the larger alkali metal ions, Na+, K+, and Rb+ ions show the metal ions sitting off the plane of the ligand, as seen for the Rb+ top (C) and side view (D). Dashed lines represent C-I···N halogen bonds and I···M+ binding interactions. The color representation is as follows: white (H), gray (C), blue (N), light pink (Li+), dark pink (I), and purple (Rb+).
Inorganics 12 00161 g003
Inorganics 12 00161 g004
Figure 4. Linear relationship between the magnitude of the complexation energy, |CE|, and the halogen metal ion distance, dI…M+, top view (A); and the corresponding linear relationship between the magnitude of the complexation energy, |CE|, and the distance of the metal ion from the center of the plane formed by the three halogen atoms, dc…M+, bottom view (B). The equation of best fit line for A is |CE| = −34.614 kcal/(mol Å) dI…M+ + 162.99 kcal/mol with R2 = 0.98. The equation of best fit line for B is |CE| = −12.914 kcal/(mol Å) dc…M+ + 68.77 kcal/mol with R2 = 0.99.
Figure 4. Linear relationship between the magnitude of the complexation energy, |CE|, and the halogen metal ion distance, dI…M+, top view (A); and the corresponding linear relationship between the magnitude of the complexation energy, |CE|, and the distance of the metal ion from the center of the plane formed by the three halogen atoms, dc…M+, bottom view (B). The equation of best fit line for A is |CE| = −34.614 kcal/(mol Å) dI…M+ + 162.99 kcal/mol with R2 = 0.98. The equation of best fit line for B is |CE| = −12.914 kcal/(mol Å) dc…M+ + 68.77 kcal/mol with R2 = 0.99.
Inorganics 12 00161 g004
Inorganics 12 00161 g005
Figure 5. The linear relationship between the magnitude of the complexation energy, |CE|, and the NBO second-order delocalization energy, E2, associated with the halogen-metal ion interaction, C-I···M+. The equation of best fit line for |CE| = 1.134 E2 + 32.02 kcal/mol, with R2 = 1.00.
Figure 5. The linear relationship between the magnitude of the complexation energy, |CE|, and the NBO second-order delocalization energy, E2, associated with the halogen-metal ion interaction, C-I···M+. The equation of best fit line for |CE| = 1.134 E2 + 32.02 kcal/mol, with R2 = 1.00.
Inorganics 12 00161 g005
Inorganics 12 00161 g006
Figure 6. Optimized geometries for Li+ (A) and Na+ (B) complexed ions by the macrocycle ligand via I···M+ and N···M+ interactions. The corresponding optimized geometries of the K+ and Rb+ complexes are shown at the bottom of the figure (C,D). Dashed lines represent C-I···N halogen bonds and the N···M+ and I···M+ binding interactions. The color representation is as follows: white (H), gray (C), blue (N), light pink (Li+), and dark pink (I). The metal ion is found within the macrocycle ligand, with the color intensifying from light pink (Li+) to dark purple (Rb+).
Figure 6. Optimized geometries for Li+ (A) and Na+ (B) complexed ions by the macrocycle ligand via I···M+ and N···M+ interactions. The corresponding optimized geometries of the K+ and Rb+ complexes are shown at the bottom of the figure (C,D). Dashed lines represent C-I···N halogen bonds and the N···M+ and I···M+ binding interactions. The color representation is as follows: white (H), gray (C), blue (N), light pink (Li+), and dark pink (I). The metal ion is found within the macrocycle ligand, with the color intensifying from light pink (Li+) to dark purple (Rb+).
Inorganics 12 00161 g006
Inorganics 12 00161 g007
Figure 7. Optimized geometries of the transition state structures connecting the two different modes of binding the metal ion, M+. The various figures shown correspond to Li+ (A), Na+ (B), K+ (C), and Rb+ (D). The color representation is as follows: white (H), gray (C), blue (N), light pink (Li+), and dark pink (I). The color of the metal ion intensifies from light pink (Li+) to dark purple (Rb+).
Figure 7. Optimized geometries of the transition state structures connecting the two different modes of binding the metal ion, M+. The various figures shown correspond to Li+ (A), Na+ (B), K+ (C), and Rb+ (D). The color representation is as follows: white (H), gray (C), blue (N), light pink (Li+), and dark pink (I). The color of the metal ion intensifies from light pink (Li+) to dark purple (Rb+).
Inorganics 12 00161 g007
Table 1. Relevant distances (Å) and angles (degrees) for the optimized alkali metal ion complex with the macrocyclic ligand via I···M+ interactions.
Table 1. Relevant distances (Å) and angles (degrees) for the optimized alkali metal ion complex with the macrocyclic ligand via I···M+ interactions.
SystemdC-I…NAC-I…NdI…M+dc…M+
Macrocycle_Li+2.919171.82.7950.000
Macrocycle_Na+2.952171.13.0431.152
Macrocycle_K+2.966168.83.5022.137
Macrocycle_Rb+2.966168.53.6832.434
Table 2. BSSE-corrected complexation energies, CE, and deformation energies, ∆Edef, for alkali metal ion complexes via I···M+ interactions. Energies in kcal/mol.
Table 2. BSSE-corrected complexation energies, CE, and deformation energies, ∆Edef, for alkali metal ion complexes via I···M+ interactions. Energies in kcal/mol.
SystemCE∆EdefCE + ∆Edef
Macrocycle_Li+−67.871.81−66.06
Macrocycle_Na+−55.692.16−53.53
Macrocycle_K+−40.771.60−39.17
Macrocycle_Rb+−36.841.49−35.35
Table 3. Second-order delocalization energies, E2 (kcal/mol), for each of the halogen bonds, C-I···N, and each of the halogen metal ion interactions, C-I···M+, in the macrocycle-M+ complexes.
Table 3. Second-order delocalization energies, E2 (kcal/mol), for each of the halogen bonds, C-I···N, and each of the halogen metal ion interactions, C-I···M+, in the macrocycle-M+ complexes.
SystemE2C-I…N E2C-I…M+
Macrocycle_Li+7.4330.01
Macrocycle_Na+6.7319.05
Macrocycle_K+6.355.87
Macrocycle_Rb+6.303.28
Table 4. Electron density values at bond critical points, ρc (a.u.), for each of the halogen bonds, C-I···N, and each of the halogen metal ion interactions, C-I···M+, in the macrocycle-M+ complexes.
Table 4. Electron density values at bond critical points, ρc (a.u.), for each of the halogen bonds, C-I···N, and each of the halogen metal ion interactions, C-I···M+, in the macrocycle-M+ complexes.
System ρC-I…N ρC-I…M+
Macrocycle_Li+0.02150.0117
Macrocycle_Na+0.02020.0132
Macrocycle_K+0.01970.0094
Macrocycle_Rb+0.01970.0087
Table 5. Relevant distances (Å) and angles (degrees) for the optimized alkali metal ion complex with the macrocyclic ligand via I···M+ and N···M+ interactions.
Table 5. Relevant distances (Å) and angles (degrees) for the optimized alkali metal ion complex with the macrocyclic ligand via I···M+ and N···M+ interactions.
SystemdC-I…NAC-I…NdI…M+dN…M+
Macrocycle_Li+2.890166.63.0892.019
3.049163.04.3855.142
3.989112.72.8274.762
Macrocycle_Na+2.821170.63.1452.398
3.089162.93.8324.864
4.095108.33.0934.341
Macrocycle_K+2.870169.83.5482.857
3.139163.13.7385.116
4.24099.53.4963.699
Macrocycle_Rb+2.886169.53.7183.009
3.131162.93.8805.253
4.171102.43.6673.763
Table 6. BSSE-corrected complexation energies, CE, and deformation energies, ∆Edef, for alkali metal ion complexes via I···M+ and N···M+ interactions. Energies in kcal/mol.
Table 6. BSSE-corrected complexation energies, CE, and deformation energies, ∆Edef, for alkali metal ion complexes via I···M+ and N···M+ interactions. Energies in kcal/mol.
SystemCE∆EdefCE + ∆Edef
Macrocycle_Li+−77.206.27−70.93
Macrocycle_Na+−65.117.13−57.98
Macrocycle_K+−51.137.75−43.38
Macrocycle_Rb+−46.287.29−38.99
Table 7. Second-order delocalization energies, E2 (kcal/mol), for each of the halogen bonds, C-I···N, halogen metal ion interactions, I···M+, and metal ion nitrogen interactions, N···M+, in the complexes via I···M+ and N···M+ interactions.
Table 7. Second-order delocalization energies, E2 (kcal/mol), for each of the halogen bonds, C-I···N, halogen metal ion interactions, I···M+, and metal ion nitrogen interactions, N···M+, in the complexes via I···M+ and N···M+ interactions.
SystemE2C-I…NE2I…M+E2N…M+
Macrocycle_Li+7.9215.987.60
3.911.910.00
0.0026.010.00
Macrocycle_Na+9.6615.704.93
3.577.630.13
0.0015.850.22
Macrocycle_K+8.157.852.35
3.226.580.11
0.006.150.62
Macrocycle_Rb+7.765.601.66
3.354.830.11
0.004.470.53
Table 8. Electron density values at bond critical points, ρc (a.u.), for each of the halogen bonds, C-I···N, halogen metal ion interactions, I···M+, and metal ion nitrogen interactions, N···M+, in the complexes via I···M+ and N···M+ interactions.
Table 8. Electron density values at bond critical points, ρc (a.u.), for each of the halogen bonds, C-I···N, halogen metal ion interactions, I···M+, and metal ion nitrogen interactions, N···M+, in the complexes via I···M+ and N···M+ interactions.
SystemρC-I…NρI…M+ρN…M+
Macrocycle_Li+0.02290.00640.0261
0.01680.00000.0000
0.00000.01050.0000
Macrocycle_Na+0.02580.01070.0211
0.01570.00260.0000
0.00000.01150.0000
Macrocycle_K+0.02340.00870.0147
0.01450.00570.0000
0.00320.00900.0000
Macrocycle_Rb+0.02270.00820.0141
0.01470.00570.0000
0.00340.00850.0000
Table 9. Gibbs free energy barriers (kcal/mol) relative to the more stable metal ion complex (ΔG1ǂ) and the less stable metal ion complex (ΔG2ǂ). The more stable complex involves both I···M+ and N···M+ interactions. The less stable one involves only the I···M+ interactions. The difference between the energy barriers represents the difference in Gibbs free energy between the two different binding modes of metal ion complexes.
Table 9. Gibbs free energy barriers (kcal/mol) relative to the more stable metal ion complex (ΔG1ǂ) and the less stable metal ion complex (ΔG2ǂ). The more stable complex involves both I···M+ and N···M+ interactions. The less stable one involves only the I···M+ interactions. The difference between the energy barriers represents the difference in Gibbs free energy between the two different binding modes of metal ion complexes.
SystemΔG1ǂΔG2ǂΔG1ǂ − ΔG2ǂ
Macrocycle_Li+8.361.906.46
Macrocycle_Na+6.981.655.33
Macrocycle_K+6.841.315.53
Macrocycle_Rb+6.071.614.46
Table 10. Relevant distances (Å) and angles (degrees) for the transition state complexes linking the two binding modes of the metal ion by the macrocyclic ligand.
Table 10. Relevant distances (Å) and angles (degrees) for the transition state complexes linking the two binding modes of the metal ion by the macrocyclic ligand.
SystemdC-I…NAC-I…NdI…M+dN…M+
Macrocycle_Li+2.793172.12.7992.943
3.042163.03.1364.138
3.171153.22.7824.206
Macrocycle_Na+2.862171.93.0073.335
3.013167.53.1864.114
3.099159.72.9934.112
Macrocycle_K+2.908169.73.4593.782
2.992167.73.6274.443
3.036163.73.4344.421
Macrocycle_Rb+2.915169.13.6383.922
2.992167.63.8074.595
3.032163.73.6074.561
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Parra, R.D. Alkali Metal-Ion Binding by a Model Macrocycle Containing a C-I···N Halogen Bonded Network: A DFT Study of C-I···M+ and N···M+ Binding Interactions, M+ = Li+, Na+, K+, and Rb+. Inorganics 2024, 12, 161. https://doi.org/10.3390/inorganics12060161

AMA Style

Parra RD. Alkali Metal-Ion Binding by a Model Macrocycle Containing a C-I···N Halogen Bonded Network: A DFT Study of C-I···M+ and N···M+ Binding Interactions, M+ = Li+, Na+, K+, and Rb+. Inorganics. 2024; 12(6):161. https://doi.org/10.3390/inorganics12060161

Chicago/Turabian Style

Parra, Rubén D. 2024. "Alkali Metal-Ion Binding by a Model Macrocycle Containing a C-I···N Halogen Bonded Network: A DFT Study of C-I···M+ and N···M+ Binding Interactions, M+ = Li+, Na+, K+, and Rb+" Inorganics 12, no. 6: 161. https://doi.org/10.3390/inorganics12060161

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop