Design of High Peak Power Pulsed Laser Diode Driver

Abstract

This paper attempts to describe a laser diode driver circuit using the depletion mode gallium nitride high electron mobility transistor (D-mode GaN HEMT) to generate nanosecond pulses at a repetition rate up to 10 MHz from the vertical-cavity surface-emitting laser (VCSEL). The feature of this driver circuit is a large instantaneous laser power output designed in the most efficient way. The design specifications include a pulse duration between 10 ns and 100 ns and a peak power up to above 100 W. The pulsed laser diode driver uses the D-mode GaN HEMT, which has very small C_oss difference between turn-on and turn-off states. The analysis is according to a laser diode model that is adjusted to match the VCSEL, made in National Yang Ming Chiao Tung University (NYCU). A design guide is summarized from the derivations and analysis of the proposed laser diode driver. According to the design guide, we selected the capacitor, resistor, and diode components to achieve 10 ns to 100 ns pulse duration for laser lighting. The experiment demonstrated that the maximum power-to-light efficiency can be as high as 86% and the maximum peak power can be 150 W, which matches the specifications of certain applications such as light detection and ranging (LiDAR).

1. Introduction

LiDAR is widely used in autonomous cars [1], unmanned aerial vehicles (UAVs) [2], and forest science [3]; it sends out a pulse laser signal and simultaneously gathers the information of the reflection from objects. The object distance is calculated by the optical time-of-flight (TOF) [4], thus the higher the laser peak current, or power, pulses means farther detection can be achieved, and shorter pulse duration represents better detection accuracy. For some applications, such as simultaneous localization and mapping (SLAM) [5], we additionally need a high measurement sampling rate to acquire enough information.

Two laser driver topologies, including the laser diode being in parallel [6] and series [7] with a transistor, have been introduced in the literature. The series topology is featured with a simple circuit, whereas the parallel one is characterized by high optical power and short pulses [8,9]. Some researchers integrated the power switch with its driver using CMOS technology in order to operate at megahertz frequency [7,10]; however, high switching frequency leads to more switching loss for conventional silicon-based materials. The methodology introduced in [11] uses a momentary boost in supply voltage to reduce power overhead and thus improves the power efficiency. Furthermore, some other researchers [12,13] used wide bandgap devices such as the GaN HEMT for the laser driver application due to their low products of total gate charge and conduction resistance. The wide bandgap devices implemented in laser drivers yield better compactness and power efficiency than that of MOSFET [13]. In recent years, EPC Co. have published a laser driver with an enhancement mode power GaN device that is capable of driving a laser with current pulses, with total pulse widths as short as 1.2 ns and currents of up to 28A [14].

Aside from the aforementioned advantages, GaN devices have other superior material properties, such as zero reverse recovery and low output capacitance difference between turn-on and turn-off of the transistor [15,16]. There are also challenges using D-mode GaN, for example, a negative voltage is required to be applied at the gate to turn off the normally on channel. To overcome the aforementioned challenges, several schemes [17,18,19] have transformed the normally on device into a normally off transistor with the charge pump gate drives [17], the cascode GaN structure [18], and the self-powered gate drives [19]. As the laser driving frequency is limited by the inductance of the laser and the capacitance of the driver system, we will need to reduce the parasitic inductance on the circuit board and use GaN HEMT to reduce the parasitic capacitance for higher repetition rate and shorter pulse duration [6].

In addition, high power laser emitters are critical to the LiDAR system, of which VCSEL is used mostly in high speed optical applications such as 3D sensing and light detection and ranging [20,21]. With large current density, directive emission, low divergence angle, narrow bandwidth, and low power consumption, VCSEL has become one of the most reliable and high performance lasers [22,23,24]. Some studies about the analysis of laser equivalent circuit models [25,26,27,28] considering the resonance mechanism [25], rate equations [26], contact resistance equation [27], and thermal equation [28] can yield simulation results approaching the real phenomenon.

The aim of this paper is to propose a laser driver with D-mode GaN HEMT that is capable of generating high peak power pulse within nanoseconds to VCSEL for a LiDAR system. With feedback control of pre-boosted supply voltage, the presented laser driver will yield high peak power under high power efficiency. Section 2 depicts the laser diode and the VCSEL equivalent circuit model used in this research according to rate equations and the resonance phenomenon. In Section 3, the proposed high power laser driver for VCSEL is discussed, including pre-boosted power supply and analysis of laser circuit response. The design guide for the D-mode GaN based laser driver that provides power to light efficiency improvement and high peak power is presented in Section 4. The proposed laser driver with D-mode GaN and VCSEL is verified through the PSPICE simulation and experiment. The estimation of total power received by the photodetector is shown in Section 5. The conclusion of this work is summarized in Section 6.

2. Laser Diode

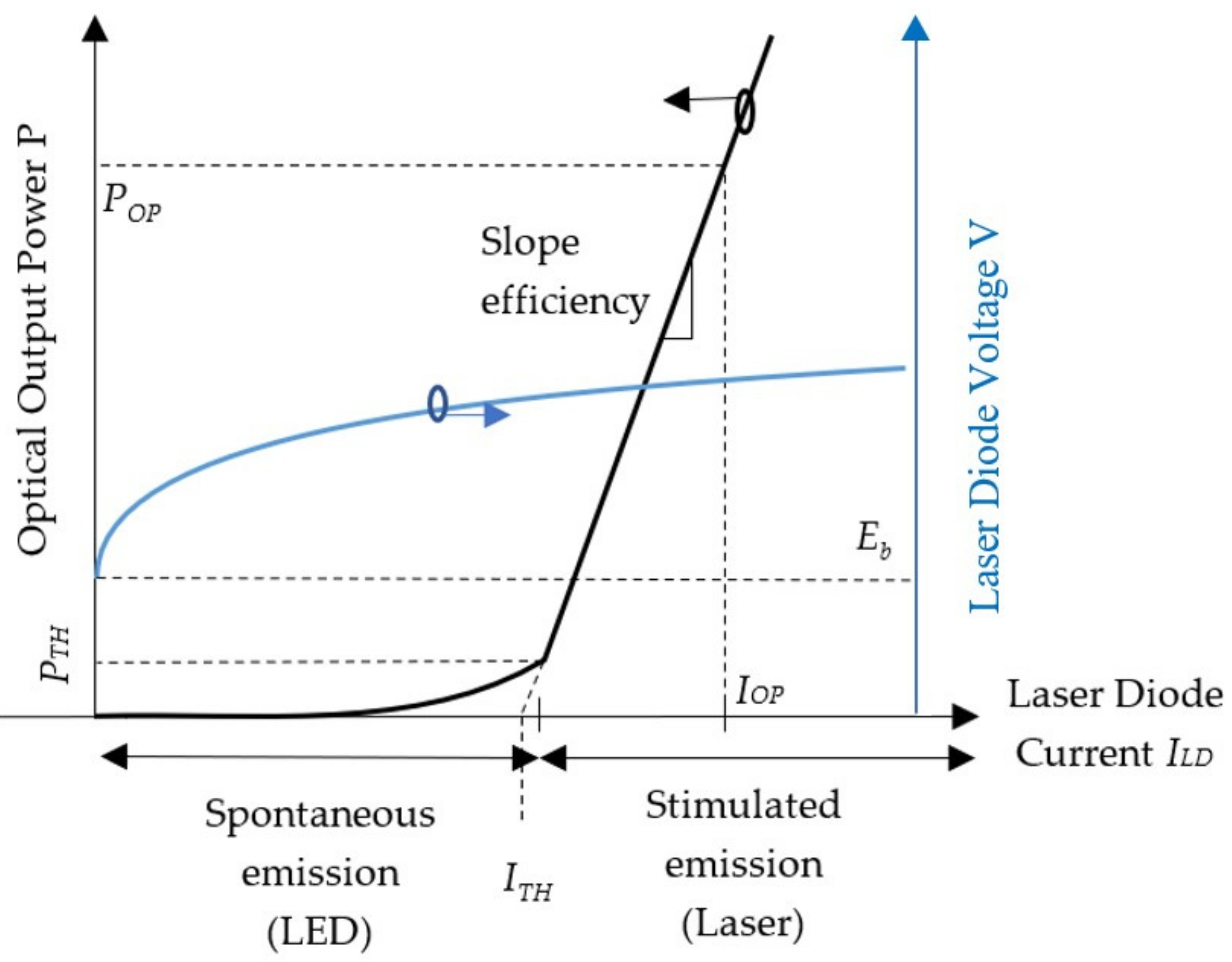
For the circuit analysis and simulation laser diode driving, we need to obtain the circuit response instead of the laser response. Thus, the equivalent circuit needs to be used to predict the waveforms of the current and voltage using circuit simulation software. As shown in Figure 1, within the maximum power rating region, the P-I curve distinguishes the spontaneous emission (LED light emitting) region from the stimulated emission (laser oscillating) region; the current level that triggers laser oscillation is the threshold current. The slope efficiency is almost constant in the stimulated emission region.

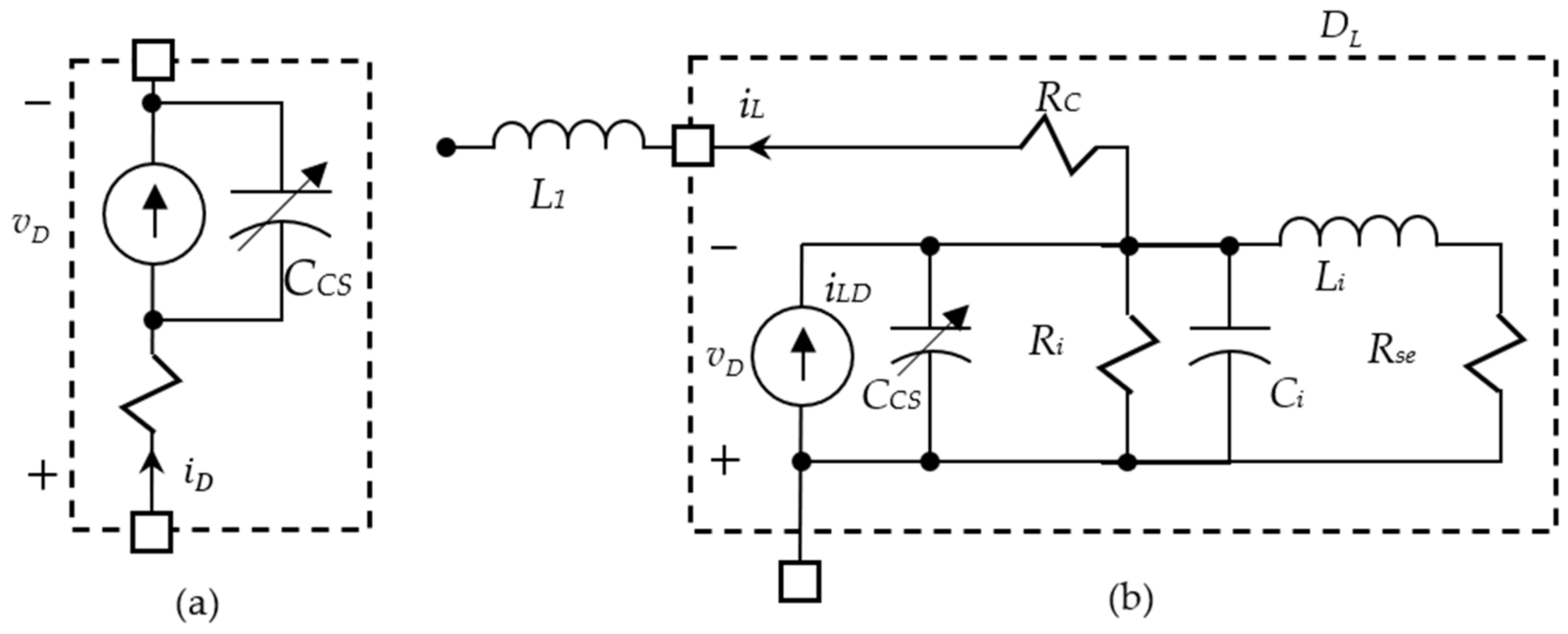
As shown in Figure 2, the major term of the current source of the PIN diode [27] can be modeled into a temperature dependent function as follows.

Table 1. Parameters used in laser diode circuit modeling.

Symbol	Unit	Value
VJ	V	1.9
Csc(o)	pF	0.6
Ci	pF	400
Ri	Ω	3.0
Li	nH	30
L1	nH	Matrix board	100
		PCB	20
Rse	mΩ	100
M		0.5
N		1
Eb	V	1.9
Iss	A	1 × 10−18
C1	µF	220
R1	Ω	100
R2	Ω	100
T1	µs	44

shows the parameters used in circuit analysis, which includes different stray inductances when using matrix board and printed circuit board (PCB).

$$I_{LD}=A{T}^n{e}^{\frac{v_D-E_b}{V_T}}=\left(A{T}^n{e}^{\frac{-E_b}{V_T}}\right)e^{\frac{v_D}{V_T}}$$

(1)

where E_b denotes band gap potential of the semiconductor in volts, n denotes temperature exponent, and A is a constant independent of the temperature T. It is modelled into a similar form as a normal PN diode as follows.

$$I_{LD}=I_{SS}\left(e^{\frac{v_D}{N{V}_T}}-1\right)$$

(2)

It may be substituted with N = 1 and the reverse saturation current as follows.

$$I_{SS}=A{T}^n{e}^{\frac{-E_b}{V_T}}$$

(3)

where E_b denotes the band gap potential of the laser diode in volts. This capacitance named the space-charge capacitance, C_SC, of the active region is given as follows.

$$C_{SC}=C_{SC\left(0\right)}{\left(1-\frac{v_D}{V_J}\right)}^{-M}$$

(4)

where C_sc(0) is the zero-bias space-charge capacitance and V_J is the heterojunction built-in potential. The active layer diffusion capacitance of the laser diode is C_i. The inductance L_i arises from the small signal analysis of the rate equations and represents the resonance phenomenon of the laser diode with capacitance C_i. The resistance R_i includes the differential resistance of the laser diode model damping due to the spontaneous and stimulated recombination terms in the rate equations. The resistance R_se models damping due to spontaneous emission coupled into the lasing mode. In the equivalent circuit we model both R_i and R_se together into R_i,se; R_c is the contact resistance, which includes the semiconductor bulk resistance. The main contribution to R_c comes from the contacts because the bulk resistance of semiconductors is very low. The inductance L₁ arises from the circuit parasitic inductance, which is always preferred to be as low as possible.

3. VCSEL Laser Diode Driver

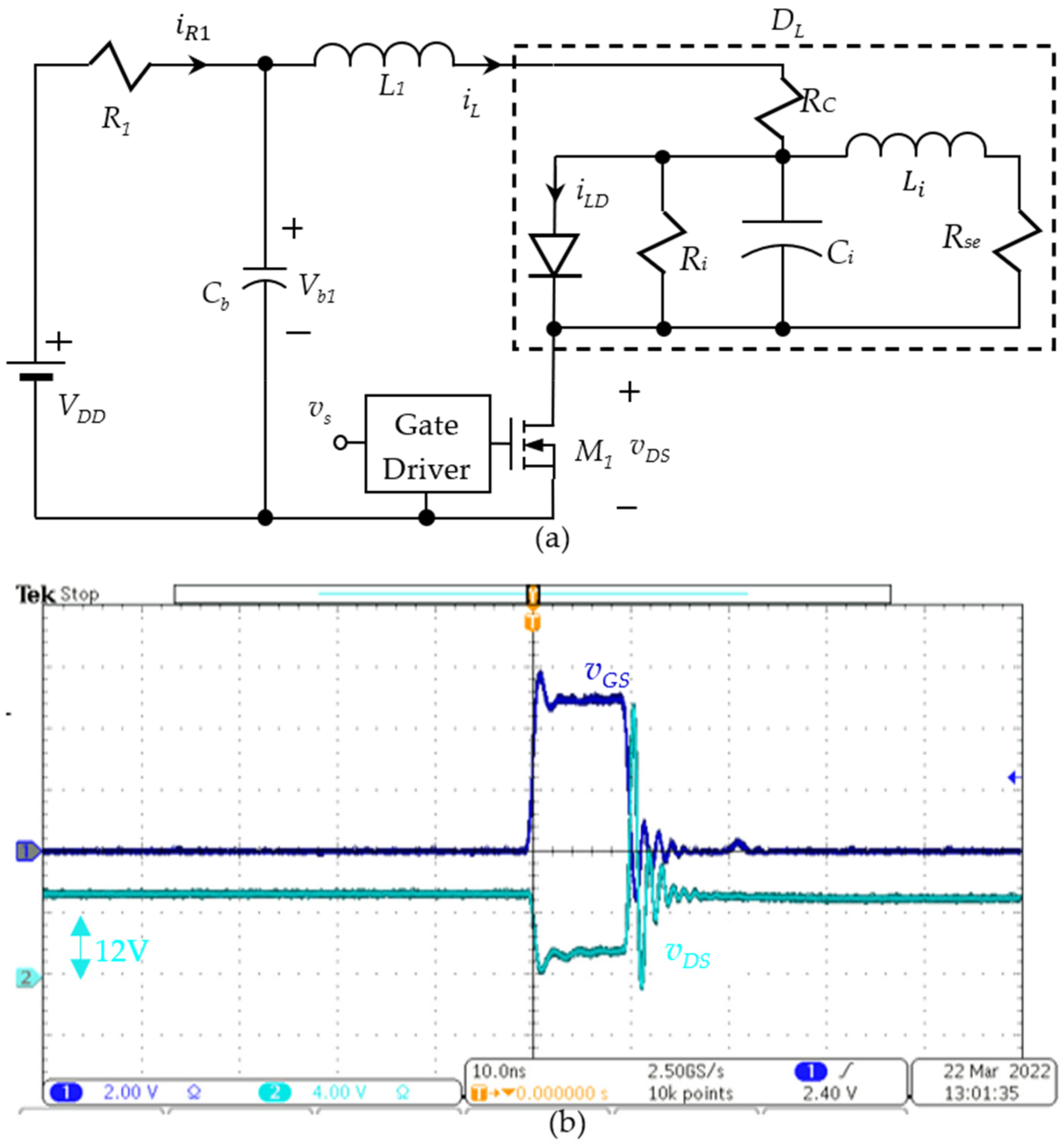
Commercial circuitry to switch on the laser is EPC9144 [14], which is simplified as shown in Figure 3a. The capacitor C_b is 1 nF, which serves as a line filter. When v_GS is high, the transistor M₁ turns on, and the current flows from the voltage source through a very small resistance R₁ to the laser diode. The reverse saturation current I_ss on the laser diode is a function of temperature when the temperature of the laser diode increases the diode current i_LD derived in Equation (1) and cannot be ignored [27] at a constant temperature operation. The moment when v_DS goes to zero is the time when the laser diode goes into the stimulated emission mode, and the rest of the oscillating response is the resonance phenomenon of the laser diode when the laser diode is likely to be in the spontaneous emission mode. The signals are taken from the transistor as shown in Figure 3b. When the gate-source voltage is operated with an on-time duration 10 ns at a pulse repetition rate 10 kHz, the transistor M₁ turns on and v_DS drops to low voltage. The actual i_LD can be roughly estimated through dividing the voltage difference V_DD − v_DS by the dynamic R_on resistance of the GaN HEMT.

The drawback of the circuit in Figure 3a is the resistor R₁ must be high enough to reduce the voltage ringing, as shown in Figure 3b, when the transistor M₁ turns off. The high resistance R₁ limits the current i_LD flowing through the diode, which is typically ten times higher than the contact resistance R_c. For the high peak laser power application, the circuit must be reconsidered.

3.1. The Proposed VCSEL Laser Diode Driver

There is a need to adjust the current level of driving due to different selections of lighting in a number of groups of laser diodes. Therefore, a boost converter used to escalate the voltage level of the capacitor is proposed and shown in Figure 4.

3.2. Power Supply

The boost switching power supply is used to control the input voltage v_DD for the laser driver circuit from a low voltage, such as V_in = 4 V from Li-ion battery. The boost power supply is used to boost the low voltage into a high voltage for the laser. The input voltage v_DD is then subsequently charging the capacitor C₁, which is the main voltage source in the laser lighting loop. On the power supply side, the boost converter circuit consists of an inductor L_b, diode D_b, transistor M_b, and capacitor C_b. The diode D_b comes into the reverse bias when the transistor M_b is switched on. During the M_b turn-on period δ_bT_b, the inductor L_b increases its magnetic energy with a current rise as follows.

$$\Delta I_b=\frac{V_{in}{\delta }_b{T}_b}{L_b}$$

(5)

This magnetic energy will be conveyed to the capacitor C_b during its M_b turn-off period. Because the output current from the power supply to the laser driver is very low, the boost converter working in the discontinuous current mode is assumed. On the path of the current flowing from the inductor L_b to the capacitor C₁, the diode D_b is forced into a forward bias. The charging current of the capacitor C_b is derived in the steady state as follows.

$$\Delta I_b=\frac{\left(V_{DD}-V_{in}\right)\alpha \left(1-{\delta }_b\right)T_b}{L_b}$$

(6)

where α, 0 ≤ α ≤ 1, denotes the fraction of the current flowing time from the M_b turn-off period $\left(1-{\delta }_b\right)T_b$. During the M_b turn-off period, the current i_Db flows into the capacitor C_b through the diode D_b.

$$\alpha =\frac{2}{\left(1-{\delta }_b\right)\Delta I_b}{I}_{R1}=\frac{2}{\left(1-{\delta }_b\right)\Delta I_b}\frac{P_L}{V_b}$$

(7)

The term V_DD denotes the average voltage across the capacitor C_b; I_R1 denotes the average current flow through resistor R₁; P_L denotes the power loss in the laser diode driver including the resistor R₁. Substituting Equation (7) into (6) and comparing Equations (5) and (6), we have the capacitor voltage v_DD as follows.

$${\delta }_b=\sqrt{\frac{2P_L}{V_{in}{}^2}\frac{L_b}{T_b}\left(1-\frac{V_{in}}{V_{DD}}\right)}$$

(8)

It is observed that the capacitor voltage is irrelevant to the capacitance when the boost converter stands alone. However, when we considered the current output i_R1 from R₁, the capacitor voltage v_DD is charged/discharged by two sources, and the total voltage can be calculated from the superposition theorem as follows.

$$v_{DD}=V_{DD}-\Delta v_{DD}=V_{DD}-\frac{\Delta Q}{C_b}$$

(9)

The capacitor voltage is then a function of the capacitance of C_b and the charge withdrawn ΔQ from the capacitor. On the laser driver side, the capacitor C₁ obtains the charges from capacitor C_b when transistor M₁ turns off. The charge redistribution between two capacitors occurs when transistor M_b turns on, and the diode D_b is under reverse bias.

$$\frac{\Delta v_{DD}}{\Delta v_{C1}}=\frac{C_1}{C_b}$$

(10)

The steady state of v_C1 is obtained when the charge redistribution is completed. The time constant may be seen as the capacitor C_b to charge the C₁, which, relatively, has a very small capacitance. The governing equation for the charge redistribution is derived as follows.

$$\frac{d{v}_{C1}}{dt}+\frac{1}{\left(R_1+R_2\right)C_1}{v}_{C1}=\frac{V_{DD}}{\left(R_1+R_2\right)C_1}$$

(11)

In order to reduce the complexity for the analysis, one may reduce charging time constant T₁ of capacitor C₁. The capacitor loses electrical energy ΔE each time when the laser diode is powered up within the pulse train period T_pp. Assuming that $V_{C1}=V_{DD}$ at steady state, we can derive the power loss from the laser diode driver circuit as follows.

$$P_L=\frac{\Delta E}{T_{pp}}=\frac{C_1{V}_{DD}}{T_{pp}}\Delta V_{C1}$$

(12)

Equation (8) is then written as follows.

$${\delta }_b=\sqrt{\Delta v_{C1}}\sqrt{\frac{2L_b{C}_1}{T_{pp}{T}_b{V}_{in}}\left(\frac{V_{DD}}{V_{in}}-1\right)}$$

(13)

The above equation states that the power supply duty cycle δ_b is proportional to the square root of the voltage drop Δv_C1 in capacitor C₁.

3.3. Laser Circuit Response

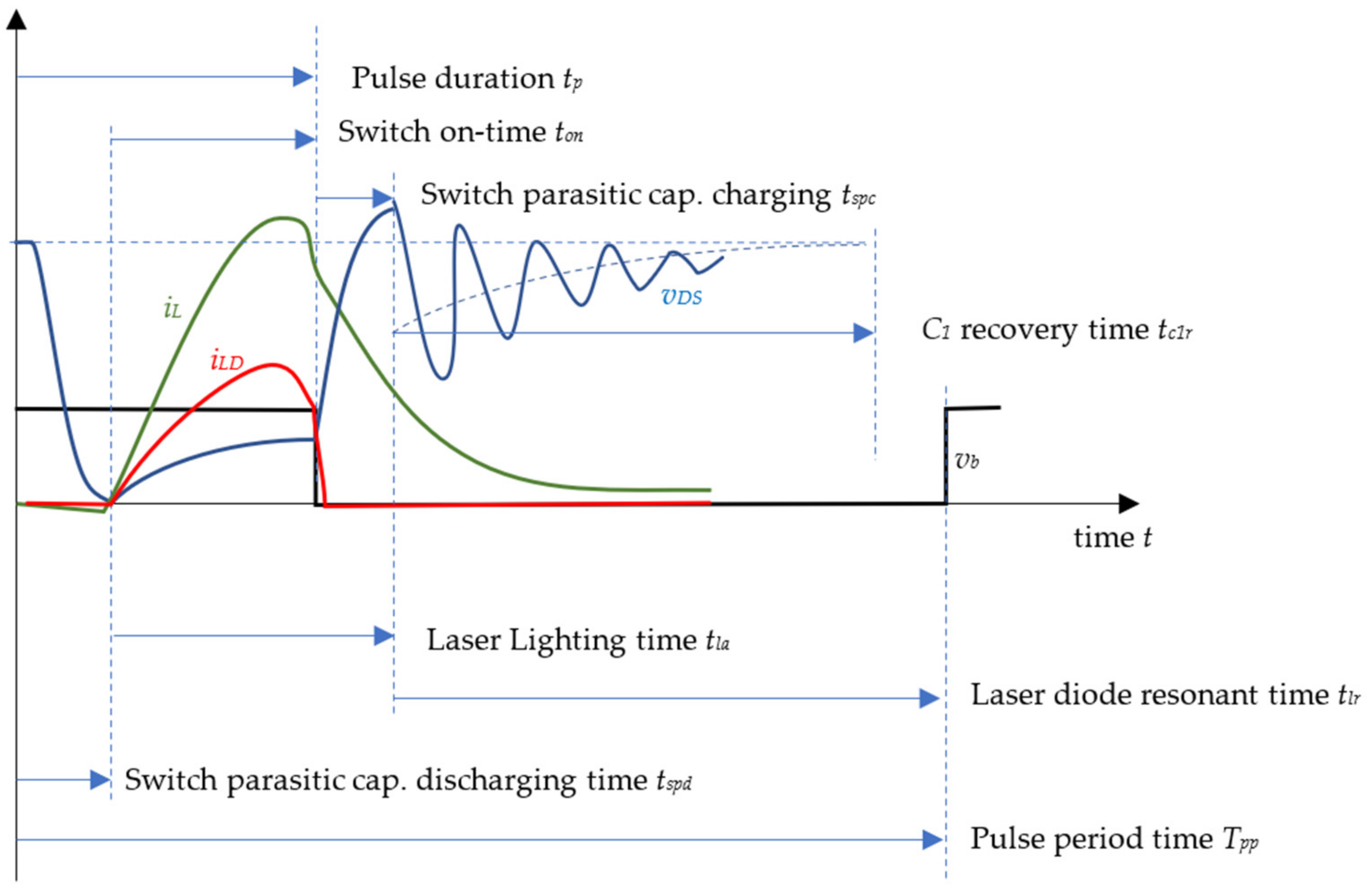
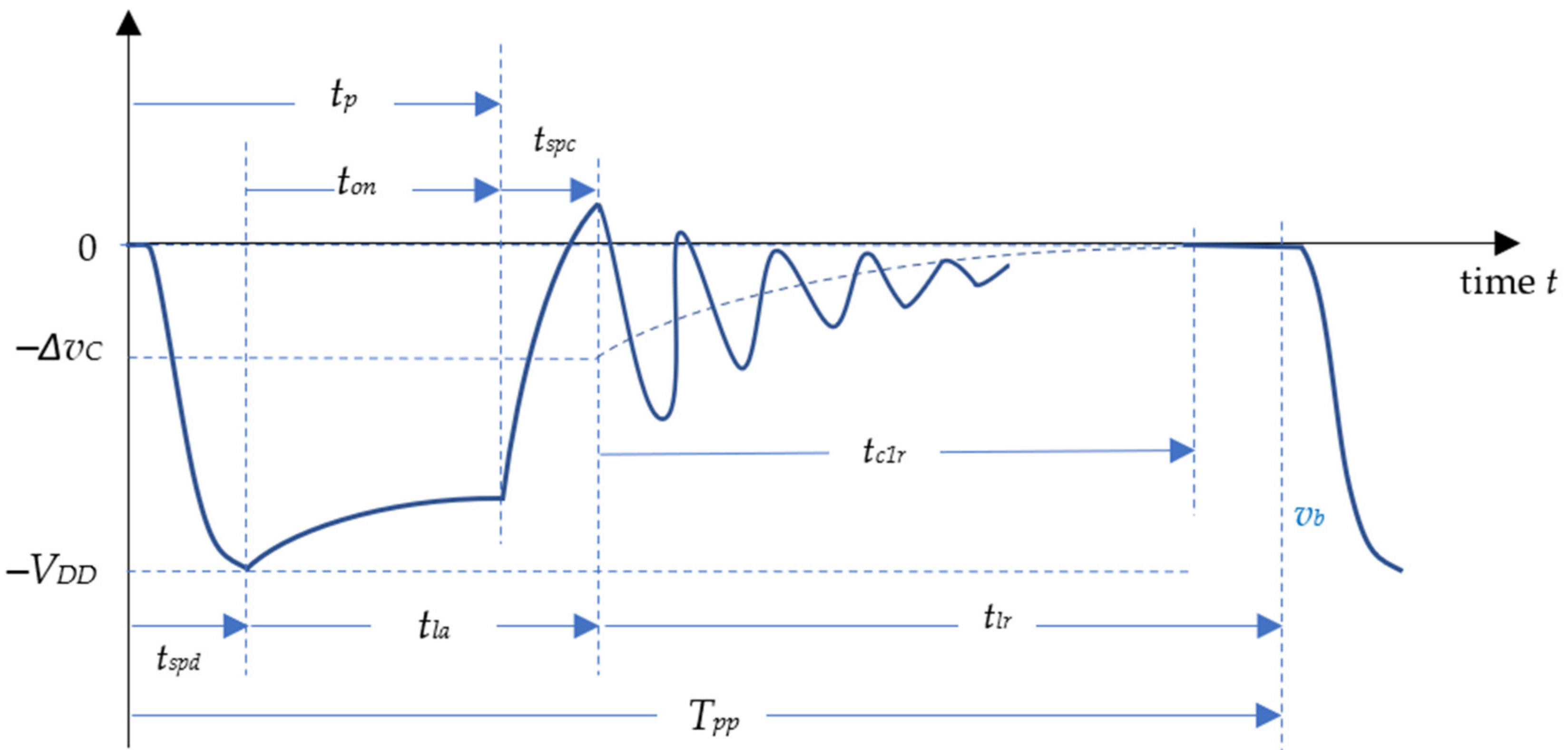
The fundamental data of the VCSEL are from a light–current–voltage (LIV) curve, which simultaneously measures the electrical and optical output power characteristics of the device. LIV characteristics are a function of laser temperature as indicated in Equation (6), which must be tightly controlled. The main reasons for performing low-duty-cycle pulsed laser driving are thermal management, thermal response, and transient response. The pulse driving technique is mainly applied to generate nanosecond pulses of high peak power with solid-state bulk lasers. In this study, we are especially interested in the repetition rate of 10 kHz and 1 MHz. As shown in Figure 5, there are four phases in a LIV pulse, namely the switch parasitic capacitor discharge time t_spd, the switch on-time t_on, the switching parasitic charge time t_spc, and the laser diode resonant time t_lr. The entire cycle between two consecutive gate turn-on signals is a pulse period time T_pp, which is the reciprocal of the laser repetition rate.

$$T_{pp}=t_{spd}+t_{on}+t_{spc}+t_{lr}$$

(14)

where T_pp is the reciprocal of the repetition rate f_LD, that is

$$T_{pp}=\frac{1}{f_{PD}}$$

(15)

The pulse duration achieved is typically in the nanosecond range and usually well above the resonator round-trip time. The pulse duration of the laser pulse is t_p, which consists of the switch parasitic capacitor discharge time t_spd, the switch on-time t_on.

$$t_p=t_{spd}+t_{on}$$

(16)

As a simplified model, the laser lighting time driven by the switch conduction is written as follows.

$$t_{la}=t_{on}+t_{spc}$$

(17)

The power of the laser radiation builds up very quickly in the laser resonator. The large cavity power present at that time leads to further depletion of the stored energy during the time where the power decays. Usually, the energy extracted after the pulse maximum is similar to that before the pulse maximum, and the resulting pulse shape is roughly symmetric. The laser diode resonance is due to inductance L_i with capacitance C_i. The resonance mechanism of a true laser diode may be more sophisticated than the circuit model, however, it is simplified into the circuit as shown in Figure 2 and analyzed only for circuit control purposes.

3.3.1. Switch Parasitic Capacitor Discharge Time t_spd

As shown in Figure 6, at the moment after v_s turns to high voltage for switching on the transistor M₁, the parasitic capacitors in C_oss are discharged in order to bring the transistor M₁ to the linear ohmic state. The capacitors C_oss discharge through the laser diode D_L and the inductor L₁ with the governing equation as follows.

$$\frac{d^2{i}_L}{d{t}^2}+2{\xi }_{spd}{\omega }_{spd}\frac{d{i}_L}{dt}+{\omega }_{spd}{}^2{i}_L=0$$

(18)

In the above equation, the natural frequency ω_spd is a function of inductor L₁ and capacitor C_oss as follows.

$${\omega }_{spd}=\frac{1}{\sqrt{\left(L_1+L_i\right)C_{oss}}}$$

(19)

The parallel resistance R₂ can be ignored because the on-resistance of the GaN device is much smaller than R₂. However, the parallel resistance R₂ may yield a current path when the laser diode starts to flow and thus weaken the laser diode current. Therefore, we may add an extra diode to prevent R₂ current from flowing in the same direction as the laser diode. The damping ratio of the current oscillation is as follows.

$${\xi }_{spd}=\frac{\left(R_C+R_{se}\right)}{2}\sqrt{\frac{C_{oss}}{\left(L_1+L_i\right)}}$$

(20)

where R_c is the contact resistance of the laser diode. The discharging is under a very light damping, hence the rise time of the current response, i.e., the discharging time, is estimated as follows.

$$t_{r,spd}=\frac{\pi }{{\omega }_{spd}}$$

(21)

According to the parameters of the inductance, parasitic capacitance, and the resistance provided as shown in

Table 2. Parameters used in laser diode circuit modeling equations.

Symbol		Unit	Value
Coss(GaN)	On	pF	70
	Off		250
RC (Laser Diode)		mΩ	100
Rse (Laser Diode)		mΩ	50
L1 + Li		nH	130
ωspd		Mrad/sec	332
${\xi }_{spd}$			0.001
tr,spd		ns	9.5

, the capacitor discharging time together with the gate drive delay is, in total, around 1 ns. The switch parasitic capacitor discharge time t_spd forms a barrier for the laser current to flow; that is, the pulse duration shall not be smaller than t_r,spd in order to have the laser diode come to its stimulated emission.

3.3.2. Switch On-Time t_on

During the switch on-time, the switch conducts the current from the capacitor C₁ through the laser diode D_L and the inductor L₁ to the transistor M₁ with the governing equation as follows. It is assumed that the diode holds a constant voltage V_LD,on depending on the I_SS of the laser diode. It may also be considered that the capacitor C₁ charges both the inductor and the on-resistance of the transistor R_D. Assuming the on-resistance of the transistor R_D is small and the damping ratio ${\xi }_{on}$ is negligibly small, the governing equation is derived as follows.

$$\frac{d^2{v}_{C1}}{d{t}^2}+{\omega }_{on}{}^2{v}_{C1}=0$$

(22)

In the above equation, the natural frequency ω_on is a function of inductor L₁ and capacitor C₁ as follows.

$${\omega }_{on}=\frac{1}{\sqrt{L_1{C}_1}}$$

(23)

Substituting the initial voltage of v_C1 as $V_{C1}=V_{DD}$ into Equation (22), we obtain

$$v_{C1}=\left(V_{DD}-V_{LD,on}\right)\cos {\omega }_{on}t$$

(24)

The capacitor voltage of v_C1 is reducing along the time when the transistor M₁ is on, and the lost voltage of the capacitor will be refilled during the M₁ turn-off time. The capacitor voltage drop when ignoring V_LD,on is derived as follows.

$$\Delta v_{C1}=V_{DD}\left(1-\cos \left({\omega }_{on}{t}_{on}\right)\right)$$

(25)

The energy loss in the capacitor C₁ is mainly consumed by the laser diode, hence the power transferred to the laser diode for the lighting pulse is then derived as follows.

$$P=\frac{C_1}{t_{on}}\left(V_{DD}-\frac{1}{2}\Delta v_{C1}\right)\Delta v_{C1}$$

(26)

The maximum power that can be transferred for each pulse can then be derived from taking the first derivative of the above equation.

$$\frac{d}{d{t}_{on}}P=C_1{V}_{DD}{}^2\frac{d}{d{t}_{on}}\frac{\left(\frac{1}{2}+\cos {\omega }_{on}{t}_{on}\right)\left(1-\cos {\omega }_{on}{t}_{on}\right)}{t_{on}}=0$$

(27)

One trivial solution of the above equation is t_on = π/ω_on, that is, the electrical energy stored in the capacitor is used up during each pulse of laser switching. The inductor current i_L1 is then derived in terms of the capacitor voltage as follows.

$$i_L=-L_1\frac{d{v}_{C1}}{dt}={\omega }_{on}{L}_1\left(V_{DD}-V_{LD,on}\right)\sin {\omega }_{on}t$$

(28)

Although all current of i_L flows through the laser diode, only a portion of the current becomes the lighting current i_LD stated in Equation (1). The fraction between i_LD and i_L during the on-time is mainly a function of the resistance R_i, including the differential resistance of the laser diode model damping due to the spontaneous and stimulated recombination terms in the rate equations. The larger the resistance R_i, the higher the lighting current i_LD is. The other current branch of the laser diode includes the current path through the inductance L_i, representing the resonance phenomenon of the laser diode, the resistance R_se, representing damping due to spontaneous emission coupled into the lasing mode, and the current through the active layer diffusion capacitance of the laser diode C_i. The resonance phenomenon and the active layer diffusion will prolong the current of i_L after the lighting current i_LD cuts off from the diode equation.

The significance of this proposed circuit, obtained from Equation (22), is that there is no other resistor presented on the path of the laser diode lighting during the switch turn-on time. The damping ratio of the lighting current is subjected only to the dynamic on-resistance of the transistor M₁. When the on-resistance R_D of the transistor is made very small, the maximum light current is proportional to the V_DD and not limited by the resistance in the current loop.

3.3.3. Transistor Parasitic Capacitor Charge Time t_spc

As shown in Figure 6, at the moment after v_s turns to low voltage for switching off the transistor M₁, the parasitic capacitors in C_oss shall be charged in order to bring the transistor M₁ to the off-state. The capacitors C_oss are charged through the laser diode D_L and the inductor L₁ with the governing equation as follows.

$$\frac{d^2{i}_L}{d{t}^2}+2{\xi }_{spc}{\omega }_{sps}\frac{d{i}_L}{dt}+{\omega }_{spc}{}^2{i}_L=0$$

(29)

In the above equation, the natural frequency ω_spc and ${\xi }_{spc}$ are the same as ω_spd and ${\xi }_{spd}$ derived in Equations (19) and (20), respectively. The charging is under a very light damping, hence the rise time of the current response, the charging time, is the same as derived in Equation (21). The only difference between charging and discharging of the parasitic capacitors is that the laser diode is conducting current i_LD during the charging time only.

$$t_{r,spc}=\frac{\pi }{{\omega }_{spc}}$$

(30)

During the same time, the current keeps flowing to drain out the zero-voltage junction capacitor of the laser diode, as shown in Figure 5.

3.3.4. Laser Diode Resonant Time t_lr

In the case where the GaN HEMT transistor M₁ turns off at the time t_r,spc passed the v_s turn-off time, then the output parasitic capacitor C_oss of the transistor M₁ has been filled up; however, the resonance through the same capacitor as the current in the inductor has no zero first-derivative.

$$\frac{d^2{i}_L}{d{t}^2}+2{\xi }_{lr}{\omega }_{lr}\frac{d{i}_L}{dt}+{\omega }_{lr}{}^2{i}_L=0$$

(31)

The value of R₂ is mapped into the dynamic impedance Z₂ from the parallel connection with L₁ and C_oss into a series connection as follows.

$$Z_2=\frac{L_1+L_i}{R_2\left(C_{oss(GaN,off)}+C_i\right)}$$

(32)

When the GaN HEMT transistor M₁ turns off, the parallel resistance R₂ can contribute to the damping ratio. The damping ratio ${\xi }_{lr}$ when R_C + R_se = Z₂ is then written as follows.

$${\xi }_{lr}=\frac{\left(R_C{+R}_{se}+Z_2\right)}{2}\sqrt{\frac{C_{oss(GaN,off)}+C_i}{L_1+L_i}}\approx \frac{1}{R_2}\sqrt{\frac{L_1+L_i}{C_{oss(GaN,off)}+C_i}}$$

(33)

The damping ratio is preferable to be critical damping without causing too much turn-off overshoot voltage on v_DS.

Table 3. Parameters for switch on-time.

Symbol	Unit	Value
L1	nH	100
Li	nH	30
Coss(GaN,off) + Ci	$\mathrm{pF}$	500
Rc + Rse	$m\mathsf{\Omega }$	200
R2	$\mathsf{\Omega }$	8	100
${\xi }_{lr}$		2	0.16

shows the R₂ adjusted according to the damping desired.

3.3.5. C₁ Recovery Time

There is another important time that determines the repetition rate of the laser diode switching: the capacitor C₁ recovery time. The recovery time is critical when the repetition rate increases, thus for the same pulse duration, the duty of the transistor switching increases. The supply of charges from resistor R₁ through the path from R₁ to C₁ and then to R₂ is activated only when the transistor turns off. The loss of charges from C₁ during the transistor turn-on time must be refilled through its turn off time in order to maintain the capacitor C₁ at the same voltage as the voltage source v_s. The time constant for the charging T_c1 can be obtained from the RC charging equation as follows.

$$T_{c1}=\left(R_1+R_2\right)C_1\approx R_1{C}_1$$

(34)

The capacitor C₁ recovery time t_c1r may be estimated as four times the time constant T_c1, which is nearly 98% of the full voltage to V_DD.

3.4. Sensing the Laser Diode Current

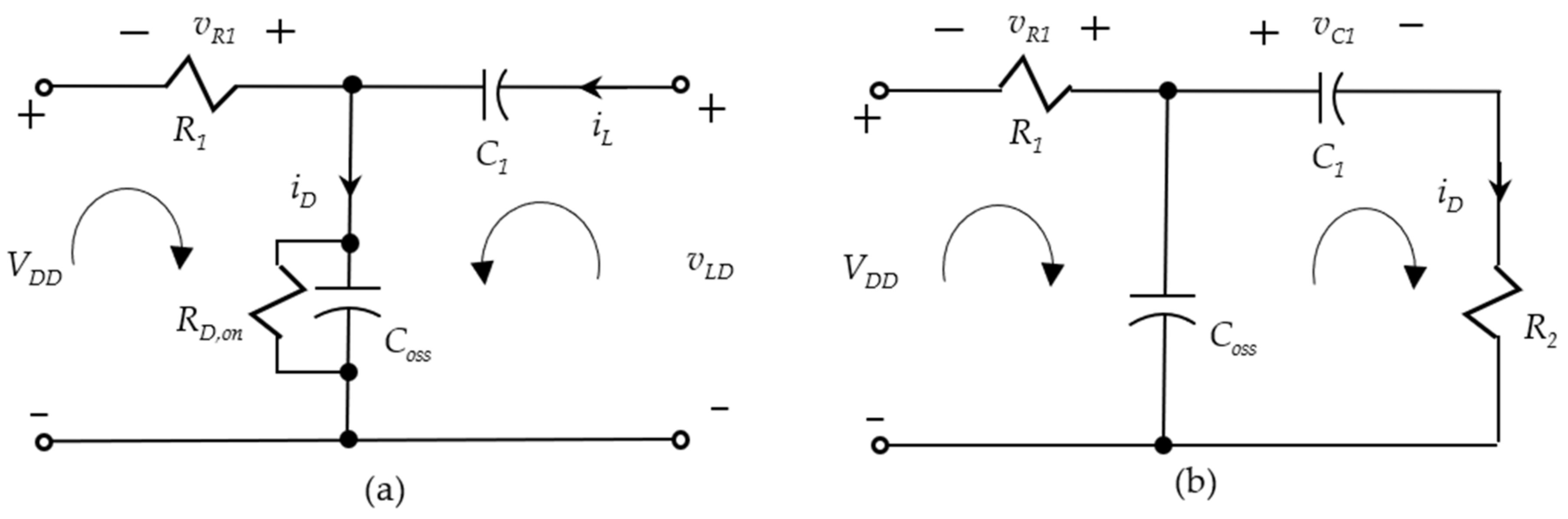
In the small pulse duration or high repetition rate applications, it is difficult to directly measure either the current i_D or the voltage v_DS without interfering with the laser driver circuit. However, the state sensing is of extreme importance during the feedback control of the laser power. In Figure 7, we simplified the laser driver circuit from the view of resistor R₁. The resistor voltage is labeled in the opposite way such that it matches the wave form of the supposed v_DS. In Figure 7a, the total laser diode current i_L can be obtained from the branch current solution as follows when $R_1>>R_{D,on}$ is assumed.

$$i_L=\frac{V_{DD}}{R_{D,on}}-\frac{v_{R1}}{R_{D,on}\left|\right|R_1}\approx \frac{V_{DD}-v_{R1}}{R_{D,on}}$$

(35)

In the above equation, the input voltage V_DD is controlled through the power supply, the voltage v_R1 is sensed, and the dynamic-on resistance of the transistor is assumed. In Figure 7b, the supplement voltage to the capacitor C₁ is estimated.

$$\Delta v_{C1}=-\frac{{\displaystyle {\int }_0^{t_{c1r}}{v}_{R1}dt}}{R_1{C}_1}=-\frac{{\displaystyle {\int }_0^{t_{c1r}}{v}_{R1}dt}}{T_{c1}}\approx -\frac{{\displaystyle {\int }_0^{t_{c1r}}{v}_{R1}dt}}{t_{c1r}/m}=-m\overline{v_{R1}}$$

(36)

The recovery time to time constant ratio m is suggested to be 4, as stated previously, when the 2% voltage error is considered to be the settling time clearance. The average voltage $\overline{v_{R1}}$ on the resistor R₁ can be estimated by taking the average of the integration.

Figure 8 shows the standard voltage response template on resistor R₁. With the voltage response, we can easily label the timing of the individual states of the laser driving process. The anomaly cases include:

(a)

Due to either the resistance of R₁ being too high or the capacitance C₁ being too small, the voltage of v_R1 is below zero voltage all the time during the high repetition rate operation.

(b)

The voltage of v_R1 does not fall to ─V_DD during the short pulse duration operation.

(c)

Due to either the damping of the laser driver circuit being too high or the charge pump gate drive being subjected to high gate resistance, the voltage of v_R1 does not oscillate during the laser diode resonant time t_lr.

4. Design Guide

The parameter used in the proposed circuit consists of mainly the input voltage to the laser diode driver V_DD, which is controlled by the power supply, as stated previously. In order to maintain the correct voltage, the duty cycle (δ_b) is controlled as stated in Equation (13). The other parameters, including the resistor R₁ for both experimental sensing and the charging of capacitor C₁ and the capacitance C₁, are critical to the power efficiency, maximum pulse duration, and peak laser lighting power.

4.1. Power to Light Efficiency

As shown in Figure 8, there are mainly two sessions of the power losses from the resistor R₁ as follows. The first session of power loss is due to the current conducting through R₁ to M₁ during the transistor M₁ turn-on time. The joule loss from R₁ is estimated by assuming the on-resistance of the transistor R_D is small as follows.

$$J_{L,on}=\frac{V_{DD}{}^2}{R_1}{t}_{on}$$

(37)

The second session of power loss is to refill the capacitor C₁ to again reach the voltage V_C1. The joule loss from R₁ during the transistor M₁ turn-off time is derived from the integration of the exponential current charging of the capacitor C₁.

$$J_{L,off}=\int \left(\Delta v_{C1}{e}^{-t/\left(R_1{C}_1\right)}\right)\times \frac{\Delta v_{C1}{e}^{-t/\left(R_1{C}_1\right)}}{R_1}dt=\frac{C_1\Delta v_{C1}{}^2}{2}$$

(38)

The voltage loss Δv_C1 in capacitor C₁ is due to the lighting, and the remaining voltage is derived in Equation (25), which is proportional to V_C1. The electrical power loss of the laser diode driver is then derived as follows.

$$P_L=\frac{J_{L,on}+J_{L,off}}{T_{pp}}$$

(39)

where T_pp is defined previously as the repetition period, which is the reciprocal of the repetition rate f_LD. The electrical power loss is proportional to the repletion rate as well as the square of the voltage V_C1. In order to reduce the electrical power loss, we will need to (a) reduce the capacitance C₁ and (b) increase the resistance R₁. The lighting current i_LD is proportional to V_C1 and the laser diode voltage holds constant V_LD,on. Therefore, the power to light efficiency is in proportion to the product of the repetition rate and the V_DD.

$$\eta \propto \frac{1}{f_{LD}{V}_{DD}}$$

(40)

4.2. Maximum Pulse Duration and Repetition Rate f_LD

Because the lighting current i_LD of the laser diode will turn off when the current reverses, as shown in Figure 6, the maximum pulse duration t_p,max is restrained by Equation (28) and i_L > 0 as follows.

$$t_P<t_{p,\max }=\frac{\pi }{{\omega }_{on}}=\pi \sqrt{L_1{C}_1}$$

(41)

In order to have a small pulse duration, we will need to decrease either the parasitic inductance L₁ or the capacitance C_oss(GaN,on) + C_i. It will need four times the time constant R₁C₁ to recover the capacitor C₁ back into V_DD; therefore, the repetition rate is limited by the reciprocal of R₁C₁ as follows.

$$f_{LD}<\frac{1}{4R_1{C}_1}$$

(42)

In order to increase the repletion rate, we will need to decrease both R₁ and C₁.

4.3. Peak Power

The peak power is determined by the electrical energy storage in the capacitor as follows.

$$P_{LD}\propto \frac{1}{t_p}{\displaystyle \int V_{LD,on}}d{i}_L>>\frac{1}{2}{C}_1{V}_{DD}{}^2\frac{1-\cos {\omega }_{on}{t}_p}{t_p}$$

(43)

Substituting t_p as its maximum value t_p,max from Equation (41), we obtain the P_LD follows.

$$P_{LD}\propto V_{DD}{}^2\sqrt{\frac{C_1}{L_1}}$$

(44)

In order to increase the peak power of laser lighting, we will need to increase the input voltage V_DD and C₁ as well; however, we can also decrease L₁ to increase the peak power.

Table 4. Design guide of the proposed laser driver circuit.

Task	Preference
	VDD	R1	C1	L1
Increase repetition rate fLD		decrease	decrease
Decrease pulse duration tp,max			decrease	decrease
Increase peak power PLD	increase		increase	decrease
Increase power to light efficiency η	decrease	increase

summarizes the design guide for different purposes of the applications; all agree that the inductance L₁ is to be minimized. Except for the high peak power of laser output, the capacitance C₁ is preferred to be small. In order to increase the repetition rate, we will have to choose a low resistance R₁. In order to increase peak power of the laser output, we will need to increase the input voltage V_DD.

5. Simulation and Experiment

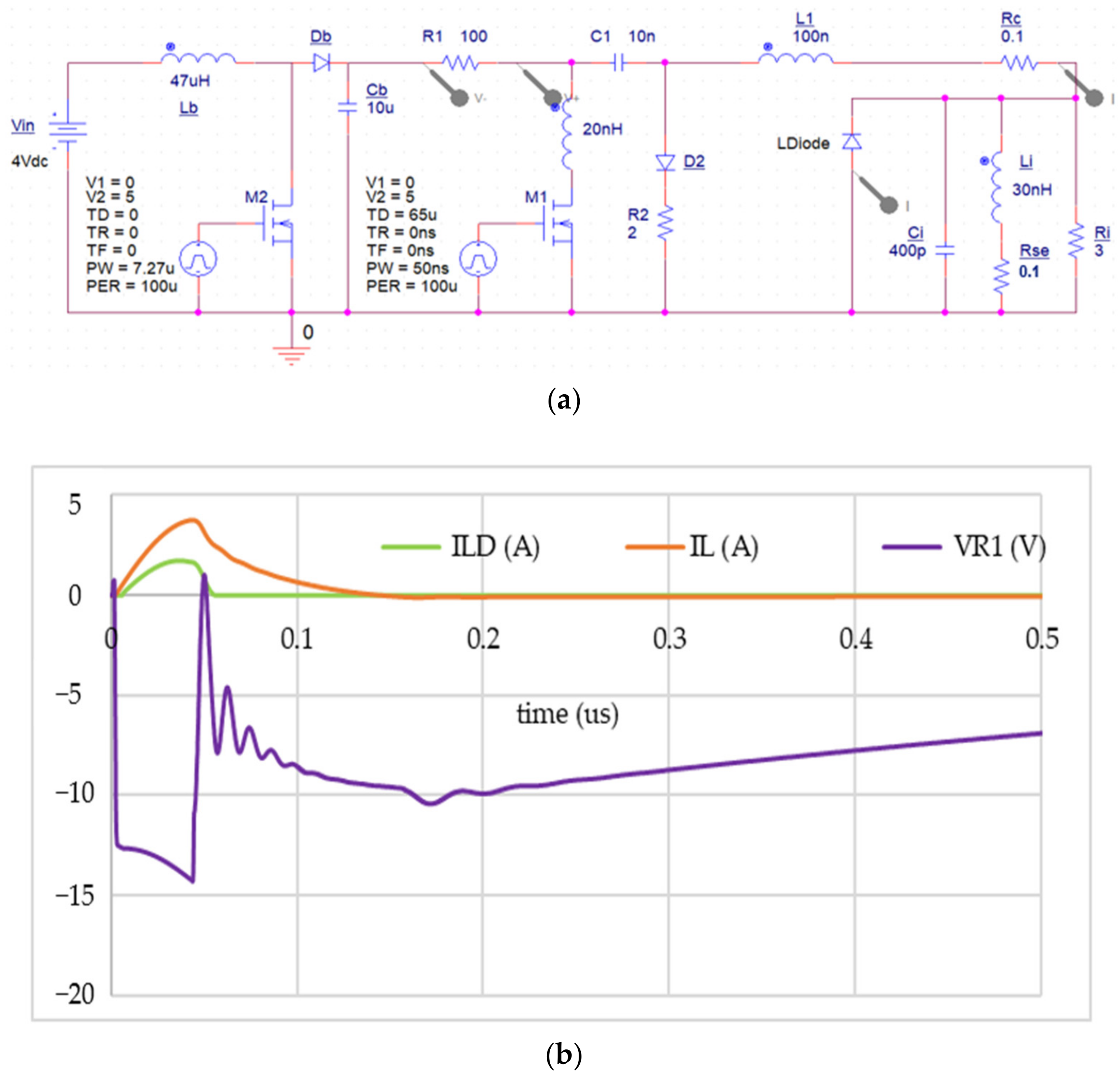
The laser diode SPICE model is based on the laser diode model specified in Table 1. The boost power supply on the left part of the PSPICE circuit model, shown in Figure 9a, is so operated that the V_DD shown in capacitor C_b is 15 V while the simulation result for t_p = 50 ns at its steady state is shown in Figure 9b. There is a parasitic inductance due to bonding connected in series with the transistor M₁. The parameters used in the simulation as experiment as well are shown in

Table 5. Parameters for laser diode driver simulation and experiment.

Symbol	Unit	Value
L1	nH	100
C1	nF	10
R1	Ω	100
ωon	Mrad/s	31.6
tp,max	ns	100
$f_{on}={\omega }_{on}/2\pi$	MHz	5

. The ω_on derived in Equation (23) is also calculated and converted to 5 MHz, as shown Table 5. The maximum pulse duration t_p,max is calculated from Equation (41) as 100 ns. The pulse duration t_p = 50 ns is half of t_p,max = 100 ns; one half of total electrical energy previously stored in the capacitor C₁ was released during the laser light process. Therefore, the Δv_C1 is calculated as 0.3V_DD = 4.5 V from Equation (25) when the switch parasitic capacitor discharge time t_spd is negligibly small and t_on ≈ t_p. The simulation result shows, in Figure 9b, the voltage v_R1 (purple curve line) measured on the resistor R₁ goes from 0 V at 0 s representing the M₁ turn-off state, immediately drops down to −V_DD representing when the transistor M₁ turns on, then jumps to 0 V again at 50 ns, indicating the transistor has been turned off again, and later falls back to the voltage −(V_DD − Δv_C1) = −10 V at 150 ns, which is inconsistent with the result predicted in Equation (25). For a shorter pulse duration, say, one-tenth of 100 ns (t_p,max), the repetition rate can be as high as 10 MHz.

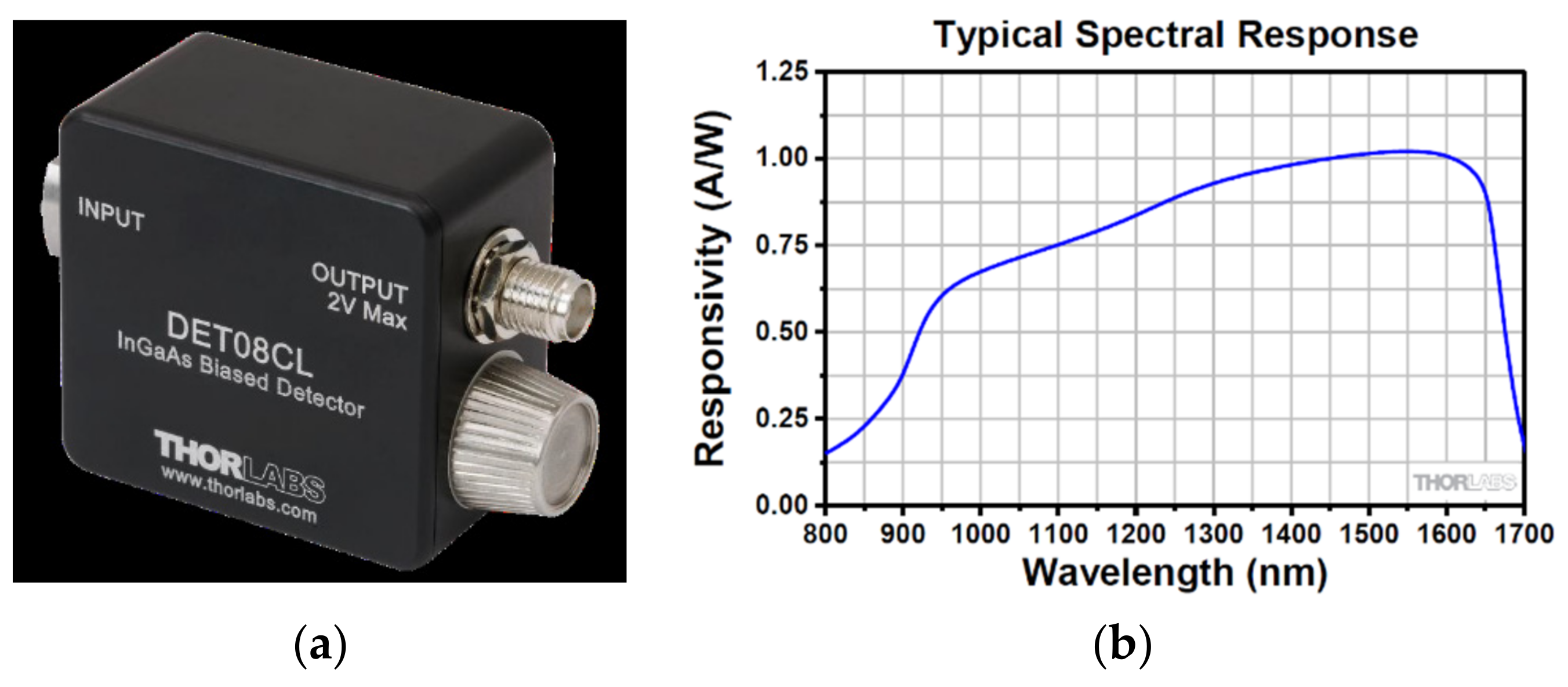
For estimating the output power of a laser diode, the photodiode detector DET08CL(/M) is used, which is an InGaAs junction photodiode (an intrinsic device), and a 50 Ω terminator is used in conjunction with a 50 Ω coaxial cable in our measurements. It behaves similarly to an ordinary signal diode, but it generates a photocurrent when light is absorbed in the depleted region of the junction semiconductor. It determines the expected level of the output current (I_OUT) and the responsivity based upon the incident light.

$$I_{OUT}=I_{DARK}+I_{PD}\cong I_{PD}$$

(45)

The definition of photodiode responsivity R(λ) = I_PD/P is the ratio of generated photocurrent I_PD to the incident light power P at a given wavelength λ. According to the response curve, the photodiode responsivity R(λ) is around 0.6 A/W at wavelength 940 nm. Ignoring the dark current (I_DARK), junction capacitance (C_J), and the other electric characters in the circuit, the received power can be carried out via measured photocurrent (I_PD) at wavelength 940 nm.

$$P=\frac{I_{PD}}{R\left(\lambda \right)@940nm}\cong \frac{I_{PD}}{0.6}$$

(46)

To estimate the total out power of the laser diode, the diverging solid angle of the laser beam is checked, and the solid angle of the photodetector is calculated from the active area diameter. The solid angle of a cone with its apex at the apex of the solid angle, and with the full divergence angle 2θ, is the area of a spherical cap on a unit sphere. The value of θ defined in this paper is the half angle of the beam plane.

$$\mathsf{\Omega }={{\displaystyle \int }}_0^{2\pi }{{\displaystyle \int }}_0^{\theta }\sin \vartheta d\vartheta d\varphi =2\pi (1-\cos \theta )=4\pi {\sin }^2\frac{\theta }{2}\left(steradian\right)$$

(47)

For the PCSEL L13395-04 (HAMAMATSU), its beam spread angle is only 1 degree when its operating power is around 150 mW, $\Delta \mathrm{\Omega }\cong 9.70\times {10}^{-5}\left(steradian\right)$. For a 940 nm VCSEL V3-7-2000-S (EGISMOS), its beam spread angle along the wide axis is 60 degrees and is 45 degrees along the narrow axis, $\Delta \mathrm{\Omega }\cong 0.24\left(steradian\right)$.

The photodiode detector for the experiment and the experimental setup are shown in Figure 10 and Figure 11, respectively. In the experiment, we used the 940 nm VCSEL fabricated in the Department of Photonics at NYCU. The V_DD in this experiment is 15 V. The prototyping board is used in the experiment, and the parasitic inductance L₁ is approximately 100 nH according to the model fitting of the frequency response using Equation (22). The thickness of the prototyping board is 1.55 mm. The spacing between the VCSEL and the photodiode detector is 5 mm, which can also be observed from the Figure 11a side view to compare the thickness with the distance. The active area diameter of the DET08CL(/M) InGaAs junction photodiode is Ø80 µm, and its received solid angle was calculated as follows when $\theta \cong {\sin }^{-1}\left(80\mu m/5mm\right)\approx 0.016rad$.

$$\Delta \mathrm{\Omega }=4\pi {\sin }^2\frac{\theta }{2}\cong 8\times {10}^{-4}\left(steradian\right)$$

(48)

The power correcting factor for a 940 nm VCSEL V3-7-2000-S is around 300. As for the PCSEL L13395-04, the estimated received power does not have to be corrected because its divergence solid angle is smaller than that of the DET08CL. The D-mode GaN HEMT is used in the experiment, as shown in Figure 11b, as the transistor M₁. We used a 10 nF capacitor C₁ to produce a t_p,max = 100 ns pulse, which is inconsistent with the simulation. 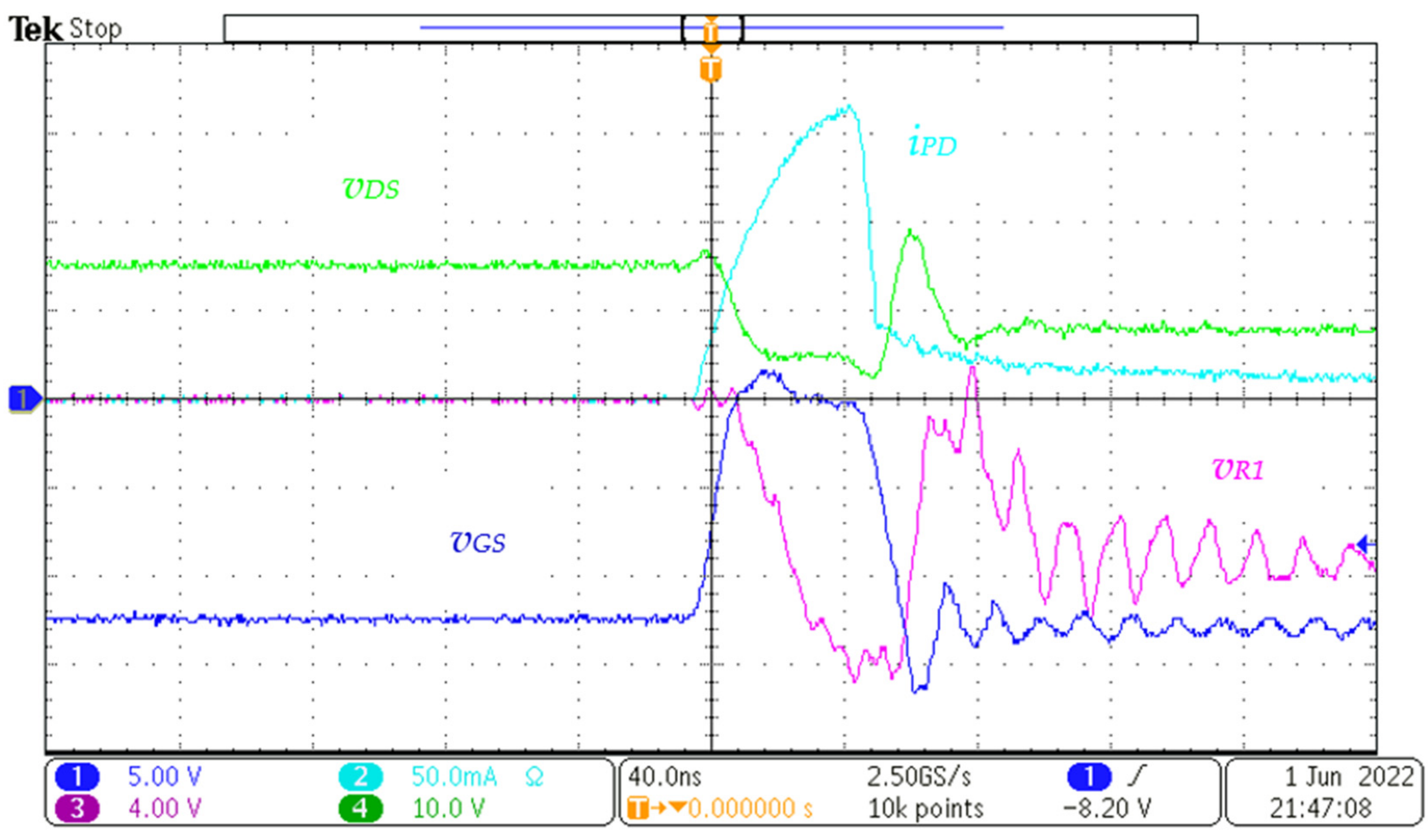The result is shown in Figure 12. In Figure 12, there are four curves. The first curve, in blue, is the gate-source voltage v_GS of the D-mode GaN HEMT. Because the D-mode GaN HEMT is a normally on device and the turn-on voltage of the D-mode GaN HEMT is −7 V, a charge pump gate drive is used, as shown in Figure 6. The second curve, in green, is the drain-source voltage v_DS response of the D-mode GaN HEMT. We directly measured the v_DS using a difference voltage probe that has very low capacitance. The third curve, in purple, is the v_R1. As stated in Section 3.4, the voltage response of v_R1 is similar to v_DS, with the only difference being in voltage shift. Comparing v_R1 in 4 V/div and v_DS in 10 V/div from the experimental result, we actually found the v_R1 is oscillating more than v_DS and with some amount of delay. The fourth curve, in cyan is the current taken from the photodetector, and the peak ampere is 165 mA. According to the power correcting factor calculated from 5 mm distance according to Equation (48) and the power conversion according to Equation (46), the peak power is calculated to be 81 W. It is also observed from Figure 12 that there is still some amount of residual laser light showing on the photodetector, which may be due to the VCSEL resonance.

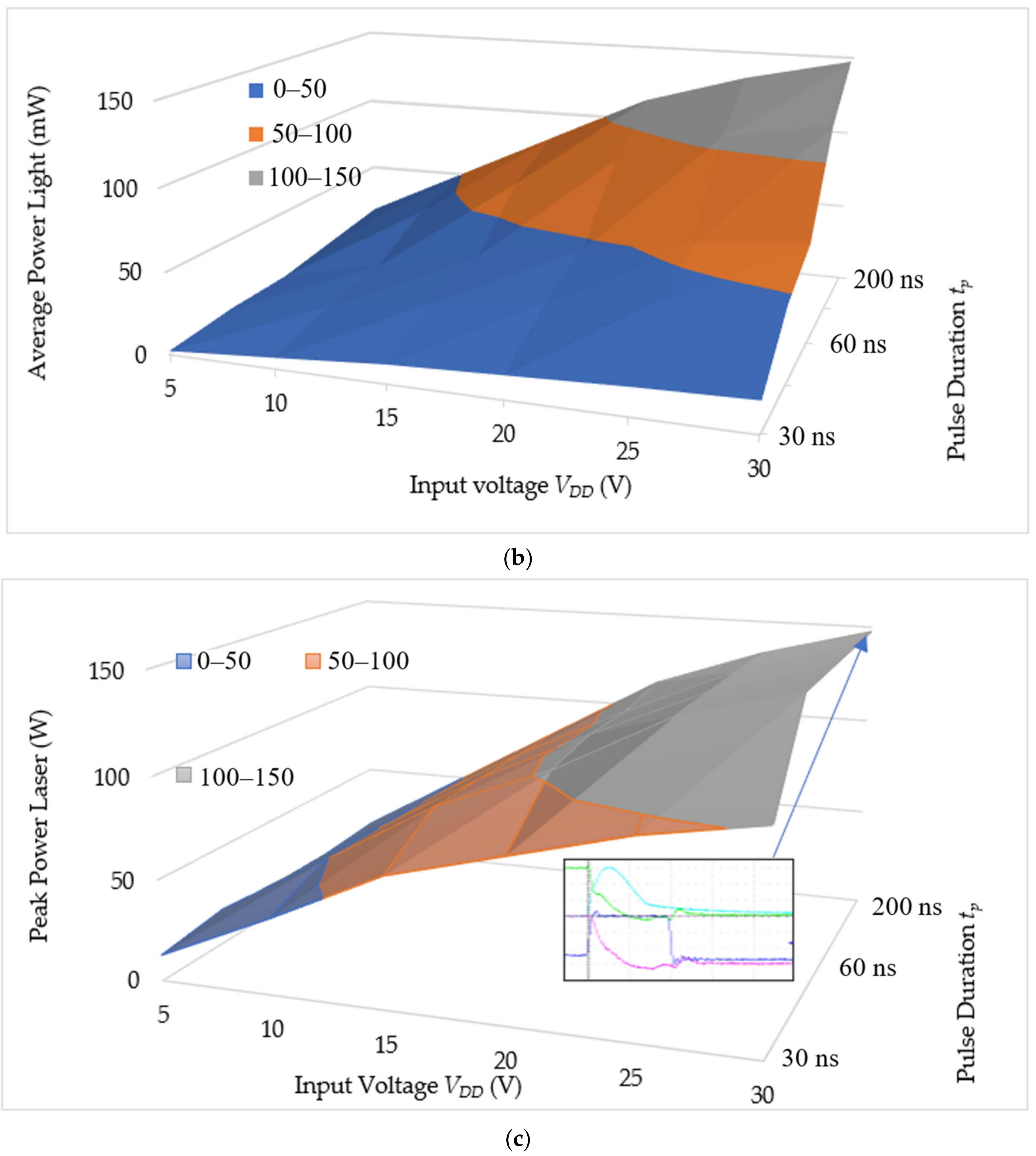
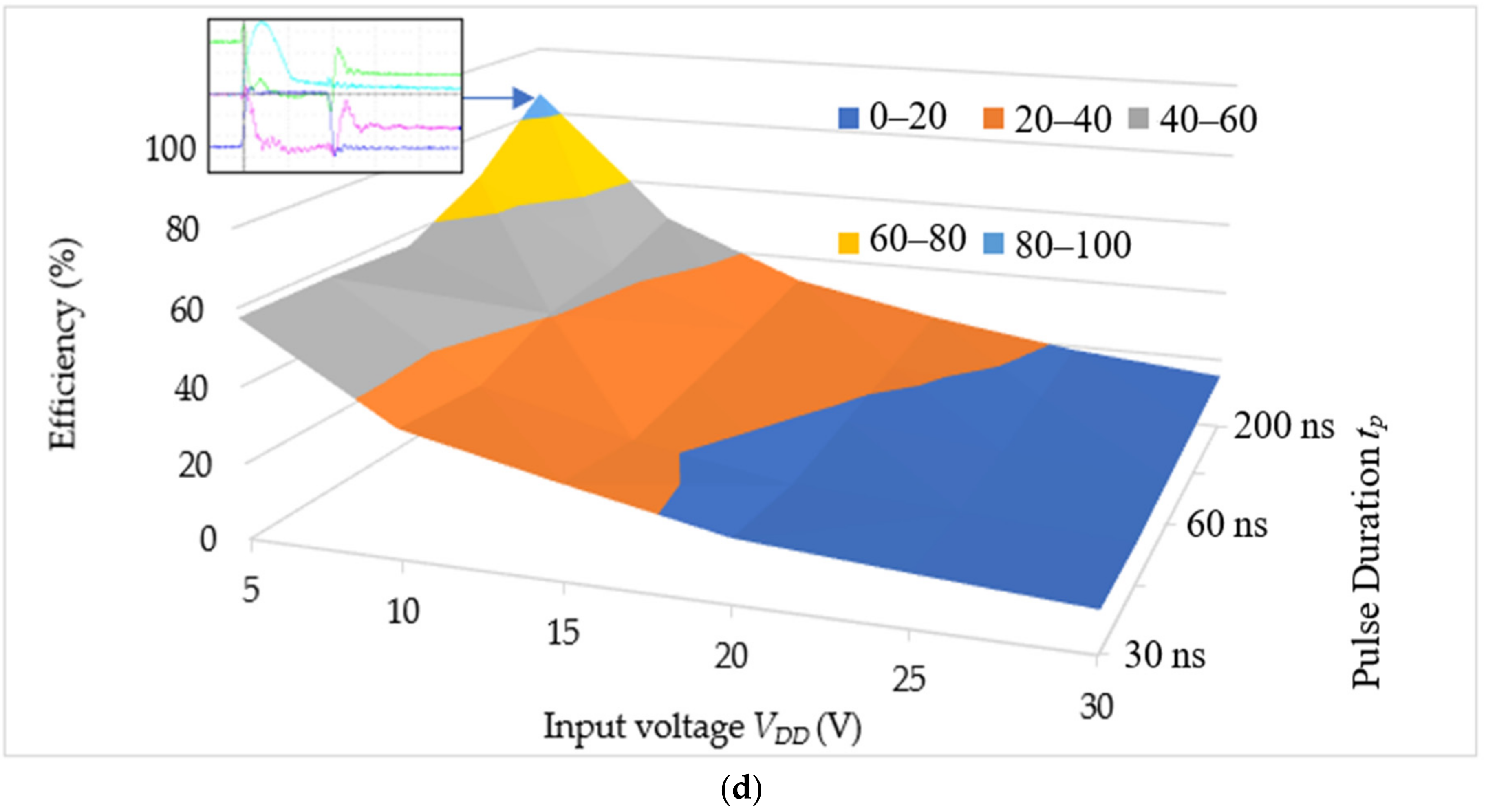
The performance measurement is summarized from many more experiments on the same experiment setup as shown in Figure 11. The input power measured from the power supply reading is shown in Figure 13a. The average lighting power is shown in Figure 13b. The peak power shown in Figure 13c is inconsistent with the power estimated in Equation (44): the higher the input voltage to the laser driver, the larger the peak power from the laser is. The efficiency from the electrical power input to the average laser output power is shown in Figure 13d, which is inconsistent with Equation (40): the lower the input voltage, the higher the efficiency is. As a result, calculated from the experiments, we conclude that, for the current implementation, the highest efficiency is 86% and the maximum power is 150 W. Both the efficiency and the peak power stands for the turn-on time t_on, which should be no less than the pulse duration t_p,max. In Figure 12, it is observed that when t_on is larger than t_p,max, the pulse duration remained at t_p,max = 100 ns when ignoring the residual light.

6. Discussion

When the VCSEL (around 30~40%) efficiency is unknown, the direct measurement, which imposed extra measurement inductance and capacitance on the VCSEL, is inappropriate for calculating the output power; therefore, we estimated the output power of a laser diode using the photodiode detector (PD) DET08CL. A standard method, such as the integrating sphere, collects electromagnetic radiation from a source completely external to the optical device and can be used to precisely measure the output power of the VCSEL laser. Other methods that split the optical beam into two branches [23]—one is directed to an optical spectrum analyzer (OSA), and the other to the optical input of an oscilloscope—may also be used to measure the output power of the VCSEL laser. Although PD is not the best component for the absolute measurement mean, for the circuit designer it is simple and can provide enough relative information for the circuit designer to understand the relationships among the repetition rate, pulse duration, and the laser output power.

There are state-of-the-art commercial drivers for laser diode that can output higher repetition and short pulse duration, such as those from Analog Modules, Inc. (Longwood, Orlando, USA) Model 7612 A [29] is capable of 1.25 W, 10 ns pulse width, and 50 MHz repetition rate. The driver circuit of this paper is oriented to yield a large instantaneous laser power output in an efficient way. The design specifications include a pulse duration of 10~100 ns and a 10 MHz repetition rate when the peak power is 100W. The high instantaneous laser power is due to our circuit design, as shown in Figure 6. Our driver uses the D-mode GaN HEMT, which has a very small C_oss difference between turn-on and turn-off states, and which is used to drive the VCSEL made in NYCU. There are still areas for improvement, such as circuit fabrication, SiP (system in a package) IC design, and VCSEL efficiency, to be achieved in order to catch up with those state-of-the-art products.

The key factors of the output stability in the experiment include the stray inductance due to the wiring path of the laser diode (VCSEL in this study), the input parasitic capacitance C_iss of the GaN HEMT, and the cooling of the circuit board. Among these factors, the stray inductance is most critical factor. Extra stray inductance may result in reduction of the maximum output current and the maximum laser output power, which can be improved through shortening the current path from the laser to the capacitor C₁ and to the transistor M_1. Thus, flip-chip bonding instead of wire bonding is recommended for future work. The input parasitic capacitance is critical to achieve shorter pulse duration as well as higher repetition rate, which can be reduced by fabricating the GaN HEMT with a smaller gate width. A 20 mm GaN HEMT device will be introduced to replace the 120 mm device used in this paper, of which the differences between the devices and the laser output characteristics will be reported in future work. The copper pours, the clip bond, and the ribbon bond are solutions to enhance the heat dissipation of the laser diode driver circuit, which actually help the laser output stability.

7. Conclusions

A laser diode driver circuit is proposed in this paper, which has the advantages that only a single Li-ion battery is needed to provide the adjustable voltage to the laser diode driver, as well as that feedback control can be achieved through the resistor voltage reading without interfering with the current path of laser lighting. The other advantage is its high peak power due to the parallel topology for the power input and the laser emitting. In this paper, the mathematical model of the laser driver is derived according to the laser driver topology to yield the preliminary parameter design of the electronic components. In the experiment, we used the 940 nm VCSEL fabricated in the Dept. of Photonics at NYCU. The circuit model of the VCSEL made at NYCU was acquired by comparing the results between the experiments and the PSPICE simulation. With the SPICE circuit model, we then derived the design guide for different application purposes. The results of a power efficiency of 86% and a maximum peak power of 150 W were obtained for the flash LiDAR application. It will still need further improvement through fabricating the GaN HEMT at NCTU with smaller parasitic capacitances and reducing the parasitic inductance on the circuit board for future application of the VCSEL as the laser emitter on the LiDAR system, which needs a repetition rate as high as 25 MHz with a pulse duration as short as 5 ns.