Deep Deconvolution of Object Information Modulated by a Refractive Lens Using Lucy-Richardson-Rosen Algorithm
Abstract
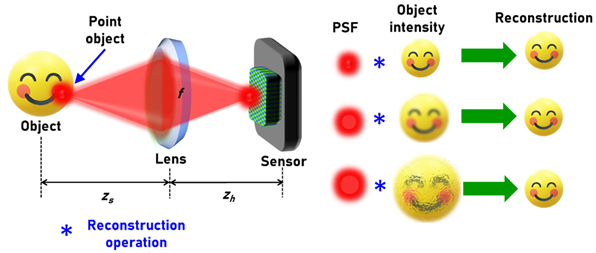
:1. Introduction
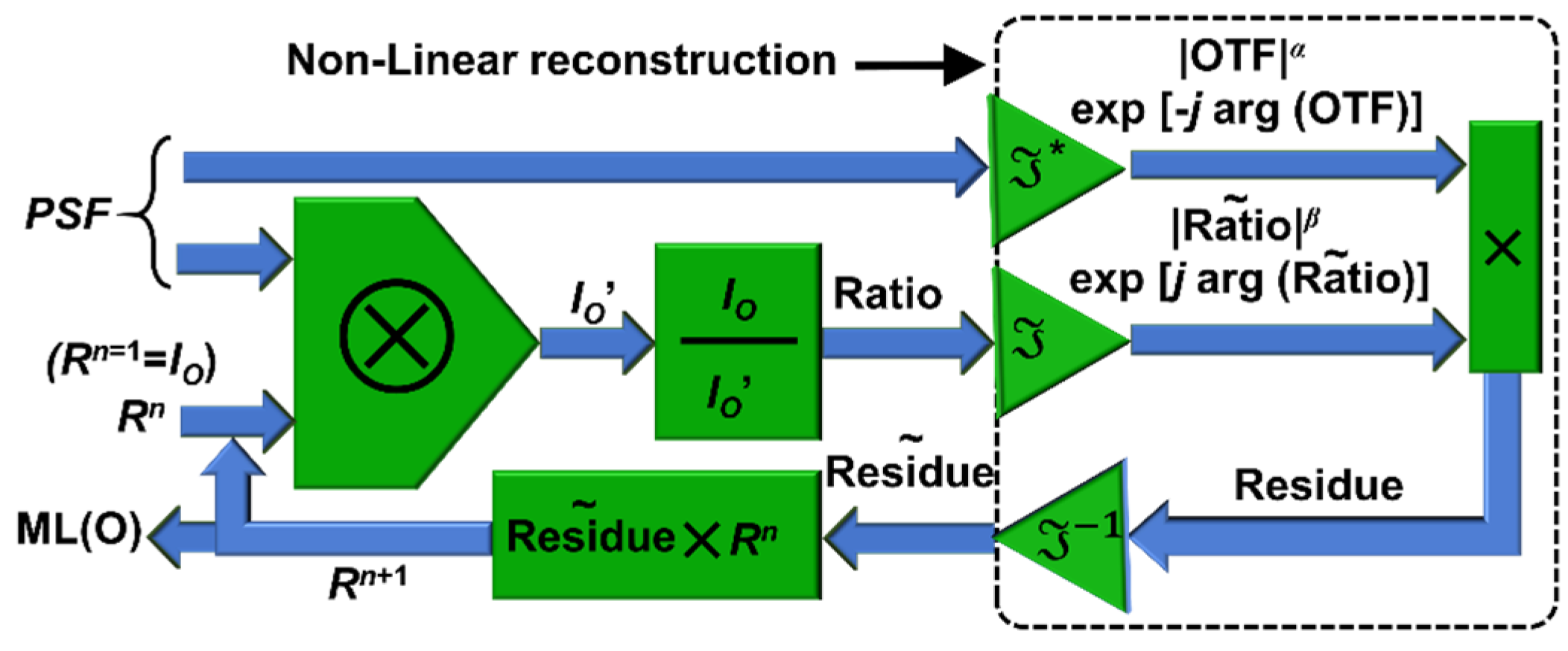
2. Materials and Methods
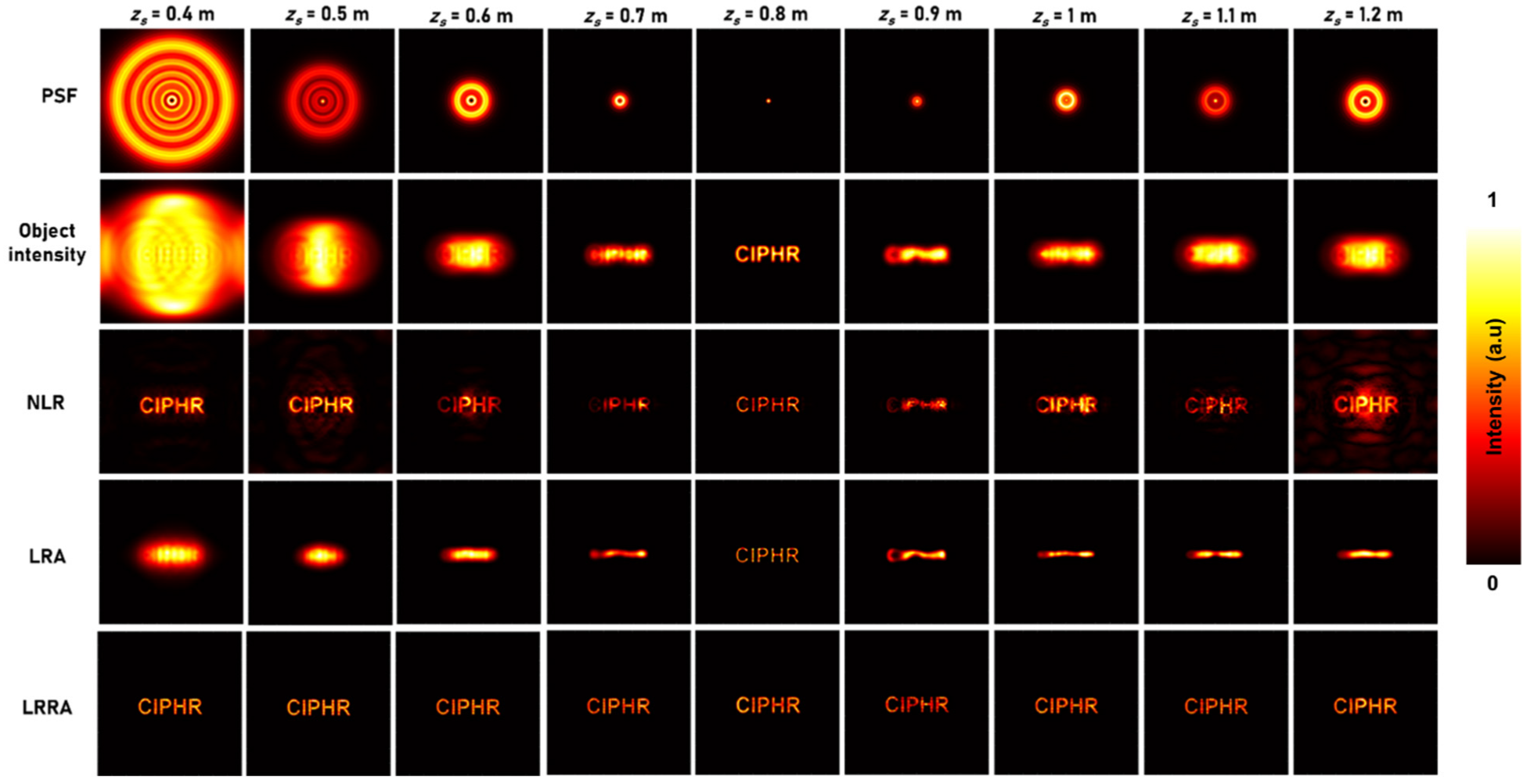
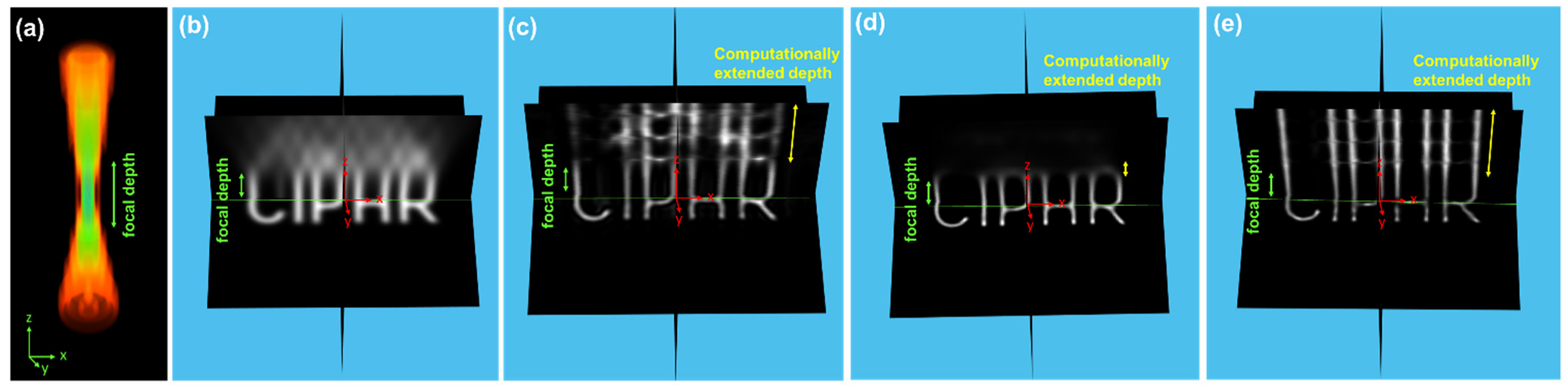
3. Simulation Studies
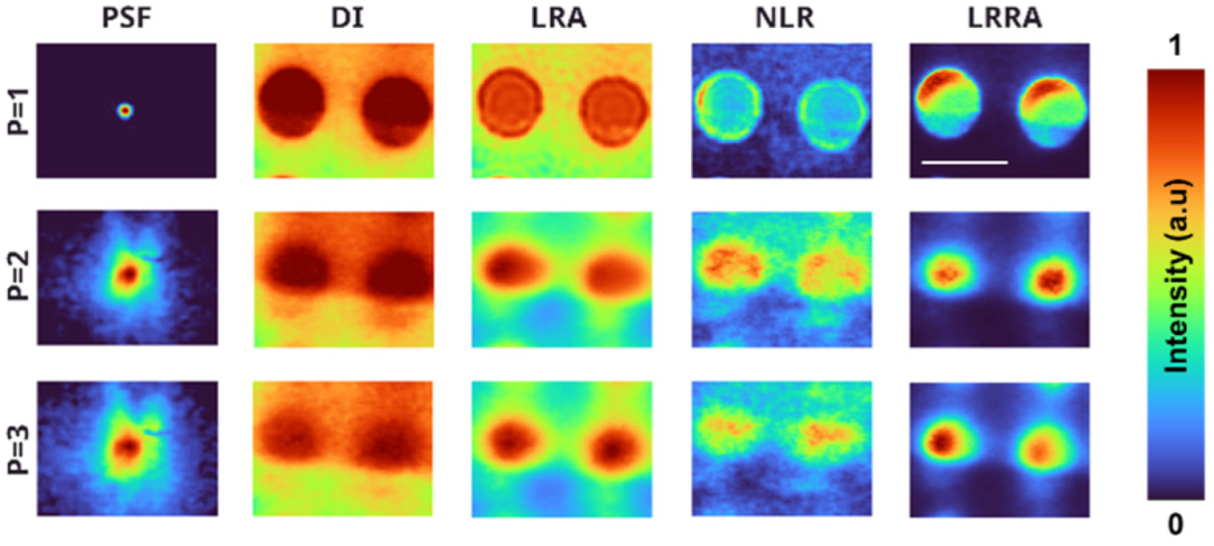
4. Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosen, J.; Vijayakumar, A.; Kumar, M.; Rai, M.R.; Kelner, R.; Kashter, Y.; Bulbul, A.; Mukherjee, S. Recent advances in self-interference incoherent digital holography. Adv. Opt. Photon. 2019, 11, 1–66. [Google Scholar] [CrossRef]
- Lichtman, J.W.; Conchello, J.A. Fluorescence microscopy. Nat. Methods 2005, 2, 910–919. [Google Scholar] [CrossRef]
- Kim, M.K. Adaptive optics by incoherent digital holography. Opt. Lett. 2012, 37, 2694–2696. [Google Scholar] [CrossRef]
- Liu, J.-P.; Tahara, T.; Hayasaki, Y.; Poon, T.-C. Incoherent Digital Holography: A Review. Appl. Sci. 2018, 8, 143. [Google Scholar] [CrossRef]
- Poon, T.-C. Optical Scanning Holography—A Review of Recent Progress. J. Opt. Soc. Korea 2009, 13, 406–415. [Google Scholar] [CrossRef]
- Rosen, J.; Alford, S.; Anand, V.; Art, J.; Bouchal, P.; Bouchal, Z.; Erdenebat, M.-U.; Huang, L.; Ishii, A.; Juodkazis, S.; et al. Roadmap on Recent Progress in FINCH Technology. J. Imaging 2021, 7, 197. [Google Scholar] [CrossRef]
- Murty, M.V.R.K.; Hagerott, E.C. Rotational shearing interferometry. Appl. Opt. 1966, 5, 615. [Google Scholar] [CrossRef]
- Sirat, G.; Psaltis, D. Conoscopic holography. Opt. Lett. 1985, 10, 4–6. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef]
- Kim, M.K. Incoherent digital holographic adaptive optics. Appl. Opt. 2013, 52, A117–A130. [Google Scholar] [CrossRef] [Green Version]
- Kelner, R.; Rosen, J.; Brooker, G. Enhanced resolution in Fourier incoherent single channel holography (FISCH) with reduced optical path difference. Opt. Express 2013, 21, 20131–20144. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography–a new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef] [PubMed]
- Ables, J.G. Fourier Transform Photography: A New Method for X-Ray Astronomy. Publ. Astron. Soc. Aust. 1968, 1, 172–173. [Google Scholar] [CrossRef]
- Dicke, R.H. Scatter-Hole Cameras for X-Rays and Gamma Rays. Astrophys. J. Lett. 1968, 153, L101. [Google Scholar] [CrossRef]
- Cieślak, M.J.; Gamage, K.A.; Glover, R. Coded-aperture imaging systems: Past, present and future development–A review. Radiat. Meas. 2016, 92, 59–71. [Google Scholar] [CrossRef]
- Anand, V.; Rosen, J.; Juodkazis, S. Review of engineering techniques in chaotic coded aperture imagers. Light. Adv. Manuf. 2022, 3, 1–9. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Rosen, J. Interferenceless coded aperture correlation holography–a new technique for recording incoherent digital holograms without two-wave interference. Opt. Express 2017, 25, 13883–13896. [Google Scholar] [CrossRef]
- Singh, A.K.; Pedrini, G.; Takeda, M.; Osten, W. Scatter-plate microscope for lensless microscopy with diffraction limited resolution. Sci. Rep. 2017, 7, 10687. [Google Scholar] [CrossRef]
- Antipa, N.; Kuo, G.; Heckel, R.; Mildenhall, B.; Bostan, E.; Ng, R.; Waller, L. DiffuserCam: Lensless single-exposure 3D imaging. Optica 2018, 5, 1–9. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Tang, D.; Dang, C. Single-shot multispectral imaging with a monochromatic camera. Optica 2017, 4, 1209–1213. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Rosen, J. Spectrum and space resolved 4D imaging by coded aperture correlation holography (COACH) with diffractive objective lens. Opt. Lett. 2017, 42, 947. [Google Scholar] [CrossRef] [PubMed]
- Anand, V.; Ng, S.H.; Maksimovic, J.; Linklater, D.; Katkus, T.; Ivanova, E.P.; Juodkazis, S. Single shot multispectral multidimensional imaging using chaotic waves. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Anand, V.; Ng, S.H.; Katkus, T.; Juodkazis, S. Spatio-Spectral-Temporal Imaging of Fast Transient Phenomena Using a Random Array of Pinholes. Adv. Photon. Res. 2021, 2, 2000032. [Google Scholar] [CrossRef]
- Rai, M.R.; Anand, V.; Rosen, J. Non-linear adaptive three-dimensional imaging with interferenceless coded aperture correlation holography (I-COACH). Opt. Express 2018, 26, 18143–18154. [Google Scholar] [CrossRef]
- Horner, J.L.; Gianino, P.D. Phase-only matched filtering. Appl. Opt. 1984, 23, 812–816. [Google Scholar] [CrossRef]
- Smith, D.; Gopinath, S.; Arockiaraj, F.G.; Reddy, A.N.K.; Balasubramani, V.; Kumar, R.; Dubey, N.; Ng, S.H.; Katkus, T.; Selva, S.J.; et al. Nonlinear Reconstruction of Images from Patterns Generated by Deterministic or Random Optical Masks—Concepts and Review of Research. J. Imaging 2022, 8, 174. [Google Scholar] [CrossRef]
- Richardson, W.H. Bayesian-Based Iterative Method of Image Restoration. J. Opt. Soc. Am. 1972, 62, 55–59. [Google Scholar] [CrossRef]
- Lucy, L.B. An iterative technique for the rectification of observed distributions. Astron. J. 1974, 79, 745. [Google Scholar] [CrossRef]
- Anand, V.; Han, M.; Maksimovic, J.; Ng, S.H.; Katkus, T.; Klein, A.; Bambery, K.; Tobin, M.J.; Vongsvivut, J.; Juodkazis, S.; et al. Single-shot mid-infrared incoherent holography using Lucy-Richardson-Rosen algorithm. Opto-Electron. Sci. 2022, 1, 210006. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Beck, A.; Teboulle, M. Fast Gradient-Based Algorithms for Constrained Total Variation Image Denoising and Deblurring Problems. IEEE Trans. Image Process. 2009, 18, 2419–2434. [Google Scholar] [CrossRef] [PubMed]
- Biemond, J.; Lagendijk, R.; Mersereau, R. Iterative methods for image deblurring. Proc. IEEE 1990, 78, 856–883. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Tao, D. Recent progress in image deblurring. arXiv 2014, arXiv:1409.6838. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praveen, P.A.; Arockiaraj, F.G.; Gopinath, S.; Smith, D.; Kahro, T.; Valdma, S.-M.; Bleahu, A.; Ng, S.H.; Reddy, A.N.K.; Katkus, T.; et al. Deep Deconvolution of Object Information Modulated by a Refractive Lens Using Lucy-Richardson-Rosen Algorithm. Photonics 2022, 9, 625. https://doi.org/10.3390/photonics9090625
Praveen PA, Arockiaraj FG, Gopinath S, Smith D, Kahro T, Valdma S-M, Bleahu A, Ng SH, Reddy ANK, Katkus T, et al. Deep Deconvolution of Object Information Modulated by a Refractive Lens Using Lucy-Richardson-Rosen Algorithm. Photonics. 2022; 9(9):625. https://doi.org/10.3390/photonics9090625
Chicago/Turabian StylePraveen, P. A., Francis Gracy Arockiaraj, Shivasubramanian Gopinath, Daniel Smith, Tauno Kahro, Sandhra-Mirella Valdma, Andrei Bleahu, Soon Hock Ng, Andra Naresh Kumar Reddy, Tomas Katkus, and et al. 2022. "Deep Deconvolution of Object Information Modulated by a Refractive Lens Using Lucy-Richardson-Rosen Algorithm" Photonics 9, no. 9: 625. https://doi.org/10.3390/photonics9090625
APA StylePraveen, P. A., Arockiaraj, F. G., Gopinath, S., Smith, D., Kahro, T., Valdma, S.-M., Bleahu, A., Ng, S. H., Reddy, A. N. K., Katkus, T., Rajeswary, A. S. J. F., Ganeev, R. A., Pikker, S., Kukli, K., Tamm, A., Juodkazis, S., & Anand, V. (2022). Deep Deconvolution of Object Information Modulated by a Refractive Lens Using Lucy-Richardson-Rosen Algorithm. Photonics, 9(9), 625. https://doi.org/10.3390/photonics9090625









