Abstract
Mixed-Fixed/Flex-Grid Optical Networks (MFGONs) are a new paradigm that emerged during the brown-field migration from fixed-grid Wavelength Division Multiplexing (WDM) optical networks to flex-grid Elastic Optical Networks (EONs). Based on the flex-grid, we can accommodate IP traffic directly to the optical layer by configuration. Considering the different granularities of spectrum resources and complex constraints in MFGONs, it is difficult to apply Routing and Wavelength/Spectrum Allocation (RWA/RSA) algorithms proposed in either fixed-grid or flex-grid optical networks. This paper first proposes two concepts, i.e., Link Spectrum Compactness (LSC) and Radiancy of Nodes (RoNs), to evaluate different scenarios of candidate paths for the end-to-end requests in MFGONs. Then, based on these two concepts, a Spectrum Entropy (SE) model is proposed in MFGONs. Here, the SE is the metric that combines LSC and RoNs to judge the fragmentation of network resources, and the value of SE is treated as the cost of candidate paths during the RSA operation. Finally, an SE-minimized RSA algorithm in MFGONs is designed. Simulation results prove that the proposed algorithm can effectively reduce the Bandwidth Blocking Ratio (BBR) and increase the revenues for upgrading the nodes compared to the state-of-the-art RSA algorithm. Particularly, the performance improvement is more obvious for highly connected networks.
1. Introduction
Because of the popularity of video streaming, cloud computing services, and mobile applications, the IP traffic is continually increasing, which causes the burden of optical networks to increase considerably. To meet the increasing capacity requirement of services, Wavelength Division Multiplexing (WDM) systems with up to 40 or 100 Gb/s per channel have been deployed in backbone networks. However, traditional WDM optical networks strictly follow the International Telecommunication Union’s (ITU-T) fixed uniform spacing and grid (typically at 50 or 100 GHz) [1], which will lead to inflexible spectrum allocation and low spectrum utilization [2]. To increase the spectrum utilization and elasticity of WDM networks, Elastic Optical Networks (EONs) were proposed a few years ago [3]. In EONs, the fixed-wavelength grid of WDM optical networks is further subdivided into narrower spectrum units, which are called Frequency Slots (FSs) [4]. Furthermore, EONs can adaptively assign routes, bandwidths, modulation levels, and transmit optical powers, which is more accommodating to the end-user demands than WDM optical networks. To accommodate a traffic demand in EONs, the Routing and Spectrum Allocation (RSA) problem should be carefully considered, which is more challenging than the traditional Routing and Wavelength Allocation (RWA) problem in WDM optical networks. Meanwhile, the traditional RWA solutions [5,6] are no longer applicable in EONs because EONs should satisfy not only spectrum consistency, but also spectrum continuity and spectrum conflict constraints.
A lot of research has been conducted with respect to the RSA problem. To effectively resolve the RSA problem in a large-scale network, two efficient algorithms, namely, the K-Shortest Paths (KSPs) with maximum spectrum reuse algorithm and the balanced load spectrum allocation algorithm, were proposed [7]. With the technology of Orthogonal Frequency Division Multiplexing (OFDM), the multipath configuration scheme and optical grooming approach can be used to aggregate and distribute traffic directly at the optical layer, respectively [8,9], which improve the spectrum utilization efficiency to a great extent. Since different modulation formats affect the spectrum utilization, spectrum allocation algorithms were proposed based on Integer Linear Programming (ILP) models and dynamic traffic allocation models to solve the internal relationship between the modulation formats and RSA [10,11,12,13]. In addition, by leveraging conflict graphs, the unified theoretical framework for the performance analysis of RSA algorithms was proposed [14].
EONs are more flexible and efficient to meet the growing demands compared to WDM optical networks. However, the upgrading from WDM optical networks to EONs is a brown-field migration. On the one hand, the high prices of the key equipment in EONs have not fallen sufficiently for large-scale deployment; on the other hand, operating the existing WDM optical network can achieve greater benefits and avoid additional losses in the upgrade process before the existing optical network capacity is exhausted [15,16,17]. Therefore, a more reasonable strategy is to gradually upgrade the nodes in the legacy networks, forming a mixed network supporting both fixed and flexible grid operations, namely, a Mixed-Fixed/Flex-Grid Optical Network (MFGON). Many studies on upgrading strategies from WDM optical networks to EONs have been proposed from the fields of academia and industry [18,19], and the problems of when to upgrade and how to upgrade have been answered in [17]. For the growth of network traffic, the multi-stage conception of gradual upgrading from WDM optical networks to EONs was mentioned again, and the specific upgrading process was further developed by the authors of [20]. It analyzed the difficulties that will be faced in each stage and highlighted the RSA problem that was not solved.
As we know, the RWA problem is NP-complete and heuristics are typically used [21]. In MFGONs, the complexity of the RSA problem is even higher because some network resources are in spectrum granularity, while others remain in the wavelength granularity for the partial upgrade. There has not been enough research about how to rationally choose paths, allocate resources, and establish stable optical channels to provide high-quality services in MFGONs. Some researchers have preliminarily explored the RSA problem, but it was still limited to the problem of node upgrade [22]. Moreover, in [23], though an RSA algorithm based on backbone networks was proposed, it was not suitable for dynamic traffic scenarios. Based on the shortcomings of the above related work, we propose an SE model and the corresponding SEM-RSA algorithm, which considers the RSA problem in the evolution of MFGONs in dynamic scenarios. This paper first proposes a Spectrum-Entropy (SE) model for evaluating different situations of candidate paths for requests in MFGONs, and then introduces an RSA algorithm for MFGONs based on the proposed model. The rest of this study is organized as follows. Section 2 introduces the problems of the existing technology and further illustrates the necessity of the proposed algorithm. The core calculation formula and the process of the algorithm are detailed in Section 3. Section 4 evaluates the algorithm through simulations, and Section 5 summarizes this paper.
2. Problem Statement
In an RSA problem, optical paths are established for a set of requests by selecting routing paths and allocating spectrum resources [24]. Although RSA is the extension of RWA, unlike RWA, RSA has more complicated constraints, which makes the relevant algorithms on RWA not applicable to RSA. To date, the research on RSA has made initial progress, such as the KSPs with a maximum spectrum reuse algorithm and the balanced load spectrum allocation algorithm [7]. With the technology of Orthogonal Frequency Division Multiplexing (OFDM), we can aggregate and distribute traffic directly at the optical layer [8,9]. However, in MFGONs, the following problems still exist.
In MFGONs, a part of network resources is affected by the upgrade of the technology and changes from wavelength granularity to spectrum granularity, while the other part remains in the wavelength granularity. Unlike in EONs, the RSA problem in MFGONs not only needs to satisfy the constraints of spectrum continuity, spectrum consistency, and spectrum conflict, but also needs to allocate spectrum according to the strict spectrum resource standards; that is, spectrum compatibility constraints. Therefore, the RSA problem in MFGONs becomes more complex.
Figure 1 shows four typical scenarios and an example network topology in MFGONs. The wavelength granularity of a fixed-grid node is assumed to be 50 GHz, and the FS of a flex-grid node is 12.5 GHz. Figure 1a shows the path of fully fixed-grid nodes. In this case, only the RWA restriction is needed. For example, although a 100 Gb/s request only needs a 37.5 GHz spectrum, it occupies a 50 GHz spectrum due to the fixed wavelength granularity. Figure 1b shows a path where the source node is a fixed-grid node and passes through flex-grid nodes. For the request needing a 37.5 GHz spectrum, since the source node is a fixed-grid node, the bandwidth of 50 GHz is needed even though the path passes through a flex-grid node. Figure 1c shows the situation of establishing a super-channel in a path connecting fully flex-grid nodes. Figure 1d shows a path where the source node is a flex-grid node and passes through fixed-grid nodes. At this point, only a 25 GHz spectrum is required by the 40 Gb/s request from a flex-grid node, but the spectrum must be limited within a fixed granularity due to passing fixed-grid nodes.
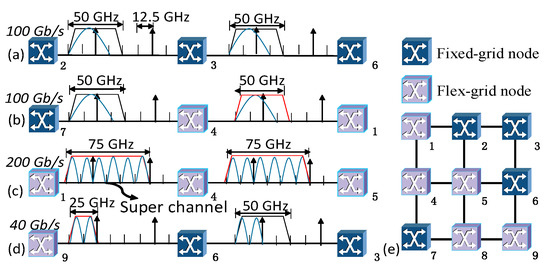
Figure 1.
Four typical scenarios in MFGONs: (a) the path of fully fixed-grid nodes; (b) the path where the source node is a fixed-grid node and passes through flex-grid nodes; (c) the path of fully flex-grid nodes; (d) the path where the source node is a flex-grid node and passes through fixed-grid nodes; (e) network topology.
Furthermore, RSA and resource defragmentation are usually considered as two independent phases [25,26,27]. For example, the defragmenting operation is performed when the fragmentation gradually accumulates to a certain threshold or blocking appears, which means that the performance of the network is bad. In fact, the RSA for each request should consider the defragmentation of the optical network to decrease the defragmentation. In addition, the definition of spectrum fragmentation should be changed due to two different spectrum granularities and more complex constraints in MFGONs.
Finally, there are limitations in the current RSA algorithms. Mathematical ILP models and dynamic traffic optimization models are used to solve RSA problems. However, the RSA problem is solved by choosing the best path as far as possible without considering the impact of the current connection on subsequent requests. This limitation is not conducive to efficient spectrum utilization.
In view of the above problems, an evaluation metric called Spectrum Entropy (SE) is proposed based on the newly defined Link Spectrum Compactness (LSC) and Radiancy of Nodes (RoNs), in order to represent the cost of alternative paths for requests in MFGONs. The SE is further used as a basic reference value during the process of RSA in MFGONs. Moreover, in our research, we take flex-grid distance modulation conversion into consideration, but do not account for wavelength converter, signal regeneration, physical impairments of WDM transmission, and wavelength routing.
3. Spectrum-Entropy-Minimized Routing and Spectrum Allocation
This paper proposes an SE-Minimized Routing and Spectrum Allocation (SEM-RSA) algorithm in MFGONs. The core of the algorithm is the cost of a path; that is, the SE of a path. The SE is based on LSC and RoNs, and is used as a reference for evaluating alternative paths. In this section, we introduce the SE model and the SEM-RSA algorithm in detail. Before detailing these, the following sets and parameters need to be defined.
3.1. Link Spectrum Compactness (LSC)
Spectrum compactness is proposed to evaluate the spectrum continuity of the link in EONs by abstracting the spectrum distribution characteristics [27]. A higher LSC means a denser spectral distribution. However, this concept cannot be fully applied to MFGONs as a result of the different resource granularities; thus, the calculation formula should be changed considering the following two different scenarios.
3.1.1. The Initial Node of the Link Is a Flex-Grid Node
Ever since the original concept of LSC was proposed in EONs [27], it has been suitable for the scenario in which the link’s initial node is a flex-grid node. Its definition is shown in Equation (1). The notations and definitions in Equation (1) are shown in Table 1.

Table 1.
Notations and definitions.
3.1.2. The Initial Node of the Link Is a Fixed-Grid Node
In MFGONs, even if the spectrum resources spanning fixed grids can meet the quantity requirements of the service bandwidth, it cannot satisfy the spectrum-compatibility constraint, because the wavelength allocation of fixed-grid optical network resources needs to be limited to the same wavelength channel. These continuous spectrum resources therefore form discrete small-grained spectrum blocks. The discrete spectrum blocks that are difficult to be utilized in MFGONs due to the spectrum compatibility constraint are called unique new spectrum fragments, and are referred to as spectrum fragments hereafter for unified explanation. The LSC in this case should be modified as follows. When an idle spectrum spans two different channel positions, it needs to be divided into two discrete small-grained spectrum blocks. Hence, parameter H, which represents the number of spectrum blocks in Equation (1), needs to be revised as explained in the next lines. The revised H is denoted as H’ in Equation (2).
To further illustrate two different scenarios, an example of a calculation is show in Figure 2a,b, where C_flex denotes the LSC of the link whose initial node is a flex-grid node, and C_fixed denotes the LSC of the link whose initial node is a fixed-grid node. Note that the square with the plaid pattern denotes an occupied spectrum slot and the blank square denotes an unused spectrum slot. When the initial node is a fixed-grid node and because the fixed grid occupies 50 GHz (corresponding to 4 frequency slots of 12.5 GHz each), the first spectrum block shown in Figure 2a is divided into two spectrum blocks by the dashed line shown in Figure 2b, so the value of H that was 3 if the starting node is a flex-grid node according to Figure 2a now changes to H′ = 4.
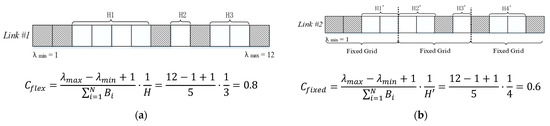
Figure 2.
Link spectrum compactness calculation example: (a) LSC of link #1; (b) LSC of link #2.
3.2. The Radiancy of Nodes (RoNs)
In view of the limitations of the current RSA algorithms, we proposed RoNs to reflect the connection states of the corresponding nodes. RoNs can reflect the impact of establishing connections on network resources and the subsequent requests. Because of different spectrum granularities and complex restrictions, a low spectrum utilization mode emerges on the link that starts from a node whose type is different from the type of source node and ends at a node whose type is the same as the type of source node. At the same time, this low utilization mode affects other links connected with it. Therefore, the routing distribution can be optimized by considering the connection states of nodes on the paths to further break through the limitation. The calculation formulation of RoNs is defined in Equation (3), where D is the value of RoNs, d is defined as the degree of the node, so as to reflect the position of the node in the whole network topology. The smaller the RoNs value, the higher the status of the node in the network, and the less likely the link spectrum is wasted. The specific value of n is related to the type of source node and current node. It can be divided based on the following two situations:
When the node is the same type as the source node:
When the node is the different type as the source node:
The value of n represents the number of flex/fixed-grid nodes adjacent to the node in the network. Where is the number of fixed-grid nodes connected to a flex-grid node when the source node is a flex-grid node, and is the number of flex-grid nodes connected to a fixed-grid node when the source node is a fixed-grid node, is the number of flex-grid nodes connected to a fixed-grid node when the source node is a flex-grid node, and is the number of flex-grid nodes connected to a flex-grid node when the source node is a fixed-grid node.
3.2.1. The Same Type with the Source Node
- The source node is a flex-grid node.
When the source node is a flex-grid node, the low spectrum utilization patterns emerge on the link starting from a node with a different type than the source node. With less nodes of the different type in the path, there is less chance of wasting resources. Therefore, the value of n in this case is the number of fixed-grid nodes connected to the flex-grid node, for example, in the topology shown in Figure 1e, for flex-grid node 5 in the path 4-5-2-3. There are two connected fixed-grid nodes that include nodes 2 and 6, so the value of n is 2 and the value of D is 2/4.
- The source node is a fixed-grid node.
When the source node is a fixed-grid node, the spectrum must satisfy the wavelength granularity, which leads to a certain degree of spectrum waste (for fixed-grid nodes, the spectrum can only be selected at the wavelength granularity regardless of resource utilization). To avoid the unnecessary waste of the flex-grid spectrum, it is more advantageous to select nodes with more fixed-grid nodes. In the path 3-6-9-8, the fixed-node, node 6, has two connected flex-grid nodes, including nodes 5 and 9, so the value of n is 2 and the value of D is 2/3.
3.2.2. The Different Type with the Source Node
- The source node is a flex-grid node.
When the source node is a flex-grid node, the low spectrum utilization mode emerges on the link starting from a fixed-grid node. Considering the subsequent requests, the inefficient occupancy radiates to flex-grid nodes when the source node is a flex-grid node. Therefore, the value of n in this case is the number of flex-grid nodes connected to the fixed-grid node. For example, in the topology shown in Figure 1e, spectrum wastage is caused by fixed-grid node 2 whose type is different from that of flex-grid node 4 in the path 4-1-2-3. For fixed-grid node 2, there are two connected flex-grid nodes that include nodes 1 and 5, so the value of n is 2 and the value of D is 2/3.
- The source node is a fixed-grid node.
The spectrum must meet the wavelength granularity when the source node of a link is a fixed grid, which leads to the low spectrum utilization on the link starting from a fixed-grid node. The inefficient occupation radiates to flex-grid nodes. There is only one directly connected flex-grid node for node 1 in the path 3-2-1-4, so the value of n is 1 and D is 1/2.
3.3. The Spectrum Entropy (SE) of Optical Path
Based on the above concepts, the SE of an optical path is proposed to evaluate the cost of each alternative path. The SE of a path is defined as shown in Equation (5).
where represents a node in the path; means traversing all the nodes except the destination; L represents the alternate path; and are Boolean values. For node with the same type as the source node, , ; otherwise, , , C represents the LSC with v as the initial node, and the calculation method is related to the type of ; D and D’ are the RoNs of node , and the calculation method is related to the type of the source node and .
The cumulative process implies the consideration of the nodes on the path when finding the routing path for the connection request. Generally, the more the nodes on the path, the greater the cumulative sum. The path with the lower SE becomes the final path to establish a connection at a lower bandwidth blocking ratio. For example, as shown in Figure 3b, the path whose source node is a flex-grid node has two links. The calculation has two summed parts. Node 2 is different from the type of source node, so it is necessary to calculate the D of node 2, which is 1/2. The final SE is obtained by substituting the parameters into Equation (4). The calculation of SE in other scenarios is similar to the above. These examples are relevant to the topology shown in Figure 1e.
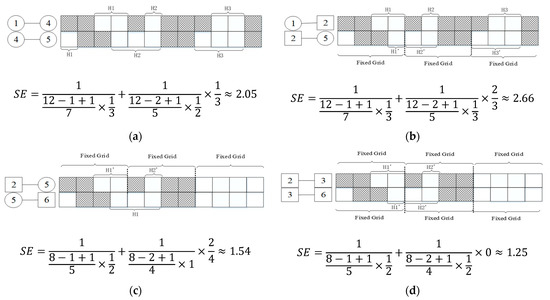
Figure 3.
Example of the calculation of SE in four different situations. (a) A path where all nodes are flex-grid nodes. (b) A path where the source node is a flex-grid node and passing through some fixed-grid nodes. (c) A path where the source node is a fixed-grid node and passing through some flex-grid nodes. (d) A path where all nodes are fixed-grid nodes.
3.4. Spectrum-Entropy-Minimized Routing and Spectrum Allocation (SEM-RSA)
Based on the concepts mentioned above, the proposed SEM-RSA algorithm (Algorithm 1) is described as follows. The values of and K need to be initialized at first. It should be noted that the setting of the K value affects the time complexity of the algorithm and the value is related to the topology (line 1). After the initialization, the algorithm determines whether the connection can be established based on the requested rate and the type of the source node. If the request-rate from the fixed-grid node exceeds , the service cannot be accommodated. When the result is judged to be successful, K paths are calculated using the KSP algorithm and are saved in Ω (line 2–7). Then, all the paths in Ω are traversed and the path with sufficient resources is selected to calculate the value of SE. These paths are stored in θ (line 9–12). When θ is not an empty set, the algorithm selects the path with the minimum SE to establish the connection. Otherwise, the type of the source node needs to be judged at this time. When the source node is a flex-grid node and is greater than , the request is divided into sub-requests with small rates and the algorithm executes line 3 for each sub-request. If not, the connection fails to be established (lines 13–21). Finally, the RESULT is output and the network spectrum states are updated.
| Algorithm 1 Spectrum-Entropy-Minimized Routing and Spectrum Allocation (S EM-RSA) Algorithm. |
| SEM-RSA Algorithm |
| Input: G, r(), , K; |
| Output: SEM-RSA algorithm, RESULT; |
| 1: Initialize the value of K based on delay and performance requirements as well as determine the value of ; |
| 2: for each request r() do |
| 3: if is a fixed-grid node && > |
| 4: RESULT = FAILED; |
| 5: else 6: Ω ⬅ Routing computation with K disjoint paths (G, k); |
| 7: end if |
| 8: for ∈ Ω do |
| 9: if adequate spectrum resources exist on path to establish connections |
| 10: Compute the corresponding to path ; 11: θ⬅ (, ); |
| 12: end if |
| 13: if θ ≠ |
| 14: Choose the with the smallest ; |
| 15: = ; |
| 16: RESULT = SUCCEED |
| 17: else if is a flex-grid node && > |
| 18: Divide super-wavelength request into sub-requests; |
| 19: Execute line 3 for each sub-request; |
| 20: else RESULT = FAILED; |
| 21: end if |
| 22: Output RESULT and update network spectrum states; |
| 23: end for 24: end for |
The time complexity of lines 1–7 was O () determined by the KSP algorithm. For each path, lines 8–18 were traversed once, so the time complexity of this part was O (KF). The time complexity of the step of judging the final path was O (K), which did not affect the overall performance. Thus, the overall time complexity of this SEM-RSA algorithm was approximately O (+).
4. Performance Evaluation and Analysis
For evaluating the performance of the proposed SEM-RSA algorithm in MFGONs, we used two network topologies, i.e., 30-Node-CONUS (30 nodes and 36 links) and COST-239NET (11 nodes and 26 links) in the simulations, respectively, as shown in Figure 4. 30-Node-CONUS is a network topology for the United States, which has a large number of nodes and low node connectivity; COST-239NET is a network topology for Europe that has fewer nodes and greater node connectivity. The simulations were performed on a computer with a 2.5 GHz Intel Core i5-7200U CPU and 8 GB RAM. We set different parameters in our simulation in terms of bandwidth, topology, and traffic, and verified their impact on the algorithm performance under end-user demand with different arrival/duration times and different bandwidths. Every data we obtained was based on 105 requests to ensure the accuracy and stability of the simulation. Each fiber had 400 FSs or 100 wavelengths. The value of K was set to 3 and was set to 100 Gb/s. Traffic of the requests was divided into four levels: 40 Gb/s, 100 Gb/s, 200 Gb/s, and 400 Gb/s. The four traffic requirements of requests were uniformly distributed, except in Section 4.2.
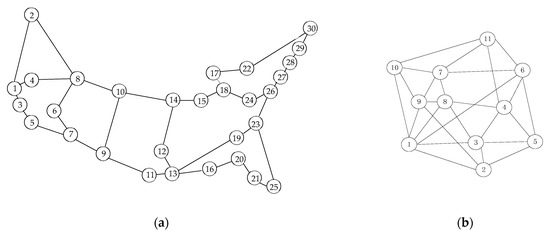
Figure 4.
Network topologies used for simulations: (a) 30-Node-CONUS; (b) COST-239NET.
4.1. Bandwidth Blocking Ratio (BBR) under Different Flex-Grid Nodes’ Proportions
In order to prove the advantages of the proposed algorithm, we compared the algorithm under the same network and traffic with the baseline MDRA algorithm proposed in the-state-of-the-art work [28], which proposed a routing and spectrum allocation strategy and considered modulation-format allocation in mixed-grid optical networks. The results are shown in Figure 5. There are different migration strategies from fixed grid to flex grid, including updating the nodes one by one [15] and partially updating the wavelength-selective switches in a node [29]. In this simulation, we chose the former migration strategy. Two different scenarios were set up, including 50% and 70% flex-grid nodes out of all the nodes, which were scenarios A and B, respectively. Figure 5a shows that SEM-RSA has a lower bandwidth blocking ratio (BBR) than the baseline algorithm under the same traffic load. It is shown that the SEM-RSA algorithm is applicable to MFGON with different flex-grid-node ratios. Additionally, only considering a single metric of LSC or RoNs was also simulated. The results show that the SEM-RSA algorithm can always achieve the best performance.
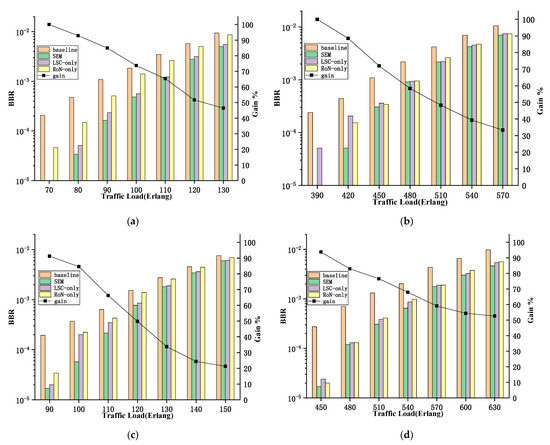
Figure 5.
BBR performance in (a) 30-Node-CONUS under scenario A; (b) COST-239NET under scenario A; (c) 30-Node-CONUS under scenario B; (d) COST-239NET under scenario B.
The curves in Figure 5 represent the performance gains of the SEM-RSA algorithm relative to the baseline algorithm. It can be observed that, with the increase in traffic load, the gain gradually decreases. The reason for this phenomenon is that, when the traffic is at a low level, the connection request arrives and leaves, resulting in a higher possibility of fragmentations in the network. At this time, the improvement of the SEM-RSA algorithm is more obvious. With the increase in traffic load, the connection lasts longer in the network; as a result, there are relatively fewer fragments in the network and the improvement space is limited. However, the overall advantage of the algorithm still exists.
Moreover, by comparing the curves in scenarios A and B, we can see that, with the increasing proportion of flex-grid nodes in the network, the SEM-RSA algorithm can achieve better results. In addition n, further simulations were conducted in COST-239NET, which has a higher network node connectivity compared to 30-Node-CONUS, to prove that the SEM-RSA algorithm is effective for different network topologies. By comparing Figure 5a,c and Figure 5b,d, it can be found that, when the network connectivity was lower, the performance improvement of SEM-RSA was more obvious. This was because, as the connectivity of the nodes increased, there was more selectivity in establishing connections. Moreover, the smaller number of nodes means the smaller routing probability between the nodes, the greater impact of each connection on the network, and the lower chances of blocking. As a result, the performance improvement of the SEM-RSA algorithm was more obvious.
4.2. BBR under Different Bandwidth Requirement Proportions
The above results were obtained on the premise that the bandwidth requirements of requests were uniformly distributed. In order to prove the wide applicability of the algorithm, we changed the proportion of each bandwidth and designed different scenarios. It was assumed that the total bandwidth required by requests had four different levels: 2, 3, 6, and 10 FSs. This paper simulated four different scenarios, low-bandwidth-requirement concentration (LBR), middle-bandwidth-requirement concentration (MBR), high-bandwidth-requirement concentration (HBR), and uniform-bandwidth-requirement (UBR), where the proportions of the requests for the above bandwidth requirement were 3:3:2:2, 2:3:3:2, 2:2:3:3, and 1:1:1:1, respectively. The simulation results are presented in Figure 6.
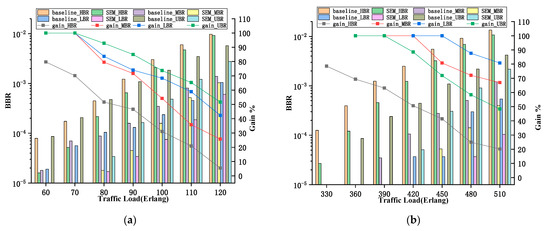
Figure 6.
BBR of different routing algorithms with different request ratios in (a) 30-Node-CONUS; (b) COST-239NET.
As shown in Figure 6a, the simulation results show that the SEM-RSA algorithm still has relatively good improvement under different scenarios, but the overall BBR shows an upward trend as the proportion of high-bandwidth-demand increases. In addition, the curve in the simulation diagram shows the performance gain of the SEM-RSA algorithm relative to the benchmark algorithm in terms of BBR under different scenarios. It can be seen that, in the scenario of LBR, the improvement effect of the SEM-RSA algorithm is more obvious. This is because when low bandwidth demands are concentrated, it is easier to form small-grained spectrum fragments with frequent arrivals and departures of requests. In the case of more spectrum fragments, the degree of fragmentation of the network is fully considered in the SEM-RSA algorithm, so the improvement effect of the SEM-RSA algorithm is better. In addition, the trend in Figure 6b for COST-239NET is similar to Figure 6a, which shows that the performance improvement of the SEM-RSA algorithm in terms of BBR can also be adapted to different topologies in different traffic distribution conditions.
4.3. Revenue Analysis of Node Upgrading
The MFGON exists for a long time, and upgrading the fixed-grid nodes until all the nodes in the network are flex-grid nodes will be the main tone for a period of time. From the perspective of operators, it is hoped that the upgrading of the nodes can produce the maximum benefits. Therefore, this paper also compared the gains produced by the two algorithms after upgrading a single node, and the results are shown in Figure 7. We used “BU” to denote “before upgrading” “AU” to denote “after upgrading”.
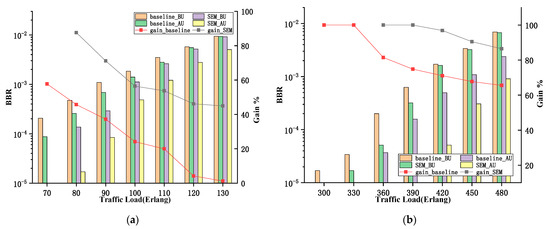
Figure 7.
Gain from upgrading nodes of different routing algorithms. (a) 30-Node-CONUS; (b) COST-239NET.
Figure 7a shows BBR under different traffic loads. We can see that the BBR of both algorithms decreases with upgrading on the whole. Moreover, the curve reflects the performance improvement after upgrading. The missing points are because the BBR is 0, before and after node upgrading. The results show that the gain of the baseline algorithm is maintained at a low level under different traffic loads. This indicates that, although the BBR decreases considerably after upgrading, the benefits of upgrading are low. On the contrary, the gain of upgrading for the SEM-RSA algorithm is close to 100% when the traffic load is at a low value. Although the gain becomes worse with the increase in traffic load, the worst-case benefit of upgrading is still 35.4% higher than that of the baseline algorithm. In particular, this trend is consistent with the pattern shown in Figure 5. It is shown that the single-node upgrade also has the effect of improving the BBR, but it is not as obvious as the multi-node upgrade. Figure 7b shows the simulation results for COST-239NET. The trend of the curve is basically similar to that in Figure 7a, but the overall gain is better for the same traffic load. The minimum gain is about 12.5%, which is also better than the results for the 30-Node-CONUS topology.
Normally, in a practical network, the highly connected nodes tend to carry services in a more centralized way. In order to further verify the performance of the SEM-RSA algorithm after upgrading several nodes, the corresponding simulation was conducted and the results are shown in Figure 8. Scenario C represents 50% requests from flex-grid nodes and scenario D represents 70% requests from flex-grid nodes. As can be seen from Figure 8a,b, the overall performance of the SEM-RSA algorithm decreases with the increase in traffic, which conforms to the above rules. In addition, through these three curves, it can be found that the better performance of the SEM-RSA algorithm can be achieved when more requests come from flex-grid nodes. On the other hand, the probability of requests from these nodes is also one of the factors worth considering when updating nodes, in addition to giving priority to those nodes with high connectivity. In order to show the simulation results more clearly, we enumerated the main points, as shown in Table 2.
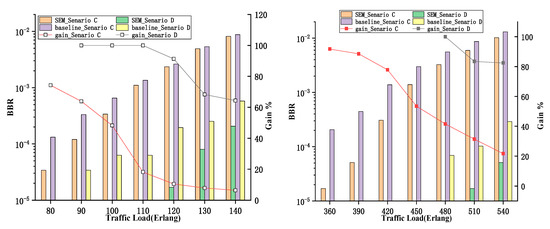
Figure 8.
BBR of different routing algorithms with different occurrence ratios in (a) 30-Node-CONUS; (b) COST-239NET.

Table 2.
BBR performance of the SEM algorithm compared to the baseline.
5. Conclusions
In this paper, the shortcomings of the existing research and the possible problems in MFGONs were summarized. To cope with the new challenges of the RSA problem in MFGONs, the concepts of LSC and RoNs were proposed. Based on them, an SE model that can be used to estimate the quality of a path and a novel SEM-RSA algorithm was designed for MFGONs. The simulation results show that the SEM-RSA algorithm has obvious advantages in terms of BBR, especially in the scenarios with a low-bandwidth-demand aggregation. However, this advantage may become less obvious with the increase in traffic load. To illustrate the wide application of the SEM-RSA algorithm, the simulation was performed in two topologies, including 30-Node-CONUS and COST-239NET.Furthermore, the results show that the SEM-RSA algorithm is more effective for the scenarios with a low-bandwidth-demand aggregation or high possibility of fragmentation. The paper also simulated the gains of different algorithms for upgrading nodes. The results show that the SEM-RSA algorithm can increase the benefits of updating. Realistic factors were fully taken into account in the simulation process. In addition, by analyzing the simulation results further, it was possible to infer that a greater gain could be obtained from the nodes with a higher connectivity.
Author Contributions
Conceptualization, X.Y.; methodology, X.Y. and Y.Z.; software, L.L.; validation, L.L. and Q.Z.; writing—original draft preparation, X.Y. and L.L.; writing—review and editing, Q.Z., Y.Z., A.N. and J.Z.; supervision, Y.Z. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program under Grant 2018YFB1800504.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brackett, C.A. Dense wavelength division multiplexing networks: Principles and applications. IEEE J. Sel. Areas Commun. 1990, 8, 948–964. [Google Scholar] [CrossRef]
- Rival, O.; Morea, A. Cost-efficiency of mixed 10-40-100Gb/s networks and elastic optical networks. In Proceedings of the Optical Fiber Communication Conference 2011, Los Angeles, CA, USA, 6–10 March 2011; Optical Society of America: Washington, DC, USA, 2011; p. OTul4. [Google Scholar]
- Kozicki, B.; Takara, H.; Tsukishima, Y.; Yoshimatsu, T.; Yonenaga, K.; Jinno, M. Experimental demonstration of spectrum-sliced elastic optical path network (SLICE). Opt. Express 2010, 18, 22105–22118. [Google Scholar] [CrossRef] [PubMed]
- Jinno, M.; Takara, H.; Kozicki, B.; Tsukishima, Y.; Sone, Y.; Matsuoka, S. Spectrum-efficient and scalable elastic optical path network: Architecture, benefits, and enabling technologies. IEEE Commun. Mag. 2009, 47, 66–73. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, K.; Sahasrabuddhe, L.; Yoo, S.B.; Mukherjee, B. On the study of routing and wavelength assignment approaches for survivable wavelength-routed WDM mesh networks. Opt. Netw. Mag. 2003, 4, 16–28. [Google Scholar]
- Ramaswami, R.; Sivarajan, K.N. Routing and wavelength assignment in all-optical networks. IEEE/ACM Trans. Netw. 1995, 3, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Cao, X.; Hu, Q.; Pan, Y. Towards elastic and fine-granular bandwidth allocation in spectrum-sliced optical networks. J. Opt. Commun. Netw. 2012, 4, 906–917. [Google Scholar] [CrossRef]
- Ruan, L.; Xiao, N. Survivable multipath routing and spectrum allocation in OFDM-based flexible optical networks. J. Opt. Commun. Netw. 2013, 5, 172–182. [Google Scholar] [CrossRef]
- Zhang, G.; De Leenheer, M.; Mukherjee, B. Optical traffic grooming in OFDM-based elastic optical networks. J. Opt. Commun. Netw. 2012, 4, B17–B25. [Google Scholar] [CrossRef]
- Yu, X.; Zhao, Y.; Zhang, J.; Mukherjee, B.; Zhang, J.; Wang, X. Static Routing and Spectrum Assignment in Co-existing Fixed/Flex Grid Optical Networks. In Proceedings of the Optical Fiber Communication Conference 2014, San Francisco, CA, USA, 9–13 March 2014; Optical Society of America: Washington, DC, USA, 2014; pp. 1–3. [Google Scholar]
- Christodoulopoulos, K.; Tomkos, I.; Varvarigos, E.A. Routing and spectrum allocation in OFDM-based optical networks with elastic bandwidth allocation. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM, Miami, FL, USA, 6–10 December 2010; pp. 1–6. [Google Scholar]
- Chatterjee, B.C.; Sarma, N.; Oki, E. Routing and spectrum allocation in elastic optical networks: A tutorial. IEEE Commun. Surv. Tutor. 2015, 17, 1776–1800. [Google Scholar] [CrossRef]
- Afsharlar, P.; Deylamsalehi, A.; Plante, J.M.; Zhao, J.; Vokkarane, V.M. Routing and spectrum assignment with delayed allocation in elastic optical networks. J. Opt. Commun. Netw. 2017, 9, B101–B111. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, F.; Zhu, Z.; Chen, Y. Analysis framework of RSA algorithms in elastic optical rings. J. Lightwave Technol. 2018, 37, 1113–1122. [Google Scholar] [CrossRef]
- Yu, X.; Tornatore, M.; Xia, M.; Wang, J.; Zhang, J.; Zhao, Y.; Zhang, J.; Mukherjee, B. Migration from fixed grid to flexible grid in optical networks. IEEE Commun. Mag. 2015, 53, 34–43. [Google Scholar] [CrossRef]
- Pastorelli, R.; Bosco, G.; Piciaccia, S.; Forghieri, F. Network planning strategies for next-generation flexible optical networks. J. Opt. Commun. Netw. 2015, 7, A511–A525. [Google Scholar] [CrossRef]
- Yu, X.; Tornatore, M.; Zhao, Y.; Zhang, J.; Wang, X.; Zhang, S.; Wang, R.; Wang, J.; Zhang, J.; Mukherjee, B. When and how should the optical network be upgraded to flex grid? In Proceedings of the 2014 The European Conference on Optical Communication (ECOC), Cannes, France, 21–25 September 2014; pp. 1–3. [Google Scholar]
- Meusburger, C.; Schupke, D.A.; Lord, A. Optimizing the migration of channels with higher bitrates. J. Lightwave Technol. 2010, 28, 608–615. [Google Scholar] [CrossRef]
- Morais, R.M.; Pedro, J.; Pinto, A.N. Techno-economic analysis of fixed and flexible node architectures in multiperiod scenarios. J. Opt. Commun. Netw. 2015, 7, B109–B121. [Google Scholar] [CrossRef]
- Mayoral, A.; Lopez, V.; de Dios, O.G.; Fernandez-Palacios, J.P. Migration steps toward flexi-grid networks. J. Opt. Commun. Netw. 2014, 6, 988–996. [Google Scholar] [CrossRef]
- Zang, H.; Jue, J.P.; Mukherjee, B. A review of routing and wavelength assignment approaches for wavelength-routed optical WDM networks. SPIE Opt. Netw. Mag. 2000, 1, 47–60. [Google Scholar]
- Yu, X.; Zhao, Y.; Zhang, J. Optical grooming with spectrum engineering (og-se) in flexi-grid networks. In Proceedings of the Optical Fiber Communication Conference 2014, San Francisco, CA, USA, 9–13 March 2014; Optical Society of America: Washington, DC, USA, 2014; p. W3H-4. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Bose, S.K.; Shen, G. Migration from fixed to flexible grid optical networks with sub-band virtual concatenation. J. Lightwave Technol. 2017, 35, 1752–1765. [Google Scholar] [CrossRef]
- Christodoulopoulos, K.; Tomkos, I.; Varvarigos, E.A. Elastic bandwidth allocation in flexible OFDM-based optical networks. J. Lightwave Technol. 2011, 29, 1354–1366. [Google Scholar] [CrossRef]
- Zhang, M.; You, C.; Jiang, H.; Zhu, Z. Dynamic and adaptive bandwidth defragmentation in spectrum-sliced elastic optical networks with time-varying traffic. J. Lightwave Technol. 2014, 32, 1014–1023. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Kim, I.; Palacharla, P.; Sekiya, M. Utilization entropy for assessing resource fragmentation in optical networks. In Proceedings of the Optical Fiber Communication Conference 2012, Los Angeles, CA, USA, 4–8 March 2012; Optical Society of America: Washington, DC, USA , 2012; p. OTh1A-2. [Google Scholar]
- Yu, X.; Zhang, J.; Zhao, Y.; Peng, T.; Bai, Y.; Wang, D.; Lin, X. Spectrum compactness based defragmentation in flexible bandwidth optical networks. In Proceedings of the OFC/NFOEC, Los Angeles, CA, USA, 4–8 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–3. [Google Scholar]
- Ahmed, T.; Rahman, S.; Ferdousi, S.; Tornatore, M.; Mitra, A.; Chatterjee, B.C.; Mukherjee, B. Dynamic routing, spectrum, and modulation-format allocation in mixed-grid optical networks. J. Opt. Commun. Netw. 2020, 12, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Tornatore, M.; Xia, M.; Zhao, Y.; Zhang, J.; Mukherjee, B. Brown-field migration from fixed grid to flexible grid in optical networks. In Proceedings of the Optical Fiber Communication Conference 2015, Los Angeles, CA, USA, 22–26 March 2015; Optical Society of America: Washington, DC, USA, 2015; p. W1I-4. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).