Abstract
By combining a spiral zone plate (SZP) and a grating, we propose a single optical element, termed a composited spiral zone plate grating (CSZPG), to generate flower mode vortices with the equicohesive petals and has long focal depths. Theoretical analysis reveals that the CSZPG can generate flower mode vortices with approximately equicohesive petals, and that it has longer focal depths compared with the conventional SZP. Moreover, the performance of the CSZPG on the period, focal length and radius is investigated. The experimental results are also presented, agreeing well with the theoretical predictions. The unique characteristics of the proposed CSZPG make it attractive for many applications such as particle trapping and optical imaging.
1. Introduction
In 1992, Swartzlander and his coworkers discovered optical vortex solitons on the basis of the theory and the experiment [1]. In the same year, Allen and his coworkers used Maxwell’s equations to prove that optical vortices [2,3,4,5,6,7] can have a certain orbital angular momentum [8]. The central intensity of the vortex beams on the axis is equal to zero [9]. In addition, the light intensity of the vortex beams is distributed in a ring shape during the propagation and the structure of wavefront is spiral. The spiral phase of optical vortex distribution can be written as exp(ilθ), where l denotes the topological charge (TC) and θ denotes the azimuthal angle. Optical vortex has enabled many diverse applications, such as twisting metal [10], optical communication [11], particle manipulation [12] and super-resolution imaging [13]. So far, to enable emerging applications, various techniques have been proposed to generate vortex beams, such as diffractive optical elements [14], spatial light modulators [15], active vortex laser generators [16] and metasurfaces [17]. In these methods, diffractive optical elements are one of the most efficient and all-purpose ways to generate optical vortex because of its eminent characteristics including small size, light weight and flexible design.
In recent years, the complex flower mode vortices have also been proposed, which can be generated by composited fork holograms [18], composited dammann vortex grating (CDVG) [19], superposition of Laguerre–Gaussian beams with opposite-signed charges [20] and spatial light modulator [21], azimuthal phase-shifted zone plate [22], petal-like zone plate [23], etc. These flower mode vortices which possess some unique properties such as the sinusoidal intensity pattern and features angular self-reconstruction [24] have been widely used in some new and traditional applications. For example, flower mode vortices with multi-ring petal-like lobes have opened a new avenue to research the Hofstadter–Hubbard model and observe interactions fractional quantum Hall physics [25], the generation of high orbital angular momentum harmonics and amplification mechanism [26] and ultrasensitive angular measurement [27].
In this paper, by combining a spiral zone plate and a grating, we propose a single optical element-composited spiral zone plate grating (CSZPG) to generate flower mode vortices. The design, performance analysis, fabrication and experimental demonstration of the CSZPG were presented in detail. It was proved in the simulations and experiments that the CSZPG can generate flower mode vortices with approximately equicohesive petals, and that it has long focal depths. The proposed CSZPG can be fabricated by standard planar process with low cost and convenient fabrication, and it will have wide applications in particle manipulation and optical imaging.
2. Design
For the conventional spiral zone plate (SZP), the functional form of the SZP can be written as:
where (r, φ) represents the polar coordinates, l represents the topological charge, λ denotes the wavelength and f represents the focal length. After binarization, the transmittance function of the SZP can be expressed as:
where (x, y) represents the cartesian coordinates. The functional form of the grating can be expressed as:
where k = 2 π/d, d is the grating period. The transmittance function of the grating by binarization can be expressed as:
where n = 0, 1, 2, 3, …, w is line width of the grating. In this paper, w is equal to half of the period.
A CSZPG is composed by the inner zones of a spiral zone plate and the outer zones of a grating. The transmittance function of the CSZPG can be written as:
where tf is transmittance function of the filter, which is composed of the circle zone. Additionally, tf can be written as:
The designing process of the CSZPG is shown in Figure 1. The spiral zone plate and the grating with parameters of f = 250 mm, d = 400 μm and l = 6 are shown in Figure 1a and Figure 1c, respectively. The filter with the parameter of R = 1500 μm is shown in Figure 1b. The structure shown in Figure 1d is inversed with the filter in Figure 1b. The inner spiral zone plate by multiplying the spiral zone plate and the filter in Figure 1a,b is shown in Figure 1e. The outer grating by multiplying the grating and the inverse filter in Figure 1c,d is shown Figure 1f. The designed CSZPG composed by the inner spiral zone plate and the outer grating is shown in Figure 1g.
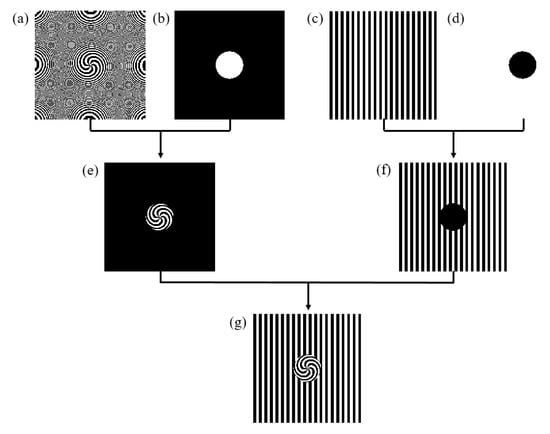
Figure 1.
The construction method of the CSZPG; the schematic diagrams of (a) the SZP, (b) the filter, (c) the grating, (d) the inversed filter, (e) the inner spiral zone plate, (f) the outer grating, and (g) the CSZPG, respectively.
3. Properties of the CSZPG
When a plane wave illuminates the proposed CSZPG, the intensity distribution in the observation plane can be written as:
where and are the coordinates of the observation plane and the CSZPG plane, respectively, z is the propagating distance from the CSZPG to the observation plane.
In order to compute quickly in the simulation, a fast Fourier transform (FFT) method is used to calculate the intensity distribution. So, Equation (7) can be rewritten as:
where F represents the FFT, F−1 denotes an inverse FFT.
In the simulations, the CSZPG is composed by the inner spiral zone plate and the outer grating with l = 6, f = 250 mm and d = 400 μm. The parameter R of the filter is 1500 μm. Figure 2a–c show the schematic diagrams of the grating, the SZP and the proposed CSZPG, respectively. The diffraction patterns of the grating, the SZP and the CSZPG at the location of z = 250 mm are shown in Figure 2d–f, respectively. It can be seen from Figure 2d,e that the grating can generate multiple diffraction orders and the SZP can generate optical vortex at the location of z = 250 mm. While the proposed CSZPG can generate flower mode vortices with six approximately equicohesive petals at the same position of z = 250 mm, and the number of petals in the flower mode vortices is the same with the topological charge l of the SZP. In addition, the normalized intensity distributions along the red lines in Figure 2e,f are shown in Figure 3 for comparison. Obviously, the intensity distributions of the SZP and the CSZPG have some differences. The vortex size of the CSZPG is larger than that of the SZP, and high-order diffractions can clearly be seen in the observed plane. The main reason is that the CSZPG combines the advantages of the grating and the SZP, which makes the CSZPG simultaneously possess the capability of dispersion and focus. Thus, the intensity profile of the CSZPG can be obtained from the focused spot in the SZP to the flower mode vortices.
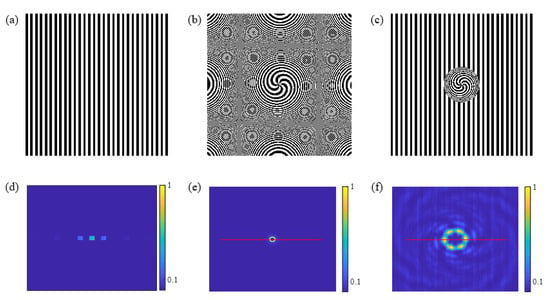
Figure 2.
Schematic diagrams of (a) the grating, (b) the SZP and (c) the CSZPG. (d–f) show the corresponding simulated normalized diffraction patterns for (a–c), respectively.
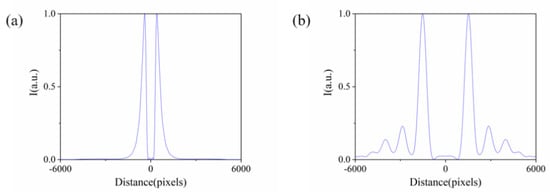
Figure 4a–i show the transverse diffraction patterns of the propagating CSZPG beams at the location of z = 250 mm with topological charge l = 2, 3, 4, 5, 6, 7, 8, 9 and 10, respectively. It can be clearly seen that the CSZPG generates flower mode vortices with 2, 3, 4, 5, 6, 7, 8, 9 and 10 petals which is same with the topological charge. Since the radius of the vortex increases as the topological charge increases in the SZP [28], the CSZPG composed by the inner SZP and the outer grating also follows this principle, and the region of the flower mode vortices gradually increases with the increase in the topological charge. Additionally, the spiral directions outside the central petal are reversed when the TCs are different signs in Figure 5, but the flower mode vortices are approximately the same. Thus, the CSZPG composed by the inner SZP and the outer grating can generate flower mode vortices, and the number of petals coincides with the topological charge of the corresponding SZP.
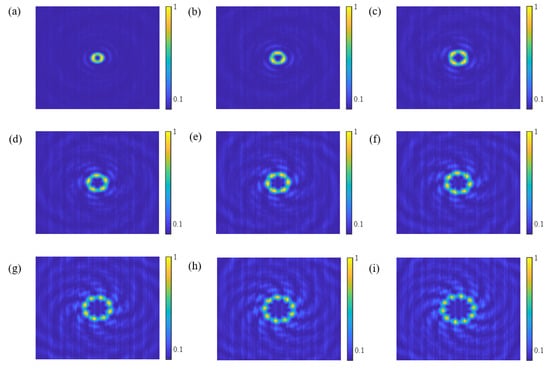
Figure 4.
Simulated normalized diffraction patterns for the CSZPG with (a) l = 2, (b) l = 3, (c) l = 4, (d) l = 5, (e) l = 6, (f) l = 7, (g) l = 8, (h) l = 9 and (i) l = 10, respectively.
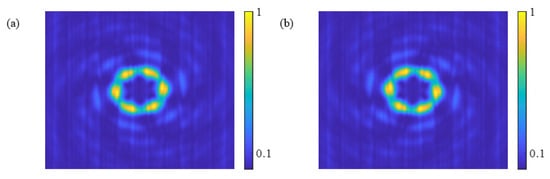
Figure 5.
Simulated normalized diffraction patterns for the CSZPG with (a) l = 6 and (b) l = −6, respectively.
Due to further research studies, it is indicated that the CSZPG can not only generate flower mode vortices, but that it also has an ultra-long depth of focus. We selected cross-section patterns of the vortex along the propagating direction, and the propagating distance is from 200 mm to 300 mm. Figure 6a,b show the cross-section patterns of the propagating SZP and the CSZPG, respectively. The horizontal axis represents the propagating distance, and the vertical axis denotes the size of the vortex beams in Figure 6. It can be found in Figure 6a that the propagating beam focuses at the location of z = 250 mm and quickly diverges on both sides of the SZP. However, in Figure 6b high-order diffractions exist in the region away from the center of the vortex, and the central focal spots are approximately same at the position from z = 230 mm to z = 270 mm for the CSZPG. Figure 7a,b show the diffraction patterns for the CSZPG at the positions of z = 230 mm and z = 270 mm, respectively. It can be found that the two patterns have the same size and image approximately. Therefore, compared with the SZP, the CSZPG has longer focal depths.
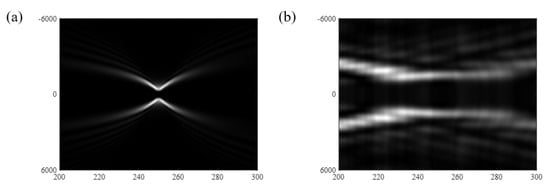
Figure 6.
The sampling cross–section patterns along the propagation from z = 200 mm to z = 300 mm for (a) the SZP and (b) the CSZPG.
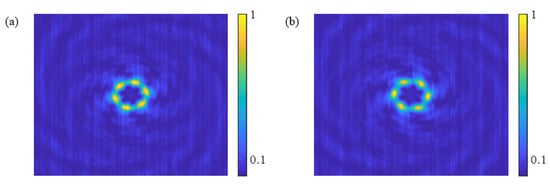
Figure 7.
The simulated normalized diffraction patterns at the position of (a) z = 230 mm and (b) z = 270 mm.
The focusing performance of the CSZPG composed by the inner SZP and the outer grating is determined by the parameters with period, radius, topological charge and focal length. In the following, we will investigate the effect of structural parameters on the focusing performance of the proposed samples.
Figure 8a–c show the schematic diagrams of three CSZPGs with d = 100 μm, 400 μm and 800 μm, respectively. Figure 8d–f show the simulated normalized intensity profiles of the propagating CSZPG beams corresponding to Figure 8a–c, respectively. It can be found that the intensity of the vortex is proportional to the period compared with the patterns in Figure 8d,e. We can attribute this phenomenon to the fact that the dispersion ability of the grating becomes weaker corresponding to the increase in the period, which makes the diffraction intensity concentrate in the region of the vortex. However, when the period is very large, such as 800 μm, the dispersion of the grating is extremely weak, and the intensity profiles are approximately same as those seen in Figure 8e,f.
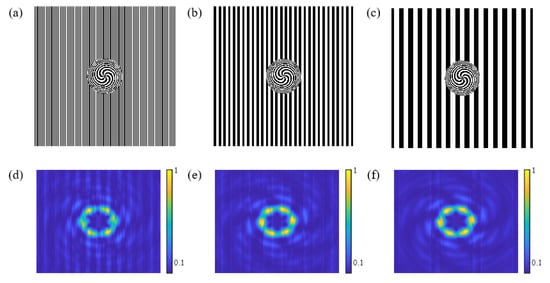
Figure 8.
Schematic diagrams of the CSZPG with the parameter of (a) d = 100 μm, (b) d = 400 μm and (c) d = 800 μm. (d–f) show the corresponding normalized diffraction patterns for (a–c), respectively.
Focal length of the CSZPG determines the focused position, and the intensity distribution in different focal lengths has some differences. For example, Figure 9a–c show the intensity distributions of the CSZPG by combining the SZP and the grating with the parameter of f = 200 mm, 250 mm and 300 mm, respectively. It is clearly seen that the intensity profiles of three CSZPGs are different. As the focal length increases from 200 mm to 300 mm, the vortex size also gradually increases. The main reason is that the dispersion characteristic of the grating exists in the CSZPG. The distance between different grating orders increases along the direction of propagation. So, for the CSZPG with the bigger focal length, the vortex size will be larger in the observed plane.
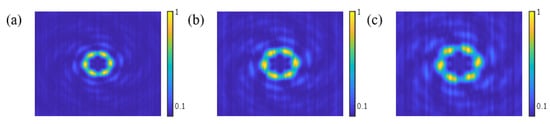
Figure 9.
The intensity distributions of the CSZPG with the parameter of (a) f = 200 mm, (b) f = 250 mm and (c) f = 300 mm.
The radius of the filter determines the proportion of the SZP in the CSZPG, which affects focusing performance. Figure 10a–c show the schematic diagrams of three CSZPGs with R = 1000 μm, 1500 μm and 3000 μm, respectively. Figure 10d–f show the transverse diffraction patterns of the propagating CSZPG beams corresponding to Figure 10a–c, respectively. In Figure 10, the CSZPG can generate flower mode vortices with approximately equicohesive petals. Moreover, it should be noted that the focusing characteristic changes corresponding to the increase in the radius. In Figure 10d, we can clearly see the flower mode vortices with scattered petals, and the intensity is not concentrated in the focal area but distributed over the whole area. As the radius increases to 1500 μm, the flower mode vortices with six centralized petals can be observed in the focal area and the intensity is mainly concentrated in the focal area in Figure 10e. While the radius is 3000 μm, six centralized petals of the flower mode vortices merge into a whole in Figure 10f. Thus, as the radius becomes larger, the area of the SZP is also increasing in the CSZPG, which leads the transmittance function of the SZP playing a major role in the transmittance function of the CSZPG. As a result, the vortex with scattered petals is constantly merged and finally the intensity pattern is approximately the same as the intensity profile of the SZP in Figure 2e.
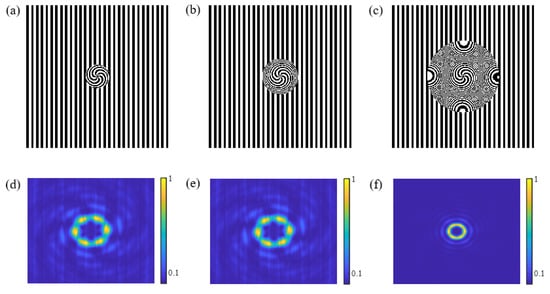
Figure 10.
Schematic diagrams of the CSZPG with the parameter of (a) R = 1000 μm, (b) R = 1500 μm and (c) R = 3000 μm. (d–f) show the corresponding diffraction patterns for (a–c).
4. Experiments
In order to prove the result in the simulations, the CSZPGs with TC of 2, 4, 6, 8, 10 and 12 were fabricated and tested. The parameters of the CSZPG are set as λ = 632.8 nm, d = 400 μm, R = 1500 μm and f = 250 mm. The fabrication procedure started with patterning the binary CSZPG onto the photoresist by using the direct writing laser lithography technology. After that, we used the wet etching to transfer the fabricated pattern onto the chrome layer and remove the residual photoresist with organic solution. Finally, the CSZPG was rinsed and dried. Figure 11b,c show the contourgraph images of the fabricated CSZPG corresponding to the red and blue circles shown in Figure 11a, respectively. The observed binary CSZPG reveals that the pattern of simulation design is in good agreement with those of actual fabrication, and the designed CSZPG has strong process compatibility.

Figure 11.
(a) Simulation design of the CSZPG with TC = 2, (b) fabricated CSZPG from the selected red circle in the simulation design shown in (a,c) fabricated CSZPG from the selected blue circle in the simulation design shown in (a).
The fabricated CSZPG was characterized by using the designed experimental setup demonstrated in Figure 12. Linearly polarized light with λ = 632.8 nm passed through the beam expander to increase the area of the beam. Then, the beam illuminated the fabricated CSZPG. The far-field diffraction pattern from the CSZPG was recorded by a charge coupled device (CCD, Lumenera LW230) with 1600 × 1200 pixels and 4.4 μm pixel size.
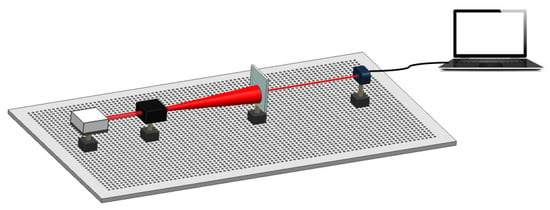
Figure 12.
Sketch map of the experimental setup. From left to right are laser source, beam expander, the CSZPG, CCD and computer.
As expected, it is experimentally demonstrated that in Figure 13a–f the CSZPG can generate flower mode vortices with approximately equicohesive petals, and the number of the petals is 2, 4, 6, 8, 10 and 12, which are equal to the topological charges, respectively. Moreover, the captured patterns are approximately the same as the corresponding numerical patterns in Figure 4. It should be noted that the intensity of the generated flower mode vortices becomes weaker as the topological charge increases. The main reason is that the CSZPG composed by the SZP and the grating possess the capability of dispersion, which makes the total light intensity evenly distribute over each petal. So, with the increase in topological charge, the intensity of the single petal gradually decreases.
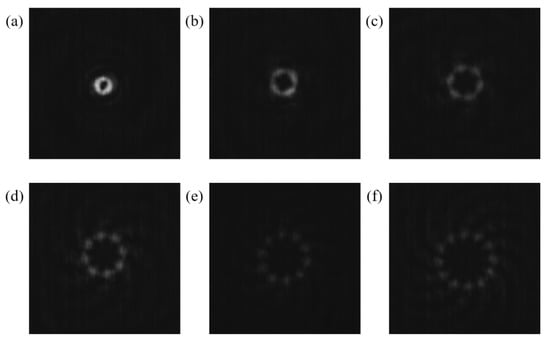
Figure 13.
Measured diffraction patterns for the CSZPG with (a) l = 2, (b) l = 4, (c) l = 6, (d) l = 8, (e) l = 10 and (f) l = 12, respectively.
Finally, we research the diffraction patterns of the design element away from the focal length. So, we measured the images of the CSZPG located at the positions of z = 230 mm, 250 mm and 270 mm in Figure 14b–d, respectively. It can be seen that the intensity and the size of the flower mode vortices generated by fabricated CSZPG at different positions are approximately the same. In addition, the shapes of the beams are well preserved at the positions of z = 220 mm and 290 mm in Figure 14a,e. Thus, the experiments show that CSZPG can achieve the long focal depths.

Figure 14.
Captured images of the CSZPG at the positions of (a) z = 220 mm, (b) z = 230 mm, (c) z = 250 mm, (d) z = 270 mm and (e) z = 290 mm, respectively.
5. Conclusions
In conclusion, we proposed a CSZPG to generate flower mode vortices by combining a SZP and a grating, and analyzed the influence of the period, focal length and radius on CSZPG performance. Both numerical and experimental results have verified that the CSZPG can generate flower mode vortices with approximately equicohesive petals, and the number of the petals is equal to topological charge. Moreover, the CSZPG has longer focal depths compared with the SZP, and the diffraction patterns are approximately the same at the position from z = 230 mm to z = 270 mm. The proposed CSZPG will have wide applications in particle trapping and optical imaging.
Author Contributions
Methodology, H.H., Y.Z. and F.C.; software, H.H.; validation, H.H., Y.Z. and F.C.; data curation, H.H.; writing—original draft preparation, H.H.; writing—review and editing, H.H., Y.Z. and F.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Key Research and Development Program of China (Grant Nos. 2017YFA0206002, 2021YFB3601304); National Natural Science Foundation of China (Grant Nos. U1832217, 61875225, 61804169, 61774166, 61888102).
Institutional Review Board Statement
Not applicable for studies not involving humans or animals.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Swartzlander, G.A.; Law, C.T. Optical vortex solitons observed in Kerr nonlinear media. Phys. Rev. Lett. 1992, 69, 2503. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A. Converting an array of edge dislocations into a multivortex beam. J. Opt. Soc. Am. A 2021, 38, 719–726. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Zaitsev, V.D. Topological Charge of Light Fields with a Polarization Singularity. Photonics 2022, 9, 298. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G.; O’Faolain, L.; Kotlyar, M.V. A dual-functionality metalens to shape a circularly polarized optical vortex or a second-order cylindrical vector beam. Photonics Nanostructures-Fundam. Appl. 2021, 43, 100898. [Google Scholar] [CrossRef]
- Kovalev, A.A.; Kotlyar, V.V.; Porfirev, A.P. Orbital angular momentum and topological charge of a multi-vortex Gaussian beam. J. Opt. Soc. Am. A 2020, 37, 1740. [Google Scholar] [CrossRef]
- Nalimov, A.G. Spin-Orbital Conversion of a Strongly Focused Light Wave with High-Order Cylindrical–Circular Polarization. Sensors 2021, 21, 6424. [Google Scholar]
- Rasouli, S.; Amiri, P.; Kotlyar, V.V.; Kovalev, A.A. Characterization of a pair of superposed vortex beams having different winding numbers via diffraction from a quadratic curved-line grating. J. Opt. Soc. Am. B 2021, 38, 2267–2276. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and transformation of Laguerre Gaussian Laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Vaughan, J.M.; Willetts, D.V. Interference properties of a light beam having a helical wave surface. Opt. Commun. 1979, 30, 263–267. [Google Scholar] [CrossRef]
- Toyoda, K.; Miyamoto, K.; Aoki, N.; Morita, R.; Omatsu, T. Using Optical Vortex to Control the Chirality of Twisted Metal Nanostructures. Nano Lett. 2012, 12, 3645–3649. [Google Scholar] [CrossRef]
- Park, S.R.; Cattell, L.; Nichols, J.M.; Watnik, A.; Rohde, G.K. De-multiplexing vortex modes in optical communications using transport-based pattern recognition. Opt. Express 2018, 26, 4004. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Cai, Y.; Wang, Z.; Ming, L.; Cao, Z.; Wang, Y.; Li, M.; Yan, S.; Bianco, P.R.; Yao, B. Aberration correction in holographic optical tweezers using a high-order optical vortex. Appl. Opt. 2018, 57, 3618–3623. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Cheng, Y.; Yue, G.; Xiang, L.; Wang, H. Super-resolution radar imaging based on experimental OAM beams. Appl. Phys. Lett. 2017, 110, 164102. [Google Scholar]
- Zang, H.; Zheng, C.; Fan, Q.; Wang, C.; Liang, E. Generation of X-ray vortex with ultra-long depth of focus using axial line-focused spiral zone plates. Chin. Opt. Lett. 2018, 16, 080501. [Google Scholar] [CrossRef] [Green Version]
- Pinnell, J.; Rodriguez-Fajardo, V.; Forbes, A. Probing the limits of orbital angular momentum (OAM) generation and detection with spatial light modulators. J. Opt. 2020, 23, 015602. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, C.; Xiao, S.; Wang, Y.; Fan, Y.; Liu, Y.; Zhang, N.; Qu, G.; Ji, H.; Han, J. Ultrafast control of vortex microlasers. Science 2020, 367, 1018–1021. [Google Scholar] [CrossRef]
- Xie, J.; Guo, H.; Zhuang, S.; Hu, B. Polarization-controllable perfect vortex beam by a dielectric metasurface. Opt. Express 2021, 29, 3081–3089. [Google Scholar] [CrossRef]
- Wang, E.; Liang, Y.; Li, H.; Xie, C. Composited holograms for the generation of cylindrical optical latticesand flower modes. Appl. Opt. 2018, 57, 4633. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, C.; Jia, W.; Wu, J.; Zhu, L.; Lu, Y.; Xiang, C.; Li, S. Generation of controllable rotating petal-like modes using composited Dammann vortex gratings. Appl. Opt. 2015, 54, 1667–1672. [Google Scholar] [CrossRef]
- Moreno, I.; Davis, J.A.; Womble-Dahl, T.; Cottrell, D.M. Azimuthal multiple-beam interference effects with combinations of vortex beams. Opt. Lett. 2015, 40, 2341–2344. [Google Scholar] [CrossRef]
- Lu, T.H.; Huang, T.D.; Wang, J.G.; Wang, L.W.; Alfano, R.R. Generation of flower high-order Poincaré sphere laser beams from a spatial light modulator. Sci. Rep. 2016, 6, 39657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sabatyan, A.; Rafighdoost, J. Azimuthal phase-shifted zone plates to produce petal-like beams and ring lattice structures. JOSA B 2017, 34, 919–923. [Google Scholar] [CrossRef]
- Arash, S.; Marjan, G. Petal-like zone plate: Long depth bifocal diffractive lens and star-like beam generator. J. Opt. Soc. Am. A 2018, 35, 1243–1253. [Google Scholar]
- Litvin, I.A.; Burger, L.; Forbes, A. Angular self-reconstruction of petal-like beams. Opt. Lett. 2013, 38, 3363–3365. [Google Scholar] [CrossRef] [Green Version]
- Cki, M.; Pichler, H.; Sterdyniak, A.; Lyras, A.; Zoller, P. Quantum Hall Physics with Cold Atoms in Cylindrical Optical Lattices. Physics 2015, 93, 013604. [Google Scholar]
- Vieira, J.; Trines, R.; Alves, E.P.; Fonseca, R.A.; Mendonca, J.T.; Bingham, R.; Norreys, P.; Silva, L.O. High Orbital Angular Momentum Harmonic Generation. Phys. Rev. Lett. 2016, 117, 265001. [Google Scholar] [CrossRef] [Green Version]
- Lavery, M.; Speirits, F.; Barnett, S.M.; Padgett, M.J. Detection of a Spinning Object Using Light’s Orbital Angular Momentum. Science 2013, 341, 537–540. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Wang, E.; Hua, Y.; Xie, C.; Ye, T. Single-focus spiral zone plates. Opt. Lett. 2017, 42, 2663. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).