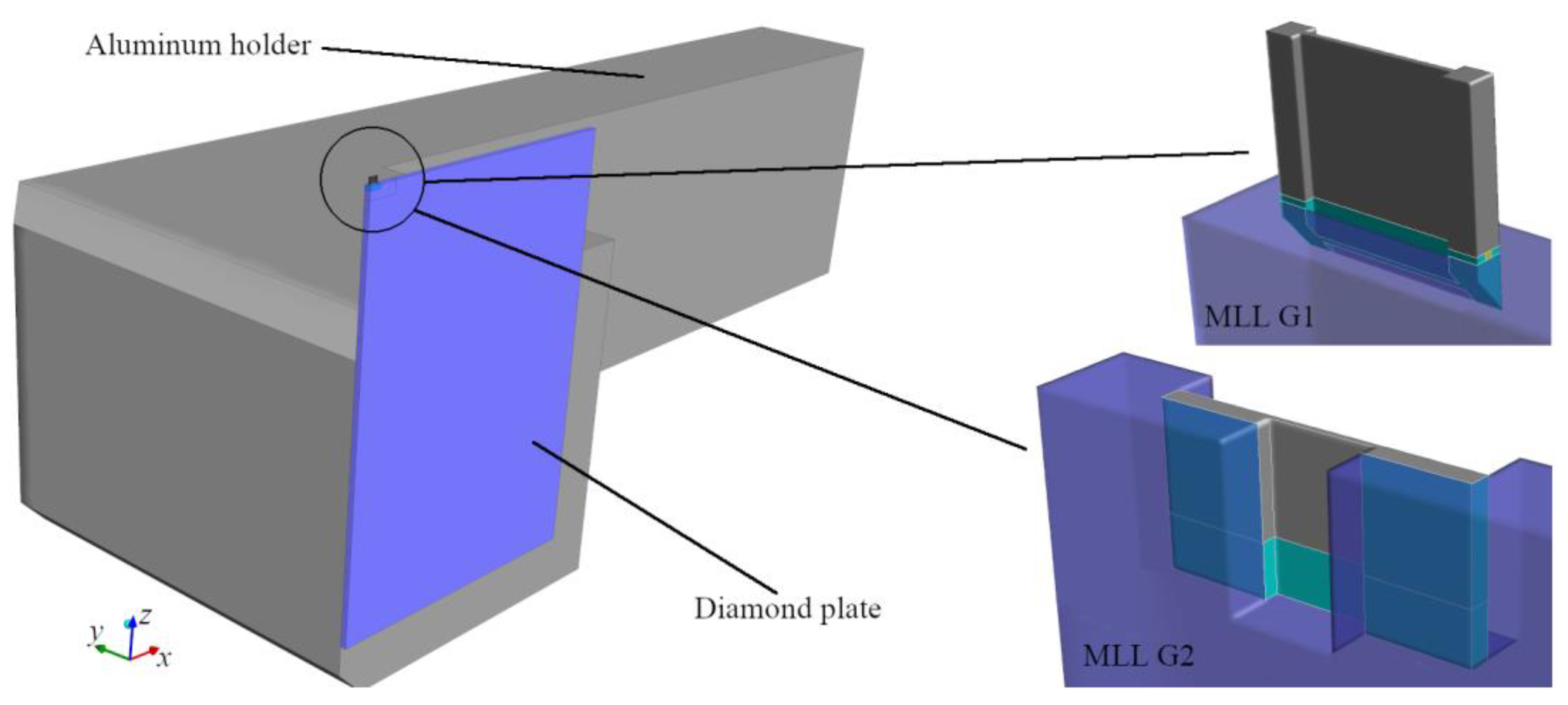
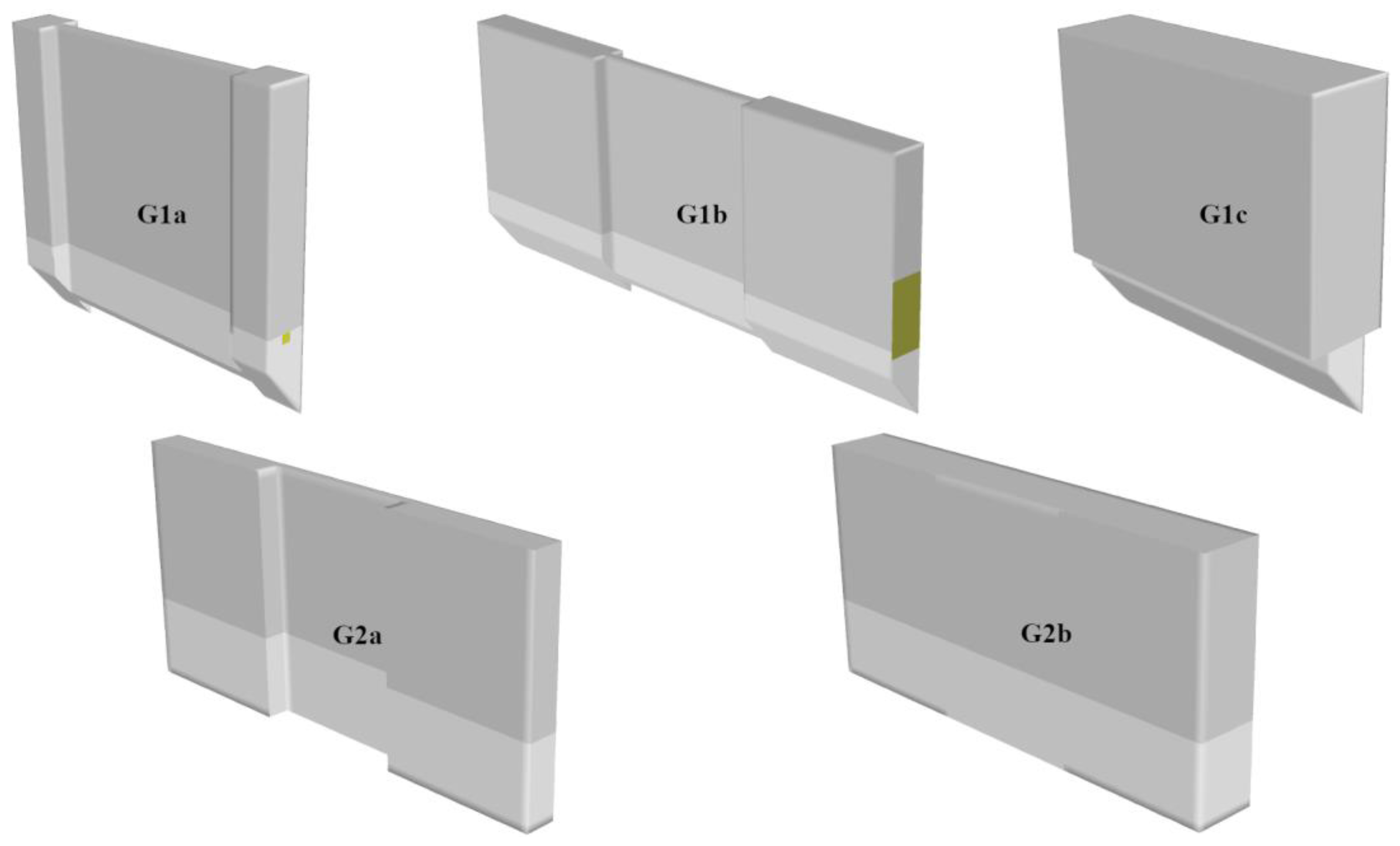
4.1. Comparison of Geometries and Materials for a Constant Absorbed Energy Per Pulse
In the following, we present the results of the numerical study of the heating of MLLs using the model described above and with an absorbed energy per pulse of = 15.6 µJ, similar to the experimental conditions, as well as for higher absorbed energies. In particular, we studied the responses of different lens geometries, mounting, and materials, under various XFEL beam conditions (intensity, number of pulses, etc.).
The numerical simulations predict that each XFEL beam pulse causes a huge instantaneous and volumetrically uniform heat load on the MLL (Equation (5) and
Table 3).
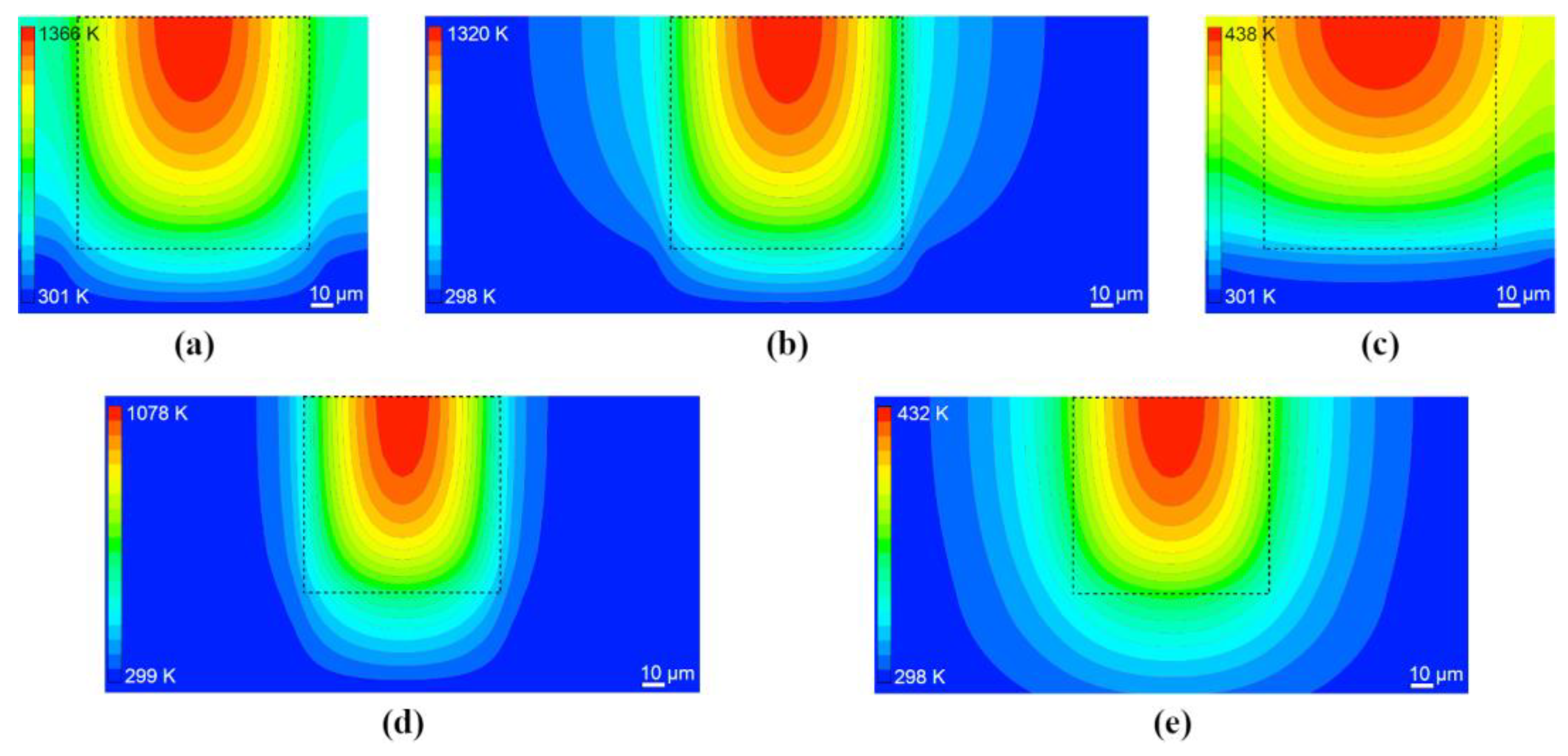
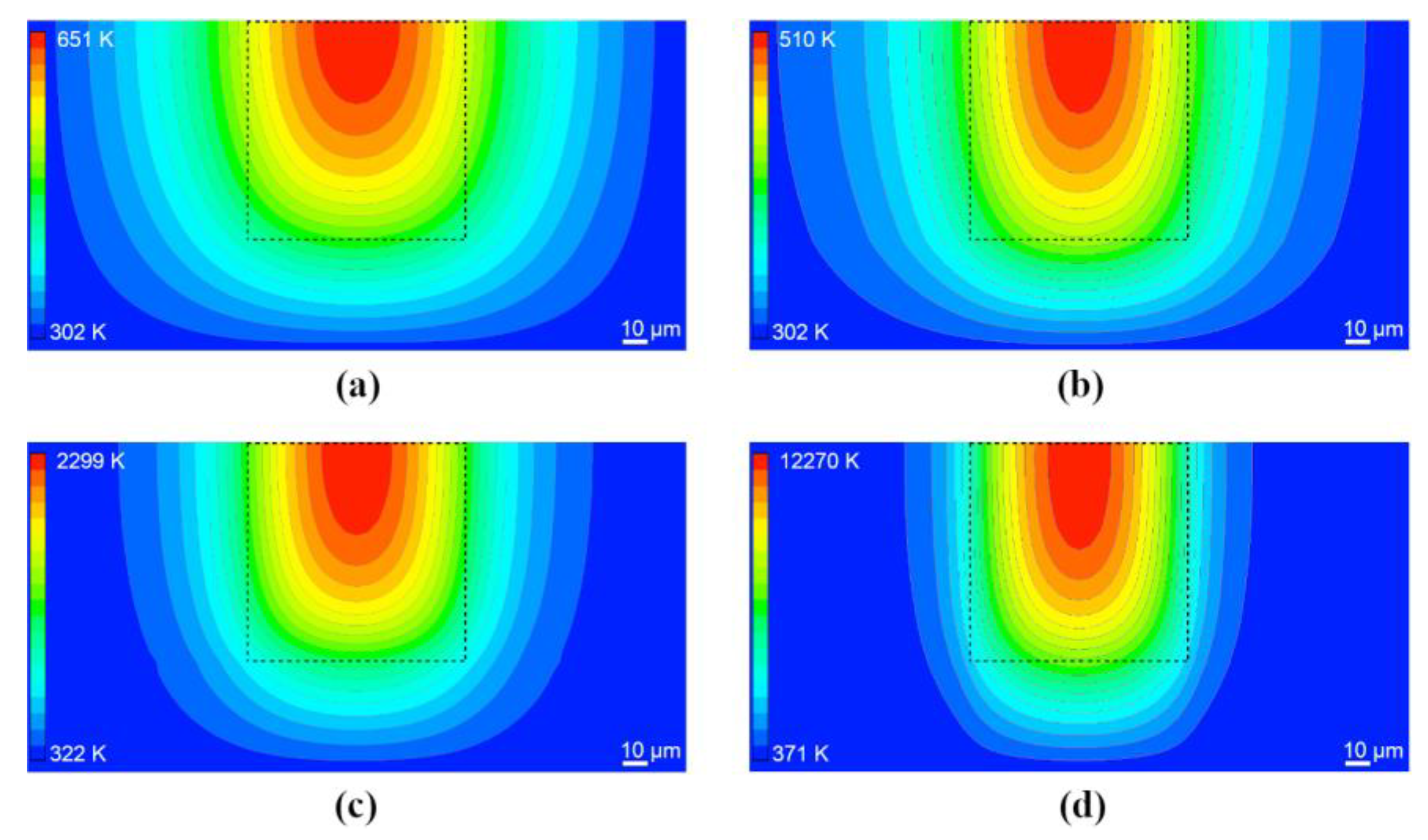
Figure 7 shows the simulated temperature field in a vertical plane perpendicular to the X-ray beam direction and intersecting the center of MLL, at a time
(after 20 X-ray pulses) for all considered geometric variants, assuming the same absorbed energy
15.6 µJ and that all lenses consist of WC/SiC multilayer. As expected, the thermal load of the MLL was reduced by increasing the support structures (G1b vs. G1c) or by using a new mounting method (G2a vs. G1a). The thicker lenses (G1c and G2b) had a substantially reduced temperature simply because the energy was absorbed in a larger volume, and thus the dose was lower. The temperature field distributions show some differences for the different geometries. In the geometries G1b, G2a and G2b, the temperature distribution in the central (illuminated) part is similar to G1a, since the X-ray beam cross-section absorption area is the same. However, G1b had a larger volume of support columns, which reduced the temperature in the entire lens due to improved heat conduction and surface radiation to the surroundings. A similar effect was achieved with G2a and G2b, where the contact area between the lens and the diamond plate increased, except that the heat dissipation was even better, and thus the temperatures were further reduced. The distribution for G1c differs most from the temperature distribution for G1a. This is due to the reduced dose caused by distributing the energy over a larger volume. Note that for a given X-ray pulse fluence, the dose (an intrinsic property) is independent of thickness and thus the absorbed energy, but the optimal thickness for focusing efficiency is dictated by the materials and photon energy, so the thickness is not a parameter that can be chosen arbitrarily. Here, we can infer that a B
4C/SiC MLL of 45 µm thickness (listed in
Table 2) heats to a much lesser extent than a WC/SiC MLL of optimal thickness.
Figure 8 shows how the temperature in the hottest part of WC/SiC MLLs changed with time. The absorbed energy per pulse was taken to be 15.6 µJ. The first 200 µs are displayed so that the temperature evolution between the X-ray pulses (3.56 µs apart) as well as between pulse trains (100 ms apart) is visible. As we can see, the lens did not cool significantly between two pulses near the beginning of the pulse train when the materials were still at a low temperature. At these lower temperatures, the predominant mechanism of heat transfer is convection. With each pulse, the temperature rises stepwise, according to
from
Table 3. When the temperature exceeds about 573 K, the mechanism of heat transfer by radiation starts to prevail, such that in 3.56 μs the temperature of the lens drops by a considerable fraction of the rising temperature. As the temperature rises, this process becomes even more pronounced. Thus, between the penultimate and last pulse, the decrease in the lens temperature was 314.3 K for geometry G1a.
As we observed from the simulations of the thick lenses (geometries G1c and G2b) and anticipated from
Table 2, the maximum temperature was considerably lower for thick lenses (
Table 5), indicating that they can therefore tolerate much higher incident absorbed energies and possibly higher incident pulse fluences. As a result, we conducted numerical simulations for the geometries G1c and G2b for absorbed energies ranging from 0.0156 mJ to 0.156 mJ (see
Figure 9 and
Table 6).
These allow us to find the dependence of the maximum lens temperature after 20 pulses on the absorbed energy per pulse. For data from
Table 6, the linear regression curve is
where
for geometry G1c, and
for the G2b geometry with WC/SiC multilayers. The goodness of fit is
. If we know the maximum allowable temperature, we can calculate from Equation (6) the highest possible absorbed energy, and thus the tolerable incident pulse energy, for a particular lens design.
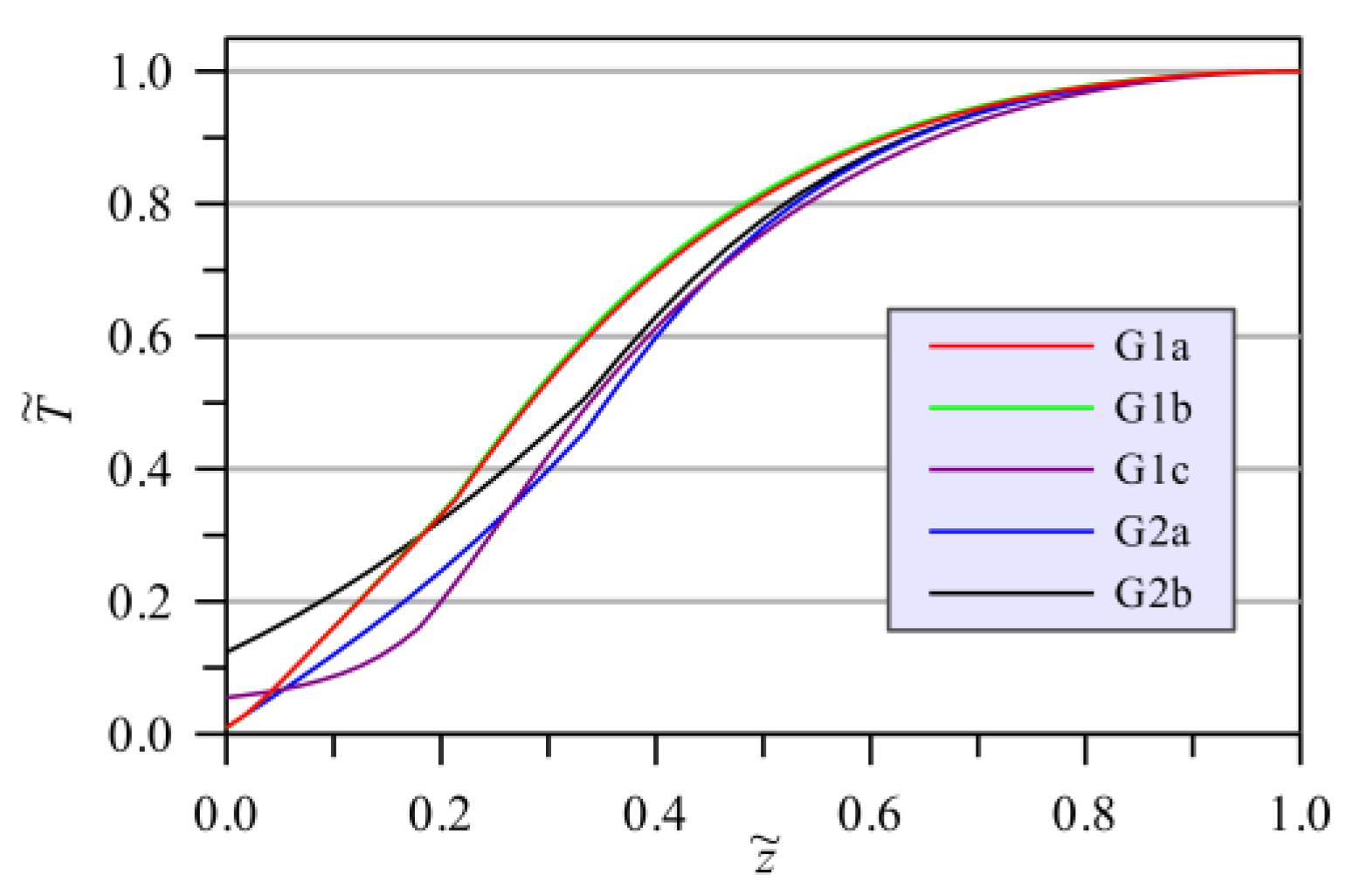
The vertical temperature profiles
through the MLL center after 20 X-ray pulses are presented in
Figure 10 as a function of the dimensionless temperature defined as
and the dimensionless vertical coordinate defined as
. The coordinate system refers to the one shown in
Figure 3. Dimensionless quantities were used for ease of comparison, as the lens heights were different for geometries G1 and G2, and maximum temperatures also varied by an order of magnitude between cases. The minimum and maximum
coordinates of the MLL are
and
, respectively. Geometry G2b was the most favorable since it led to the smallest temperature difference. Consequently, the stresses, and thus the deformations, due to the heat load, are also expected to be the smallest.
However, the thick-lens geometry of G2b is not suitable for WC/SiC MLLs since it would not efficiently focus X-rays. As shown in Equation (1), the optimal thickness is inversely proportional to the refractive contrast
of the materials. The contrast between WC and SiC is high, giving an optimal thickness of only 4.5 µm at 8 keV. The optimal thickness is much higher for the materials Be/SiC and B
4C/SiC, as well as for higher photon energies, as seen in
Table 2. The thickness of 45 µm is close to the optimum for B
4C/SiC at 8 keV and Be/SiC at 17.5 keV photon energy. We simulated these multilayer combinations for the G2b geometry with the same absorbed energy of 15.6 µJ, 20 pulses per train and 3.56 μs separation between the pulses. This absorbed energy was caused by an incident pulse energy of 409 µJ for Be/SiC and 59.2 µJ for B
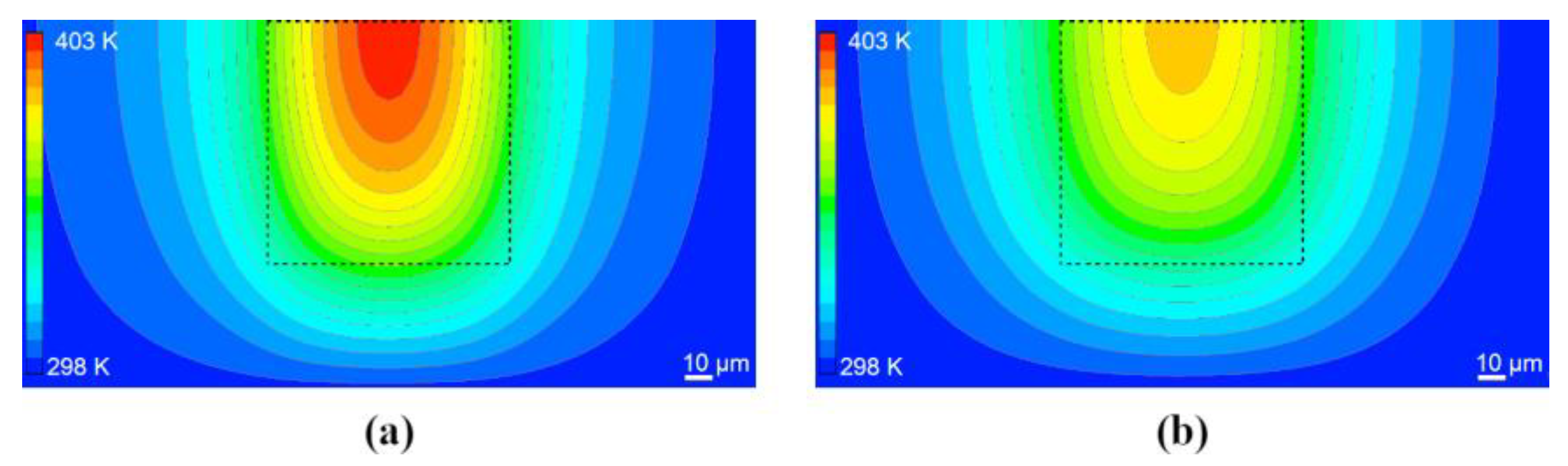
4C/SiC. The temperature distribution for the two cases is shown in
Figure 11, and
Figure 12 compares the evolution of the maximum lens temperature over the course of the pulse train. The highest temperatures for these B
4C/SiC and Be/SiC MLLs were considerably lower than for the cases discussed above, even though the incident X-ray pulse fluences were higher. For Be/SiC at 409 µJ incident pulse energy, the highest temperature is 401.47 K, and for B
4C/SiC at a 59.2 µJ incident pulse energy, the highest temperature reached was 383.71 K. It is predicted, therefore, that Be/SiC MLLs can withstand higher fluence pulses than B
4C/SiC or WC/SiC MLLs.
Figure 11 also shows a benefit of the 100 µm wide supporting posts for these particular materials. Because of the greater thickness of the lens there, more conduction of heat occurred transversely. In this case, the support posts acted as a heat sink, as can be seen from the temperature outside the illumination area as defined by the dashed lines in
Figure 11 as compared with the much higher temperature gradients that occurred for the thinner WC/Sic MLLs depicted in
Figure 7.
4.2. Comparison of Optimized MLLs of Different Materials
We also calculated the highest average and maximum temperatures of lenses made from different multilayer material pairs given in
Table 2, for a photon energy of 17.5 keV, the G2 geometry, and an incident pulse energy of 1 mJ. The thicknesses of the lenses were set to their optimal values
given by
Table 2. The incident energy of 1 mJ is much higher than the pulse energy experienced in the current XFEL experiments and represents utilizing the entire output of an FEL beamline to obtain focused intensities of higher than anything achieved to date. The absorbed energy
for the 1 mJ incident pulse is shown in
Table 2. The number of pulses per X-ray pulse train and time separation between two consecutive pulses remained the same as in the previous simulations.
The time evolution of the average and maximum temperatures for the MLLs of four multilayer systems are shown in
Figure 13, and the maximum temperature profiles are shown in
Figure 14. The highest maximum and highest average temperatures reached during irradiation by the pulse train are presented in
Table 7. The melting temperature
is also provided for comparison.
The simulation results presented in
Figure 13 and
Figure 14 show that an incident pulse energy of 1 mJ at a photon energy of 17.5 keV is too high for the WC/SiC MLL as the temperature quickly exceeds the melting point. Lenses made from the three other material pairs can tolerate high pulse energies. For TiC/SiC, the maximum temperature is lower than the melting point, but it is still very high, which means that the lens is very likely to deform due to temperature loads and stresses. The maximum temperatures of B
4C/SiC and Be/SiC lenses are both lower than 673 K and much lower than their melting temperatures.