Abstract
This paper proposes and evaluates the use of machine learning (ML) techniques for mitigating the effect of the random inter-core crosstalk (ICXT) on 256 Gb/s short-reach systems employing weakly coupled multicore fiber (MCF) and Kramers–Kronig (KK) receivers. The performance improvement provided by the k-means clustering, k nearest neighbor (KNN) and feedforward neural network (FNN) techniques are assessed and compared with the system performance obtained without employing ML. The FNN proves to significantly improve the system performance by mitigating the impact of the ICXT on the received signal. This is achieved by employing only 10 neurons in the hidden layer and four input features for the training phase. It has been shown that k-means or KNN techniques do not provide performance improvement compared to the system without using ML. These conclusions are valid for direct detection MCF-based short-reach systems with the product between the skew (relative time delay between cores) and the symbol rate much lower than one (). By employing the proposed FNN, the bit error rate (BER) always stood below on all the time fractions under analysis (compared with 100 out of 626 occurrences above the BER threshold when ML was not used). For the BER threshold of and compared with the standard system operating without employing ML techniques, the system operating with the proposed FNN shows a received optical power improvement of almost 3 dB.
1. Introduction
Current optical fiber networks are reaching the so-called capacity crunch of 100 Tb/s per single core fiber [1]. Over the last years, the traffic in data centers has been increasing exponentially, demanding new cost-efficient solutions for short-reach optical communications [2]. Space division multiplexing (SDM) has been indicated as a powerful solution to provide an ultimate capacity increase as it explores the only known physical dimension left to be exploited in optical networks [3,4].
SDM can be based on MCFs, where N independent cores provide a capacity increase of N-fold compared with standard single-mode fiber used in current networks. The simultaneous transmission in multiple cores of the MCF leads to ICXT, which is usually considered as the main impairment of MCF systems [5]. The ICXT varies randomly along the fiber length, time, and frequency, which may affect the system’s performance. High ICXT levels have been observed over several minutes or even hours, which leads to service shutdown or outage over large time periods [6]. For minimizing the impact of the ICXT on MCF-based systems, the techniques proposed so far include adaptive modulation [7], MIMO techniques [8], or optical code division multiple access spreading technique [9]. However, these techniques only provide incremental improvements of the system performance.
Due to cost purposes, short-reach MCF-based networks should employ direct-detection (DD) receivers. However, these receivers lead to nonlinear impairments that can severely limit the achievable capacity and reach. Thus, advanced DD receivers based on Kramers–Kronig (KK) technique have been proposed for performance improvement and complexity reduction compared with coherent detection counterpart [10]. With the KK technique, linearization of the receiver is attained, and the signal phase information can be recovered.
Recently, machine learning has been employed in optical communications to recover from nonlinear distortions, including non-Gaussian additive noise, non-white laser phase noise, and fiber nonlinearities in both IM/DD and coherent systems [11,12]. Simplest machine learning techniques include k-means and k nearest neighbor (KNN), which represent an unsupervised technique used for clustering and a supervised learning technique used for classification, respectively [13]. Feedforward neural networks (FNNs) are one of the simplest machine learning techniques where a set of perceptrons are organized into layers to form a fully connected neural network (NN). FNNs are suitable for memoryless systems and have been employed in optical fiber communications to perform equalizations, as shown in [11]. Beside FNN, more advanced NN architectures have been studied in optical communications, such as deep learning [12,14]. These more advanced NN are used to predict different strategies for routing and spectrum assignments for elastic optical networks [14]. They can also be used to mitigate the non-linearities, such as signal-to-signal beat interference caused by the square-law detection [12]. In SDM systems, machine learning techniques were proposed to support the design of crosstalk-aware schemes used for resources allocation [15] or to mitigate the impact of the crosstalk power between mode groups in mode-multiplexed M-quadrature amplitude modulation (QAM) OFDM-IM-DD systems [16]. NNs were also used to speed up coating loss estimation in heterogeneous trench-assisted MCF design [17].
In this work, k-means clustering and KNN, as well as a low-complexity FNN, are proposed to mitigate the effects of the random variation of the ICXT along time, induced by weakly coupled MCF in short-reach systems employing KK receivers.
2. System Modelling
Figure 1 depicts the system model considered in this work. The system is composed of the optical transmitter which transmits root-raised-cosine (RRC) pulses. Then, the signals at the output of the transmitter are launched into two different cores of an MCF: (i) core n, that is the interfered core, and (ii) core m, that is the interfering core which induces ICXT in core n. Then, the optical receiver includes a PIN photodetector, an electrical amplifier (which induces thermal noise), the RRC filter, the KK algorithm, and the ML block for ICXT mitigation. Finally, the bit error ratio (BER) is estimated using Monte Carlo simulation.
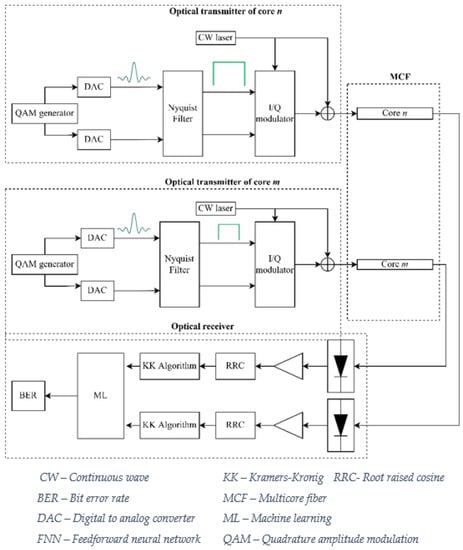
Figure 1.
Schematic diagram of the short-reach MCF based system employing KK receivers.
2.1. Optical Transmitter
The optical transmitter is responsible for converting the information signal from the electrical to the optical domain. First, a 16-QAM Nyquist signal with a roll-off factor of 5% and symbol rate of 64 Gbaud is generated using distinct random sequences for both components (in-phase and quadrature) of the signal. The modulator is a dual parallel Mach-Zehnder modulator (DPMZM) with the ability to modulate the I and Q components of the electrical field. This is achieved by biasing the inner MZMs in the null bias point and the outer MZM in the quadrature bias point.
Figure 2 shows the spectrum of the signal at the output of the transmitter. In Figure 2a, an illustrative spectrum is presented. The optical tone is added to the signal to fulfill the minimum phase condition for the KK receiver [10]. Figure 2b shows the power spectral density (PSD) of the signal at the transmitter output obtained by simulation. The spacing between the carrier and the signal is 5% of the signal bandwidth. This spacing was chosen to maximize the spectral efficiency without adding distortion to the received signal.
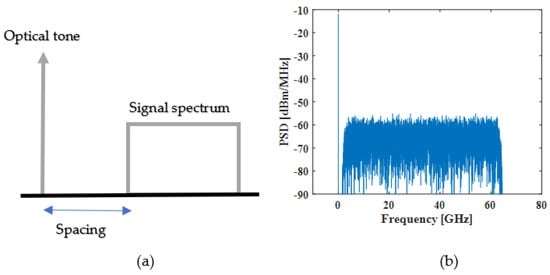
Figure 2.
(a) Illustrative spectrum of the signal at the transmitter output. (b) Power spectral density obtained by simulation of the signal at the transmitter output.
2.2. MCF Model
The MCF allows the transmission of multiples optical channels in different cores. In this work, only two cores are considered: one serving as the interfering core, i.e., the core that induces the ICXT, and the other acting as the interfered core, i.e., the core impaired by the ICXT. The ICXT induced by the MCF is modeled by the dual polarization discrete changes model (DCM) [18,19,20]. Each core operates as a linear single mode fiber (SMF), i.e., it is modulated by the SMF propagation transfer function. The random polarization rotation induced by the fiber birefringence is also included in the transmission model [19].
To validate the ICXT simulation model, the statistical properties of the in−phase (I) and quadrature (Q) components of the ICXT obtained by simulation must agree with the theoretical analysis.
Figure 3 shows the probability density function (PDF) of the in-phase and quadrature components of the ICXT field in both polarizations (x and y) directions. The simulation results of the ICXT are obtained with 1000 random phase shifts and for a ICXT level of −15 dB. The ICXT level is the ratio between the mean ICXT power and signal power, at the output of interfered core [6]. A Gaussian PDF obtained from the mean and variance of the simulation results is also shown in Figure 3 as reference. The results of Figure 3 show that the ICXT components are well described by a Gaussian PDF, as predicted theoretically in [18], which validates the ICXT simulation model.
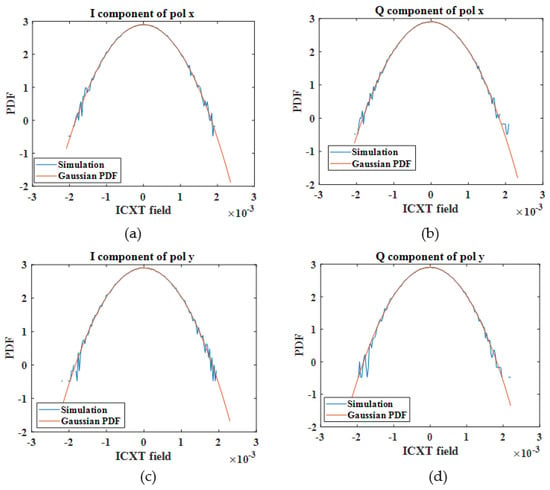
Figure 3.
PDF of the quadrature components of the ICXT in x and y polarization. (a,b) ICXT fields of polarization x. (c,d) ICXT fields of polarization y.
2.3. Optical Receiver
The receiver includes a PIN photodetector, an electrical amplifier, the RRC filter, and the symbol decision circuit.
The KK algorithm is based on the Kramers−Kronig relation, and it enables to retrieve the complex field at the PIN input from the photocurrent detected by the PIN if the minimum phase condition is ensured [10,21].
Figure 4 depicts the structure of an ideal KK receiver. The main goal of this paper is to propose a simple ML algorithm to mitigate the impact of the ICXT on the system performance. For this reason, limitations due to the practical implementation of KK receivers are not addressed. After reconstructing the complex QAM signal at the KK receiver output, fiber dispersion is fully compensated using an analog filter.
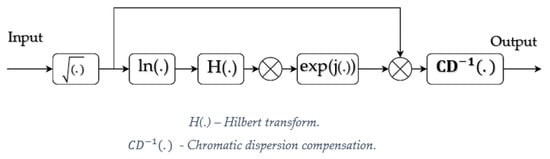
Figure 4.
Schematic diagram of the KK receiver scheme.
2.4. Machine Learning
In this work, three different ML techniques are implemented and assessed: a FNN, k-means clustering, and KNN. These algorithms are chosen due to their low complexity and memoryless configurations, which are indicated for short-reach networks.
2.4.1. K-Means Clustering
In this work, the k-means clustering algorithm is implemented and the performance of the system is evaluated.
K-means clustering focuses on dividing the input into k clusters (attributed during training process) according to dissimilarity metrics and it creates groups centered on the mean of all the samples of each cluster (centroids). The algorithm uses Euclidean distance to perform the symbol decision [13]. As features for the classification, the k-means algorithm receives the in-phase and the quadrature components of the QAM signal transmitted in the interfered core at the end of the KK receiver.
2.4.2. K Nearest Neighbor
KNN algorithm is based on the distance between the new data and the neighbors counted by the k parameter. The neighbor symbols are attributed to the training process where every input symbol has a correspondent output that matches with a class with the same characteristics. On the active phase, a new input symbol is classified into the group of data with the greatest number of nearest neighbor symbols according to the number of neighbors defined by the k parameter [13]. The classification used in the algorithm is also based on the Euclidean distance.
2.4.3. Feedforward Neural Network
In this work, a shallow feedforward neural network is employed to mitigate the impact of the random ICXT on the system performance. This FNN is implemented to learn the behavior of the ICXT and then transform the ICXT-impaired received signal into a new output showing higher ICXT tolerance.
One of the main constraints of machine learning algorithms is the complexity. In this work, we are addressing MCF-based short-reach systems with a product between the skew and the symbol rate much lower than one () [6]. This means that the ICXT induced in a given symbol of the interfered core only depends on the symbol transmitted in the interfering core at the same time instant [6].
Figure 5 depicts the scheme of the FNN employed in this work. The FNN is fed with four inputs (features): the in-phase and the quadrature components of the signal transmitted in the interfered and interfering cores at the end of the KK receivers. The main target of the FNN is to predict the I and Q components of the transmitted signal at core n without the effect of the transmission impairments. As the ICXT depends on the signal injected into the interfering core m [6,22], we need to provide the signal detected at the output of core m as a training feature.
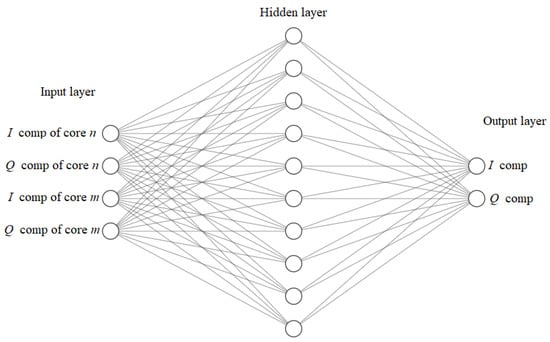
Figure 5.
Schematic diagram of the FNN used to mitigate the impact of the ICXT in DD-MCF short-reach networks.
2.5. Simulation Conditions and Parameters
This subsection presents the simulation conditions used to evaluate the effectiveness of the ML techniques to mitigate the impact of the random ICXT on the system performance. This work is focused on short-reach connections, and thus, the length of the MCF does not exceed 50 km.
For the simulation, a thermal noise with a noise equivalent power (NEP) of is considered. To estimate the BER, Monte Carlo simulation using a bit stream with bits is performed. To evaluate each BER value, 100 errors are considered. All parameters used are indicated in Table 1, Table 2 and Table 3.

Table 1.
Signal parameters.

Table 2.
MCF parameters.

Table 3.
FNN parameters.
The FNN is trained using 20,000 symbols, as indicated in Table 3. These 20,000 symbols correspond to a transmission time of 0.3 µs. The complexity and online requirements of the algorithm depend on the time required by the training phase of the FNN and the update rate. The rate at which the network must be trained depends on the variation of the ICXT along time. In particular, the neural network should be trained in time intervals over which the variation of the ICXT is almost negligible. Previous works have been shown that the decorrelation time of the ICXT is of the order of a few minutes or higher [20]. This means that, if we choose to train the network once per second, to guarantee that the ICXT is constant during the active phase of the network, the training overhead is negligible. The training phase will also require some processing time to optimize the weights and biases of the FNN. Although this processing time is dependent on the real time implementation employed, we expect that it will not affect the symbol rate of the system.
To use a KK receiver, we need to ensure the minimum phase condition. Thus, the carrier-to-signal power ratio (CSPR) must be optimized according to a noise equivalent power (NEP) of .
Figure 6 shows the BER as a function of the CSPR for four different fiber lengths. Results are obtained considering the absence of ICXT and perfect dispersion compensation. Figure 6 shows that the optimum CSPR is approximately 13 dB. This optimum operation point results from a trade-off between signal-to-noise ratio and verification of the minimum phase condition. For low CSPR levels, the condition is not satisfied. For high CSPR levels, the SNR degrades.
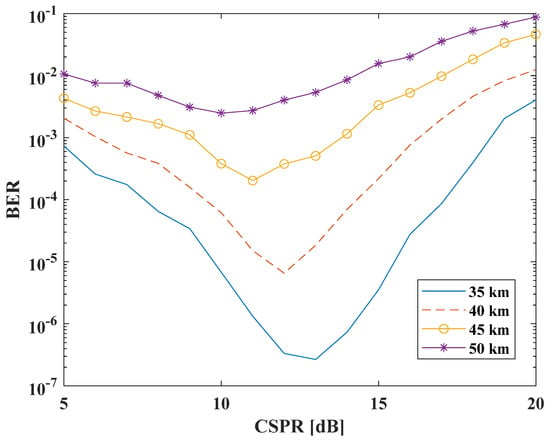
Figure 6.
BER as a function of the CSPR and fiber length for 16−QAM without ICXT.
The FNN has one single hidden layer with 10 neurons. Further investigation showed that the FNN has a similar performance with number of neurons higher than 2, although the lower the number of neurons, the longer the training time. The algorithm used for training is the scaled conjugate gradient and the activation function used is the tangent sigmoid.
3. Results and Discussion
3.1. Impact of the ICXT on the System Performance
The ICXT varies randomly over time. The time variations can be of the order of a few minutes or even hours [20]. Therefore, the concept of time fraction and short-term average inter-core crosstalk (STAXT) has been introduced to assess the performance of MCF-based systems [20]. A time fraction is a small-time duration much shorter than the ICXT decorrelation time, where the ICXT is considered constant [18]. STAXT is the average power of the ICXT measured during a time period much shorter than the ICXT decorrelation time. If the time interval between time fractions is much larger than the ICXT decorrelation time, then the ICXT varies from time fraction to time fraction. This random variation of the ICXT can cause high performance changes over time.
Figure 7 shows the impact of the ICXT on the system. In Figure 7a, the STAXT is presented as a function of the time fractions. The results show the high variation of the ICXT power at the output of the interfered core, such as reported in [5,18,20,22]. In Figure 7a,b, the ICXT level is −15 dB. Figure 7b shows the calculation of the BER along 500 different time fractions. The results show that the ICXT can cause high BER variations along time which can remain for several minutes or even hours, leading to system outage.
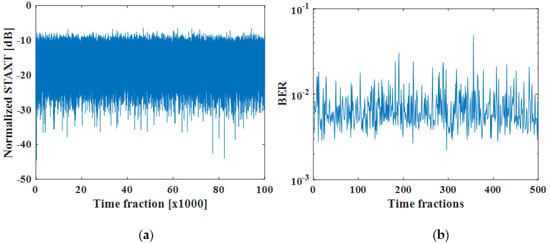
Figure 7.
(a) Normalized STAXT as a function of time fractions. (b) BER as a function of time fraction.
3.2. Performance of Short-Reach MCF-Based System Employing ML Techniques
In this subsection, the BER obtained with and without using ML techniques is evaluated by simulation. The performance improvement enabled by shallow FNNs, k−means or KNN techniques are identified and insight about the design of ML-assisted short-reach MCF−based systems is provided.
Figure 8 shows the BER of the received signal before and after using ML algorithms, considering a ICXT level of −13 dB. The results obtained show that k−means and KNN algorithms do not provide performance improvement when compared with the performance obtained without using ML. This occurs because the ICXT is random and the simplest redesign of the decision boundaries does not allow to better identify the different clusters, as inferred from the constellations shown in Figure 9a–c. In contrast, Figure 8 shows that the FNN enables the mitigation of the ICXT-induced BER degradation. This is confirmed by the comparison between the constellations obtained without ML and after employing the FNN, shown in Figure 9a,d, respectively. For instance, if we consider a BER threshold of to define the system outage [6], then the BER before applying ML techniques presents 100 occurrences (out of 626) above the threshold (the ones shown in Figure 8). By applying the proposed FNN, the BER always stood below the threshold. We chose to represent only the BER occurrences above the threshold in Figure 8, as the goal is to evaluate the system performance improvement provided by FNN in extreme degradation scenarios.
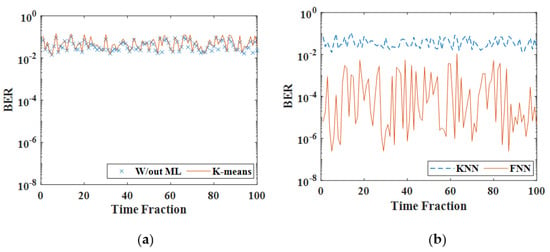
Figure 8.
BER as a function of time fractions for: (a) without the use of ML (crosses), k−means clustering (line); (b) KNN (dashed line), FNN (line).
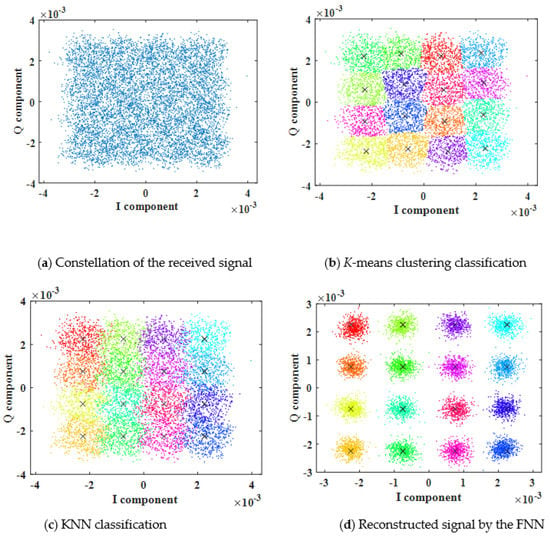
Figure 9.
Constellation of the 16−QAM signal before and after using ML techniques.
In order to conclude the analysis of the performance improvement provided by the FNN, we also evaluated the mean BER as a function of the received optical power (ROP). Figure 10 shows the mean BER as a function of the ROP considering an ICXT level of −15 dB. The BER is averaged over 500 time fractions to obtain stabilized mean BER estimates. The results show that, for the BER = (corresponding to the 20% FEC threshold), the FNN provides an additional ROP tolerance of almost 3 dB compared with the case in which ML is not employed. It is also shown that the BER = is attained for ROP = −10 dBm. If we consider the typical power levels launched into the optical fiber (between 0 and 10 dBm), this ROP level means a link budget between 10 and 20 dB. This link budget enables us to use recently fabricated MCFs where fiber loss does not exceed 0.2 dB/km and fan/in fan/out insertion losses are typically bellow 1 dB [23,24]. For ROPs below −14 dBm, the FNN does not provide performance improvement as the system is limited by the thermal noise.
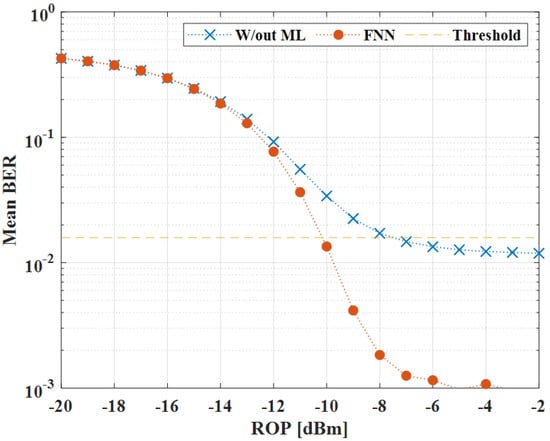
Figure 10.
Mean BER as a function of the received optical power using FNN (circles) and without the use of ML (crosses).
4. Conclusions
In this paper, k-means, KNN, and FNN techniques are proposed and optimized to improve the tolerance of 256 Gb/s DD short−reach systems to the ICXT induced by weakly coupled MCF. It has been shown that memoryless FNNs provide significant improvement of the system performance and may represent a simple and effective solution to mitigate the impact of the ICXT induced in MCFs. This conclusion is valid for short-reach systems with , where the ICXT induced in the interfered core at a given time instant only depends on the signal transmitted in the interfering core at the same time instant. The k-means clustering and KNN techniques have shown to be useless to mitigate the ICXT. With the proposed FNN, the ICXT−impaired MCF system recovered from 100 occurrences (out of 626) with BER above the BER threshold, which is used to declare system outage, to a full operation with no outage. We also confirmed that, for a BER = (20% FEC threshold), the FNN provides an additional ROP tolerance of almost 3 dB when compared with the system without the use of ML.
Author Contributions
Conceptualization, T.A., T.B. and D.P.; methodology, T.A., T.B. and D.P.; software, D.P.; validation, T.A. and T.B.; formal analysis, T.A. and T.B.; investigation, T.A., T.B. and D.P.; resources, T.A. and D.P.; data curation, D.P.; writing—original draft preparation, D.P.; writing—review and editing, D.P., T.A. and T.B.; visualization, D.P.; supervision, T.A. and T.B.; project administration, T.A.; funding acquisition, T.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Fundação para a Ciência e a Tecnologia (FCT) from Portugal under the internal projects of instituto de Telecomunicações DigCore/UIDP/50008/2020, UIDB/EEA/50008/2020, and grant BI Nº22-09-04-2021. ISTAR projects UIDB/04466/2020 and UIDP/04466/2020, and SELFIE projects are also acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Richardson, D.J.; Fini, J.M.; Nelson, L.E. Space-division multiplexing in optical fibres. Nat. Photonics 2013, 7, 354–362. [Google Scholar] [CrossRef] [Green Version]
- Perin, J.K.; Shastri, A.; Kahn, J.M. Data center links beyond 100 Gbit/s per wavelength. Opt. Fiber Technol. 2018, 44, 69–85. [Google Scholar] [CrossRef]
- Winzer, P.J.; Neilson, D.T.; Chraplyvy, A.R. Fiber optic transmission and networking: The previous 20 and the next 20 years [Invited]. Opt. Express 2018, 26, 24190–24239. [Google Scholar] [CrossRef] [PubMed]
- Butler, D.L.; Li, M.-J.; Li, S.; Geng, Y.; Khrapko, R.R.; Modavis, R.A.; Nazarov, V.N.; Koklyushkin, A.V. Space division multiplexing in short reach optical interconnects. J. Light. Technol. 2016, 35, 677–682. [Google Scholar] [CrossRef]
- Alves, T.M.F.; Cartaxo, A.V.T. Theoretical modelling of random time nature of inter-core crosstalk in multicore fibers. In Proceedings of the 2016 IEEE Photonics Conference (IPC), Waikoloa, HI, USA, 2–6 October 2016; pp. 521–522. [Google Scholar] [CrossRef]
- Alves, T.F.; Cartaxo, A.V.T.; Rebola, J.L. Stochastic properties and outage in crosstalk-impaired OOK-DD weakly-coupled MCF applications with low and high skew×bit-rate. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–8. [Google Scholar] [CrossRef]
- Alves, T.M.F.; Luís, R.S.; Puttnam, B.J.; Cartaxo, A.; Awaji, Y.; Wada, N. Performance of adaptive DD-OFDM multicore fiber links and its relation with intercore crosstalk. Opt. Express 2017, 25, 16017–16027. [Google Scholar] [CrossRef] [PubMed]
- Luís, R.S.; Rademacher, G.; Puttnam, B.J.; Awaji, Y.; Wada, N. Long distance crosstalk-supported transmission using homogeneous multicore fibers and SDM-MIMO demultiplexing. Opt. Express 2018, 26, 24044–24053. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Saitoh, K. Inter-core crosstalk mitigation in multicore fibers by optical CDMA spreading technique with referenced channels. In Proceedings of the Asia Communications and Photonics Conference (ACPC), OSA Technical Digest (Optica Publishing Group), Chengdu, China, 2–5 November 2019; p. M4A.177. [Google Scholar]
- Le, S.T.; Schuh, K.; Chagnon, M.; Buchali, F.; Dischler, R.; Aref, V.; Buelow, H.; Engenhardt, K.M. 1.72-Tb/s Virtual-carrier-assisted direct-detection transmission over 200 km. J. Light. Technol. 2018, 36, 1347–1353. [Google Scholar] [CrossRef]
- Gaiarin, S.; Pang, X.; Ozolins, O.; Jones, R.T.; Da Silva, E.P.; Schatz, R.; Westergren, U.; Popov, S.; Jacobsen, G.; Zibar, D. High Speed PAM-8 optical interconnects with digital equalization based on neural network. In Proceedings of the Asia Communications and Photonics Conference, Wuhan, China, 2–5 November 2016; pp. 1–3. [Google Scholar]
- Xu, Z.; Sun, C.; Ji, T.; Manton, J.H.; Shieh, W. Computational complexity comparison of feedforward/radial basis function/recurrent neural network-based equalizer for a 50-Gb/s PAM4 direct-detection optical link. Opt. Express 2019, 27, 36953–36964. [Google Scholar] [CrossRef] [PubMed]
- Rafique, D.; Velasco, L. Machine learning for network automation: Overview, architecture, and applications. J. Opt. Commun. Netw. 2018, 10, D126–D143. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Cheng, B.; Hang, C.; Hu, Y.; Liu, S.; Wang, Y.; Shen, J. A deep learning based RSA strategy for elastic optical networks. In Proceedings of the 18th International Conference on Optical Communications and Networks (ICOCN), Huangshan, China, 5–8 August 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Yao, Q.; Yang, H.; Zhu, R.; Yu, A.; Bai, W.; Tan, Y.; Zhang, J.; Xiao, H. Core, mode, and spectrum assignment based on machine learning in space division multiplexing elastic optical networks. IEEE Access 2018, 6, 15898–15907. [Google Scholar] [CrossRef]
- Zhang, Q.W.; Liu, M.; Zhou, H.; Wang, F.; Chen, J.; Cao, B.Y.; Song, Y.X.; Zhang, J.J.; Li, Y.C.; Wang, M. A machine learning enabled optical IMDD SDM OFDM system. In Proceedings of the 23rd Opto-Electronics and Communications Conference (OECC), Jeju, Korea, 2–6 July 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Mu, X.; Ottino, A.; Ferreira, F.M.; Zervas, G. Optimization of 125-µm Heterogeneous multi-core fibre design using artificial intelligence. IEEE J. Sel. Top. Quantum Electron. 2021, 28, 1–13. [Google Scholar] [CrossRef]
- Soeiro, R.O.J.; Alves, T.M.F.; Cartaxo, A.V.T. Dual polarization discrete changes model of inter-core crosstalk in multi-core fibers. IEEE Photonics Technol. Lett. 2017, 29, 1395–1398. [Google Scholar] [CrossRef]
- Pinheiro, B.R.P.; Rebola, J.L.L.; Cartaxo, A.V.T. Analysis of inter-core crosstalk in weakly-coupled multi-core fiber coherent systems. J. Light. Technol. 2021, 39, 42–54. [Google Scholar] [CrossRef]
- Alves, T.M.F.; Cartaxo, A.V.T. Characterization of the stochastic time evolution of short-term average intercore crosstalk in multicore fibers with multiple interfering cores. Opt. Express 2018, 26, 4605–4620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Honda, E.; Mori, Y.; Hasegawa, H.; Sato, K.-I. Intra- and inter-datacentre converged networks utilising Kramers-Kronig receivers. In Proceedings of the 45th European Conference on Optical Communication (ECOC), Dublin, Ireland, 22–26 September 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Luis, R.S.; Puttnam, B.J.; Cartaxo, A.; Klaus, W.; Mendinueta, J.M.D.; Awaji, Y.; Wada, N.; Nakanishi, T.; Hayashi, T.; Sasaki, T. Time and modulation frequency dependence of crosstalk in homogeneous multi-core fibers. J. Light. Technol. 2016, 34, 441–447. [Google Scholar] [CrossRef]
- Matsui, T.; Sagae, Y.; Sakamoto, T.; Nakajima, K. Design and applicability of multi-core fibers with standard cladding diameter. J. Light. Technol. 2020, 38, 6065–6070. [Google Scholar] [CrossRef]
- Kopp, V.; Park, J.; Singer, J.; Neugroschl, D.; Gillooly, A. Low return loss multicore fiber-fanout assembly for SDM and sensing applications. In Proceedings of the Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 8–12 March 2020; pp. 1–3. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).