Multiphoton Resonance in Attosecond Transient Absorption
Abstract
:1. Introduction
2. Theoretical Model
2.1. 3D-TDSE
2.2. Time-Dependent Perturbation Theory
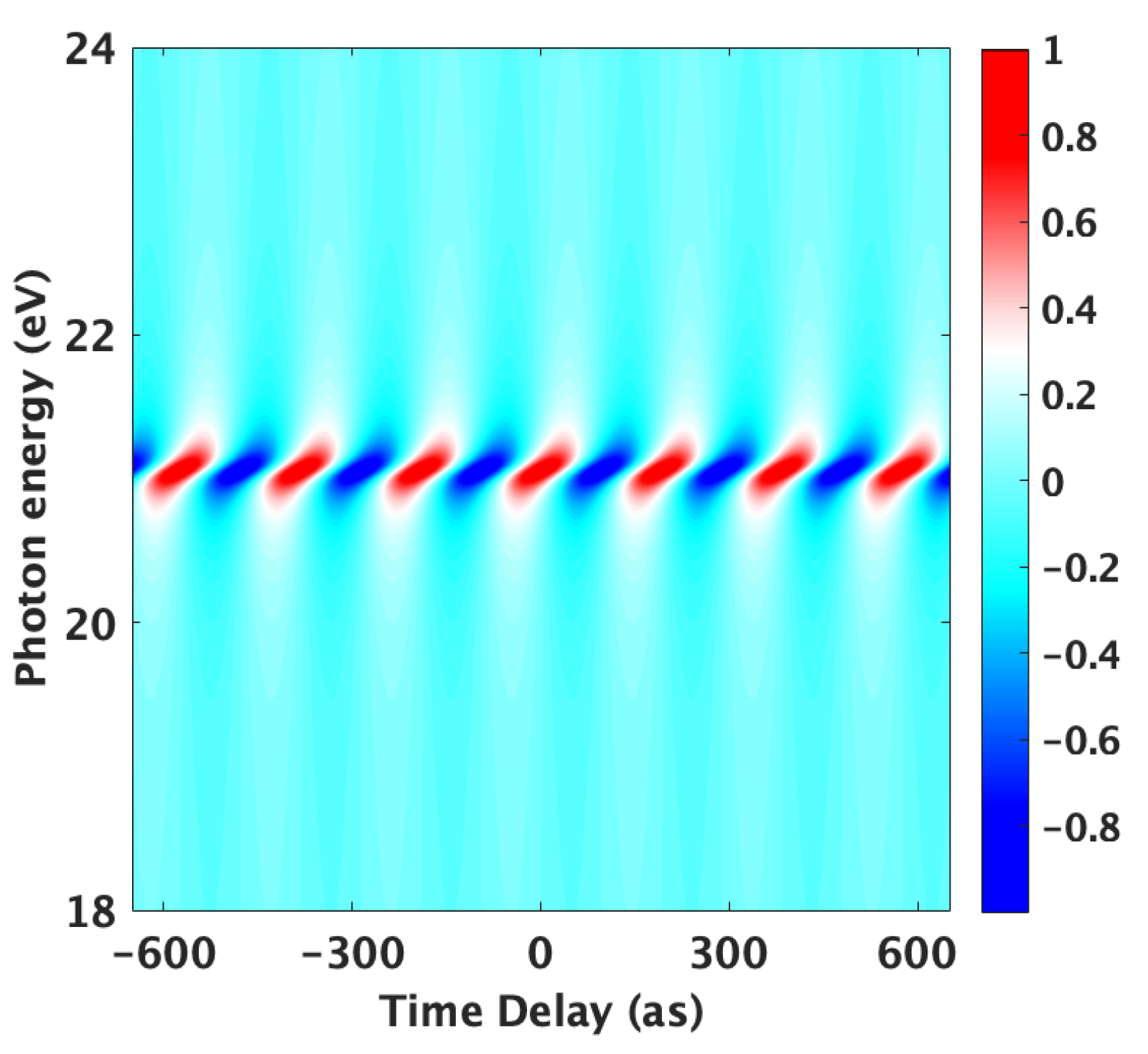
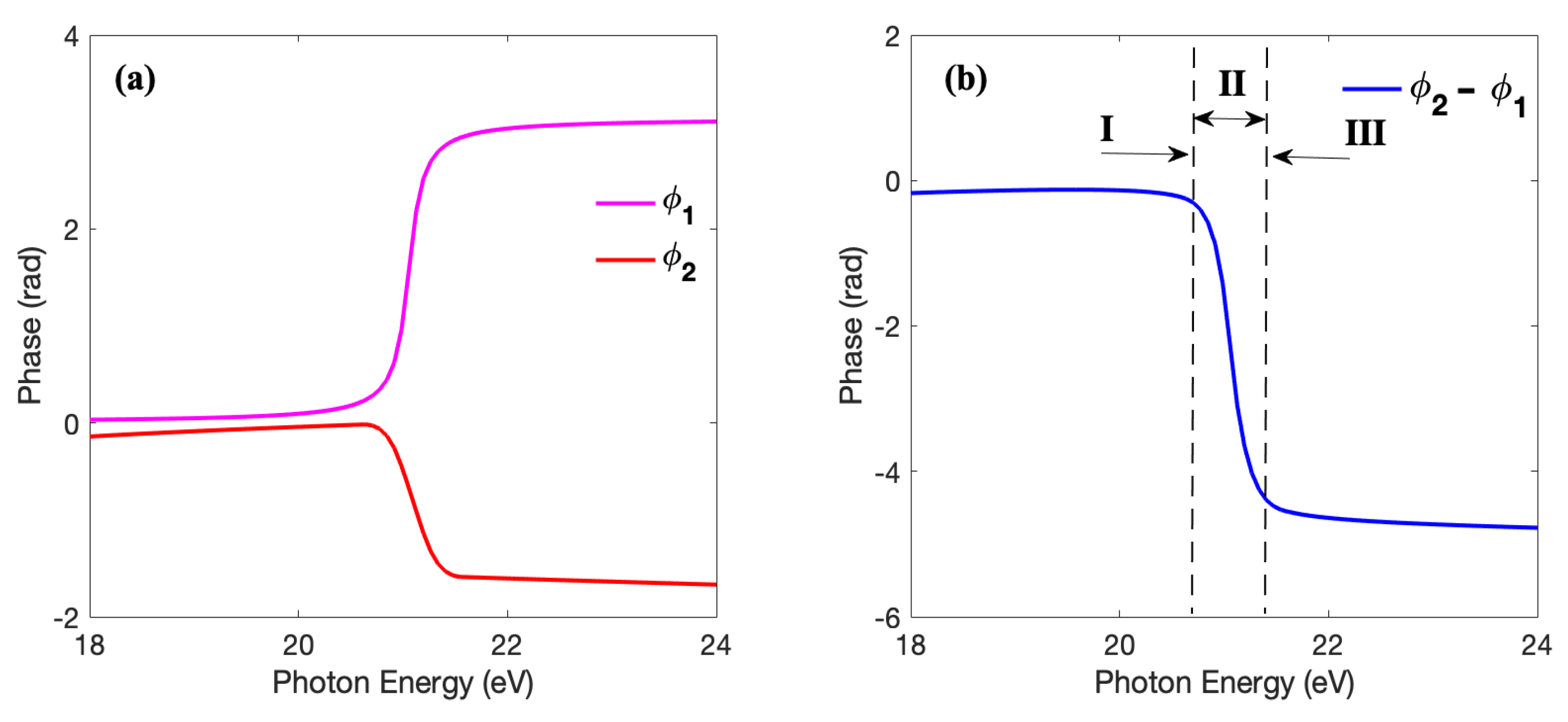
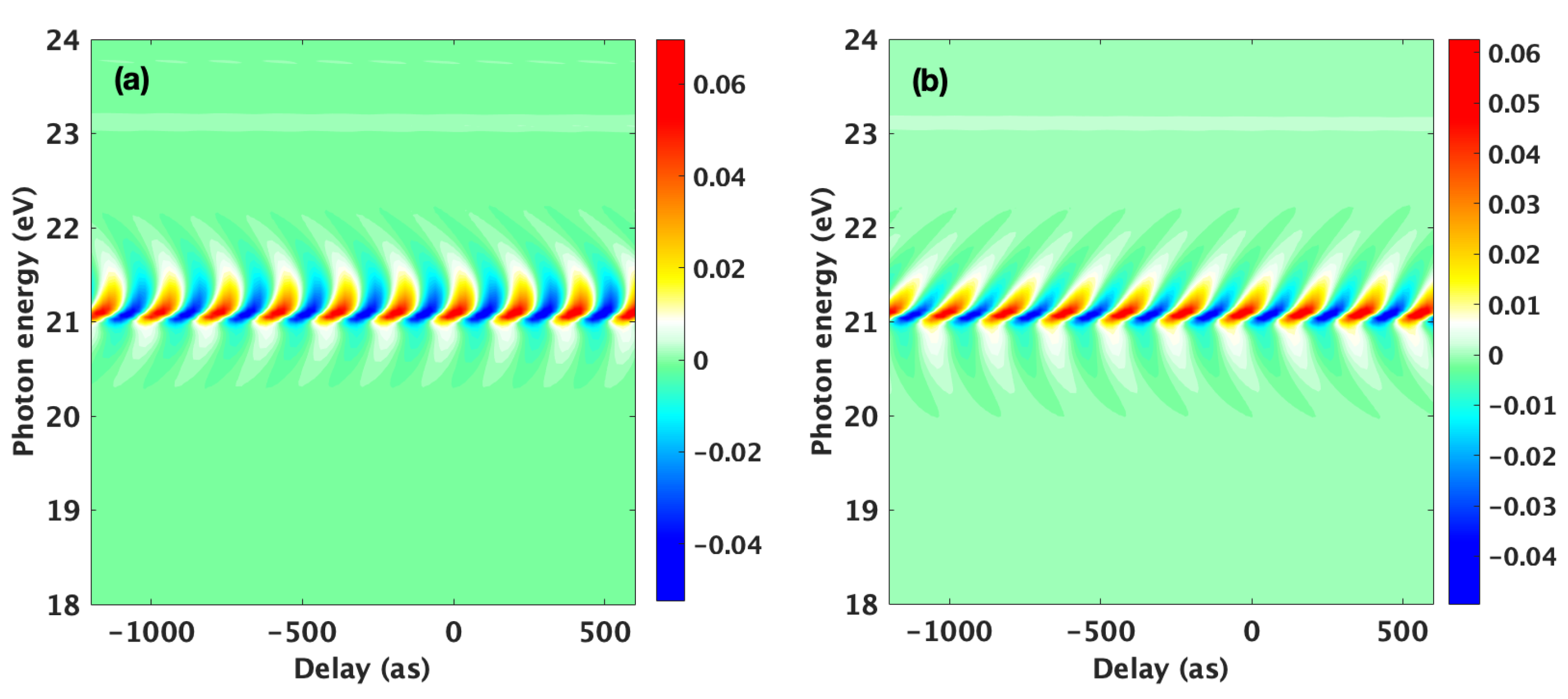
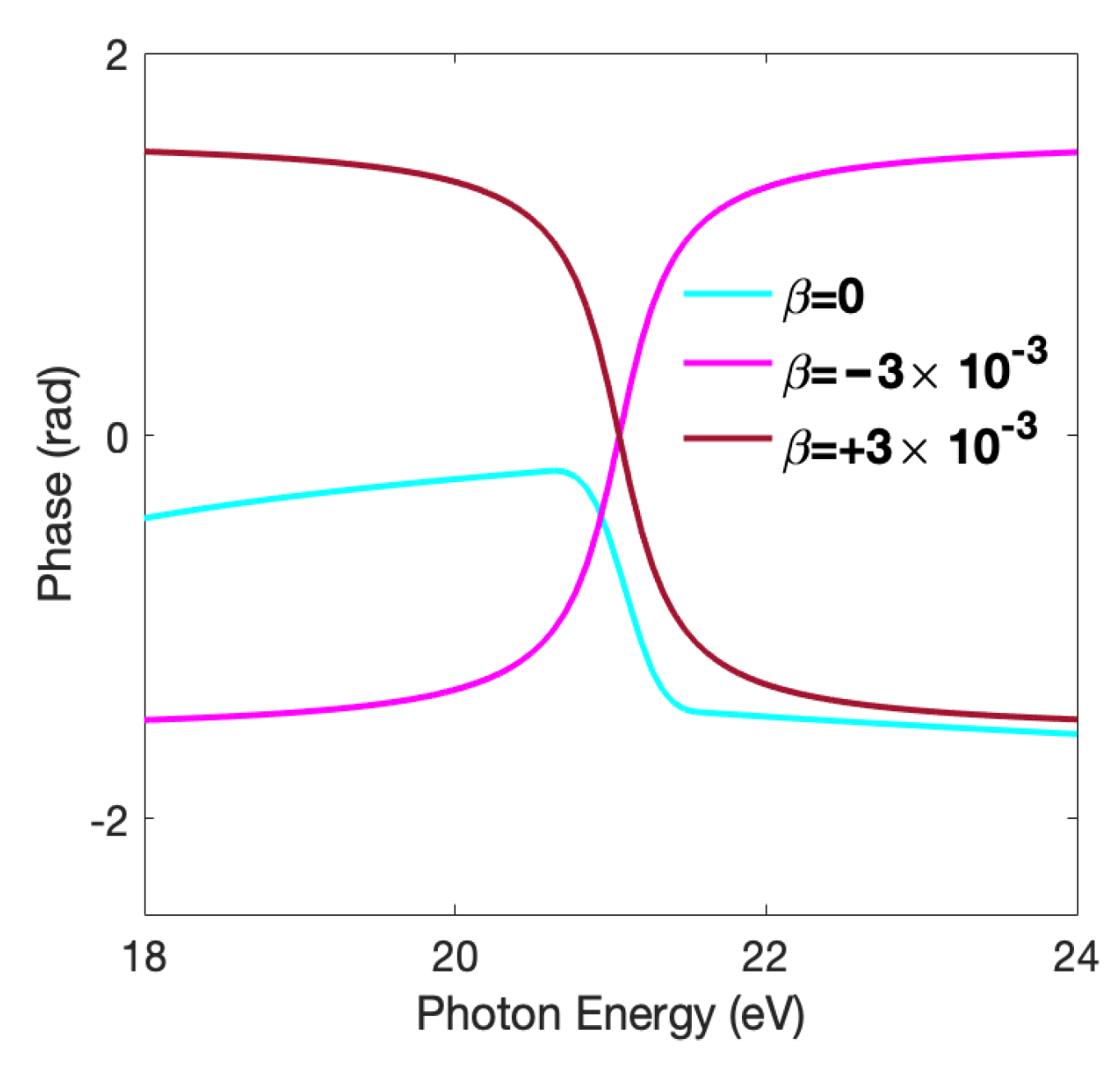
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VUV | vacuum ultraviolet |
| XUV | extreme ultraviolet |
| IR | infrared |
| ATAS | attosecond transient absorption spectrograms |
| 3D-TDSE | 3-dimensional time-dependent Schrödinger equation |
| ADK | Ammosov M. V., Delone N. B. and Krainov V. P. |
| KBBF | KBe2BO3F2 crystal |
References
- Goulielmakis, E.; Loh, Z.H.; Wirth, A.; Santra, R.; Rohringer, N.; Yakovlev, V.S.; Zherebtsov, S.; Pfeifer, T.; Azzeer, A.M.; Kling, M.F.; et al. Real-time observation of valence electron motion. Nature 2010, 466, 739–743. [Google Scholar] [CrossRef] [PubMed]
- Loh, Z.H.; Greene, C.H.; Leone, S.R. Femtosecond induced transparency and absorption in the extreme ultraviolet by coherent coupling of the He 2s2p (1Po) and 2p2 (1Se) double excitation states with 800 nm light. Chem. Phys. 2008, 350, 7–13. [Google Scholar] [CrossRef] [Green Version]
- Chu, W.C.; Zhao, S.F.; Lin, C. Laser-assisted-autoionization dynamics of helium resonances with single attosecond pulses. Phys. Rev. A 2011, 84, 033426. [Google Scholar] [CrossRef] [Green Version]
- Holler, M.; Schapper, F.; Gallmann, L.; Keller, U. Attosecond Electron Wave-Packet Interference Observed by Transient Absorption. Phys. Rev. Lett. 2011, 106, 123601. [Google Scholar] [CrossRef] [PubMed]
- Ott, C.; Kaldun, A.; Raith, P.; Meyer, K.; Laux, M.; Evers, J.; Keitel, C.H.; Greene, C.H.; Pfeifer, T. Lorentz meets Fano in spectral line shapes: A universal phase and its laser control. Science 2013, 340, 716–720. [Google Scholar] [CrossRef] [Green Version]
- Ott, C.; Kaldun, A.; Argenti, L.; Raith, P.; Meyer, K.; Laux, M.; Zhang, Y.; Blättermann, A.; Hagstotz, S.; Ding, T.; et al. Reconstruction and control of a time-dependent two-electron wave packet. Nature 2014, 516, 374–378. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Bernhardt, B.; Beck, A.R.; Warrick, E.R.; Pfeiffer, A.N.; Bell, M.J.; Haxton, D.J.; McCurdy, C.W.; Neumark, D.M.; Leone, S.R. Investigation of coupling mechanisms in attosecond transient absorption of autoionizing states: Comparison of theory and experiment in xenon. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 125601. [Google Scholar] [CrossRef] [Green Version]
- Beck, A.R.; Bernhardt, B.; Warrick, E.R.; Wu, M.; Chen, S.; Gaarde, M.B.; Schafer, K.J.; Neumark, D.M.; Leone, S.R. Attosecond transient absorption probing of electronic superpositions of bound states in neon: Detection of quantum beats. New J. Phys. 2014, 16, 113016. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Chini, M.; Cheng, Y.; Wu, Y.; Tong, X.M.; Chang, Z. Subcycle laser control and quantum interferences in attosecond photoabsorption of neon. Phys. Rev. A 2013, 87, 063413. [Google Scholar] [CrossRef] [Green Version]
- Sabbar, M.; Timmers, H.; Chen, Y.J.; Pymer, A.K.; Loh, Z.H.; Sayres, S.G.; Pabst, S.; Santra, R.; Leone, S.R. State-resolved attosecond reversible and irreversible dynamics in strong optical fields. Nat. Phys. 2017, 13, 472–478. [Google Scholar] [CrossRef]
- Wang, H.; Chini, M.; Chen, S.; Zhang, C.H.; He, F.; Cheng, Y.; Wu, Y.; Thumm, U.; Chang, Z. Attosecond time-resolved autoionization of argon. Phys. Rev. Lett. 2010, 105, 143002. [Google Scholar] [CrossRef] [PubMed]
- Chew, A.; Douguet, N.; Cariker, C.; Li, J.; Lindroth, E.; Ren, X.; Yin, Y.; Argenti, L.; Hill III, W.T.; Chang, Z. Attosecond transient absorption spectrum of argon at the L2,3 edge. Phys. Rev. A 2018, 97, 031407. [Google Scholar] [CrossRef] [Green Version]
- Pabst, S.; Sytcheva, A.; Moulet, A.; Wirth, A.; Goulielmakis, E.; Santra, R. Theory of attosecond transient-absorption spectroscopy of krypton for overlapping pump and probe pulses. Phys. Rev. A 2012, 86, 063411. [Google Scholar] [CrossRef] [Green Version]
- Birk, P.; Stooß, V.; Hartmann, M.; Borisova, G.D.; Blättermann, A.; Heldt, T.; Bartschat, K.; Ott, C.; Pfeifer, T. Attosecond transient absorption of a continuum threshold. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 124002. [Google Scholar] [CrossRef]
- Bækhøj, J.E.; Yue, L.; Madsen, L.B. Nuclear-motion effects in attosecond transient-absorption spectroscopy of molecules. Phys. Rev. A 2015, 91, 043408. [Google Scholar] [CrossRef] [Green Version]
- Warrick, E.R.; Cao, W.; Neumark, D.M.; Leone, S.R. Probing the dynamics of Rydberg and valence states of molecular nitrogen with attosecond transient absorption spectroscopy. J. Phys. Chem. A 2016, 120, 3165–3174. [Google Scholar] [CrossRef] [Green Version]
- Peng, P.; Marceau, C.; Hervé, M.; Corkum, P.; Naumov, A.Y.; Villeneuve, D. Symmetry of molecular Rydberg states revealed by XUV transient absorption spectroscopy. Nat. Commun. 2019, 10, 5269. [Google Scholar] [CrossRef] [Green Version]
- Golubev, N.V.; Vaníček, J.c.v.; Kuleff, A.I. Core-Valence Attosecond Transient Absorption Spectroscopy of Polyatomic Molecules. Phys. Rev. Lett. 2021, 127, 123001. [Google Scholar] [CrossRef]
- Warrick, E.R.; Bækhøj, J.E.; Cao, W.; Fidler, A.P.; Jensen, F.; Madsen, L.B.; Leone, S.R.; Neumark, D.M. Attosecond transient absorption spectroscopy of molecular nitrogen: Vibrational coherences in the b′1Σ+u state. Chem. Phys. Lett. 2017, 683, 408–415. [Google Scholar] [CrossRef] [Green Version]
- Schultze, M.; Ramasesha, K.; Pemmaraju, C.; Sato, S.; Whitmore, D.; Gandman, A.; Prell, J.S.; Borja, L.; Prendergast, D.; Yabana, K.; et al. Attosecond band-gap dynamics in silicon. Science 2014, 346, 1348–1352. [Google Scholar] [CrossRef]
- Reimann, J.; Schlauderer, S.; Schmid, C.; Langer, F.; Baierl, S.; Kokh, K.; Tereshchenko, O.; Kimura, A.; Lange, C.; Güdde, J.; et al. Subcycle observation of lightwave-driven Dirac currents in a topological surface band. Nature 2018, 562, 396–400. [Google Scholar] [CrossRef] [PubMed]
- Silva, R.; Jiménez-Galán, Á.; Amorim, B.; Smirnova, O.; Ivanov, M. Topological strong-field physics on sub-laser-cycle timescale. Nat. Photonics 2019, 13, 849–854. [Google Scholar] [CrossRef] [Green Version]
- Sommer, A.; Bothschafter, E.; Sato, S.; Jakubeit, C.; Latka, T.; Razskazovskaya, O.; Fattahi, H.; Jobst, M.; Schweinberger, W.; Shirvanyan, V.; et al. Attosecond nonlinear polarization and light–matter energy transfer in solids. Nature 2016, 534, 86–90. [Google Scholar] [CrossRef] [PubMed]
- Oguri, K.; Mashiko, H.; Suda, A.; Gotoh, H. Lightwave-driven electronic phenomena in solids observed by attosecond transient absorption spectroscopy. In Progress in Ultrafast Intense Laser Science XIV; Springer: Berlin/Heidelberg, Germany, 2018; pp. 219–238. [Google Scholar]
- Hanus, V.; Csajbók, V.; Pápa, Z.; Budai, J.; Márton, Z.; Kiss, G.Z.; Sándor, P.; Paul, P.; Szeghalmi, A.; Wang, Z.; et al. Light-field-driven current control in solids with pJ-level laser pulses at 80 MHz repetition rate. Optica 2021, 8, 570–576. [Google Scholar] [CrossRef]
- Cistaro, G.; Plaja, L.; Martín, F.; Picón, A. Attosecond x-ray transient absorption spectroscopy in graphene. Phys. Rev. Res. 2021, 3, 013144. [Google Scholar] [CrossRef]
- Petersen, J.C.; Farahani, A.; Sahota, D.G.; Liang, R.; Dodge, J.S. Transient terahertz photoconductivity of insulating cuprates. Phys. Rev. B 2017, 96, 115133. [Google Scholar] [CrossRef] [Green Version]
- Chini, M.; Zhao, B.; Wang, H.; Cheng, Y.; Hu, S.; Chang, Z. Subcycle ac stark shift of helium excited states probed with isolated attosecond pulses. Phys. Rev. Lett. 2012, 109, 073601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chini, M.; Wang, X.; Cheng, Y.; Wu, Y.; Zhao, D.; Telnov, D.A.; Chu, S.I.; Chang, Z. Sub-cycle oscillations in virtual states brought to light. Sci. Rep. 2013, 3, 1105. [Google Scholar] [CrossRef] [Green Version]
- Bell, M.J.; Beck, A.R.; Mashiko, H.; Neumark, D.M.; Leone, S.R. Intensity dependence of light-induced states in transient absorption of laser-dressed helium measured with isolated attosecond pulses. J. Mod. Opt. 2013, 60, 1506–1516. [Google Scholar] [CrossRef]
- Reduzzi, M.; Hummert, J.; Dubrouil, A.; Calegari, F.; Nisoli, M.; Frassetto, F.; Poletto, L.; Chen, S.; Wu, M.; Gaarde, M.B.; et al. Polarization control of absorption of virtual dressed states in helium. Phys. Rev. A 2015, 92, 033408. [Google Scholar] [CrossRef] [Green Version]
- Dong, W.; Li, Y.; Wang, X.; Yuan, J.; Zhao, Z. Analysis of interference in attosecond transient absorption in adiabatic condition. Phys. Rev. A 2015, 92, 033412. [Google Scholar] [CrossRef] [Green Version]
- Rørstad, J.J.; Bækhøj, J.E.; Madsen, L.B. Analytic modeling of structures in attosecond transient-absorption spectra. Phys. Rev. A 2017, 96, 013430. [Google Scholar] [CrossRef] [Green Version]
- Ravn, N.S.; Madsen, L.B. Nonadiabatic effects in attosecond transient absorption spectroscopy. arXiv 2021, arXiv:2103.01582. [Google Scholar]
- Wu, M.; Chen, S.; Gaarde, M.B.; Schafer, K.J. Time-domain perspective on Autler-Townes splitting in attosecond transient absorption of laser-dressed helium atoms. Phys. Rev. A 2013, 88, 043416. [Google Scholar] [CrossRef]
- Wu, M.; Chen, S.; Camp, S.; Schafer, K.J.; Gaarde, M.B. Theory of strong-field attosecond transient absorption. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 062003. [Google Scholar] [CrossRef]
- Chini, M.; Wang, X.; Cheng, Y.; Chang, Z. Resonance effects and quantum beats in attosecond transient absorption of helium. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 124009. [Google Scholar] [CrossRef]
- Pfeiffer, A.N.; Leone, S.R. Transmission of an isolated attosecond pulse in a strong-field dressed atom. Phys. Rev. A 2012, 85, 053422. [Google Scholar] [CrossRef] [Green Version]
- Eberly, J.; Grobe, R.; Law, C.; Su, Q. Numerical experiments in strong and super-strong fields. In Advances in Atomic, Molecular, and Optical Physics; Elsevier: Amsterdam, The Netherlands, 1992; pp. 301–334. [Google Scholar]
- Schafer, K.J.; Kulander, K.C. High harmonic generation from ultrafast pump lasers. Phys. Rev. Lett. 1997, 78, 638. [Google Scholar] [CrossRef] [Green Version]
- Gaarde, M.B.; Buth, C.; Tate, J.L.; Schafer, K.J. Transient absorption and reshaping of ultrafast XUV light by laser-dressed helium. Phys. Rev. A 2011, 83, 013419. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Nisoli, M. Complete characterization of a coherent superposition of atomic states by asymmetric attosecond photoionization. Phys. Rev. A 2012, 85, 053423. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, C.; Zheng, Y.; Zeng, Z.; Li, R. Attosecond chirp effect on the transient absorption spectrum of laser-dressed helium atom. Opt. Express 2017, 25, 7707–7718. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Liu, C.; Zeng, Z.; Li, R.; Xu, Z. Multiple-fringe structure of attosecond transient absorption spectrum driven by mid-infrared laser. Chin. Opt. Lett. 2019, 17, 082601. [Google Scholar]
- Penetrante, B.; Bardsley, J.; Wood, W.M.; Siders, C.; Downer, M.C. Ionization-induced frequency shifts in intense femtosecond laser pulses. JOSA B 1992, 9, 2032–2040. [Google Scholar] [CrossRef]
- Chang, Z. Fundamentals of Attosecond Optics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hertel, I.V.; Schulz, C.P. Atoms, Molecules and Optical Physics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Chen, S.; Wu, M.; Gaarde, M.B.; Schafer, K.J. Quantum interference in attosecond transient absorption of laser-dressed helium atoms. Phys. Rev. A 2013, 87, 033408. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Tang, D.; Ye, N.; Chen, C. Linear and nonlinear optical properties of the KBe2BO3F2 (KBBF) crystal. Opt. Mater. 1996, 5, 105–109. [Google Scholar] [CrossRef]
- Chen, C. Recent advances in deep and vacuum-UV harmonic generation with KBBF crystal. Opt. Mater. 2004, 26, 425–429. [Google Scholar] [CrossRef]
- Kanai, T.; Kanda, T.; Sekikawa, T.; Watanabe, S.; Togashi, T.; Chen, C.; Zhang, C.; Xu, Z.; Wang, J. Generation of vacuum-ultraviolet light below 160 nm in a KBBF crystal by the fifth harmonic of a single-mode Ti: Sapphire laser. JOSA B 2004, 21, 370–375. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, G.; Guo, L.; Geng, A.; Bo, Y.; Cui, D.; Xu, Z.; Li, R.; Zhu, Y.; Wang, X.; et al. 175 to 210 nm widely tunable deep-ultraviolet light generation based on KBBF crystal. Appl. Phys. B 2008, 93, 323–326. [Google Scholar] [CrossRef]
- Ermolov, A.; Mak, K.F.; Frosz, M.H.; Travers, J.C.; Russell, P.S.J. Supercontinuum generation in the vacuum ultraviolet through dispersive-wave and soliton-plasma interaction in a noble-gas-filled hollow-core photonic crystal fiber. Phys. Rev. A 2015, 92, 033821. [Google Scholar] [CrossRef] [Green Version]
- Van Bramer, S.; Johnston, M. Tunable, coherent vacuum ultraviolet radiation for photoionization mass spectrometry. Appl. Spectrosc. 1992, 46, 255–261. [Google Scholar] [CrossRef]
- Brahms, C.; Grigorova, T.; Belli, F.; Travers, J.C. High-energy ultraviolet dispersive-wave emission in compact hollow capillary systems. Opt. Lett. 2019, 44, 2990–2993. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Joly, N.Y.; Finger, M.A.; Babic, F.; Wong, G.K.; Travers, J.C.; Russell, P.S.J. Deep-ultraviolet to mid-infrared supercontinuum generated in solid-core ZBLAN photonic crystal fibre. Nat. Photonics 2015, 9, 133–139. [Google Scholar] [CrossRef]
- Dahiya, S.; Sidhu, M.S.; Tyagi, A.; Mandal, A.; Nandy, B.; Rost, J.M.; Pfeifer, T.; Singh, K.P. In-line ultra-thin attosecond delay line with direct absolute-zero delay reference and high stability. Opt. Lett. 2020, 45, 5266–5269. [Google Scholar] [CrossRef] [PubMed]
- Kretschmar, M.; Vrakking, M.; Schütte, B. Intense narrowband XUV pulses from a compact setup. arXiv 2021, arXiv:2106.15920. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, J.; Wang, M.; Zhou, C.; Ruan, S. Multiphoton Resonance in Attosecond Transient Absorption. Photonics 2022, 9, 257. https://doi.org/10.3390/photonics9040257
Xue J, Wang M, Zhou C, Ruan S. Multiphoton Resonance in Attosecond Transient Absorption. Photonics. 2022; 9(4):257. https://doi.org/10.3390/photonics9040257
Chicago/Turabian StyleXue, Jinxing, Meng Wang, Cangtao Zhou, and Shuangchen Ruan. 2022. "Multiphoton Resonance in Attosecond Transient Absorption" Photonics 9, no. 4: 257. https://doi.org/10.3390/photonics9040257
APA StyleXue, J., Wang, M., Zhou, C., & Ruan, S. (2022). Multiphoton Resonance in Attosecond Transient Absorption. Photonics, 9(4), 257. https://doi.org/10.3390/photonics9040257



