Abstract
The digital image correlation (DIC) method is widely used in deformation measurement due to the advantages of being non-contact, high precision, full field measurement, and requiring simple experimental equipment. Traditionally, the grayscale speckle patterns captured by a monochromatic camera are used in the DIC method. With the growing development of consumer color cameras, there is a great potential for developing color information in the DIC method. This paper proposes a scaling- and rotation-invariant DIC (SRI-DIC) method based on the color speckle patterns. For the integer-pixel matching stage, the scaling- and rotation-invariant color histogram feature is used to estimate the initial value of the deformation parameters. For the sub-pixel matching stage, a new error function using the three-channel information of color camera is proposed to avoid the influence of illumination changes. In addition, this paper proposes a reverse retrieve strategy instead of the forward search to reduce the search time. Experiments show that the proposed SRI-DIC algorithm not only has scaling and rotation invariance, robustness, and high efficiency, but also that the average accuracy of the strain result can reach 0.1%.
1. Introduction
Digital image correlation (DIC) is a non-contact optical method which measures the deformation of the objects by comparing the grey intensity of the images. Since the traditional DIC method only needs grayscale information, monochrome camera is widely used in DIC method, but color camera is rarely used. Although monochrome camera can provide grayscale information, such as contour and texture, it loses color information. In recent years, due to the rapid development of consumer color cameras, a large selection of color camera is available. Therefore, the research goal of this paper is to extend the capabilities of the traditional DIC method by introducing the additional color information.
In 1987, although color cameras were not easily available, E. Badique et al. studied image correlation based on color features, and their research pointed out that the exploitation of both spatial and chromatic attributes of images can improve recognition performances [1]. Satoru Yoneyama et al. also stated that the use of color information can improve the measurement accuracy and can use smaller sub-region to calculate the correlation [2]. David Hang et al. proved that color DIC is usually better than grayscale DIC, and the smaller the sub-region size, the greater the advantage [3]. To make full use of color information, Nghia V. Dinh et al. proposed a new error function, which take into account the three channels of color image, and minimized it by the Newton-Raphson method [4]. A. Forsey et al. combined the red, green and blue channels to create a monochrome image suitable for traditional grayscale DIC [5]. However, this method only improved the input image of DIC algorithm, but not the DIC algorithm. In addition, some scholars used a color camera to capture two different perspectives simultaneously via its blue and red channels, by this, 3D-DIC method using a color camera was achieved [6,7]. To avoid the effect of out-plane motion and non-perpendicular alignment, Wang et al. proposed that the red and blue channels of the color camera are used for 2D-DIC processing and compensation respectively [8].
In general, the existing DIC methods using color information can be divided into the following three categories: (i) using only a single channel, and the other two channels are abandoned or used for other purposes [6,7,8]; (ii) computing the luminance from the three channels and using it as a “standard” monochrome image [1,5]; and (iii) extending the error function to process all of the three channels’ data [2,3,4]. In the first category, one of the channels is chosen and used for traditional DIC processing, discarding the other channels, which is easy to operate and efficient. In the second category, the intensity of the three channels is combined into a single monochrome image for traditional DIC processing, which reduces the influence of noise that may exist in one of the camera channels. However, these two methods do not improve the DIC algorithm or make full use of the three-channel information. In the third category, the color image is treated as a superposition of three grayscale images, and the error functions of the three grayscale images are added to form the total error function. However, this method only considers the three-channel information at the mathematical level, and does not use color features. Moreover, this method requires interpolation and derivation of the three grayscale images separately, which greatly reduces the efficiency.
We aim to improve the DIC algorithm with the aid of color information, so that it has the following features: (i) it is scaling- and rotation-invariant so it can still match even if the object undergoes a large rotation or scaling deformation; and (ii) it has high efficiency and illumination invariance. To fulfill it, the color histogram features, which inherently have scaling and rotation invariance, are used to obtain the initial value of deformation parameters. Subsequently, the initial value is optimized to minimize the error function, which is calculated by the hue value of the color image, and eventually the deformation results can be measured. Since the illumination change and shift will affect the RGB values but not the hue values of the image, the hue-based error function has the advantage of illumination invariance. Furthermore, optimizing the hue-based error function only needs to interpolate and derive one hue image, instead of interpolating and deriving three channels separately, thereby improving the computational efficiency. To improve the search efficiency, this paper also proposes a search strategy based on reverse retrieve to replace the traditional forward search. In sum, this paper proposes a scaling- and rotation-invariant DIC (SRI-DIC) algorithm, which has higher efficiency and illumination invariance. The contributions of this work are as follows: (i) the color histogram features are introduced into DIC algorithm, so that the SRI-DIC algorithm has scaling and rotation invariance; (ii) the hue value is used to calculate the error function, which makes the DIC algorithm have illumination invariance; and (iii) a novel search strategy based on reverse retrieve is proposed, which greatly improves the efficiency.
The outline of this paper is described as follows. Section 1 introduces the motivation and background of this study. Section 2 mentions the basic principle of DIC algorithm. In Section 3, the integer-pixel matching algorithm based on color histogram feature is introduced in detail; To increase illumination invariance and matching accuracy, hue-based sub-pixel matching algorithm is proposed in Section 4. Section 5 analyses the performances of the proposed SRI-DIC algorithm by simulation and real experiments. Concluding remarks are summarized in Section 6.
2. Basic Principle of Digital Image Correlation Algorithm
The DIC method measures the displacement of the tracking points by correlation matching between images before and after deformation. Given a point in the reference image, a square sub-region of pixels centered at P is selected as reference sub-region. The corresponding position and deformation parameters of the reference sub-region in the deformed image are determined by minimizing the error function. The widely used error function is the zero-mean normalized sum of squared difference (ZNSSD) correlation criteria, as shown in Equation (1).
The shape function is used to describe the shape deformation related the corresponding coordinates in the reference and deformed sub-regions. The most widely used shape function is the first-order shape function, as shown in Equation (2).
where the deformation parameter . can describe the first-order deformations, such as translation, rotation, scaling, shearing. The most effective algorithm in finding the optimal deformation parameters is iterative optimization, which starts from a reasonable initial value and then iteratively refines the desirable parameter to minimize the error function. Before iterative optimization, integer-pixel matching must be performed to obtain the initial value of the deformation parameters. The initial value of the deformation parameters can be obtained by calculating the correlation coefficients by point-by-point traversal. However, when the deformed image undergoes large rotation or scaling, the correlation coefficient will drop sharply and cause mismatch, which is called de-correlation phenomenon.
Fortunately, the additional color information of color images provides a new alternative solution to the de-correlation caused by large rotation or scaling deformation. In this paper, the color histogram feature is used for integer-pixel matching to obtain the translation and the scaling factor . In addition, the color codes feature is proposed to measure the rotation angle . To determine the initial value of the deformation parameter , only the effects of translation, rotation and scaling on the shape function are considered, as shown in Figure 1. The center of the sub-region is shown with point nearby, after deformation, the point coordinates become .
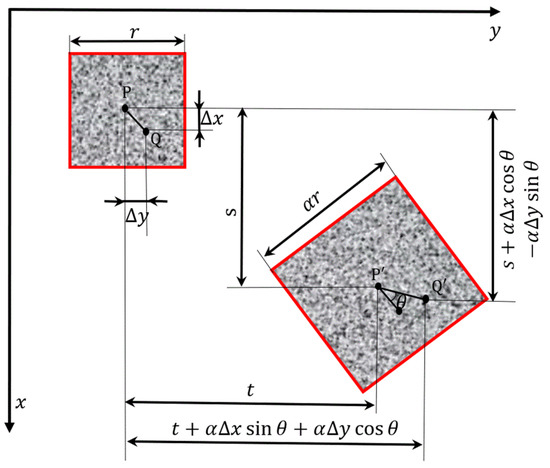
Figure 1.
Sub-region before and after rigid body rotation and scaling.
Combining Equations (2) and (3), the initial value of the deformation parameter is obtained as follows:
When the initial value is obtained, the error function is minimized by inverse compositional Gauss-Newton (IC-GN) or forward additive Newton–Raphson (FA-NR) iterative algorithm to obtain sub-pixel measurement results. To make full use of color information, this paper proposes to use color information again to calculate the error function, which is invariant to illumination change and shift.
3. Integer-Pixel Matching Based on Color Information
The traditional integer-pixel matching is no longer effective when the object surface undergoes large rotation or scaling. Thanks to the color information, many scaling- and rotation-invariant color features, which are widely used in the field of image retrieval [9,10], can be introduced into the DIC algorithm. An integer-pixel matching method based on color histogram feature is proposed to obtain the initial value of deformation parameter. In this way, the image pairs with arbitrary rotation angle and scaling factor can be matched. Subsequently, the color codes feature is proposed to obtain the rotation angle, and eventually the initial value of the deformation parameter can be determined. To improve the efficiency of integer-pixel matching method, a search strategy using reverse retrieve instead of forward search is also proposed.
3.1. Image Matching Based on Color Histogram Feature
In the field of content-based image retrieval, color information is usually used for feature extraction and matching, with good results. However, to the best of our knowledge, there is no existing literature that introduces color features into the DIC method. To make use of color features, this section introduces the color histogram feature into the integer-pixel matching. The color histogram feature can simply describe the global distribution of colors in an image, and interestingly, it has scaling and rotation invariance. With the aid of the color histogram feature, the reference and deformed image pairs with arbitrary rotation angle and scaling factor can be matched.
To calculate the color histogram feature, the color space is divided into several small color intervals, each of which becomes a bin of the histogram, this process is called color quantization. The HSI color space is chosen for color quantization, and the hue, saturation, and intensity are divided into eight, four, and two intervals respectively, for a total of 64 cube bins. Subsequently, the color histogram is calculated by counting the number of pixels whose color value belongs to each cube bin. The feature is used to describe the color histogram of the image as follows:
where represents the normalized color value; is the total number of color values; is the total number of pixels with a color value of ; and is the total number of image pixels. Since the color histogram describes the statistical distribution of the image color, it has translation, scaling, and rotation invariance. When the image is scaled and rotated, the proportions of the various colors of the image are the same, that is, the color histogram feature remains unchanged with the scaling and rotation of the image. Therefore, a scaling- and rotation-invariant integer-pixel matching algorithm based on color histogram features is proposed in this paper, and its flowchart is shown in Figure 2.
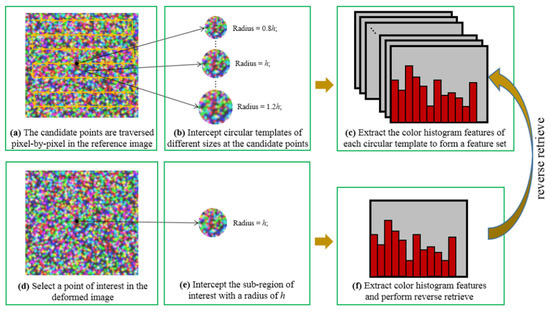
Figure 2.
Detailed flowchart of the scaling- and rotation-invariant integer-pixel matching algorithm based on color histogram features.
Due to the circular window is isotropic, the circular window is used to replace the traditional square window for image matching to ensure the rotation invariance. The multi-scale templates are extracted and matched with the sub-region of interest to determine the best matching position and scaling factor, as shown in Figure 2b. Assuming that the sub-region of interest is a circular area with a radius of pixels, the multi-scale templates are composed of circular sub-regions with a radius of 0.8 to 1.2 pixels (which can be adjusted according to the actual scaling range of the image). The color histogram features are extracted on the multi-scale templates and the sub-region of interest respectively, and then the Euclidean distance is used to evaluate the correlation between these color histogram features. Subsequently, the matching position and the scaling factor are determined by the templates with the greatest correlation. Therefore, the integer-pixel translation and the scaling factor are obtained.
As can be seen from Equation (4), not only the translation and the scaling factor but also the rotation angle must be determined to obtain the initial value of the deformation parameter . To obtain the rotation angle, the color codes feature is proposed in this paper. The polar coordinate system is established by taking the center of the sub-region as the coordinate origin, and the color codes feature of image T can be written as follows:
where and are the radius and angle in the polar coordinate system, respectively; is the radius of the circular window actually used, and is the RGB value of the corresponding pixel in polar coordinates ; represents the length of the color codes, which determines how many sectors the image is divided into; and is the total number of pixels on each sector. Therefore, the color codes feature depicts the average color of each sector regions, as shown in Figure 3. Obviously, when the image is rotated in any angle, the color codes feature of the image will undergo cyclic shift. The rotation angle can be determined by the number of cyclic shifts corresponding to the maximum correlation.
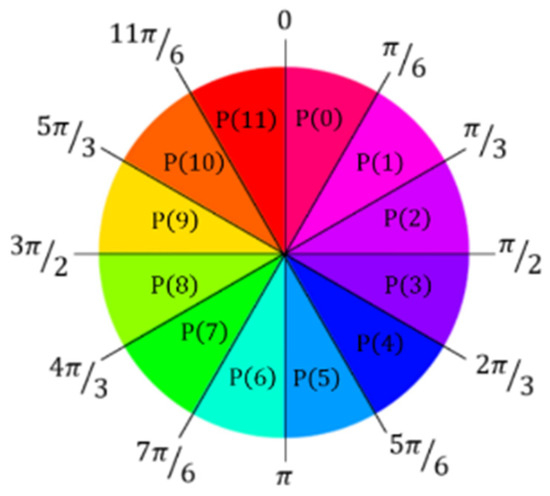
Figure 3.
Illustration of color codes ().
The color codes’ features of the image pair are extracted and marked as , , respectively. The normalized Euclidean distance of the color codes feature is used to represent the correlation of the image pair, as shown in Equation (8).
where denotes the color codes feature cyclically shifted by bins. The correlation value corresponding to each cyclic shift is calculated by Equation (8), and the maximum value among them can be obtained. Subsequently, the corresponding value of -shifts is obtained, and the rotation angle is determined by . Eventually, the integer-pixel translation , the scaling factor and the rotation angle all are available, and the initial value of the deformation parameter can be determined by Equation (4).
3.2. Search Strategy Based on Reverse Retrieve
As can be seen in Figure 2, the computational burden is greatly increased due to the color histogram features of the templates with different scales need to be extracted and matched. For example, the radius of the sub-region of interest is 30 pixels, and then the multi-scale templates contain a total of 13 template images with a radius from 24 to 36 pixels, which means that the computational burden is increased by 13 times. Moreover, when the range of scaling factor is unclear, the computational burden will be much greater. To improve the search efficiency, this paper proposes a search strategy based on reverse retrieve method.
The traditional integer-pixel matching method adopts a forward search strategy, that is, the reference sub-region is searched pixel-by-pixel in all deformed images to find the best matching position, as shown in Figure 4. With the continuous updating of deformed images, the search space of forward matching methods will also change. Once the search space is changed, it is necessary to perform feature extraction on all templates in the new search space, which is very time-consuming. To avoid redundant calculations, a reverse search method is proposed, in which, some fixed deformed sub-regions are selected and match in the reference image, as shown in Figure 4. By this method, the search space is the reference image, which is constant and can be precalculated. The reverse search strategy only needs to perform feature extraction on the search space once, therefore, it is more efficient than the forward search strategy.

Figure 4.
Comparison between forward search and reverse search strategy. In top figures, the reference sub-region (the red box) is searched in different deformed images. The bottom figures show that the reverse search method search the deformed sub-regions (the yellow and green box) in the reference image, which is constant and precalculated. For clarity, only two deformed images are displayed.
To further improve the search speed, we introduce an image retrieval method to replace the traditional pixel-by-pixel search, as shown in Figure 2c,f. Before the matching, the color histogram features of the multi-scale templates in the reference image are extracted pixel-by-pixel and stored in a feature sets Q, which are constant and do not need to be updated. When the deformed image is updated, it only needs to extract the color histogram features of the new deformed sub-region, and then retrieve them in the feature sets Q. The value of color histogram is quantized into eight intervals to build octree, and the retrieval method based on octree is used to speed up the image retrieval. Eventually, the reverse retrieval strategy avoids the repeated feature extraction of the search space and greatly improves the search efficiency.
4. Sub-Pixel Matching Based on Color Speckle Pattern
Sub-pixel matching is an iterative optimization of the error function using the Gauss-Newton or Newton-Raphson method to obtain the optimal solution of the deformation parameters [11,12]. Traditional grayscale DIC generally uses ZNSSD as an error function, as shown in Equation (1). Some scholars have proposed new error functions based on color speckle pattern [2,3,4,5], but these error functions are time-consuming and susceptible to illumination conditions. This paper proposes a hue-based error function which comprehensively uses the three-channel information and is invariant to the illumination changes.
4.1. Previous Work
To improve the accuracy of sub-pixel matching, the error function should make full use of the three-channel information of the color image. To fulfill it, the normalized cross-correlation function based on color information is proposed [2], as shown in Equation (9). In addition, the normalized sum of square distances function based on color information is proposed [3,4] and is widely used by color DIC algorithm, as shown in Equation (10).
where and refer to the intensity values for the red, green and blue channels of the template and deformed sub-region respectively. The optimal deformation parameters can be obtained by minimizing the above error function, which makes use of the three-channel information.
Although the above error functions are widely used in the color DIC algorithm, they still have some disadvantage. For example, the intensity values of the three channels may be affected by the illumination change, which result in a low matching accuracy. Moreover, the optimization of the above error function requires the derivation and interpolation of three monochrome images, which reduce the efficiency of the color DIC algorithm.
4.2. Hue-Based Sub-Pixel Matching
Hue is insensitive to surface orientation, illumination direction, intensity and highlights [9]. Therefore, this paper proposes a hue-based sub-pixel matching algorithm to increase illumination invariance and matching accuracy.
4.2.1. Photometric Analysis
The change in illumination can be modeled by diagonal mapping [13] as follows:
where is the image taken under an unknown light source; is the same image after transformation, which can be regarded as an image taken under reference light (called canonical illuminant); is a diagonal matrix that maps the color captured under the unknown light source to the corresponding color under the canonical light source :
To include the ‘diffuse’ light term, Finlayson et al. introduced the offset into the diagonal model to obtain the diagonal-offset model [14]:
Light intensity offsets are due to diffuse lighting including scattering of a white light source, object highlights under a white light source, interreflections and infrared sensitivity of the camera sensor [9]. Based on the diagonal-offset model, the change of image intensity is discussed. First, when the intensity of the light source changes, the three-channel values in the color image change by a constant factor (i.e., ). Second, the intensity values of the three channels are equally offset (i.e., ). A comprehensive model of image intensity change is as follows:
Of course, () or () will also occur, and this type of image change is called light color change. Since the wavelength of the light source is relatively constant and the spectral response range of the camera is broad, this work does not consider light color change. The purpose of this section is to find an error function that is invariant to illumination intensity change.
The RGB value of the object image may change significantly, due to the varying circumstances such as a change in object orientation, illumination intensity and position. Fortunately, hue is insensitive to these unfavorable factors as can be seen from:
It is seen that the hue value under the canonical light source is equal to that under the unknown light source , that is, the hue of the object is independent of the illumination change. Therefore, there is no doubt that using the hue value to describe the error function will achieve better results.
4.2.2. Hue-Based Error Function
Since digital images are generally displayed using RGB color space, the hue value can be calculated from the RGB value by [15]:
As can be seen from the above formula, hue value is defined as an angle in the range with red at angle 0, green at , blue at and red again at . Two similar colors may have very different hue values, for example, both 0.01π and 1.99π belong to the red category. Therefore, it is not feasible to use the cumulative sum of the differences of the hue values as the error function. Fortunately, the range of hue can be regard as a unit circle, and each hue value represents a point on the unit circle, by this, the cumulative sum of the secant between the hue values can be used as the error function, as shown below:
where and are the hue values of the pixel in the template and deformed sub-region, respectively; and is the total number of pixels in the sub-region. In this work, Equation (17) is used as the error function, which is optimized by the IC-GN method to obtain the final deformation parameters.
The core of the Gauss-Newton method is to calculate the Hessian matrix, and the key to calculating the Hessian matrix is the derivation of image. The traditional derivative formula is as follows:
To avoid the situation where the derivative of two similar colors is too large (e.g., the hue values of two adjacent pixels are 0.01π and 1.99π, respectively. = 1.98π obtained from Equation (18), the derivative formula is redefined as:
With the help of the new derivation method, the proposed error function can be optimized by IC-GN method to obtain the optimal solution. The error function not only uses three-channel information, but also is robust to the change of light intensity and direction. In addition, only one hue image need be interpolated and derived during the optimization process, so the efficiency is also improved. We highlight that the ZNSSD error function is also robust to illumination change, but it does not work when the sub-region has uneven illumination changes, while the error function based on hue can still work.
5. Experimental Verification
To experimentally evaluate the proposed SRI-DIC algorithm, simulation experiments and real experiments were carried out. The simulated speckle images were used to evaluate the integer-pixel matching and sub-pixel matching of the proposed SRI-DIC algorithm. To verify the feasibility of the SRI-DIC algorithm in practical applications, the uniaxial tension experiment was conducted on a dog-bone-type polypropylene plastic specimen.
5.1. Simulation Experiments
The first experiment concerns the scaling invariance of the integer-pixel matching method, where a 200 × 200 pixels color speckle pattern was generated for verification, as shown in Figure 5a. Figure 5a is scaled by 0.7 and 1.4 times to obtain Figure 5b,c, and Figure 5d is obtained by stretching 1.2 times in the vertical direction. To better conform the actual measurement situation, the shear and rotation deformation is randomly added to these images, as shown in Figure 5. Subsequently, nine seed points are uniformly selected in Figure 5a, and these seed points is matched in Figure 5b–d using the SRI-DIC algorithm. Since the deformation of the generated image is pre-designed, the true displacement of these seed points is known. The performance of the SRI-DIC algorithm is evaluated by the error between the measurement results and the true displacements, as shown in Figure 6. It is seen that the SRI-DIC algorithm can perform integer-pixel matching on images with different scaling factors, and the maximum error is about three pixels. As the convergence range of the iterative optimization method is about seven pixels [16], the accuracy of the SRI-DIC algorithm completely satisfies the accuracy requirement of the initial value.

Figure 5.
A series of generated speckle images with different scales (where (b–d) are deformed by (a) according to different deformation parameter).
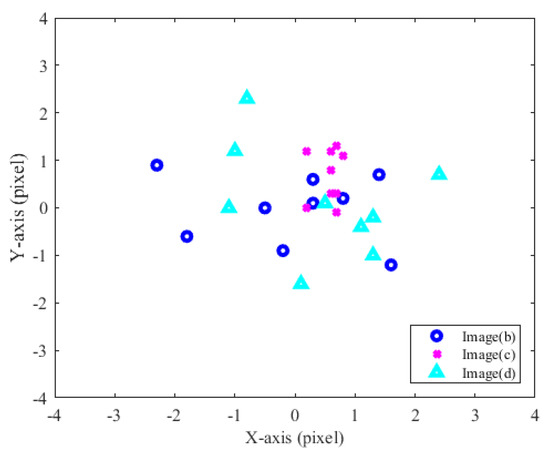
Figure 6.
The integer-pixel matching error corresponding to different scale images.
The second experiment concerns the rotation invariance of the integer-pixel matching method. Figure 5a was rotated at 30°, 60°, 90°, 120°, 150° and 180°, respectively, to obtain a series of color speckle images. All of the rotational angles are set to be in the counter-clockwise direction in this section, as shown in Figure 7. The calculation of the displacement and measurement errors is the same as in the first experiment, and the results are displayed in Table 1. As can be seen from Table 1, the proposed method can perform integer-pixel matching on images with different rotation angles, and the maximum error of position and angle is less than 3 pixels and 2.4°, respectively. To avoid the de-correlation phenomenon, the error of angle measurement should not exceed 3° [17]. Therefore, the accuracy of the SRI-DIC algorithm completely satisfies the accuracy requirement even though the image is rotated at different angles. We highlight that the angle measurement resolution is related to the length of the color codes, for example, the length of the color codes is 100 in this experiment and the angle resolution is 3.6°. If necessary, the length of the color codes can be increased to achieve higher angle accuracy.
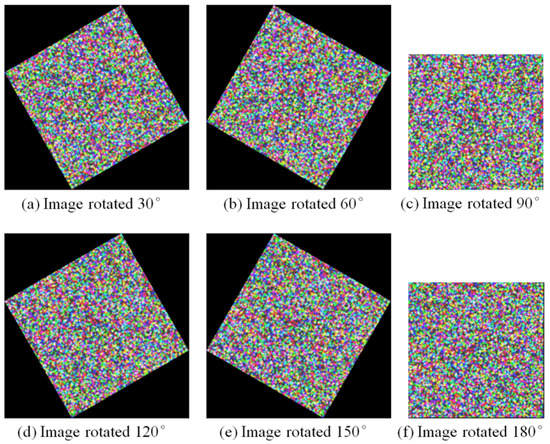
Figure 7.
A set of simulated images with different rotation angles.

Table 1.
Measurement results of the deformed images with different rotation angles.
The third experiment concerns the calculation efficiency of the reverse retrieve search strategy in the SRI-DIC algorithm. To evaluate the efficiency of the proposed algorithm, a comparative experiment with the Fourier-Mellin transform-based cross correlation (FMT-CC) method was conducted. Since the FMT-CC algorithm only calculates the correlation of a pair of deformed and reference sub-region without pixel-by-pixel searching, it is the fastest method among the existing rotation invariant initial value estimation algorithm. However, when the displacement is large (more than half of the width of the sub-region), the FMT-CC algorithm will does not work. The images of different scales in Figure 5 were reused and 10 seed points were randomly selected and matched using SRI-DIC algorithm and FMT-CC algorithm. The FMT-CC algorithm can only process grayscale image, so the color images are converted into grayscale images using the MATLAB function ‘rgb2gray’. The average computation time of 10 seed points is used to evaluate the calculation efficiency, and the results are shown in Table 2. It is seen that the SRI-DIC algorithm using image retrieval strategy costs less time than the FMT-CC algorithm. In addition, since the search space of the SRI-DIC algorithm is extracted pixel-by-pixel in the reference image, it is more robust than the FMT-CC algorithm when the displacement is large. Therefore, the SRI-DIC algorithm is not only highly efficient but also very robust.

Table 2.
Experimental results of comparing the efficiency of the proposed algorithm with the FMT-CC algorithm.
The fourth experiment concerns the illumination invariance of the SRI-DIC algorithm. A comparative experiment between the SRI-DIC algorithm and the traditional color DIC algorithm was carried out. According to Equation (14), the image intensity was changed to obtain a set of color speckle images with different brightness, as shown in Figure 8, and these images were matched by the SRI-DIC algorithm and the traditional color DIC algorithm. The measurement errors are shown in Table 3, and note that the measurement error in Table 3 is the root mean square error of randomly selecting 10 seed points. It can be seen from Table 3 that the measurement accuracy of the SRI-DIC method does not change significantly regardless of the brightness of the color speckle image changes. In contrast, the accuracy of the traditional color DIC method will deteriorate with illumination change. Therefore, we can conclude that the SRI-DIC algorithm proposed in this paper is invariant to illumination change.

Figure 8.
A set of simulated images with different brightness.

Table 3.
Experimental results of comparing the accuracy of the proposed algorithm with the traditional color DIC algorithm.
5.2. Real Experiments
To further investigate the practicality of the proposed method, uniaxial tensile tests were conducted, as shown in Figure 9. In this experiment, a dynamic test system (Instron E3000) and a dynamic extensometer (2620-601) were involved to stretch and measure the test specimen, which was a dog-bone-type polypropylene plastic specimen with 80 mm length, 10 mm width and 4 mm thickness. Two 2048 × 2448 pixels industrial color cameras (Basler_acA2440-75uc) with a 25 mm lens were used in the experiment.

Figure 9.
The physical diagram of the uniaxial tension experiment based on the 3D-DIC measurement device; (a) the physical map of the experiment; (b) the speckle images of different scales taken by the two cameras.
The test specimen was installed on the dynamic test system, and the dynamic extensometer was fixed at the back of the region of interest to obtain the true value of the strain. Before the experiment, color paint was sprayed on the surface of the specimen to form a speckle pattern. The two cameras were installed at different distances from the specimen, so the scale of the two images was different, as shown in Figure 9b. Since the scales of the two images are different, the traditional DIC method will have a de-correlation phenomenon, however, the SRI-DIC algorithm can still work.
The experimental steps were as follows: we (i) applied a 5N pre-tension on the specimen, and then capture the first image as the reference image; (ii) turned on the two cameras and shoot at a rate of two frames per second; (iii) turned on the dynamic extensometer which sends the measured strain data to the computer in real time; (iv) turned on the dynamic test system to stretch the specimen at a rate of 5 mm/min; and (v) turned off the dynamic test system within the range of the extensometer and complete the experiment.
The SRI-DIC algorithm was used to match the images of the two cameras, subsequently, three-dimensional reconstruction was performed to obtain the displacement and strain of each seed point, as displayed in the Figure 10a. For displacement calculation through DIC, the sub-region size is a circular window with a diameter of 51 pixels, and the stride size of grid nodes is 10 pixels. Since the sample material is very uniform, it can be considered that the strain values are equal everywhere in the sample. Therefore, the average strain value of all seed points can be calculated as the final strain value, and the measurement result is shown in Figure 10b. It is seen that the strain curve measured by the SRI-DIC algorithm is exactly consisted with that measured by the dynamic extensometer. The result of the dynamic extensometer is regarded as the true value, and the error of the SRI-DIC algorithm can be calculated and shown by the green line in Figure 10b. It can also be seen that the SRI-DIC algorithm can match images of different scales, and the maximum measurement error of the strain value does not exceed 0.3%, and the average error is about 0.1%. We highlight that the maximum measurement range of the dynamic extensometer is about 13%, and the measurement result will be abnormal if it exceeds this range.
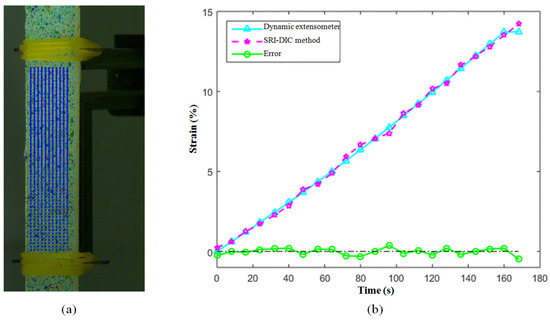
Figure 10.
The measurement results of uniaxial tensile test; (a) the displacement vector diagrams of various seed points in X and Y directions; (b) comparison results of strain values measured by dynamic extensometer and SRI-DIC algorithm.
6. Discussion
The integer-pixel matching of the SRI-DIC algorithm uses the color histogram features, which has the advantages of scaling and rotation invariance. The reverse retrieve strategy is also proposed to improve the efficiency of the SRI-DIC algorithm. In addition, the hue-based error function makes the SRI-DIC algorithm have illumination invariance. Therefore, four simulation experiments are respectively conducted for the evaluation of the scaling invariance, rotation invariance, computational efficiency and illumination invariance of the SRI-DIC algorithm in the experiment section. It can be seen from the experimental results that the integer-pixel matching method based on color histogram features has scaling, rotation and illumination invariance, and its accuracy meets the requirements of sub-pixel methods. Furthermore, the search strategy based on reverse retrieval can greatly improve the matching speed, which is faster than the state-of-the-art FMT-CC method.
In real experiments, a dynamic test system and a dynamic extensometer were involved to stretch and measure the test specimen. The SRI-DIC algorithm was used to measure the deformation of the test specimen, and the error of is about 0.1%, which can meet most measurement requirements.
The proposed method focuses on solving the deformation measurement of objects in mechanical testing. At the present stage, speckle pattern must be carefully sprayed with colored paint and not a natural surface. Improvement on feature acquisition and matching method are expected to address the problems.
7. Conclusions
The color information has brought great advantages to the fields of computer vision, image retrieval, etc. However it has not been fully utilized in DIC method. To exploit the additional color information of the color speckle pattern, this paper improves the DIC algorithm from two parts: integer-pixel matching and sub-pixel matching. Specifically, this paper proposes (i) color histogram feature based integer-pixel matching algorithm; (ii) reverse retrieve based search strategy; and (iii) hue based error function to enhance the performance of the DIC method. For validation, experiments with simulated color images were performed, and shown our method have the advantages of scaling and rotation invariance, high efficiency and illumination invariance. For real material property measurement, uniaxial tension tests were conducted, where the average error of strain results reach 0.1%.
Funding
This research was funded by the Fundamental Research Funds for the Central Universities, grant number D5000210659.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The author declare no conflict of interest, and the funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Badique, E.; Komiya, Y.; Ohyama, N.; Tsujiuchi, J.; Honda, T. Color Image Correlation: Principle and Application. In Optics and the Information Age; International Society for Optics and Photonics: Bellingham, WA, USA, 1987; Volume 813, pp. 195–196. [Google Scholar]
- Yoneyama, S.; Morimoto, Y. Accurate displacement measurement by correlation of colored random patterns. JSME Int. J. Ser. A Solid Mech. Mater. Eng. 2003, 46, 178–184. [Google Scholar] [CrossRef][Green Version]
- Hang, D.; Hassan, G.M.; MacNish, C.; Dyskin, A. Characteristics of color digital image correlation for deformation measurement in geomechanical structures. In Proceedings of the 2016 International Conference on Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, QLD, Australia, 30 November–2 December 2016; pp. 1–8. [Google Scholar]
- Dinh, N.V.; Hassan, G.M.; Dyskin, A.V.; MacNish, C. Digital image correlation for small strain measurement in deformable solids and geomechanical structures. In Proceedings of the 2015 IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3324–3328. [Google Scholar]
- Forsey, A.; Gungor, S. Demosaicing images from color cameras for digital image correlation. Opt. Lasers Eng. 2016, 86, 20–28. [Google Scholar] [CrossRef]
- Zhong, F.Q.; Shao, X.X.; Quan, C. 3D digital image correlation using a single 3CCD color camera and dichroic filter. Meas. Sci. Technol. 2018, 29, 045401. [Google Scholar] [CrossRef]
- Felipe-Sesé, L.; Molina-Viedma, Á.J.; López-Alba, E.; Díaz, F.A. RGB colour encoding improvement for three-dimensional shapes and displacement measurement using the integration of fringe projection and digital image correlation. Sensors 2018, 18, 3130. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, Y.; Li, H.; Kemao, Q.; Gu, Y.; Zhai, C. Out-of-plane motion and non-perpendicular alignment compensation for 2D-DIC based on cross-shaped structured light. Opt. Lasers Eng. 2020, 134, 106148. [Google Scholar] [CrossRef]
- Geusebroek, J.M.; Van den Boomgaard, R.; Smeulders, A.W.M.; Geerts, H. Color invariance. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1338–1350. [Google Scholar] [CrossRef]
- Van De Sande, K.; Gevers, T.; Snoek, C. Evaluating color descriptors for object and scene recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1582–1596. [Google Scholar] [CrossRef] [PubMed]
- Pan, B.; Asundi, A.; Xie, H.; Gao, J. Digital image correlation using iterative least squares and pointwise least squares for displacement field and strain field measurements. Opt. Lasers Eng. 2009, 47, 865–874. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Wang, Z. Equivalence of digital image correlation criteria for pattern matching. Appl. Opt. 2010, 49, 5501–5509. [Google Scholar] [CrossRef] [PubMed]
- Gevers, T.; Ghebreab, S.; Smeulders, A.W.M. Color Invariant Snakes. In Proceedings of the BMVC 1998, Southampton, UK, 14–17 September 1998; pp. 1–11. [Google Scholar]
- Finlayson, G.D.; Hordley, S.D.; Xu, R. Convex programming color constancy with a diagonal-offset model. In Proceedings of the IEEE International Conference on Image Processing 2005, Genova, Italy, 14 September 2005; Volume 3, p. III-948. [Google Scholar]
- Welch, E.; Moorhead, R.; Owens, J.K. Image processing using the HSI color space. In Proceedings of the SOUTHEASTCON’91, Williamsburg, VA, USA, 7–10 April 1991; pp. 722–725. [Google Scholar]
- Vendroux, G.; Knauss, W.G. Submicron deformation field measurements: Part 2. Improved digital image correlation. Exp. Mech. 1998, 38, 86–92. [Google Scholar] [CrossRef]
- Pan, B.; Wang, Y.; Tian, L. Automated initial guess in digital image correlation aided by Fourier–Mellin transform. Opt. Eng. 2017, 56, 014103. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).