Distance Measurement of a Frequency-Shifted Sub-Terahertz Wave Source
Abstract
:1. Introduction
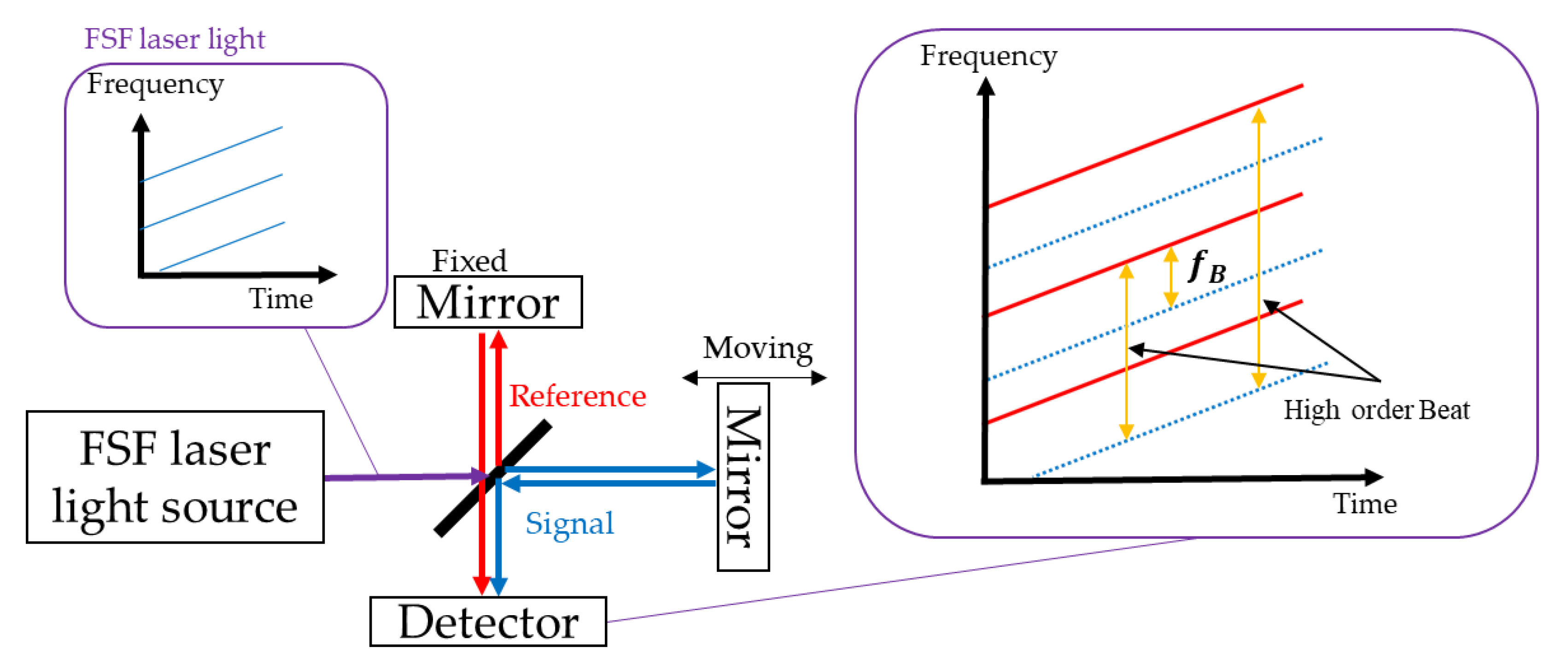
2. Optical Frequency Domain Reflectometry by Frequency-Shifted Feedback Laser
3. Frequency-Shifted Terahertz Waves
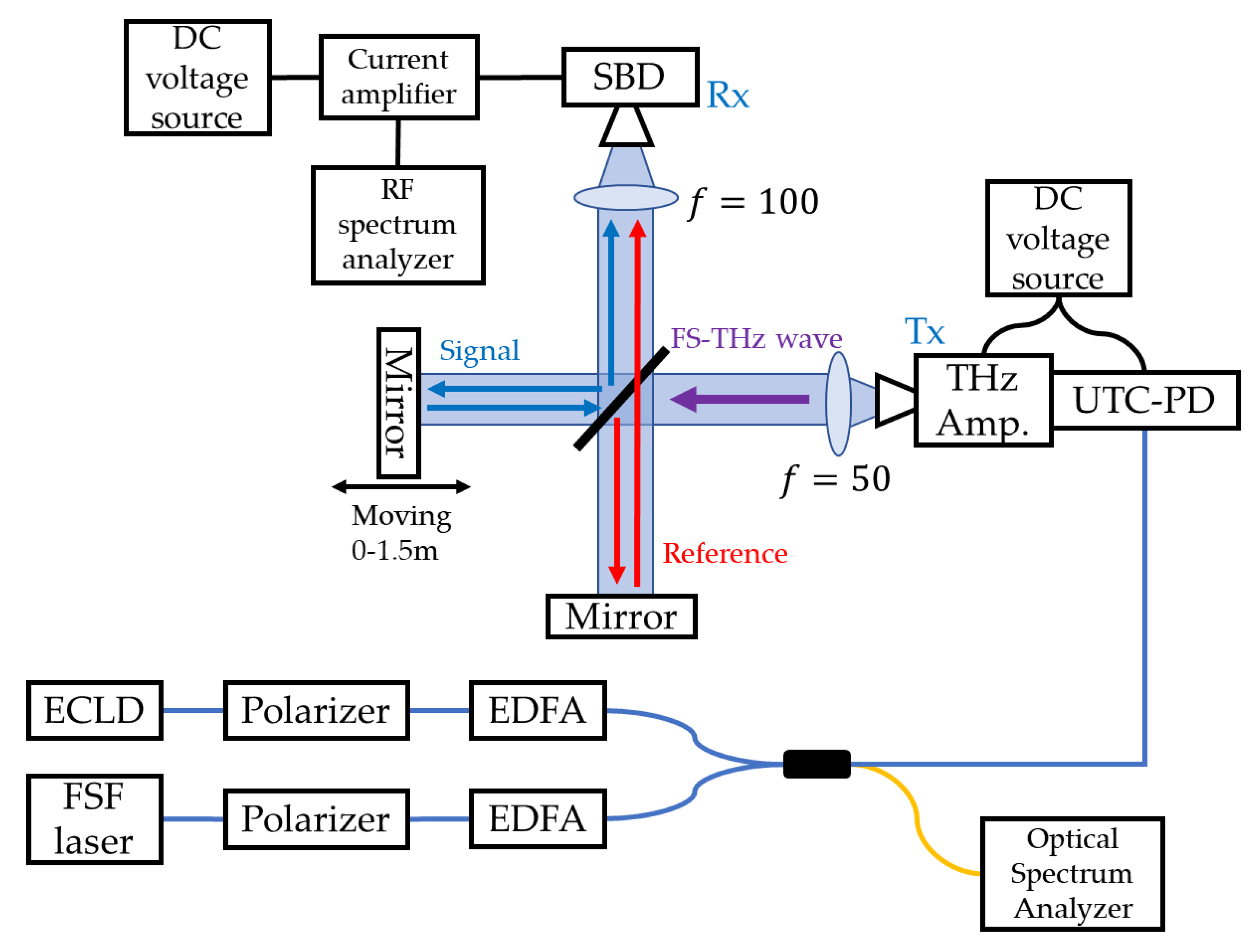
4. Distance Measurement Experiments Using Frequency-Shifted Terahertz Waves
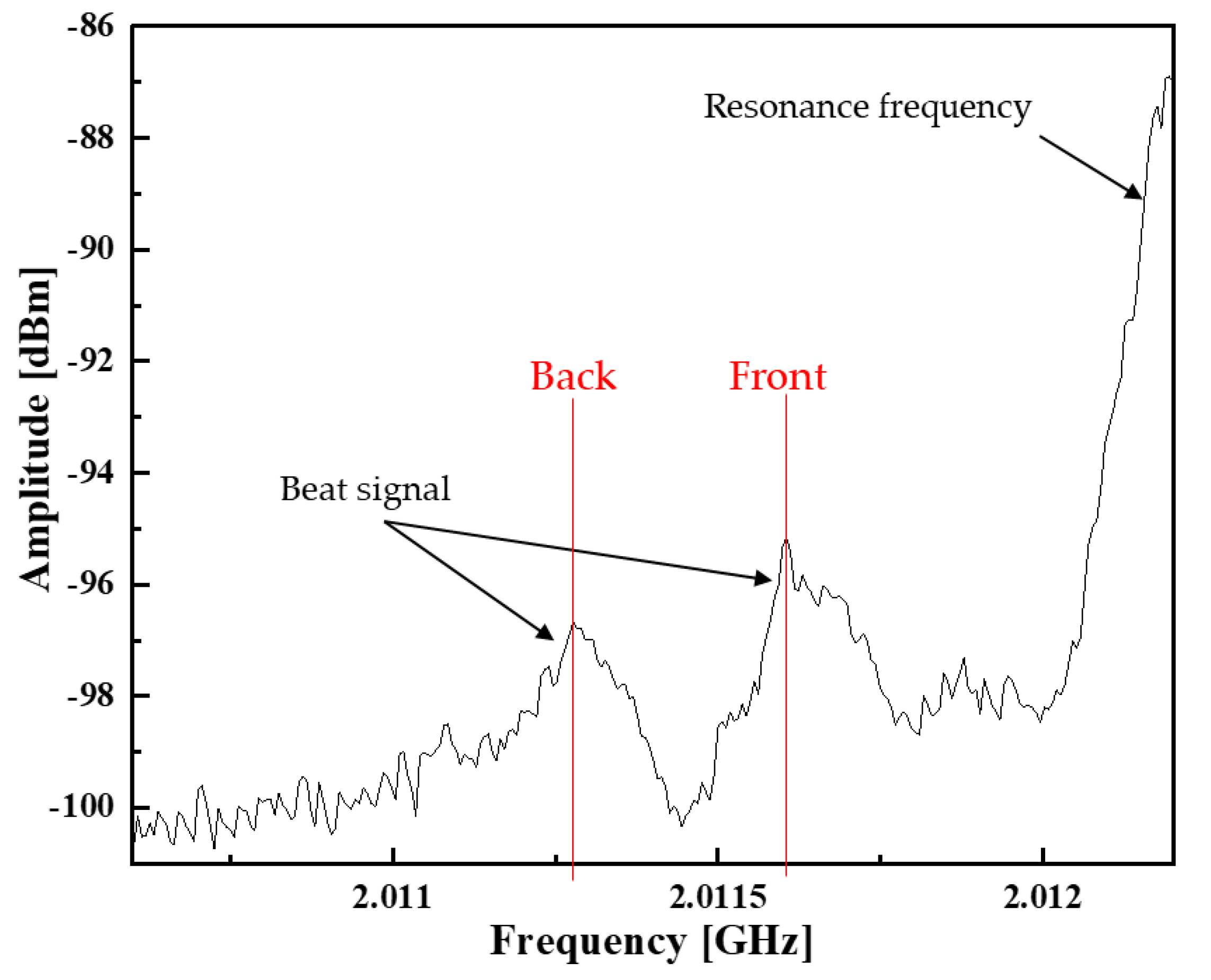
5. Results
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mittleman, D.M.; Jacobsen, R.H.; Nuss, M.C. T-ray imaging. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 679–692. [Google Scholar] [CrossRef] [Green Version]
- Guillet, J.P.; Recur, B.; Frederique, L.; Bousquet, B.; Canioni, L.; Manek-Hönninger, I.; Desbarats, P.; Mounaix, P. Review of Terahertz Tomography Techniques. J. Infrared Millim. Terahertz Waves 2014, 35, 382–411. [Google Scholar] [CrossRef] [Green Version]
- Tonouchi, M. Cutting-edge THz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Yan, Z.; Ying, Y.; Zhang, H.; Yu, H. Research progress of terahertz wave technology in food inspection. Proc. SPIE 2006, 6373, 63730R. [Google Scholar] [CrossRef]
- Krügener, K.; Schwerdtfeger, M.; Busch, S.F.; Soltani, A.; Castro-Camus, E.; Koch, M.; Viöl, W. Terahertz meets sculptural and architectural art: Evaluation and conservation of stone objects with T-ray technology. Sci. Rep. 2015, 5, 14842. [Google Scholar] [CrossRef] [Green Version]
- Jackson, J.B.; Mourou, M.; Whitaker, J.F.; Duling, I.N., III; Williamson, S.L.; Menu, M.; Mourou, G.A. Terahertz imaging for non-destructive evaluation of mural paintings. Opt. Commun. 2008, 281, 527–532. [Google Scholar] [CrossRef]
- Wietzke, S.; Jördens, C.; Krumbholz, N.; Baudrit, B.; Bastian, M.; Koch, M. Terahertz imaging: A new non-destructive technique for the quality control of plastic weld joints. J. Eur. Opt. Soc.-Rapid Publ. 2007, 2, 07013. [Google Scholar] [CrossRef] [Green Version]
- Stoik, C.D.; Bohn, M.J.; Blackshire, J.L. Nondestructive evaluation of aircraft composites using transmissive terahertz time domain spectroscopy. Opt. Express 2008, 16, 17039–17051. [Google Scholar] [CrossRef]
- Zimdars, D.; White, J.S.; Stuk, G.; Chernovsky, A.; Flchter, G.; Williamson, S. Large area terahertz imaging and non-destructive evaluation applications. Br. Inst. Non-Destr. Test. 2006, 48, 537–539. [Google Scholar] [CrossRef]
- Hoshina, H.; Sasaki, Y.; Hayashi, A.; Otani, C.; Kawase, K. Noninvasive Mail Inspection System with Terahertz Radiation. Appl. Spectrosc. 2009, 63, 81–86. [Google Scholar] [CrossRef]
- Oyama, Y.; Zhen, L.; Tanabe, T.; Kagata, M. Sub-terahertz imaging of defects in building blocks. NDT E Int. 2009, 42, 28–33. [Google Scholar] [CrossRef]
- Tanabe, T.; Kanai, T.; Kuroo, K.; Nishiwaki, T.; Oyama, Y. Non-Contact Terahertz Inspection of Water Content in Concrete of Infrastructure Buildings. World J. Eng. Technol. 2018, 6, 275–281. [Google Scholar] [CrossRef] [Green Version]
- Redo-Sanchez, A.; Karpowicz, N.; Xu, J.; Zhang, X.C. Damage and defect inspection with terahertz waves. In Proceedings of the 4th International Workshop on Ultrasonic and Advanced Methods for Nondestructive Testing and Material Characterization, North Dartmouth, MA, USA, 19 June 2006; Volume 11, p. 7. [Google Scholar]
- Karpowicz, N.; Zhong, H.; Zhang, C.; Lin, K.; Hwang, J.S.; Xu, J.; Zhang, X.C. Compact continuous-wave subterahertz system for inspection applications. Appl. Phys. Lett. 2005, 86, 054105. [Google Scholar] [CrossRef] [Green Version]
- Cooper, K.B.; Dengler, R.J.; Llombart, N.; Thomas, B.; Chattopadhyay, G.; Siegel, P.H. THz Imaging Radar for Standoff Personnel Screening. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 169–182. [Google Scholar] [CrossRef]
- Liebermeister, L.; Nellen, S.; Kohlhaas, R.B.; Lauck, S.; Deumer, M.; Breuer, S.; Schell, M.; Globisch, B. Optoelectronic frequency-modulated continuous-wave terahertz spectroscopy with 4 THz bandwidth. Nat. Commun. 2021, 12, 1071. [Google Scholar] [CrossRef]
- Nakamura, K.; Miyahara, T.; Yoshida, M.; Hara, T.; Ito, H. A New Technique of Optical Ranging by a Frequency-Shifted Feedback Laser. IEEE Photonics Technol. Lett. 1998, 10, 1772–1774. [Google Scholar] [CrossRef]
- Ito, H.; Hara, T.; Ndiaye, C. Frequency-Shifted-Feedback Laser for Precise Remote 3D Measurement for Industry Applications. Rev. Laser Eng. 2008, 36, 1038–1041. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, K.; Abe, F.; Kasahara, K.; Hara, T.; Sato, M.; Ito, H. Spectral Characteristics of an All Solid-State Frequency-Shifted Feedback Laser. IEEE J. Quantum Electron. 1997, 33, 103–111. [Google Scholar] [CrossRef]
- Umemoto, S.; Hara, T.; Kubota, K.; Miyamoto, N.; Fujino, Y.; Okamoto, T. Verification of high-accuracy and contact measurement system using FSF laser optical coordinate. In Proceedings of the 3rd International Conference on Structural Health Monitoring of Intelligent Infrastructure, Vancover, BC, Canada, 13–16 November 2007; Volume 3. [Google Scholar]
- Ellrich, F.; Bauer, M.; Schreiner, N.; Keil, A.; Pfeiffer, T.; Klier, J.; Weber, S.; Jonuscheit, J.; Friederich, F.; Molter, D. Terahertz Quality Inspection for Automotive and Aviation Industries. J. Infrared Millim. Terahertz Waves 2020, 41, 470–489. [Google Scholar] [CrossRef] [Green Version]
- Friederich, F.; May, K.H.; Baccouche, B.; Matheis, C.; Bauer, M.; Jonuscheit, J.; Moor, M.; Denman, D.; Bramble, J.; Savage, N. Terahertz Radome Inspection. Photonics 2018, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Rizzolo, S.; Périsse, J.; Boukenter, A.; Ouerdane, Y.; Marin, E.; Mace, J.-R.; Cannas, M.; Girard, S. Real time monitoring of water level and temperature in storage fuel pools through optical fibre sensors. Sci. Rep. 2017, 7, 8766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakamura, K.; Hara, T.; Yoshida, M.; Miyahara, T.; Ito, H. Optical Frequency Domain Ranging by a Frequency-Shifted Feedback Laser. IEEE J. Quantum Electron. 2000, 36, 305–316. [Google Scholar] [CrossRef]
- Ishibashi, T.; Shimizu, N.; Kodama, S.; Ito, H.; Nagatsuma, T.; Furuta, T. Uni-Traveling-Carrier Photodiodes. OSA Trends Opt. Photonics Ser. 1997, 13, 83–87. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honjo, M.; Suizu, K.; Yamaguchi, M.; Ikari, T. Distance Measurement of a Frequency-Shifted Sub-Terahertz Wave Source. Photonics 2022, 9, 128. https://doi.org/10.3390/photonics9030128
Honjo M, Suizu K, Yamaguchi M, Ikari T. Distance Measurement of a Frequency-Shifted Sub-Terahertz Wave Source. Photonics. 2022; 9(3):128. https://doi.org/10.3390/photonics9030128
Chicago/Turabian StyleHonjo, Minoru, Koji Suizu, Masaki Yamaguchi, and Tomofumi Ikari. 2022. "Distance Measurement of a Frequency-Shifted Sub-Terahertz Wave Source" Photonics 9, no. 3: 128. https://doi.org/10.3390/photonics9030128
APA StyleHonjo, M., Suizu, K., Yamaguchi, M., & Ikari, T. (2022). Distance Measurement of a Frequency-Shifted Sub-Terahertz Wave Source. Photonics, 9(3), 128. https://doi.org/10.3390/photonics9030128




