Two-Phonon Blockade in Quadratically Coupled Optomechanical Systems
Abstract
:1. Introduction
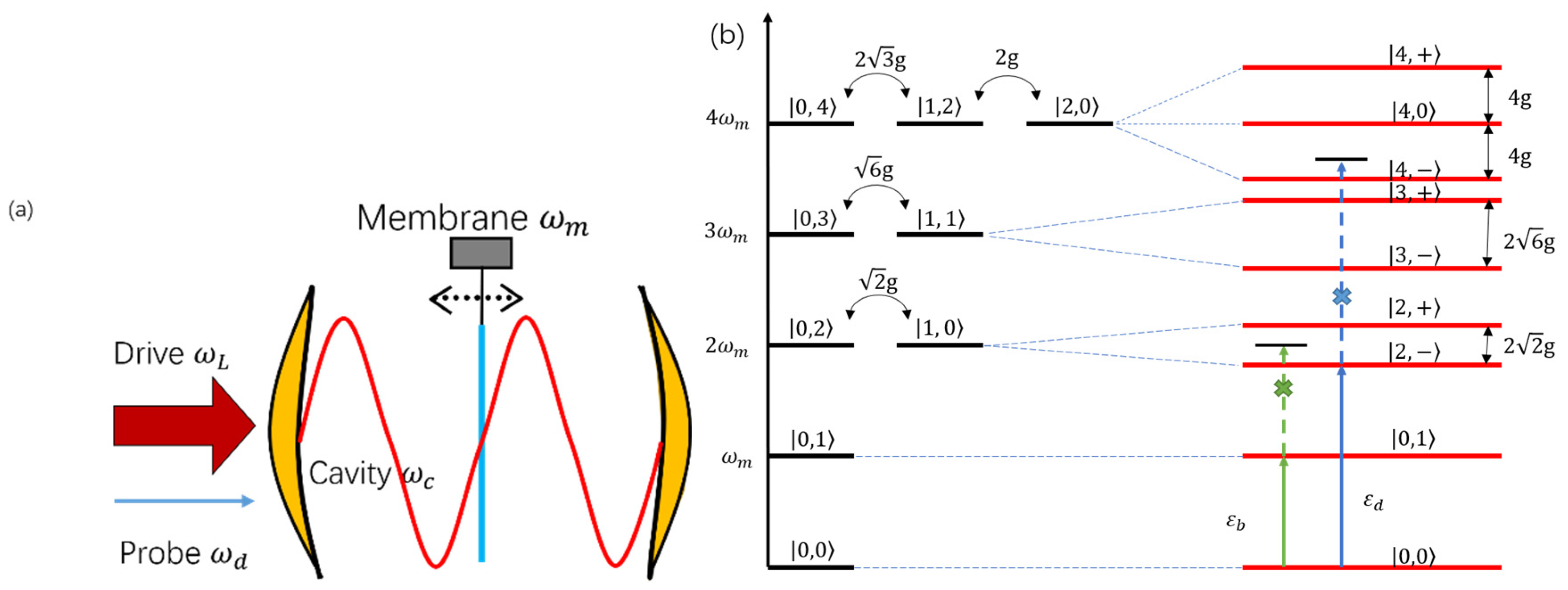
2. Model and Hamiltonian
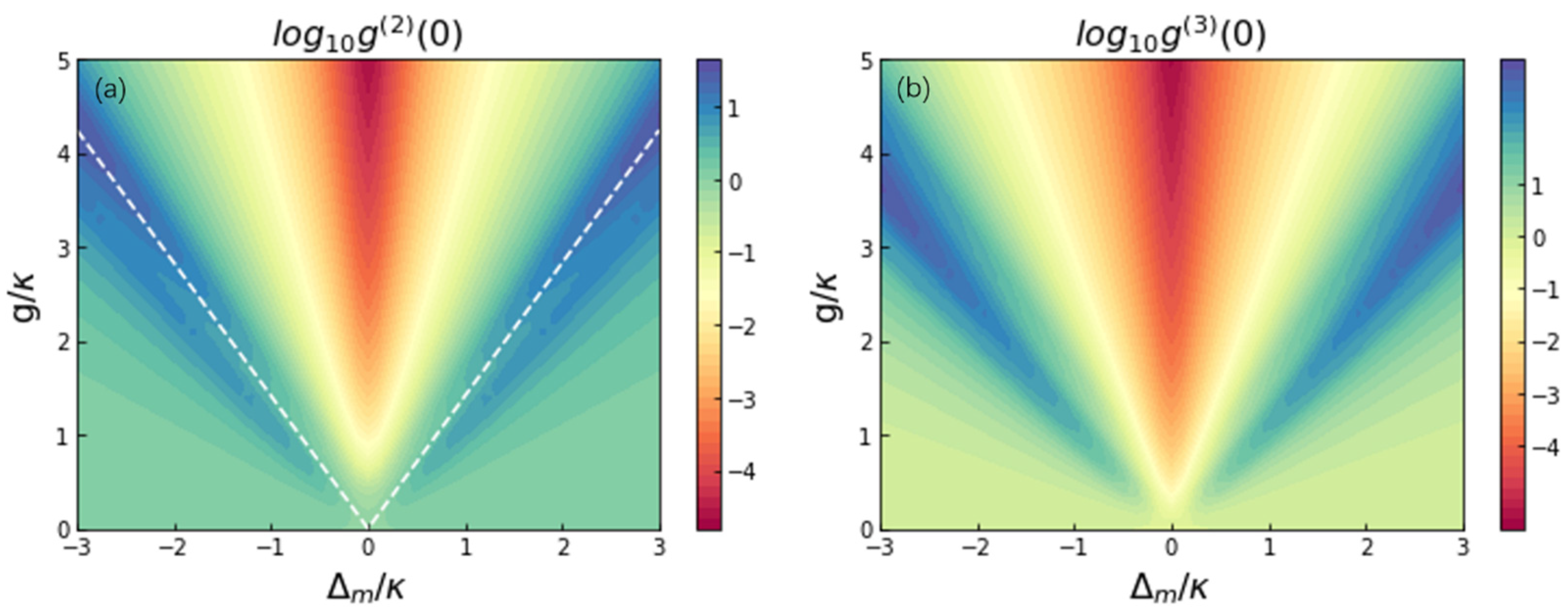
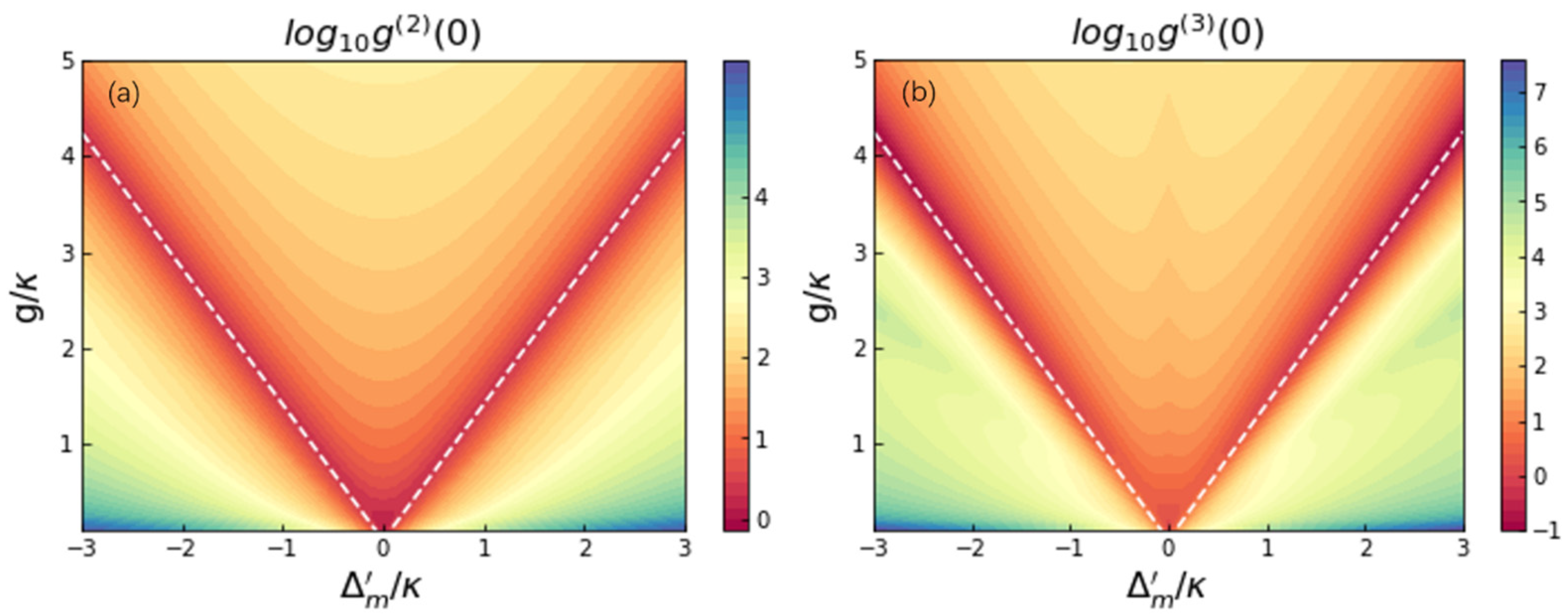
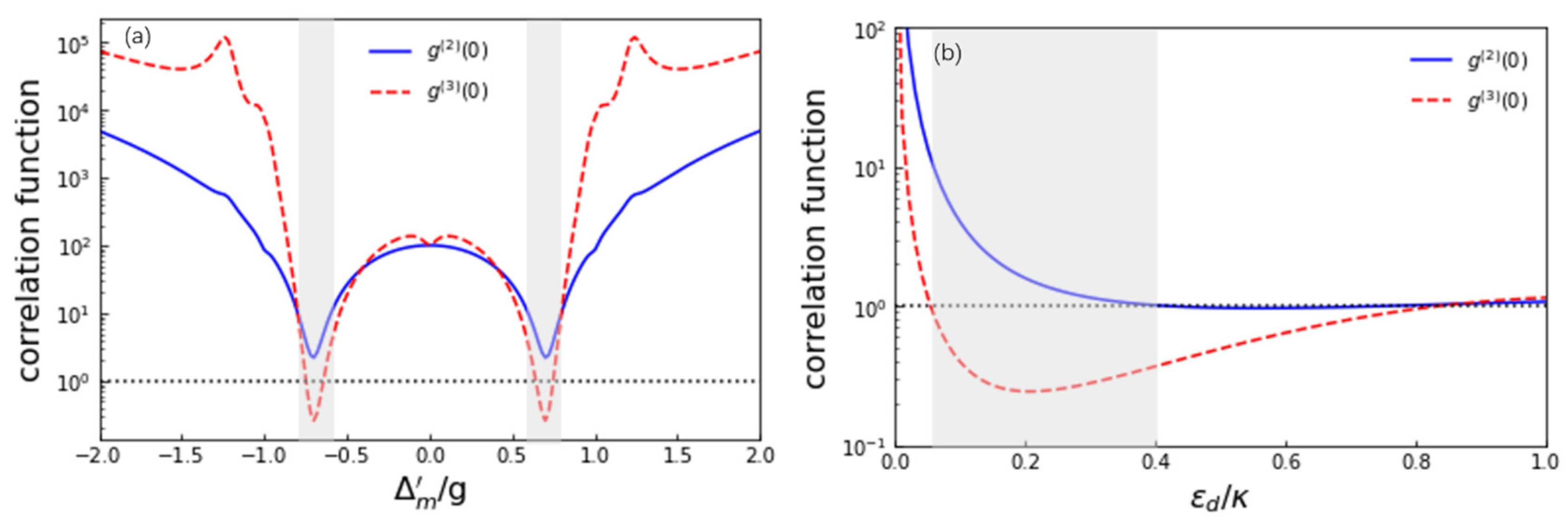
3. Two-Phonon Blockade via Weakly Driving the Optical Cavity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Aspelmeyer, M.; Meystre, P.; Schwab, K. Quantum optomechanics. Phys. Today 2012, 65, 29–35. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 2008, 321, 1172–1176. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, F.; Girvin, S.M. Trend: Optomechanics. Physics 2009, 2, 40. [Google Scholar] [CrossRef] [Green Version]
- Meystre, P. A short walk through quantum optomechanics. Ann. Phys. 2013, 525, 215–233. [Google Scholar] [CrossRef] [Green Version]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef] [Green Version]
- Chan, J.; Alegre, T.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef] [Green Version]
- Wilson-Rae, I.; Nooshi, N.; Zwerger, W.; Kippenberg, T.J. Theory of Ground State Cooling of a Mechanical Oscillator Using Dynamical Backaction. Phys. Rev. Lett. 2007, 99, 093901. [Google Scholar] [CrossRef] [Green Version]
- Marquardt, F.; Chen, J.P.; Clerk, A.A.; Girvin, S.M. Quantum Theory of Cavity-Assisted Sideband Cooling of Mechanical Motion. Phys. Rev. Lett. 2007, 99, 093902. [Google Scholar] [CrossRef] [Green Version]
- Corbitt, T.; Wipf, C.; Bodiya, T.; Ottaway, D.; Sigg, D.; Smith, N.; Whitcomb, S.; Mavalvala, N. Optical Dilution and Feedback Cooling of a Gram-Scale Oscillator to 6.9 mK. Phys. Rev. Lett. 2007, 99, 160801. [Google Scholar] [CrossRef] [Green Version]
- Heikkilä, T.T.; Massel, F.; Tuorila, J.; Khan, R.; Sillanpää, M.A. Enhancing Optomechanical Coupling via the Josephson Effect. Phys. Rev. Lett. 2014, 112, 203603. [Google Scholar] [CrossRef] [Green Version]
- Johansson, J.R.; Johansson, G.; Nori, F. Optomechanical-like coupling between superconducting resonators. Phys. Rev. A 2014, 90, 053833. [Google Scholar] [CrossRef] [Green Version]
- Xuereb, A.; Genes, C.; Dantan, A. Strong Coupling and Long-Range Collective Interactions in Optomechanical Arrays. Phys. Rev. Lett. 2012, 109, 223601. [Google Scholar] [CrossRef]
- Xuereb, A.; Genes, C.; Dantan, A. Collectively enhanced optomechanical coupling in periodic arrays of scatterers. Phys. Rev. A 2013, 88, 053803. [Google Scholar] [CrossRef]
- Genes, C.; Xuereb, A.; Pupillo, G.; Dantan, A. Enhanced optomechanical readout using optical coalescence. Phys. Rev. A 2013, 88, 033855. [Google Scholar] [CrossRef] [Green Version]
- Via, G.; Kirchmair, G.; Romero-Isart, O. Strong Single-Photon Coupling in Superconducting Quantum Magnetomechanics. Phys. Rev. Lett. 2015, 114, 143602. [Google Scholar] [CrossRef] [Green Version]
- Lü, X.-Y.; Wu, Y.; Johansson, J.R.; Jing, H.; Zhang, J.; Nori, F. Squeezed Optomechanics with Phase-Matched Amplification and Dissipation. Phys. Rev. Lett. 2015, 114, 093602. [Google Scholar] [CrossRef] [Green Version]
- Bose, S.; Jacobs, K.; Knight, P.L. Preparation of nonclassical states in cavities with a moving mirror. Phys. Rev. A 1997, 56, 4175–4186. [Google Scholar] [CrossRef] [Green Version]
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Ponderomotive control of quantum macroscopic coherence. Phys. Rev. A 1997, 55, 3042–3050. [Google Scholar] [CrossRef] [Green Version]
- Marshall, W.; Simon, C.; Penrose, R.; Bouwmeester, D. Towards Quantum Superpositions of a Mirror. Phys. Rev. Lett. 2003, 91, 130401. [Google Scholar] [CrossRef] [Green Version]
- Stannigel, K.; Komar, P.; Habraken, S.J.M.; Bennett, S.D.; Lukin, M.D.; Zoller, P.; Rabl, P. Optomechanical Quantum Information Processing with Photons and Phonons. Phys. Rev. Lett. 2012, 109, 013603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kómár, P.; Bennett, S.D.; Stannigel, K.; Habraken, S.J.M.; Rabl, P.; Zoller, P.; Lukin, M.D. Single-photon nonlinearities in two-mode optomechanics. Phys. Rev. A 2013, 87, 013839. [Google Scholar] [CrossRef] [Green Version]
- Rabl, P. Photon Blockade Effect in Optomechanical Systems. Phys. Rev. Lett. 2011, 107, 063601. [Google Scholar] [CrossRef] [PubMed]
- Kronwald, A.; Ludwig, M.; Marquardt, F. Full photon statistics of a light beam transmitted through an optomechanical system. Phys. Rev. A 2013, 87, 013847. [Google Scholar] [CrossRef] [Green Version]
- Liao, J.Q.; Law, C.K. Correlated two-photon scattering in cavity optomechanics. Phys. Rev. A 2013, 87, 043809. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Gu, X.; Liu, Y.X.; Miranowicz, A.; Nori, F. Tunable photon blockade in a hybrid system consisting of an optomechanical device coupled to a two-level system. Phys. Rev. A 2015, 92, 033806. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.; Lin, G.W.; Chen, X.; Chen, Z.H.; Lin, X.M. Single-photon nonlinearities in a strongly driven optomechanical system with quadratic coupling. Phys. Rev. A 2016, 93, 063860. [Google Scholar] [CrossRef]
- Nunnenkamp, A.; Børkje, K.; Girvin, S.M. Single-Photon Optomechanics. Phys. Rev. Lett. 2011, 107, 063602. [Google Scholar] [CrossRef] [Green Version]
- Thompson, J.; Zwickl, B.; Jayich, A.; Marquardt, F.; Girvin, S.; Harris, J. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72–75. [Google Scholar] [CrossRef] [Green Version]
- Sankey, J.C.; Yang, C.; Zwickl, B.M.; Jayich, A.M.; Harris, J.G. Strong and tunable nonlinear optomechanical coupling in a low-loss system. Nat. Phys. 2010, 6, 707–712. [Google Scholar] [CrossRef] [Green Version]
- Purdy, T.P.; Brooks, D.W.C.; Botter, T.; Brahms, N.; Ma, Z.-Y.; Stamper-Kurn, D.M. Tunable Cavity Optomechanics with Ultracold Atoms. Phys. Rev. Lett. 2010, 105, 133602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilson, D.J.; Regal, C.A.; Papp, S.B.; Kimble, H.J. Cavity Optomechanics with Stoichiometric SiN Films. Phys. Rev. Lett. 2009, 103, 207204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nunnenkamp, A.; Børkje, K.; Harris, J.G.E.; Girvin, S.M. Cooling and squeezing via quadratic optomechanical coupling. Phys. Rev. A 2010, 82, 021806. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharya, M.; Uys, H.; Meystre, P. Optomechanical trapping and cooling of partially reflective mirrors. Phys. Rev. A 2008, 77, 033819. [Google Scholar]
- Liao, J.-Q.; Nori, F. Photon blockade in quadratically coupled optomechanical systems. Phys. Rev. A 2013, 88, 023853. [Google Scholar] [CrossRef] [Green Version]
- Seok, H.; Wright, E.M. Antibunching in an optomechanical oscillator. Phys. Rev. A 2017, 95, 053844. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.; Liao, C.-G.; Shang, X.; Ye, M.-Y.; Lin, X.-M. Phonon blockade in a quadratically coupled optomechanical system. Phys. Rev. A 2017, 96, 013861. [Google Scholar]
- Xu, X.-W.; Shi, H.-Q.; Chen, A.-X.; Liu, Y.-X. Cross-correlation between photons and phonons in quadratically coupled optomechanical systems. Phys. Rev. A 2018, 98, 013821. [Google Scholar]
- Xie, H.; Liao, C.-G.; Shang, X.; Chen, Z.-H.; Lin, X.-M. Optically induced phonon blockade in an optomechanical system with second-order nonlinearity. Phys. Rev. A 2018, 98, 023819. [Google Scholar]
- Liu, Y.-X.; Miranowicz, A.; Gao, Y.B.; Bajer, J.C.V.; Sun, C.P.; Nori, F. Qubit-induced phonon blockade as a signature of quantum behavior in nanomechanical resonators. Phys. Rev. A 2010, 82, 032101. [Google Scholar]
- Wang, X.; Miranowicz, A.; Li, H.-R.; Nori, F. Method for observing robust and tunable phonon blockade in a nanomechanical resonator coupled to a charge qubit. Phys. Rev. A 2016, 93, 063861. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.-W.; Chen, A.-X.; Liu, Y.-X. Phonon blockade in a nanomechanical resonator resonantly coupled to a qubit. Phys. Rev. A 2016, 94, 063853. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.-L.; Yin, T.-S.; Bin, Q.; Lü, X.-Y.; Wu, Y. Single-photon-induced phonon blockade in a hybrid spin-optomechanical system. Phys. Rev. A 2019, 99, 013804. [Google Scholar] [CrossRef]
- Yin, T.-S.; Bin, Q.; Zhu, G.-L.; Jin, G.-R.; Chen, A. Phonon blockade in a hybrid system via the second-order magnetic gradient. Phys. Rev. A 2019, 100, 063840. [Google Scholar] [CrossRef]
- Ramos, T.; Sudhir, V.; Stannigel, K.; Zoller, P.; Kippenberg, T.J. Nonlinear Quantum Optomechanics via Individual Intrinsic Two-Level Defects. Phys. Rev. Lett. 2013, 110, 193602. [Google Scholar] [CrossRef] [Green Version]
- Bin, Q.; Lü, X.-Y.; Laussy, F.P.; Nori, F.; Wu, Y. N-Phonon Bundle Emission via the Stokes Process. Phys. Rev. Lett. 2020, 124, 053601. [Google Scholar] [CrossRef] [Green Version]
- Flowers-Jacobs, N.E.; Hoch, S.W.; Sankey, J.C.; Kashkanova, A.; Jayich, A.M.; Deutsch, C.; Reichel, J.; Harris, J.G.E. Fiber-cavity-based optomechanical device. Appl. Phys. Lett. 2012, 101, 221109. [Google Scholar] [CrossRef] [Green Version]
- Paraïso, T.K.; Kalaee, M.; Zang, L.; Pfeifer, H.; Marquardt, F.; Painter, O. Position-Squared Coupling in a Tunable Photonic Crystal Optomechanical Cavity. Phys. Rev. X 2015, 5, 041024. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.-Y.; Jin, G.-R.; Yin, T.-S.; Chen, A. Two-Phonon Blockade in Quadratically Coupled Optomechanical Systems. Photonics 2022, 9, 70. https://doi.org/10.3390/photonics9020070
Li Z-Y, Jin G-R, Yin T-S, Chen A. Two-Phonon Blockade in Quadratically Coupled Optomechanical Systems. Photonics. 2022; 9(2):70. https://doi.org/10.3390/photonics9020070
Chicago/Turabian StyleLi, Zi-Yuan, Guang-Ri Jin, Tai-Shuang Yin, and Aixi Chen. 2022. "Two-Phonon Blockade in Quadratically Coupled Optomechanical Systems" Photonics 9, no. 2: 70. https://doi.org/10.3390/photonics9020070
APA StyleLi, Z.-Y., Jin, G.-R., Yin, T.-S., & Chen, A. (2022). Two-Phonon Blockade in Quadratically Coupled Optomechanical Systems. Photonics, 9(2), 70. https://doi.org/10.3390/photonics9020070




