Linearity and Optimum-Sampling in Photon-Counting Digital Holographic Microscopy
Abstract
1. Introduction
2. Methods
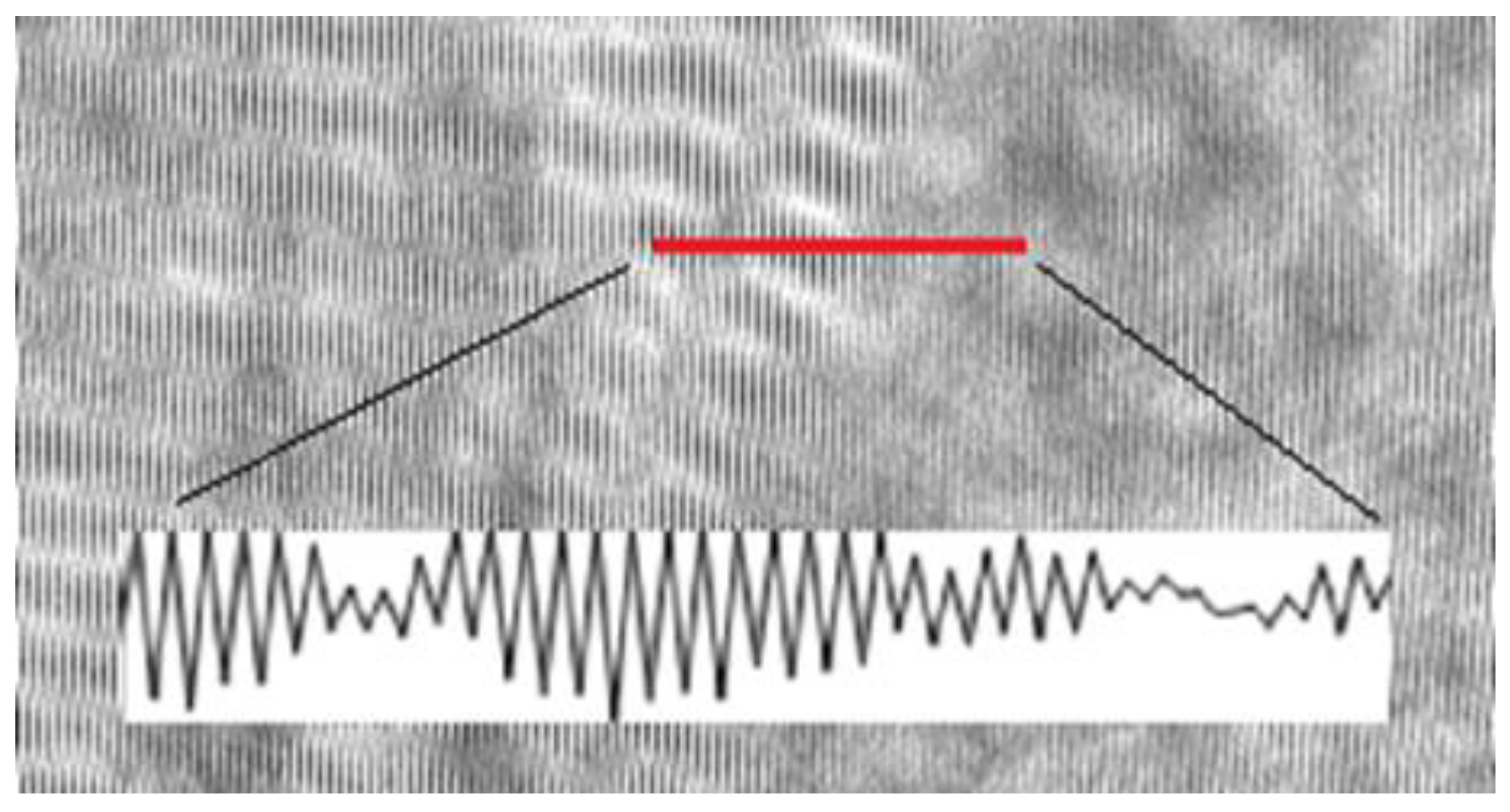
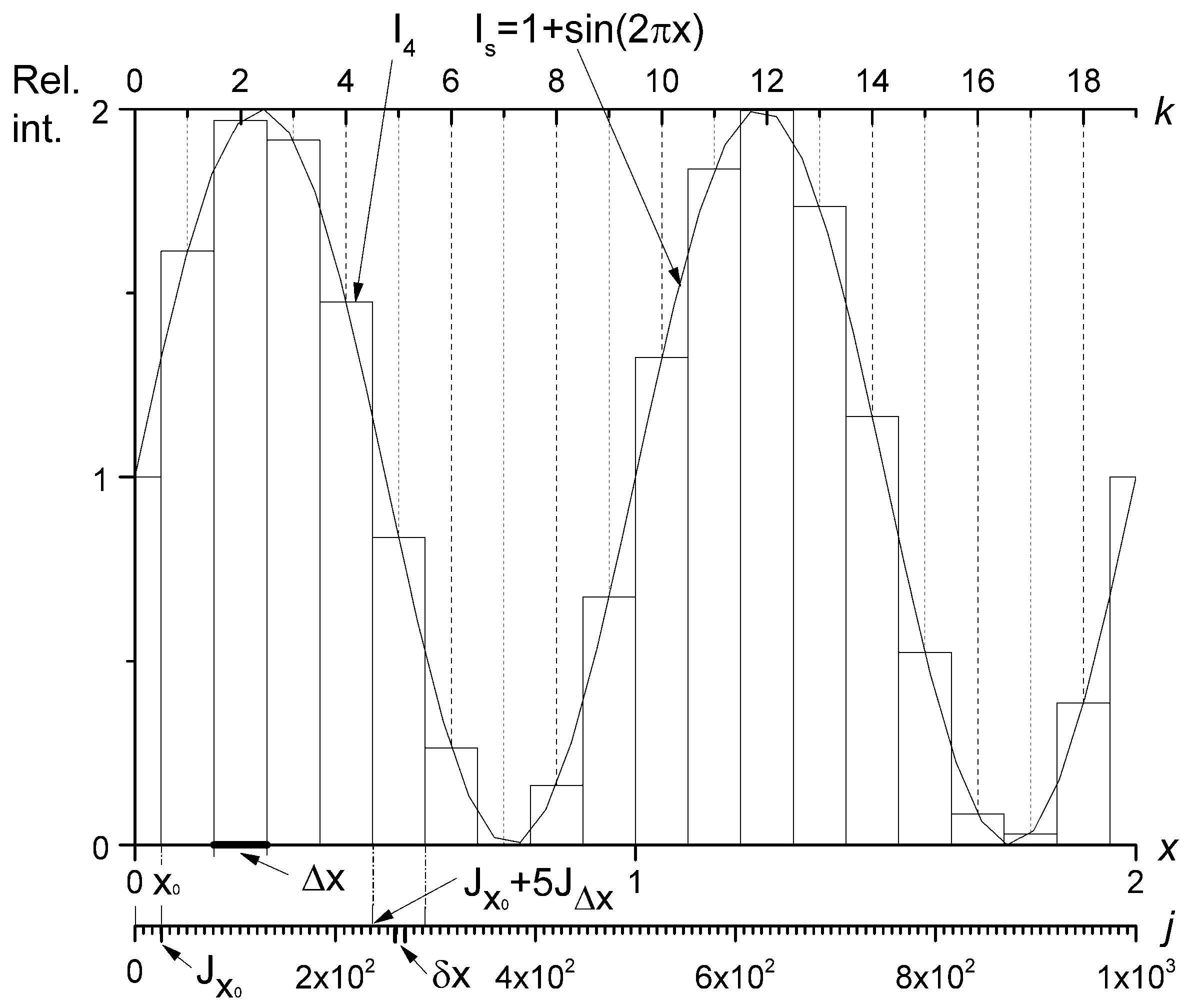
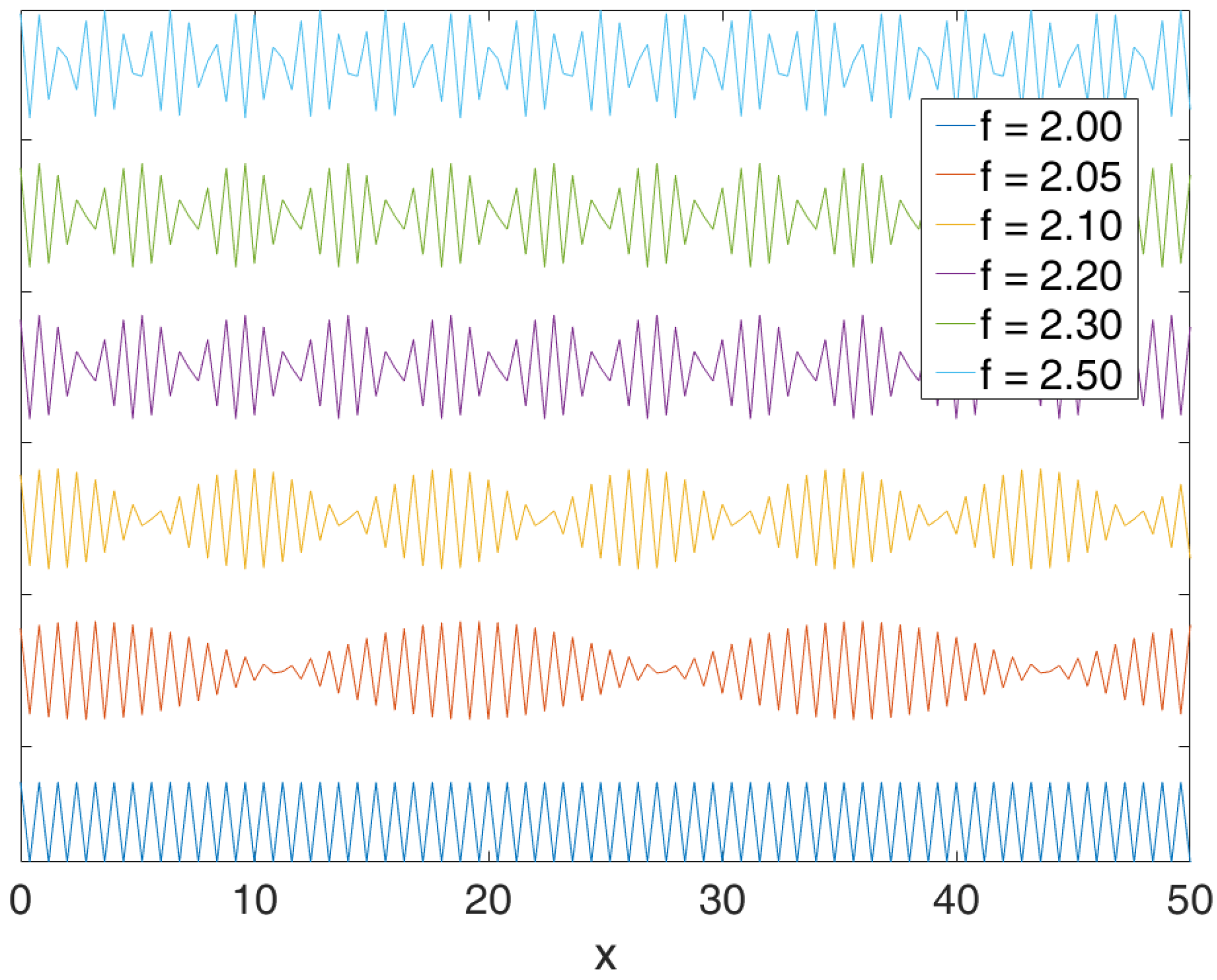
2.1. Optimum Sampling Conditions
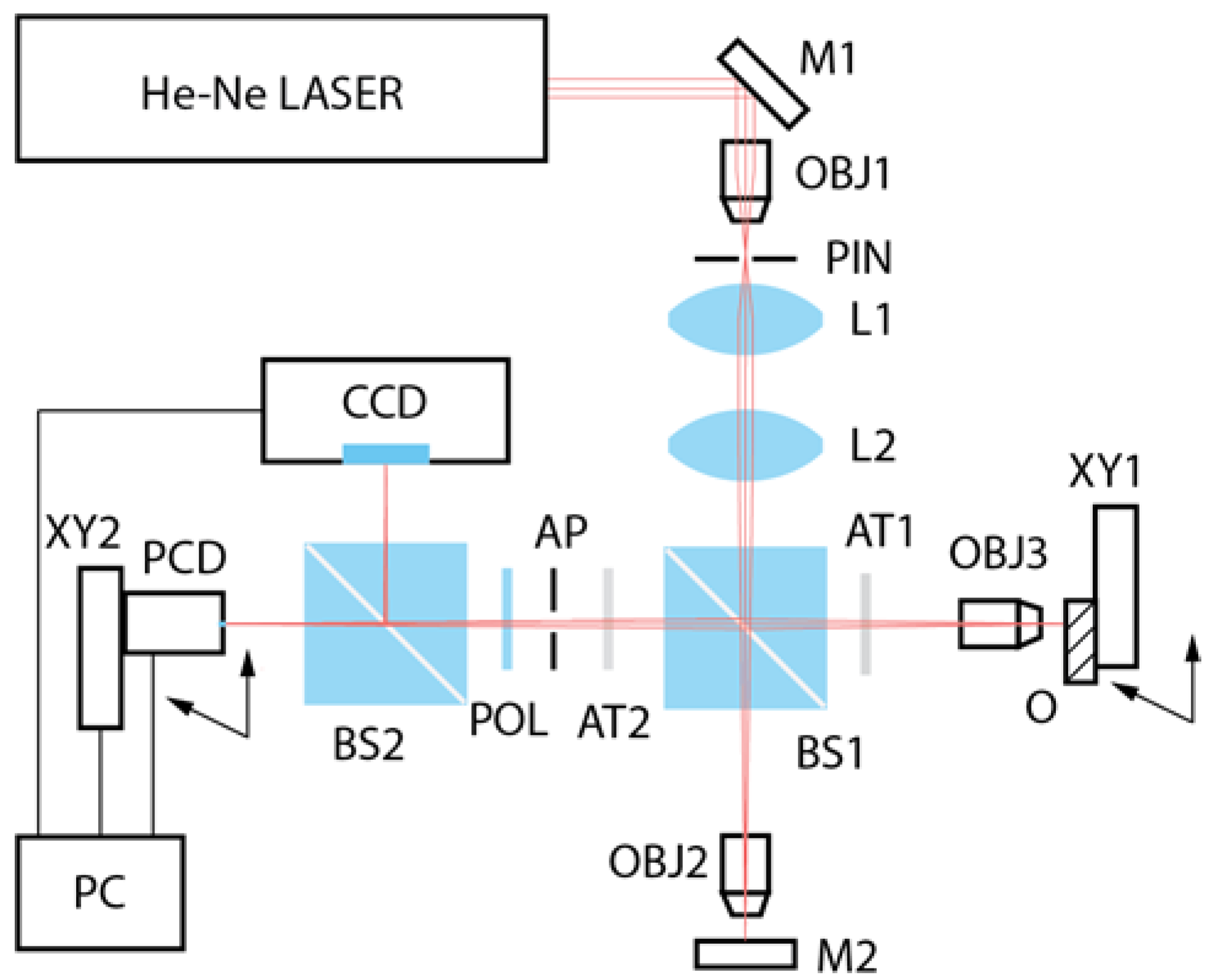
2.2. Experimental Setup
3. Results
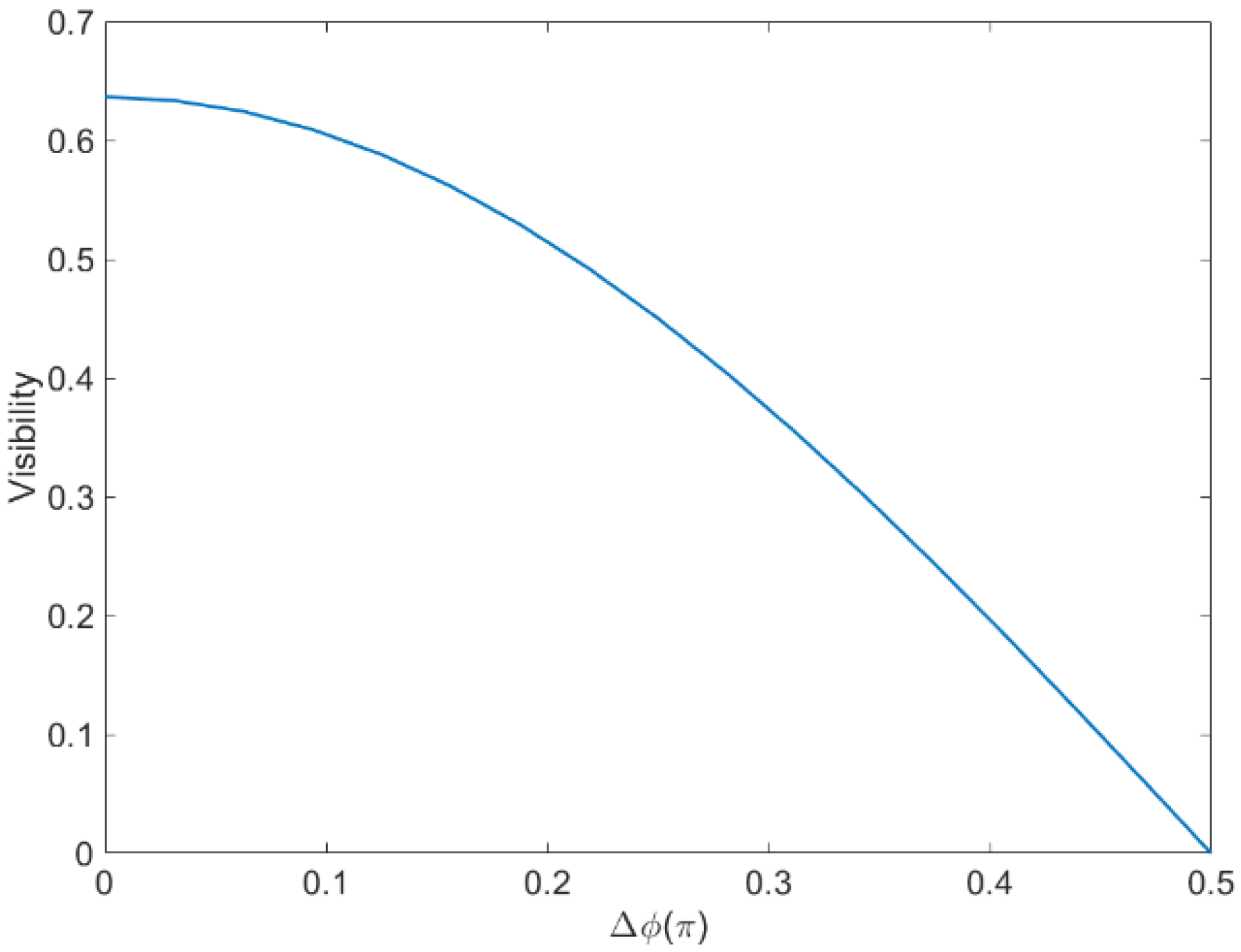
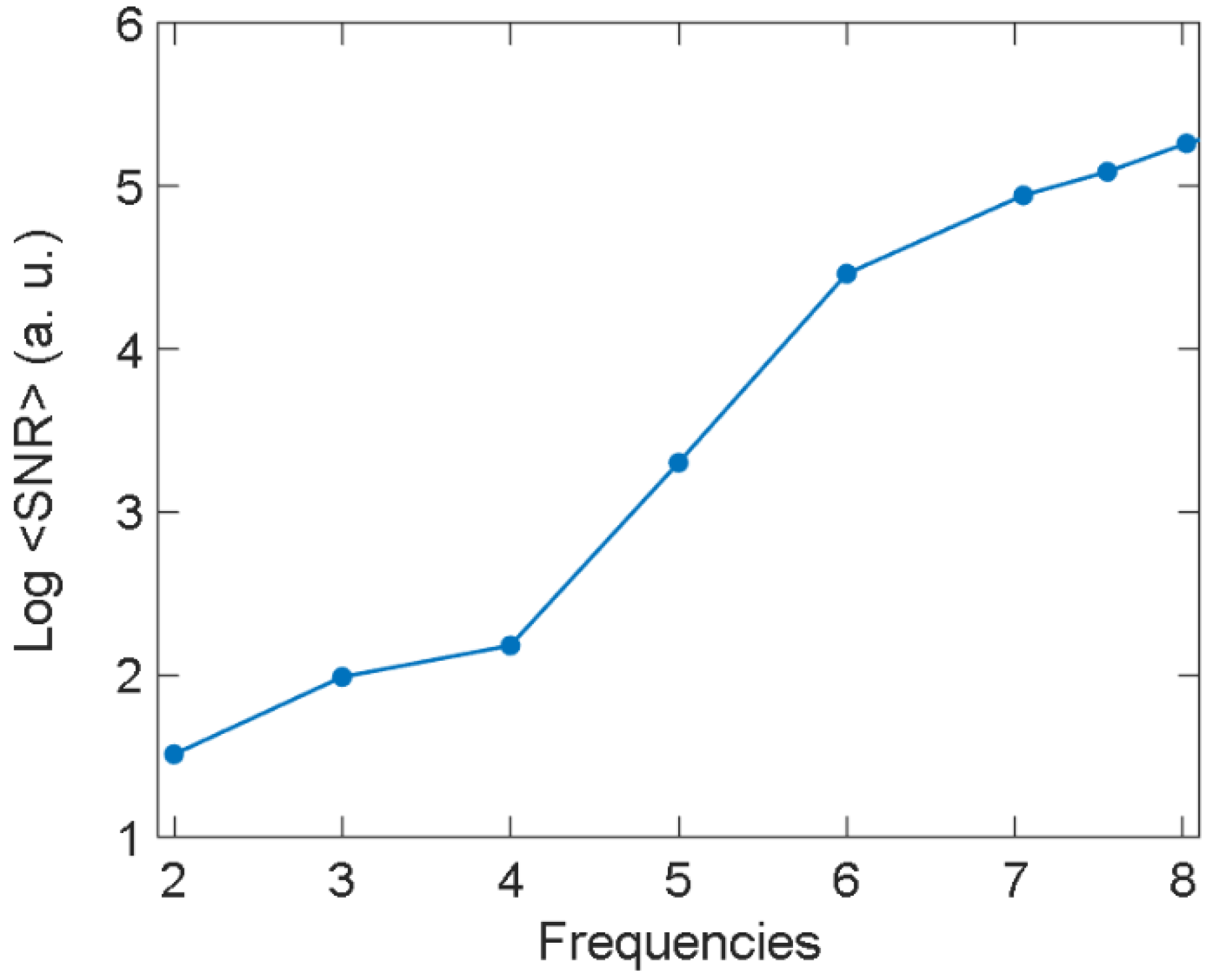
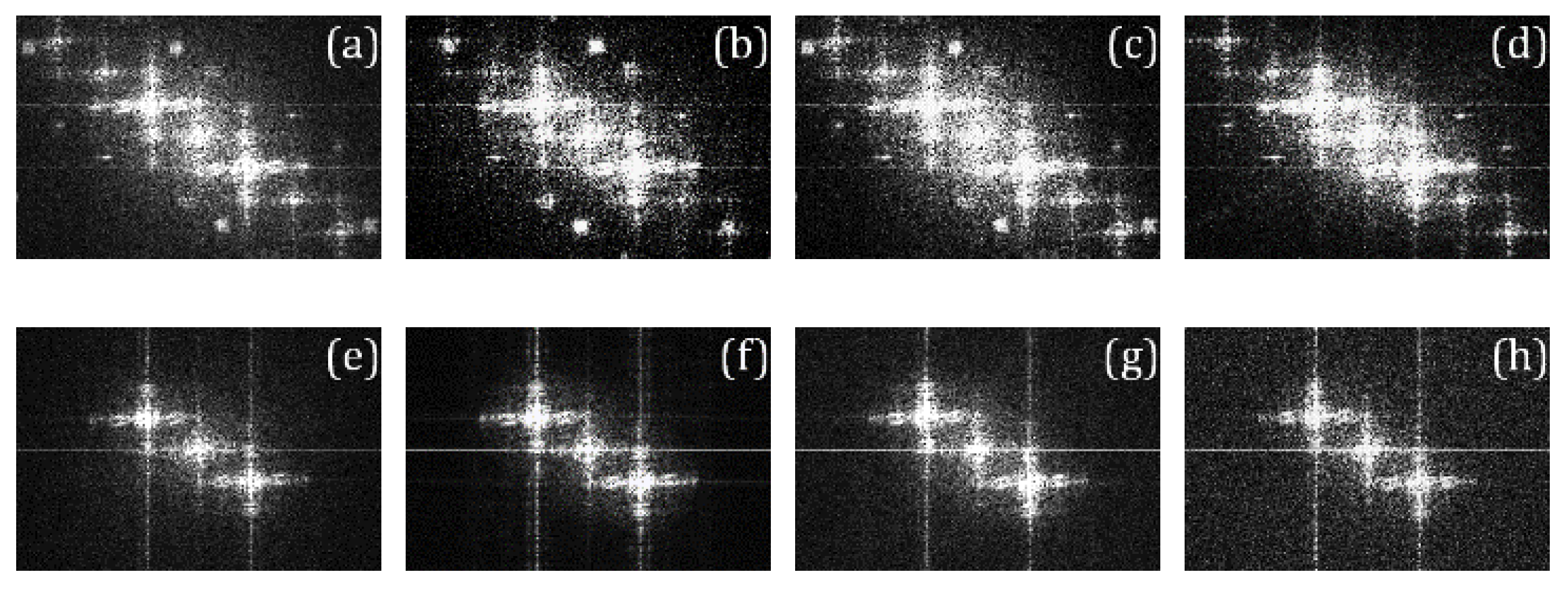
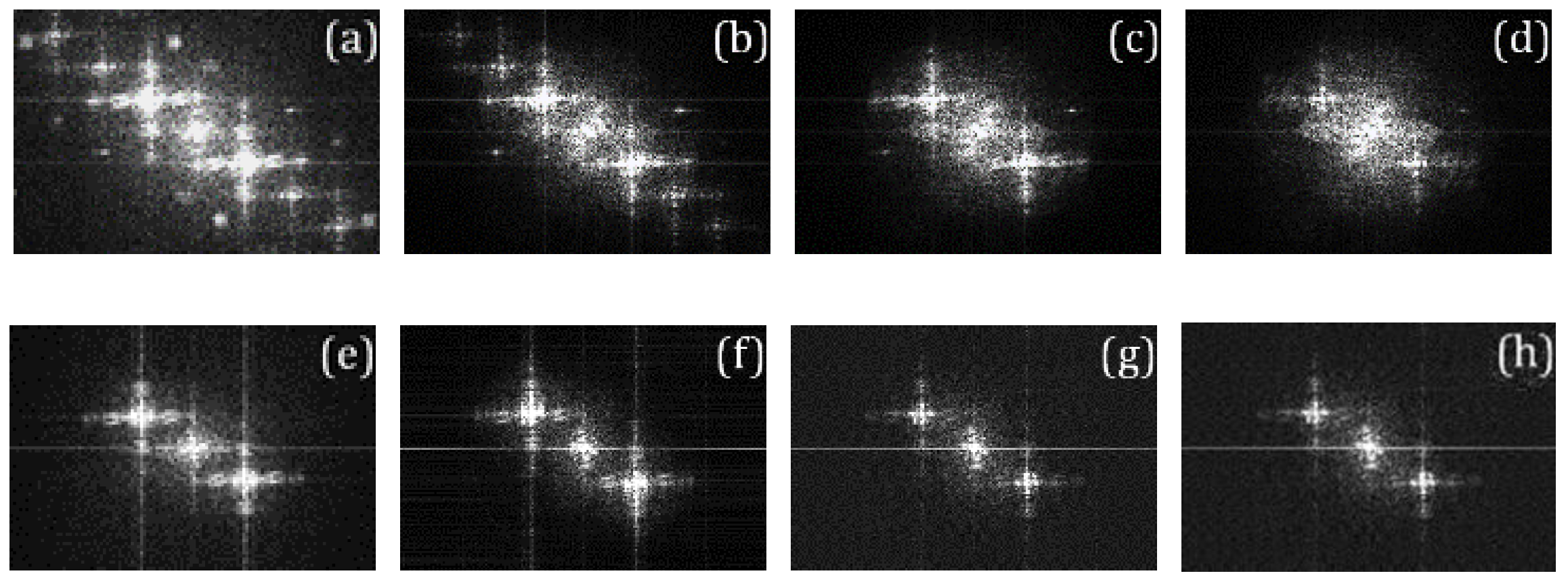
3.1. Nonlinear Recording
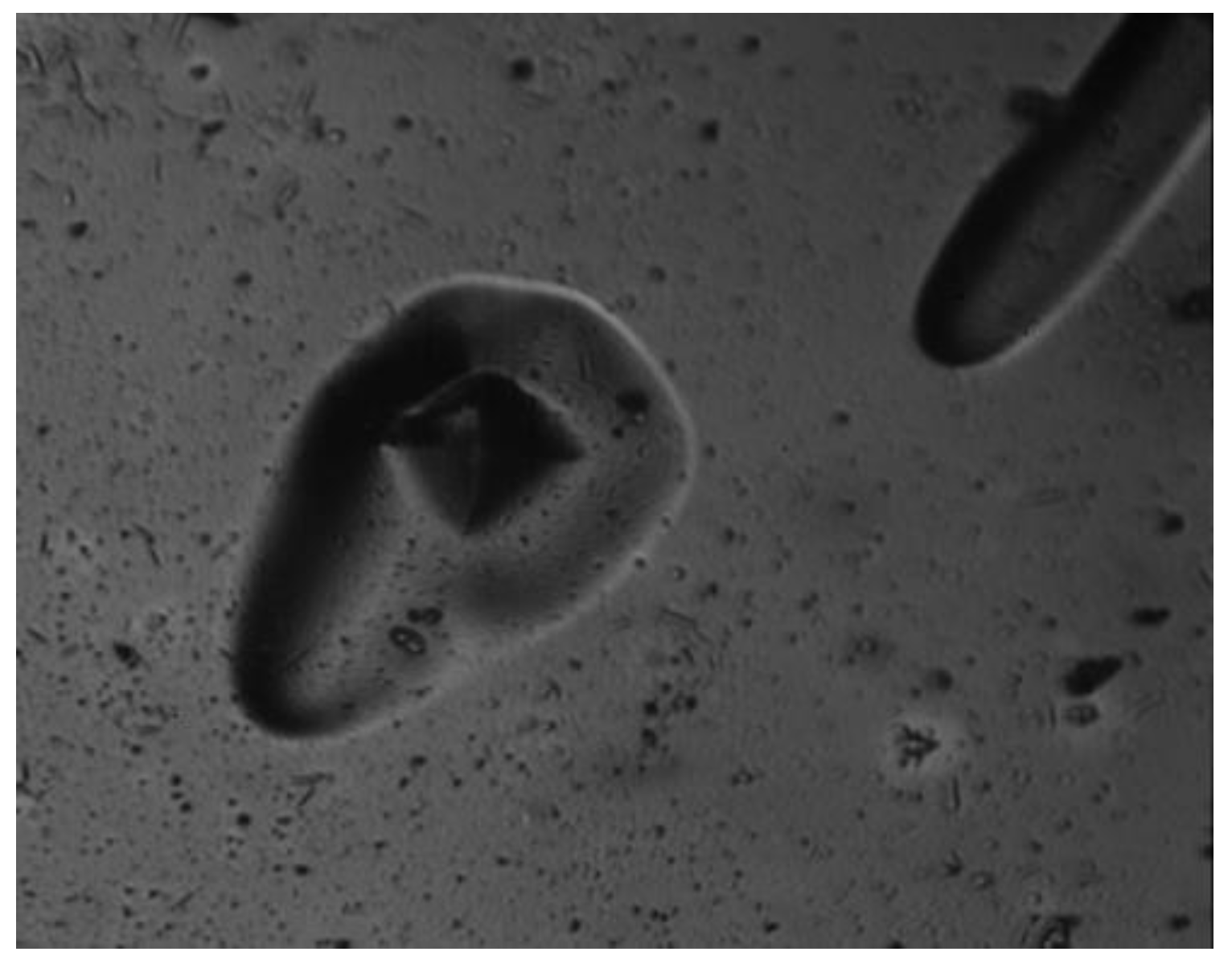
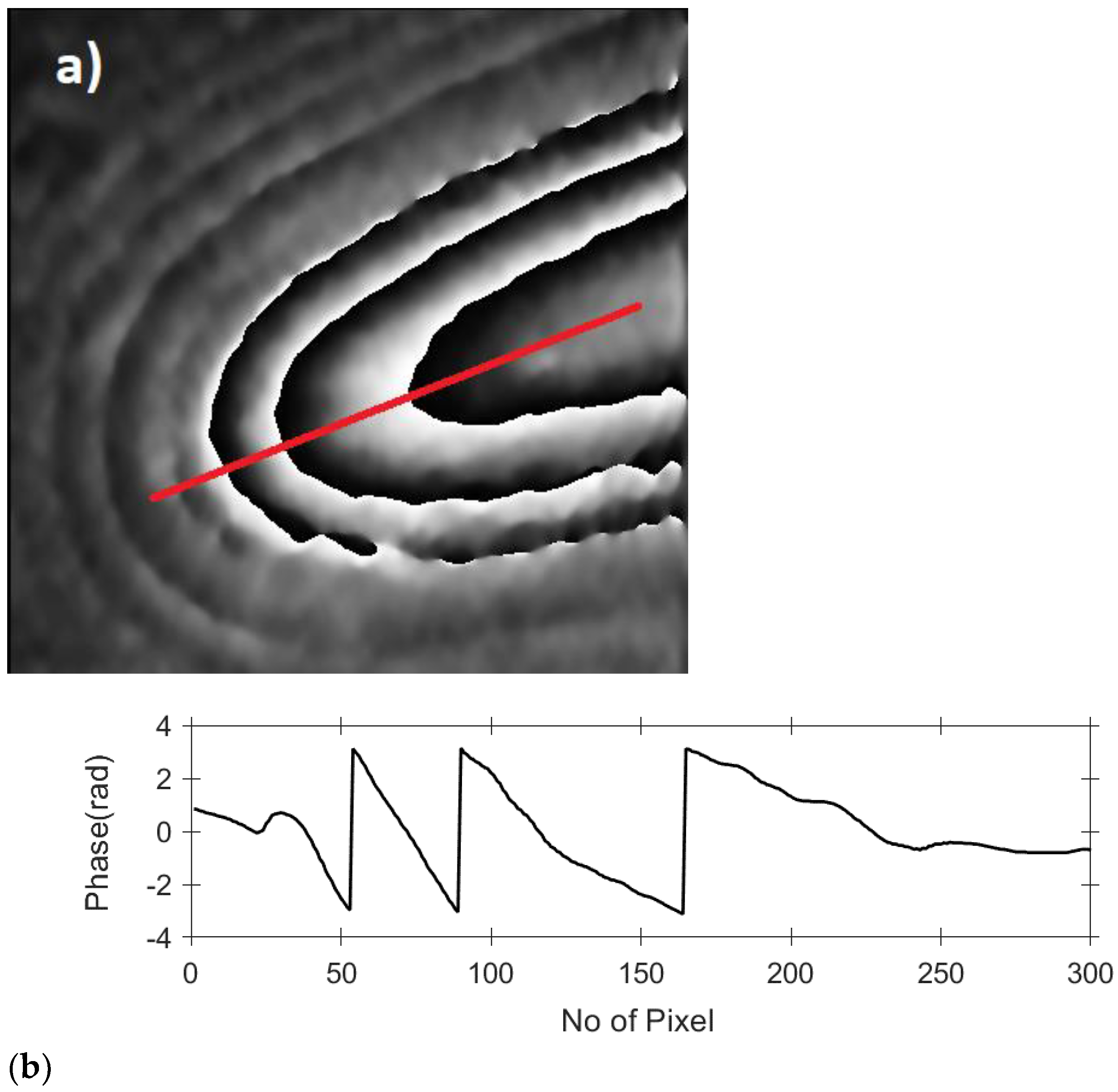
3.2. Thin Metallic Filmbuckling
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Kim, M.K. Digital Holographic Microscopy; Springer Series in Optical Sciences; Springer: New York, NY, USA, 2011; Volume 162, ISBN 978-1-4419-7792-2. [Google Scholar]
- Anand, A.; Chhaniwal, V.; Javidi, B. Tutorial: Common path self-referencing digital holographic microscopy. APL Photon. 2018, 3, 071101. [Google Scholar] [CrossRef]
- Bishara, W.; Su, T.-W.; Coskun, A.F.; Ozcan, A. Lensfree on-chip microscopy over a wide field-of-view using pixel super-resolution. Opt. Express 2010, 18, 11181. [Google Scholar] [CrossRef] [PubMed]
- Serabyn, E.; Liewer, K.; Lindensmith, C.; Wallace, J.; Nadeau, J. Compact, lensless digital holographic microscope for remote microbiology. Opt. Express 2016, 24, 28540. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Khare, K. Single-shot full resolution region-of-interest (ROI) reconstruction in image plane digital holographic microscopy. J. Mod. Opt. 2018, 65, 1127. [Google Scholar] [CrossRef]
- Goodman, J.W. Speckle Phenomena in Optics Theory and Applications; Roberts and Company: Englewood, CO, USA, 2007; ISBN 978-1-9362-2114-1. [Google Scholar]
- Bianco, V.; Memmolo, P.; Leo, M.; Montresor, S.; Distante, C.; Paturzo, M.; Picart, P.; Javidi, B.; Ferraro, P. Strategies for reducing speckle noise in digital holography. Light. Sci. Appl. 2018, 7, 48. [Google Scholar] [CrossRef] [PubMed]
- Charriére, F.; Rappaz, B.; Kühn, J.; Colomb, T.; Marquet, P.; Depeursinge, C. Influence of shot noise on phase measurement accuracy in digital holographic microscopy. Opt. Express 2007, 15, 8818. [Google Scholar] [CrossRef]
- Monaldi, A.C.; Romero, G.G.; Cabrera, C.M.; Blanc, A.V.; Alanís, E.E. Rolling Shutter Effect aberration compensation in Digital Holographic Microscopy. Opt. Commun. 2016, 366, 94. [Google Scholar] [CrossRef]
- Remmersmann, C.; Stürwald, S.; Kemper, B.; Langehanenberg, P.; Von Bally, G. Phase noise optimization in temporal phase-shifting digital holography with partial coherence light sources and its application in quantitative cell imaging. Appl. Opt. 2009, 48, 1463. [Google Scholar] [CrossRef]
- Bothe, T.; Burke, J.; Helmers, H. Spatial phase shifting in electronic speckle pattern interferometry: Minimization of phase reconstruction errors. Appl. Opt. 1997, 36, 5310. [Google Scholar] [CrossRef]
- Styk, A.; Patorski, K. Identification of nonlinear recording error in phase shifting interferometry. Opt. Lasers Eng. 2007, 45, 265. [Google Scholar] [CrossRef]
- Pan, B.; Kemao, Q.; Huang, L.; Asundi, A. Phase error analysis and compensation for nonsinusoidal waveforms in phase-shifting digital fringe projection profilometry. Opt. Lett. 2009, 34, 416. [Google Scholar] [CrossRef] [PubMed]
- Cywińska, M.; Trusiak, M.; Zuo, C.; Patorski, K. Enhancing single-shot fringe pattern phase demodulation using advanced variational image decomposition. J. Opt. 2019, 21, 045702. [Google Scholar] [CrossRef]
- Claus, D.; Iliescu, D.; Bryanston-Cross, P. Quantitative space-bandwidth product analysis in digital holography. Appl. Opt. 2011, 50, H116. [Google Scholar] [CrossRef] [PubMed]
- Onural, L. Sampling of the diffraction field. Appl. Opt. 2000, 39, 5929. [Google Scholar] [CrossRef] [PubMed]
- Demoli, N.; Halaq, H.; Sariri, K.; Torzynski, M.; Vukicevic, D. Undersampled digital holography. Opt. Express 2009, 17, 15842. [Google Scholar] [CrossRef]
- Demoli, N.; Meštrović, J.; Sovic, I. Subtraction digital holography. Appl. Opt. 2003, 42, 798. [Google Scholar] [CrossRef]
- Leclercq, M.; Picart, P. Digital Fresnel holography beyond the Shannon limits. Opt. Express 2012, 20, 18303. [Google Scholar] [CrossRef]
- Tahara, T.; Awatsuji, Y.; Nishio, K.; Ura, S.; Matoba, O.; Kubota, T. Space-Bandwidth Capacity-Enhanced Digital Holography. Appl. Phys. Express 2013, 6, 22502. [Google Scholar] [CrossRef]
- Agbana, T.E.; Gong, H.; Amoah, A.S.; Bezzubik, V.; Verhaegen, M.; Vdovin, G. Aliasing, coherence, and resolution in a lensless holographic microscope. Opt. Lett. 2017, 42, 2271. [Google Scholar] [CrossRef]
- Yamamoto, M.; Yamamoto, H.; Hayasaki, Y. Photon-counting digital holography under ultraweak illumination. Opt. Lett. 2009, 34, 1081. [Google Scholar] [CrossRef]
- Demoli, N.; Skenderović, H.; Stipčević, M. Digital holography at light levels below noise using a photon-counting approach. Opt. Lett. 2014, 39, 5010. [Google Scholar] [CrossRef]
- Demoli, N.; Skenderović, H.; Stipčević, M. Time-averaged photon-counting digital holography. Opt. Lett. 2015, 40, 4245. [Google Scholar] [CrossRef]
- Wallace, J.K.; Rider, S.; Serabyn, E.; Kühn, J.; Liewer, K.; Deming, J.; Showalter, G.; Lindensmith, C.; Nadeau, J.L. Robust, compact implementation of an off-axis digital holographic microscope. Opt. Express 2015, 23, 17367. [Google Scholar] [CrossRef]
- Demoli, N. Real-time monitoring of vibration fringe patterns by optical reconstruction of digital holograms: Mode beating detection. Opt. Express 2006, 14, 2117. [Google Scholar] [CrossRef]
- Stipčević, M.; Skenderović, H.; Gracin, D. Characterization of a novel avalanche photodiode for single photon detection in VIS-NIR range. Opt. Express 2010, 18, 17448. [Google Scholar] [CrossRef][Green Version]
- Freund, L.B.; Suresh, S. Thin Film Materials; Cambridge University Press: Cambridge, MA, USA, 2003; pp. 86–153. ISBN 978-0-5215-2977-8. [Google Scholar]
- Mondal, K.; Liu, Y.; Shay, T.; Genzer, J.; Dickey, M.D. Application of a Laser Cutter to Pattern Wrinkles on Polymer Films. ACS Appl. Polym. Mater. 2020, 2, 1848. [Google Scholar] [CrossRef]
- Tang, J.; Qiu, Z.; Li, T. A novel measurement method and application for grinding wheel surface topography based on shape from focus. Measurement 2019, 133, 495. [Google Scholar] [CrossRef]
- Faou, J.-Y.; Parry, G.; Grachev, S.; Barthel, E. How Does Adhesion Induce the Formation of Telephone Cord Buckles? Phys. Rev. Lett. 2012, 108, 116102. [Google Scholar] [CrossRef]
- Moon, M.; Jensen, H.; Hutchinson, J.; Oh, K.; Evans, A. The characterization of telephone cord buckling of compressed thin films on substrates. J. Mech. Phys. Solids 2002, 50, 2355. [Google Scholar] [CrossRef]
- Demoli, N.; Halaq, H.; Vukicevic, D. White light reconstruction of image plane digital holograms. Opt. Express 2010, 18, 12675. [Google Scholar] [CrossRef]
- Zappa, E.; Busca, G. Comparison of eight unwrapping algorithms applied to Fourier-transform profilometry. Opt. Lasers Eng. 2008, 46, 106. [Google Scholar] [CrossRef]
- Park, Y.; Depeursinge, C.; Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photon. 2018, 12, 578. [Google Scholar] [CrossRef]
- Balasubramani, V.; Kujawińska, M.; Allier, C.; Anand, V.; Cheng, C.-J.; Depeursinge, C.; Hai, N.; Juodkazis, S.; Kalkman, J.; Kuś, A.; et al. Roadmap on Digital Holography-Based Quantitative Phase Imaging. J. Imaging 2021, 7, 252. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demoli, N.; Abramović, D.; Milat, O.; Stipčević, M.; Skenderović, H. Linearity and Optimum-Sampling in Photon-Counting Digital Holographic Microscopy. Photonics 2022, 9, 68. https://doi.org/10.3390/photonics9020068
Demoli N, Abramović D, Milat O, Stipčević M, Skenderović H. Linearity and Optimum-Sampling in Photon-Counting Digital Holographic Microscopy. Photonics. 2022; 9(2):68. https://doi.org/10.3390/photonics9020068
Chicago/Turabian StyleDemoli, Nazif, Denis Abramović, Ognjen Milat, Mario Stipčević, and Hrvoje Skenderović. 2022. "Linearity and Optimum-Sampling in Photon-Counting Digital Holographic Microscopy" Photonics 9, no. 2: 68. https://doi.org/10.3390/photonics9020068
APA StyleDemoli, N., Abramović, D., Milat, O., Stipčević, M., & Skenderović, H. (2022). Linearity and Optimum-Sampling in Photon-Counting Digital Holographic Microscopy. Photonics, 9(2), 68. https://doi.org/10.3390/photonics9020068





