Influence of Gold Nanoantennas on the Photoluminescence of Silicon Nanocrystals
Abstract
1. Introduction
2. Fabrication
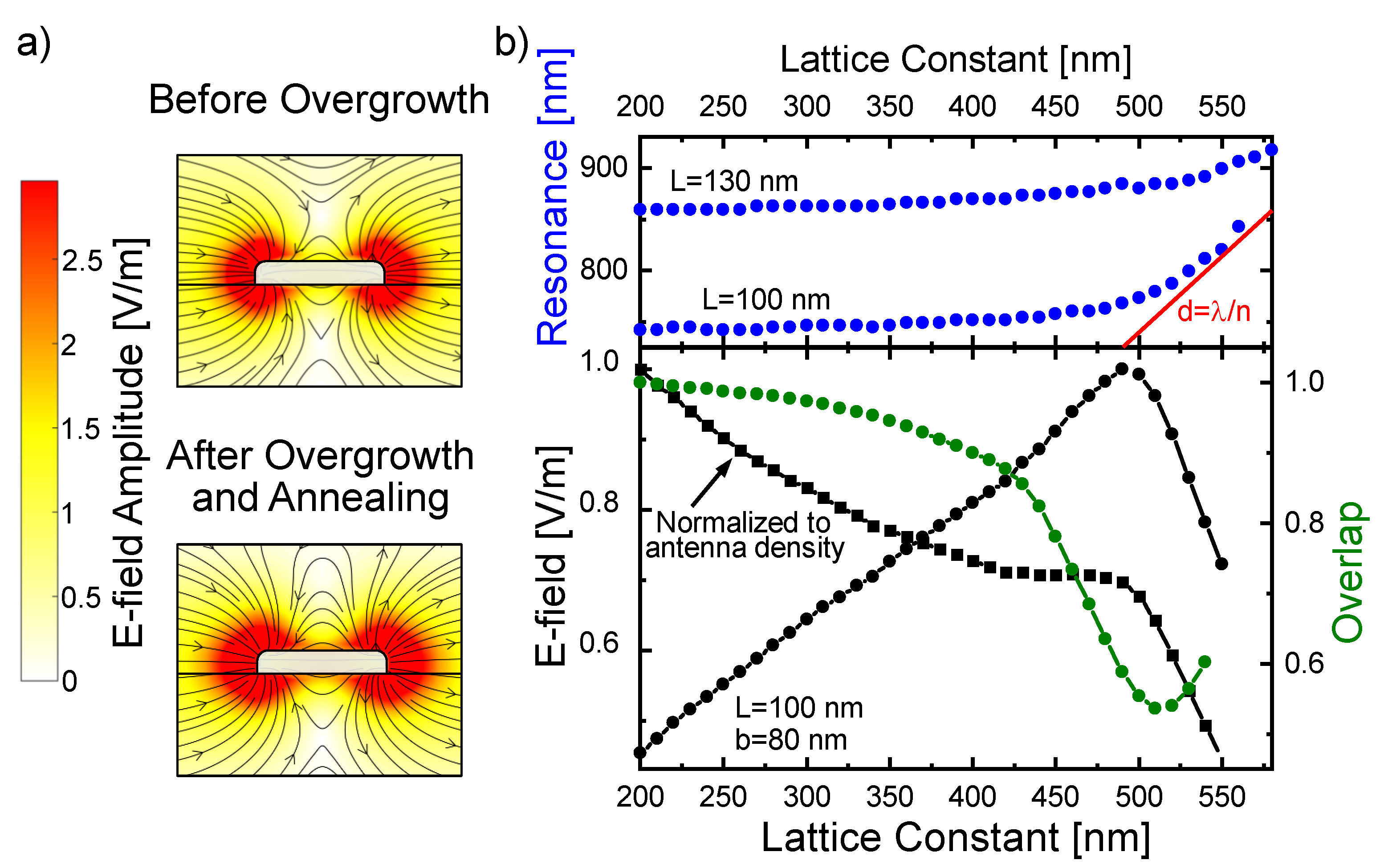
3. Theoretical Results
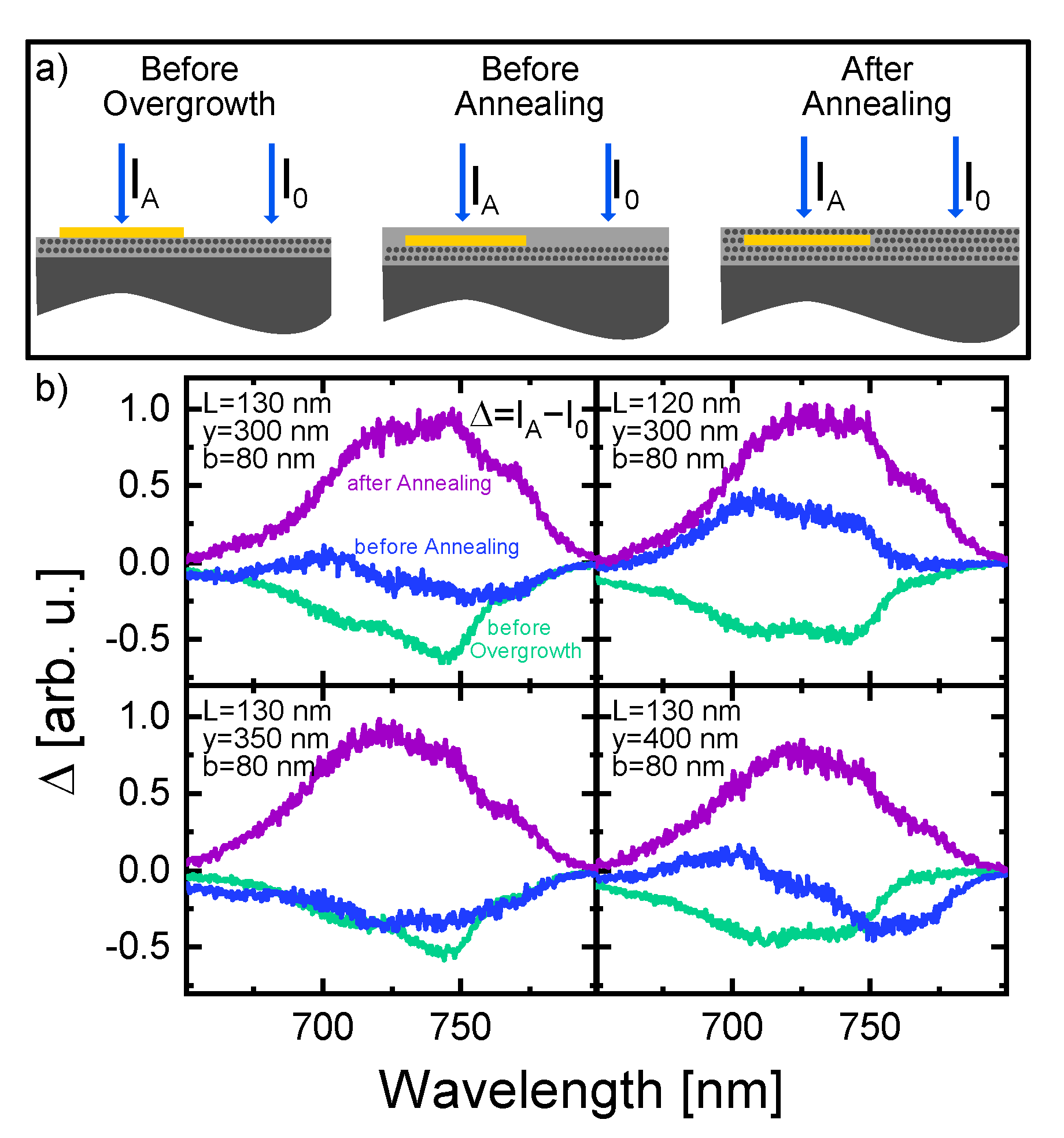
4. Experimental Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yates, J.T. A New Opportunity in Silicon-Based Microelectronics. Science 1998, 279, 335–336. [Google Scholar] [CrossRef]
- Marconi, A.; Anopchenko, A.; Pucker, G.; Pavesi, L. Silicon nanocrystal light emitting device as a bidirectional optical transceiver. Semicond. Sci. Technol. 2011, 26, 095019. [Google Scholar] [CrossRef]
- Liu, M.-C.; Chiang, T.-Y.; Kuo, P.-Y.; Chou, M.-H.; Wu, Y.-H.; You, H.-C.; Cheng, C.-H.; Liu, S.-H.; Yang, W.-L.; Lei, T.-F.; et al. SONOS memories with embedded silicon nanocrystals in nitride. Semicond. Sci. Technol. 2008, 23, 075033. [Google Scholar] [CrossRef]
- Zhao, S.; Pi, X.; Mercier, C.; Yuan, Z.; Sun, B.; Yang, D. Silicon-nanocrystal-incorporated ternary hybrid solar cells. Nano Energy 2016, 26, 305–312. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Holman, Z.C.; Kortshagen, U.R. Optimization of Si NC/P3HT Hybrid Solar Cells. Adv. Funct. Mater. 2010, 20, 2157–2164. [Google Scholar] [CrossRef]
- Pi, X.; Zhang, L.; Yang, D. Enhancing the Efficiency of Multicrystalline Silicon Solar Cells by the Inkjet Printing of Silicon-Quantum-Dot Ink. J. Phys. Chem. C 2012, 116, 21240–21243. [Google Scholar] [CrossRef]
- Dal Negro, L.; Pavesi, L.; Pucker, G.; Franzò, G.; Priolo, F. Optical gain in silicon nanocrystals. Opt. Mater. 2001, 17, 41–44. [Google Scholar] [CrossRef]
- Zacharias, M.; Heitmann, J.; Scholz, R.; Kahler, U.; Schmidt, M.; Bläsing, J. Size-controlled highly luminescent silicon nanocrystals: A SiO/SiO2 superlattice approach. Appl. Phys. Lett. 2002, 80, 661–663. [Google Scholar] [CrossRef]
- Meier, C.; Gondorf, A.; Lüttjohann, S.; Lorke, A.; Wiggers, H. Silicon nanoparticles: Absorption, emission, and the nature of the electronic bandgap. J. Appl. Phys. 2007, 101, 103112. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Burdov, V.; Lockwood, R.; Meldrum, A. Silicon Nanocrystals: Fundamental Theory and Implications for Stimulated Emission. Adv. Opt. Technol. 2008, 2008, 279502. [Google Scholar] [CrossRef]
- Hartel, A.M.; Hiller, D.; Gutsch, S.; Löper, P.; Estradé, S.; Peiró, F.; Garrido, B.; Zacharias, M. Formation of size-controlled silicon nanocrystals in plasma enhanced chemical vapor deposition grown SiOxNy/SiO2 superlattices. Thin Solid Films 2011, 520, 121–125. [Google Scholar] [CrossRef]
- Troudi, M.; Sghaier, N.; Souifi, A. Individual silicon nanocrystals photo-current response confirming the quantum single charge residence on single electron nanopixel devices. Phys. E Low-Dimens. Syst. Nanostruct. 2022, 137, 115057. [Google Scholar] [CrossRef]
- Das, P.; Metiu, H. Enhancement of molecular fluorescence and photochemistry by small metal particles. J. Phys. Chem. 1985, 89, 4680–4687. [Google Scholar] [CrossRef]
- Chen, H.; Yang, J.; Rusak, E.; Straubel, J.; Guo, R.; Myint, Y.; Pei, J.; Decker, M.; Staude, I.; Rockstuhl, C.; et al. Manipulation of photoluminescence of two-dimensional MoSe2 by gold nanoantennas. Sci. Rep. 2016, 6, 22296. [Google Scholar] [CrossRef] [PubMed]
- Genov, D.; Sarychev, A.; Shalaev, V.; Wei, A. Resonant Field Enhancements from Metal Nanoparticle Arrays. Nano Lett. 2004, 4, 153–158. [Google Scholar] [CrossRef]
- Leitner, A.; Lippitsch, M.; Draxler, S.; Riegler, M.; Aussenegg, F. Fluorescence properties of dyes adsorbed to silver islands, investigated by picosecond techniques. Appl. Phys. B 1985, 36, 105–109. [Google Scholar] [CrossRef]
- Ritchie, G.; Burstein, E. Luminescence of dye molecules adsorbed at a Ag surface. Phys. Rev. B 1981, 24, 4843–4846. [Google Scholar] [CrossRef]
- Volmert, R.; Weber, N.; Meier, C. Nanoantennas embedded in zinc oxide for second harmonic generation enhancement. J. Appl. Phys. 2020, 128, 043107. [Google Scholar] [CrossRef]
- Köthemann, R.; Weber, N.; Lindner, J.K.N.; Meier, C. High-precision determination of silicon nanocrystals: Optical spectroscopy versus electron microscopy. Semicond. Sci. Technol. 2019, 34, 095009. [Google Scholar] [CrossRef]
- McBrayer, J.D.; Swanson, R.M.; Sigmon, T.W. Diffusion of Metals in Silicon Dioxide. Electrochem. Soc. 1986, 133, 1242–1246. [Google Scholar] [CrossRef]
- Iacona, F.; Franzò, G.; Spinella, C. Correlation between luminescence and structural properties of Si nanocrystals. J. Appl. Phys. 2000, 87, 1295–1303. [Google Scholar] [CrossRef]
- Cushman, C.; Smith, N.; Kaykhaii, M.; Podraza, N.; Linford, M. An introduction to modeling in spectroscopic ellipsometry, focusing on models for transparent materials: The Cauchy and Sellmeier models. Vac. Technol. Coat. 2016, 7, 2–9. [Google Scholar]
- Yakubovsky, D.I.; Arsenin, A.V.; Stebunov, Y.V.; Fedyanin, D.Y.; Volkov, V.S. Optical constants and structural properties of thin gold films. Opt. Express 2017, 25, 25574–25587. [Google Scholar] [CrossRef] [PubMed]
- Maier-Flaig, F. Silizium-Nanokristalle für Optoelektronische Anwendungen, 1st ed.; Karlsruher Institut für Technologie: Karlsruhe, Germany, 2013; pp. 55–59. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Köthemann, R.; Golla, C.; Qu, H.; Meier, C. Influence of Gold Nanoantennas on the Photoluminescence of Silicon Nanocrystals. Photonics 2022, 9, 985. https://doi.org/10.3390/photonics9120985
Köthemann R, Golla C, Qu H, Meier C. Influence of Gold Nanoantennas on the Photoluminescence of Silicon Nanocrystals. Photonics. 2022; 9(12):985. https://doi.org/10.3390/photonics9120985
Chicago/Turabian StyleKöthemann, Ronja, Christian Golla, Hong Qu, and Cedrik Meier. 2022. "Influence of Gold Nanoantennas on the Photoluminescence of Silicon Nanocrystals" Photonics 9, no. 12: 985. https://doi.org/10.3390/photonics9120985
APA StyleKöthemann, R., Golla, C., Qu, H., & Meier, C. (2022). Influence of Gold Nanoantennas on the Photoluminescence of Silicon Nanocrystals. Photonics, 9(12), 985. https://doi.org/10.3390/photonics9120985





