Bound States in the Continuum versus Fano Resonances: Topological Argument
Abstract
1. Introduction
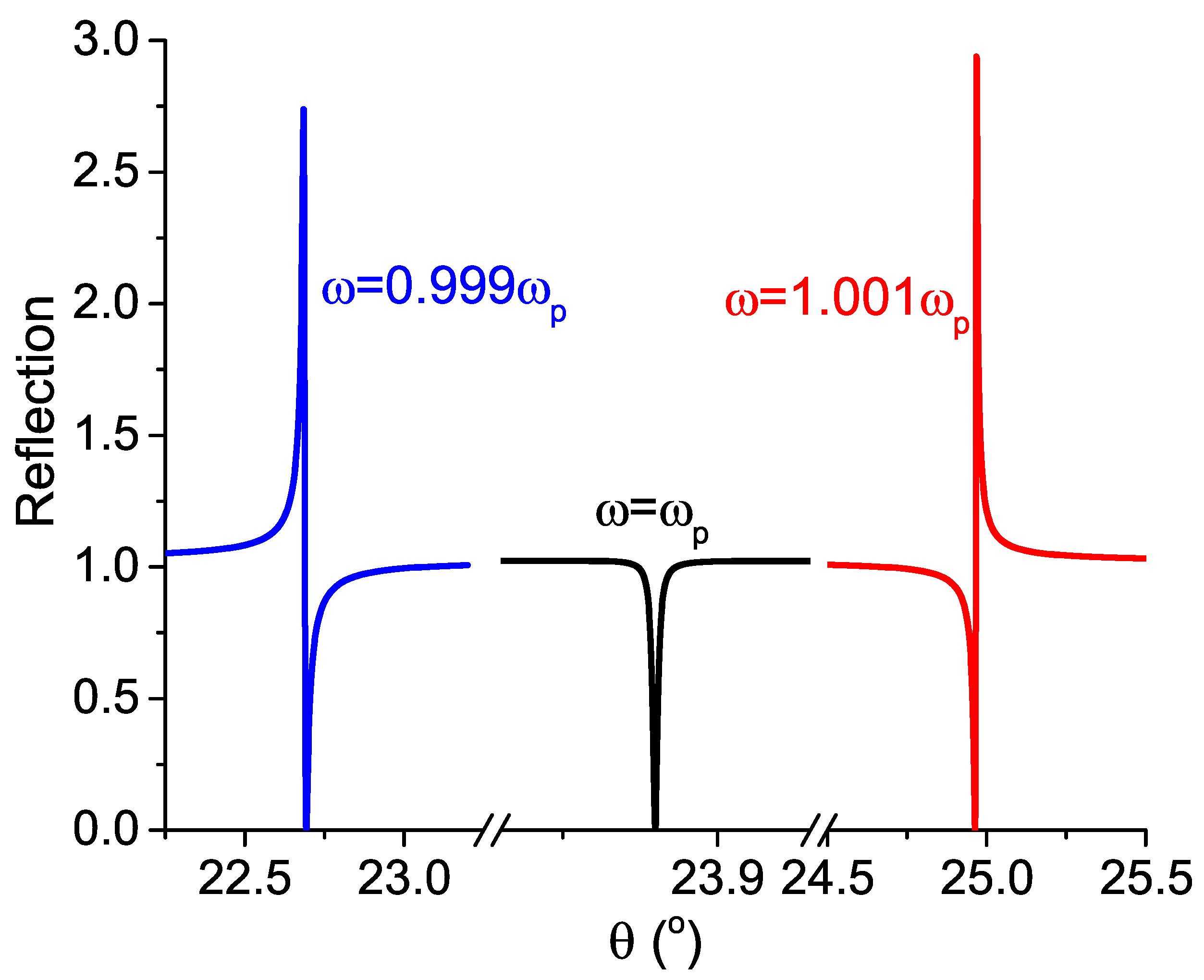
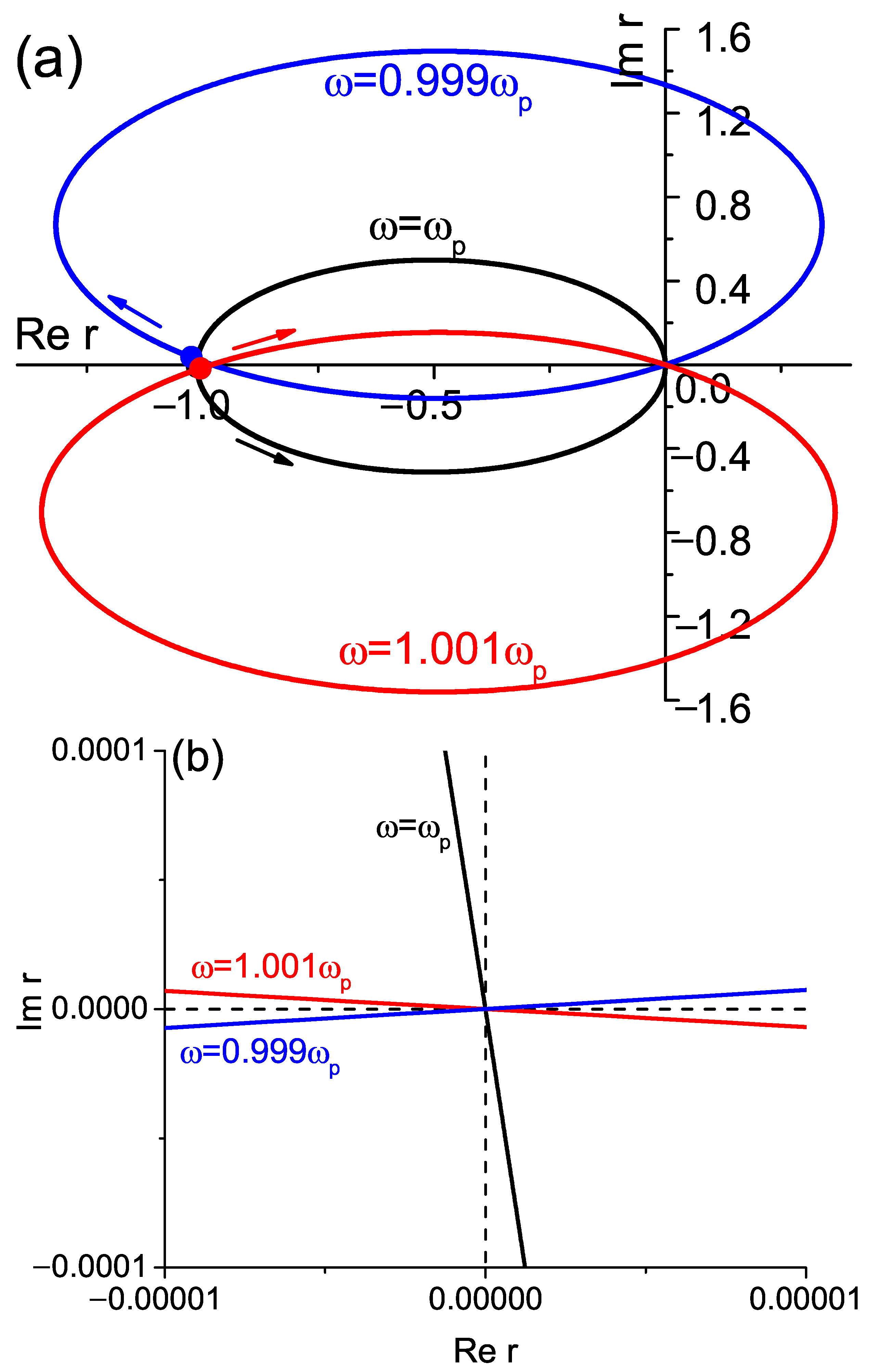
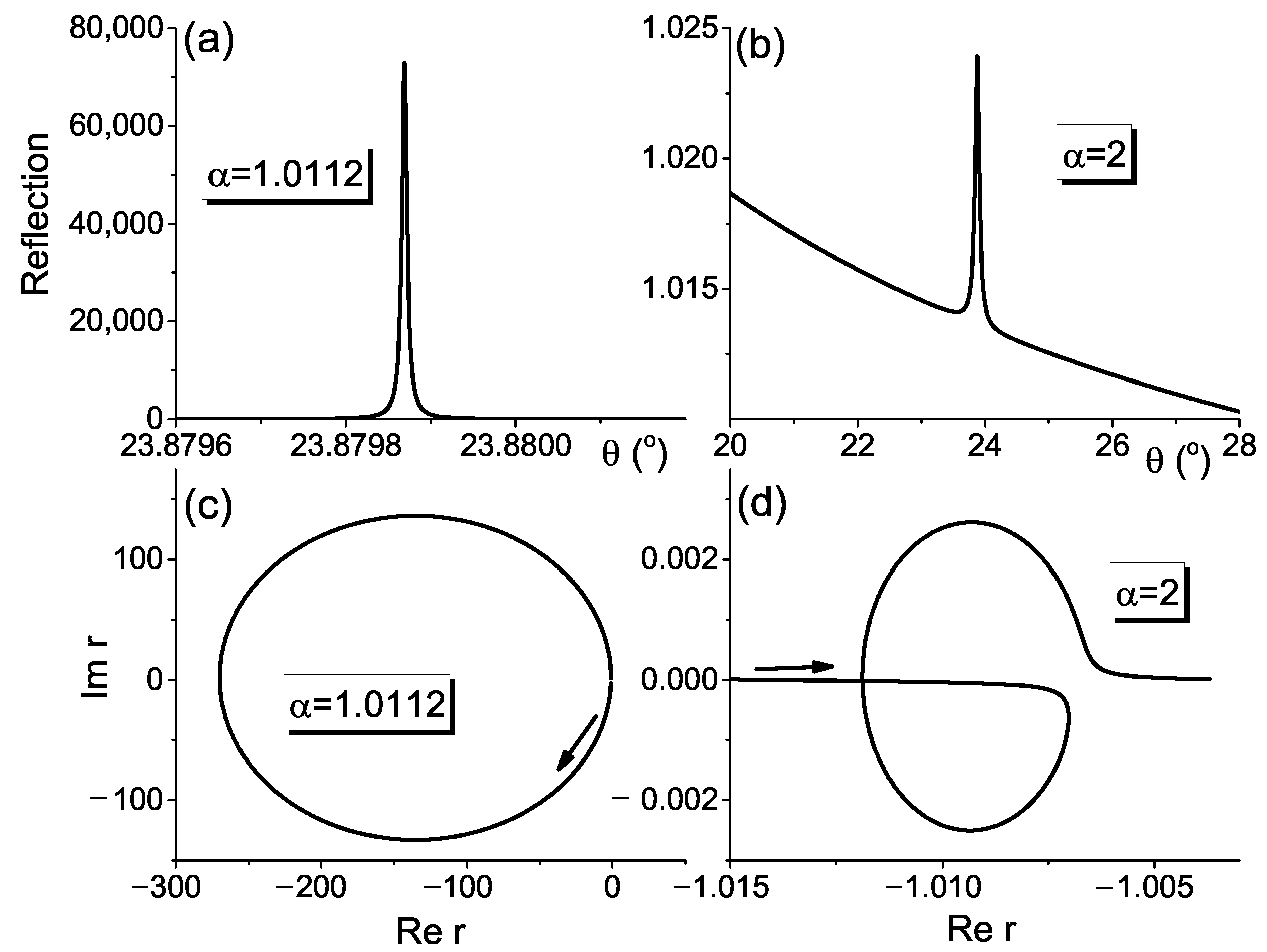
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Krasnok, A.; Baranov, D.; Li, H.; Miri, M.-A.; Monticone, F.; Alú, A. Anomalies in light scattering. Adv. Opt. Photon. 2019, 11, 892–951. [Google Scholar] [CrossRef]
- Von Neumann, J.; Wigner, E. Über merkwürdige diskrete Eigenwerte. Phys. Z. 1929, 30, 465–467. [Google Scholar]
- Stillinger, F.H.; Herrick, D.R. Bound states in the continuum. Phys. Rev. A 1975, 11, 446–454. [Google Scholar] [CrossRef]
- Friedrich, H.; Wintgen, D. Interfering resonances and bound states in the continuum. Phys. Rev. A 1985, 32, 3231–3242. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Koshelev, K.; Bogdanov, A.; Kivshar, Y. Engineering with bound states in the continuum. Opt. Photon. News 2020, 31, 38–45. [Google Scholar] [CrossRef]
- Azzam, S.I.; Kildishev, A.V. Photonic bound states in the continuum: From basics to applications. Adv. Opt. Mater. 2021, 9, 2001469. [Google Scholar] [CrossRef]
- Sadreev, A.F. Interference traps waves in open system: Bound states in the continuum. Rep. Prog. Phys. 2021, 84, 055901. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Kupriianov, A.S.; Xu, Y.; Sayanskiy, A.; Dmitriev, V.; Kivshar, Y.S.; Tuz, V.R. Metasurface engineering through bound states in the continuum. Phys. Rev. Appl. 2019, 12, 014024. [Google Scholar] [CrossRef]
- Bogdanov, A.A.; Koshelev, K.L.; Kapitanova, P.V.; Rybin, M.V.; Gladyshev, S.A.; Sadrieva, Z.F.; Samusev, K.B.; Kivshar, Y.S.; Limonov, M.F. Bound states in the continuum and Fano resonances in the strong mode coupling regime. Adv. Photon. 2019, 1, 016001. [Google Scholar] [CrossRef]
- Melik-Gaykazyan, E.; Koshelev, K.; Choi, J.-H.; Kruk, S.S.; Bogdanov, A.; Park, H.-G.; Kivshar, Y. From Fano to quasi-BIC resonances in individual dielectric nanoantennas. Nano Lett. 2021, 21, 1765–1771. [Google Scholar] [CrossRef] [PubMed]
- Novitsky, D.V.; Shalin, A.S.; Redka, D.; Bobrovs, V.; Novitsky, A.V. Quasibound states in the continuum induced by PT symmetry breaking. Phys. Rev. B 2021, 104, 085126. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Lu, L.; Stone, A.D.; Soljačić, M. Topological nature of optical bound states in the continuum. Phys. Rev. Lett. 2014, 113, 257401. [Google Scholar] [CrossRef] [PubMed]
- Dang, N.H.M.; Zanotti, S.; Drouard, E.; Chevalier, C.; Trippé-Allard, G.; Amara, M.; Deleporte, E.; Ardizzone, V.; Sanvitto, D.; Andreani, L.C.; et al. Realization of polaritonic topological charge at room temperature using polariton bound states in the continuum from perovskite metasurface. Adv. Opt. Mater. 2022, 10, 2102386. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, C.; Xiao, S.; Wang, Y.; Fan, Y.; Liu, Y.; Zhang, N.; Qu, G.; Ji, H.; Han, J.; et al. Ultrafast control of vortex microlasers. Science 2020, 367, 1018–1021. [Google Scholar] [CrossRef] [PubMed]
- Heilmann, R.; Salerno, G.; Cuerda, J.; Hakala, T.K.; Törmä, P. Quasi-BIC mode lasing in a quadrumer plasmonic lattice. ACS Photon. 2022, 9, 224–232. [Google Scholar] [CrossRef] [PubMed]
- Salerno, G.; Heilmann, R.; Arjas, K.; Aronen, K.; Martikainen, J.-P.; Törmä, P. Loss-driven topological transitions in lasing. Phys. Rev. Lett. 2022, 129, 173901. [Google Scholar] [CrossRef]
- Kang, M.; Mao, L.; Zhang, S.; Xiao, M.; Xu, H.; Chan, C.T. Merging bound states in the continuum by harnessing higher-order topological charges. Light Sci. Appl. 2022, 11, 228. [Google Scholar] [CrossRef]
- Ardizzone, V.; Riminucci, F.; Zanotti, S.; Gianfrate, A.; Efthymiou-Tsironi, M.; Suàrez-Forero, D.G.; Todisco, F.; De Giorgi, M.; Trypogeorgos, D.; Gigli, G.; et al. Polariton Bose–Einstein condensate from a bound state in the continuum. Nature 2022, 605, 447–452. [Google Scholar] [CrossRef]
- Monticone, F.; Doeleman, H.M.; Den Hollander, W.; Koenderink, A.F.; Alù, A. Trapping light in plain sight: Embedded photonic eigenstates in zero-index metamaterials. Laser Photon. Rev. 2018, 12, 1700220. [Google Scholar] [CrossRef]
- Sakotic, Z.; Krasnok, A.; Alù, A.; Jankovic, N. Topological scattering singularities and embedded eigenstates for polarization control and sensing applications. Photon. Res. 2021, 9, 1310–1323. [Google Scholar] [CrossRef]
- Huang, Y.; Shen, Y.; Veronis, G. Topological edge states at singular points in non-Hermitian plasmonic systems. Photon. Res. 2022, 10, 747–757. [Google Scholar] [CrossRef]
- Pankin, P.S.; Wu, B.-R.; Yang, J.-H.; Chen, K.-P.; Timofeev, I.V.; Sadreev, A.F. One-dimensional photonic bound states in the continuum. Commun. Phys. 2020, 3, 91. [Google Scholar] [CrossRef]
- Kivshar, Y. Resonant tunneling and bound states in the continuum. Fiz. Nizk. Temp. 2022, 48, 438–444. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambrudge University Press: Cambridge, UK, 2006; pp. 387–391. [Google Scholar]
- Ernzerhof, M.; Giguère, A.; Mayou, D. Non-Hermitian quantum mechanics and exceptional points in molecular electronics. J. Chem. Phys. 2020, 152, 244119. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Hua, J.; Lei, D.; Lu, M.; Chen, Y. Topological physics of non-Hermitian optics and photonics: A review. J. Opt. 2021, 23, 123001. [Google Scholar] [CrossRef]
- Novitsky, D.V.; Canós Valero, A.; Krotov, A.; Salgals, T.; Shalin, A.S.; Novitsky, A.V. CPA-lasing associated with the quasibound states in the continuum in asymmetric non-Hermitian structures. ACS Photon. 2022, 9, 3035–3042. [Google Scholar] [CrossRef]
- Hlushchenko, A.V.; Novitsky, D.V.; Tuz, V.R. Trapped-mode excitation in all-dielectric metamaterials with loss and gain. Phys. Rev. B 2022, 106, 155429. [Google Scholar] [CrossRef]
- Brunetti, G.; Dell’Olio, F.; Conteduca, D.; Armenise, M.N.; Ciminelli, C. Comprehensive mathematical modelling of ultra-high Q grating-assisted ring resonators. J. Opt. 2020, 22, 035802. [Google Scholar] [CrossRef]
- Yadav, G.; Sahu, S.; Kumar, R.; Jha, R. Bound States in the Continuum Empower Subwavelength Gratings for Refractometers in Visible. Photonics 2022, 9, 292. [Google Scholar] [CrossRef]
- Tang, S.; Chang, C.; Zhou, P.; Zou, Y. Numerical Study on a Bound State in the Continuum Assisted Plasmonic Refractive Index Sensor. Photonics 2022, 9, 224. [Google Scholar] [CrossRef]
- Tu, X.; Mario, L.Y.; Mei, T. Coupled Fano resonators. Opt. Express 2010, 18, 18820–18831. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V. Mesotronics: Some New, Unusual Optical Effects. Photonics 2022, 9, 762. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Novitsky, D.V.; Novitsky, A.V. Bound States in the Continuum versus Fano Resonances: Topological Argument. Photonics 2022, 9, 880. https://doi.org/10.3390/photonics9110880
Novitsky DV, Novitsky AV. Bound States in the Continuum versus Fano Resonances: Topological Argument. Photonics. 2022; 9(11):880. https://doi.org/10.3390/photonics9110880
Chicago/Turabian StyleNovitsky, Denis V., and Andrey V. Novitsky. 2022. "Bound States in the Continuum versus Fano Resonances: Topological Argument" Photonics 9, no. 11: 880. https://doi.org/10.3390/photonics9110880
APA StyleNovitsky, D. V., & Novitsky, A. V. (2022). Bound States in the Continuum versus Fano Resonances: Topological Argument. Photonics, 9(11), 880. https://doi.org/10.3390/photonics9110880





