Core Switch Using Optically Induced Long-Period Gratings

Abstract

We propose and theoretically demonstrate an optically induced long-period gratings (OLPGs) based core switching technique for multi-core fibers (MCFs). This switching technique is fully reconfigurable in terms of signal wavelength and input–output fiber cores. The switching window and its efficiency can be adjusted by changing the peak power and the shape of the pump pulses, respectively. Switching efficiencies of 76% were found. Furthermore, we also show that the switched signal can be reshaped by tuning the shape of the pump pulses.

1. Introduction

Space-division multiplexing (SDM) over multi-core fibers (MCFs) has been proposed as an alternative to current optical communication systems based on single-mode fibers (SMFs) [1]. Although MCFs provide a significant increase in transmission capacity per fiber, several tailored subsystems are required to make them commercially viable. For instance, signal switching between arbitrary fiber cores is a mandatory functionality in future flexible optical networks. These switches have been accomplished by using an array of wavelength-selective switches [2], silicon-photonic integrated circuits [3], and reconfigurable optical add/drop multiplexers based on micro-electro-mechanical system mirrors or liquid crystal on silicon pixel arrays [2]. A few in-line approaches have also been proposed, such as the nonlinear core coupling induced by high-power ultra-short pulses [4], the core switching induced by long-period gratings (LPGs) [5,6], and the acousto-optic effect [7]. In that case, the LPGs cause mode coupling between the fundamental core mode and a particular cladding mode. When two fiber cores have similar LPGs, the optical signal is switched from one particular core mode to another by a double resonant coupling with a cladding mode [5,6,7].

Conventional LPGs have an all-optical counterpart, called optically induced LPGs (OLPGs), which can in principle be used for the same purposes. They were first experimentally demonstrated by using a pulsed laser with 5 kW peak power and a pulse duration of 14 ns [8]. In [9], these were theoretically investigated as a particular scheme of inter-modal Bragg-scattering four-wave mixing (FWM) process, which can be used for mode switching with several advantages.

Here, we propose a technique for core switching in MCFs using OLPGs. We show that the switching window can be adjusted by controlling the peak power of the pumps, while the switching efficiency depends on the shape of the pump pulses. The switched signal can also be reshaped as a function of the shape of the pump pulses. This work aims to be a first step towards the realization of an optical core switch.

2. Principle of Operation

The operating principle of the core switch lies in a double resonant coupling process driven by OLPGs induced in different cores of an MCF. The signal is transferred from the fundamental mode of a particular core to a cladding mode and then from this cladding mode to the desired output core(s), see Figure 1. The two pumps are launched in the input of the MCF in different core modes at the same wavelength, which leads to the multimodal interference between them, producing a periodic refractive index variation through the Kerr effect, i.e., the OLPG. The OLPGs, in turn, can promote the signal transfer to the cladding mode, and then to the other core. The pumps are removed at the output. As the pump and the signal wavelengths are quite long, the added noise and the nonlinear distortions at the signal wavelength can be neglected. In order to accomplish an experimental validation of this technique, an experimental setup similar to the one employed in [8] is required for the two cores being tested. Besides that, an additional synchronization stage is also required between both sets of pump pulses propagated in each core.

This kind of switching is fully reconfigurable concerning the input/output ports since the OLPG can be induced/removed by turning on/off the pumps. Moreover, the switching window can be spectrally tuned by changing the optical power of the pumps. In this sense, the pump wavelength can be held fixed, allowing the central wavelength of the switching window to be tuned.

3. Theoretical Model

Here, we present the theory of OLPG-based core-to-core coupling in MCFs for co-polarized and pulsed signals. Following [9] and adding dispersion, we found the system of four coupled equations that describe the energy transfer from a given core to a cladding mode promoted by the two pump beams propagating nonlinearly. By considering two similar sets of coupled equations [10], in which the cladding mode is assumed as same, the full set of scalar coupled equations can be written as,

$$\begin{array}{c}i{\partial }_z{A}_1+D_1{A}_1+N_1=0,\hfill \\ i{\partial }_z{A}_2+D_2{A}_2+N_2=0,\hfill \\ i{\partial }_z{A}_{{\mathrm{co}}_1}+D_{{\mathrm{co}}_1}{A}_{{\mathrm{co}}_1}+N_{{\mathrm{co}}_1}(1,2)=0,\hfill \\ i{\partial }_z{A}_{\mathrm{cl}}+D_{\mathrm{cl}}{A}_{\mathrm{cl}}+N_{\mathrm{cl}}(1,2)+N_{\mathrm{cl}}(3,4)=0,\hfill \\ i{\partial }_z{A}_3+D_3{A}_3+N_3=0,\hfill \\ i{\partial }_z{A}_4+D_4{A}_4+N_4=0,\hfill \\ i{\partial }_z{A}_{{\mathrm{co}}_2}+D_{{\mathrm{co}}_2}{A}_{{\mathrm{co}}_2}+N_{{\mathrm{co}}_2}(3,4)=0.\hfill \end{array}$$

(1)

with $A_i$ and ${\partial }_z$ denoting the complex envelope amplitude and the partial derivative with respect to the longitudinal coordinate, respectively. The subindexes 1, 2, and ${\mathrm{co}}_1$ denote the two pumps and the signal propagating in the input core, while the 3, 4, and ${\mathrm{co}}_2$ denote both pumps and the signal on the output core. The subindex cl relates to the signal in the cladding mode. The term $D_i$ denotes a differential operator that accounts for dispersion. Neglecting dispersion terms higher than the second order, $D_i$, is given by

$$D_i=i({\beta }_i^{\left(1\right)}-{\beta }_1^{\left(1\right)}){\partial }_t-\frac{1}{2}{\beta }_i^{\left(2\right)}{\partial }_t^2,$$

(2)

where ${\beta }_i^{\left(n\right)}$ denotes the n-order derivative with respect to time of the propagation constant for the i mode. The nonlinear terms $N_i$ and the OLPG terms $N_l(i,j)$ are simpler than in [9] since we are considering co-polarized signals. Thus, $N_i$ is written as

$$\begin{array}{cc}\hfill N_i=& ({\gamma }_{iiii}{P}_i+2{\gamma }_{ijji}{P}_j+{\gamma }_{iiji}{A}_i{A}_j^{*}{e}^{-i\Delta {\beta }_{w}z})A_i+\hfill \\ \hfill & \left(2{\gamma }_{iiij}{P}_i{e}^{i\Delta {\beta }_{w}z}+{\gamma }_{ijjj}{P}_j{e}^{i\Delta {\beta }_{w}z}+{\gamma }_{ijij}{A}_j{A}_i^{*}{e}^{2i\Delta {\beta }_{w}z}\right)A_j,\hfill \end{array}$$

(3)

for the pump pair of modes, i.e., with i and j equal to 1 and 2 or equal to 3 and 4, and $j\ne i$. The parameter $P_i={\left|A_i\right|}^2$ denotes the power of the mode i. Lastly, the OLPG term $N_l(i,j)$ with m and $l={\mathrm{co}}_1$, co${}_2$ and cl, and $m\ne l$ is given by

$$\begin{array}{cc}\hfill N_l(i,j)=& (2{\gamma }_{liil}{P}_i+2{\gamma }_{ljjl}{P}_j+{\gamma }_{lijl}{A}_i{A}_j^{*}{e}^{-i\Delta {\beta }_{w}z}+\hfill \\ & {\gamma }_{ljil}{A}_j{A}_i^{*}{e}^{i\Delta {\beta }_{w}z})A_l+(2{\gamma }_{liim}{P}_i+2{\gamma }_{ljjm}{P}_j+\hfill \\ & {\gamma }_{lijm}{A}_i{A}_j^{*}{e}^{-i\Delta {\beta }_{w}z}+{\gamma }_{ljim}{A}_j{A}_i^{*}{e}^{i\Delta {\beta }_{w}z})A_m{e}^{i\Delta {\beta }_{p}z}.\hfill \end{array}$$

(4)

The difference of propagation constants at the corresponding central wavelengths are accounted for in the exponentials of the nonlinear terms as

$$\Delta {\beta }_w={\beta }_j-{\beta }_i,\Delta {\beta }_p={\beta }_m-{\beta }_l,$$

(5)

and the nonlinear parameters are given by,

$${\gamma }_{ijkl}={\displaystyle \frac{n_2{\omega }_i}{c}}\int E_i^{*}{E}_j{E}_k^{*}{E}_{l}dxdy,$$

(6)

with $n_2$, ${\omega }_i$, c, and $E_i$ denoting the nonlinear refractive index, the angular frequency, the vacuum speed of light and the normalized transversal scalar field of the i beam, respectively. Equation (1) takes into account all the dominant nonlinear processes, including self-phase modulation for the pumps, cross-phase modulation (XPM) between both pumps and each signal in the core/cladding, and the Bragg-scatering FWM. Lastly, (1) is solved by using a pseudo-spectral method [11].

To efficiently induce the signal transfer to the cladding mode, the phase-matching condition between both pumps, the signal, in the fundamental core mode, and the idler, in a given cladding mode, must be achieved. If the two pump beams have the same optical power, their power remains constant along the fiber [12]. For a single resonant process and in the continuous wave (CW) regime, (1) can be reduced to a system of two coupled equations for the signal and idler beams, similar to the well-known BS-FWM process. In that case, the phase-matching condition can be written as [9],

$$\Delta {\beta }_w-\Delta {\beta }_p=P_0({\gamma }_{11{\mathrm{co}}_1{\mathrm{co}}_1}+{\gamma }_{22{\mathrm{co}}_1{\mathrm{co}}_1}-{\gamma }_{11\mathrm{cl}\mathrm{cl}}-{\gamma }_{22\mathrm{cl}\mathrm{cl}}),$$

(7)

with $P_0$ denoting the optical power of the pumps. In order to estimate the optimum value of the pump powers, (7) is solved by imposing the perfect phase-matching condition. The coupling length may also be estimated by [9]

$$L_c=\pi /\left(2P_0{\gamma }_{12\mathrm{cocl}}\right).$$

(8)

4. Results

We assume a four-core MCF similar to the commercial fiber SM-4C1500 (8.0/125) from Fibercore, with cladding and core diameters of 125 and 7.2 $\mathsf{\mu }$m, respectively. The cores have a step-index profile and are disposed in a “square” arrangement with a pitch of 36.25 $\mathsf{\mu }$m. The refractive index for the core/cladding regions is estimated by a three-term Sellmeier equation with 0.052/0 mole fraction of GeO${}_2$ [7]. The $\beta$ and E were calculated using Comsol Multiphysics software package assuming a bare fiber in the air.

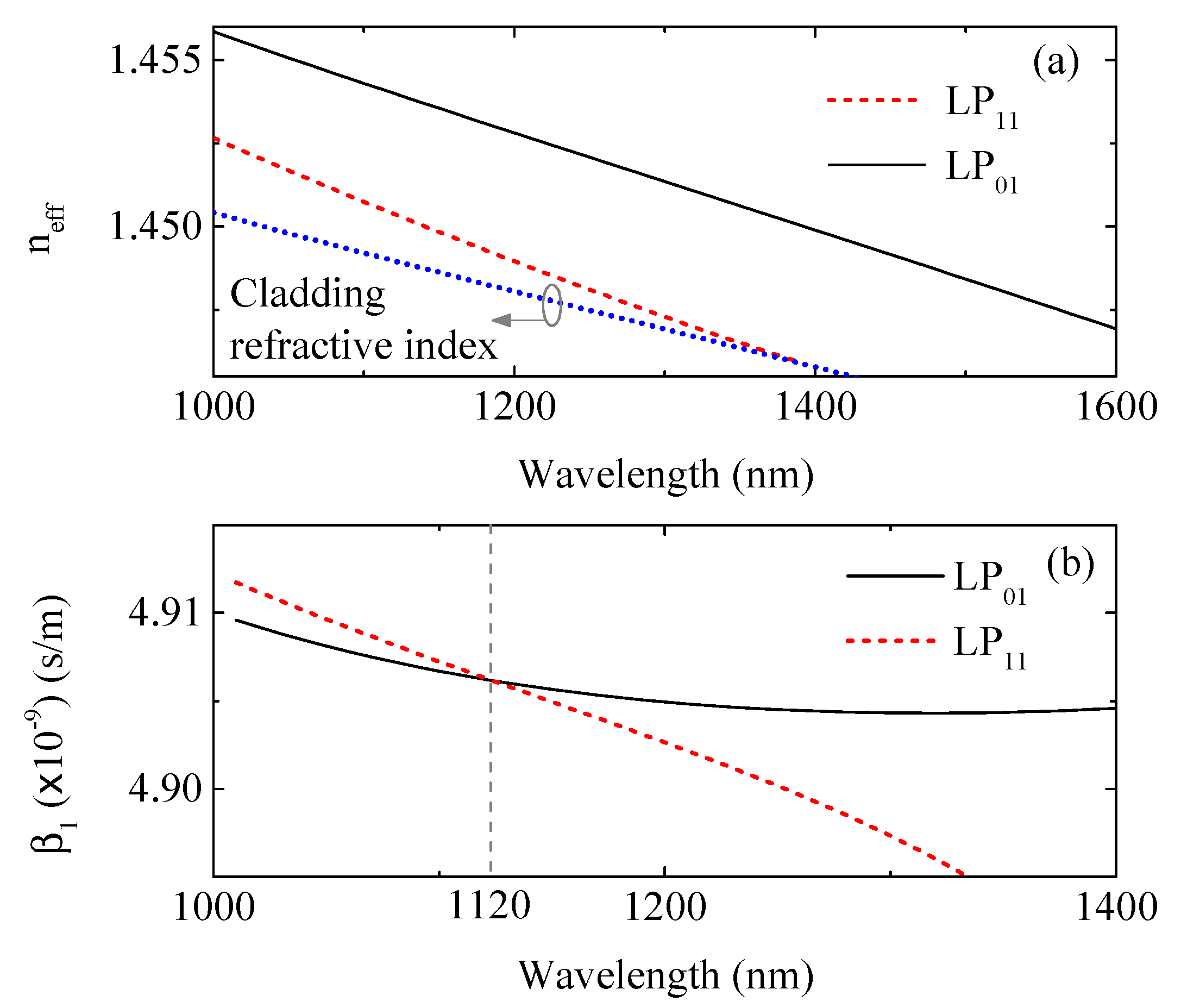
We assume a signal beam in the fundamental mode at 1550 nm and two pumps in LP${}_{01}$ and LP${}_{11}$ modes with the same wavelength and below the 1400 nm, allowing the propagation of the LP${}_{11}$, see Figure 2a. We note that the pump pulses can suffer from the modulation instability (MI) caused by XPM, but this effect can be avoided if the pump beams have similar group velocities [12], which happens at 1120 nm, see Figure 2b. Moreover, at this wavelength the walk-off length between the pumps is larger, which allows the nonlinear interaction at longer fiber lengths. In that way, the pumps are launched at 1120 nm with a super-Gaussian envelope,

$$A\left(t\right)=a\left(t\right)e^{-{(t^2/2{\sigma }^2)}^n}$$

(9)

with a, n, and $\sigma$ denoting the amplitude, the order, and the temporal width of the pulse, respectively. While, the signal has a Gaussian envelope with a peak power of 1 mW. We start by assuming a full width at half maximum (FWHM) of 12 ps for all the pulses.

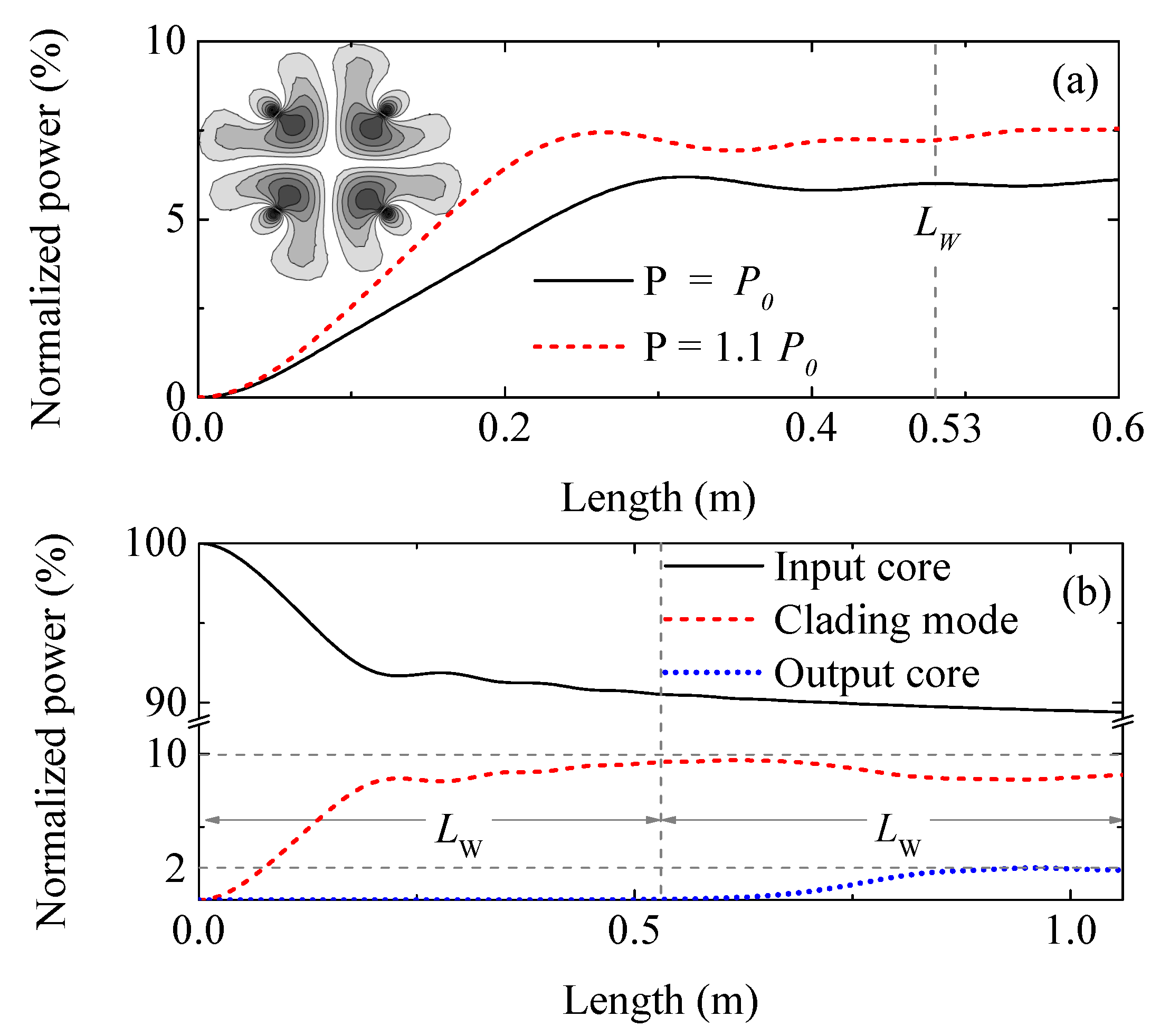
To choose the cladding mode, we consider a few tens of them for which the required optical power to induce mode conversion, $P_0$, and the characteristic coupling length, $L_C$, are estimated according to (7) and (8), respectively. Notice that longer OLPGs can become very sensitive to group velocity fluctuations and polarization effects. In that way, cladding modes with $L_c$ of tens of meters are excluded. On the other hand, shorter OLPGs tend to require high pump powers to produce a significant modulation of the nonlinear refractive index. On this basis, the cladding mode with better performance in terms of conversion/switching efficiency, henceforward defined as the signal ratio between the optical power launched in the input core and the power coupled to the desired output core or mode, is the 5th highest index cladding mode showed in the inset of Figure 3a. In

Table 1. $\Delta \beta$ and $P_0$ requirement for phase-matching of the chosen cladding mode and their neighbours.

Cladding Mode	2nd	3rd	4th	5th	6th	7th	8th
$\Delta \beta$ (m${}^{-1}$)	217	223	115	80	222	956	956
P${}_0$ (kW)	17.4	17.8	9.22	6.47	17.8	76.6	76.7

at shaded is indicated that such a mode requires pump beams with an optical power of $P_0=6.47$ kW, the lower value in the set of cladding modes under analysis. Besides the optical power, the coupling length must be kept at acceptable low values, in this case, for this cladding mode $L_c=0.79$ m. Therefore, the chosen cladding mode meets the main requirements to provide an efficient mode conversion. Moreover, Table 1 indicates that the mode coupling for a given cladding mode only happens for pumps with adequate optical power. However, $P_0$ must be numerically optimized because in the derivation of (7) the CW approximation was assumed. Starting from $P_0$ and considering a single OLPG in the MCF, we solved (1), evaluating the maximum power transfer to the cladding mode as a function of the pump peak power. The optimum value was found to be $1.1P_0=7.14$ kW, for an effective interaction length quite close to the value of the walk-off length between the core and cladding signals, $L_W=0.53$ m, see Figure 3b. As a result, $L_W$ is used to estimate the effective interaction length instead of $L_c$. However, when the values of $L_c$ and $L_W$ are similar, the coupling is enhanced.

Thereafter, we solved (1), considering two OLPGs in different cores. In a first coupling process, the signal is transferred from the core to a cladding mode in a region with a length of ≈$L_W$. Then, a second process induces the power transfer from the cladding to the other core mode, resulting in a device with a total length of 2$L_W$, see Figure 3b. Although part of the signal can remain in the cladding mode, it will be severely attenuated for large fibers lengths, resulting in negligible crosstalk. To enhance the power transfer, we must synchronize the pumps and the signal in each coupling process to increase the temporal overlap among all of them. The signal and the pumps are time-delayed to overlap at the center of the first region. On the other core, we employed the same process to synchronize the pumps and the signal in the cladding mode. Note that the shape, peak power, and FWHM of the signal remain unchanged in all scenarios considered below.

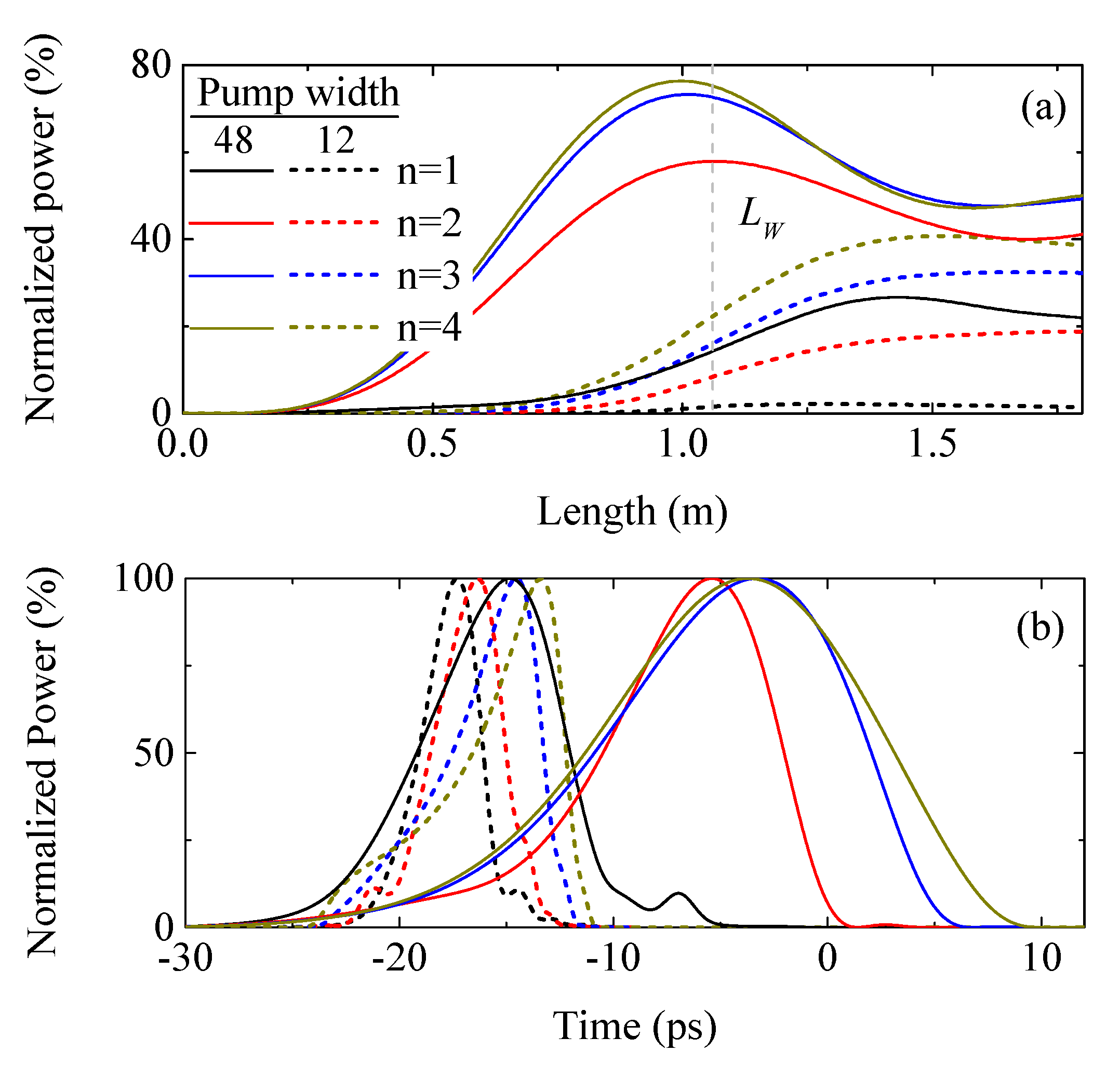
Besides the pulse synchronization, the switching efficiency also depends on the FWHM and on the shape of the pump pulses. The power transfer can be enhanced by increasing the FWHM of the pump pulse, which increases the temporal overlap among all the pulses, resulting in higher index perturbations or stronger OLPGs. In the same way, we can also increase the power transfer by changing the temporal shape of the pump pulses. For pulses with a super-Gaussian shape, we note that the power transfer increases with the order of the super-Gaussian because the temporal overlap between the pulses also increases, see Figure 4a. We note that the coupling length varies for all the cases, which can be explained by a change in the walk-off length due to the changes in the shapes and FWHM of the pump pulses. Furthermore, the coupling length tends to decrease with the order of the Gaussian pulse because the average power of the pump beams increases, in accordance with (8). A switching efficiency of 76% is accomplished for pump pulses with a super-Gaussian shape with $n=4$ and an FWHM of 48 ps, see Figure 4a. On the other hand, the shape of pump beams also changes the temporal shape of the switched pulse. In Figure 4b, it is shown that the FWHM of the switched pulse can be tunned from ≈3 up to 14 ps using super-Gaussian pump beams of order $n=1,2,3$ and 4 with FWHM of 12 and 48 ps. The shape of the switched pulse can be slightly changed by adjusting the shape of the pumps or it can be kept quite close to a Gaussian by using Gaussian pumps.

Last, we analyze the transmission spectrum of the OLPG-based core switch for two pump configurations, considering first and fourth order super-Gaussian pumps with an FWHM of 48 ps. Equation (1) is solved assuming constant wavelength and initial peak power for the pump beams, while the signal wavelength is ranged from 1548 to 1552 nm keeping the initial peak power constant. The fiber length considered is chosen to match the maximum power transfer at the output core. For the fourth order super-Gaussian pumps, the transmission spectrum shows a single peak centered at 1550 nm with an FWHM of ≈0.4 nm. The transmission window induced by the Gaussian pumps is also single peaked, centered at 1549.9 with an FWHM of 0.5 nm. In both cases, the transmission spectrum is not symmetric relative to the central wavelength, this effect being more obvious in the case of Gaussian pumps, see Figure 5. However, the transmission windows in both cases are narrow enough to enable the core switch of a single wavelength channel. Notice that the central wavelength of the switching window can be adjusted by varying only the power of the pump beams, according to (7), while the pump wavelength is kept fixed.

5. Discussion

The results presented in the previous section showed that a transmission window between two distinct cores at a given signal wavelength can be opened by two strong pump beams propagated at a distinct wavelength. The central wavelength of this transmission window can be changed by adjusting the power of the pump beams, while the switching efficiency can be tuned by changing the width and shape of pump pulses. In particular, we show that for pump pulses with FWHM of 12 and 48 ps and peak powers of 7.14 kW, a switching efficiency of 26% and 76%, respectively, can be achieved. Note that this remarkable efficiency is achieved in fiber lengths of ≈1 m. We also show that the switching efficiency tends to increase with FWHM and with the order of the super-Gaussian pulse because the walk-off between the pump pulses also increases, giving rise to strong OLPG, or, increasing the efficiency of the multimodal BS-FWM.

The core switching technique proposed in this paper can be used for several applications, such as all-optical packet switching in which each packet is independently switched for a given core [13]. The efficiency of that process can be adjusted by changing the shape and the FHWM of the pulse of the optical beam. On the other hand, the optical power of the pump beams can be reduced to lower values by increasing the MCF’s non-linearity, using materials with higher nonlinear refractive index or reducing the core size. Furthermore, the MCF’s dispersion profile can be engineered to enhance the phase-matching condition between the core and the cladding modes. For instance, double-cladding MCFs or low-index acrylate coatings can be employed to properly engineer the dispersion profile of the cladding mode, leading to a substantial power reduction of the pump beams and enabling the signal propagation in the cladding for longer distances. By combining all the aforementioned approaches, the optical power of the pump beams can be substantially reduced to enable the use of pump beams in constant wave (CW) operation. In that way, the development of highly nonlinear fiber is of paramount importance to pave the way for all-optical core switching [14].

6. Conclusions

The results provided in this paper show that OLPGs can be used for dynamic core switch in MCF. We showed that the switching window can be shifted by properly adjusting the power of the pump beams, while the switching efficiency can be tunned by changing the width and shape of pump pulses. For pump pulses with 12 and 48 ps of temporal width, we achieve a switching efficiency of 26% and 76%, respectively, in fiber lengths of ≈1 m and with peak powers of 7.14 kW for the pump beams. The pump pulses with higher super-Gaussian order and larger FWHM lead to higher switching efficiencies. When compared with the typical optical powers employed for all-optical signal processing, these values are slightly higher. However, in principle, they can be reduced to more practical levels by increasing the nonlinearity of the MCF, or by properly engineering the dispersion profile of the cladding mode. We also show that the shape of the switched signal depends on the shape of the pump pulses, paving the way for all-optical joint signal reshaping and core switching based on OLPGs. Lastly, to support future investigations, we present a theoretical model for the double resonant coupling induced by OLPGs in MCFs.