A Large Mode Area Parabolic-Profile Core Fiber with Modified Segmented in Cladding
Abstract
1. Introduction
2. Theory and Structure
3. Discussion of Proposed Fiber
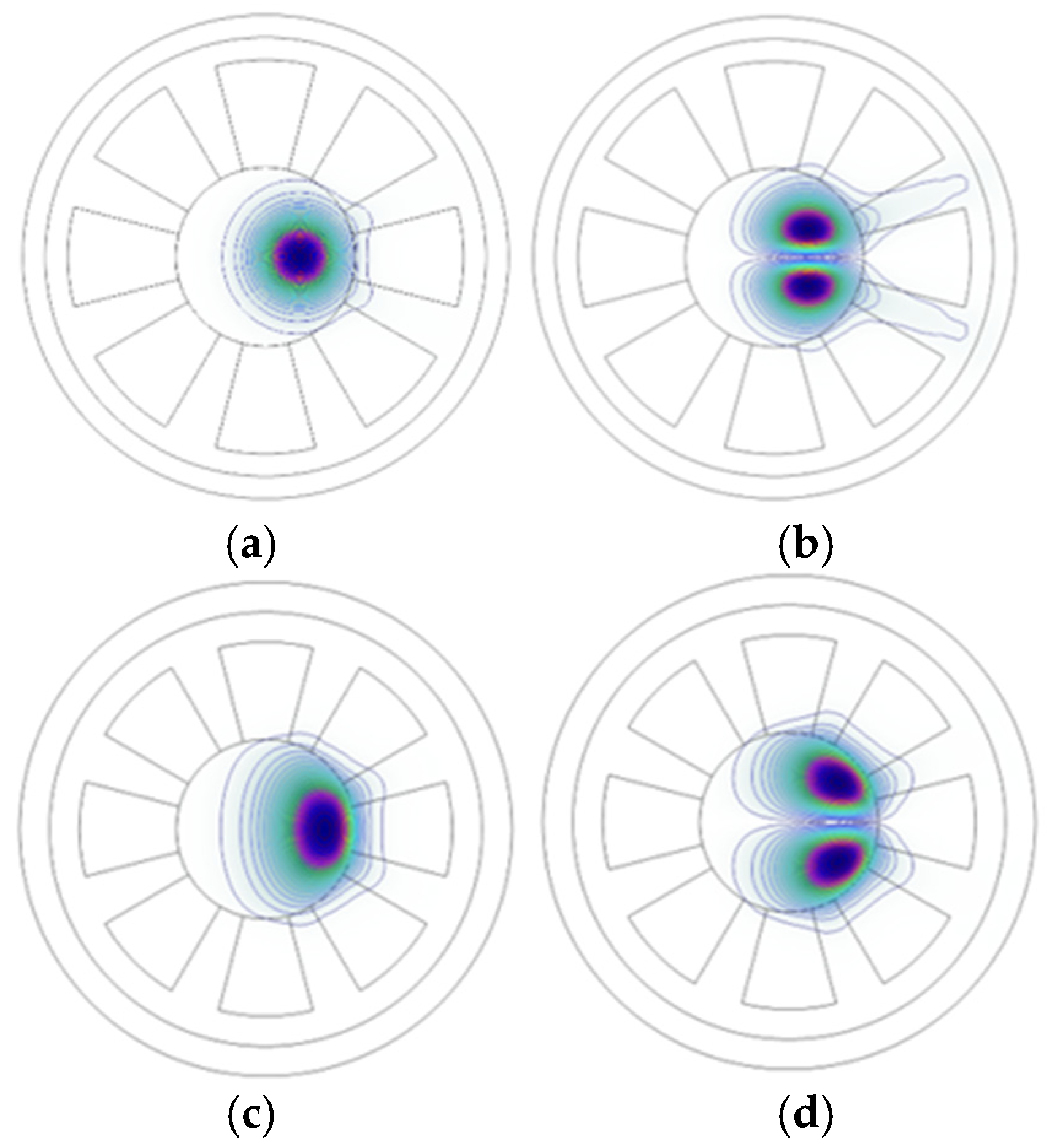
3.1. Effects of Core Radius
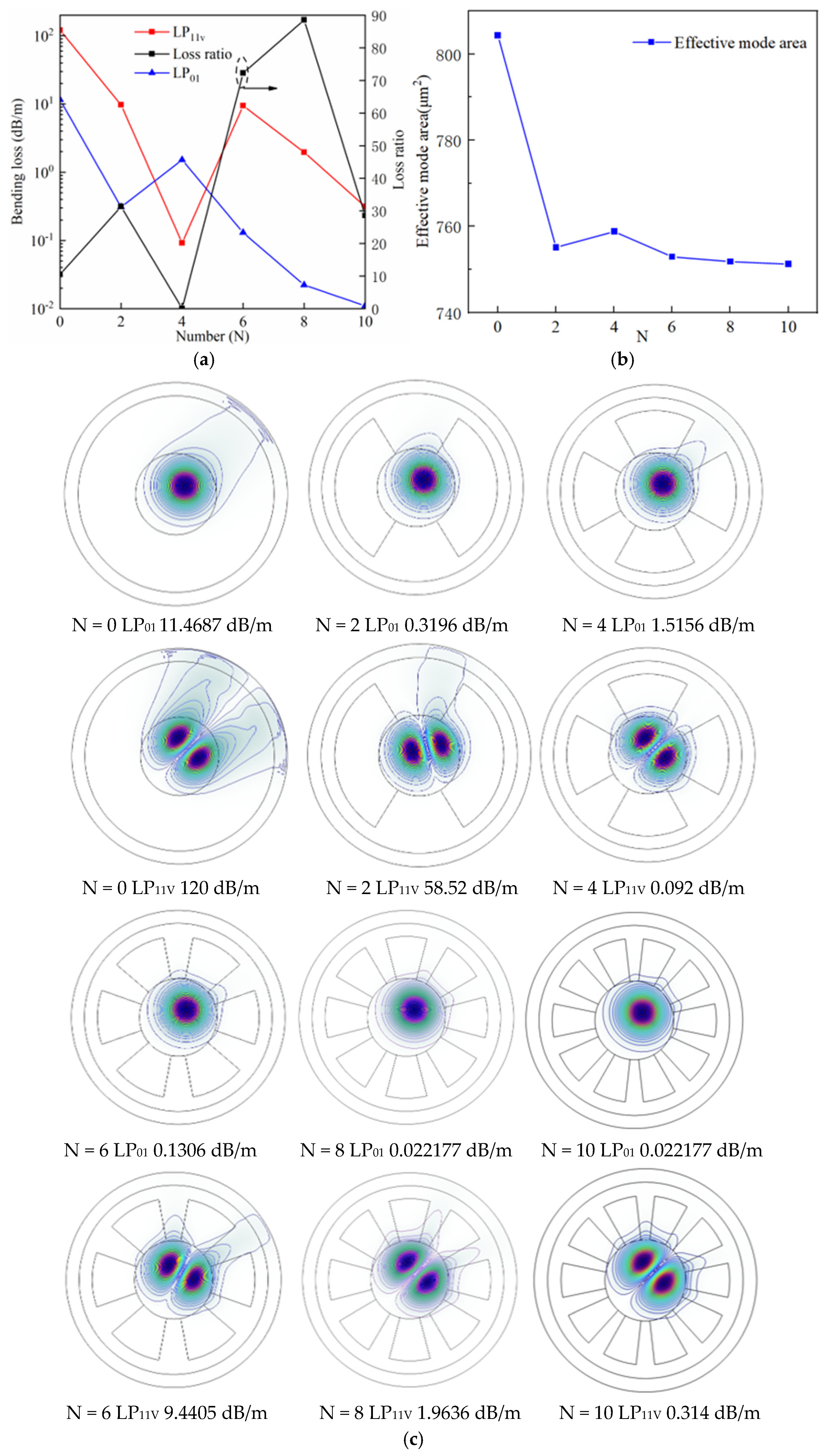
3.2. Effects of Number of Segments
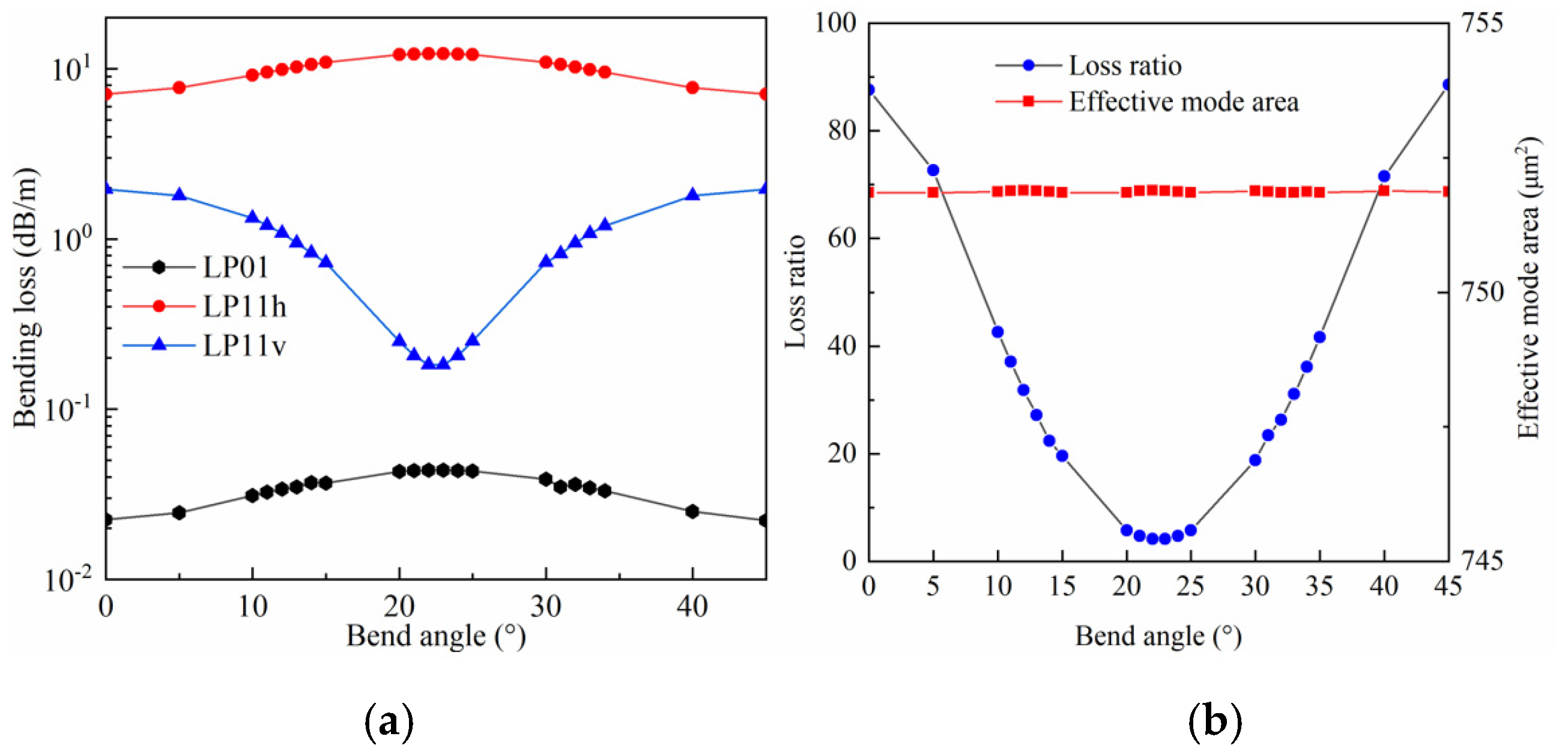
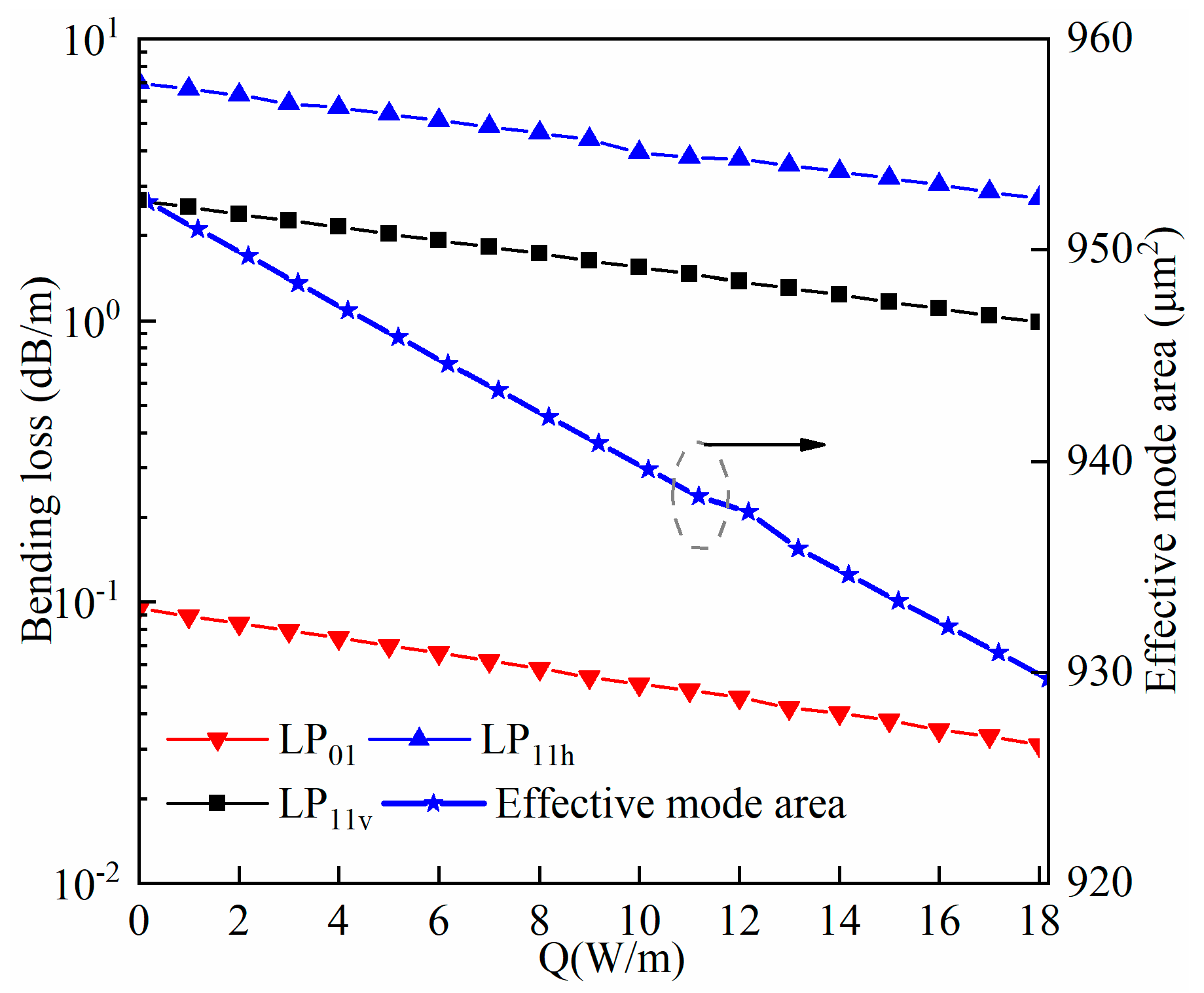
3.3. Effects of Bending Angle
3.4. Effects of Duty Cycle
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nilsson, J.; Payne, D.N. High-Power Fiber Lasers. Science 2011, 332, 921–922. [Google Scholar] [CrossRef] [PubMed]
- Richardson, D.J.; Nilsson, J.; Clarkson, W.A. High power fiber lasers: Current status and future perspectives. J. Opt. Soc. Am. B 2010, 27, B63–B92. [Google Scholar] [CrossRef]
- Jain, D.; Alam, S.; Codemard, C.; Jung, Y.; Zervas, M.N.; Sahu, J.K. High power, compact, picosecond MOPA based on single trench fiber with single polarized diffraction-limited output. Opt. Lett. 2015, 40, 4150–4153. [Google Scholar] [CrossRef] [PubMed]
- Zervas, M.N.; Codemard, C.A. High Power Fiber Lasers: A Review. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 219–241. [Google Scholar] [CrossRef]
- O’Connor, M.; Gapontsev, V.; Fomin, V.; Abramov, M.; Ferin, A. Power Scaling of SM Fiber Lasers toward 10 Kw; Optical Society of America: Washington, DC, USA, 2009. [Google Scholar]
- Dawson, J.W.; Messerly, M.J.; Beach, R.J.; Shverdin, M.Y.; Stappaerts, E.A.; Sridharan, A.K.; Pax, P.H.; Heebner, J.E.; Siders, C.W.; Barty, C.P.; et al. Analysis of the Scalability of Diffraction-Limited Fiber Lasers and Amplifiers to High Average Power. Opt. Express 2008, 16, 13240–13266. [Google Scholar] [CrossRef] [PubMed]
- Smith, A.V.; Smith, J.J. Overview of a Steady-Periodic Model of Modal Instability in Fiber Amplifiers. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 3000112. [Google Scholar] [CrossRef]
- Otto, H.J.; Stutzki, F.; Jansen, F.; Eidam, T.; Jauregui, C.; Limpert, J.; Tünnermann, A. Temporal dynamics of mode instabilities in high-power fiber lasers and amplifiers. Opt. Express 2012, 20, 15710–15722. [Google Scholar] [CrossRef]
- Jain, D.; Jung, Y.; Barua, P.; Alam, S.; Sahu, J.K. Demonstration of ultra-low NA rare-earth-doped step-index fiber for applications in high power fiber lasers. Opt. Express 2015, 23, 7407–7415. [Google Scholar] [CrossRef]
- Smith, A.V.; Smith, J.J. Mode competition in high power fiber amplifiers. Opt. Express 2011, 19, 11318–11329. [Google Scholar] [CrossRef]
- Naderi, S.; Dajani, I.; Madden, T.; Robin, C. Investigations of modal instabilities in fiber amplifiers through detailed numerical simulations. Opt. Express 2013, 21, 16111–16129. [Google Scholar] [CrossRef]
- Liu, E.; Liang, S.; Liu, J. Double-cladding structure dependence of guiding characteristics in six-fold symmetric photonic quasi-crystal fiber. Superlattices Microstruct. 2019, 130, 61–67. [Google Scholar] [CrossRef]
- Liu, E.; Tan, W.; Yan, B.; Xie, J.; Ge, R.; Liu, J. Robust transmission of orbital angular momentum mode based on a dual-cladding photonic quasi-crystal fiber. J. Phys. D Appl. Phys. 2019, 52, 325110. [Google Scholar] [CrossRef]
- Li, C.; Yan, B.; Liu, J. Refractive index sensing characteristics in a D-shaped photonic quasi-crystal fiber sensor based on surface plasmon resonance. J. Opt. Soc. Am. A 2019, 36, 1663. [Google Scholar] [CrossRef] [PubMed]
- Liu, E.; Tan, W.; Yan, B.; Xie, J.; Ge, R.; Liu, J. Broadband ultra-flattened dispersion, ultra-low confinement loss and large effective mode area in an octagonal photonic quasi-crystal fiber. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2018, 35, 431. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; Wang, A.; Liu, E.; Tan, W.; Xie, J.; Ge, R.; Liu, J. Polarization filtering in the visible wavelength range using surface plasmon resonance and a sunflower-type photonic quasi-crystal fiber. J. Phys. D Appl. Phys. 2018, 51, 155105. [Google Scholar] [CrossRef]
- She, Y.L.; Zhou, D.J.; Chen, X.Y.; Xia, A.S. Study on ultralow bending loss of bend-insensitive single-mode optical fiber. Opt. Fiber Technol. 2019, 50, 225–232. [Google Scholar]
- She, Y.; Zhou, D.; Chen, X. Optimization design of bending performance for ultralow loss hole assisted fiber. Infrared Laser Eng. 2019, 48, 0918006. [Google Scholar]
- She, Y.L.; Zhang, W.T.; Liang, G.; Tang, Y.; Tu, S. Optimal design of Large Mode Area All-Solid-Fiber Using a Gray Relational Optimization Technique. Opt. Int. J. Light Electron Opt. 2021, 242, 167188. [Google Scholar]
- She, Y.-L.; Zhou, D.-J.; Chen, X.Y.; Ni, J.-M. Bend-resistant low bending loss and large mode area single-mode fiber with low NA-ScienceDirect. Opt. Fiber Technol. 2019, 51, 101–106. [Google Scholar]
- Huang, L.; Yao, T.; Yang, B.; Leng, J.; Zhou, P.; Pan, Z.; Gu, S. Modified Single Trench Fiber with Effective Single-mode Operation for High-power Application. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 0901409. [Google Scholar] [CrossRef]
- Xu, W.; Lin, Z.; Wang, M.; Feng, S.; Zhang, L.; Zhou, Q.; Chen, D.; Zhang, L.; Wang, S.; Yu, C.; et al. 50μm core diameter Yb3+/Al3+/F codoped silica fiber with M2<1.1 beam quality. Opt. Lett. 2016, 41, 504. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Liu, Y.; Shen, B.; Feng, X.; Huang, S.; Li, M.; Wang, J.; Guo, C.; Li, L.; Tao, R. Partially inscribed Bragg gratings suppressing high-order modes in high-power large-mode-area fiber oscillators. Opt. Int. J. Light Electron Opt. 2020, 220, 165217. [Google Scholar] [CrossRef]
- Yehouessi, J.P.; Vanvincq, O.; Cassez, A.; Douay, M.; Quiquempois, Y.; Bouwmans, G.; Bigot, L. Extreme large mode area in single-mode pixelated Bragg fiber. Opt. Express 2016, 24, 4761. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; He, D.; Yu, C.; Feng, S.; Chen, D.; Hu, L. Compact Single-Mode Nd-doped Silicate Glass Multi-Trench Fiber with 40 m Core-Diameter. IEEE J. Sel. Top. Quantum Electron. 2017, 24, 0900104. [Google Scholar]
- Wang, X.; Lou, S.; Lu, W.; Sheng, X.; Zhao, T.; Hua, P. Bend Resistant Large Mode Area Fiber With Multi-Trench in the Core. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 117–124. [Google Scholar] [CrossRef]
- Ma, S.; Ning, T.; Pei, L.; Zheng, J.; Li, J.; Xu, J.; He, X. Bend-resistant large mode area fiber with an azimuthally segmented trench in the cladding. J. Light. Technol. 2019, 37, 3761–3769. [Google Scholar] [CrossRef]
- Ma, S.; Ning, T.; Pei, L.; Li, J.; Zheng, J.; He, X.; Wen, X. Bend-resistant leaky multi-trench fiber with large mode area and single-mode operation. PLoS ONE 2018, 13, e0203047. [Google Scholar] [CrossRef]
- Kurade, B.M.; Ayyanar, N.; Raja, G.T.; Varshney, S.K. Asymmetric-clad multi-trench fibers with large-mode-area and controlled leakage loss. Opt. Fiber Technol. 2019, 48, 235–241. [Google Scholar] [CrossRef]
- Dong, L.; McKay, H.A.; Fu, L.; Ohta, M.; Marcinkevicius, A.; Suzuki, S.; Fermann, M.E. Ytterbium-doped all glass leakage channel fibers with highly fluorine-doped silica pump cladding. Opt. Express 2009, 17, 8962–8969. [Google Scholar] [CrossRef]
- Dong, L.; Wu, T.; McKay, H.A.; Fu, L.; Li, J.; Winful, H.G. All-Glass Large-Core Leakage Channel Fibers. Sel. Top. Quantum Electron. 2009, 15, 47–53. [Google Scholar] [CrossRef]
- Dong, L.; Li, J.; Peng, X. Bend-resistant fundamental mode operation in ytterbium-doped leakage channel fibers with effective areas up to 3160 μm2. Opt. Express 2006, 14, 11512–11519. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Mckay, H.A.; Marcinkevicius, A.; Fu, L.; Li, J.; Thomas, B.K.; Fermann, M.E. Extending Effective Area of Fundamental Mode in Optical Fibers. J. Light. Technol. 2009, 27, 1565–1570. [Google Scholar] [CrossRef]
- Tünnermann, A.; Schreiber, T.; Röser, F.; Liem, A.; Höfer, S.; Zellmer, H.; Nolte, S.; Limpert, J. The renaissance and bright future of fiber lasers. J. Phys. B At. Mol. Opt. Phys. 2005, 38, S681. [Google Scholar] [CrossRef]
- Jain, D.; Sahu, J.K. Large Mode Area Single Trench Fiber for 2 μm Operation. J. Light. Technol. 2016, 34, 3412–3417. [Google Scholar] [CrossRef]
- Jain, D.; Baskiotis, C.; Sahu, J.K. Bending performance of large mode area multi-trench fibers. Opt. Express 2013, 21, 26663–26670. [Google Scholar] [CrossRef]
- Wang, X.; Lou, S.; Lu, W. Bend-resistant large-mode-area photonic crystal fiber with a triangular-core. Appl. Opt. 2013, 21, 26663–26670. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Ning, T.; Lu, S.; Zheng, J.; Li, J.; Pei, L. Bending-Resistant Design of a Large Mode Area Segmented Cladding Fiber With Resonant Ring. J. Light. Technol. 2018, 36, 2844–2849. [Google Scholar] [CrossRef]
- Guo, Z.; Pei, L.; Ning, T.; Zheng, J.; Li, J.; Wang, J. Segmented cladding fiber with a high-index ring in core for wideband single-mode operation in any bending orientation. IEEE Photonics J. 2021, 13, 7101018. [Google Scholar] [CrossRef]
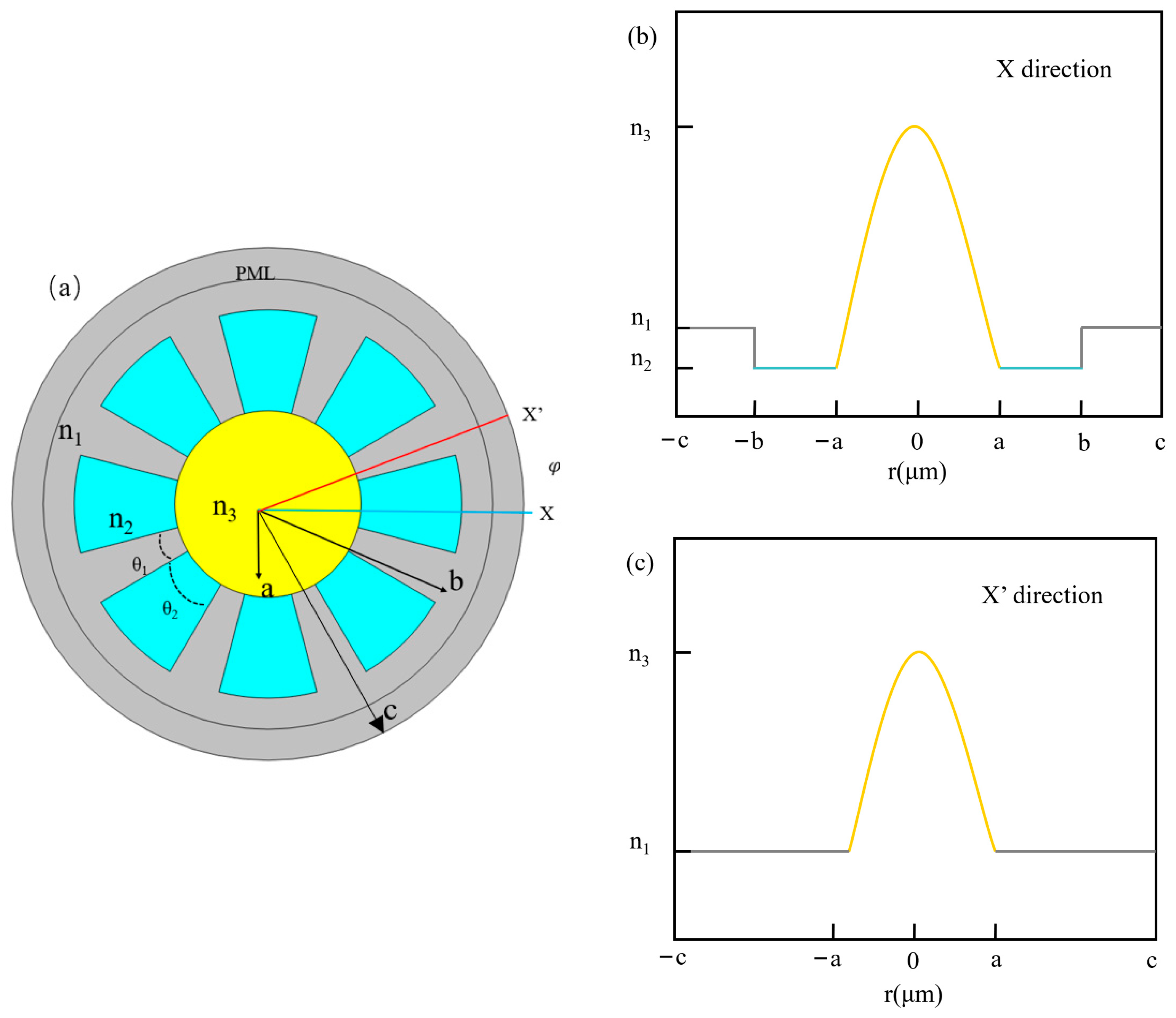






| Parameter | Value |
|---|---|
| c | 82.5 μm |
| β | 3 × 10−5/K |
| ksi | 1.38 W/(m·K) |
| kc | 0.2 W/(m·K) |
| h1 | 80 W/(m2·K) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhang, W.; She, Y.; Du, H.; Tu, S. A Large Mode Area Parabolic-Profile Core Fiber with Modified Segmented in Cladding. Photonics 2022, 9, 783. https://doi.org/10.3390/photonics9100783
Yang S, Zhang W, She Y, Du H, Tu S. A Large Mode Area Parabolic-Profile Core Fiber with Modified Segmented in Cladding. Photonics. 2022; 9(10):783. https://doi.org/10.3390/photonics9100783
Chicago/Turabian StyleYang, Song, Wentao Zhang, Yulai She, Hao Du, and San Tu. 2022. "A Large Mode Area Parabolic-Profile Core Fiber with Modified Segmented in Cladding" Photonics 9, no. 10: 783. https://doi.org/10.3390/photonics9100783
APA StyleYang, S., Zhang, W., She, Y., Du, H., & Tu, S. (2022). A Large Mode Area Parabolic-Profile Core Fiber with Modified Segmented in Cladding. Photonics, 9(10), 783. https://doi.org/10.3390/photonics9100783






