Increasing the Quality Factor (Q) of 1D Photonic Crystal Cavity with an End Loop-Mirror
Abstract
1. Introduction
2. D PhC Modeling and Q-Factor Simulations
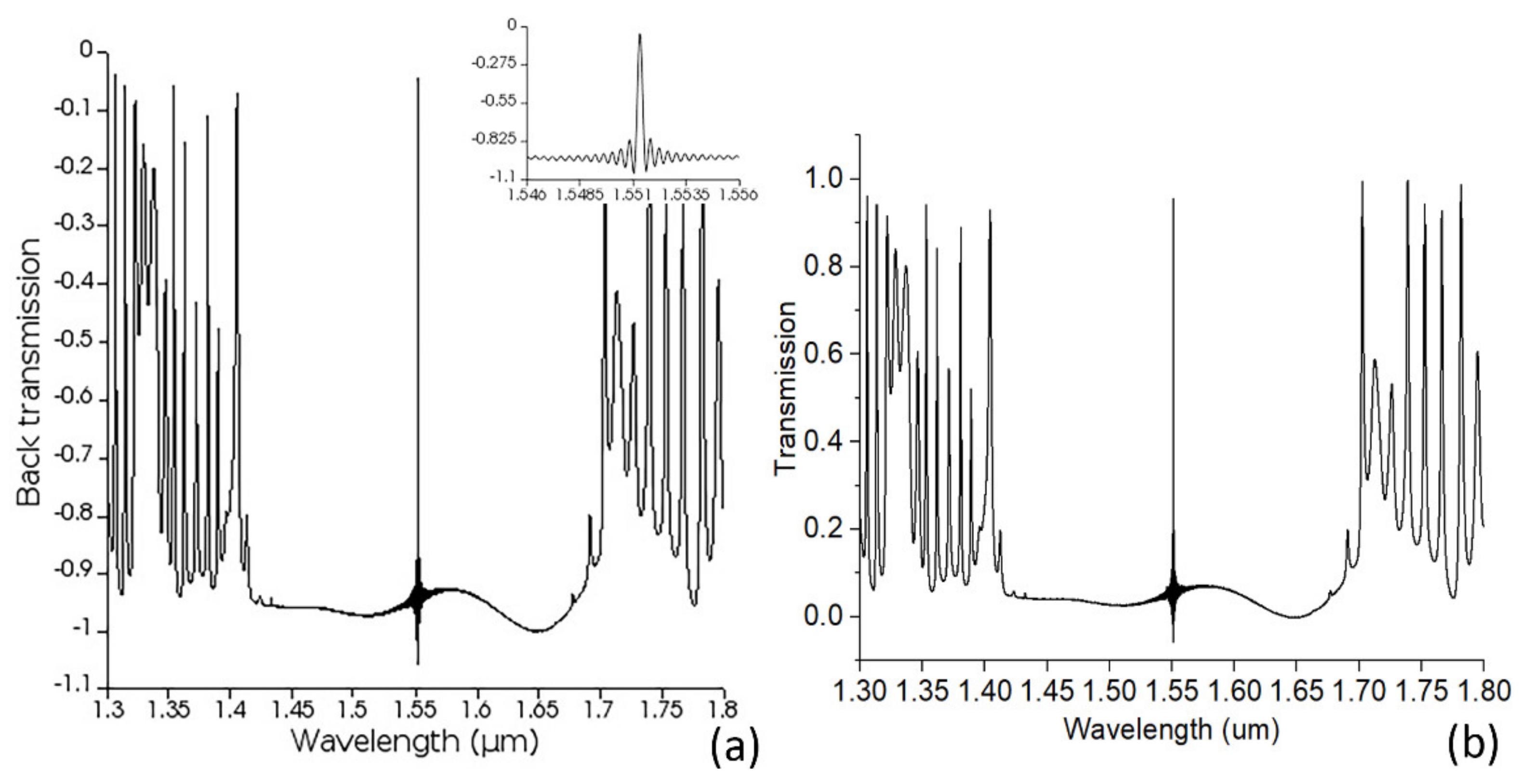
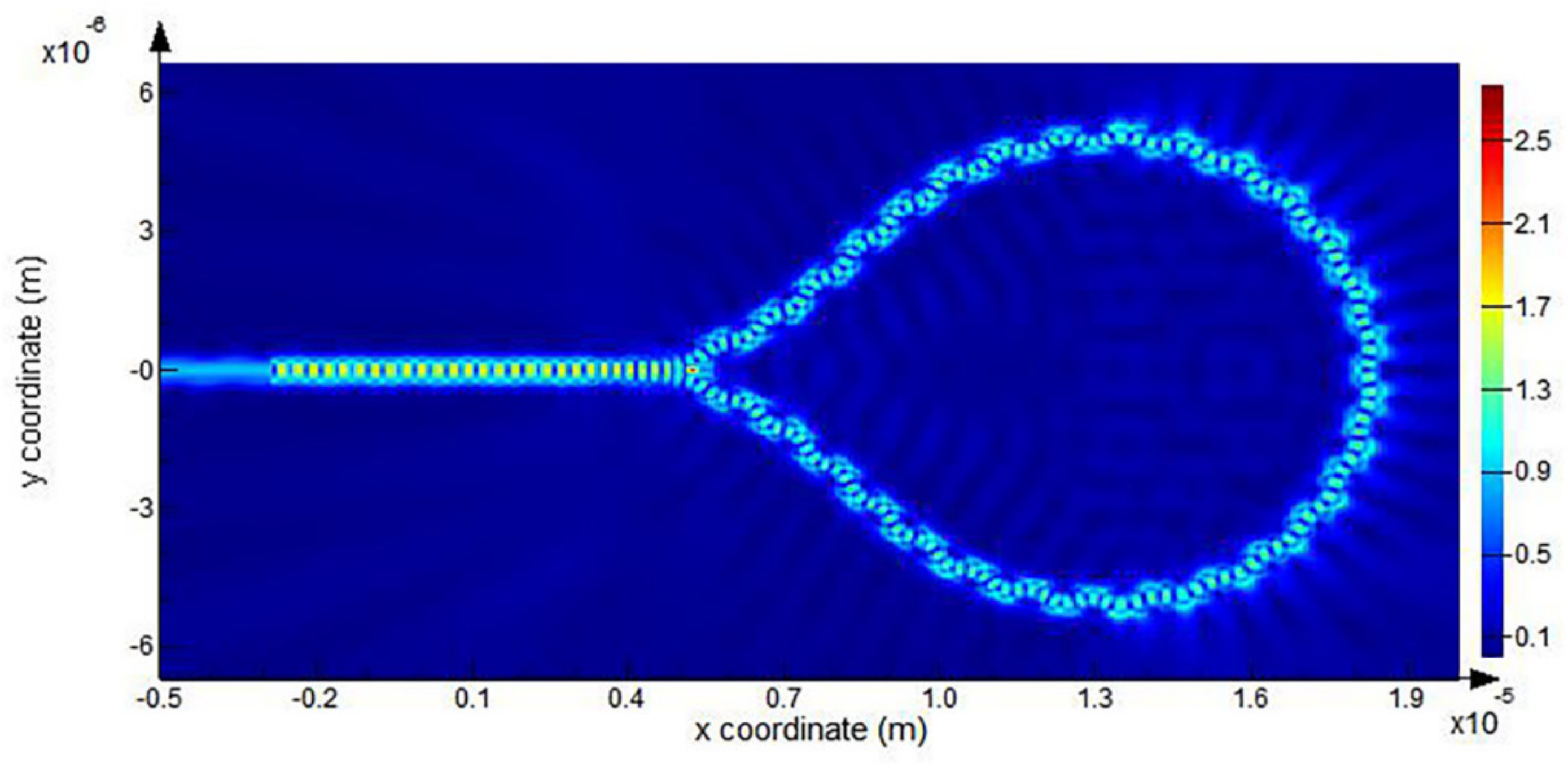
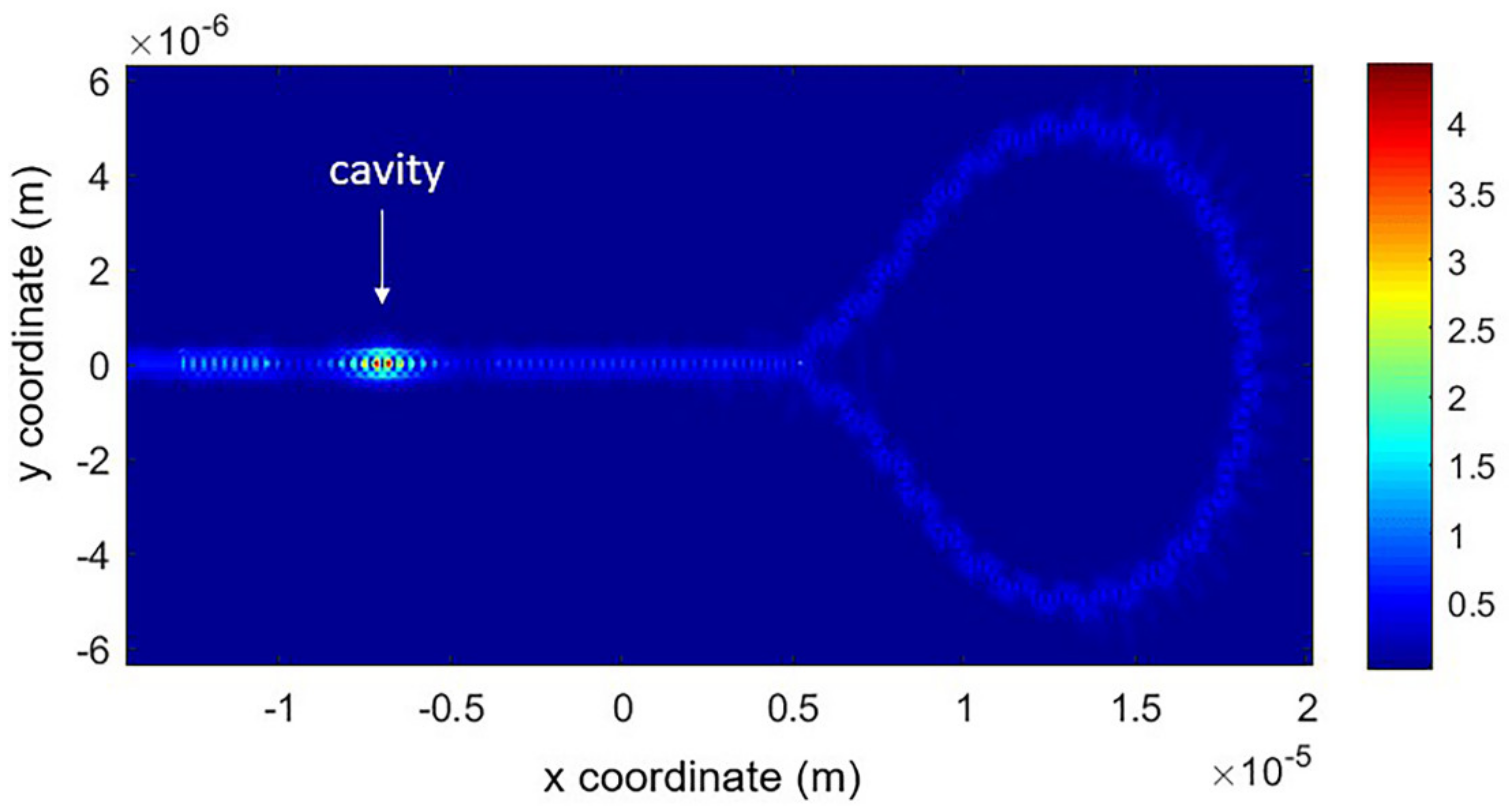
3. Inserting the End Loop-Mirror (ELM) and the Effect to Q
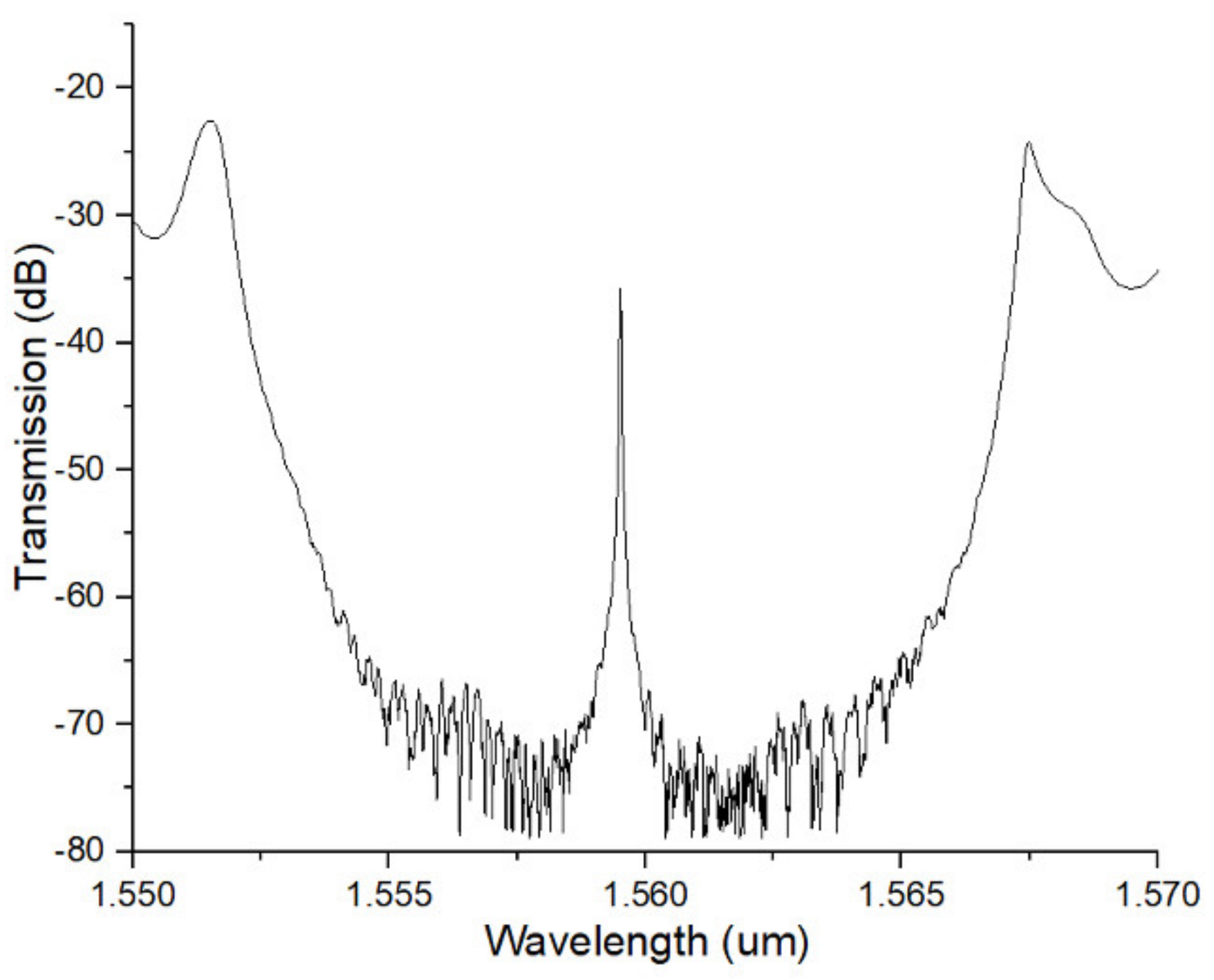
4. Fabrication and Measurement
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Absil, P.P.; Verheyen, P.; de Heyn, P.; Pantouvaki, M.; Lepage, G. Silicon photonics integrated circuits: A manufacturing platform for high density, low power optical I/O’s. Opt. Express 2015, 23, 9369–9378. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Luo, X.; Kee, J.S.; Han, K.; Li, C.; Park, M.K.; Tu, X.; Zhang, H.; Fang, Q.; Jia, L.; et al. Silicon-based optoelectronic integrated circuit for label-free bio/chemical sensor. Opt. Express 2013, 21, 2528–2533. [Google Scholar] [CrossRef]
- Dulkeith, E.; Xia, F.; Schares, L.; Green, W.M.J.; Vlasov, Y.A. Group index and group velocity dispersion in silicon-on-insulator photonic wires. Opt. Express 2006, 14, 1249–1251. [Google Scholar]
- Cherchi, M.; Ylinen, S.; Harjanne, M.; Kapulainen, M.; Aalto, T. Dramatic size reduction of waveguide bends on a micron-scale silicon photonic platform. Opt. Express 2013, 21, 819–821. [Google Scholar] [CrossRef]
- Prinzen, A.; Waldow, M.; Kurz, H. Fabrication tolerances of SOI based directional couplers and ring resonators. Opt. Express 2013, 21, 21–26. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, S.; Lim, A.E.J.; Lo, G.Q.; Galland, C.; Baehr-Jones, T.; Hochberg, M. A compact and low loss Y-junction for submicron silicon waveguide. Opt. Express 2013, 21, 1310–1316. [Google Scholar] [CrossRef]
- Mizuno, T.; Takahashi, H.; Kitoh, T.; Oguma, M.; Kominato, T.; Shibata, T. Mach—Zehnder interferometer switch with a high extinction ratio over a wide wavelength range. Opt. Lett. 2005, 30, 251–253. [Google Scholar] [CrossRef]
- Jiang, X.; Wu, J.; Yang, Y.; Pan, T.; Mao, J.; Liu, B.; Liu, R.; Zhang, Y.; Qiu, C.; Tremblay, C.; et al. Wavelength and bandwidth-tunable silicon comb filter based on Sagnac loop mirrors with Mach- Zehnder interferometer couplers. Opt. Express 2016, 24, 555–559. [Google Scholar] [CrossRef] [PubMed]
- Donzella, V.; Sherwali, A.; Flueckiger, J.; Grist, S.M.; Fard, S.T.; Chrostowski, L. Design and fabrication of SOI micro-ring resonators based on sub-wavelength grating waveguides. Opt. Express 2015, 23, 9103–9112. [Google Scholar] [CrossRef] [PubMed]
- Prabhathan, P.; Murukeshan, V.M.; Jing, Z.; Ramana, P.V. Compact SOI nanowire refractive index sensor using phase shifted Bragg grating. Opt. Express 2009, 17, 15330. [Google Scholar] [CrossRef] [PubMed]
- Donzella, V.; Sherwali, A.; Flueckiger, J.; Fard, S.T.; Grist, S.M.; Chrostowski, L. Sub-wavelength grating components for integrated optics applications on SOI chips. Opt. Express 2014, 22, 21037–21050. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, K.; de Zoysa, M.; Noda, S. Progress in photonic-crystal surface-emitting lasers. Photonics 2019, 6, 96. [Google Scholar] [CrossRef]
- Vollmer, F.; Yang, L.; Fainman, S. Label-free detection with high-Q microcavities: A review of biosensing mechanisms for integrated devices. Nanophotonics 2012, 1, 267–291. [Google Scholar] [CrossRef] [PubMed]
- Velha, P.; Rodier, J.C.; Lalanne, P.; Hugonin, J.P.; Peyrade, D.; Picard, E.; Charvolin, T.; Hadji, E. Ultra-high-reflectivity photonic-bandgap mirrors in a ridge SOI waveguide. New J. Phys. 2006, 8, 204. [Google Scholar] [CrossRef]
- Waveguides, P.C.; Ebnali-heidari, A.; Prokop, C.; Ebnali-heidari, M.; Karnutsch, C. A Proposal for Loss Engineering in Slow-Light. J. Lightwave Technol. 2015, 33, 1905–1912. [Google Scholar]
- Street, T. A theoretical analysis of scattering loss from planar optical waveguides. Opt. Quantum Electron. 1994, 26, 977–986. [Google Scholar]
- Poulton, C.G.; Koos, C.; Fujii, M.; Pfrang, A.; Schimmel, T.; Leuthold, J.; Freude, W. Radiation Modes and Roughness Loss in High Index-Contrast Waveguides. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1306–1321. [Google Scholar] [CrossRef]
- Yap, K.P.; Lapointe, J.; Lamontagne, B.; Delâge, A.; Bogdanov, A.; Janz, S.; Syrett, B. SOI Waveguide Fabrication Process Development Using Star Coupler Scattering Loss Measurements. Proc. SPIE Int. Soc. Opt. Eng. 2008, 6800, 1–12. [Google Scholar]
- Simard, A.D.; Ayotte, N.; Painchaud, Y.; Larochelle, S. Impact of Sidewall Roughness on Integrated Bragg Gratings. J. Lightwave Technol. 2011, 29, 3693–3704. [Google Scholar] [CrossRef]
- Dong, P.; Qian, W.; Liao, S.; Liang, H.; Kung, C.C.; Feng, N.N.; Shafiiha, R.; Fong, J.; Feng, D.; Krishnamoorthy, A.V. Low loss shallow-ridge silicon waveguides. Opt. Express 2010, 18, 4752–4757. [Google Scholar] [CrossRef]
- Xu, D.X.; Schmid, J.H.; Reed, G.T.; Mashanovich, G.Z.; Thomson, D.J.; Nedeljkovic, M.; Chen, X.; Van Thourhout, D.; Keyvaninia, S.; Selvaraja, S.K. Silicon Photonic Integration Platform—Have We Found the Sweet Spot? IEEE J. Sel. Top. Quantum Electron. 2014, 20, 189–205. [Google Scholar]
- Deotare, P.B.; McCutcheon, M.W.; Frank, I.W.; Khan, M.; Lončar, M. High quality factor photonic crystal nanobeam cavities. Appl. Phys. Lett. 2009, 94, 65–68. [Google Scholar] [CrossRef]
- Zain, A.R.M.; Gnan, M.; Chong, H.M.H.; Sorel, M.; de la Rue, R.M. Tapered photonic crystal microcavities embedded in photonic wire waveguides with large resonance quality-factor and high transmission. IEEE Photonics Technol. Lett. 2008, 20, 6–8. [Google Scholar] [CrossRef]
- Zain, A.R.M.; Johnson, N.P.; Sorel, M. High Quality-Factor 1-D-Suspended Photonic Crystal/Photonic Wire Silicon Waveguide Micro-Cavities. IEEE Photonics Technol. Lett. 2009, 21, 1789–1791. [Google Scholar] [CrossRef]
- Song, J.; Fang, Q.; Tao, S.H.; Liow, T.Y.; Yu, M.B.; Lo, G.Q.; Kwong, D.L. Fast and low power Michelson interferometer thermo-optical switch on SOI Abstract. Opt. Express 2008, 16, 15304–15311. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yang, S.; Guan, H.; Lim, A.E.J.; Lo, G.Q.; Magill, P.; Baehr-Jones, T.; Hochberg, M. Sagnac loop mirror and micro-ring based laser cavity for silicon-on-insulator. Opt. Express 2014, 22, 1096–1101. [Google Scholar] [CrossRef] [PubMed]
- Kuhlow, B.; Przyrembel, G.; Schlüter, S.; Fürst, W.; Steingrüber, R.; Weimann, C. Photonic crystal microcavities in SOI photonic wires for WDM filter applications. J. Light. Technol. 2007, 25, 421–431. [Google Scholar] [CrossRef]
- Alexoudi, T.; Terzenidis, N.; Pitris, S.; Moralis-Pegios, M.; Maniotis, P.; Vagionas, C.; Mitsolidou, C.; Mourgias-Alexandris, G.; Kanellos, G.T.; Miliou, A.; et al. Optics in computing: From photonic network-on-chip to chip-to-chip interconnects and disintegrated architectures. J. Light. Technol. 2019, 37, 363–379. [Google Scholar] [CrossRef]
- Hammer, M.; Ivanova, O.V. Effective index approximations of photonic crystal slabs: A 2-to-1-D assessment. Opt. Quantum Electron. 2009, 41, 267–283. [Google Scholar] [CrossRef]
- Danielmeyer, H.G.; Streifer, W.; Scifres, D.R.; Fonstad, G.; Oaks, T. The Effective Index Method and Its Application to Semiconductor Lasers. IEEE J. Quantum Electron. 1982, 18, 1083–1089. [Google Scholar]
- Haron, M.H.; Berhanuddin, D.D.; Majlis, B.Y.; Zain, A.R.M. Double-peak one-dimensional photonic crystal cavity in parallel configuration for temperature self-compensation in sensing. Appl. Opt. 2021, 60, 13–16. [Google Scholar] [CrossRef] [PubMed]
- Roth, J.; Ku, T. Low loss optical MMI-based splitter based on a semi- analytical modeling approach. Opt. Quantum Electron. 2018, 50, 1–16. [Google Scholar] [CrossRef]
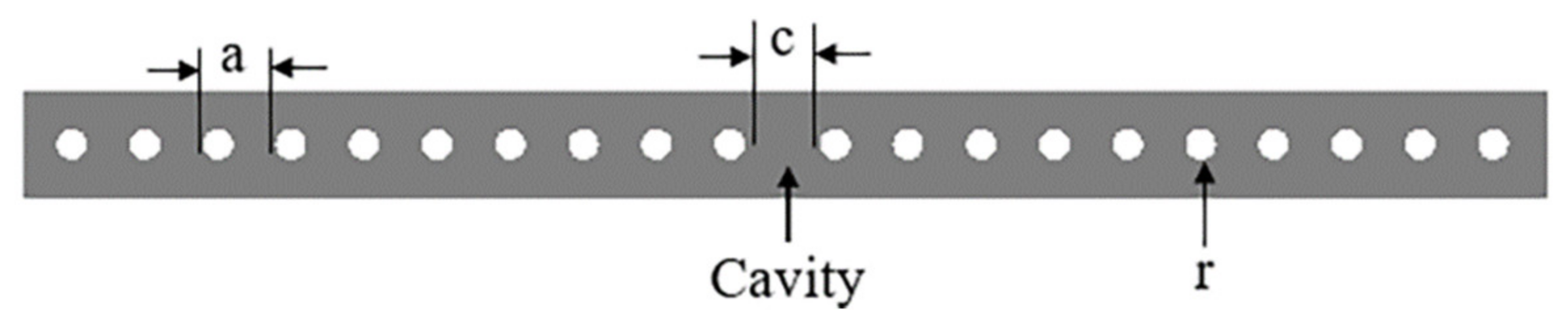
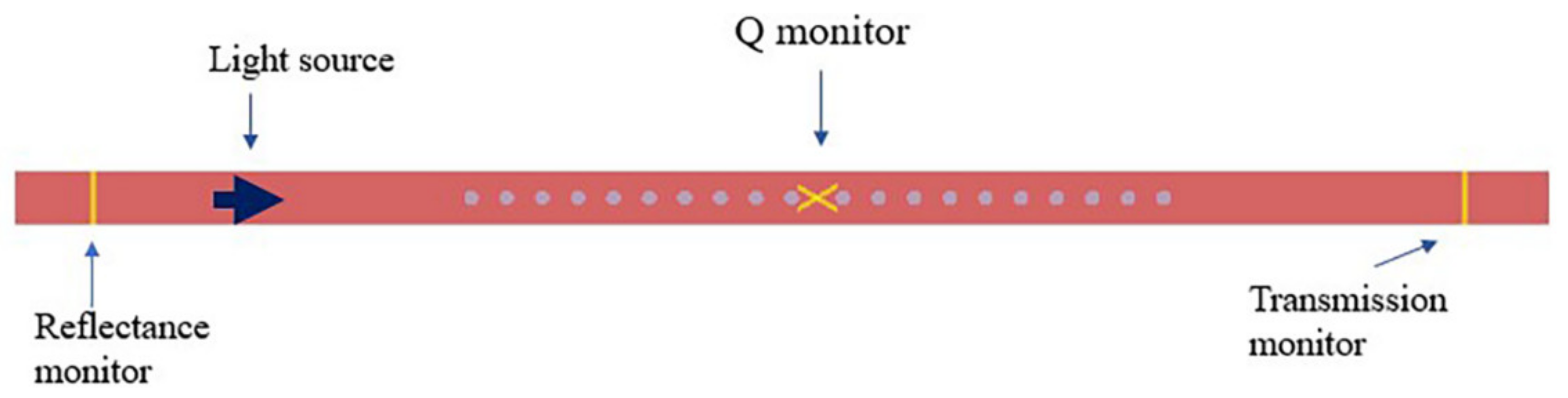
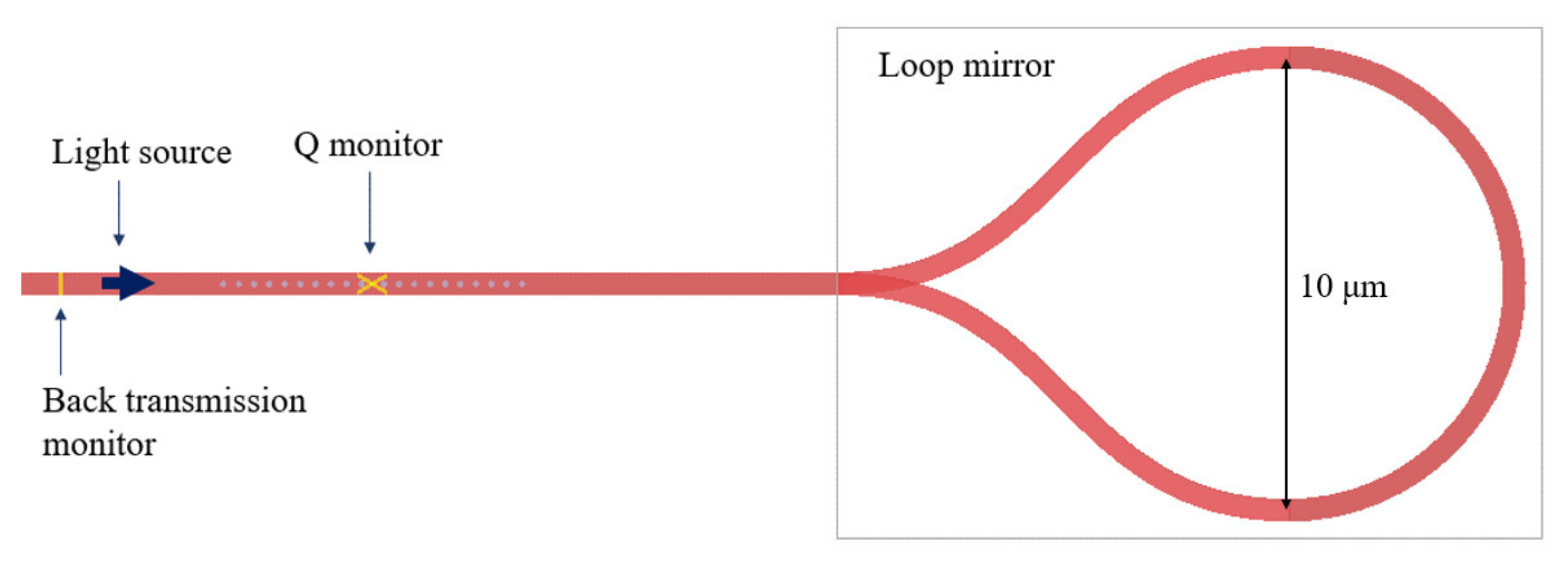

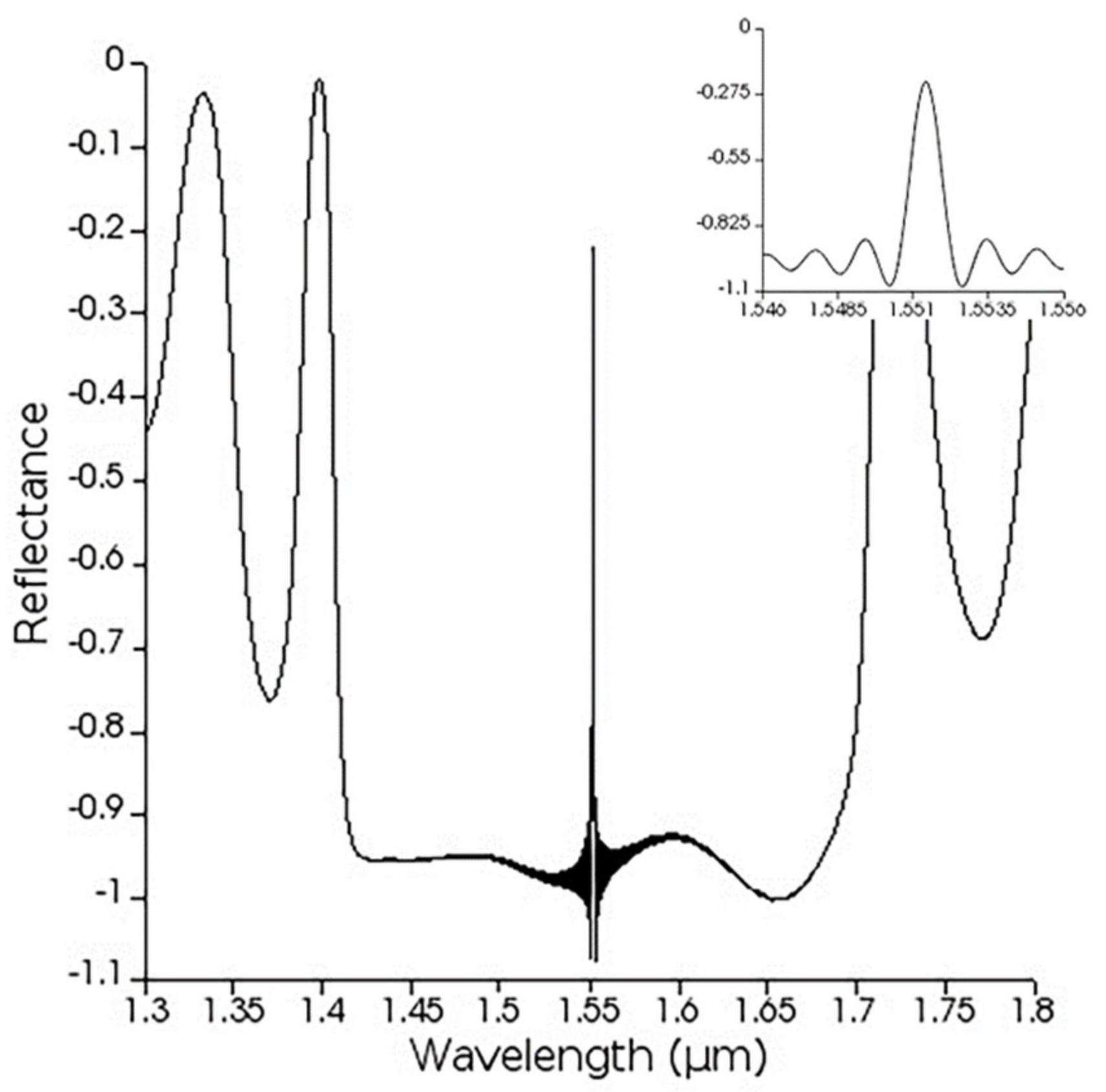


| Design | Radius (nm) | N | a (nm) | Peak Wavelength (nm) | T | Q-Factor |
|---|---|---|---|---|---|---|
| A | 70 | 20 | 367 | 1550 | 0.77 | 2409 |
| B | 70 | 22 | 367 | 1550 | 0.64 | 4324 |
| C | 50 | 40 | 358 | 1550 | 0.767 | 8332 |
| D | 50 | 46 | 358 | 1550 | 0.336 | 23881 |
| Design | Q without ELM | Q with ELM | Q Increment | Improvement Percentage (%) |
|---|---|---|---|---|
| A | 2409 | 4325 | 1916 | 79.53 |
| B | 4324 | 7542 | 3218 | 74.42 |
| C | 8332 | 14,367 | 6035 | 72.43 |
| D | 23,881 | 33,808 | 9917 | 41.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haron, M.H.; Yeop Majlis, B.; Zain, A.R.M. Increasing the Quality Factor (Q) of 1D Photonic Crystal Cavity with an End Loop-Mirror. Photonics 2021, 8, 99. https://doi.org/10.3390/photonics8040099
Haron MH, Yeop Majlis B, Zain ARM. Increasing the Quality Factor (Q) of 1D Photonic Crystal Cavity with an End Loop-Mirror. Photonics. 2021; 8(4):99. https://doi.org/10.3390/photonics8040099
Chicago/Turabian StyleHaron, Mohamad Hazwan, Burhanuddin Yeop Majlis, and Ahmad Rifqi Md Zain. 2021. "Increasing the Quality Factor (Q) of 1D Photonic Crystal Cavity with an End Loop-Mirror" Photonics 8, no. 4: 99. https://doi.org/10.3390/photonics8040099
APA StyleHaron, M. H., Yeop Majlis, B., & Zain, A. R. M. (2021). Increasing the Quality Factor (Q) of 1D Photonic Crystal Cavity with an End Loop-Mirror. Photonics, 8(4), 99. https://doi.org/10.3390/photonics8040099






