Photothermal, Photoelectric, and Photothermoelectric Effects in Bi-Sb Thin Films in the Terahertz Frequency Range at Room Temperature
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Bi1−xSbx Synthesis and Characterization
2.3. Optical Properties of Bi1−xSbx Films
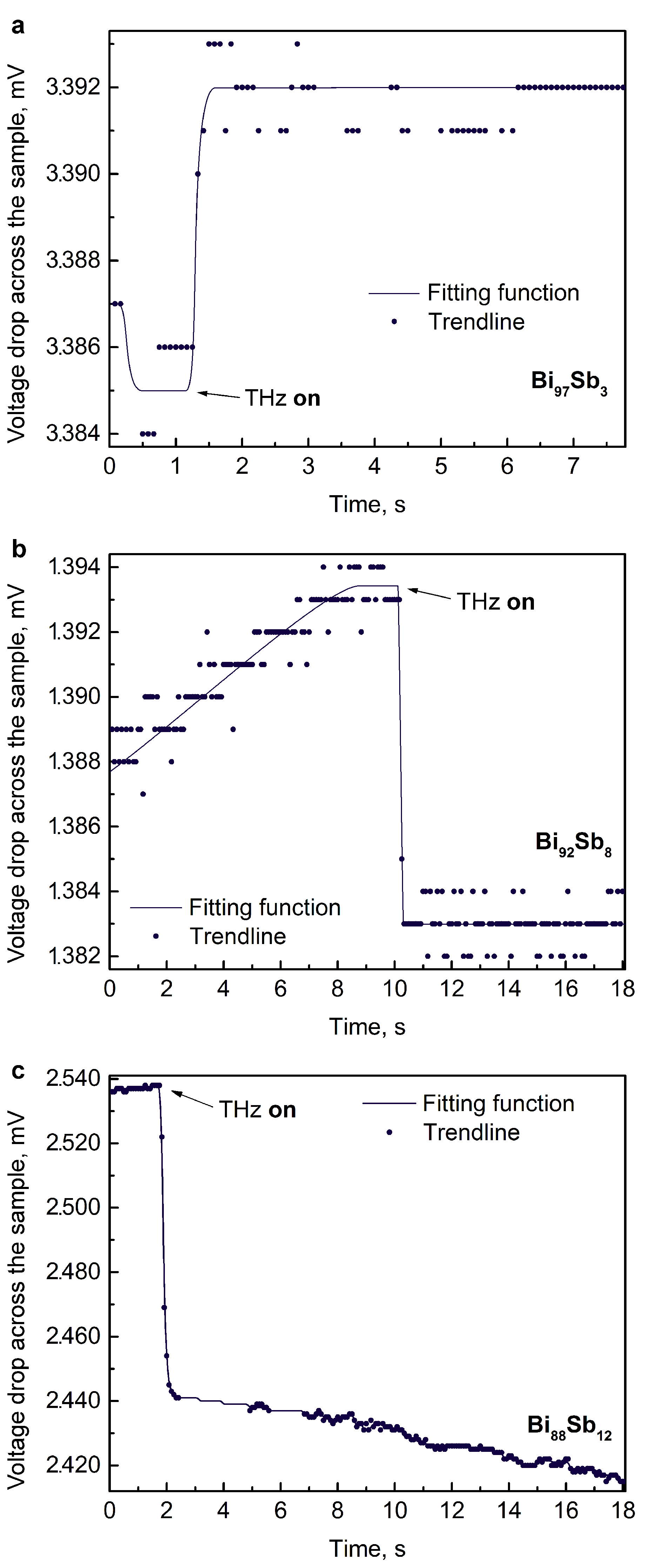
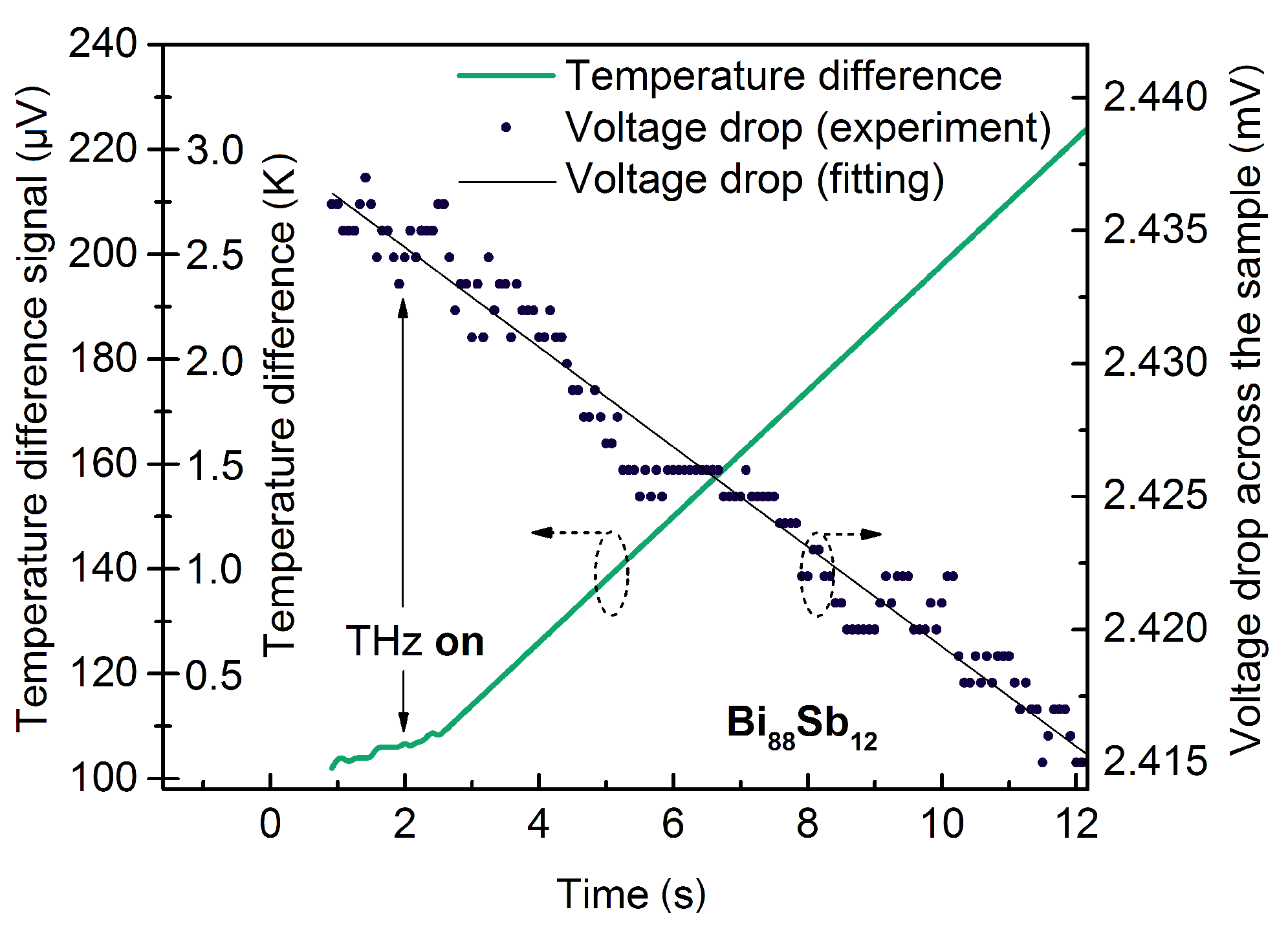
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dexheimer, S.L. Terahertz Spectroscopy: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Malhotra, I.; Jha, K.R.; Singh, G. Terahertz antenna technology for imaging applications: A technical review. Int. J. Microw. Wirel. Technol. 2018, 10, 271. [Google Scholar] [CrossRef]
- Chan, W.L.; Deibel, J.; Mittleman, D.M. Imaging with terahertz radiation. Rep. Prog. Phys. 2007, 70, 1325. [Google Scholar] [CrossRef]
- Choi, H.; Son, J.H.; Son, J.H. Terahertz imaging and tomography techniques. In Terahertz Biomedical Science and Technology; CRC Press: Boca Raton, FL, USA, 2014; pp. 47–66. [Google Scholar]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical applications of terahertz spectroscopy and imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef]
- Zaytsev, K.I.; Kudrin, K.G.; Koroleva, S.A.; Fokina, I.N.; Volodarskaya, S.I.; Novitskaya, E.V.; Perov, A.N.; Karasik, V.E.; Yurchenko, S.O. Medical diagnostics using terahertz pulsed spectroscopy. In Journal of Physics: Conference Series; IOP Publishing: Bristol, England, 2014; Volume 486, p. 012014. [Google Scholar]
- Kato, M.; Tripathi, S.R.; Murate, K.; Imayama, K.; Kawase, K. Non-destructive drug inspection in covering materials using a terahertz spectral imaging system with injection-seeded terahertz parametric generation and detection. Opt. Express 2016, 24, 6425–6432. [Google Scholar] [CrossRef]
- Ospald, F.; Zouaghi, W.; Beigang, R.; Matheis, C.; Jonuscheit, J.; Recur, B.; Guillet, J.P.; Mounaix, P.; Vleugels, W.; Bosom, P.V.; et al. Aeronautics composite material inspection with a terahertz time-domain spectroscopy system. Opt. Eng. 2013, 53, 031208. [Google Scholar] [CrossRef]
- Nagatsuma, T.; Ducournau, G.; Renaud, C.C. Advances in terahertz communications accelerated by photonics. Nat. Photonics 2016, 10, 371–379. [Google Scholar] [CrossRef]
- Sizov, F. Terahertz radiation detectors: The state-of-the-art. Semicond. Sci. Technol. 2018, 33, 123001. [Google Scholar] [CrossRef]
- Lewis, R.A. A review of terahertz detectors. J. Phys. Appl. Phys. 2019, 52, 433001. [Google Scholar] [CrossRef]
- Markov, M.; Rezaei, S.E.; Sadeghi, S.N.; Esfarjani, K.; Zebarjadi, M. Thermoelectric properties of semimetals. Phys. Rev. Mater. 2019, 3, 095401. [Google Scholar] [CrossRef]
- Rowe, D.M. CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Lu, X.; Sun, L.; Jiang, P.; Bao, X. Progress of photodetectors based on the photothermoelectric effect. Adv. Mater. 2019, 31, 1902044. [Google Scholar] [CrossRef]
- Cai, X.; Sushkov, A.B.; Suess, R.J.; Jadidi, M.M.; Jenkins, G.S.; Nyakiti, L.O.; Myers-Ward, R.L.; Li, S.; Yan, J.; Gaskill, D.K.; et al. Sensitive room-temperature terahertz detection via the photothermoelectric effect in graphene. Nat. Nanotechnol. 2014, 9, 814. [Google Scholar] [CrossRef]
- Terahertz Sources. Available online: http://terasense.com/products/terahertz-sources (accessed on 10 March 2021).
- Zaitsev, A.D.; Demchenko, P.S.; Zykov, D.V.; Korotina, E.A.; Makarova, E.S.; Tkhorzhevskiy, I.L.; Tukmakova, A.S.; Kablukova, N.S.; Asach, A.V.; Novotelnova, A.V.; et al. Optical and Galvanomagnetic Properties of Bi1-xSbx Thin Films in the Terahertz Frequency Range. Appl. Sci. 2020, 10, 2724. [Google Scholar] [CrossRef]
- Tinkham, M. Energy gap interpretation of experiments on infrared transmission through superconducting films. Phys. Rev. 1956, 104, 845. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Suslov, A.; Grabov, V.; Komarov, V.; Demidov, E.; Senkevich, S.; Suslov, M. The Band-Structure Parameters of Bi 1–x Sb x (0 ≤ x ≤ 0.15) Thin Films on Substrates with Different Thermal-Expansion Coefficients. Semiconductors 2019, 53, 611–614. [Google Scholar] [CrossRef]
- Sahu, M.K. Semiconductor nanoparticles theory and applications. Int. J. Appl. Eng. Res. 2019, 14, 491–494. [Google Scholar]
- Suslov, A.; Komarov, V.; Suslov, M. Galvanomagnetic properties of Bi85Sb15 thin films on glass and glass-ceramic substrates. In Materials Science and Condensed Matter Physics; Institute of Applied Physics: Kishinev, Moldova, 2016; p. 245. [Google Scholar]
- Demidov, E.; Grabov, V.; Komarov, V.; Kablukova, N.; Krushel’nitskii, A. Topological insulator state in thin bismuth films subjected to plane tensile strain. Phys. Solid State 2018, 60, 457–460. [Google Scholar] [CrossRef]
- TYDEX. Available online: http://tydex.ru (accessed on 10 March 2021).
- Müller, R.; Gutschwager, B.; Hollandt, J.; Kehrt, M.; Monte, C.; Müller, R.; Steiger, A. Characterization of a large-area pyroelectric detector from 300 GHz to 30 THz. J. Infrared Millim. Terahertz Waves 2015, 36, 654–661. [Google Scholar] [CrossRef]
- Virginia Diodes. Available online: http://vadiodes.com (accessed on 10 March 2021).
- Vicarelli, L.; Vitiello, M.; Coquillat, D.; Lombardo, A.; Ferrari, A.C.; Knap, W.; Polini, M.; Pellegrini, V.; Tredicucci, A. Graphene field-effect transistors as room-temperature terahertz detectors. Nat. Mater. 2012, 11, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Zagrajek, P.; Danilov, S.N.; Marczewski, J.; Zaborowski, M.; Kolacinski, C.; Obrebski, D.; Kopyt, P.; Salski, B.; But, D.; Knap, W.; et al. Time resolution and dynamic range of field-effect transistor–based terahertz detectors. J. Infrared Millim. Terahertz Waves 2019, 40, 703–719. [Google Scholar] [CrossRef]
- Chen, F.; Yang, J.; Li, Z. Modeling of an uncooled CMOS THz thermal detector with frequency-selective cross-dipole antenna and NMOS temperature sensor. Microw. Opt. Technol. Lett. 2017, 59, 3160–3166. [Google Scholar] [CrossRef]
- Zak, A.; Andersson, M.A.; Bauer, M.; Matukas, J.; Lisauskas, A.; Roskos, H.G.; Stake, J. Antenna-integrated 0.6 THz FET direct detectors based on CVD graphene. Nano Lett. 2014, 14, 5834–5838. [Google Scholar] [CrossRef] [PubMed]



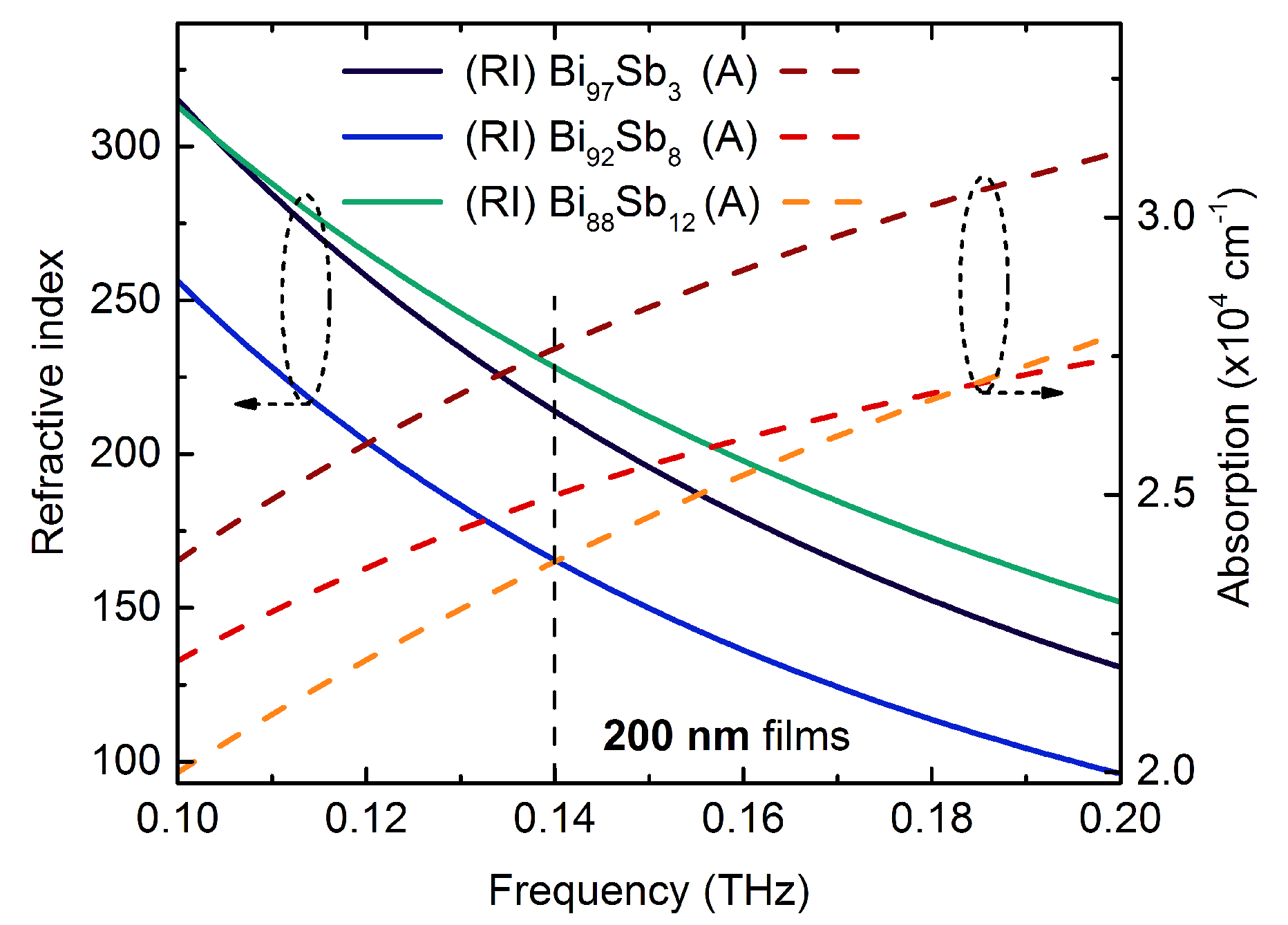


| Quantity | 3% | 8% | 12% |
|---|---|---|---|
| Conductivity [17] , (Ohm·m)−1 | 2.21 | ||
| Added conductivity | |||
| Stationary photo-conductivity | |||
| Refractive index [17] n | 214 | 166 | 228 |
| Absorption coefficient [17] , cm−1 | |||
| Stationary carrier concentration [22] , m−3 | |||
| Electron mobility [22] , m2/(V·s) | 4.1 | 2.4 | 3.2 |
| Hole mobility [22] , m2/(V·s) | 0.8 | 0.27 | 0.18 |
| Relaxation time [17] , ps | 0.371 | 0.342 | 0.335 |
| Carrier concentration under THz radiation , m−3 | 1.38 | ||
| 7.67 | 16.81 | 25.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodzitsky, M.K.; Demchenko, P.S.; Zykov, D.V.; Zaitsev, A.D.; Makarova, E.S.; Tukmakova, A.S.; Tkhorzhevskiy, I.L.; Asach, A.V.; Novotelnova, A.V.; Kablukova, N.S. Photothermal, Photoelectric, and Photothermoelectric Effects in Bi-Sb Thin Films in the Terahertz Frequency Range at Room Temperature. Photonics 2021, 8, 76. https://doi.org/10.3390/photonics8030076
Khodzitsky MK, Demchenko PS, Zykov DV, Zaitsev AD, Makarova ES, Tukmakova AS, Tkhorzhevskiy IL, Asach AV, Novotelnova AV, Kablukova NS. Photothermal, Photoelectric, and Photothermoelectric Effects in Bi-Sb Thin Films in the Terahertz Frequency Range at Room Temperature. Photonics. 2021; 8(3):76. https://doi.org/10.3390/photonics8030076
Chicago/Turabian StyleKhodzitsky, Mikhail K., Petr S. Demchenko, Dmitry V. Zykov, Anton D. Zaitsev, Elena S. Makarova, Anastasiia S. Tukmakova, Ivan L. Tkhorzhevskiy, Aleksei V. Asach, Anna V. Novotelnova, and Natallya S. Kablukova. 2021. "Photothermal, Photoelectric, and Photothermoelectric Effects in Bi-Sb Thin Films in the Terahertz Frequency Range at Room Temperature" Photonics 8, no. 3: 76. https://doi.org/10.3390/photonics8030076
APA StyleKhodzitsky, M. K., Demchenko, P. S., Zykov, D. V., Zaitsev, A. D., Makarova, E. S., Tukmakova, A. S., Tkhorzhevskiy, I. L., Asach, A. V., Novotelnova, A. V., & Kablukova, N. S. (2021). Photothermal, Photoelectric, and Photothermoelectric Effects in Bi-Sb Thin Films in the Terahertz Frequency Range at Room Temperature. Photonics, 8(3), 76. https://doi.org/10.3390/photonics8030076





