Usability of Tilted Plasmon Antenna with Structured Light
Abstract
:1. Introduction
2. Materials and Methods
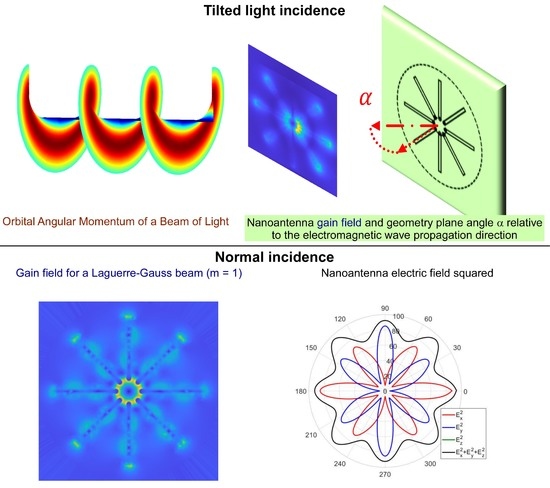
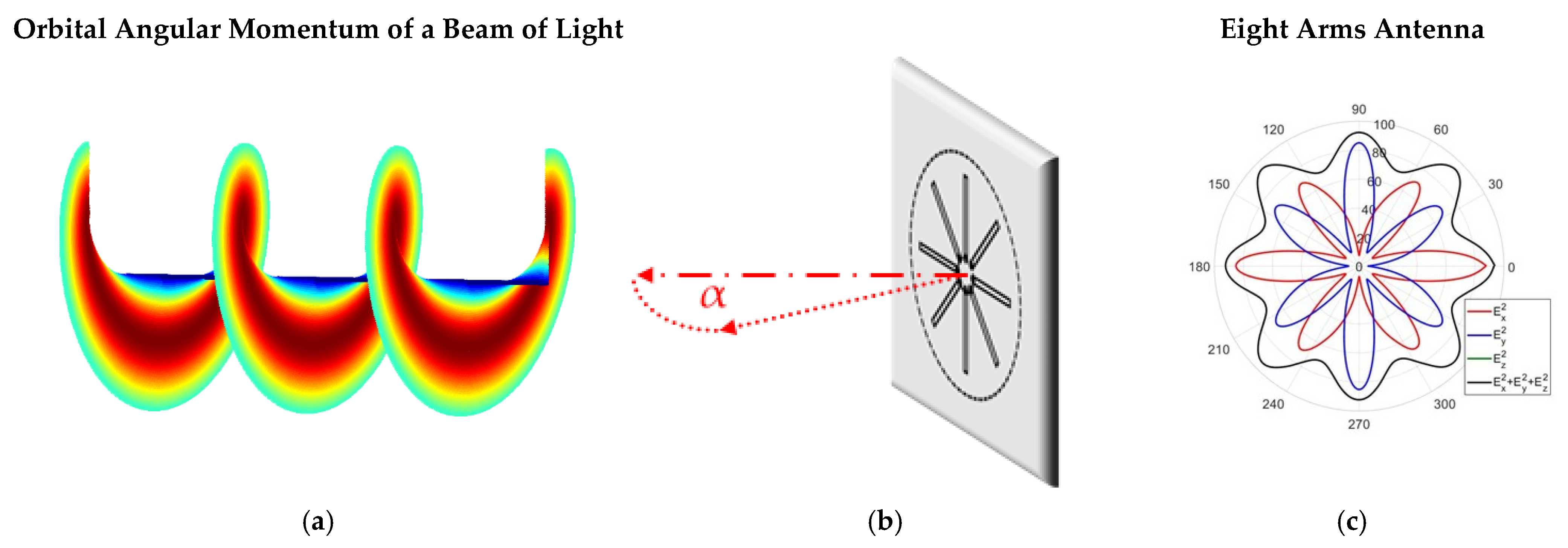
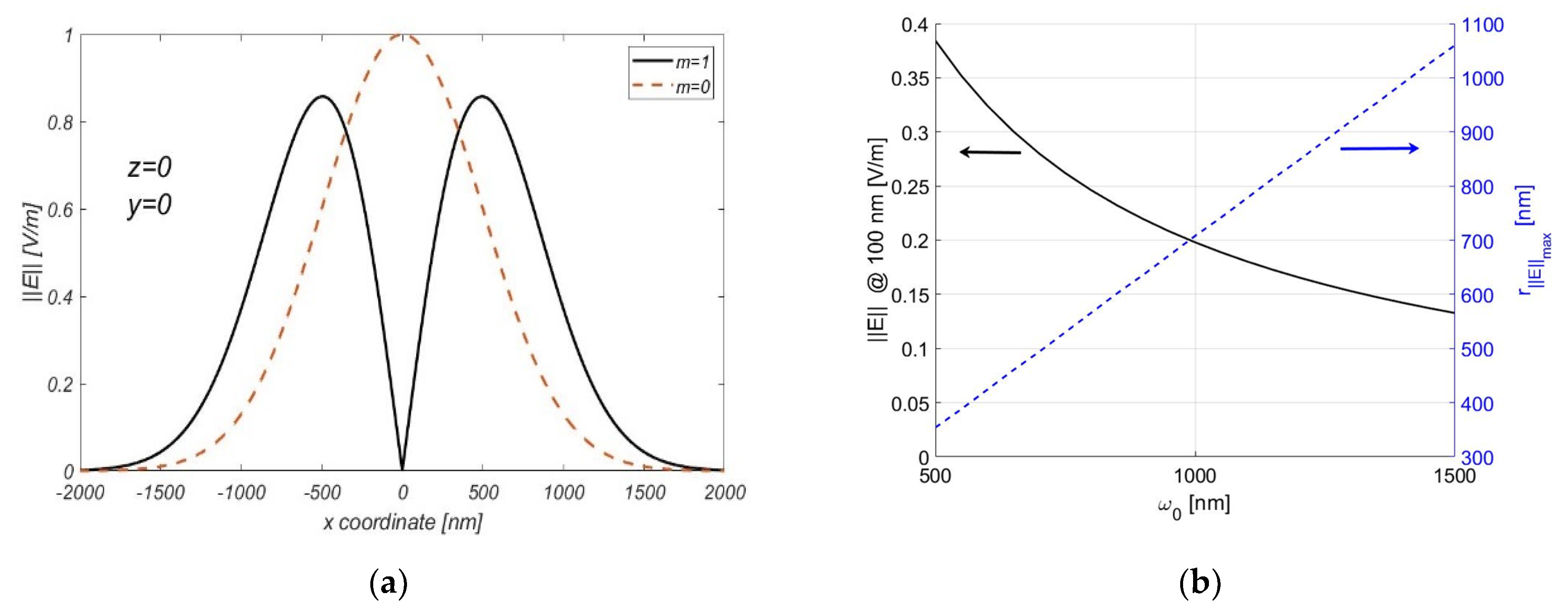
2.1. Orbital Angular Momentum (OAM) of a Beam of Light
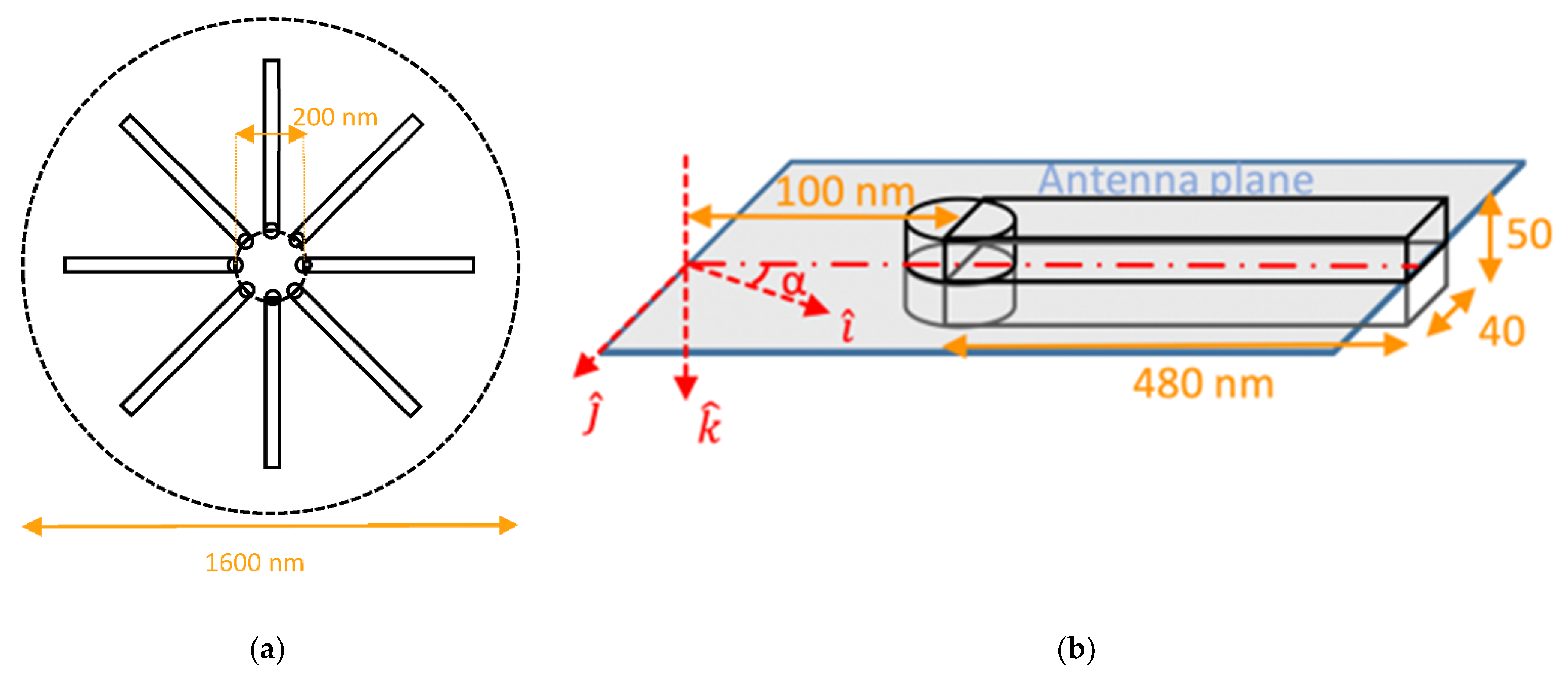
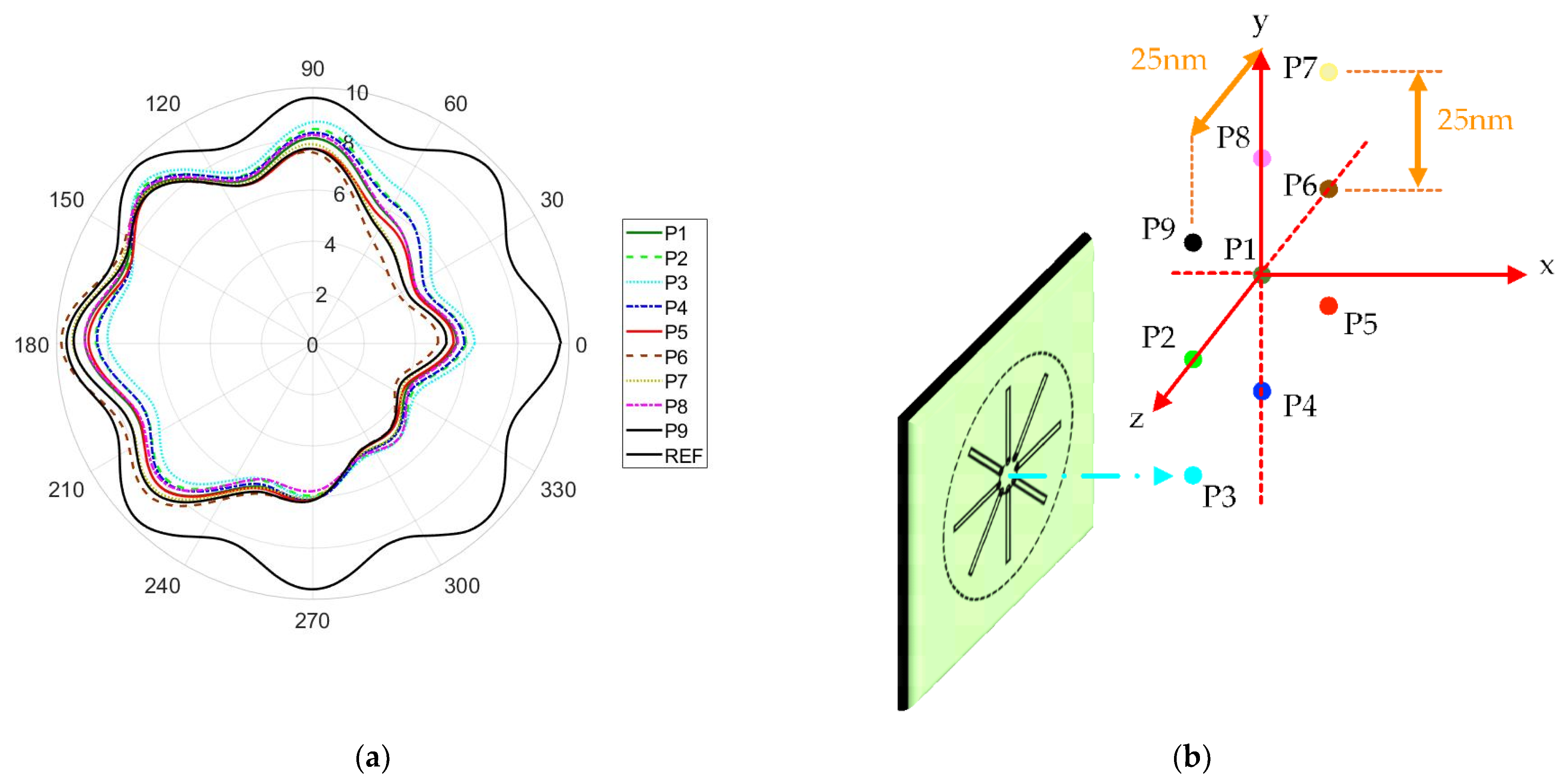
2.2. The Nanolens
2.3. Electric Field Calculations
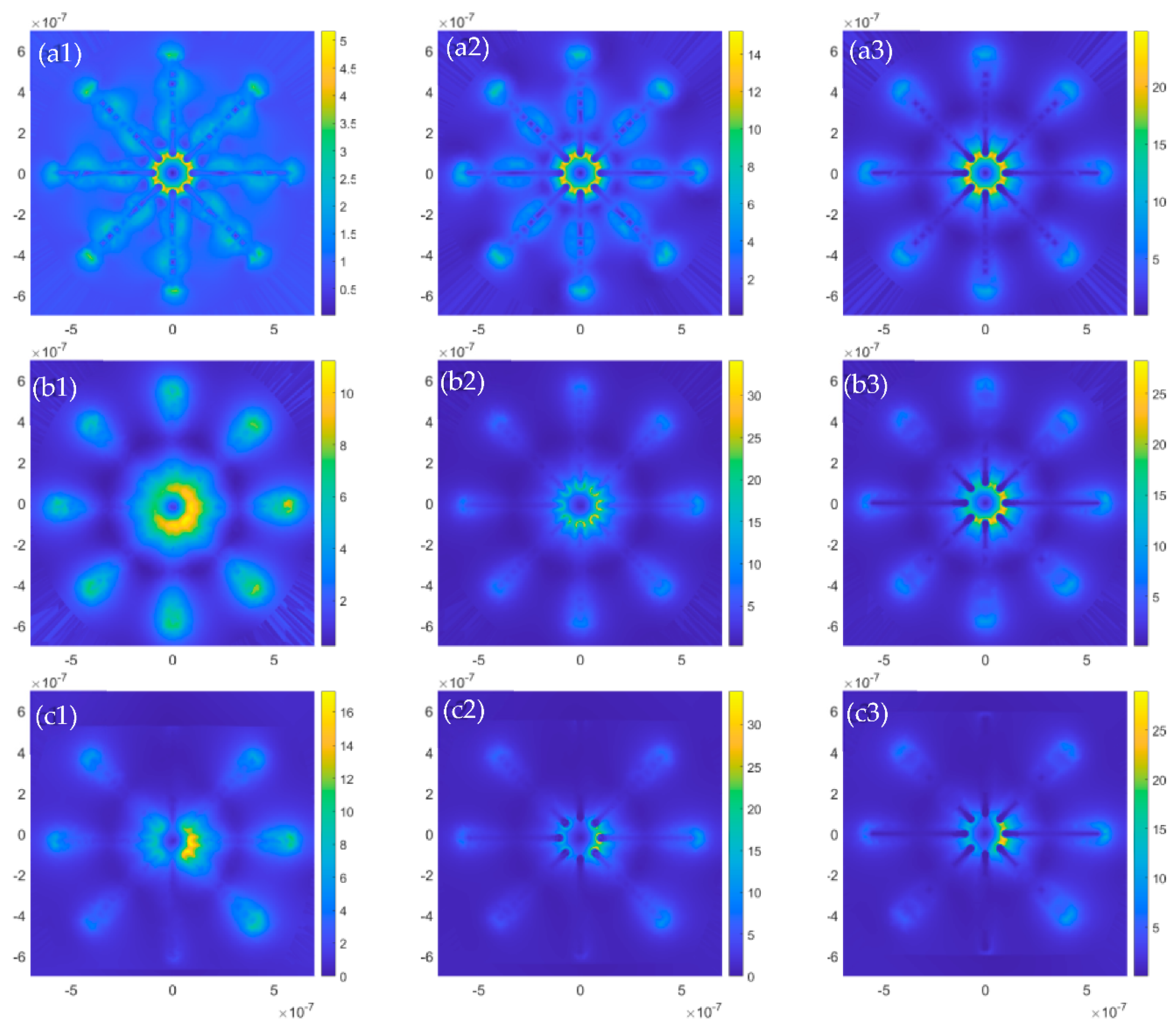
3. Results
3.1. Two-Arm Dipole Antenna Intuition
3.2. Eight-Arm Antenna: Corral
3.3. Improved Illumination with Oblique Incidence
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, H.; Peng, Y.; Yang, Y.; Li, Z.-Y. Plasmon-enhanced light–matter interactions and applications. NPJ Comput. Mater. 2019, 5, 45. [Google Scholar] [CrossRef]
- Wyrick, J.; Wang, X.; Kashid, R.V.; Namboodiri, P.; Schmucker, S.W.; Hagmann, J.A.; Liu, K.; Stewart, M.D., Jr.; Richter, C.A.; Bryant, G.W.; et al. Atom-by-Atom Fabrication of Single and Few Dopant Quantum Devices. Adv. Funct. Mater. 2019, 29, 1903475. [Google Scholar] [CrossRef]
- Kraemer, A.R.; Jones, R.W. Optical Antennas; International Foundation for Telemetering: Los Angeles, CA, USA, 14–16 November 1978. [Google Scholar]
- Krasnok, A.E.; Maksymov, I.S.; Denisyuk, A.I.; Belov, P.A.; Miroshnichenko, A.E.; Simovski, C.R.; Kivshar, Y.S. Optical nanoantennas. Physics-Uspekhi 2013, 56, 539–564. [Google Scholar] [CrossRef]
- Naidoo, D.; Roux, F.S.; Dudley, A.; Litvin, I.; Piccirillo, B.; Marrucci, L.; Forbes, A. Controlled generation of higher-order Poincaré sphere beams from a laser. Nat. Photonics 2016, 10, 327–332. [Google Scholar] [CrossRef] [Green Version]
- Holleczek, A.; Aiello, A.; Gabriel, C.; Marquardt, C.; Leuchs, G. Classical and quantum properties of cylindrically polarized beams of light via a Poincaré sphere representation. In Proceedings of the CLEO/Europe and EQEC 2011 Conference Digest, Munich, Germany, 5 May 2011; p. EA_P14. [Google Scholar]
- Shutova, M.; Shutov, A.; Sokolov, A. Spectroscopic Sensing Enhanced by Quantum Molecular Coherence and by Plasmonic Nanoantennas; SPIE OPTO: San Francisco, CA, USA, 2020; Volume 11296. [Google Scholar]
- Yue, Z.; Ren, H.; Wei, S.; Lin, J.; Gu, M. Angular-momentum nanometrology in an ultrathin plasmonic topological insulator film. Nat. Commun. 2018, 9, 4413. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, M.; Huang, Z.; Salut, R.; Suarez, M.A.; Lu, H.; Martin, N.; Grosjean, T. Plasmonic Helical Nanoantenna As a Converter between Longitudinal Fields and Circularly Polarized Waves. Nano Lett. 2021, 21, 3410–3417. [Google Scholar] [CrossRef] [PubMed]
- Carli, M.; Zilio, P.; Garoli, D.; Giorgis, V.; Romanato, F. Sub-wavelength confinement of the orbital angular momentum of light probed by plasmonic nanorods resonances. Opt. Express 2014, 22, 26302–26311. [Google Scholar] [CrossRef] [PubMed]
- Tan, Q.; Guo, Q.; Liu, H.; Huang, X.; Zhang, S. Controlling the plasmonic orbital angular momentum by combining the geometric and dynamic phases. Nanoscale 2017, 9, 4944–4949. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afanasev, A.; Carlson, C.E.; Schmiegelow, C.T.; Schulz, J.; Schmidt-Kaler, F.; Solyanik, M. Experimental verification of position-dependent angular-momentum selection rules for absorption of twisted light by a bound electron. New J. Phys. 2018, 20, 023032. [Google Scholar] [CrossRef] [Green Version]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef] [PubMed]
- Forbes, K.A.; Andrews, D.L. Spin-orbit interactions and chiroptical effects engaging orbital angular momentum of twisted light in chiral and achiral media. Phys. Rev. A 2019, 99, 023837. [Google Scholar] [CrossRef] [Green Version]
- Litvin, I.A.; Mueller, N.S.; Reich, S. Selective excitation of localized surface plasmons by structured light. Opt. Express 2020, 28, 24262–24274. [Google Scholar] [CrossRef] [PubMed]
- Fujiwara, H.; Sudo, K.; Sunaba, Y.; Pin, C.; Ishida, S.; Sasaki, K. Spin–Orbit Angular-Momentum Transfer from a Nanogap Surface Plasmon to a Trapped Nanodiamond. Nano Lett. 2021, 21, 6268–6273. [Google Scholar] [CrossRef]
- Kerber, R.M.; Fitzgerald, J.M.; Oh, S.S.; Reiter, D.E.; Hess, O. Orbital angular momentum dichroism in nanoantennas. Commun. Phys. 2018, 1, 87. [Google Scholar] [CrossRef]
- Arikawa, T.; Hiraoka, T.; Morimoto, S.; Blanchard, F.; Tani, S.; Tanaka, T.; Sakai, K.; Kitajima, H.; Sasaki, K.; Tanaka, K. Transfer of orbital angular momentum of light to plasmonic excitations in metamaterials. Sci. Adv. 2020, 6, eaay1977. [Google Scholar] [CrossRef] [PubMed]
- Jesus-Silva, A.J.; Fonseca, E.J.S.; Hickmann, J.M. Study of the birth of a vortex at Fraunhofer zone. Opt. Lett. 2012, 37, 4552–4554. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.; Yuan, C.; Yao, X.; Lu, K.; Belić, M.; Zhang, Y. Optical vortices induced in nonlinear multilevel atomic vapors. Opt. Lett. 2012, 37, 4507–4509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lesina, A.C.; Berini, P.; Ramunno, L. Vectorial control of nonlinear emission via chiral butterfly nanoantennas: Generation of pure high order nonlinear vortex beams. Opt. Express 2017, 25, 2569–2582. [Google Scholar] [CrossRef] [Green Version]
- Ding, F.; Chen, Y.; Bozhevolnyi, S.I. Focused vortex-beam generation using gap-surface plasmon metasurfaces. Nanophotonics 2020, 9, 371–378. [Google Scholar] [CrossRef] [Green Version]
- Heeres, R.W.; Zwiller, V. Subwavelength Focusing of Light with Orbital Angular Momentum. Nano Lett. 2014, 14, 4598–4601. [Google Scholar] [CrossRef] [PubMed]
- Plick, W.N.; Krenn, M. Physical meaning of the radial index of Laguerre-Gauss beams. Phys. Rev. A 2015, 92, 063841. [Google Scholar] [CrossRef] [Green Version]
- Palik, E.D. Handbook of Optical Constants of Solids: Volume 1; Elsevier Science: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef] [PubMed]
- Novotny, L.; van Hulst, N. Antennas for light. Nat. Photonics 2011, 5, 83–90. [Google Scholar] [CrossRef]
- Ghenuche, P.; Cherukulappurath, S.; Taminiau, T.H.; van Hulst, N.F.; Quidant, R. Spectroscopic Mode Mapping of Resonant Plasmon Nanoantennas. Phys. Rev. Lett. 2008, 101, 116805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Novotny, L. Optical Antennas: A New Technology That Can Enhance Light-Matter Interactions. In Proceedings of the Frontiers of Engineering Reports on Leading-Edge Engineering from the 2009 Symposium, Washington, WA, USA, 10–12 September 2009; pp. 45–56. [Google Scholar]
- Hachtel, J.A.; Cho, S.-Y.; Davidson, R.B.; Feldman, M.A.; Chisholm, M.F.; Haglund, R.F.; Idrobo, J.C.; Pantelides, S.T.; Lawrie, B.J. Spatially and spectrally resolved orbital angular momentum interactions in plasmonic vortex generators. Light Sci. Appl. 2019, 8, 33. [Google Scholar] [CrossRef] [PubMed]
- Kerber, R.M.; Fitzgerald, J.M.; Reiter, D.E.; Oh, S.S.; Hess, O. Reading the Orbital Angular Momentum of Light Using Plasmonic Nanoantennas. ACS Photonics 2017, 4, 891–896. [Google Scholar] [CrossRef] [Green Version]
- Arikawa, T.; Morimoto, S.; Tanaka, K. Focusing light with orbital angular momentum by circular array antenna. Opt. Express 2017, 25, 13728–13735. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintero-Torres, R.; Domínguez-Juárez, J.L.; Shutova, M.; Sokolov, A.V. Usability of Tilted Plasmon Antenna with Structured Light. Photonics 2021, 8, 504. https://doi.org/10.3390/photonics8110504
Quintero-Torres R, Domínguez-Juárez JL, Shutova M, Sokolov AV. Usability of Tilted Plasmon Antenna with Structured Light. Photonics. 2021; 8(11):504. https://doi.org/10.3390/photonics8110504
Chicago/Turabian StyleQuintero-Torres, Rafael, Jorge Luis Domínguez-Juárez, Mariia Shutova, and Alexei V. Sokolov. 2021. "Usability of Tilted Plasmon Antenna with Structured Light" Photonics 8, no. 11: 504. https://doi.org/10.3390/photonics8110504
APA StyleQuintero-Torres, R., Domínguez-Juárez, J. L., Shutova, M., & Sokolov, A. V. (2021). Usability of Tilted Plasmon Antenna with Structured Light. Photonics, 8(11), 504. https://doi.org/10.3390/photonics8110504