Optimization of Network Coding Resources Based on Improved Quantum Genetic Algorithm

Abstract

The problem of network coding resource optimization with a known topological structure is NP-hard. Traditional quantum genetic algorithms have the disadvantages of slow convergence and difficulty in finding the optimal solution when dealing with this problem. To overcome these disadvantages, this paper proposes an adaptive quantum genetic algorithm based on the cooperative mutation of gene number and fitness (GNF-QGA). This GNF-QGA adopts the rotation angle adaptive adjustment mechanism. To avoid excessive illegal individuals, an illegal solution adjustment mechanism is added to the GNF-QGA. A solid demonstration was provided that the proposed algorithm has a fast convergence speed and good optimization capability when solving network coding resource optimization problems.

1. Introduction

In recent years, it has become a research hotspot in the industry to complete the recovery of failures by combining the distributed recovery mechanism of the optical network with optical multicase technology [1,2]. Optical multicast technology is a kind of information transmission technology whereby an optical network transmits the sender’s information to multiple receivers at the same time. A large number of optical cross-connect devices are distributed in the optical transport network, which provides the possibility for the application of optical layer multicast technology. By converting point-to-point connections to point-to-multipoint connections, the logical structure of networks with a simple physical topology can become more compact and complex. The application of the optical tree connection in an optical transmission network can effectively enhance the broadcast ability of the network.

In addition, optical multicast technology also has many potential advantages: (a) although optical multicast requires a detailed understanding of the topology of the physical layer, it can also establish a more efficient multicast tree to allocate resources effectively and reasonably to improve utilization; (b) optical multicast cancels packet switching and network storage and forwarding, reducing traffic transmission time; (c) optical multicast can copy multicast packets through optical splitters; (d) optical multicast technology is transparent to the data bit rate and code format, which can effectively reduce the difficulty of node data processing and improve the transmission efficiency of the business. For business requests in the optical multicast network, it is also necessary to find the appropriate optical path in the optical network to transmit the business and allocate the corresponding network resources for this group of point-to-multipoint optical paths.

In order to achieve a good recovery function, the most basic work of optical transmission is to select network routing. An optical network is composed of multiple optical channels that transmit different information. The establishment of optical channels requires topology and resource information in optical networks, which means that routing selection is affected by multiple indicators such as the wavelength continuity of the optical network, different wavelengths of the optical network, the lower bound of network congestion, the network delay, the cost of routing establishment, and the average number of hops. Therefore, many factors must be taken into account when selecting routing for an optical channel to reduce the overhead of network resources and optimize the utilization of network resources.

When rerouting in optical networks, it is difficult to obtain the optimal solution because the distributed recovery mechanism only uses the local information of the network. The introduction of a shared protection link improves its performance to some extent. In the distributed recovery mechanism, all nodes do not store the link usage and reserved information; rather, each node can rely on the open shortest path routing protocol and traffic engineering technology to obtain the wavelength resource usage of the working path and the standby path. According to the information, the shared link satisfying the conditions is determined, and the resources are configured in advance. On the other hand, inspired by the coding and decoding idea of erasure codes, network coding technology can be introduced into optical transmission networks to solve the link failure recovery problem in the network [3,4]. When a limited link fails in the network, some services can be recovered by encoding and decoding at the network coding node. Network coding technology is particularly suitable for multicast networks. Through this coding multicast mode, not only can we use small network resources to construct an approximate real-time self-repair multicast communication network, but we can also obtain a high multicast transmission rate.

Network multicast allows information to be transmitted from a single point to multiple points. Compared with traditional unicast and broadcast methods, multicast greatly improves transmission efficiency. The traditional routing uses the method of “storage-forward” to transmit data, with which it is difficult to achieve the maximum network flow in theory, and this causes a waste of bandwidth resources. Ahlswede et al. [5] first proposed the basic principle of network coding in 2000. Network coding allows intermediate nodes to combine the received information during information transmission and then pass the result information to the next node. Network coding technology can effectively improve network throughput [6], enhance network robustness [7], and increase the utilization of wired and wireless networks [7,8,9], meaning that the multicast rate can reach the upper limit of the maximum flow minimum cut theory [10,11].

In the past decade, network coding technology has rapidly developed into an important research field in electrical engineering and computer science. It has a wide range of applications, such as wireless networks, distributed file storage, and network security, but the encoding operation also brings additional computational overhead [12,13]. Therefore, it is very important to reduce the number of codings in the process of network information transmission. The core purpose of network coding resource optimization is to minimize coding overhead [14] and achieve multicast rate requirements under a given topology.

Han et al. [15] first proposed the quantum genetic algorithm to solve optimization problems. The quantum genetic algorithm (QGA) combines quantum computation with the genetic algorithm. Compared with the traditional genetic algorithm, the quantum genetic algorithm uses qubit to encode, which can guarantee the diversity of populations with a small population. Therefore, the quantum genetic algorithm can be used to solve network coding resource optimization problems and has made great progress over the traditional genetic algorithm. However, when the number of nodes increases, the quantum genetic algorithm easily finds the optimal solution.

In this paper, on the basis of existing research, and considering the influence of gene number on population variation, an adaptive quantum genetic algorithm (GNF-QGA) based on gene number and fitness co-variation is proposed to solve the problem of network coding resource optimization. The rotation angle step adjustment mechanism based on the adaptive evolution mechanism is adopted, and the solution of excessive illegal solutions is proposed. The experimental data show that the proposed algorithm has a better optimization ability in solving the network coding resource optimization problem.

2. Network Coding Resource Optimization

In multicast, there are many different information transmission methods in the same topology when sending information from one source node to multiple destination nodes. Different information transmission methods consume different resources, and each additional encoding operation will increase the corresponding processing cost. The optimization problem of network coding resources aims to find a solution with the smallest number of codings under the premise of meeting the maximum flow transmission requirements; that is, finding a multicast tree with the fewest coding operations [16].

Seeing network communication as a single source node, each edge is a directed graph of unit capacity expressed as $(G,S,T,R)$, where G represents a directed graph, and S is the source node. $T=\{t_1,t_2,...,t_n\}$ is the destination node set and R is the multicast rate that the network communication can reach. It has been proved that linear network coding can meet the needs of the multicast networks [17,18], so this paper only studies simple linear network coding. Nodes with more than one input edge and at least one output edge may be coding points. When a node has more than one input edge and more than one output edge, the coding of each output edge may be different. 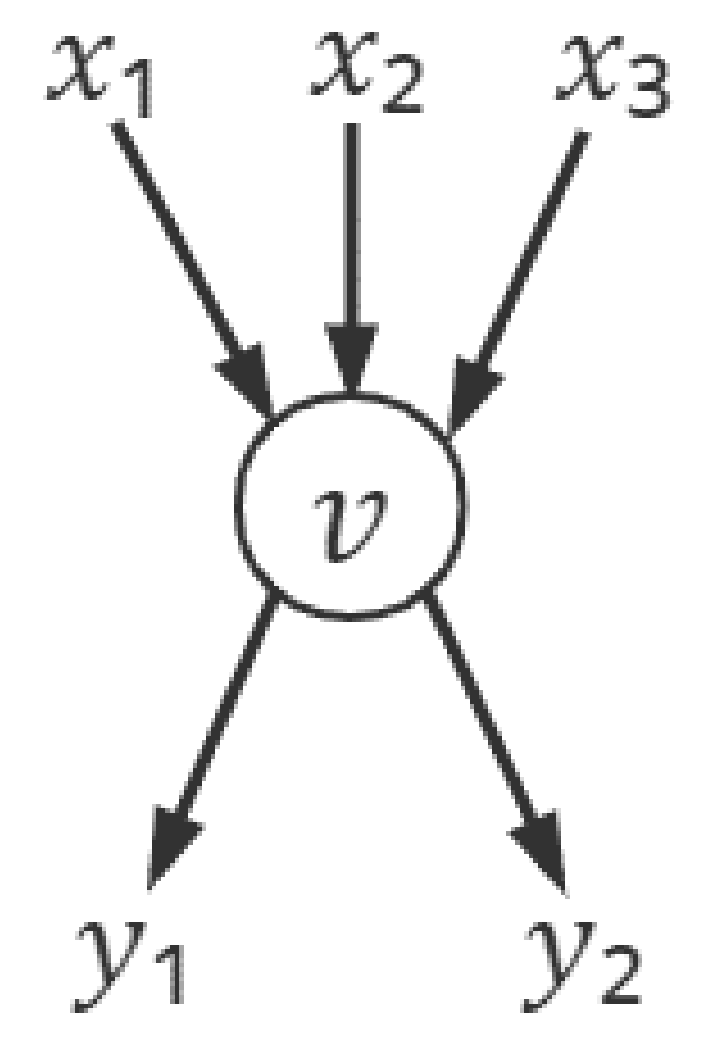Figure 1 shows the example of coding node [19]. Assuming that $y_1=x_1+x_2$ and $y_2=x_2+x_3$, node v needs to be encoded twice. Therefore, the number of encoding edges rather than the number of nodes should be recorded when calculating the optimal encoding method.

For the convenience of this research, we decompose the nodes with multiple-input edges and multiple-output edges. Each input side is pointed to a single node (input node), and each output side is projected from a single node (output node), and then a side pointing to the output node is created sequentially from the input node. Figure 2 illustrates the decomposition results of nodes in Figure 1.

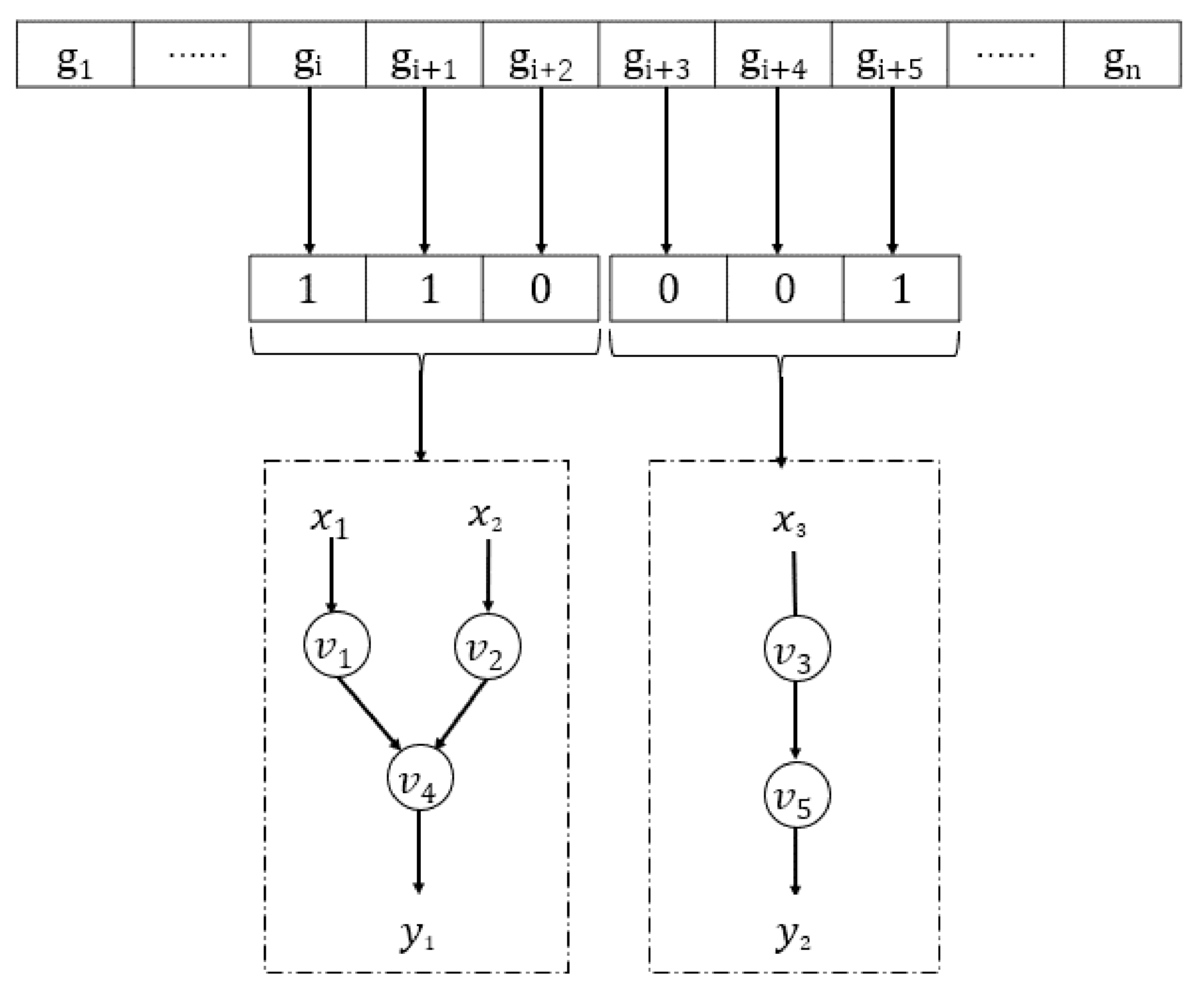
Figure 2 shows that after node v is decomposed, node $v_4$ and node $v_5$ may be the encoding points, and an encoding point will be encoded at most once (only one output edge), so the number of encodings can be calculated according to the number of encoding points. To use GNF-QGA to solve the network coding resource optimization problem, each side can be set as a binary number, and it can be assumed that 1 represents the side with data flow while 2 represents the side without data flow. Node v can be represented by a 6 bit binary number of gene coding in which the first three represent the three input edges of $v_4$ and the last three represent the three input edges of $v_5$. Figure 3 shows that node $v_4$ encodes data from node $v_1$ and node $v_2$, while node $v_5$ directly forwards the data from node $v_3$ without a coding operation.

Only nodes that may be coding points require gene coding, and the number of genes $N_{gene}$ is defined as (1), where $I_{mm}$ represents the number of input edges of the node while $O_{mm}$ represents the number of output edges of the node. When the gene is determined, the number of encodings can be calculated according to the expression pattern of the gene—namely a multicast tree structure.

$$N_{gene}=\left\{\begin{array}{cc}{I}_{mm}\times O_{mm}\hfill & I_{mm}\ge 2\wedge O_{mm}\ne 0\hfill \\ 0\hfill & I_{mm}<2\vee O_{mm}=0\hfill \end{array}\right.$$

(1)

3. Algorithm Description

The adaptive quantum genetic algorithm based on gene number and fitness cooperative mutation includes the fitness evaluation mechanism, rotation angle adaptive adjustment mechanism, the cooperative mutation mechanism based on gene number and fitness, and illegal solution adjustment mechanism.

3.1. Fitness Cooperative Mutation Mechanism

In the fitness evaluation mechanism, the fitness function of chromosome $C{h}_i$ is shown as (2), where $C_i$ represents the number of coded edges in the multicast tree built on chromosome $C{h}_i$, and $C_{max}$ represents the number of coding edges in the multicast tree constructed by chromosomes with all genes being 1. This represents the legal individual when $flag=1$ and the illegal individual when $flag=0$. The maximum flow $flow(S,t_i)$ from the source node to every destination node is calculated based on the Dinic algorithm, and the edge of the maximum flow is marked. If two or more incident edges of node $v_i$ are marked, node $v_i$ is the encoding node. The number of encoding edges is added by one based on node decomposition. Assuming the network coding multicast rate requirement is $MAX\_FLOW$, if there is a destination node $t_i$ such that $flow(S,t_i)<MAX\_FLOW$, chromosome $C{h}_i$ is an illegal solution.

$$F\left(C{h}_i\right)=\left\{\begin{array}{cc}{C}_{max}-C_i\hfill & flag=1\hfill \\ 0\hfill & flag=0\hfill \end{array}\right.$$

(2)

In the process of algorithm implementation, the topology map corresponding to chromosome X is generated first, and then the topology map is used as an input. Secondly, the Dinic algorithm is used to solve the maximum flow $flow(S,t)$ of the source node S to all other target nodes $t\in T$. If any $flow(S,t)$ is smaller than the multicast rate R, it indicates that the topology cannot meet this condition. For all target nodes $t\in T$, we use the Dijkstra algorithm to solve path set $P(s,t)=\{P_1(S,t),P_2(S,t),\dots ,P_n(S,t)\}$. For each target node, the Dijkstra algorithm should be run R times, and it should be ensured that for each path in the path set $P(S,t)$, if $i\ne j$, $P_i(S,t)\cap P_j(S,t)=⌀$. A marked array can be used to record the passing edges in each Dijkstra algorithm so that the repeated edges cannot be walked in the next iteration of the algorithm. Path set P is all edges of the network coding multicast tree. In this multicast tree, if all incident edges of a node are not less than 2, the corresponding output edge of the node is the coding edge. We can specifically define two sets for all potential encoding nodes in the Dijkstra algorithm, recording the edges emitted from that point and the edges that enter it.

3.2. Rotation Angle Adaptive Adjustment Mechanism

The quantum genetic algorithm is an improved intelligent heuristic search method combining quantum computing and the genetic algorithm. Its quantum-bit coding simulates the characteristics that quantum states can be superimposed on multiple states, which greatly increases the number of states represented by a single chromosome and greatly expands the search space of the algorithm.

3.2.1. Quantum Computing

Quantum computation is a concept proposed by Richard Feynman, a theoretical physicist, when he simulated the classical computer to realize quantum mechanical systems. Since then, Deutsch proposed that quantum computers should follow the law of quantum mechanics. The quantum state has the characteristics of interference, superposition, non-replication, entanglement, and parallelism, which means that quantum computation can greatly improve the operation efficiency of an algorithm; it is also the theoretical basis of the quantum algorithm.

3.2.2. Quantum Coding

The core of the quantum genetic algorithm is qubit coding, and the qubit is the basic information unit in quantum computing. A quantum bit represents the superposition of two quantum ground states, known as the superimposition state, and it is shown as (3).

$$|\phi \rangle =\alpha |0\rangle +\beta |1\rangle$$

(3)

The quantum state has changed the traditional representation method of either zero or one, where the probability amplitude of the quantum state is expressed by complex numbers. ${\left|\alpha \right|}^2$ represents the probability that the quantum state $\phi$ will collapse to 0 after observation while ${\left|\beta \right|}^2$ represents the probability that the quantum state $\phi$ will collapse to 1 after observation. $\alpha$ and $\beta$ need to meet the normalization condition shown as (4)

$${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$$

(4)

3.2.3. Quantum Rotation Gate

In the quantum genetic algorithm, the concept of the quantum rotation gate replaces the selection, mutation, and crossover operations in traditional genetic algorithms to complete the update operation of individuals in the population. The quantum state adjusts its mutation probability through the quantum rotation gate so that the probability of collapse to the global optimal solution in individual observation increases. It can be said that the operation of the quantum rotation gate is the key to the convergence of the entire quantum genetic algorithm. The quantum rotation gate is shown as (5).

$$U\left(\theta \right)=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$$

(5)

The renewal process of quantum state through quantum rotation gate is shown as (6).

$$\left[\begin{array}{c}{\alpha }_i^{\prime }\\ {\beta }_i^{\prime }\end{array}\right]=\left[\begin{array}{cc}cos\left({\theta }_i\right)& -sin\left({\theta }_i\right)\\ sin\left({\theta }_i\right)& cos\left({\theta }_i\right)\end{array}\right]\left[\begin{array}{c}{\alpha }_i\\ {\beta }_i\end{array}\right]$$

(6)

In Equation (6), ${\left[\begin{array}{cc}{\alpha }_i& {\beta }_i\end{array}\right]}^T$ represents the i-th quantum bit encoded by individual chromosome while ${\left[\begin{array}{cc}{\alpha }_i^{\prime }& {\beta }_i^{\prime }\end{array}\right]}^T$ is the quantum bit that has been rotated and updated through a quantum revolving gate. Furthermore, ${\theta }_i$ is the rotation angle, which is determined by the rotation angle table shown in

Table 1. Rotation angle look-up table.

${\mathit{x}}_{\mathit{i}}^{\mathit{j}}$	${\mathit{b}}_{\mathit{i}}$	$\mathit{f}\left({\mathit{x}}^{\mathit{j}}\right)\ge \mathit{f}\left({\mathit{X}}_{\mathit{best}}^{\mathit{t}}\right)$	$\mathsf{\Delta }{\mathit{\theta }}_{\mathit{i}}^{\mathit{j}}$	$\mathit{S}({\mathit{\alpha }}_{\mathit{i}}^{\mathit{j}},{\mathit{\beta }}_{\mathit{i}}^{\mathit{j}})$
				${\mathbf{\alpha }}_{\mathbf{i}}^{\mathbf{j}},{\mathbf{\beta }}_{\mathbf{i}}^{\mathbf{j}}>\mathbf{0}$	${\mathbf{\alpha }}_{\mathbf{i}}^{\mathbf{j}},{\mathbf{\beta }}_{\mathbf{i}}^{\mathbf{j}}>\mathbf{0}$	${\mathbf{\alpha }}_{\mathbf{i}}^{\mathbf{j}}=\mathbf{0}$	${\mathbf{\beta }}_{\mathbf{i}}^{\mathbf{j}}=\mathbf{0}$
0	0	$false$	${\theta }_1^j=0$	-	-	-	-
0	0	$true$	${\theta }_2^j=0$	-	-	-	-
0	1	$false$	${\theta }_3^j={\theta }^j$	$+1$	$-1$	0	$\pm 1$
0	1	$true$	${\theta }_4^j={\theta }^j$	$-1$	$+1$	$\pm 1$	0
1	0	$false$	${\theta }_5^j={\theta }^j$	$-1$	$+1$	$\pm 1$	0
1	0	$true$	${\theta }_6^j={\theta }^j$	$+1$	$-1$	0	$\pm 1$
1	1	$false$	${\theta }_7^j=0$	-	-	-	-
1	1	$true$	${\theta }_8^j=0$	-	-	-	-

. $x_i$ represents the observation state of i-th chromosome encoding of the individual. $b_i$ represents the i-th chromosome encoding of the optimal individual in the population. $\Delta {\theta }_i^j$ represents the rotation angle. $S({\alpha }_i^j,{\beta }_i^j)$ represents the directions of the rotation angles whose values are determined by the conditions in Table 1. The value of the rotation angle ${\theta }_i$ is $S({\alpha }_i^j,{\beta }_i^j)\times \Delta {\theta }_i^j$. This algorithm uses the rotation angle adaptive adjustment mechanism, by which the rotation angle is modified adaptively according to the individual fitness.

In Table 1, $x_j$ represents the j-th individual, and $b_i$ represents the i-th gene of the current optimal individual $X_{best}^t$. $f\left(x\right)$ represents the fitness of individual x. ${\theta }_j$ represents the rotation angle step of the j-th individual, which is defined by Equation (7) [10].

$${\theta }^j=\left\{\begin{array}{cc}\frac{f_j-f_{min}}{f_{max}-f_{min}}(K_2-K_1)+K_1\hfill & f_{max}\ne f_{min}\hfill \\ K_1\hfill & f_{max}=f_{min}\hfill \end{array}\right.$$

(7)

where $K_1$ represents the minimum rotation angle step, $K_2$ represents the maxmum rotation angle step and $K_1<K_2$.

3.3. Cooperative Mutation Mechanism Based on Gene Number and Fitness

The rotation angle adaptive adjustment mechanism can allocate a reasonable rotation angle step size according to the different fitness of individuals, reducing the optimization time, but it easily leads to the decline of population diversity in the later period, and the algorithm falls easily into a locally optimal solution. Based on self-adaptation, this paper proposes a cooperative mutation mechanism based on gene number and fitness, which increases the population diversity in the later stage of the algorithm and improves the optimization ability of the algorithm. The mutation operation is realized by exchanging the mutation bit probability amplitude according to mutation probability. For each individual, the mutation probability $v_j$ is determined by the results of the gene number and fitness calculation as shown in Equation (8)

$$v_j=\left\{\begin{array}{cc}{K}_3\frac{f_{max}-f_j}{f_{max}-f_{min}}(K_4-N_{gene})\hfill & f_{max}\ne f_{min}\hfill \\ K_3(K_4-N_{gene})\hfill & f_{max}=f_{min}\hfill \end{array}\right.$$

(8)

where $K_3$, $K_4$ are coefficients of variation and $K_4>N_{gene}$.

It can be seen from Equation (8) that when the number of genes is constant, the individuals with higher fitness are assigned a lower mutation probability, which can protect their genes and improve the stability of the algorithm. On the contrary, individuals with a small fitness are assigned a higher mutation probability, which can prompt them to adjust their state more quickly and move closer to the optimal solution. When the number of genes is large, the mutation probability is low, which can ensure the stability of the algorithm and reduce the illegal individuals. Conversely, when the number of genes is small, the mutation probability is high, which can accelerate the convergence of the algorithm and improve the optimization speed.

3.4. Illegal Solution Adjustment Mechanism

In solving the optimization problem of network coding resources, excessive illegal individuals will reduce the optimization efficiency of the algorithm. In order to further improve the efficiency of the algorithm and reduce the number of illegal individuals, this paper proposes the illegal solution adjustment mechanism. For the illegal solution, the probability $CP$ is equal to the optimal solution, as shown in Equation (9), where $K_5$ is a normal number less than 1.

$$CP=\left\{\begin{array}{cc}0\hfill & flag=1\hfill \\ K_5\hfill & flag=0\hfill \end{array}\right.$$

(9)

3.5. Algorithm Procedure

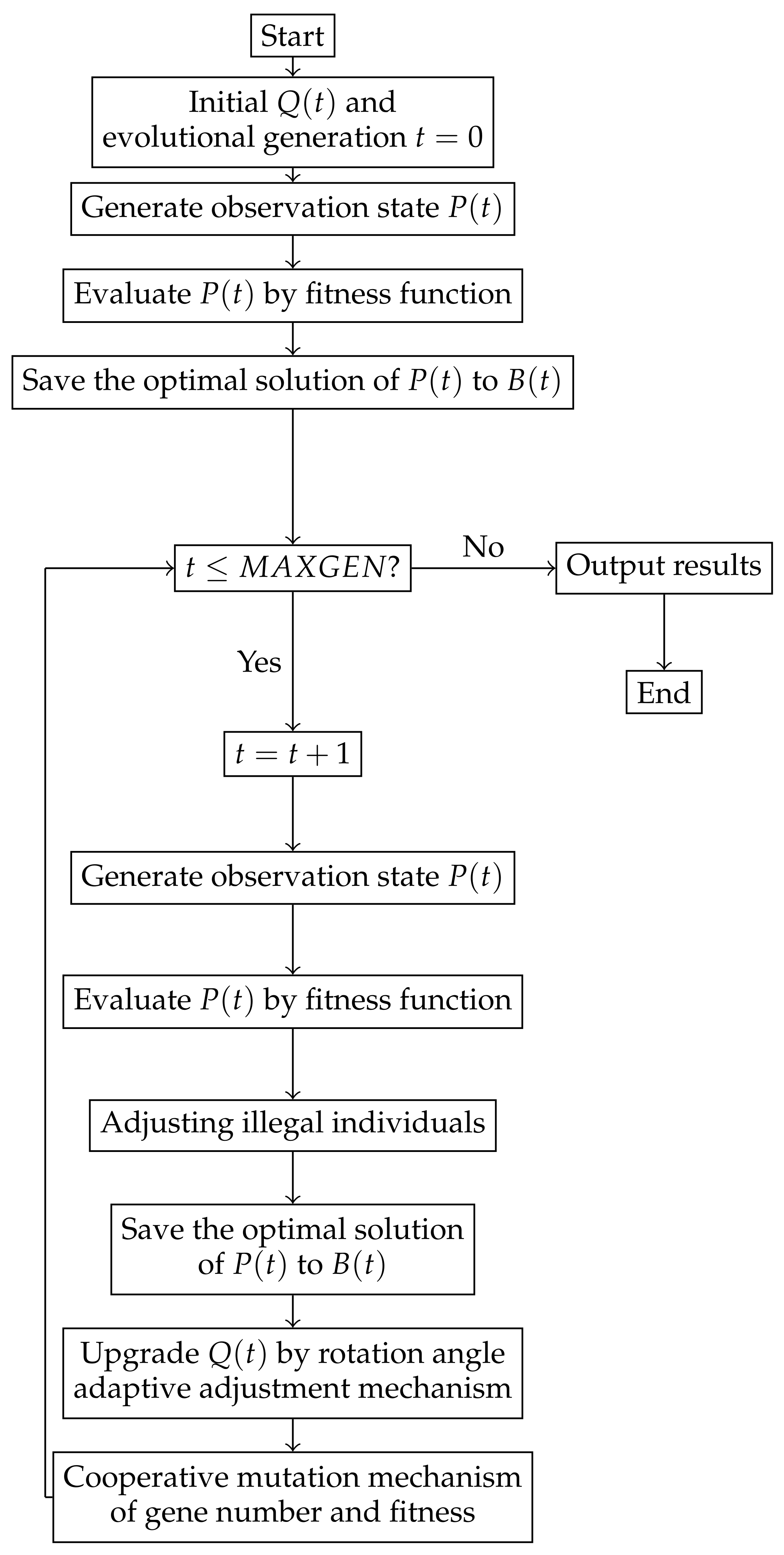
The flow of adaptive quantum genetic algorithm based on the cooperative mutation mechanism of gene number and fitness is shown in Figure 4, where $MAXGEN$ is the maximum evolutional generation set by the algorithm.

4. Experimental Analysis

In order to verify the effectiveness of GNF-QGA, this paper compares it with the traditional quantum genetic algorithm (QGA) and the quantum genetic algorithm based on the rotation angle adaptive adjustment mechanism (AM-QGA). The rotation angle step of the AM-QGA is shown in Table 1 and the mutation probability is 0.1.

The hardware and software environment used in this experiment is an Intel(R) Core(TM) i5-7300 HQ CPU with 4 cores and running with 2.50 GHz, 8 G RAM, Windows 10, CodeBlaocks 13.12, GCC 4.8.1. Each algorithm has a population size of 50 in the experiment. The maximum number of iterations is set to 1000. The relevant parameter settings for GNF-QGA are shown in

Table 2. Parameter settings for GNF-QGA.

Parameters	Settings
Minimum rotation angle step $K_1$	$0.01\pi$
Maximum rotation angle step $K_2$	$0.05\pi$
Mutation coefficient $K_3$	$0.0016$
Mutation coefficient $K_4$	200
Illegal solution adjustment constant $K_5$	$0.1$

.

The three test functions selected for the performance test of the algorithm in this paper are as follows:

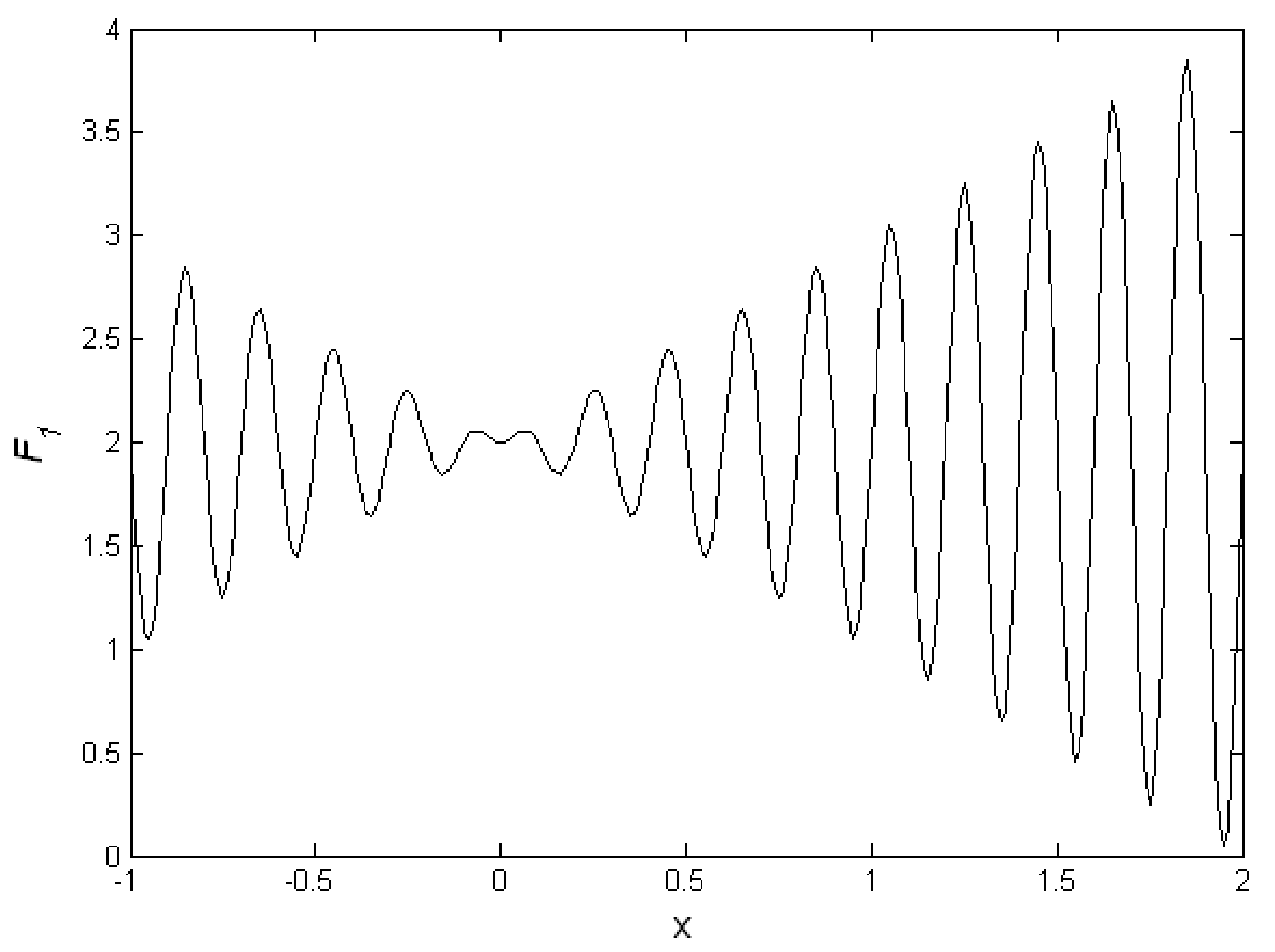
1.

Unary function (shown in Equation (10)): This function is a simple, one-dimensional multi-peak function. The range of independent variables in this paper is a, and the maximum value of the function is around 3.805. The plot of this function is shown in Figure 5.

$$F_1=xsin\left(10\pi x\right)+2.0$$

(10)

2.

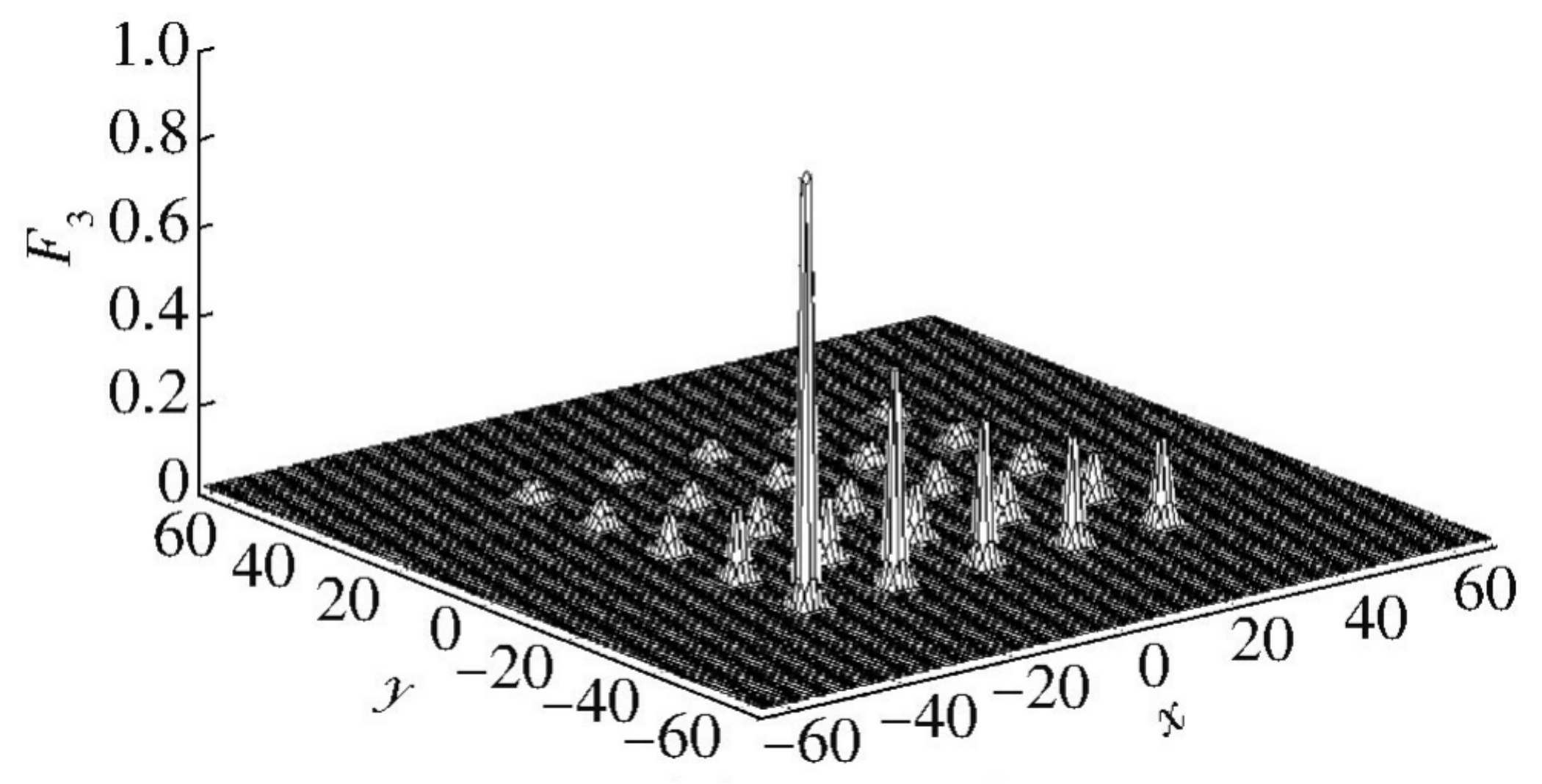
Schaffer’s F6 function (shown in Equation (11)): This function has infinite local maxima, of which only one $(0,0)$ is the global maximum and the maximum is 1. In this paper, the range of independent variables is $-10<2,y<10$. There is a circular valley around the maximum peak of this function, and its value is 0.990283. It is easy to stop at this local maximum point. The plot of this function is shown in Figure 6.

$$F_2=0.5-\frac{{sin}^2\sqrt{x^2+y^2}-0.5}{{(1+0.001(x^2+y^2))}^2}$$

(11)

3.

De Jong function (Shekel’s foxholes, shown in Equation (12)): The range of independent variables is $-65.536<x_i<65.536$. The function has multiple local maximum points, and it can be considered convergent when its function value is greater than 1. The plot of this function is shown in Figure 7

$$F_3=0.02+\sum _{j=1}^{25}\frac{1}{j+{\sum }_{i=1}^2\left(x_i-a_{ij}\right)}$$

(12)

where:

$$\begin{array}{c}{\left(a_{ij}\right)}_{2\times 25}=\hfill \end{array}\left(\begin{array}{ccccccccccc}-32& -16& 0& 16& 32& -32& -16& \dots & 0& 16& 32\\ -32& -32& -32& -32& -32& -16& -16& \dots & 32& 32& 32\end{array}\right)$$

The parameters of the algorithm and function in the test are set as follows: the coding accuracy for three test functions is $0.000001$; the population size for the three algorithms’ solving function $F_1$ is 40 and the number of iterations is 100; the population size for the three algorithms’ solving function $F_2$ and $F_3$ is 100 and the number of iterations is 400. In AM-QGA, $K_1=0.001\pi$, $K_2=0.05\pi$, and the initial mutation probability $p=0.2$. The comparison results of QGA, AM-QGA, and GNF-QGA are shown in

Table 3. Test results and comparison of typical functions.

Functions	Algorithm	Mean Computation Time	Optimum Value	Mean Value
$F_1$	QGA	3.1094	3.8503	3.8491
	AM-QGA	10.2969	3.8503	3.8503
	GNF-QGA	11.7813	3.8503	3.8503
$F_2$	QGA	2.1133	1.0000	0.9913
	AM-QGA	8.0282	1.0000	0.9927
	GNF-QGA	9.1375	1.0000	0.9987
$F_3$	QGA	5.4628	1.0200	0.9121
	AM-QGA	20.8914	1.0200	0.9362
	GNF-QGA	22.7656	1.0200	0.9857

, in which the mean value means the mean value of the optimal solution obtained by three algorithms running 1000 times independently. When solving $F_1$, AM-QGA and GNF-QGA run 1000 times independently can search the optimal solution, but QGA can not search the optimal solution each time. When solving $F_2$, the mean value obtained by GNF-QGA is the highest, but the calculation time of GQA is the least. When solving $F_3$, the calculation time of AM-QGA is less than that of GNF-QGA, but the mean value obtained by AM-QGA is the lowest, and the optimization effect of QGA is the worst. It can be seen that GNF-QGA has the best optimization effect on the above three continuous functions, but the high computational complexity leads to a long operation time.

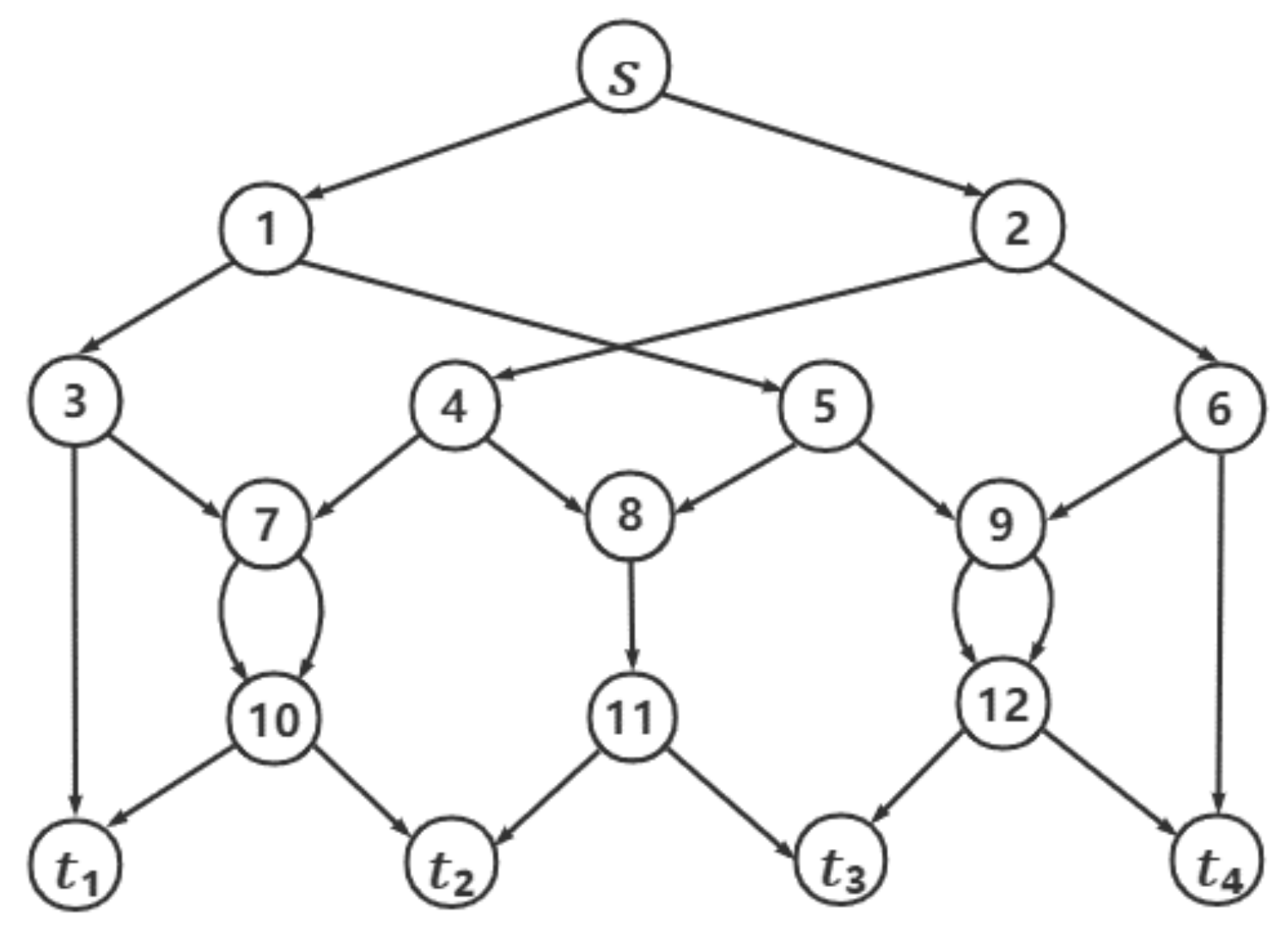
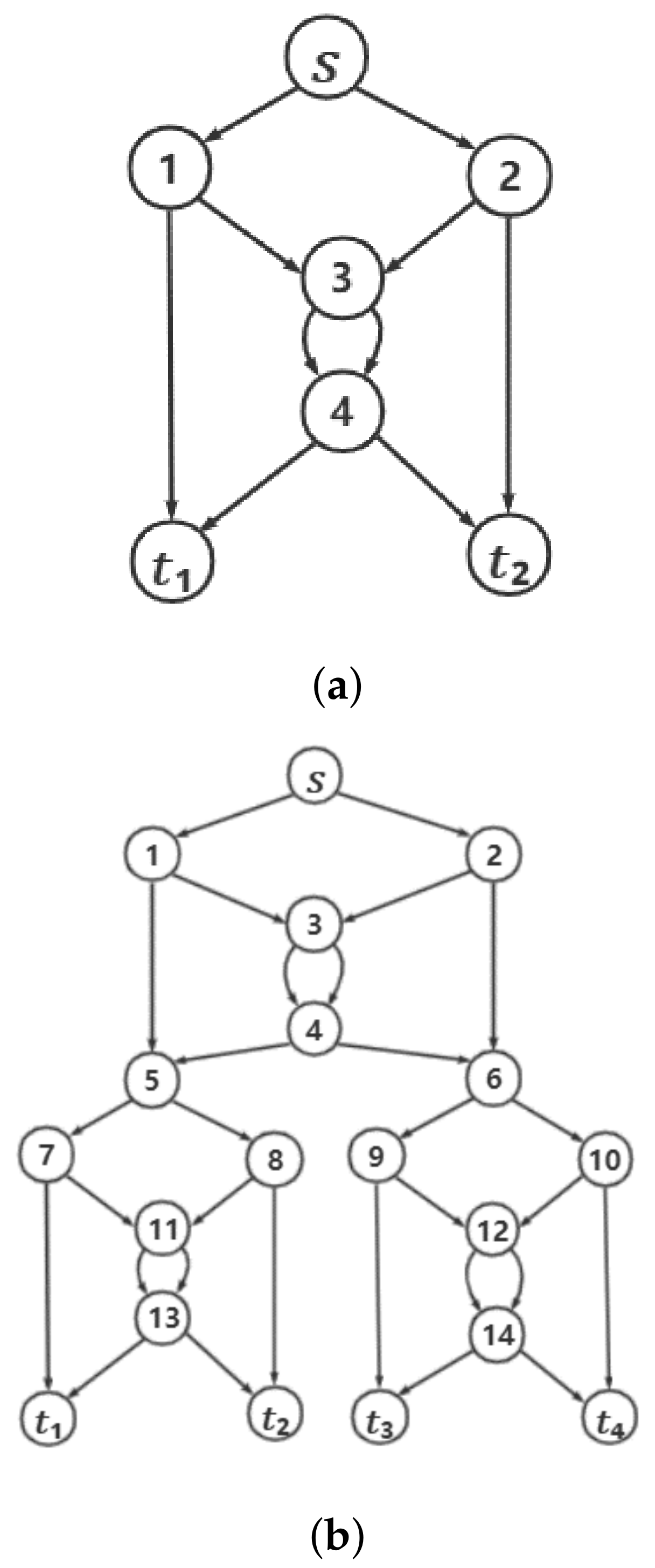
For the optimization problem of network coding resources, this paper selects five networks with known topological structures. One of them is shown in Figure 8, in which S represents the source node and t represents the destination node. Its code number is 1 based on the exhaustive method. The remaining four networks are from [20], known as 3-copy, 7-copy, 15-copy, and 31-copy networks. Figure 9 explains the structure of the n-copy network. Figure 9a is the initial network and Figure 9b is the three-copy network made up of three initial networks. For the n-copy network, the source node is at the top and the destination node is at the bottom. The network coding multicast rate requirement selected in this paper is 2.

The parameters of four n-copy networks are shown in

Table 4. Parameters of networks.

Network	3-Copy	7-Copy	15-Copy	31-Copy
Number of nodes	19	43	91	187
Number of sides	30	70	150	310
Number of destination nodes	4	8	16	32
Number of potential coding nodes	7	19	43	91
Number of individual chromosome bits	34	98	226	482
Maximum number of coding operations	15	43	99	211
Number of all possible coding operations	32,768	8.79 × 10${}^{12}$	6.33 × 10${}^{29}$	3.29 × 10${}^{63}$

including the number of nodes, number of sides, number of destination nodes, number of potential coding nodes, number of individual chromosome bits, maximum number of coding operations, and number of all the possible coding operations.

Table 5. Experiment results.

Networks	Algorithm	MNI	ON	Optimal Solution
Figure 8	QGA	8.4	10	0
	AM-QGA	6.3	10	0
	GNF-QGA	4	10	0
3-copy	QGA	57.9	10	0
	AM-QGA	38.2	10	0
	GNF-QGA	28.3	10	0
7-copy	QGA	301.4	10	0
	AM-QGA	6181.7	10	0
	GNF-QGA	147	10	0
15-copy	QGA	807.5	5	0
	AM-QGA	449.0	9	0
	GNF-QGA	303.0	10	0
31-copy	QGA	NG	0	3
	AM-QGA	952.1	1	0
	GNF-QGA	563.1	8	0

shows the experimental results of the network coding problem. The mean number of iterations (MNI) is the average number of evolutionary generations finding the optimal solutions running 10 times. The MNIs of those that cannot find the optimal solutions are calculated by the maximum number of iterations. The occurrence number (ON) is the occurrence number of the optimal solutions in 10 runs, and the optimal solution is the optimal solution found by the algorithm—not necessarily the theoretically optimal solution.

As can be seen from Table 5, the proposed GNF-QGA has the best performance, with a faster convergence speed in solving simple networks. With the increase of network complexity, the advantages of GNF-QGA are gradually highlighted. In the 15-copy network, the search success rate of QGA and AM-QGA decreased, and GNF-QGA still maintained a success rate of 100%. In the 31-copy network, QGA did not find the optimal solution, AM-QGA found the optimal solution only once, and GNF-QGA found it 8 times. It can be seen that GNF-QGA has a strong optimization ability. The GNF-QGA mutation mechanism based on gene number and fitness can provide a more appropriate mutation probability for the population and avoid the premature convergence of the algorithm into a locally optimal solution. The illegal adjustment mechanism can reduce the proportion of illegal individuals and accelerate the convergence speed of the algorithm. Therefore, it can quickly find the optimal solution in the whole optimization process.

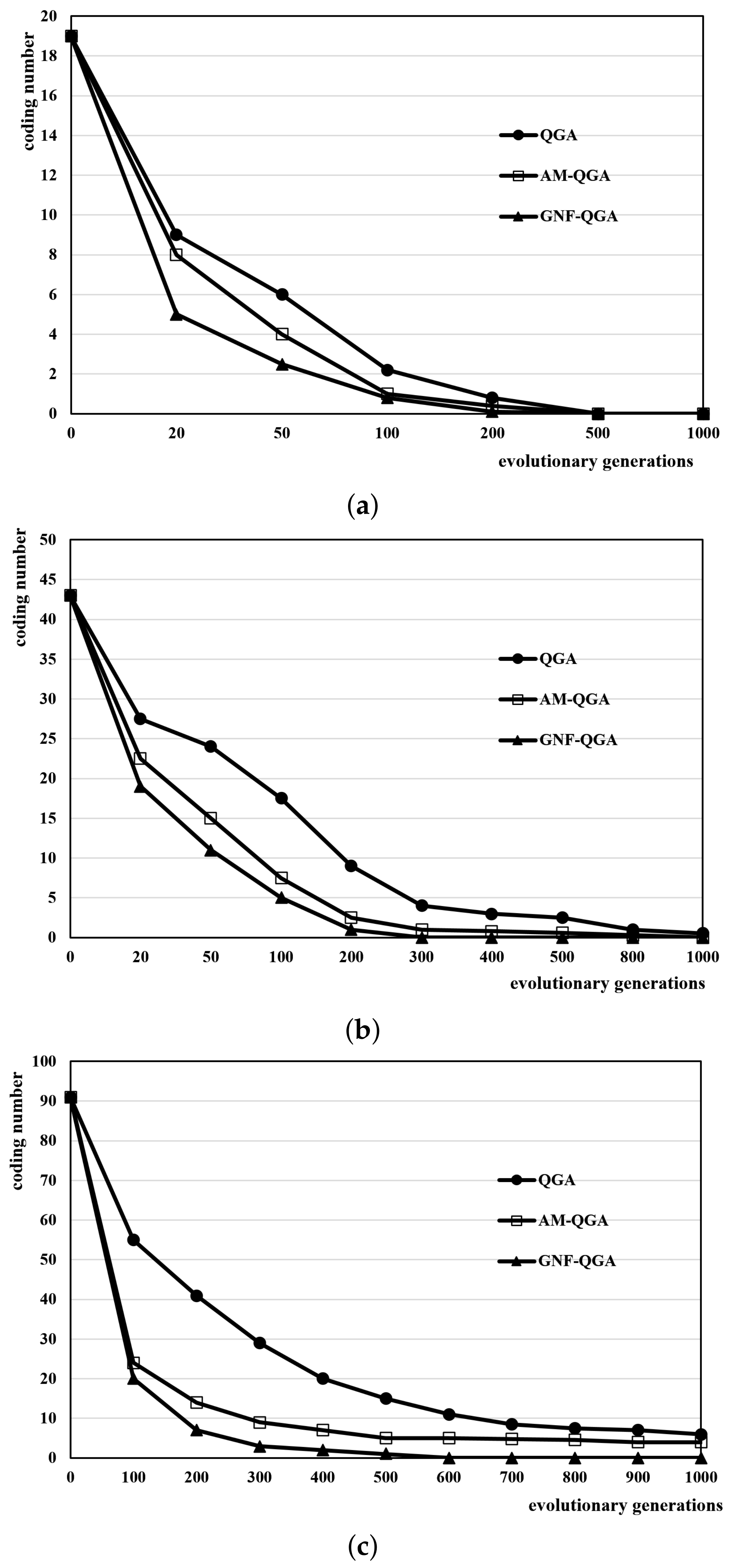
Figure 10 shows the relationship between the coding number and evolution generations in different algorithms solving 7-copy, 15-copy and 31-copy networks, from which we can see that the coding number of GNF-QGA is less than those of two other algorithms. Additionally, the coding number of GNF-QGA decreases the fastest, which indicates that its convergence speed is better than others. In Figure 10b, the search speed of QGA decreases significantly, and in Figure 10c, it is difficult for QGA and AM-QGA to find the optimal solution after 600 generations, indicating that it easily falls into a local optimal solution. The unique algorithm mechanism of GNF-QGA enables it to prevent premature convergence and maintain good optimization ability.

From the above experimental results, it can be found that GNF-QGA has the fastest convergence rate, especially in the early stage of the algorithm, and has the best global search ability and anti-early maturity ability. The convergence performance of AM-QGA is second only to GNF-QGA. The convergence performance and anti-local searchability of the QGA algorithm are the worst. Because of the adaptive adjustment mechanism and multi-operator co-evolution mechanism adopted by GNF-QGA, the search efficiency of the algorithm is greatly improved, the algorithm does not easily fall into a local optimum, and the performance is the best among the three algorithms. Because AM-QGA uses quantum bit coding, the population diversity is better than the genetic algorithm, so its algorithm performance is better than the QGA algorithm. In addition, from Figure 10, it can be found that QGA and AM-QGA algorithms cannot find the optimal solution after 500 generations when calculating graphs with a large amount of data, indicating that the quantum genetic algorithm very easily falls into the local optimum although it has a fast convergence speed. The GNF-QGA algorithm has a strong global search ability in solving the resource allocation network coding problem and can maintain the population diversity well in the later stage of the algorithm, easily jumping out of the local optimal solution. It can be concluded that the GNF-QGA algorithm with a multi-operator co-evolution mechanism has better stability and better global convergence performance after fully considering the distribution of population individuals and adjusting the mutation probability.

5. Conclusions

This paper proposes an adaptive quantum genetic algorithm based on the cooperative mutation of gene number and fitness (GNF-QGA) and applies it to the optimization of network coding resources. The fitness evaluation mechanism, rotation angle adaptive adjustment mechanism, the cooperative mutation mechanism based on gene number and fitness, and illegal solution adjustment mechanism are introduced in detail. The fitness evaluation mechanism can provide individual fitness for the algorithm. The rotation angle adaptive adjustment mechanism can dynamically allocate the rotation step length according to the individual fitness. The cooperative mutation mechanism based on gene number and fitness can provide a reasonable mutation probability and maintain population diversity. The illegal solution adjustment mechanism can avoid excessive illegal individuals and accelerate the convergence speed of the algorithm. Finally, GA, AM-QGA, and GNF-QGA are experimentally compared and analyzed. The experimental results show that the convergence speed and optimization ability of GNF-QGA proposed in this paper are higher than those of the other two algorithms in solving the optimization problem of network coding resources, showing strong comprehensive performance.